Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Aug 7;3:2328. doi: 10.1038/srep02328

A self-assembled three-dimensional cloak in the visible

Stefan Mühlig 1,5, Alastair Cunningham 2,5, José Dintinger 3,5, Mohamed Farhat 1,4, Shakeeb Bin Hasan 1, Toralf Scharf 3, Thomas Bürgi 2, Falk Lederer 1, Carsten Rockstuhl 1,a
PMCID: PMC3736173  PMID: 23921452

Abstract

An invisibility cloak has been designed, realized and characterized. The cloak hides free-standing sub-wavelength three-dimensional objects at the short wavelength edge of the visible spectrum. By a bottom-up approach the cloak was self-assembled around the object. Such fabrication approach constitutes a further important step towards real world applications of cloaking; leaving the realm of curiosity. The cloak and the way it was fabricated opens an avenue for many spectacular nanooptical applications such as non-disturbing sensors and photo-detectors, highly efficient solar cells, or optical nanoantenna arrays with strongly suppressed cross-talk to mention only a few. Our results rely on the successful combination of concepts from various disciplines, i.e. chemistry, material science, and plasmonics. Consequently, this work will stimulate these fields by unraveling new paths for future research.

After finding widespread interest in literature and movies, the concept of cloaking was scientifically substantiated in 20051,2. At this time, two suggestions based on different theoretical approaches were simultaneously put forward describing how an object can be concealed from an external observer. On the one hand, by relying on conformal mapping, Leonhardt has shown that for two-dimensional objects, i.e. restricting the considerations to cylindrical geometries with in-plane propagation, light trajectories are bent around an object with a suitably smooth refractive index profile in a surrounding shell3. By appreciating that, according to Fermat's principle, light always chooses the path where it accumulates the minimal phase change; the specific shell design yields an identical phase accumulation for all possible ray trajectories4. This prevents an incident plane wave from being distorted; independent of the propagation direction. An implementation requires the refractive index to attain quite unusual values, i.e. varying between zero and unity, inaccessible with ordinary materials5. Alternatively, based on transformation optics, Pendry et al. suggested a cloak that can even hide three dimensional objects6. However, this became only possible by considering artificial electromagnetic materials7,8 exhibiting a suitably tailored and inhomogeneous bi-axial anisotropic permittivity and permeability9. Likewise, this cloak prevents phase disturbances and reflection losses at the interface between the shell and the surroundings10.

Although the material requirements in both approaches are challenging and potentially unachievable, a well-defined goal was set for a functional device. The race was on to demonstrate the cloaking functionality in the optical regime where visual perception takes place11. For a device to be truly termed a “cloak of invisibility” it must operate in this spectral regime. Various simplifications were made to demonstrate the cloaking concept in principle, even experimentally. The challenges can usually be slightly lifted while resorting to cylindrical objects. Then, rather than dealing with the full vectorial set of electric and magnetic fields, Maxwell's equations can be decomposed into two uncoupled sets, i.e. those for transverse electric (TE) and transverse magnetic (TM) polarization. By further accepting a spurious reflection due to an impedance mismatch, cloaks in the micro-wave frequencies were demonstrated12. An alternative successful strategy for a simplification consists in restricting the consideration to a half-space and hiding the object above a ground plate (carpet cloak)13. Then, the reflected light from the ground plate with the object to be cloaked should be identical to that in the absence of the object. The carpet cloak concept enabled novel experimental realizations14,15,16. At present this concept has been implemented both for two-dimensions and three-dimensional objects to be cloaked17,18,19,20,21,22. However, it is obvious that carpet cloaks are not the ultimate solution to hide isolated three-dimensional objects. For the sake of completeness it should be mentioned that alternative approaches for broadband and free-standing cloaking devices can be obtained while lifting these strict requirements. Specifically, manifold approaches to cloak objects can be perceived while considering the problem from a ray optical perspective instead of treating the system in the realm of electromagnetics. Then, even natural materials can be used for the fabrication of the cloak23. These cloaks, however, are limited to a restoration of a proper intensity and do not consider the phase distribution. Nonetheless, perceiving the problem from a macroscopic perspective this is often sufficient. In contrast to such previous work, however, in this contribution the cloaking device is developed by solving Maxwell's equations, i.e. the electromagnetic fields exhibit amplitude and phase.

Further simplifications with respect to the carpet cloak can be made if only sub-wavelength objects are considered24. Then, the optical response is usually most conveniently expressed in the quasi-static limit and only an electric dipole contributes to the scattered far-field. Suppressing this scattered field results in the cloaking of the three-dimensional object. Although related ideas existed in literature for quite some time25, Alù and Engheta reinforced this approach26 by its analytical description. They derived an expression that imposes conditions on the geometrical and material properties of the shell of a spherical core-shell structure to suppress the scattering response27. It reads as:

graphic file with name srep02328-m1.jpg

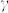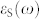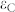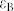where Inline graphic is the ratio of the core to the shell radius. Here the shell radius is understood as the outer radius of the structure and Inline graphic, Inline graphic, and Inline graphic are the permittivity of the shell, the core, and the background material, respectively. Here, for simplicity but without loss of generality, only the shell material is assumed to be dispersive. The solution to Eq. 1 suggests that the magnitude of the electric dipolar polarization of the core is identical to that of the shell whereas their phases differ by π. This causes destructive interference in the far-field and a suppression of the scattering response.

Although, at a first glance it might look less impressive to hide sub-wavelength objects, the effect has major implications on controlling light-matter interaction and may entail the implementation of various functional devices28. For example, in an aperture-less scanning near-field optical microscope a tip is excited at its apex by an external source29. There, the localized light can interact with other nanoscale objects. Information on these objects is determined in the far-field by measuring amplitude and phase of the scattered light. A major issue of such microscopes consists in suppressing the background radiation originating from light scattered at the tip. This can be achieved by suitably cloaking the tip30. Another example is the manipulation of the force and the torque exerted on nanometric objects by such cloaks. This will enable novel schemes to manipulate nano-mechanical objects in free space31. These promising applications among with others32,33 represent a strong motivation to implement such cloaks.

Recently, successful implementations have been presented at microwave frequencies34,35. There, a cylinder has been covered by a shell made of an artificial material. The cloak was optimized to suppress the scattered light at the dominant linear polarization36. The required material properties for the shell were provided by periodically arranged sub-wavelength unit cells. Another verification of this concept has been experimentally performed recently for a cylindrical cloaked sensor in the visible. By placing a silicon nanowire on a metallic ground plate and covering it partially by a metallic shell, the scattered light was considerably reduced while the nanowire was still functional as a photodetector37. Such application is exciting, since it allows the measurement of an optical signal while being minimally invasive; and demonstrates moreover the successful merger of photonics and electronics in a single device38. However, to date a cloak that hides an isolated three-dimensional object in free space in the visible range has not yet been demonstrated.

Here, we present the design, the fabrication, and the characterization of a cloak for free-standing three-dimensional objects in the visible. We achieve this by taking advantage of a metamaterial for the shell that is composed of an amorphous arrangement of metallic nanoparticles (NPs). The cloak is fabricated by self-assembly techniques39,40. As a result several million cloaking core-shell structures are fabricated. The use of a metamaterial shell rather than a homogeneous metallic thin film has the key advantages of a considerably less absorption, relaxed fabrication constraints, a large durability of the device, and avoiding the fabrication of extremely thin homogeneous metallic shells41,42,43. We characterize the cloak by an appropriate experimental set-up where the scattered light is measured upon depositing the cloaks on a dielectric substrate. The excellent agreement with supporting simulations proves the reliability and robustness of the entire concept.

Results

Design consideration

The basic concept of the cloak is shown by an artistic illustration in Fig. 1. By analyzing Eq. 1, it is easily appreciated that while fixing the geometry and the permittivities of the core and the surroundings, the equation exhibits two solutions for the shell permittivity. One of them results in a large and negative permittivity; this solution is termed the negative cloaking resonance. In contrast, the second one results in a permittivity that is only slightly larger than zero but less than unity; this solution is termed the positive cloaking resonance. Both requirements can, in principle, be met using ordinary metal films for the shell44. However, due to the onset of interband absorption, the spectral domain where the real part of the permittivity takes appropriate values is associated with strong absorption, i.e. a huge imaginary part in the permittivity45. This prevents a real-valued solution for γ in Eq. 1 leading to imperfect cloaking.

Figure 1. Artistic view of the considered cloak.

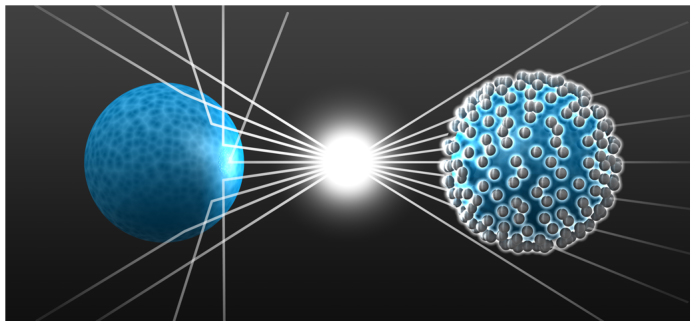
Figure 1

Open in a new tab

On the left it is seen that a dielectric object reveals its presence to an external observer by scattering the light. This is different on the right. There, a shell made from metallic nanoparticles scatters the same amount of light as the core but π out-of-phase. This suppresses the scattered field. It therefore makes the object undetectable.

To circumvent this issue, the metallic shell film can be advantageously replaced by an arrangement of metallic nanoparticles. Here, silver is considered as the metal material. The silver nanoparticles exhibit localized plasmon polariton resonances and their arrangement forms an effective plasmonic shell material46. In what follows we focus on an amorphous arrangement which is easy to implement with self-assembly techniques and represents a metamaterial with the required effective optical properties. A metamaterial made from silver nanoparticles exhibits a Lorentzian dispersion in the permittivity around the plasmon resonance of the single silver nanoparticle, as can be seen in Figure 2 (a). Two different filling fractions are considered and the strength of the Lorentzian resonance and the FWHM strongly depend on them. The denser the silver NPs are arranged the stronger the variation of the real part of the effective permittivity appears. Therefore, negative values, necessary for the negative cloaking resonance, can only be obtained at suitably high filling fractions. However, high filling fractions cause large imaginary parts of the effective permittivity in wavelength ranges where the real part is negative. This is very detrimental and suggests that the negative cloaking approach is not practical for a shell of silver nanoparticles.

Figure 2. Effective parameters of the metamaterials shell.

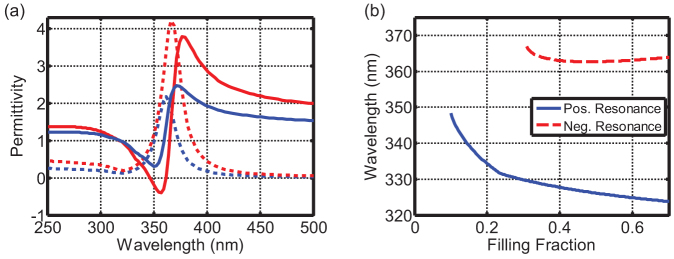
Figure 2

Open in a new tab

(a) Effective permittivity of a metamaterial shell consisting of amorphously arranged silver NPs. The permittivity is obtained by using the Maxwell-Garnett formula (details are given in the Methods section). Two filling fractions of silver NPs are shown: 0.11 (blue) and 0.18 (red). Solid and dashed curves designate real and imaginary part of the permittivity, respectively. (b) Positive and negative cloaking resonance for a silica core sphere (55 nm radius, ε = 2.18) and a metamaterial shell (67 nm radius) with permittivity from (a) as a function of the filling fraction of silver NPs.

However, one can take advantage of the second solution, the positive cloaking resonance. At wavelengths appreciably shorter than that of the Lorentzian resonance, absorption decreases rapidly41. This includes just the wavelength domain (about 325–350 nm) where the real part of the effective permittivity varies in the desired range between zero and unity. Therefore, further considerations will exclusively cover the positive cloaking resonance. Another advantage of this choice is that the required parameters can even be achieved for relatively low filling fractions.

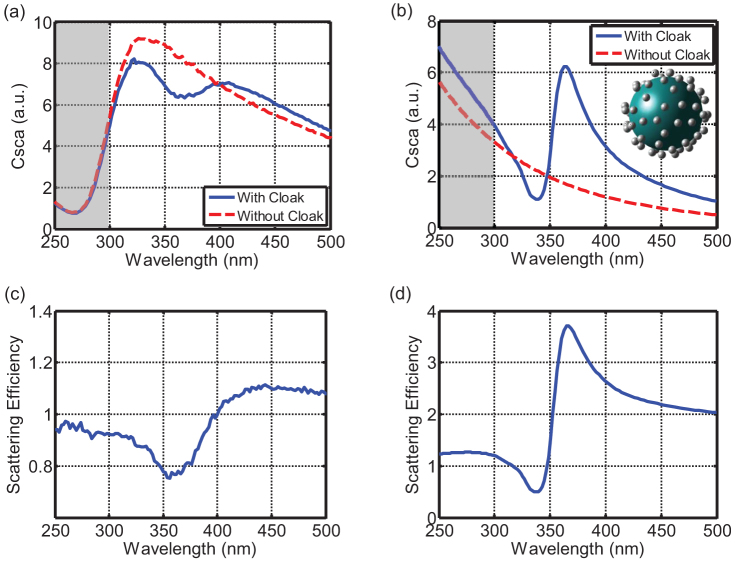
To make the design definite, we have chosen to cloak a fused silica sphere with a radius of 55 nm because well-mastered silica chemistry, which allows for a surface functionalization, simplifies the fabrication procedure47. Its permittivity in the spectral domain of interest, i.e. slightly below 400 nm, can be assumed to be constant (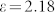Inline graphic). We define the scattering efficiency as the ratio of scattered light of the object to be cloaked and of the bare object. Small scattering efficiencies account for highly suppressed scattered fields and therefore a cloaking of the object, i.e. the silica sphere. Generally, a smaller scattering efficiency than that for silica can be anticipated for spheres with a larger permittivity. The stronger the scattering signal the easier to suppress the scattering response41. Thus, in these cases the scattering efficiency might even be much less than we expect to observe in our experiments.

The shell is formed by amorphously arranged silver NPs (r = 6 nm). Thus the radius of the shell amounts to 67 nm. Using this data Eq. 1 can be solved for the two shell permittivities required to suppress the scattering. The negative and positive cloaking resonances appear for 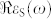Inline graphic = −2.69 and 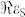Inline graphic = 0.41, respectively. Therefore, if the shell is a metamaterial composed of amorphously arranged silver NPs, its effective permittivity depends on the filling fraction [c.f. Figure 2 (a)] and can thus meet these values at different wavelengths as shown in Figure 2 (b). It can be clearly seen, that for experimentally achievable filling fractions (< 30%) only the positive cloaking resonance might be observable.

Fabrication and sample preparation

For the fabrication a self-assembly technique for colloidal nanoparticles has been used. The reliability of this technique has been proven in the past48,49,50,51,52. There, layered arrays of gold nanoparticles were deposited on planar or spherical substrates. These works aimed at achieving, for example, plasmonically active substrates or unit cells with a strong artificial magnetic scattering response. Since we had to cope with the challenge of using silver as the metallic material, we used a modified Lee-Meisel method53 to first fabricate silver nanoparticles by reducing AgNO3 with sodium borohydride. Nanoparticles with 6 nm radius were fabricated. Details of the fabrication process can be found in the Methods section. The main advantage of this method is the availability of nanoparticles in solution. In addition, the adsorption of citrate ions on the silver surface leads to a weak negative charge of the NPs. In a separate fabrication procedure, silica cores with a radius of 55 nm were deposited on a planar substrate and functionalized to be slightly positively charged using well established silica chemistry47. Details are likewise documented in the Methods section. By merging the array of silica spheres with the silver nanoparticle solution and exploiting the electrostatic interaction, the metallic nanoparticles tend to deposit on the silica cores. Moreover, since the nanoparticles are equally charged they tend to maximize the distance to their nearest neighbor on the surface of the core to lower their energy. This is extremely beneficial since agglomeration and clustering are avoided; while simultaneously assuring a sufficiently high filling fraction (approximately between 0.1 and 0.3).

The entire fabrication process is extremely robust and shows a great resistance against imperfections. Moreover, quite a few parameters exist, such as pH and salt concentration, which allow for a flexible and easy control of particle sizes and density. Both of them can affect the functionality of the cloak. To inspect the fabricated cloaks and to characterize them spectroscopically, the silica cores covered with silver nanoparticles on a glass substrate are perfectly suitable. A referential scanning electron micrograph image from such a sample, prepared in exactly the same manner on a silicon substrate, is shown in Figure 3 where the homogeneity is quite reasonable. The deposition on the glass substrate also allows for an unambiguous analysis of the scattering response since it better resembles the scenario if analyzing an isolated cloak as considered in simulations. Moreover, the arrangement on a dielectric substrate is not expected to affect the response54, since scattering may be well described in the dipole limit and the particle density is moderate. For reference purposes the bare dielectric spheres were equally deposited on the same substrate at the same concentration. This facilitates the identification of the scattering efficiency as defined above.

Figure 3. SEM image of fabricated core-shell cloaks.

Figure 3

Open in a new tab

The large dielectric silica core spheres and their decoration with the silver nanoparticles can be seen.

Optical characterization

To optically characterize the samples, a well-adapted setup based on a Perkin Elmer spectrometer has been used. The details of the setup are explained in the Methods section. In short, using different configurations, it allows the measurement of the total transmittance, i.e. the share of energy that is transmitted into the half-space behind the sample, the diffuse transmittance, i.e. the same as the total transmittance but excluding a specular region of about ±5°, the total reflectance, and the diffuse reflectance, for the same sample. The latter ones are analogously defined as their transmittance counterparts. Various important parameters can be derived; but most notably the total scattering cross-section. It is obtained as the sum of the diffuse transmittance and the diffuse reflectance. The results for the scattering cross-sections of the referential samples with the bare silica spheres and the cloaked structures are shown in Figure 4 (a). There, we have shaded a spectral region below 300 nm since the borosilicate substrate used was absorptive in this spectral domain. Therefore, the light scattered in forward direction is attenuated. This, however, is not detrimental since the positive cloaking resonance occurs for larger wavelengths [c.f. Figure 2 (b)]. Moreover, the scattering efficiency, we are primarily interested in, is only marginally affected since both samples (bare silica spheres and the cloaked sample) suffer from the same absorption. Overall, we see for the bare sphere a typical scattering response for an object in the electric dipolar limit, i.e. it scales with the fourth power of the inverse wavelength. This scattering response is expected to be reduced for the appropriately decorated core.

Figure 4. Measured and simulated cloaking performance.

Figure 4

Open in a new tab

Measured (a) and simulated (b) scattering cross section of the core object with (blue solid) and without the cloaking silver nanoparticle shell (red dashed) are shown on top. The inset in (b) shows the structure as considered in the simulation. The gray shaded areas mark the wavelength domain where the borosilicate substrate absorbs. Since the substrate is disregarded in simulations the experimental and simulated curves show different dependencies inside the gray shaded area. The measured (c) and simulated (d) scattering efficiencies are shown at the bottom. Different scaling for the scattering efficiency has been used for measurement and simulation. Although the functional dependency is perfectly reproduced, the cloaking efficiency (inverse of scattering efficiency) is enhanced in the simulations; a deviation that is attributed to the fact that the measurement is an ensemble average whereas the simulation corresponds to a single structure.

Indeed, a strong suppression of the scattering response around 360 nm can be recognized. Moreover, a characteristic increase in the scattering cross section occurs at wavelengths exceeding 400 nm. Disregarding the absorption in the substrate the comparison to simulations, shown in Figure 4 (b), shows a remarkable agreement. All characteristic features are reproduced. For illustrative purposes, the inset of Figure 4 (b) shows exactly the structure used in the simulations. Specifically, for the sake of precision, we did not resort to an effective medium description of the shell. Rather than we used an extended Mie scattering formalism where the mutual interaction of the scattered fields from a huge number of spheres is exactly taken into account55,56. The given arrangement was derived from inspecting various SEM images to extract the particle density at the surface. In simulations the filling fraction of silver NPs was set to 0.11. The core and the nanoparticle radii were assumed to be 55 nm and 6 nm, respectively. Details of the simulations are documented in the Methods section. The only aspect that is not reproduced in the simulation is the effect of substrate absorption at shorter wavelengths because particles were assumed to be surrounded by air. The scattering efficiencies as shown in Figure 4 (c) and (d) are extracted from the measured and the simulated results, respectively.

Discussion

From the functional dependency of the scattering efficiency on wavelength a very intuitive explanation of the operation principle of such cloak can be drawn. Obviously, a spectral interference phenomenon occurs, where a weakly dispersive background scattering signal, i.e. caused by the bare silica core sphere, interferes with a sufficiently narrow plasmonic resonance of the shell. The latter can be explained on phenomenological grounds with a harmonic oscillator model. The phase of this plasmonic resonance changes by π near the resonance wavelength. At wavelengths above the resonance, where the induced polarization can follow the excitation, the scattered field from the shell is in phase with that from the core object. This results in an enhancement of the scattering efficiency. At wavelengths below the resonance, the induced polarization in the shell material is lagging by π with respect to the excitation. This causes a reduction of the scattering efficiency. Perfect cloaking would occur at a wavelength where the amplitudes of both scattering contributions are identical. The asymmetric line shape of the cloaking efficiency resembles Fano type resonances57. There, a continuous background of modes spectrally interferes with an isolated mode; just as it occurs in the present sample.

Although the scattering efficiencies in measurement and simulation are qualitatively identical, there is a quantitative difference. We attribute this difference to the fact that the measurement is performed with an ensemble whereas the simulation is performed for an isolated decorated core. Moreover, variations in the geometrical parameters of the cloak evoked by the self-assembly process cause a smoothening of the resonances and a lowering of their extreme values. This is unavoidable in the chosen bottom-up approach. Whereas the filling fraction can be precisely controlled this does not hold for the geometrical properties, as e.g. the size of the silica core sphere and the silver nanoparticles. Consequently, some uncertainty exists in the structure, which inhomogeneously broadens every spectral feature. This broadening is evidenced comparing Figure 4 (c) and (d). However, larger metallic nanoparticles, a higher filling fraction, and a larger core permittivity would improve the cloaking performance. This optimization towards an improvement is currently in progress, but the demonstration of this proof-of-principle device is a significant step towards the application of functional cloaks.

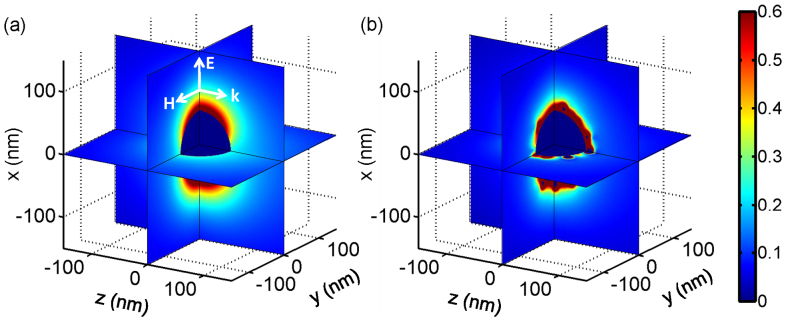
Thus, the functionality of a cloak to hide a free-standing three-dimensional object is demonstrated. The suppression of the scattered field can be also seen in Figure 5, where the simulated near-field amplitude of the scattered electric field is displayed. Even though each nanoparticle interacts resonantly with the external illumination, their scattered field cancels some fraction of the scattered field from the core object; and all together they suppress the scattering signal of the object to a noticeable extent. Of course, in close proximity to the silver NPs the electric field is enhanced due to the excitation of localized surface plasmon resonances. But these fields do not propagate into the far field, as can be clearly seen in Figure 5 (b).

Figure 5. Field distributions of the cloak.

Figure 5

Open in a new tab

Simulated magnitude of the scattered electric field of the object without (a) and with cloak (b) at the wavelength where the scattering efficiency is minimized (at 338 nm) under plane wave illumination as sketched in (a). Whereas for the isolated element an appreciable scattering effect occurs, visible through the excitation of an electric dipole along the x-axis in (a) it is significantly suppressed if the cloak is used in (b).

In summary, we demonstrated a self-assembled three-dimensional cloak. The structure may find applications in cloaked sensors or in optical nanoantenna arrays to strongly suppress the cross-talk. Although the scattering efficiency has to be further minimized the functionality is demonstrated. However, beyond this specific contribution we have established a novel design and fabrication paradigm that exploits bottom-up approaches for realizing nanooptical devices. Functional devices with comparable properties can be prepared in short time, in ultra-large quantities, and, perhaps above all, at low costs. The control over nanometric dimensions by assembling a finite number of metallic nanoparticles into complicated agglomerates might be the key to control the light-matter interaction at the nanoscale. This ability is essential for the architecture of future nanophotonic devices. They are of major scientific importance. This holds especially if their interaction with external light is not considered as an isolated element but if coupled to other quantum objects, e.g. molecules, atoms, or quantum dots, to form hybrid devices. Examples for applications in reach can be found in such high impact areas like optical signal processing, desirable even at the single photon level to entail applications such as quantum logical elements and quantum computing. Alternatively, ultrafast nanooptical devices that access length and time scales of elementary electronic, vibrational, and structural excitations in matter would equally benefit from the functionality that can be offered by the self-assembly of a few, but strongly interacting, nanoparticles.

Methods

Fabrication

Silver nanospheres stabilized by citrate molecules were prepared by first cooling 196 mL of water in an ice-bath. 2 mL of aqueous solutions of AgNO3 (25 mM) and sodium citrate (25 mM) were added under vigorous magnetic stirring before the reducing agent, 600 μL of an aqueous solution of NaBH4 (0.1 M) was introduced in a dropwise fashion. The solution was left stirring in the ice-bath for a period of two hours to allow the reaction to achieve completion before the silver nanospheres were stored in a fridge.

Glass and silicon substrates, used for spectral measurements and electron microscopy, respectively, were prepared according to the same method. They were first rinsed with water and ethanol before being dried under a stream of compressed air. The surfaces were then cleaned and hydroxylated through immersion in a piranha solution (3:1 mixture of concentrated sulphuric acid to 30% hydrogen peroxide) for 30 minutes. Piranha solution is strongly acidic and highly oxidising and should be handled with caution. The substrates were next rinsed with copious amounts of water and again dried under a stream of compressed air. Subsequently, the surface chemistry was altered through the functionalisation with an organosilane. Here, the substrates were immersed in a 5% (v/v) solution of N-[3-(trimethoxysilyl)propyl] ethylenediamine in ethanol for 30 minutes before being rinsed with water, dried, and set in an oven at 120°C for a further 30 minutes.

Large area arrays of SiO2 microspheres were deposited on functionalised glass or silicon substrates by immersing the substrates in a solution of the particles which had been adjusted to pH 5 through the addition of a dilute solution of HCl. The substrate was then removed, washed with water and dried in a stream of compressed air. The microsphere array was then functionalised by exposing to a 5% (v/v) solution of N-[3-(trimethoxysilyl)propyl]ethylenediamine in ethanol for 30 minutes before rinsing with water and drying under a stream of compressed air. The microspheres were then decorated with the silver nanoparticles by immersing the substrate in the silver nanoparticle solution for a period of two and a half hours before washing with water and drying in a stream of compressed air.

Optical characterization

The optical measurements were performed with a double-beam UV-Vis spectrophotometer (Lambda 900, Perkin Elmer) equipped with a 150 mm Spectralon coated integrating sphere to collect reflected or transmitted light from the samples over a full hemisphere. A combination of deuterium and halogen lamps is used to cover the 250–500 nm wavelength range, and detection is performed by a photomultiplier located at the bottom of the integrating sphere. The sphere contains different apertures that can be opened to reject the specular reflected [Figure 6 (a)] or transmitted [Figure 6 (b)] light (with an angular resolution of ±5°) in order to collect only the diffuse light, i.e. scattered in the backward and forward directions respectively. The probed area (defined by the area of the sphere apertures) is 15 × 10 mm2. For reflectance and transmittance measurements, the sample is fixed at the front or rear aperture respectively with the incoming light impinging on the substrate side in both cases so as to retrieve the total amount of light scattered by the sample by summing the two contributions (diffuse reflectance + diffuse transmittance).

Figure 6.

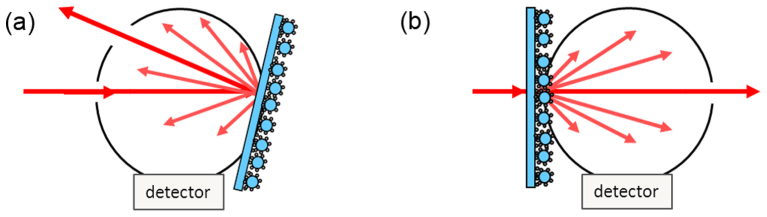
Figure 6

Open in a new tab

Integrating sphere configuration for (a) diffuse reflectance - the sample is inclined at an angle of 8° - and (b) diffuse transmittance measurements.

Optical simulation

The results of Figure 2 showing effective permittivities for a shell made of silver nanoparticles where obtained by the Maxwell-Garnett Formula59

graphic file with name srep02328-m9.jpg

where εB is the permittivity of the surroundings and f the filling fraction of silver nanoparticles on the shell. The permittivity of silver (εAg) was taken from literature45 with a size correction of the imaginary part59 to account for the finite radius of the silver spheres of 6 nm. The positive and negative cloaking resonance wavelengths of Figure 2 (b) where obtained by solving Eq. 1. The core radius was set to 55 nm and the shell radius to 67 nm. Furthermore, the surrounding was set to vacuum εB = 1 and the core was assumed as fused silica εc = 2.18. The two solutions of Eq. 1 yield the shell permittivities of εS = 0.41 and εS = −2.69 for the positive and negative cloaking resonance, respectively. These permittivities were inserted in the above given Maxwell-Garnett formula to find the cloaking resonance wavelengths.

The numerical results of Figure 4 (b), (d) and Figure 5 were not obtained by using an effective medium approach as for Figure 2. Quite contrary, an extension of the well-known Mie theory was applied that exactly solves Maxwell's equations for an arbitrary arrangement of spheres55,56. So the interaction between every silver NP as sketched in the inset of Figure 4 (b) was fully taken into account. Since this so-called extended Mie theory is based on a series expansion of the electric field into eigenfunctions we took five orders of this expansion into account. After four orders full convergence of the fields was observed. In all simulations the cloak was illuminated by an x-polarized plane wave propagating along z-direction.

Author Contributions

S.M., M.F. and C.R. conceived the idea. S.M., M.F. and S.B.H. made the design and performed all numerical simulations. A.C. and T.B. fabricated the sample. J.D. and T.S. characterized the sample. C.R., S.M. and F.L. wrote the manuscript. All authors discussed the manuscript and worked on its improvement.

Acknowledgments

Financial support by the German Federal Ministry of Education and Research (PhoNa), by the Thuringian State Government (MeMa), and the European Union's Seven Framework Programme (FP7/2007–2013) under grant agreement no. 228455 is acknowledged. We also thank Karsten Verch (www.karstenverch.com) for his artistic view of the device shown in Fig. 1.

References

  1. Pendry J. B., Aubry A., Smith D. R. & Maier S. A. Transformation optics and subwavelength control of light. Science 337, 549–552 (2012). [DOI] [PubMed] [Google Scholar]
  2. Greenleaf A., Kurylev Y., Lassas M., Leonhardt U. & Uhlmann G. Cloaked electromagnetic, acoustic, and quantum amplifiers via transformation optics. PNAS 109, 10169–10174 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Leonhardt U. Optical conformal mapping. Science 312, 1777–1780 (2006). [DOI] [PubMed] [Google Scholar]
  4. Born M. & Wolf E. Principles of Optics. Cambridge, University Press (1999). [Google Scholar]
  5. Schmiele M., Rockstuhl C. & Lederer F. Strategy for cloaking of twisted domains. Phys. Rev. A 79, 053854 (2009). [Google Scholar]
  6. Pendry J. B., Schuring D. & Smith D. R. Controlling electromagnetic fields. Science 312, 1780–1782 (2006). [DOI] [PubMed] [Google Scholar]
  7. Soukoulis C. M. & Wegener M. Past achievements and future challanges in the development of three-dimensional photonic metamaterials. Nature Photon. 5, 523–530 (2011). [Google Scholar]
  8. Shalaev V. M. Optical negative-index metamaterials. Nature Photon. 1, 41–48 (2007). [DOI] [PubMed] [Google Scholar]
  9. Simovski C. R. Material parameters of metamaterials (a review). Opt. Spectrosc. 107, 726–753 (2009). [Google Scholar]
  10. Cummer S. A., Popa B.-I., Schuring D., Smith D. R. & Pendry J. B. Full-wave simulations of electromagnetic cloaking structures. Phys. Rev. E 74, 036621 (2006). [DOI] [PubMed] [Google Scholar]
  11. Halimeh J. C., Ergin T., Mueller J., Stenger N. & Wegener M. Photorealistic images of carpet cloaks. Opt. Express 17, 19328–19336 (2009). [DOI] [PubMed] [Google Scholar]
  12. Schuring D. et al. Metamaterial electromagnetic cloak at microwave frequencies. Science 314, 977–980 (2006). [DOI] [PubMed] [Google Scholar]
  13. Li J. & Pendry J. B. Hiding under a carpet: a new strategy for cloaking. Phys. Rev. Lett. 101, 203901 (2008). [DOI] [PubMed] [Google Scholar]
  14. Chen X. et al. Macroscopic invisibility cloaking of visible light. Nature Commun. 2, 176 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Zhang B., Luo Y., Liu X. & Barbastathis G. Macroscopic invisibility cloak for visible light. Phys. Rev. Lett. 106, 033901 (2011). [DOI] [PubMed] [Google Scholar]
  16. Liang D. et al. Robust large dimension terahertz cloaking. Adv. Mater. 24, 916–921 (2012). [DOI] [PubMed] [Google Scholar]
  17. Valentine J., Li J., Zentgraf T., Bartal G. & Zhang X. An optical cloak made of dielectrics. Nature Mater. 8, 568–571 (2009). [DOI] [PubMed] [Google Scholar]
  18. Zhou F. et al. Hiding a realistic object using a broadband terahertz invisibility cloak. Sci. Rep. 1, 78; 10.1038/srep00078 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Ergin T., Stenger N., Brenner P., Pendry J. B. & Wegener M. Three-dimensional invisibility cloak at optical wavelengths. Science 328, 337–339 (2010). [DOI] [PubMed] [Google Scholar]
  20. Liu R. et al. Broadband ground-plane cloak. Science 323, 366–369 (2009). [DOI] [PubMed] [Google Scholar]
  21. Ma H. F. & Cui T. J. Three-dimensional broadband ground plane cloak made of metamaterials. Nature Commun. 1, 21 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Gabrielli L. H., Cardenas J., Poitras C. B. & Lipson M. Silicon nanostructure cloak operating at optical frequencies. Nature Photon. 3, 461–463 (2009). [Google Scholar]
  23. Chen H. & Zheng B. Broadband polygonal invisibility cloak for visible light. Sci. Rep. 2, 255 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Chen P.-Y., Soric J. & Alu A. Invisibility and cloaking based on scattering cancellation. Adv. Mater. 24, OP281–OP304 (2012). [DOI] [PubMed] [Google Scholar]
  25. Kerker M. Invisible bodies. J. Opt. Soc. A 65, 376–379 (1975). [Google Scholar]
  26. Alu A. & Engheta N. Achieving transparency with plasmonic and metamaterial coatings. Phys. Rev. E 72, 016623 (2005). [DOI] [PubMed] [Google Scholar]
  27. Alu A. & Engheta N. Plasmonic and metamaterial cloaking: physical mechanisms and potentials. J. Opt. A: Pure Appl. Opt. 10, 093002 (2008). [Google Scholar]
  28. Rockstuhl C. & Scharf T. Amorphous Nanophotonics. Heidelberg, Springer (2013). [Google Scholar]
  29. Vogelgesang R. & Dmitriev A. Real-space imaging of nanoplasmonic resonances. Analyst. 135, 1175–1181 (2010). [DOI] [PubMed] [Google Scholar]
  30. Bilotti F., Tricarico S., Pierini F. & Vegni L. Cloaking apertuless near-field scanning optical microscopy tips. Opt. Lett. 36, 211–213 (2011). [DOI] [PubMed] [Google Scholar]
  31. Tricarico S., Bilotti F. & Vegni L. Reduction of optical forces exerted on nanoparticles covered by scattering cancellation based plasmonic cloaks. Phys. Rev. B 82, 045109 (2010). [Google Scholar]
  32. Monti A., Bilotti F., Toscano A. & Vegni L. Possible implementation of epsilon-near-zero metamaterials working at optical frequencies. Opt. Commun. 285, 3412–3418 (2012). [Google Scholar]
  33. Monti A. et al. Overcoming mutual blaockage between neighboring dipole antennas using a low-profile patterned metasurface. IEEE Antennas Wireless Propag. Lett. 11, 1414–1417 (2012). [Google Scholar]
  34. Rainwater D. et al. Experimental verification of three-dimensional plasmonic cloaking in free-space. New J. Phys. 14, 013054 (2012). [Google Scholar]
  35. Edwards B., Alu A., Silverinha M. & Engheta N. Experimental verification of plasmonic cloaking at microwave frequencies with metamaterials. Phys. Rev. Lett. 103, 153901 (2009). [DOI] [PubMed] [Google Scholar]
  36. Bilotti F., Tricarico S. & Vegni L. Electromagnetic cloaking devices for TE and TM polarizations. New J. Phys. 10, 115035 (2008). [Google Scholar]
  37. Fan P. et al. An invisible metal-seminconductor photodetector. Nature Photon. 6, 380–385 (2012). [Google Scholar]
  38. Alu A. & Engheta N. Claoking a sensor. Phys. Rev. Lett. 102, 233901 (2009). [DOI] [PubMed] [Google Scholar]
  39. Urzhumov Y. A. et al. Plasmonic nanoclusters: a path towards negative-index metafluids. Opt. Express 15, 14129–14145 (2007). [DOI] [PubMed] [Google Scholar]
  40. Rockstuhl C., Lederer F., Etrich C., Pertsch T. & Scharf T. Design of an artificial three-dimensional composite metamaterial magnetic resonances in the visible range of the electromagnetic spectrum. Phys. Rev. Lett. 99, 017401 (2007). [DOI] [PubMed] [Google Scholar]
  41. Mühlig S., Farhat M., Rockstuhl C. & Lederer F. Cloaking dielectric spherical objects by a shell of metallic nanoparticles. Phys. Rev. B 83, 195116 (2011). [Google Scholar]
  42. Monti A., Bilotti F. & Toscano A. Optical cloaking of cylindrical objects by using covers made of core-shell nanoparticles. Opt. Lett. 36, 4479–4481 (2011). [DOI] [PubMed] [Google Scholar]
  43. Bilotti F., Tricarico S. & Vegni L. Plasmonic metamaterial cloaking at optical frequencies. IEEE Trans. Nanotech. 9, 55–61 (2010). [Google Scholar]
  44. Alu A. & Engheta N. Plasmonic materials in transparency and cloaking problems: mechanism, robustness, and physical insights. Opt. Express 15, 3318–3332 (2007). [DOI] [PubMed] [Google Scholar]
  45. Johnson P. B. & Christy R. W. Optical constants of noble metals. Phys. Rev. B 6, 4370–4379 (1972). [Google Scholar]
  46. Rockstuhl C. & Scharf T. A metamaterial based in coupled metallic nanoparticles and ist band-gap property. J. Micros. 229, 281–286 (2008). [DOI] [PubMed] [Google Scholar]
  47. Iller R. K. The chemistry of silica – solubility, polymerization, colliod and surface properties, and biochemistry. New York, Wiley (1979). [Google Scholar]
  48. Decher G. Fuzzy nanoassemblies: towards layered polameric multicomposites. Science 277, 1232–1237 (1997). [Google Scholar]
  49. Cunningham A., Mühlig S., Rockstuhl C. & Bürgi T. Coupling of plasmon resonances in layered arrays of gold nanoparticles. J. Phys. Chem. C 115, 8955–8960 (2011). [Google Scholar]
  50. Mühlig S. et al. Self-assembled plasmonic core-shell clusters with an isotropic magnetic dipole resonance in the visible range. ACS Nano 5, 6586–6592 (2011). [DOI] [PubMed] [Google Scholar]
  51. Cunningham A., Mühlig S., Rockstuhl C. & Bürgi T. Exciting bright and dark eigenmodes in strongly coupled asymmertric metallic nanoparticle arrays. J. Phys. Chem. C 116, 17746–17752 (2012). [Google Scholar]
  52. Bassim N. D. et al. Layer-by-layer assembly of heterogeneous modular nanocomposites. J. Phys. Chem. C 116, 1694–1701 (2012). [Google Scholar]
  53. Lee P. C. & Meisel D. Adsorption and surface-enhanced Raman of dyes on silver and gold sols. J. Phys. Chem. 86, 3391–3395 (1982). [Google Scholar]
  54. Farhat M. et al. Understanding the functionality of an array of invisibility cloaks. Phys. Rev. B 84, 235105 (2011). [Google Scholar]
  55. Xu Y.-L. Electromagnetic scattering by an aggregate of spheres. Appl. Opt. 34, 4573–4588 (1995). [DOI] [PubMed] [Google Scholar]
  56. Mühlig S. et al. Three-dimensional metamaterial nanotips. Phys. Rev. B 81, 075317 (2010). [Google Scholar]
  57. Luk'yanchuk B. et al. The Fano resonance in plasmonic nanostrutures. Nature Mater. 9, 707–715 (2010). [DOI] [PubMed] [Google Scholar]
  58. Sihvola A. Electromagnetic mixing formulas and applications. IEEE Publication Series (2000). [Google Scholar]
  59. Okamoto T. Near-field spectral analysis of metallic beads. In: Kawata, S. Ed. Near-field optics and surface plasmon polaritons. Topics. Appl. Phys. 81, 97–123. Berlin, Springer (2001). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES