The Effect of HAART on HIV RNA Trajectory Among Treatment Naïve Men and Women: a Segmental Bernoulli/Lognormal Random Effects Model with Left Censoring

Abstract

Background

Highly active antiretroviral therapy (HAART) rapidly suppresses human immunodeficiency virus (HIV) viral replication and reduces circulating viral load, but the long-term effects of HAART on viral load remain unclear.

Methods

We evaluated HIV viral load trajectories over 8 years following HAART initiation in the Multicenter AIDS Cohort Study and the Women’s Interagency HIV Study. The study included 157 HIV-infected men and 199 HIV-infected women who were antiretroviral naïve and contributed 1311 and 1837 semiannual person-visits post-HAART, respectively. To account for within-subject correlation and the high proportion of left-censored viral loads, we used a segmental Bernoulli/lognormal random effects model.

Results

Approximately 3 months (0.30 years for men and 0.22 years for women) after HAART initiation, HIV viral loads were optimally suppressed (ie, with very low HIV RNA) for 44% (95% confidence interval = 39%–49%) of men and 43% (38%–47%) of women, whereas the other 56% of men and 57% of women had on average 2.1 (1.5–2.6) and 3.0 (2.7–3.2) log10 copies/mL, respectively.

Conclusion

After 8 years on HAART, 75% of men and 80% of women had optimal suppression, whereas the rest of the men and women had suboptimal suppression with a median HIV RNA of 3.1 and 3.7 log10 copies/mL, respectively.

INTRODUCTION

Observational studies and clinical trials^1–4 have shown that highly active antiretroviral therapy (HAART) has dramatically extended the time to development of acquired immunodeficiency syndrome (AIDS) and to death in human immunodeficiency virus (HIV)–infected individuals. The primary mechanism of action is suppressing plasma HIV RNA to “undetectable” levels by using sensitive assays (eg, to suppress viremia below 50 copies/mL by using the Roche ultrasensitive assay) that in turn allows an increase in CD4-postive T-lymphocyte (CD4 cell) count and function.^5,6 Although suppressing HIV RNA levels may be necessary to prevent drug resistance, 1 of the major causes of treatment failure,⁷ undetectable levels of HIV RNA in plasma do not imply that viral replication has been stopped.^8–10 Moreover, after achieving suppression, many patients experience intermittent episodes of detectable viremia (“viral blips”), which may raise concerns about drug resistance and alterations in therapies.^11–14

In the Multicenter AIDS Cohort Study (MACS) of men, Tarwater et al.¹⁵ reported that regardless of CD4 cell counts at HAART initiation, there was a significant increase in CD4 cell count during the first 2 years, followed by CD4 cell count stabilization between 2 and 3.5 years. Chu et al.,¹⁶ using a Bayesian random change points model, reported that after large initial increases in CD4 count, 35% of men in MACS compared with 25% of women in the Women’s Interagency HIV Study (WIHS) had a statistically significant flattening in CD4 cell count trajectory within 7 years after HAART initiation, which suggests that HIV RNA response to HAART may also have a nonlinear trajectory. From a clinical standpoint, the determination of change points (ie, when the post-HAART initiation changes of longitudinal HIV RNA or CD4 cell count trajectory become apparent) may identify the optimal time to change antiretroviral therapy, and from a pathogenic perspective, this may reflect the time at which the HIV has developed resistance to the current therapy.¹⁷

Li and coworkers¹⁸ have shown that for each year following HAART initiation HIV RNA levels in both therapy-experienced and therapy-naïve men and women can be modeled with bimodal distributions, with each mode corresponding to optimal and suboptimal responders, that is, very low and relatively high HIV RNA levels. In their study, even though most patients achieved optimal virologic response with model-based median of HIV RNA less than 20 copies/mL, substantial proportions (32% of men and 44% of women) had suboptimal suppression with median HIV RNA higher than 5000 copies/mL among suboptimal responders even in the fifth year after HAART initiation. However, this evaluation of longitudinal patterns of viral RNA measurements was potentially confounded from selection bias and correlation among repeated measurements¹⁹. Moreover, because their analysis was conducted separately for each yearly interval (from within 1 year before HAART initiation up to 5 years after HAART initiation), a time of change in HIV viral load trajectory cannot be estimated.

We thus undertook this investigation to study the longitudinal patterns of HIV viral load after HAART initiation and to test for the presence of change points of HIV RNA trajectories (ie, points at which the change of HIV viral load trajectories become apparent) by using data from 2 prospective cohort studies — the MACS and the WIHS. Various approaches have been considered for modeling the trajectories of HIV RNA, including random regression models with informative drop-out,²⁰ a joint model for longitudinal CD4 cell count and HIV RNA,²¹ and a marginal structure left-censored mean model.²² We extended a Bernoulli/lognormal random effects model with left censoring for HIV RNA levels below detection limits^23–25 to 1) test whether the longitudinal HIV RNA can be well characterized by Bernoulli/lognormal mixture models, possibly corresponding to optimal and suboptimal suppression, and 2) identify potential change points in the longitudinal trajectory that may shed some light on the optimal time to change therapies and the time to successful resistance of the virus. This random effects model provides a unified approach to model repeatedly measured biomarker data with undetectable levels. Unlike a simple 2-step approach (ie, that models the binary probability of having detectable compared with undetectable values in the first step and then models the conditional viral load values among detectables in the second step) that assumes all undetectable values correspond to optimal suppression, this extended approach allows a proportion of undetectable HIV RNA to be left-censored values of a continuous distribution to characterize the distribution of HIV RNA for those with suboptimal suppression (ie, reflected by having frequent episodes of detectable viremia, see statistical methods section).²³

METHODS

POPULATION AND STUDY DESIGN

The MACS is a multicenter prospective cohort study initiated in 1983 to investigate the natural history of HIV-1 infection among homosexual and bisexual men in the United States. The study design has been previously described.²⁶ A total of 3512 infected participants were either HIV-positive at enrollment (83.8%) or became infected with HIV during follow-up (16.2%). The WIHS is a multicenter prospective cohort study initiated in 1993 to examine the natural history of HIV-1 infection among women in the United States. The baseline WIHS cohort characteristics have been described previously.²⁷ A total of 2809 infected women were either HIV-positive at enrollment (99.4%) or became infected with HIV during follow-up (0.6%). The MACS and WIHS protocols were approved by institutional review boards of each of the participating centers, and informed consent was obtained from all participants.

In both the MACS and WIHS, participants return every 6 months for clinical visits at which detailed questionnaires and physical examinations are administered, and biologic specimens are collected for testing and storage. Antiretroviral medications in the preceding 6 months are self-reported at each semiannual visit and summarized to define HAART usage in the preceding 6 months. Highly active antiretroviral therapy is defined according to the U.S. Department of Health and Human Services/Kaiser Panel guidelines.^28,29 The date of HAART initiation is considered to be the midpoint between the last visit reporting no HAART use (last no HAART) and the first visit at which HAART use is reported (first HAART). In the MACS, HIV RNA is determined using the Roche Amplicor RNA kit (Hoffman-LaRoche, Nutley, NJ) with a limit of detection (LOD) of 400 copies/mL. If this kit does not detect HIV RNA, the Roche Ultrasensitive RNA PCR assay with an LOD of 50 copies/mL (Hoffman-LaRoche) is performed. In the WIHS, HIV RNA is measured using the NASBA assay (Organon Teknika Corp., Cambridge, UK) with an LOD of 4000 copies/mL¹⁵ up to September 1998, and by the NucliSens assay (Organon Teknika Corp.) with an LOD of 400 copies/mL through March 1999 and 80 copies/mL beginning in April 1999.¹⁶ Acquired immunodeficiency syndrome was defined as clinical conditions consistent with the 1993 Centers for Disease Control and Prevention case definition³⁰ but did not include the criteria of only having a CD4 cell count below 200 cells/mL.

We used MACS and WIHS data collected up to 30 September 2005 (end of semiannual visit 43 of MACS and visit 22 of WIHS). We restricted the analysis to participants who 1) initiated HAART on or after 1 July 1995 with 1 year or less between their last no HAART and first HAART use visits; 2) had an HIV RNA measurement available at their last pre-HAART visit and at least 1 post-HAART measurement; 3) did not use any antiretroviral therapy before HAART initiation; and 4) reported HAART usage for at least 80% of all post-HAART visits. Of the HIV-positive participants who were alive as of 1 July 1995 and were seen at a visit afterward, 709 of 1733 men and 1336 of 2576 women reported use of HAART after enrollment with 1 year or less between last no HAART and first HAART visit. Of these, 203 men and 315 women did not use any antiretroviral therapy before HAART initiation. Finally, 157 MACS men (contributing 1311 person-visits) and 199 WIHS women (contributing 1837 person-visits) met all eligibility criteria. The HIV RNA measurements from the visit prior to HAART initiation and all subsequent visits were used in the analysis.

STATISTICAL METHODS: A SEGMENTAL BERNOULLI/LOGNORMAL RANDOM EFFECTS MODEL WITH LEFT CENSORING

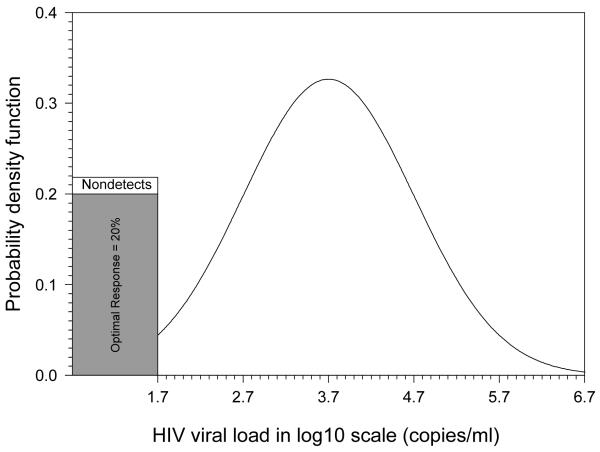
The classic longitudinal model for the analysis of progression of biomarkers in HIV-infected individuals is the linear mixed-effects model.³¹ However, longitudinal studies of viral load are complicated by left censoring of the measures due to values below detection limits³² and the possible existence of mixture distributions, especially in the era of HAART.^18,33 To model adequately longitudinal HIV viral load measures, which have a high proportion of values below the LOD, a Bernoulli/lognormal random effects mixture model with left censoring was used.²³ This Bernoulli/lognormal mixture model assumes that there exists a lower component with extremely low plasma viral load levels (ie, < 1 copy/mL or approximately equal to 0 copy/mL), representing those with fully suppressed or optimal virologic response. For those with suboptimal virologic response, the HIV viral load values are assumed to be lognormally distributed because the log transformation has often been used to stabilize variances when modeling the longitudinal HIV viral load data.^18,33,34 Figure 1 illustrates the probability density function for a cross-sectional Bernoulli/lognormal mixture model with 20% being optimal suppression for HIV viral load in log10 scale.³⁵ For those with suboptimal suppression, it is log10-normally distributed as lognormal (3.7, 1) corresponding to a median of HIV RNA = 5000 copies/mL. When the LOD is 50 copies/mL (or 1.7 copies/mL in log10 scale), 2.3% of those with suboptimal suppression (ie, 80% × 2.3% = 1.8% of all observations) cannot be detected and thus are indistinguishable from the 20% observations with true optimal suppression.

Figure 1.

An illustration of Bernoulli/lognormal model.

An illustration of a mixture distribution

Let P_ij be the Bernoulli probability of having an optimal suppression for the i^th subject at the j^th time point after HAART initiation for the i^th individual measured at time t_ij, i =1, …, N, and j = 1, …, n_i, where t_ij is the time lag between time of HAART initiation and HIV viral load measurement, N represents the number of individuals, and n_i represents the total number of HIV viral load measurements collected for the i^th individual. Let the random variable Y_ij denote the log₁₀-transformed HIV viral load conditional on the individual having a suboptimal suppression. We extended the Bernoulli/lognormal random effects mixture model²³ allowing for up to 2 change points to separate the possible acute, intermediate, and long-term effects of HAART on HIV viral load. Specifically, the probability of having optimal suppression (ie, P_ij, the Bernoulli part) is modeled by a random effects logistic regression model with 3 pieces as

$$\text{logit}\left(P_{\mathit{ij}}\right)={\alpha }_0+{\alpha }_1{\left(t_{\mathit{ij}}-{\mathit{CP}}_{1a}\right)}^{-}+{\alpha }_2{\left(t_{\mathit{ij}}-{\mathit{CP}}_{1a}\right)}^{+}+{\alpha }_3{\left(t_{\mathit{ij}}-{\mathit{CP}}_{2a}\right)}^{+}+a_i,$$

where CP_1a and CP_2a denote the unknown change points between acute and intermediate, and intermediate and long-term effects for the probability of having optimal suppression, respectively; (t_ij–CP_1a)⁻ equals t_ij–CP_1a if t_ij<CP_1a and equals zero if t_ij≥CP_1a; (t_ij–CP_ia)⁺ equals zero if t_ij≤CP_ia and equals t_ij–CP_ia if t_ij>CP_ia (i=1, 2). The parameter α₀ can be interpreted as the expected log odds of the probability of optimal suppression at the change point CP_1a; α₁, α₂ and α₂+α₃ represent the log odds ratio of annual acute, intermediate, and long-term changes of the probability of optimal suppression, respectively. A similar 3-piece linear regression model for the values of suboptimal suppression (ie, the lognormal part because Y_ij is the log10-transformed viral load) takes the form of

$$Y_{\mathit{ij}}={\mu }_{\mathit{ij}}+{\epsilon }_{\mathit{ij}}={\beta }_0+{\beta }_1{\left(t_{\mathit{ij}}-{\mathit{CP}}_{1b}\right)}^{-}+{\beta }_2{\left(t_{\mathit{ij}}-{\mathit{CP}}_{1b}\right)}^{+}+{\beta }_3{\left(t_{\mathit{ij}}-{\mathit{CP}}_{2b}\right)}^{+}+b_i+{\epsilon }_{\mathit{ij}},$$

where ε_ij represents the random error in the model prediction for the i^th individual at the j^th time point. The structure of the random error ε_ij is assumed to be independently and identically distributed as Gaussian N(0, σ²). The parameter β₀ can be interpreted as the estimated log10 HIV viral load at change point CP_1b; 10^β₁, 10^β₂, and 10^β₂+β₃ represent the annual acute, intermediate, and long-term relative (proportional) rate of changes in HIV viral load with suboptimal suppression, respectively. The random effects are assumed to be joint bivariate normally distributed as $\left(\begin{array}{c}\hfill a_i\hfill \\ \hfill b_i\hfill \end{array}\right)~N\left[\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}\right),\left(\begin{array}{cc}\hfill {\sigma }_a^2\hfill & \hfill \rho {\sigma }_a{\sigma }_b\hfill \\ \hfill \rho {\sigma }_a{\sigma }_b\hfill & \hfill {\sigma }_b^2\hfill \end{array}\right)\right]$. In general, the change points for the logistic and the linear models are allowed to be different (ie, CP_1a≠ CP_1b and CP_2a≠ CP_2b). However, for ease of interpretation, it might be more logical to assume CP_1a=CP_1b=CP₁ and CP_2a=CP_2b=CP₂ in practice.

Given the random effects, the likelihood function for the segmental Bernoulli/lognormal random effects model with left censoring is as follows,

$$L(\mathbf{Y};\theta )=\prod _{i=1}^N\prod _{j=1}^{n_i}{\left\{P_{\mathit{ij}}+\left(1-P_{\mathit{ij}}\right)\Phi \left[(D_{\mathit{ij}}-{\mu }_{\mathit{ij}})∕\sigma \right]\right\}}^{1-{\delta }_{\mathit{ij}}}{\left\{{\sigma }^{-1}\left(1-P_{\mathit{ij}}\right)\phi \left[(Y_{\mathit{ij}}-{\mu }_{\mathit{ij}})∕\sigma \right]\right\}}^{{\delta }_{\mathit{ij}}},$$

where D_ij denotes the assay detection limits for the i^th individual measured at time t_ij on log10 scale, δ_ij denotes whether the assay measurement is below detection limits D_ij, φ(·) and Φ(·) are the standard Gaussian probability density function and cumulative distribution function, respectively. In the absence of fully suppressed or optimal suppression to HAART (ie, the observations with values below LOD can be subsumed by the left tail of a continuous distribution, or equivalently P_ij=0), the likelihood of left censored model becomes

$$L(\mathbf{Y};\theta )=\prod _{i=1}^N\prod _{j=1}^{n_i}{\left\{\Phi \left[(D_{\mathit{ij}}-{\mu }_{\mathit{ij}})∕\sigma \right]\right\}}^{1-{\delta }_{\mathit{ij}}}{\left\{{\sigma }^{-1}\phi \left[(Y_{\mathit{ij}}-{\mu }_{\mathit{ij}})∕\sigma \right]\right\}}^{{\delta }_{\mathit{ij}}}\cdot$$

In the previous models, we, as others,²³ assumed conditional independence given random effects a_i and b_i. In the presence of residual correlation (ie, ε_ij s are not independent), the conditional independence can often be relaxed by allowing an appropriate, more general residual covariance structure Σ_i for the vector ε_i of subject-specific error components for the linear regression model.³¹ We considered the simple but often-reasonable residual covariance structure of Σ_i=σ²I_ni where I_ni denotes the identity matrix of dimension n_i.

The SAS version 9 was used for all analyses (SAS Institute Inc, Cary, NC). Specifically, we used the NLMIXED procedure to obtain maximum likelihood estimates. The NLMIXED procedure is able to compute general functions of estimated parameters with standard errors computed using the delta method. The finite sample corrected Akaike Information Criterion (AIC),³⁶ provided from SAS NLMIXED output as a measure of goodness-of-fit (ie, the smaller the AIC, the better the fit.), was used to compare the mixture model with the left-censored model and to select the number of change points. The AIC is computed as $-2\times \mathcal{l}\left(\widehat{\theta }\right)+2\mathit{np}∕(n-p-1)$, where l(·) is the marginal log likelihood, $\widehat{\theta }$ denotes the vector of maximum likelihood parameter estimates, n is the number of observations, and p is the number of parameters. The SAS code is available on request from the first author. To obtain the population average estimates for the probabilities of optimal suppression at each time point after HAART initiation, numerical integration over the estimated distributions of random effects was implemented.³⁷

RESULTS

eTable 1 (available with the electronic version of this manuscript) presents descriptive statistics at HAART initiation according to cohort. The 157 men had a median number of 6 longitudinal HIV RNA measurements with a median of 2.8 post-HAART follow-up years. Among men, 127 (81%) were Caucasian, 21 (13%) African American, and 8 (5%) Latino. Among the 199 women, the median number of longitudinal HIV RNA measurements was 8 with a median of 3.2 post-HAART follow-up years. Among women, 8 (4%) were Caucasian, 120 (60%) African American, and 70 (35%) Latina. The mean calendar years at which HAART was initiated were 2002.4 and 2000.5 for the MACS and WIHS, respectively, reflecting that a considerable amount of MACS men were recruited during 2001–2003 when the study expanded. Compared with women in the WIHS, men in the MACS were about 2 years older, had 20–30 more CD4 cells/mm³, and had higher HIV RNA levels at the visit within 6 months before HAART initiation. Fewer men had a history of an opportunistic infection or malignancy diagnostic of AIDS³⁰ prior to HAART. All-cause mortality during the follow-up was about 5% and 10% for the MACS and WIHS participants, respectively.

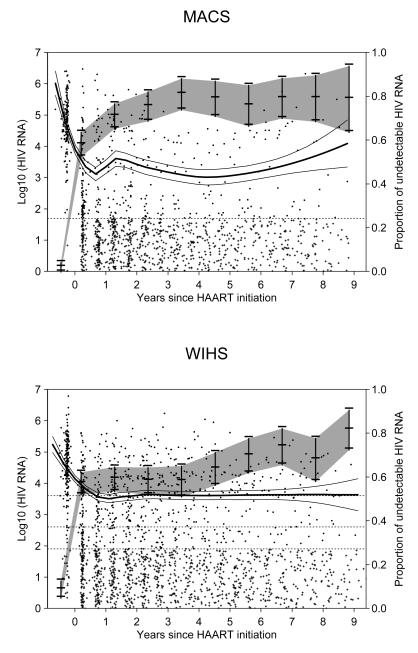
Figure 2 presents longitudinal measurements of HIV RNA in log10 scale for the 157 men in the MACS (upper panels) and the 199 women in the WIHS (lower panels), including the pre-HAART baseline viral load values. For the purpose of demonstrating the high proportions of left censoring, those measurements with values below LOD have been randomly assigned a value from a uniform distribution between 1 copy/mL and LOD; in the model fitting, however, they were treated as left-censored values. Specifically, 827 of 1311 (63%) MACS measurements were below LOD (50 copies/mL); 1034 of the 1837 (56%) WIHS measurements were below LOD, including 1015 with LOD = 80 copies/mL, 17 with LOD = 400 copies/mL, and 2 with LOD = 4000 copies/mL. The vertical bars in gray-shaded area represent the observed annual proportions of HIV RNA measures below LOD with its point-wise 95% confidence interval (CI). The solid line represents the nonparametric LOWESS smoothed curves for those with detectable values. It suggests that after a significant, rapid decrease within a half-year post-HAART initiation, HIV RNA appears subsequently to stabilize or only gradually increase on the population level.

Figure 2.

Longitudinal measurements of HIV RNA (in log10 scale) for the MACS (upper panels) and the WIHS (lower panels). For the purpose of demonstrating the high proportions of left censoring, those measurements with values below LOD have been randomly assigned a value from a uniform distribution between 1 copy/mL and LOD, and plotted with symbols “+”. Those measurements with detected values were plotted using symbols “•”. The vertical bars in the gray-shaded area represent the observed annual proportions of HIV RNA measures below LOD with its point-wise 95% CI. The solid line represents the nonparametric smoothed LOWESS curves for those with detectable values. The dashed line represents lower detections limits (ie, LOD = 50 copies/mL for the MACS; and LOD = 4000, 400, and 80 copies/mL for the WIHS depending on the calendar time of measurements).

eTables 2 and 3 summarize the maximum likelihood estimates and the goodness-of-fit for the MACS and WIHS under the assumption CP_1a=CP_1b and CP_2a=CP_2b=CP₂, respectively. We fitted 6 models to the data, that is, the random effects left-censored model (I) and the random effects mixture model (II) with a) no change point, b) 1, and c) 2 change points, respectively. Twice the negative value of log-likelihood and the finite sample corrected AIC were used to measure the goodness-of-fit. The mixture models provided a significantly better fit than the left-censored models, suggesting the existence of optimal and suboptimal suppression to HAART. A mixture model with 2 change points provided the best fit for the MACS, whereas a mixture model with 1 change point provided the best fit for the WIHS. However, the differences in the goodness-of-fit for a mixture model with 1 change point compared with a mixture model with 2 change points was relatively small for both the MACS and the WIHS, suggesting similar response to HAART for the MACS men and the WIHS women.

Based on the model with best fit in eTables 2 and 3, at the first change point, that is, about 3 months (0.30 years for MACS and 0.22 years for WIHS) following HAART initiation, HIV viral loads were fully suppressed for 44% (95% CI = 39%–49%) of men and 43% (38%–47%) of women, whereas the other 56% of men and 57% of women had on average 2.1 (1.5–2.6) and 3.0 (2.7–3.2) log10 copies/mL respectively. The proportion of men with fully suppressed viral loads increased with an annual odds ratio (OR) of 2.16 (CI = 0.84–5.53) between 3 months and 3 years following HAART initiation, and slightly increased after 3 years with annual OR of 1.11 (0.88–1.41), whereas for women, the proportion with fully suppressed HIV RNA increased with an annual OR of 1.49 (1.33–1.68) from 3 months after HAART initiation. However, the mean log10 viral loads among those not fully suppressed remained stable for men (annual increase of 0.08 log10 copies/mL with 95% CI = −0.23 to 0.38 between 3 months and 3 years, and 0.17 log10 copies/mL with CI = −0.10 to 0.44 after 3 years from HAART initiation) and slightly increased for women starting at 3 months following HAART initiation (annual increase of 0.09 log10 copies/mL with CI = 0.05–0.13).

For sensitivity analyses, we also fit mixture models allowing different change points for the logistic and linear models (ie, CP_1a≠CP_1b and CP_2a≠CP_2b). Although those models slightly improved the goodness-of-fit compared with their counterparts (results not shown), the statistical inferences were similar to the mixture models assuming equal change points for the logistic and linear models (ie, CP_1a=CP_1b=CP₁ and CP_2a=CP_2b=CP₂) for both men and women. Furthermore, to test whether our models are sensitive to LOD and to test whether the observed differences between men and women in eTables 2 and 3 were due to the differences in the LOD, we artificially increased the detection limit to 80 copies/mL for the MACS, and left censored those 52 MACS measurements (4.0%) with viral load values of more than 50 copies/mL but less than or equal to 80 copies/mL and refitted those models. The point estimates and their standard errors were very similar to those reported in eTable 2 (results not shown) with similar conclusions.

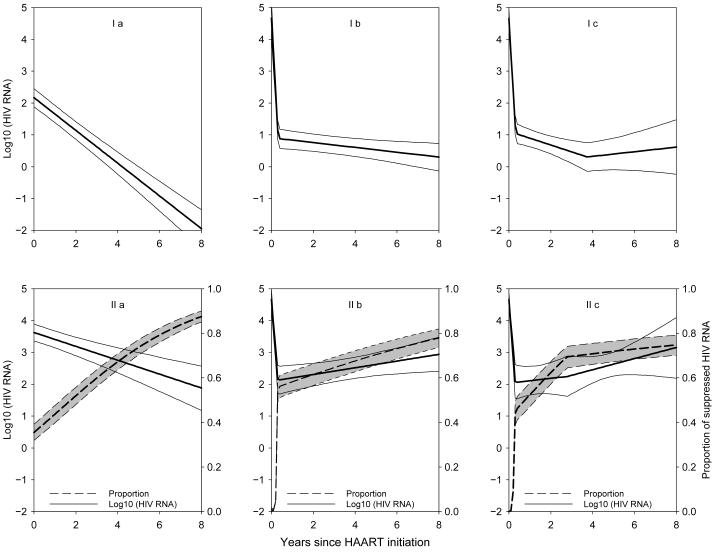
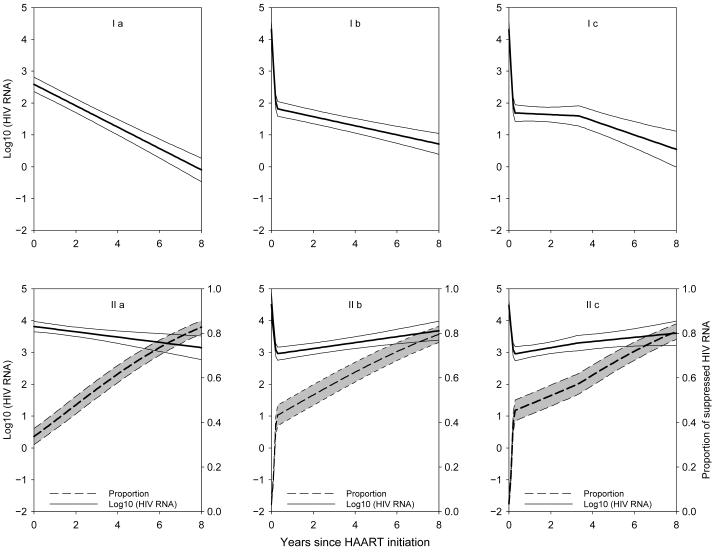
Figures 3 and 4 present the predicted trajectories for men and women, respectively, based on the parameter estimates in the different models of eTables 2 and 3 up to 8 years after HAART initiation. The dramatic differences in the predicted trajectories yielding differing information for public health emphasize the need of carefully selecting a good model to reflect the HIV RNA longitudinal patterns. For example, based on the model that fit the MACS data best (ie, a mixture model with 2 change points, Model IIc), after 8 years on HAART, although the majority (ie, 75%) of men had optimal suppression, 25% were suboptimal responders with a median HIV RNA of 3.1 log10 copies/mL. Yet based on the left-censored model with no change points, one would conclude that after 8 years the median of HIV RNA is less than 1 copy/mL (ie, 0.01 copy/mL) which, although not inconsistent with Model IIc, does not capture the finding that a substantial portion (25%) of men still had very high levels of HIV RNA. Surprisingly, even though a different model had the best fit for women (ie, a mixture Model IIb with 1 change point), after 8 years on HAART, 80% of women had optimal suppression, and 20% had suboptimal suppression with a median HIV RNA of 3.7 log10 copies/mL.

Figure 3.

Predicted trajectory for the MACS based on the parameter estimates in eTable 2. Models Ia, Ib, Ic, IIa, IIb, and IIc correspond to the left-censored model (I) and the mixture model (II) respectively, with a) no change point, b) 1, and c) 2 change points, respectively. Dashed lines represent the estimated proportions of fully suppressed viral load, and solid lines represent the population averaged trajectory for those incompletely suppressed.

Figure 4.

Predicted trajectory for the WIHS based on the parameter estimates in eTable 3. Models Ia, Ib, Ic, IIa, IIb, and IIc correspond to the left-censored model (I) and the mixture model (II) respectively, with a) no change point, b) 1, and c) 2 change points, respectively. Dashed lines represent the estimated proportions of optimal or fully suppressed viral load, and solid lines represent the population averaged trajectory for those incompletely suppressed.

DISCUSSION

The longitudinal data for antiretroviral therapy–naïve men and women who subsequently initiated and continuously used HAART (reported use in at least 80% of biannual visits following initiation), allowed us to model the average HIV RNA changes up to 8 years after initiation of HAART. Specifically, our study focused on how to model longitudinal HIV RNA data that have high proportions of left-censored observations, and how the inferences would differ based on different models. In summary, the data suggest that when modeling longitudinal HIV RNA data following HAART initiation, it may be better to use a segmental Bernoulli/lognormal random effects model to reflect trajectory changes (ie, acute, intermediate, and long-term effects) and the existence of optimal and suboptimal suppression. Based on the models with best fit, after 8 years on HAART, although the 75% of men and 80% of women (who survived and continued to use HAART regularly) had optimal suppression, but there were 25% of men and 20% of women who had suboptimal suppression with a median HIV RNA of 3.1 and 3.7 log10 copies/mL, respectively. Despite the differences between the MACS and WIHS cohorts and slightly different models used to fit the data, it is interesting that these long-term estimates of proportions with optimal suppression and level of HIV RNA among suboptimal responders are very similar.

In this article, we did not consider subject-specific change points, which may be more attractive, for 2 reasons: 1) it is technically difficult to implement subject-specific change points in this setting, that is, it is not directly implementable using SAS NLMIXED; and 2) it requires a relatively large number of data points per subject. For example, Chu et al.¹⁶ used a Bayesian approach requiring 2 data points before and after the subject-specific change points to model the longitudinal CD4 trajectories in the absence of detection limits and mixture distribution and were only able to consider 1 change point per subject. Here we are interested in the population level change points and considered 2 change points corresponding to acute and intermediate effects.

Although the Bernoulli/lognormal mixture model can be easily extended to handle baseline covariates without significant difficulty, given the relatively small study sample sizes (ie, 157 men and 199 women), and the very high percentages of HIV RNA below detection limits as shown in Figure 2, we did not consider potential baseline factors associated with the heterogeneity of patterns, which may include pre-HAART CD4 cell counts, age at HAART initiation, and host genotype. Furthermore, due to the same reasons and the potential difficulty of including time-dependent covariates in the model, we did not consider the effect of different types of HAART, and the effect of switching or interrupting HAART. Further research along the lines, such as by adjusting baseline and time-dependent confounding factors and compliance, may shed additional light on the effects of HAART on HIV RNA trajectory.

Caution is necessary when comparing the WIHS and MACS cohorts because they differ in several characteristics in addition to sex. In the MACS, 81% were Caucasian compared with only 8% Caucasian in the WIHS and the 2 cohorts have other substantially different sociodemographic characteristics. Furthermore, only 5.7% of the participants in MACS compared with 32.7% of the those in WIHS had clinical AIDS before HAART initiation. Generalizations to the current era in which individuals are encouraged to go directly from no treatment to HAART may also be limited because the MACS men and WIHS women in this study may not be representative of the HIV-infected men and women in the current population due to recent changes in sociodemographic characteristics and other factors within the HIV-infected populations. As a technical note, in the presence of left censoring due to the LODs, the models are locally identified, that is, the choice of a Bernoulli/lognormal random effects model results in identification. However, different results may be found with a different parametric distribution.