The Delicate Bistability of CaMKII

Abstract

Calcium/calmodulin-dependent protein kinase II (CaMKII) is a synaptic, autophosphorylating kinase that is essential for learning and memory. Previous models have suggested that CaMKII functions as a bistable switch that could be the molecular correlate of long-term memory, but experiments have failed to validate these predictions. These models involved significant approximations to overcome the combinatorial complexity inherent in a multisubunit, multistate system. Here, we develop a stochastic particle-based model of CaMKII activation and dynamics that overcomes combinatorial complexity without significant approximations. We report four major findings. First, the CaMKII model system is never bistable at resting calcium concentrations, which suggests that CaMKII activity does not function as the biochemical switch underlying long-term memory. Second, the steady-state activation curves are either laserlike or steplike. Both are characterized by a well-defined threshold for activation, which suggests that thresholding is a robust feature of this system. Third, transiently activated CaMKII can maintain its activity over the time course of many experiments, and such slow deactivation may account for the few reports of bistability in the literature. And fourth, under in vivo conditions, increases in phosphatase activity can increase CaMKII activity. This is a surprising and counterintuitive effect, as dephosphorylation is generally associated with CaMKII deactivation.

Introduction

The processes of learning and memory require long-term changes in the neural network to assimilate and store new information (1). At the cellular level, these changes are thought to include the formation, elimination, and modification of synapses, all of which fall under the general category of synaptic plasticity (2–4). Two of the most well studied examples of synaptic plasticity are long-term potentiation (LTP), a persistent increase in the efficacy of synaptic transmission (5), and its converse, long-term depression (LTD), a persistent decrease in the efficacy of synaptic transmission (6). At the molecular level, LTP is usually characterized by an increase in the size of dendritic spines (7) and an increase in the number of synaptic AMPA receptors (AMPARs) (8), whereas LTD is usually characterized by the opposite changes. LTP and LTD are controlled by a vast signaling network whose functional properties are still being elucidated (9). In particular, it is at present unknown which signaling molecule(s) undergoes permanent changes leading to the persistent changes in spine size and synaptic AMPAR numbers.

Several possible molecular mechanisms have been proposed to account for the permanent changes at the synapse, including changes in local transcription rates, changes in kinase/phosphatase activities, changes in the organization of scaffolding proteins, and changes in the localization/aggregation of certain proteins (10,11). The common requirement for any molecular correlate of long-term memory is that it must be stable in the presence of protein turnover (12), because protein turnover times are on the order of seconds to a few weeks, whereas long-term memories can last for a lifetime. A leading candidate for a permanent molecular switch that is stable to protein turnover is a system composed of an autophosphorylating kinase coupled to a phosphatase (13). Under certain conditions, such a system can form a bistable switch, where at basal conditions states of low and high kinase activity are both stable, and the current activity state depends on the history of the system (13).

Calcium/calmodulin-dependent protein kinase II (CaMKII) is an autophosphorylating kinase (14,15) that constitutes up to 2% of total protein in certain regions of the brain and is highly enriched at synapses (16). CaMKII is activated by calcium-saturated calmodulin (CaM) (17), and once activated, it can autophosphorylate at T286 (18). Once phosphorylated at this site, CaMKII is autonomously active, that is, active even in the absence of Ca²⁺/CaM (19). This site can be dephosphorylated by several synaptically localized protein phosphatases, including PP1 and PP2A (20). This CaMKII-phosphatase system satisfies the minimum requirements of the autophosphorylating kinase-phosphatase system described above, and it is therefore possible that a bistable CaMKII switch forms the molecular basis of synaptic plasticity and long-term memory (21).

Indeed, there is strong evidence that CaMKII plays a central role in synaptic plasticity and memory. CaMKII activation is necessary (22,23) and sufficient (24,25) for hippocampal NMDAR-dependent LTP, and CaMKII knockout (26–28) and knockdown (29) mice show severe deficits in several learning tasks. Phosphorylation of T286 is significantly increased after LTP induction (30–33), and CaMKII autonomy is required for LTP induction (34,35) and normal learning and memory (36). However, investigations of persistent autonomous activity during LTP have given mixed results. Early studies showed a sustained increase in autonomous activity after LTP induction (37,38) and suggested that LTP maintenance requires autonomous activity (39,40). More recent work showed that although LTP induction indeed generates persistent T286 phosphorylation, it only transiently increases CaMKII autonomy (41), which suggests the involvement of additional deactivation mechanisms. In addition, many groups have shown that autonomy is required for LTP induction but not LTP maintenance (42–45). An in vitro study of the CaMKII-PP1 system found no evidence of bistability (46), but it is possible that the authors did not use large enough CaMKII concentrations to observe potential bistability.

The synaptic activity of CaMKII is regulated by a large biochemical signaling network with contributions from both calcium and cAMP pathways (9), and several groups have studied this network using computational models of varying complexity (47,48). In many cases, the models show that CaMKII activity is bistable at the basal state under a wide range of kinetic parameters and model assumptions (49–53). Although the models differ, a common requirement for bistability is that the phosphatase operate at saturation. In the postsynaptic density (PSD), the concentration of CaMKII subunits is 100–200 μM, whereas the Michaelis-Menten constants of the relevant phosphatases are on the order of 10 μM (46). Phosphatases should be saturated in such a situation, and thus the most important theoretical requirement for bistability is satisfied at the synapse.

Given the prevailing experimental evidence, it is reasonable to question the model predictions of robust bistability. In fact, modeling of CaMKII is difficult because of the combinatorial complexity that arises from its multisubunit holoenzyme structure (54), and most published models involve severe approximations that may invalidate their results. Here, we develop a detailed model of CaMKII activation that includes several physiologically relevant states not usually included in other models. We implement this model using particle-based, stochastic, network-free simulations that overcome combinatorial complexity and allow for an exact study of the system properties. Our major finding is that bistability is possible but physiologically irrelevant because it occurs over just a narrow range of calcium concentrations that are much higher than basal calcium levels. At low phosphatase concentrations, CaMKII activates through a laser transition, which differs from a more conventional Hill-type activation curve in that activity is nearly zero below a threshold, and above that threshold, the activity turns on in a linear fashion. Although the system is not bistable at basal conditions, autonomous activity decays very slowly after the system returns to resting calcium levels. Under physiological conditions, the decay times are on the order of several hours, which may account for the conflicting reports of in vivo bistability. Finally, we show that basal levels of inhibitory phosphorylation can greatly diminish the amount of autonomous activity generated by stimulation protocols and can change the function of phosphatases from CaMKII inhibitors to CaMKII activators.

Model

Calmodulin activation

Calmodulin (CaM) is a relatively small, dumb-bell-shaped calcium-binding protein that can bind four calcium ions, two at its N-lobe and two at its C-lobe (55). The lobes act independently of one another, but calcium binding at each lobe is a highly cooperative process (56–58). Models that take this lobe structure into account are required to study CaM dynamics over very short timescales (59,60), but for our purposes it is sufficient (61) to ignore the lobe structure and assume that CaM binds four calcium ions in a sequential manner. The five states of CaM are denoted CaM_i, i = 0,…,4, where i indicates the number of bound calcium ions. The calcium binding kinetics are extremely fast, with some of the largest on and off rates ever measured (62), and we therefore assume that the calcium-binding reactions are in rapid equilibrium. This assumption is valid for all of the simulations presented here except for the LTP protocols discussed below, where we consider Ca²⁺ pulses at 100 Hz. In these cases, our assumption will tend to overestimate the amount of calcium-saturated CaM, but in that section our main focus will be on the kinetics of deactivation, which occurs on very long timescales where again the rapid equilibrium assumption is valid.

Using the fact that CaM is buffered in all of the situations studied here, we have

$$\begin{array}{l}{\text{CaM}}_0={\text{CaM}}_{\text{tot}}{\left(1+\frac{\text{Ca}}{K_0}+\frac{{\text{Ca}}^2}{K_0{K}_1}+\frac{{\text{Ca}}^3}{K_0{K}_1{K}_2}+\frac{{\text{Ca}}^4}{K_0{K}_1{K}_2{K}_3}\right)}^{-1},\hfill \\ {\text{CaM}}_i=\left(\frac{\text{Ca}}{K_{i-1}}\right){\text{CaM}}_{i-1},i=1,\dots ,4\hfill \end{array}$$ (1)

where Ca is the free Ca²⁺ concentration (assumed buffered), K_i is the dissociation constant for the reaction ${\text{CaM}}_i+{\text{Ca}}^{2+}\rightleftharpoons {\text{CaM}}_{i+1}$, and ${\text{CaM}}_{\text{tot}}=\sum {\text{CaM}}_i$ is the total, buffered concentration of cytosolic calmodulin (that is, not bound to CaMKII). The K_i values used here are listed in Table S1 in the Supporting Material.

CaMKII structure and states

A single CaMKII subunit is composed of an association domain, a linker region, a regulatory domain, and a kinase domain (63), as depicted in Fig. 1 A. CaMKII subunits cluster together through their association domains to form a 12-subunit holoenzyme, shown schematically in Fig. 1 B, with the association domains forming a central hub and the kinase domains protruding in a gear shape (64–66). In its initial inactive form, D_uu, the CaMKII subunit is autoinhibited because the regulatory domain blocks the ATP and substrate binding sites on the kinase domain (67). An active form, C_u, is generated when fully saturated CaM (CaM₄) binds to and displaces the regulatory domain, which exposes the ATP and substrate sites (67). This also exposes T286 in the regulatory domain, which can be phosphorylated by a neighboring active subunit (68–70), giving state C_p. Phosphorylation of T286 prevents the regulatory domain from fully inhibiting the kinase domain, even in the absence of Ca²⁺/CaM and thus generates a Ca²⁺-independent (autonomous) subunit, D_pu, whose activity is usually 20–80% of CaM-stimulated activity (71). Dissociation of CaM exposes T305/T306, which can be autophosphorylated through an intrasubunit reaction (69). Phosphorylation at these sites prevents CaM binding and locks the subunit in a partially active state, D_pp (72,73). In addition, the initial autoinhibited subunit can undergo a Ca²⁺-independent basal autophosphorylation on T305/T306 (74). The resulting state, D_up, must be dephosphorylated before activation by CaM, and we will refer to this state as the doubly inhibited state. Basal autophosphorylation is very slow in vitro (74) but may be accelerated by some scaffolding proteins in vivo (75). For simplicity, in our model we treat the double phosphorylation event on T305/T306 as a single event on T305.

Figure 1.

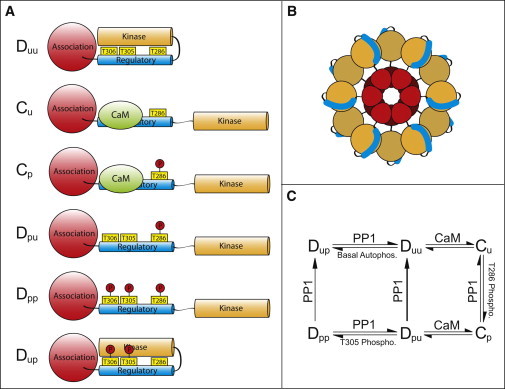
Model states and reactions. (A) A CaMKII subunit can exist in one of six states depending on CaM binding and phosphorylation at several sites. The six states are as follows: D_uu, autoinhibited; C_u, CaM-bound, unphosphorylated; C_p, CaM-bound, phosphorylated on T286; D_pu, phosphorylated on T286; D_pp, phosphorylated on T286, T305, and T306; and D_uu, phosphorylated on T305 and T306. States D_uu and D_up are inactive; the other states have varying activity levels. (B) A schematic view of the dodecameric CaMKII holoenzyme. Association domains are shown in red, regulatory domains in blue, and kinase domains in orange. (C) Reaction diagram describing conversion between the six states of CaMKII. See the text for details.

CaMKII reactions

Fig. 1 C shows a schematic representation of the CaMKII reaction diagram. The reactions can be loosely grouped into three categories.

Calmodulin binding

Although partially saturated CaM can bind to CaMKII, it only weakly stimulates kinase activity compared to fully saturated CaM (76,77). Thus, we only allow fully saturated CaM (CaM₄) to bind to and activate CaMKII. In Pepke et al. (60), it was shown that this assumption overestimates the amount of CaMKII activation on short timescales compared to models that allow binding by partially saturated CaM. The timescales considered here are long enough so that our assumption is valid, except during the rapid calcium pulses considered during LTP and LTD protocols. However, as mentioned above, our primary interest in these cases is the kinetics of CaMKII deactivation, which occurs over timescales long enough for our assumption to be valid.

CaM binding kinetics strongly depend on the phosphorylation state of T286 (78,79). We therefore introduce two on rates, k_on,u and k_on,p, to describe binding to the unphosphorylated and phosphorylated T286 species, respectively. We allow CaM dissociation to proceed through one of two pathways: either CaM₄ directly dissociates from CaMKII, or CaM loses two Ca²⁺ and then rapidly dissociates as CaM₂. As we do not include states with partially saturated CaM bound to CaMKII, this second dissociation pathway is described by a calcium-dependent off rate for CaM₄. The full CaM dissociation rate is given by

$$k_{\text{off},i}=k_{\text{off},i}^{\left(1\right)}+\frac{k_{\text{off},i}^{\left(2\right)}}{1+{\left(\text{Ca}/K_{\text{Ca},i}\right)}^2},$$ (2)

where i = u or i = p, depending on the phosphorylation state of T286, $k_{\text{off},i}^{\left(1\right)}$ is the dissociation rate of fully saturated CaM, $k_{\text{off},i}^{\left(2\right)}$ is the maximal effective dissociation rate for the Ca²⁺-dependent dissociation pathway, and K_Ca,i is the calcium concentration giving the half-maximal calcium-dependent dissociation rate. The values for the CaM-CaMKII binding rates are listed in Table S1.

Recent experimental evidence suggests that CaMKII subunits in the holoenzyme pair up through their regulatory domains (80,81) and that this interaction leads to positive cooperativity in CaM binding (82). It is difficult to reconcile this evidence of positive cooperativity with previous studies that showed no cooperativity in CaM binding (83,46). Therefore, we have not included such an interaction in the model considered in the main text. In the Supporting Material, we do consider a model with cooperative CaM binding and compare it to the results shown below for the noncooperative model. We find that cooperative CaM binding has a negligible effect on CaMKII activation and does not change any of our major conclusions, which justifies its omission from the main model considered here. See the Supporting Material for a full description of the cooperative CaM binding mode.

Autophosphorylation

Phosphorylation of T286 is an intersubunit reaction whereby an active subunit phosphorylates a neighboring, CaM-bound subunit. We make the common assumption (61,84) that phosphorylation proceeds in a unidirectional manner around the holoenzyme. Autophosphorylation is a first-order reaction that may occur at different rates depending on the state of the kinase subunit (the substrate subunit is always C_u) (84). We therefore introduce four autophosphorylation rates depending on the state of the kinase subunit: r₁ for C_u, r₂ for C_p, r₃ for D_pu, and r₄ for D_pp. Based on activities toward exogenous substrates, we assume that r₂ = r₁ (85), r₃ = 0.8r₁ (83), and r₄ = r₃ (73). This leaves r₁ as the only free autophosphorylation rate.

Phosphorylation of T305 is an intrasubunit reaction that can occur in one of two first-order reactions. The autoinhibited subunit can directly phosphorylate T305 with a slow basal rate, r_b. Alternatively, the autonomously active subunit, D_pu, rapidly phosphorylates T305 with a rate r₃₀₅. The values for all autophosphorylation rates are listed in Table S1.

Dephosphorylation

The phosphatases PP1 and PP2A dephosphorylate T286 and T305 in vivo, with most PP1 activity in the PSD and most PP2A activity in the cytosol (20). Here, we will use PP1 to denote all phosphatase activity. Dephosphorylation proceeds through a standard irreversible Michaelis-Menten reaction with reaction flux

$$J_{X,\text{PP}1}=\frac{n_X{k}_c\text{PP}{1}_{\text{act}}X}{K_m+{\Sigma }_P},$$ (3)

where X is the species being dephosphorylated, n_X is the number of phosphorylated residues on X, k_c is the catalytic rate constant, K_m is the Michaelis-Menten constant, PP1_act is the concentration of active PP1, and Σ_p = C_p + D_pu + D_up + 2D_pp is the total concentration of phosphorylated residues. We assume that PP1 has equal activity toward T286 and T305 (same k_c and K_m), and we assume that there is no preference for the order in which these residues are dephosphorylated. Parameter values are listed in Table S2.

PP1 regulation

PP1 is deactivated by binding to phosphorylated inhibitor-1 (I1) (86,87). I1 is dephosphorylated by the phosphatase calcineurin (CaN) (86), whose activity is regulated by calcium and calcium-bound CaM (88). I1 is phosphorylated by protein kinase A (PKA) (86), whose activity is stimulated by cAMP (89). As the levels of cAMP are controlled (at least partially) by CaM-activated adenylyl cyclases (90,91) and CaM-activated phosphodiesterases (92), the activity of PKA can be treated as a function of CaM. A schematic diagram of this regulatory network is shown in Fig. S1. Following the methods of Zhabotinsky (51) and Graupner and Brunel (52), we assume that CaN and PKA are in rapid equilibrium with CaM and write their activities as Hill functions:

$$\begin{array}{c}{V}_{\text{CaN}}=k_{\text{CaN}}^{\left(0\right)}+\frac{k_{\text{CaN}}{\left({\text{CaM}}_4/K_{\text{CaN}}\right)}^{n_{\text{CaN}}}}{1+{\left({\text{CaM}}_4/K_{\text{CaN}}\right)}^{n_{\text{CaN}}}},\\ V_{\text{PKA}}=k_{\text{PKA}}^{\left(0\right)}+\frac{k_{\text{PKA}}{\left({\text{CaM}}_4/K_{\text{PKA}}\right)}^{n_{\text{PKA}}}}{1+{\left({\text{CaM}}_4/K_{\text{PKA}}\right)}^{n_{\text{PKA}}}},\end{array}$$ (4)

where $k_{\text{CaN}}^{\left(0\right)}$ is the basal activity of CaN, k_CaN is the maximum CaM-stimulated CaN activity, K_CaN is the CaM₄ concentration at half-maximal CaN activity, and n_CaN is the Hill exponent. The symbols with subscript PKA have the same meanings but apply to PKA activity.

Although the concentration of active PP1 is a function of calcium, it is not necessary to include this dependence when studying the steady-state activation of CaMKII. As pointed out in Graupner and Brunel (52), it is sufficient to determine steady-state activation as a function of calcium for various concentrations of PP1 and then combine these curves to make a phase diagram depicting CaMKII activity as a function of calcium and PP1. Assuming a specific functional form for steady-state active PP1 as a function of calcium then picks out a particular curve in this phase diagram.

For studies of the system dynamics the calcium dependence of PP1 activity must be included in the simulation because both active PP1 and I1 are dynamic variables. The concentrations of these evolve according to

$$\begin{array}{l}\frac{d\text{I}{1}_p}{dt}=-k_{\text{on},\text{PP}1}\text{I}{1}_p{P}_{\text{act}}+k_{\text{off},\text{PP}1}{P}_{\text{inact}}-V_{\text{CaN}}\text{I}{1}_p+V_{\text{PKA}}\text{I}{1}_{\text{tot}},\hfill \\ \frac{d{P}_{\text{act}}}{dt}=-k_{\text{on},\text{PP}1}\text{I}{1}_p{P}_{\text{act}}+k_{\text{off},\text{PP}1}{P}_{\text{inact}},\hfill \end{array}$$ (5)

where I1_p is the concentration of phosphorylated I1, I1_tot is the total cytosolic concentration of unphosphorylated I1 (assumed buffered), P_act is the concentration of active PP1, P_inact is the concentration of inactive PP1, and P_tot = P_act + P_inact is the total concentration of PP1.

Modeling platforms

It is not practical to implement the model described above using conventional deterministic simulations based on ordinary differential equations, because an exact implementation of the multistate, multisubunit holoenzyme would require a network of thousands of species and reactions (54). Such combinatorial complexity can be overcome by using a particle-based stochastic simulation, an approach frequently called network-free modeling because there is no need to enumerate the entire reaction network before the simulation (93). Instead, the simulation keeps track of the exact state of each subunit in every holoenzyme, and different holoenzyme configurations arise naturally as the system evolves. Reaction probabilities are calculated for each individual subunit, and the system is updated according to Gillespie’s exact stochastic simulation algorithm (SSA) (94). We implemented the model using a custom Java program, which is described in the Supporting Material and is available upon request.

Results

Model validation

We validated the dynamic properties of the model by reproducing the experimental results of De Koninck and Schulman (83), where CaMKII activation was shown to be frequency dependent. We validated the steady-state properties of the model by reproducing the results of Bradshaw et al. (46), which explored steady-state CaMKII activation as a function of calcium and PP1. The comparisons to these two experiments are discussed in the Supporting Material and shown in Figs. S2 and S3. In both cases, the model results are in excellent qualitative and quantitative agreement with the experimental results. We conclude that the model accurately captures CaMKII dynamics and steady-state activation.

Steady-state solutions and bistability

To investigate steady-state solutions and search for regions of bistability, we began with a system with no activity (Ca²⁺ = 0 μm) and increased calcium in increments. At each increment, the system is run to steady state, and then Ca²⁺ is increased again. We continue in this manner until the system plateaus at a high steady-state activity. We then run this process in reverse, beginning with the high-activity steady state and decrementing Ca²⁺ until we again reach the system with no activity. If, for a certain Ca²⁺ level, the steady-state activity during the decrementing phase is different from that during the incrementing phase, then we conclude that the system exhibits bistability at that Ca²⁺ level. An example of this process is shown in Fig. 2 A, where we show the time course of CaMKII activity during the entire process of increasing and decreasing Ca²⁺. Fig. 2 B shows the average steady-state activity as a function of Ca²⁺ for this same simulation, with the data points color-coded to indicate the activity values as we increased and decreased calcium. Here, the system evolves to the same level of activity regardless of the direction of calcium changes, and thus we conclude that the system does not exhibit bistability for the chosen parameters.

Figure 2.

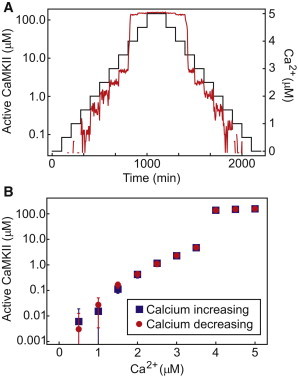
Illustrative example of the incremental calcium scan used to search for bistability. (A) A plot of the concentrations of Ca²⁺ (black) and active subunits (red) as a function of time. Here, calcium is increased in increments of 0.5 μM every 100 min, which is about twice as long as required to reach steady state under these conditions. (B) A plot of steady-state CaMKII activity as a function of Ca²⁺, as derived from the time course in A. The system equilibrates to the same activity level whether calcium is increasing or decreasing, and thus there is no evidence of bistability under these conditions.

We used the process described above to generate steady-state activity curves for several values of r₁, CaM, and PP1 (CaM_tot = 0.1, 1.0, 10.0, and 100.0 μm, r₁ = 1.0, 10.0, and 100.0 s⁻¹, and PP1 = 0.01–50.0 μm to cover a broad range that is guaranteed to contain the in vivo concentration, estimated at 0.1–1.0 μm (51)). The range of parameters was chosen to cover all relevant physiological concentrations and rates, and also samples some extreme cases. Fig. 3 shows typical steady-state activity curves obtained with 0.1 μm CaM and the slower set of phosphorylation rates (r₁ = 1 s⁻¹, etc.). Results for other combinations of CaM concentrations and autophosphorylation rates are shown in Figs. S4–S11. Each curve in Fig. 3 shows the steady-state activity as a function of calcium for different concentrations of PP1, from very low PP1 (A) to very high PP1 (L). At low PP1, there is no indication of bistability, but nor does the system respond in a simple Hill-like fashion. Instead, the activation curve resembles an imperfect transcritical bifurcation (also called a laser transition), where the activity remains very low until calcium increases above a threshold, at which point the system activity increases in a linear fashion (linearity does not continue indefinitely, because the activity must saturate). As PP1 increases, the slope of the linear activation region increases (see Fig. 3, A–D). At a critical value of PP1, the slope diverges and a gap opens between regions of low and high activity, as shown in Fig. 3 E. As PP1 is further increased, the region of high activity continues to slide backward over the region of low activity (see Fig. 3, F and G), creating a region of bistability. As PP1 continues to increase, the region of bistability shifts to higher calcium concentrations and eventually begins to narrow (Fig. 3, H and I), and the low activity curve begins to bend more sharply upward and the high-activity curve bends more sharply downward, so that the gap between high and low activity regions decreases (Fig. 3, J and K). At a second critical value of PP1, these curves touch in a cusp (infinite slope) (Fig. 3 K is very close to this threshold). As PP1 continues to increase, the cusp is softened and the region of high activity occurs only at very high calcium concentrations. (In Fig. 3 J, high activity occurs only at much higher calcium concentrations than are shown. See, for example, Fig. S5, J–L, for plots with a softened cusp.)

Figure 3.

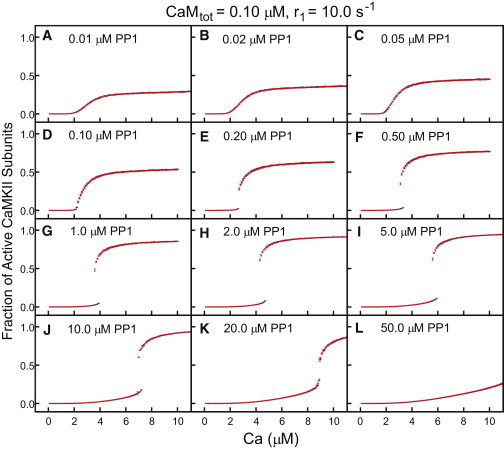
CaMKII activation curves. CaMKII activity is plotted as a function of Ca²⁺ for various concentrations of PP1, as labeled in the figures. As in Fig. 2B, activity levels at increasing Ca²⁺ increments are shown in blue and those at decreasing Ca²⁺ increments are shown in red. Regions of bistability are easily identified by blue points at the edge of the lower activity curve. The interesting features and notable trends are discussed in the text. The simulations used standard parameters and 200 μM CaMKII.

This general trend is observed in all of our simulations. Changes in CaM or the phosphorylation rates do not affect the overall qualitative behavior but do affect the values of specific features like the initial slope above threshold in the transcritical bifurcation and the width and location of the bistable region. For one parameter set, 10 μM CaM and r₀ = 1 s⁻¹ (Fig. S7), a region of bistability was not observed, but it may be that in this case the width of the bistable region is smaller than the calcium increment.

Two important features should be noted: 1), the width of the bistable region is narrow (relative to the calcium concentrations at which it occurs); and 2), the bistable region never extends down to include the basal calcium concentration. The location of the bistable region is shifted to lower calcium as CaM and r₁ increase, but even at the highest, nonphysiological values investigated here, bistability required Ca²⁺ > 0.5 μM (see Fig. S11, G and H). Kinase activity always remains low at resting calcium, and there is no way for this system to act as a memory switch. The narrowness of the bistable regions suggests that bistability will be difficult to observe in vitro. Experimental data would likely show steplike behavior with very high Hill coefficients.

The location of the activation thresholds and narrow bistable regions depends most strongly on the autophosphorylation rates and on the binding affinities between calcium and CaM. Experimental estimates of the autophosphorylation rates vary by about an order of magnitude, from 1 s⁻¹ to about 30 s⁻¹, and we had already varied these parameters. On the other hand, the calcium-CaM binding affinities are well determined under a variety of experimental conditions (57) and we treated these as fixed parameters. Nevertheless, it was of interest to determine the affinities required to produce bistable regions at basal calcium levels. To do so, we rescaled all four calcium-CaM dissociation constants by the same factor, K_i → K_i/β, such that affinity increases with increasing β. We chose other parameters to provide the greatest chance of shifting the activity curves to lower thresholds: r₁ = 100 s⁻¹ (three times the largest estimate) and CaM_tot = 10 μM (large but plausible) or 100 μM (extreme). Figs. S12–S15 show a sample of the activation curves with β = 2 and 5. We found that activation thresholds scaled nearly linearly with β. For example, with CaM_tot = 100 μM and PP1 = 2 μM, a tiny region of bistability occurs at 0.6 μM Ca²⁺ for β = 1 (Fig. S11 H), and is shifted to about 0.3 μM and about 0.13 μM for β = 2 (Fig. S14 H) and β = 5 (Fig. S15 H), respectively. However, the qualitative features of the activation curves did not change. It is important to note that regions of bistability remained very narrow and were frequently narrowed further or lost altogether (for example, compare Figs. S11 G and S14 G). Thus, even if calcium-CaM affinities are increased dramatically in vivo, this model predicts that no physiologically useful region of bistability will emerge.

In Fig. 4, we assemble the individual curves from Fig. 3 to form a phase diagram of CaMKII activity as a function of Ca²⁺ and PP1. The regions of bistability are too small to be of any interest on this scale, and we have made no attempt to show them in the phase diagram. Phase diagrams for the other five combinations of CaM and r₁ are shown in Fig. S16. The phase plot reveals an interesting and unexpected feature of this model; at high calcium concentrations and low to intermediate PP1 concentrations, increases in PP1 increase the total kinase activity of the system. It is generally assumed that increasing PP1 will reduce activity, because it will reduce the concentration of the autonomous state. Our model tracks the concentration of each CaMKII state, and we can therefore examine these curves to investigate the source of this surprising feature.

Figure 4.

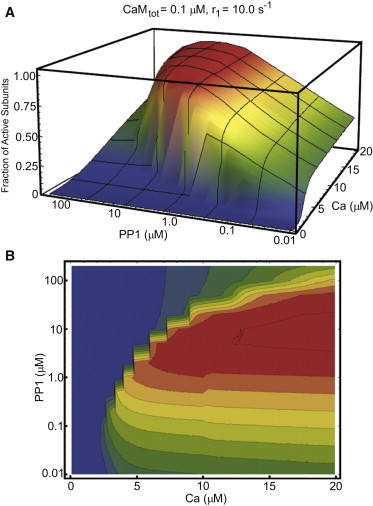
CaMKII activation phase diagram. (A) The curves shown in Fig. 3 are assembled into a single phase diagram showing CaMKII activity as a function of Ca²⁺ and PP1. (B) The phase diagram is shown as a contour plot.

In Fig. 5, we plot the concentration of all six subunit states along with the concentration of active subunits as a function of PP1 at a fixed, high calcium concentration of 19.8 μM. At low PP1, the dominant species is D_up, the doubly inactive state that must be dephosphorylated before it can be activated by CaM. Increasing PP1 converts more subunits to the unphosphorylated autoinhibited state, which can be directly activated by CaM. Thus, in this regime, PP1 aids in CaMKII activation by increasing the concentration of subunits available for CaM activation. Physiological PP1 concentrations are estimated to be in the 0.1- to 1.0-μM range, and therefore, this effect might be important in vivo. The demonstration of such an effect would be missed by less detailed models.

Figure 5.

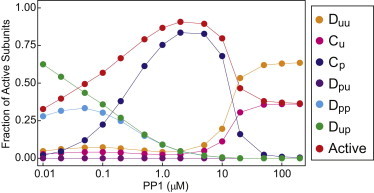
Detailed subunit distribution. The fraction of subunits in each state is plotted as a function of PP1 at high Ca²⁺ concentration, along with the fraction of active subunits. At low PP1, the dominant species are the doubly inhibited D_up and the autonomously active D_pp. At intermediate PP1, most subunits are CaM-bound and phosphorylated at T286. At very high PP1, all phosphorylation is suppressed and all subunits are either in the autoinhibited D_uu or the activated C_u state.

In the Supporting Material, we present results for a model with cooperative CaM binding to CaMKII, a mechanism suggested by some recent experimental results (82). There we show that the effects of cooperativity are negligible in the sense that cooperative CaM binding does not allow for any new qualitative behavior and does not shift activation thresholds or bistable regions down to basal calcium levels. This result is not surprising because the main model already contains strong cooperativity in calcium binding to CaM and in autophosphorylation of T286, so that a third additional source of cooperativity is unlikely to significantly alter the activation curves. See the Supporting Material for more details.

Dynamic behavior and response to stimuli

In this section, we examine the dynamic response of the system using typical in vivo concentrations and system parameters: CaMKII_tot = 200 μM, CaM_tot = 5 μM, r₁ = 1 s⁻¹, and other parameters as listed in Tables S1 and S2. The CaM concentration used here is lower than that typically measured in vivo, but we use this lower value because our model does not include other CaM-binding proteins that significantly reduce the amount of CaM available for CaMKII activation. We varied I1 and PP1 to cover a range of in vivo estimates: 0, 0.01, and 0.1 μM $\text{I}{1}_{\text{tot}}$; 0.05, 0.1, 0.2, 0.5, and 1.0 μM $\text{PP}{1}_{\text{tot}}$. We used two different stimulation protocols, an LTP protocol consisting of high-amplitude, high-frequency stimulation (10 μM, 5 ms Ca²⁺ pulses at 100 Hz for 1 s), and an LTD protocol consisting of lower-amplitude, low-frequency stimulation (2 μM, 200 ms Ca²⁺ pulses at 1 Hz for 10 min). As discussed in the Model section, our assumptions of rapid equilibrium between Ca²⁺ and CaM break down on these fast timescales, as does the assumption that only fully saturated CaM can activate CaMKII. The activation curves shown here therefore overestimate the amount of CaMKII activation, but the qualitative features will be the same. Moreover, as shown below, the timescales of deactivation are slow enough for our model assumptions to be valid, and we can therefore make both qualitative and quantitative statements about the kinetics of deactivation.

Typically, stimulation protocols are modeled with initial conditions such that all CaMKII is in the autoinhibited state, D_uu (51). We hypothesized that applying these protocols to a system already in steady state would produce a significantly attenuated response because of the large concentration of doubly inhibited subunits. Thus, for all simulations, we applied the stimulation protocol twice: all simulations begin with 100% D_uu, and the stimulation protocol is applied. After the stimulation protocol, calcium is returned to basal levels and the system is allowed to relax to its basal steady state. Once steady state is achieved, the stimulation protocol is applied a second time and the time evolution of the system is followed until the system again relaxes back to its basal steady state.

Fig. 6 shows illustrative examples of the CaMKII activity produced by these protocols. In Fig. 6 A, the LTD protocol is applied to the system with 0.1 μM $\text{I}{1}_{\text{tot}}$ and 1.0 μM $\text{PP}{1}_{\text{tot}}$. This generates low levels of CaMKII activity, and the activity of CaMKII simply oscillates at the same frequency of the stimulation. The response to the second stimulation is nearly identical to the response to the first stimulation, because steady-state PP1 activity is high enough to keep only a negligible fraction of subunits in the doubly inhibited state. In Fig. 6 B, the LTD protocol is applied to a system with 0 μM $\text{I}{1}_{\text{tot}}$ and 0.05 μM $\text{PP}{1}_{\text{tot}}$ Here, CaMKII activity slowly but steadily increases with each pulse, and the activity does not plateau during the stimulation protocol. This system has lower PP1 activity, and here it is easy to see the effect of T305 phosphorylation on the second stimulation. CaMKII activity increases at a much slower rate, because dephosphorylation must occur before CaMKII activation, and this greatly reduces the total amount of activation. In Fig. 6 C, the LTP protocol is applied to the same system in Fig. 6 B, and this shows a typical response to the LTP protocol. CaMKII activity rapidly increases and then begins to plateau. As in Fig. 6 B, inhibitory T305 phosphorylation significantly reduces the amount of activity generated in response to the second stimulation.

Figure 6.

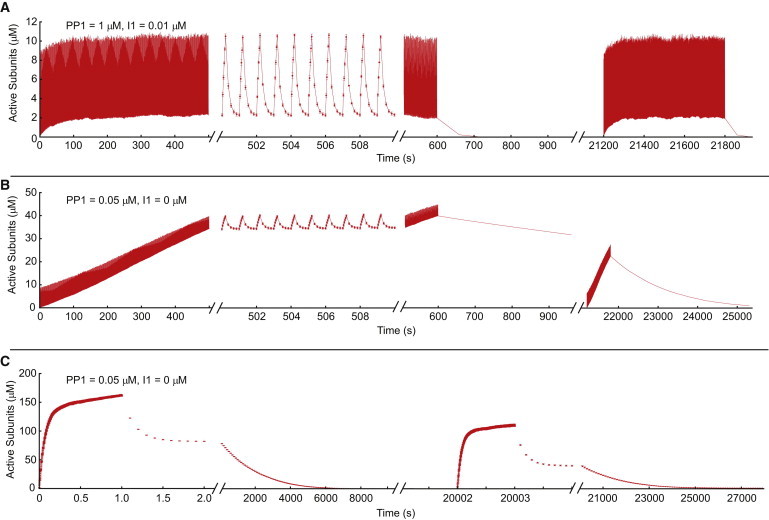
Response to LTP and LTD protocols. In each figure, the system begins with all subunits in the D_uu state, and the first stimulation protocol is applied at t = 0. After the first stimulation protocol, the system is allowed to relax to its steady state at basal calcium. We then apply a second stimulation protocol (identical to the first), after which the system is again allowed to relax to steady state. The axes are cut to highlight various sections of interest. (A) LTD protocol. In this case, CaMKII activity oscillates in time with the stimulation and there is no significant accumulation of active subunits. The first and second stimuli produce identical responses. (B) LTD protocol. In this case, CaMKII activity slowly accumulates with each pulse, and does not plateau during the time course of the stimulation. The response to the second stimulus is significantly attenuated, because a significant fraction of subunits are doubly inhibited in the steady state. (C) LTP protocol. CaMKII is rapidly activated and then plateaus. Activity decays in a biexponential manner with a very fast and a very slow time constant, as discussed in the text. The response to the second stimulus is attenuated, as in B. See the text for more details.

It is obvious from Fig. 6 C that CaMKII activity decays with two timescales: the first represents calmodulin rapidly dissociating from CaMKII after the stimuli, whereas the second represents the slow decrease in autonomous activity due to the action of PP1. To characterize this decay we fit it to a double exponential,

$$\text{Activity}\left(t\right)=a_1{e}^{-\left(t-t^{\ast }\right)/{\tau }_1}+a_2{e}^{-\left(t-t^{\ast }\right)/{\tau }_2},$$ (6)

where t^∗ is the time the last calcium pulse finishes and τ₁ and τ₂ characterize the fast and slow decay times, respectively. By requiring that τ₂ > τ₁, we can interpret $\left(a_1+a_2\right)$ as the total CaMKII activity generated by the stimulation, and a₂ as the total autonomy generated by the stimulation.

We used this fit to characterize the result of the LTP stimulation as the concentrations of PP1 and I1 were varied. In Fig. 7, we show the dependence of the fitted parameters as a function of PP1 for I1 = 0.01 μM. Additional examples are shown in Fig. S17. Several trends are evident. First, a₁, τ₁, and a₂ are independent of PP1 for the first pulse. This makes sense, as all of the simulations begin with the same initial conditions and the first pulse occurs on a timescale too short to be affected by PP1. Second, the time constant for the decay of autonomous activity is a highly nonlinear function of PP1, increasing dramatically as PP1 decreases. At 0.05 μM PP1, autonomous activity decays with a time constant of ∼2 h.

Figure 7.

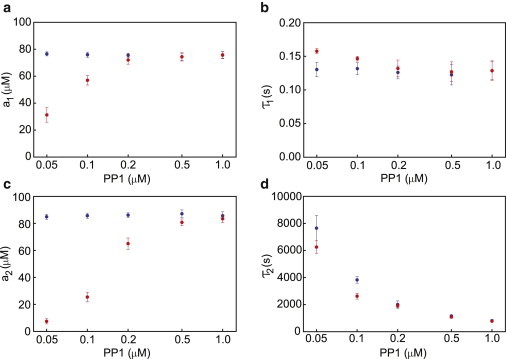
Characterization of response to LTP protocols. The decay of CaMKII activity after LTP stimulation was fit to a double exponential, and the fitted parameters are plotted as functions of PP1. The response to the first stimulation is shown in blue and the response to the second stimulation in red. (a) a₁ gives the concentration of active subunits that are CaM-bound but not phosphorylated, i.e., the nonautonomous portion of CaMKII activity. (b) τ₁ is the fast decay time, which is controlled by the dissociation of CaM from nonautonomous subunits. (c) a₂ gives the concentration of autonomous CaMKII generated in response to the stimulation protocol. (d) τ₂ characterizes the slow decay time for the loss of autonomous activity due to dephosphorylation.

For the second pulse (applied after steady state is reached), both the total activity and the amount of autonomous activity are significantly reduced at low PP1 concentrations. This reflects the fact that a significant fraction of the subunits are in the doubly inhibited D_up state at low PP1, and must be dephosphorylated before they can be activated by CaM. The fast and slow time constants are no different than during the first pulse, which is expected because τ₁ characterizes the dissociation of CaM and is not affected by phosphorylation, whereas τ₂ characterizes total PP1 activity, which is also unaffected by the initial phosphorylation state of the holoenzymes.

The simulations discussed above considered synaptic activation in the absence of background noise, and it is worthwhile to investigate the effects of noise on the system dynamics. In vivo, the largest source of noise is likely to be transient calcium fluctuations due to basal synaptic firing rates, which occur at ∼1 Hz. A single synaptic activation produces postsynaptic calcium transients in the range 0.3–1.3 μM (95–97), although the duration of such transients in the spine is only 10–20 ms (97). We have repeated the LTP protocol in the presence of noise with a range of amplitudes and frequencies (0.1–2 Hz), and found that its effects were minimal. At the largest amplitudes and frequencies, spontaneous calcium transients could increase the deactivation time constant by about 10–20%, which is insignificant given uncertainties in other parameters, and in most cases spontaneous calcium transients produced no noticeable changes.

Discussion

We have investigated the dynamic and steady-state properties of a detailed model of CaMKII by using a network-free simulation scheme, which allowed us to study the system without making the severe approximations that have characterized previous modeling efforts. We were particularly interested to determine whether bistability, a major feature of coarse-grained models, would still be present in a more detailed simulation. We found that our model produces regions of bistability, but for any reasonable choice of parameters bistability only occurs at calcium concentrations much higher than basal calcium levels, and then only over a relatively narrow calcium range. Because bistability does not occur at basal calcium levels, our model suggests that bistability is not a physiologically relevant feature of the CaMKII system, and therefore, despite its theoretical appeal, the CaMKII-PP1 system does not function as the bistable biochemical switch underlying synaptic plasticity and memory.

We reached this conclusion after sampling the parameter space over both physiological and extreme cases. Nevertheless, the full parameter space is too large to sample entirely, and it is possible that parameters could be found that would give broad regions of bistability at basal calcium levels. Furthermore, although we have included CaMKII phosphorylation sites known to affect kinase activity and/or CaM binding, there are several other phosphorylation sites whose functional role is unknown. It is possible that other CaMKII states would change the conclusions of this study, and the model may need to be revised as more biochemical details become known. Ultimately, careful experimental investigations will be required to reach a definitive conclusion on the existence and/or role of CaMKII bistability.

Our model predicts that CaMKII activity is not a simple Hill-like function of calcium for any physiologically reasonable choice of parameters. Rather, for low PP1, CaMKII activity turns on in a laser transition, whereas for higher PP1, CaMKII activity turns on abruptly just past the narrow region of bistability. Both types of activation curves are characterized by a threshold calcium level below which there is almost no activity. A sharp activation threshold is therefore a robust feature of our model, and it is interesting to speculate on the advantage of this characteristic as opposed to the robust bistability that emerged from other models. In a bistable system, there is a threshold stimulation required to drive the system to its high-activity state, but thereafter, all information about the threshold is lost and the system is insensitive to the characteristics of additional stimuli. With laserlike or steplike activity curves, activation always requires an above-threshold stimulus. A bistable system has a built-in frequency dependence because repetitive subsaturating (but above threshold) stimuli can drive the system to a high-activity state, provided the activating stimuli are fast enough to prevent the system from fully relaxing to the low-activity state between stimuli. The laserlike and steplike activation curves possess the same type of frequency dependence but are able to discriminate between a larger range of frequencies, because they are not automatically driven to a permanently active state once a critical activity level is attained. The frequency response at a specific synapse could be tuned by changing PP1 activity, which controls the decay rate to the low-activity state.

Our model included inhibitory autophosphorylation on T305, a feature that has been omitted in previous studies of bistability (but has been included in some models investigating very-short-time in vitro dynamics (84)). We found that this phosphorylation site dramatically changes the steady-state activity levels of CaMKII. In particular, at low-to-intermediate PP1 concentrations, the effect of T305 phosphorylation is to make CaMKII activity an increasing function of PP1 concentration. This was a surprising discovery, because PP1 deactivates autonomous activity, and is thus usually associated with reduced CaMKII activity. However, at low PP1, a significant fraction of subunits are phosphorylated on T305 in the steady state, and these subunits must be dephosphorylated before they can undergo CaM-mediated activation. Increasing PP1 therefore increases the fraction of subunits available for CaM binding, and increases the overall activity level of the system. It is only at very high PP1 that increasing PP1 decreases total activity.

It is conventional to characterize the system response to different LTP protocols under different conditions by the probability of switching to the highly active state (51). Such a characterization is impossible here, because our system does not exhibit bistability at basal calcium levels. In fact, the main differences between different stimulation protocols are in the rate at which CaMKII is activated and the maximum activity level attained. For example, there is no fundamental difference between LTP and LTD protocols in this model; LTD protocols are simply characterized by a slower increase in CaMKII activity and a lower overall activity level compared to LTP protocols. As with the steady-state activity, we find that inhibitory phosphorylation at T305 has a significant effect on the dynamic response of the system. The total activity level achieved during a stimulation protocol is significantly reduced if the system begins in the basal steady state instead of with all subunits in the nonphosphorylated autoinhibited state. It takes time for the stimulation to dephosphorylate doubly inhibited subunits to make those subunits available for CaM binding, and this delay is sufficient to reduce the total activity achieved.

Basal inhibitory autophosphorylation on T305 is usually omitted in models, because the basal phosphorylation rate is extremely slow, r_b = 5 × 10⁻⁴ s⁻¹ in vitro (74). Thus, it is questionable whether the effects discussed above are relevant in vivo, where basal phosphatase activity might be sufficient to keep inhibitory autophosphorylation at negligible levels. However, the total fraction of phospho-T305 at resting levels is much higher than would be predicted by the slow measured in vitro phosphorylation rate (98), which suggests that basal autophosphorylation is accelerated by some undetermined mechanism. One potential mechanism is binding to the scaffold protein CASK, which has been shown to increase T305 phosphorylation 40-fold (75).

A significant feature of our model is the extremely slow PP1-mediated deactivation reaction. The decay from a highly active transient state to the resting level at basal calcium can take hours to days under relevant in vivo conditions. Most experiments that investigate in vivo bistability only track CaMKII activity for about an hour after stimulation protocols (37), and the longest experiment we are aware of only followed CaMKII activity for 8 h after stimulation (33). Our model suggests that a transiently active state could maintain autonomy over such timescales and may be interpreted as permanently elevated CaMKII activity. This observation suggests that the conflicting reports of CaMKII bistability may reflect the fact that transient activity could last for the duration of the experiment under typical conditions.

During LTP induction, CaMKII translocates to the PSD (99,100) by binding to NMDARs and other scaffold proteins (101,102). The CaMKII-NMDAR interaction is known to alter several important reaction rates (103), for example, decreasing the T286 dephosphorylation rate (104), and NMDAR-binding generates autonomous activity even without T286 phosphorylation (105). Our model does not include NMDAR binding, and we are therefore not able to investigate the effects of this important in vivo interaction. It is possible that NMDAR interactions could generate bistable kinase activity at basal calcium levels, but we feel that this is unlikely. The major effect of NMDAR binding appears to be on the rate of dephosphorylation, which could have an effect on the qualitative aspects of the activation curve but would not shift the region of bistability to low calcium concentrations. Note that this only applies to bistability in CaMKII kinase activity. The CaMKII-NMDAR interaction is required for LTP maintenance (106), which suggests that CaMKII may play a structural role in synaptic plasticity.

In conclusion, our detailed model strongly suggests that CaMKII kinase activity is not the bistable molecular correlate to long-term memory. It also shows that the often overlooked inhibitory autophosphorylation on T305 can alter the system response to PP1 in such a way that PP1 actually increases CaMKII activity. Finally, the model suggests that previous observations of in vivo bistability were in fact observations of extremely long-lived transient states of high activity.