Pressure and Temperature Dependence of Growth and Morphology of Escherichia coli: Experiments and Stochastic Model

Abstract

We have investigated the growth of Escherichia coli, a mesophilic bacterium, as a function of pressure (P) and temperature (T). Escherichia coli can grow and divide in a wide range of pressure (1–400 atm) and temperature (23–40°C). For T > 30°C, the doubling time of E. coli increases exponentially with pressure and exhibits a departure from exponential behavior at pressures between 250 and 400 atm for all the temperatures studied in our experiments. The sharp change in doubling time is followed by a sharp change in phenotypic transition of E. coli at high pressures where bacterial cells switch to an elongating cell type. We propose a model that this phenotypic change in bacteria at high pressures is an irreversible stochastic process, whereas the switching probability to elongating cell type increases with increasing pressure. The model fits well the experimental data. We discuss our experimental results in the light of structural and thus functional changes in proteins and membranes.

Introduction

A vast majority of bacteria and archaea can grow in diverse environmental conditions. Those conditions include high pressures (1,2), high temperature (3), low temperature (4), high salinity, low pH (5), and high pH (6,7). Because these conditions are not hospitable for other life forms, these organisms have been named extremophiles (1,3,8–12). One of the first isolated extremophiles was Thermus aquaticus, thermophilic bacteria that can survive at near-boiling temperatures (3). Adaptation of these organisms to such harsh conditions raises many interesting questions, such as how do they adapt to these conditions? Does the adaptation occur at a single-component level such as by mutations in proteins leading to their barostability and thermostability, or does the adaptation to these conditions have a collective nature, in which more than one cellular component acts in compliance to preserve the functionality of the other?

Recent studies on the taxonomy, ecology, and enzymology of these microorganisms have provided insights into the adaptation of these organisms to their environmental conditions (9,13,14). For example, the bacterial cytoplasmic membrane must maintain its liquid-crystalline structure and semipermeability with changing conditions (15). It was shown that bacterial membranes adapt to the temperature changes by changing their lipid composition (16). Adaptation of a protein to nonambient conditions requires that it maintains its catalytic activity as well as its structure (17,18). Most globular proteins denature at high as well as low temperatures. Moreover, even if a protein does not denature at low temperature, small thermal fluctuations will lead to decreased catalytic activity at low temperatures (19,20). In fact, in one study on proteins from psychrophilic organisms, it was found that proteins are more flexible (21). However, increase of flexibility also leads to high propensity of unfolding of the protein. Hence, a fine balance between the structural flexibility and stability is required (22). Recent comparative study of an essential recombination protein RecA from mesophilic and thermophilic bacteria suggests that its function of binding to single-stranded DNA is adapted to the conditions in which organisms grow (23). A study of SSB, a single-stranded DNA binding protein from mesophilic and piezophilic bacteria, shows a similar adaptation (24).

While there is a large body of work on the stability and kinetics of proteins and adaptation of different components of prokaryotes obtained from extremophiles, the growth of bacteria is only approached using conventional methods such as plate counting (25). Such studies have provided killing curves of saturated bacterial solutions upon increasing pressures, and hence a pressure-temperature phase diagram of the bacterial survival is obtained (26).

To understand the adaptation of bacterial cells to extreme pressure and temperature, it is important to have knowledge of growth bottlenecks and physical changes induced by different thermodynamic conditions on bacteria that thrive at ambient pressure and temperature. In this article, we study the pressure-temperature dependence of growth and phenotypic changes of a mesophilic bacterium, E. coli, using an optical method that allows us to measure the growth of bacteria in real-time at different pressures and temperatures. We have investigated the growth and morphological changes in a wide range of pressure and temperature. In Methods, we describe our experimental setup and protocol to measure the growth of bacteria. In Results, we summarize the results of the pressure-temperature dependence on growth followed by a stochastic model to account for the morphological changes induced by high pressure, and conclude with the Discussion.

Methods

Experimental Setup

Measurement of growth at normal conditions is rather easy, as there are many commercial photometers available. High pressure and temperature require that photometer optics are built around a high-pressure cell to obtain the growth curve. Below we describe our experimental setup to measure the growth.

Bacteria absorb and scatter light with an intensity that depends on the scattering angle and absorption coefficient (27). Most commonly used for measuring bacterial concentration in a solution is the turbidity method, in which the extinction of light is measured at a fixed angle, usually in the forward direction. The method relies on many assumptions, including:

1. Each bacterial cell is an independent scatterer;

2. The shape of bacterial cell is uniform; and

3. Multiple scattering of the light is negligible.

The extinction cross-section C_ext is a sum of cross-section attributable to scattering C_sca and absorption C_abs, and can be written as

$$C_{\text{ext}}=C_{\text{sca}}+C_{\text{abs}}.$$ (1)

Then the coefficient of extinction α is

$$\alpha =\rho C_{\text{ext}},$$ (2)

where ρ is the number density of bacterial cells. The intensity I_t, detected by a light detector after the incident light traverses a distance x in the scattering medium, is given by

$$I_t=I_0{e}^{-\alpha x},$$ (3)

where I₀ is the intensity of the light incident on the medium. Hence, the difference of the logarithm of the intensities of incident and the transmitted light is proportional to the concentration of scatterers in the medium. The optical density (OD) of the medium is defined as

$$OD=log\left(\frac{I_0}{I_t}\right).$$ (4)

A schematic of our experimental setup to measure the pressure-temperature dependence of growth is shown in Fig. 1. A sample of bacteria with Luria Broth (LB) medium (as in Bertani (28)) is contained in a rectangular cuvette (volume: 400 μL; Spectrocell, Oreland, PA) made up of fused silica and having a square cross-section (6 × 6 mm). The cuvette with a flexible movable cap made of Teflon (E. I. DuPont de Nemours, Paris, France) is loaded into the high-pressure cell (ISS, Champaign, IL). A piston is used to pressurize the water inside the pressure cell, with the pressure measured by a pressure gauge. The growth of the bacteria is measured in real-time by shining a white light (Xenon lamp), which passes through an excitation bandpass filter (FF01-586/15-25; Semrock, Rochester, NY) and is focused onto the cuvette holding the sample. We chose light with a 586-nm wavelength to keep our measurements consistent with measurements done with most of the commercially available photometers.

Figure 1.

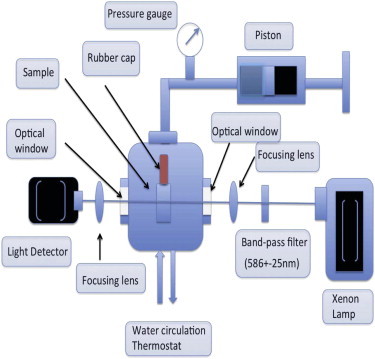
Schematic of the experimental setup to measure bacterial growth.

The transmitted light is focused on a light detector on the other side of the cuvette, which measures the intensity of the transmitted light. The light detector is built around a photosensor chip, model No. TSL230R (TAOS, AMS, Yeolmbridge, Launceston, Cornwall, UK). The TSL230R photosensor consists of a silicon photodiode with a current-to-frequency converter built into it. The nonlinearity error is typically 0.2% at 100 kHz. The frequency of the transistor-transistor logic signal from the detector proportional to the incident light intensity is measured using an AT-MIO-16 frequency counter chip interfaced to the software LABVIEW (both by National Instruments, Austin, TX). We maintain the intensity of the light source such that all our experiments fall into the linear regime of the sensor. The distance between the light sensor and the cuvette was 10 cm. Distance between the detector and the sample dictates the angular integration of the scattered light incident on the sensor. The temperature of the high-pressure cell is regulated using a circular water-bath thermostat. The time for growth measurement ranged between 200 and 1000 min, depending on the pressure-temperature-dependent growth rate of bacteria. The entirely closed structure of our experimental setup imposes a major limitation on the regulation of oxygen in our experiments. The growth measurements were done in oxygen-limited conditions. The partial pressure of oxygen in LB medium was 20 kPa.

Cell Culture and Growth Medium

Bacteria and media

For all the experiments reported here, the DH5α strain of E. coli was used. While other wild-type strains of E. coli such as MG1655 (K-12) or MC4100 are common for studying the physiology of bacterial cells based on lowest number of genetic mutations, DH5α offers certain advantages for our work. Earlier studies have shown that a major effect of pressure on cell morphology is the elongation of cells. The SOS response system is implicated in the change of morphology at high pressures where cell elongation occurs. The recA1 mutation in DH5α causes the elimination of the homologous recombination, an initiator process for the SOS pathway upon UV irradiation (29). Lack of RecA-mediated recombination in DHα removes the effect of pressure on the SOS pathway. Hence, our experimental results would be able to distinguish the high-pressure effects where the recombination system is not involved (see Discussion). The drawback of using DH5α is that, because it lacks the homologous recombination system, the cells are sickly and the growth is slower compared to other wild-type strains. Due to its slow growth, cells were grown in standard LB medium (28), which is a rich medium for bacterial growth. The pH of the growth medium was kept to 7 by adding NaOH to the solution. For the consistency of the experiments, cells were first grown on a LB plate for ∼10 h and then subsequently used for experiments as described below.

Growth conditions and measurements

Bacterial cells picked from LB plate were first grown in LB medium at atmospheric pressure and T = 37°C in an incubator until the OD of the solution is ∼1.0. A small amount of freshly grown bacterial cells was then added to a cuvette containing 800 μL of medium to bring the initial OD to 0.005 and was used as the starting point for all the pressure-temperature measurements. The final bacterial solution with LB medium was then transferred to a high-pressure cuvette at room temperature and pressure and was closed with a Teflon cap. The cuvette with the bacterial solution was then put into the high-pressure chamber (see the experimental setup) equilibrated at the temperature of interest and the piston of the high-pressure setup was slowly moved until the pressure-gauge reading reaches the desired value of the pressure. The growth of the bacterial cells then was assessed by measuring optical density (Eq. 4). Growth measurements were done in a sealed high-pressure cell. Images were taken using a cooled charge-coupled device camera (SensiCam, Romulus, MI) connected to an Axiovert 35 microscope (Carl Zeiss, Jena, Germany) with 40× Olympus (Melville, NY) and 100× Zeiss objectives. For visualization of DNA, we used NucBlue reagent from Life Technologies (Guilford, CT). Image analysis of bacterial cells was done using the software IMAGEJ (National Institutes of Health, Bethesda, MD) (30).

Results

Exponential dependence of double time with pressure

In Fig. 2, we show three growth curves (OD as a function of time), represented by three different symbols, obtained in our experiments at P = 1 atm and T = 37°C. The starting OD for all the growth curves is ≈0.05. The growth curves show an exponential growth regime followed by a saturation regime. The value of the saturation OD (<0.5) is smaller compared to the saturation OD (typically 1.0) reached when oxygen is not a growth-limiting agent. In the oxygen-limited environment, both the division time and saturation OD are affected.

Figure 2.

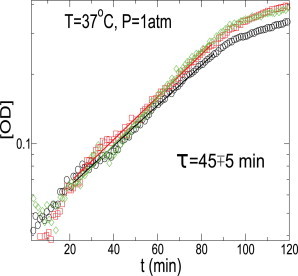
Set of three growth curves at P = 1 atm and T = 37°C. τ is the doubling time in minutes. The typical error on τ in our experiments is ∼10% of the value of τ.

The biomass of bacterial cells at time t in the exponential regime can be written as

$$m\left(t\right)=m\left(0\right)e^{t/\tau },$$ (5)

where m(0) is the biomass of bacterial cell at the beginning of the exponential phase and τ is the doubling time (which, effectively, is a measure of the timescale over which bacterial biomass is doubled). The value τ is a function of both pressure and temperature. Because focal volume is constant during the course of experiments, the OD(t) of bacterial solution at a given t in the exponential regime can be written as

$$OD\left(t\right)=OD\left(0\right)e^{t/\tau },$$ (6)

where OD(0) is the optical density at the beginning of the exponential phase. In Fig. 2, we also show exponential fits (solid lines) and the value of doubling time τ = 45 ± 5 min obtained by measuring the slope of log(OD) versus time in the exponential regime. Typical error in the measurement of τ in our experiments is ∼10% of the value of τ.

In Fig. 3, a and b, we show the growth curve for various pressures at T = 31°C and T = 34°C, respectively. We find that where the saturation is reached within the timescale of our experiments, the time profile of the growth curves show the typical characteristics of growth at P = 1 atm and T = 37°C. In Fig. 3, c and d, we show τ extracted from Fig. 3, a and b, for various pressures at T = 31°C and 34°C, respectively. We find that τ(P) increases, and hence the rate of growth decreases, upon increasing pressure. We further find that the OD corresponding to the saturation regime decreases upon increasing pressure. Earlier studies on the effect of pressure on the total biomass production of different bacteria have found a similar decrease in total mass as a function of pressure (31). The doubling time τ(P) at a given temperature increases with pressure but shows a discontinuous jump at high pressures. We find that the discontinuous jumps in τ occurs between P = 250 and 400 atm for all the temperatures studied in our experiments. To further characterize the low-pressure regime of τ, in Fig. 4, we show the doubling time τ(P) as a function of pressure for two different temperatures T = 31°C and T = 34°C on a linear-log plot. We find that the low-pressure regime of increase of doubling time with pressure can be fit by an exponential function where the exponent increases with decreasing temperature. The discontinuous change in τ(P) coincides with departure from exponential behavior.

Figure 3.

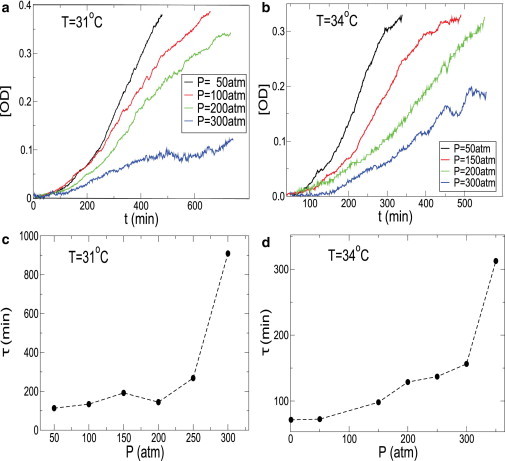
(a) Growth curves at different pressures for T = 31°C. (b) Growth curves at different pressures for T = 34°C. (c) Doubling time τ(P) extracted from Fig. 3a. (d) Doubling time τ(P) extracted from Fig. 3b. Pressure dependence of τ(P) is marked by a sharp increase at high pressures where the cells still grow, but the growth is extremely slow.

Figure 4.

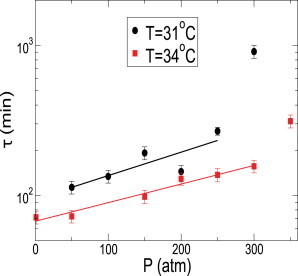
Dependence of τ(P) for two different temperatures T = 31°C (solid black circles) and T = 34°C (solid red squares) on a linear-log plot. Error bars plotted are the estimated 10% error on the values of τ (see Fig. 2 for details). The low-pressure linear dependence on a linear-log plot suggests that τ(P) follows an exponential behavior. The discontinuous jump in τ(P) at a given temperature is marked by its departure from the initial exponential behavior.

Pressure and temperature do not only affect the structural stability of biomolecules but can also affect the thermodynamic force driving different biochemical processes inside the cell. In general, the timescale of a given chemical reaction is proportional to $e^{\frac{P\Delta V}{k_{\text{B}}T}},$ where k_B is the Boltzmann constant and ΔV is the volume change across the chemical reaction. It is easy to see that any chemical reaction accompanied by a positive volume change will exponentially slow down with pressure. In this context, the exponential dependence of τ(P) with pressure (Fig. 4) is not a surprise. Note that it is a very simple consideration, as most of the biochemical processes are not individual, usually involving a cascade of chemical reactions corresponding to any cellular module. Nonetheless, the exponential dependence of the doubling time with pressure does suggest an overall positive volume change. Furthermore, ΔV itself is a function of pressure and temperature. At moderate pressures and temperature, one may assume it to be a constant. It is hard to speculate the mechanisms responsible for slow growth, and further experiments must be carried out to precisely figure out the decrease of growth rate at high pressure.

The other remarkable feature of the pressure dependence of division time is the abrupt increase of τ(P) in the range of pressures 250–400 atm for all the temperatures studied here. Where does this discontinuity in the pressure dependence of growth come from? Discontinuity in the growth as a function of pressure suggests that something abrupt must happen in this pressure range. The range of pressures where we see a discontinuous jump in the doubling time cannot be attributed to protein denaturation, because the pressure is not high enough to denature the proteins. While protein stability is relatively unaffected, the functionality of proteins may show a large variability in this range of pressures (23). We hypothesize that the discontinuous jump in the doubling time stems from functional changes in biomolecules.

Pressure-temperature phase diagram of the doubling time of E. coli

In Fig. 5, we show the surface plot of pressure-temperature dependence of τ(P,T). It shows smooth change as a function of pressure and temperature, but at high pressures as well as low temperature growth are both marked by sharp change in τ. We further find that the slope of the locus of the points in the (P,T) plane, where τ(P,T) shows sharp transition with respect to pressure, resembles the functional phase diagram of a typical protein (shown as dotted blue curve in Fig. 5) (23,24). A careful observation of the τ(P,T) data reveals that at low T, there is a region where τ exhibits a nonmonotonic behavior with pressure. In this narrow region of pressure and temperature, τ_T(P) first decreases and then increases further upon increasing pressure. The purple dotted line with dP/dT < 0 marks the boundary between this anomalous behavior and the normal behavior of increasing division time with increasing pressure. We hypothesize that this anomalous behavior of doubling time as a function of pressure results from structural transition in the phospholipids present in the cell membrane at low temperatures (32).

Figure 5.

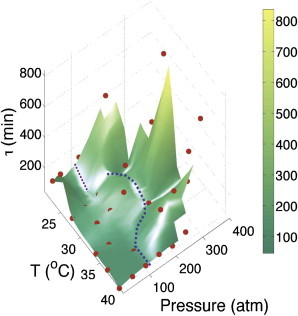
Pressure-temperature surface plot of doubling time τ(P,T). (Solid red circles) Experimental data points. (Blue dotted line) Loci of the points where τ changes abruptly. (Purple dotted line) dP/dt < 0 is the region separating anomalous pressure dependence of the doubling time. (Color bar) Value of τ in minutes.

Bacterial cell elongation, length distribution, and heterogeneities

Besides the slow growth of the population of bacterial cells at high pressures, the other interesting features of the response to high pressure are found in the morphological changes in bacterial cells (33,34). We found that bacterial cell-length exhibited large degrees of heterogeneity upon increasing pressures. Specifically, cells with lengths much larger than the typical length of bacteria at normal pressures (≈2 μm) were observed. Moreover, we find that the degrees of heterogeneity of bacterial population increases upon increasing pressure (see Fig. 6, a–f). We have also bright-field images of bacteria at P = 200 atm and T = 31°C at larger magnification (100×) (Fig. 6, g and h). A fluorescent image of an elongated bacteria at P = 200 atm and T = 31°C shows the DNA in blue color. Our experiments suggest that the cells are able to replicate DNA faithfully in the range of pressure and temperature where elongation is observed.

Figure 6.

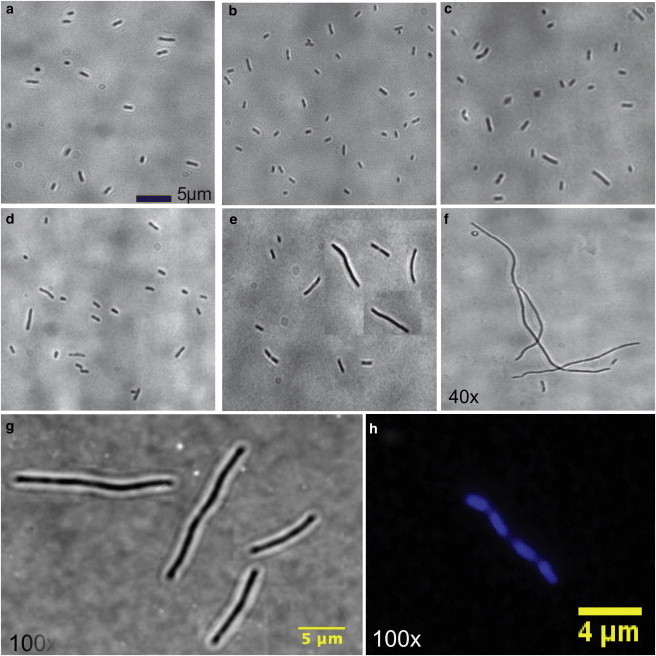
Progressive elongation of bacterial cells at different pressures for T = 31°C: (a) 1 atm, (b) 50 atm, (c) 100 atm, (d) 200 atm, (e) 250 atm, and (f) 300 atm. The images were taken and analyzed at the end of experiments for all the pressures. (g) Bright-field images of bacteria at P = 200 atm at 100× magnification, suggesting that bacteria still retain the normal morphology. (h) A fluorescent image of an elongated bacteria at P = 200 atm and T = 31°C, showing the DNA (blue). Our experiments suggest that the cells are able to replicate DNA faithfully in the range of pressure and temperature where elongation is observed.

To further characterize the bacterial elongation, we looked at the distribution of bacterial cell length at various pressures at a given temperature. Bacterial cells were grown at a given pressure and temperature for a fixed amount of time. The cells were then taken from the pressure chamber and imaged using a microscope. The images obtained in the previous steps were then analyzed in the software IMAGEJ (30). Cells were detected using the particle-search method. Cell length was assessed by measuring the surface area of the cells, which was then converted to length in microns by assuming the same diameter.

In Fig. 7, we show the distribution of bacterial cell length l at the end of our experiments for pressures P = 1, 100, 200, and 300 atm, respectively, for T = 31°C. The distribution P(l) of l at P = 1 atm follows a Gaussian distribution. As the pressure is increased, P(l) starts developing a non-Gaussian tail, suggesting growing bacterial cell-length heterogeneities. A major fraction of the cells still retain the same morphology as P = 1 atm, but there is an increase in the population of elongated cells upon increasing pressure.

Figure 7.

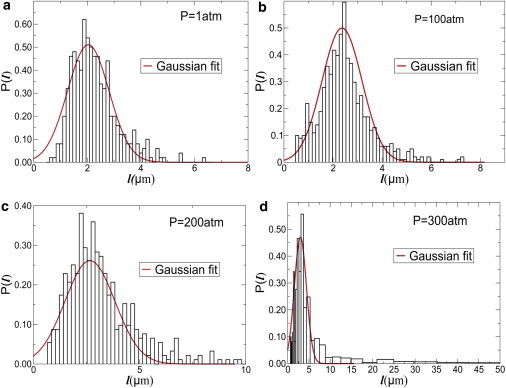
Histogram of length of bacterial cells at different pressures for T = 31°C: (a) 1 atm, (b) 100 atm, (c) 200 atm, and (d) 300 atm. Also shown are the Gaussian fits to the distribution. At high pressures, the distribution P(l) becomes increasingly non-Gaussian and develop a long tail.

The average value of the cell length 〈l〉 increases upon increasing pressure, and shows a sharp increase at the same pressure where the doubling time also shows a sharp increase (see Fig. 8). While the bacterial cell elongation at high pressure is known, the sharp transition at high pressure is new. The exponential increase of doubling time with pressure as we saw in the earlier section can be interpreted as exponential decrease of overall kinetics, leading to slow growth due to cell elongation at high pressure. While the increased cell length upon increasing pressure would explain the decreased rate of growth, it is not clear whether the elongated cells would grow more slowly than the cells with normal morphology. For example, if the elongated cells lack the ability of cell division but still replicate their genome normally, then one would expect the growth rate per unit cell size not to change unless other kinetic processes are also affected by the increase of pressure.

Figure 8.

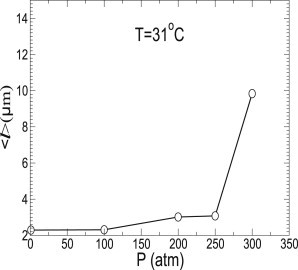
Average bacterial cell length 〈l〉 as a function of pressure at T = 31°C. Average length of bacterial cells shows a sharp transition between P = 250 and 300 atm.

The elongation of bacterial cells at high pressure has been a subject of intense research, and to our knowledge, no consensus on the molecular mechanism responsible for it has been reached (34). To account for the bacterial cell-length heterogeneities and elongation upon increased pressure, we propose a stochastic model in the next section.

A stochastic irreversible switch model for the morphological changes at high pressures

A quick overview of Figs. 6 and 7 suggests that while the average length of the bacterial cells undergoes a sharp transition at high pressures, a major fraction of bacteria still retain the morphology of a normal cell. If increased pressure affects the cell division that leads to elongated cells, then we can describe the cell division or lack of it using a simple stochastic process. Below, we develop a simple stochastic model that captures the progressive heterogeneity in cell-length distribution. The model is based upon the following assumptions:

• 1.Cells either divide into two identical cells with probability α or, lacking the ability to divide, grow into an elongating bacteria with probability β = (1 – α). Probability for switching to an elongating cell type depends on the pressure.
• 2.Once a cell is unable to divide, it then continues to grow without dividing (i.e., now grows by elongating) during its course of bacterial growth. (This assumption is based upon the fact that the cell-division machinery requires localization of the many proteins involved to create a cell-septum site for the division. We expect that, as the cells elongate, the localization of those proteins in extended cells would be more difficult.)
• 3.Whenever a cell does not divide from one generation n to the next generation n + 1, the cell length just doubles.
• 4.Our observation of DNA in elongated cells suggests that DNA is replicated faithfully in the range of pressure and temperature where elongation of cells is observed, and that the number of DNA is proportionate with cell length for all pressure and temperature values (see Fig. 6). We then further assume that the biomass growth rate of both normal and elongating cells is the same per unit DNA, and, based on that, the doubling time will be independent of cell length.

A schematic of the model is shown in Fig. 9. Let us assume that we start with a cell with length l₀ at time t = 0. Hence, at the end of the n generations of division, the system will have different distributions of bacterial cell length:

$$l\in \left\{l_0,2l_0,4l_0,8l_0,\dots ,2^n{l}_0\right\}.$$

Figure 9.

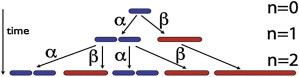
Schematic of the stochastic irreversible switching of normal bacterial cell (blue) to elongating bacterial cells (red). A normal cell can either divide into two cells with probability α or switch to an elongating phenotype with a probability β. Once a bacterial cell’s fate changes to elongating cell type, it just grows without dividing.

It can be shown easily that the above scheme of irreversible stochastic switching leads to a number of various lengths l of bacterial cells at the end of n generations, given by

$$N\left(l=l_0\right)={\left(2\alpha \right)}^n,$$

$$N\left(l=2l_0\right)={\left(2\alpha \right)}^{\left(n-1\right)}\beta ,$$

$$N\left(l=4l_0\right)={\left(2\alpha \right)}^{\left(n-2\right)}{\beta }^2,$$

$$N\left(l=8l_0\right)={\left(2\alpha \right)}^{\left(n-3\right)}{\beta }^3.$$

Hence, in the extreme cases, either:

• 1.A case of no switching will lead to no changes in the bacterial length, α = 1; or
• 2.All the cells elongate to the maximum, limited by growth and number of divisions, α = 0.

In general, the number of bacterial cells of length l = 2^al₀ is given by

$$N\left(l=2^a{l}_0\right)={\left(2\alpha \right)}^{\left(n-a\right)}{\beta }^a.$$ (7)

The total number of bacterial cells at the end of n generation can be given by

$$N=\sum _{a=0}^n{\left(2\alpha \right)}^{\left(n-a\right)}{\beta }^a={\left(2\alpha \right)}^n\sum _{a=0}^n{\left(\frac{\beta }{2\alpha }\right)}^a={\left(2\alpha \right)}^n\frac{1-{\left(\beta /2\alpha \right)}^{n+1}}{1-\beta /2\alpha }.$$ (8)

Now the probability p(l = 2^al₀) of a bacterial cell with length 2^al₀ is given by

$$p\left(l=2^a{l}_0\right)=\frac{N\left(l=2^a{l}_0\right)}{N}=\frac{{\left(2\alpha \right)}^{\left(n-a\right)}{\beta }^a}{{\left(2\alpha \right)}^n\frac{1-{\left(\beta /2\alpha \right)}^{n+1}}{1-\beta /2\alpha }},$$ (9)

which, in terms of the switching probability β, can be written as

$$p\left(l=2^a{l}_0\right)={\left(\frac{\beta }{2\left(1-\beta \right)}\right)}^a\frac{1-\frac{3}{2}\beta }{\left(1-\beta \right)\left[1-{\left(\frac{\beta }{2\left(1-\beta \right)}\right)}^{n+1}\right]}.$$ (10)

Hence, the expectation value of length 〈l_n〉 at the end of n generation is given by

$$\langle l_n\rangle =\sum _{a=0}^n{2}^a{l}_0·p\left(l=2^a{l}_0\right)=l_0\frac{1-\frac{3}{2}\beta }{\left(1-\beta \right)\left[1-{\left(\frac{\beta }{2\left(1-\beta \right)}\right)}^{n+1}\right]}\sum _{a=0}^n{\left(\frac{\beta }{1-\beta }\right)}^a,=\frac{\left(1-\frac{3}{2}\beta \right)}{\left(1-2\beta \right)}\frac{\left[1-{\left(\frac{\beta }{1-\beta }\right)}^{n+1}\right]}{\left[1-{\left(\frac{\beta }{2\left(1-\beta \right)}\right)}^{n+1}\right]}{l}_0.$$

The distribution of l at t = 0 is a Gaussian, and as suggested by our experimental data, a Gaussian given by

$$P\left(l,t=0\right)=\frac{1}{\sqrt{2\pi {\sigma }_0^2}}{e}^{-\frac{{\left(l-l_0\right)}^2}{2{\sigma }_0^2}},$$ (11)

where l₀ is the average value and σ₀ is the standard deviation of cell length, respectively. The distribution of length at the end of n generations can be written as

$$\begin{array}{c}{P}_n\left(l\right)=\sum _{a=0}^n{\left(\frac{\beta }{2\left(1-\beta \right)}\right)}^a\frac{1-\frac{3}{2}\beta }{\left(1-\beta \right)\left[1-{\left(\frac{\beta }{2\left(1-\beta \right)}\right)}^{n+1}\right]},\\ \frac{1}{\sqrt{2\pi {\sigma }_0^2{2}^{2a}}}{e}^{-\frac{{\left(l-2^a{l}_0\right)}^2}{\left({2.2}^{2a}{\sigma }_0^2\right)}},\end{array}$$ (12)

where the sum over a takes into account the probability of obtaining length 2^al after n generations where l is the length of the cell at n = 0. Note that the maximum length of a cell starting with length l at t = 0 cannot be longer than 2ⁿl after n generations.

In Fig. 10 a, we show the evolution of the distribution of l for a fixed value of β = 0.5. As the time progresses, the distribution develops a long tail. Note that for β > β_c = 2/3, the system would undergo an irreversible fate where, after a few generations, the population will be dominated by elongated cells and cells with normal length will vanish from the population at the long time limit. We further show the expectation value of length 〈l〉 in Fig. 10 b as a function of β for a fixed number of generations. The value 〈l〉 increases slowly for small β-values and grows sharply with increasing β. To further test our model, we compare the data of P(l) at P = 300 atm with our model in Fig. 11. We find that the model can reasonably reproduce the length distribution.

Figure 10.

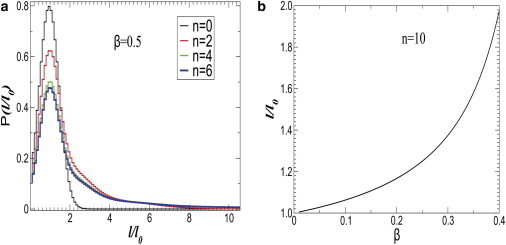
(a) Evolution of the distribution of the length of bacterial cells for β = 0.5. (b) Model prediction of the average length as a function of switching probability β.

Figure 11.

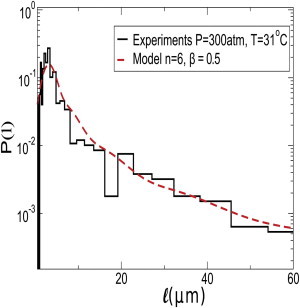
Comparison of model prediction of P_n(l) with experimental data at P = 300 atm and T = 31°C with model parameters β = 0.5 and n = 6. (Solid black line) Experimental data. (Dashed red line) Model prediction.

To further characterize the heterogeneities in the population of bacterial cell length, we calculate a non-Gaussian measure ϕ (35) of the distribution P_n(l) defined by

$$\varphi =\frac{\langle \Delta l^4\rangle }{3{\left(\langle \Delta l^2\rangle \right)}^2}-1,$$ (13)

where 〈Δl²〉 and 〈Δl⁴〉 are the second and fourth central moments of the distribution P_n(l), respectively. The value ϕ = 0 corresponds to a Gaussian distribution, while a deviation of ϕ from zero corresponds to the degree of deviation from a Gaussian distribution.

In Fig. 12 a, we show the dependence of switching probability β on pressure for T = 31°C. The values of β for different pressures is calculated by fitting Eq. 12 to the distribution of cell lengths obtained in our experiments. The value β increases monotonically with increasing pressure. In Fig. 12 a, we show the dependence of ϕ on switching probability β for n = 6 from the model (solid line). We find that ϕ grows slowly first, but increases sharply with β. In Fig. 12 b, we also show the non-Gaussian parameter ϕ measured from the experimental distribution of cell lengths at pressures P = 50, 100, 150, and 200 atm and temperature T = 31°C (solid red circles). Note that the model assumes a transition, but is not able to give much information about the physical origin of such phenotypic transitioning.

Figure 12.

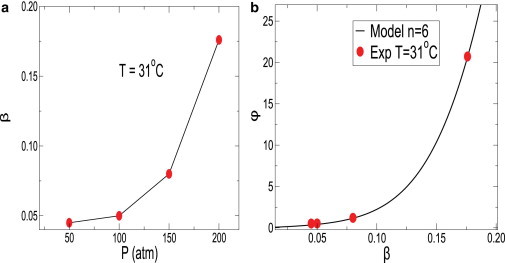
(a) Dependence of switching probability β on pressure for T = 31°C. The value β increases monotonically with increasing pressure. (b) Dependence of the non-Gaussian parameter of the distribution ϕ on the switching probability β. (Solid black curve) Model data. We have also plotted the values of β extracted from experimental distribution of cell length at T = 31°C for pressures P = 50, 100, 150, and 200 atm (solid red circles).

What are the biophysical mechanisms responsible for the cell elongation? And where does the stochasticity come from? The clue to the stochasticity problem comes from the measured transition in the cell length observed here and the polymerization of one of the cytoskeletal proteins responsible for cell division, FtsZ. Recent experiments on FtsZ in vivo and in vitro suggests that FtsZ protein depolymerizes at high pressures leading to delocalization of FtsZ in the cell (34). Furthermore, it was shown that FtsZ is not able to form the Z-ring, due to the increased depolymerization that is considered responsible for the mechanical forces required for the cell division.

Could FtsZ be responsible for the sharp transition in the growth and the cell division observed in our experiments? Or could a set of other processes, including the formation of Z-ring by FtsZ, lead to the observed transition? Is the cell elongation phenomenon due only to the depolymerization of FtsZ at high pressures, or is more than one cellular process responsible for it? The answers to these unresolved questions can only come from further experiments.

Discussion

We have investigated the growth of E. coli in real-time as a function of pressure and temperature. We find that E. coli can grow and divide in a wide range of pressures (1–400 atm) and temperatures (20–40°C). The doubling time of bacteria increases upon increasing pressure at a given temperature. Furthermore, doubling time at a constant temperature exhibits an exponential dependence on pressure for moderate values of pressure. Moreover, we find that for all the temperatures studied, doubling time shows an abrupt increase at pressures between 250 and 400 atm. Although at high T this sharp increase in doubling time with pressure is very large, where τ can be larger than 500 min, at low T, τ increases by a few folds. Furthermore, we find that the doubling time shows an anomalous decrease and then increase with pressure at low temperature. We hypothesize that this anomalous behavior of doubling time is a manifestation of the structural changes in phospholipids in the membrane. Further experiments on a variety of cell types where the lipid composition is known would be required to address this.

We next looked at the bacterial cell morphology after application of pressure until the time of saturation in which we could reach the saturation or a few generation time in which the saturation was hard to reach over the timescale of our experiments. We find that average bacterial length increases upon pressure. While the bacterial elongation at high pressures (33,34) is known, we find that E. coli shows a behavior of morphology very similar to growth rate or doubling time, whereas the average cell length also displays a sharp increase at pressures between 250 and 400 atm. Moreover, the heterogeneities in the cell length of bacteria increases upon increasing pressure. To explain the changes in heterogeneity of the cell-length distribution with change in pressure, we propose a simple stochastic irreversible switch model of bacterial phenotypes (normal and elongating). We find that the model fits well the experimental data of distribution of bacterial cell length at different pressure. Moreover, the model allows us to extract the switching probability of E. coli bacteria to elongating phenotype, which increases upon increasing pressure.

While the model captures the cell elongation phenomenon and explains the cell-length distribution, it leaves us with one more question: what biophysical processes give rise to the stochasticity in the phenotypic transitions as a function of pressure? A clue to this comes from the measured transition in the cell elongation observed here and depolymerization of FtsZ protein responsible for cell division. Note that because the bacterial strain used in our experiments (DH5α) lacks the homologous recombination system, the cell elongation cannot be interpreted as the conventional SOS response of the system. Hence, FtsZ depolymerization and delocalization, leading to nonformation of a Z-ring, is a biophysical process that may potentially lead to the phenotypic transitions proposed here. Further experiments are required where the polymerization of cytoskeletal proteins such as MreB and FtsZ can be visualized along with cell division, at various pressures and temperatures.

Because growth is coupled to various other processes, the bottlenecks could be either the structural integrity (such as protein denaturation or membrane structural changes) or the time integrity of various processes. There is a large body of literature on the behavior of different biomolecules at varied physical conditions. These studies indicate that, at high pressures and temperatures, the essential components that make up a cell may become unstable. Proteins can unfold and membranes can undergo structural transitions at high pressures, leading to death of a cell (17,18). The other issue, which has been rather overlooked in the past, is the variation in the timescales of various processes. Because pressure and temperature not only change the stability but also modify the thermodynamic driving force of a chemical reaction, they can lead to changes in the timescales of various processes. How the time integrity of various processes is maintained by a cell is an interesting question. A better understanding can only come from a systematic study of the mutations in the protein/enzymes or regulatory circuits involved in various processes.