Abstract
We study effects of oscillatory convective flow in extracellular space on the velocity of chemical signal propagation having a form of a front wave above a cellular layer. We found that the time-averaged propagation velocity under oscillatory flow for a particular Péclet number amplitude is slower than the velocity under steady laminar flow regime for the same value of the Péclet number, but significantly faster than under no-flow conditions. We derive asymptotic values of the propagation velocity and asymptotic characteristics of the corresponding concentration fronts in high- and low-frequency regimes and show that the reason for the observed velocity increase under the oscillatory flow stems from a nonlinear dependence of the propagation velocity on the Péclet number, particularly from the convex character of the dependence. Our findings suggest that the specific responses of cellular cultures to different flow conditions in the extracellular space (for example, expression of atherosclerosis protective genes under steady laminar flow but not under oscillatory flow) is a consequence of a nonlinear coupling between the extracellular transport and complex intracellular reaction cascades forming a positive feedback loop of the autocrine signaling. This mechanism can operate independently of, or in conjunction with, a direct stress-sensing due to mechanotransduction.
Introduction
Convective transport in tissues plays an important role in many developmental processes. It has been shown that the convective transport is necessary for the left-right body axis formation (1), vascular and lymphatic systems development (2), cancer cell movement (3,4), and cell migration in inflammatory or injury events (5–7). Pressure gradients and the convective fluid flow velocity in porous media are related via the Darcy law (8). Consequently, pressure gradients emerging in a body induce interstitial flow despite the compactness of bones, cartilage, or muscles (9).
A mechanism by which the convective flow can contribute to the signal transmission is to bring about spatial asymmetries in the distribution of morphogens in the extracellular matrix (8,10). The asymmetries induce chemical signal transmission in corresponding directions due to the morphogen-related activation of integrins and other cellular receptors (11,12).
Endothelia (vascular epithelia) are naturally exposed to permanent convective transport. Hence, much experimental and theoretical work has been focused on the effects of steady convective flow and shear stress on endothelial cell development (2,10,11,13). Affected cells chemotactically organize along morphogen gradients and respond by releasing new morphogen molecules (11,14,15). It has been shown that only a joint action of the convective transport and the vascular endothelial growth factor leads to formation of organized vascular capillaries (10,13,16).
In the previously mentioned studies, steady laminar flow was typically considered. In real biological systems, convective transport is distinctly nonstationary because of the periodic character of changes in the body. The heart is responsible for convective transport in the vascular system with a period of ∼1 s, lung epithelium is affected by a breathing period of ∼4 s, walking or running induces pressure gradients in bones, muscles, and cartilage with a period <1 s, certain smooth muscles (gut, womb) contract with periods of several minutes, and circadian rhythms and human habits repeat every 24 h. As a result, a considerable body of experimental work examined effects of oscillatory and pulsatile flow on cell cultures or tissues in vitro or in vivo (e.g., see the literature (17–24)). To be more specific, we define the oscillatory flow as a flow with zero average value, i.e., the flow direction is periodically flipped. Oscillatory flow is usually observed at vascular bifurcations (17). On the other hand, the pulsatile flow is defined as flow with a nonzero average value, i.e., the flow periodically accelerates and decelerates but the flow direction usually remains unchanged.
A number of studies have focused on developmental processes occurring in endothelial cells under nonstationary flow with the characteristic frequency ∼1 Hz. Endothelial cells typically behave differently under static and oscillatory conditions. Moreover, response of the endothelial cells under the oscillatory flow is different from that under the pulsatile regime (17). Oscillatory flow in endothelium leads to an increased production of cell attachment proteins (18), NADH oxidase activity (19), metalloproteinase expression (20), sphingosine kinase-1 gene expression (21), JNK protein activity (22), etc. Conversely, endothelial cells under oscillatory flow lose the ability to increase the concentration of free calcium (23) or do not increase nitric oxide synthase gene expression as observed under steady laminar flow (24). Atherosclerosis can develop as a result of the overexpression or suppression of specific genes under oscillatory flow, with possible fatal impacts (19,20,24). This differs significantly from the steady laminar flow that shows rather protective effects (25–27). Information that is more comprehensive can be found in reviews (17,28). In endothelium, the classical ligand-receptor signal transduction influenced by convective flow is accompanied by various mechanotransduction processes mediating the linkage between extracellular shear stress and intracellular signaling cascades (29).
Furthermore, effects of oscillatory flow on the cell behavior are widely studied in connective tissues, especially in bones. For example, the oscillatory flow in osteoblasts increases the activity of enzymes such as mitogen-activated protein kinases or alkaline phosphatase (30,31), activation of integrins and related kinase cascades (31), and expression of specific genes (32–34). It also affects the concentration of the free intracellular calcium (35). Oscillatory flow imposed on in vitro osteoblast cultures or mesenchymal stem cell cultures provides homogeneous cell seeding and proliferation as well as increased cell viability (30,36,37), which is an important finding for the artificial bone engineering (38).
Theoretical studies focusing on the effects of oscillatory flow on cell cultures are rather rare. Qin et al. (39) developed a mathematical model to investigate the interaction of the pulsatile and oscillatory flows with endothelial cells, especially the impacts of various flow regimes on the chloride transmembrane transport and the corresponding electric current. They showed that the endothelial cell can distinguish between the flow types by different electric current responses. John and Barakat (40) developed a mathematical model that allows for determination of ATP concentration above endothelial layers under the influence of various convective regimes. They assumed that the ATP source term depends directly on shear stress. Other mathematical models were developed to study mechanotransduction processes in the endothelium (41,42). The cells were considered to be solid bodies. It was found that the velocity of cellular sensor responses depends on the character of flow and oscillation frequency. Barakat (41) found that the cell deformation becomes frequency-independent above certain critical frequency. Oscillatory flow with the frequency ∼1 Hz results in a smaller cell deformation than under steady convective flow (42).
Unfortunately, the mechanisms that lead to a specific gene expression profile under oscillatory flow have not been fully understood. In this work, we show that the levels of enzyme activities or gene expressions under oscillatory flow differ from those under steady laminar flow, and not only due to direct mechanotransduction. Another and probably sufficient mechanism relies only on the classical extracellular ligand-transmembrane receptor signal transmission. Typical examples of the transduction process are:
-
1.
Growth factor binding to tyrosinkinase receptors on the outer cytosolic membrane surface.
-
2.
Membrane-bound protein phosphorylation.
-
3.
MAPK cascade activation.
-
4.
Intracellular protein and/or transcription factor modification (Fig. 1).
Figure 1.
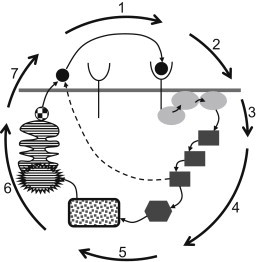
Scheme of positive feedback loop in autocrine signaling: (1) ligand-receptor binding; (2) phosphorylation of membrane-associated proteins; (3) activation of MAPK cascades; (4) transcription factor modification; (5) transcription; (6) translation, posttranslation modification of the ligand; and (7) new ligand release. (Dashed line) Alternative process of the ligand release based on a direct (transcription-independent) activation of intracellular or extracellular proteases.
As a starting point for our study, we begin with the mathematical model of such a transduction formulated by Přibyl et al. (43) with a single positive feedback between the ligand binding and ligand release in a simple cellular layer. The model has been recently modified (44) to allow for convective flow. Here we present the frequency/period and amplitude characteristics of the averaged signal propagation velocity in a cellular layer under the influence of oscillatory flow. The results are compared with those obtained for steady-flow or no-flow cellular systems. The dependences of the propagation velocity and other characteristics on the period of oscillations are explained with the help of analysis in asymptotic (high- and low-frequency) regimes.
Mathematical Model
Domain description
Both intracellular and extracellular reaction-transport processes are necessary to establish a positive feedback loop in a tissue to start a chemical signal transmission and signal propagation in a cellular layer (Fig. 1). Whereas complex reaction-transport processes inside cells are responsible for the release of new ligand molecules, the convective and diffusive transports in the extracellular domain are necessary for ligand spreading. The main reaction steps of the intracellular part of the positive feedback are depicted in Fig. 1. The positive feedback loop does not necessarily rely on the transcription; it can also exploit available cytosolic and membrane-bound proteins (45). However, the corresponding reaction cascades are still complex, case-dependent, and able to be affected by either random or oriented intracellular transport. Because we focus on general effects of extracellular oscillatory flow on the cell behavior in this work, a detailed description of the intracellular reaction-transport was deemed unnecessary. Instead, a simple switch-like sigmoidal dependence between the surface concentration of ligand-receptor complexes and ligand release rate was used (44). Admittedly, this assumption results in a strong simplification of the positive feedback loop mechanism. However, the sigmoidal character of the response is typical for enzyme intracellular cascades with a high degree of cooperativity (46). Moreover, it has been shown that introduction of time delays between the ligand-receptor complex formation and ligand release leads only to a decrease of signal propagation velocity; the qualitative character of the signaling remains unchanged (43).
The modeling domain considered in this work (Fig. 2) consists of the extracellular part with solid top and bottom boundaries. The top boundary represents either a ligand-impermeable membrane or a symmetry axis. The bottom boundary corresponds to a homogeneous cellular layer that is assumed to be continuous in space. Receptor-related chemical reactions and the release of new ligand molecules are described in terms of boundary conditions at the bottom boundary. Specific effects coming from the discrete character of the cells have been reported in Přibyl et al. (47).
Figure 2.
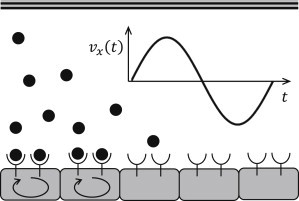
Modeling domain.
Ligand dynamics
In the extracellular gap (Fig. 2), the ligand molecules are transported via diffusion and convection. Diffusion is assumed in both directions, but only longitudinal convective transport along the cellular layer (x axis) is considered in
| (1) |
where symbols S, t, x, y, and DS denote the ligand molar concentration, time, spatial coordinates parallel and perpendicular to the cellular layer, and the ligand diffusivity, respectively. The oscillatory convective transport is represented by a time-dependent harmonic function
| (2) |
with the amplitude vA and the frequency f. Here, we assume that the longitudinal convective transport has the character of a time-varying plug flow. As we showed earlier (44), the Taylor dispersion effect coming from the laminar character of the flow in the extracellular space is negligible in a wide range of physically realistic regimes.
The reflecting boundary condition is used at the top boundary:
| (3) |
The bottom boundary condition at the cellular layer balances the diffusive transport of the ligand, its release by the ligand-releasing protease with activity P, ligand consumption, and release due to the ligand-receptor interactions
| (4) |
where R and C represent the surface concentrations of the free receptors and ligand-receptor complexes. The symbols , , and gS denote the kinetic constants of the ligand-receptor binding, ligand-receptor complex dissociation, and ligand release, respectively.
Equation 1 can be simplified if the thickness of the extracellular gap H is significantly smaller than the characteristic spatial extent of the ligand trafficking (48) in the extracellular space (44). Such conditions occur in compact tissues. In this case, we can introduce a spatially averaged ligand concentration by means of the thin fin approximation (49),
| (5) |
After the corresponding averaging of Eq. 1 with the use of the boundary conditions from Eqs. 3 and 4, we obtain
| (6) |
The equations describing the dynamics of the surface receptors, ligand-receptor complexes, and protease activation are the same as those in Nebyla et al. (44). They are also briefly described in Appendix A.
Dimensionless model
With the use of the scaling factors defined in Appendix B, the model equations are transformed into a dimensionless form:
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
We identify 10 dimensionless parameters of the model (see Appendix B for their definitions). Their physical meaning is explained in Table 1. We investigate the amplitude and frequency/period characteristics of the autocrine signaling for three sets of the dimensionless parameters listed in Table 2. We call Set 1 the basic set, for which the parameter values were taken as the averaged values of experimentally available data (44). The dimensionless period of the flow oscillations is .
Table 1.
Physical meaning of dimensionless parameters
| Parameter | Meaning |
|---|---|
| α | Ratio of gap height/spatial extent of ligand transport |
| βS | Relative strength of ligand-receptor complex endocytosis |
| γ | Ratio of Ligand/receptor generation rates |
| Tuning parameter for the sharpness of the sigmoidal function | |
| τC | Ratio of protease/complex deactivation rate constants |
| τR | Ratio of protease deactivation/receptor endocytosis rate constants |
| τS | Ratio of protease deactivation rate constant/ligand diffusion timescale |
| Switch on-/off threshold of protease activation | |
| PeA | Amplitude of the Péclet number |
| Frequency of the oscillatory flow |
Table 2.
Parameter values
| Parameter | Set 1 (basic set) | Set 2 | Set 3 |
|---|---|---|---|
| α | 0.1 | 0.1 | 0.1 |
| βS | 0.5 | 0.5 | 0.5 |
| γ | 1 | 1 | 1 |
| 0.01 | 0.01 | 0.01 | |
| τC | 0.1 | 1 | 0.01 |
| τR | 0.5 | 1 | 0.01 |
| τS | 0.002 | 1 | 0.01 |
| 0.3 | 0.3 | 0.3 | |
| f/kP | f/kP | f/kP |
There are two limiting spatially uniform steady states of Eqs. 7–10 corresponding to the on- and off- states of the autocrine signaling. The off-state is
| (12) |
and the on-state is
| (13) |
Numerical Methods and Analysis
Solvers
Equations 7–10 were solved with the use of the COMSOL 3.5 software (COMSOL Multiphysics, Palo Alto, CA). The relative and absolute tolerances of the femtime solver were set to 1 × 10−4. The spatial domain was discretized into uniform finite elements of size 0.01. The domain size was chosen large enough to follow the development and motion of oscillatory concentration fronts. The on- and off-steady states, Eqs. 12 and 13, were used on the left and right boundaries, respectively. As for the initial condition, the domain was divided into two parts. We assumed spatially uniform on- and off-steady states in the left and right parts, respectively.
The numerical results were verified using a program based on a finite difference method employing the ode45 MATLAB solver (The MathWorks, Natick, MA). We used symmetric and asymmetric three-point differential formulae. The relative difference between the front velocities provided by COMSOL (COMSOL Multiphysics) and finite difference codes was always <1%. Moreover, the propagation velocity of nonoscillating traveling concentration fronts (for a time-independent Péclet number) was in agreement with that obtained by the continuation of the corresponding heteroclinic orbit (50) connecting the on- and off-steady states.
Velocity evaluation
The harmonic character of the oscillatory flow gives rise to periodic changes in the chemical signal propagation velocity above the cellular layer. After an initial transient, the periodic character becomes sustained. In all our simulations, the oscillatory response of the wave and the oscillations of the flow are 1:1 frequency-locked, i.e., we observe the same frequencies of variations of the propagation velocity and oscillatory flow velocity. The position of the concentration front of the ligand-receptor complex in the space-time coordinates is plotted in Fig. 3 A. Here, the position of the concentration front in space is evaluated at the concentration equal to the complex threshold . Within one period of the oscillatory flow, the profiles of the front change significantly (Fig. 3 B). The averaged propagation velocity is then found as the slope of the linear fit in the stable periodic regime (Fig. 3 A).
Figure 3.
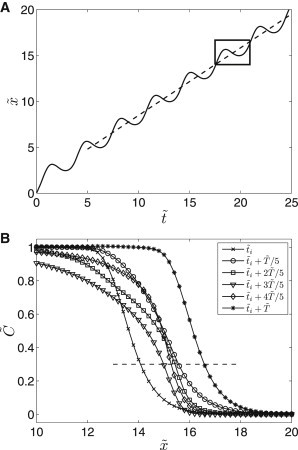
(A) (Solid line) Position of on the complex concentration front in space and time; (dashed line) linear fit of the data for evaluation of the averaged propagation velocity ; (box) one period starting at for the visualization of concentration profiles. (B) Detail of the propagating front at different times during the highlighted period; (dashed line) threshold concentration . Parameter Set 1, PeA = 4, .
Results
Frequency characteristics
Dependences of the average propagation velocity on the period of the oscillatory flow are plotted in Fig. 4. The characteristics are typically nonlinear with lower and upper asymptotes (dashed lines). Several inflection points as well as a distinct velocity maximum at are identified for two of the three considered parameter sets. The common feature of all these dependences is that larger periods of the oscillatory flow accelerate the autocrine communication more significantly than the shorter ones. The velocity increase amounts to several tens of percent for parameter Sets 1 and 2 and >100% for parameter Set 3. As we will show in the discussion, the character of these dependences results from different timescales of the reaction and transport processes at the cellular layer.
Figure 4.
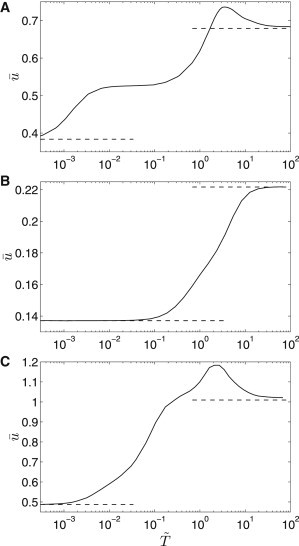
Dependence of the propagation velocity on the period of oscillations. (A) Parameter Set 1; (B) parameter Set 2; (C) parameter Set 3, PeA = 4. (Dashed lines) Upper and lower velocity asymptotes.
In general, the quantitative character of the calculated frequency characteristics depends on the choice of the sharpness parameter in Eq. 11. To document this effect, we selected a periodic regime corresponding to the maximum in Fig. 4 A and studied the effect of the parameter on the propagation velocity (see the Supporting Material). The propagation velocity attains an asymptotic value for ∼<0.02, and this value corresponds to the Heaviside dependence of the protease activity on the complex concentration. An increase of above 0.02 leads to an increase of the propagation velocity. However, the relative difference between the propagation velocities in the asymptotic regime and for does not exceed 5%, i.e., our results are not significantly affected in a wide range of the sharpness parameter.
Amplitude characteristics
All amplitude characteristics showing versus PeA plotted in Fig. 5 are monotonous and increasing in the studied range. In certain ranges of periods of the flow oscillations , the velocity increase exceeds 100%. For , we find to be the same as the velocity of the signal propagation in the absence of the convective transport. The amplitude characteristics are plotted only for Set 1; qualitatively identical behavior is found for the other sets.
Figure 5.
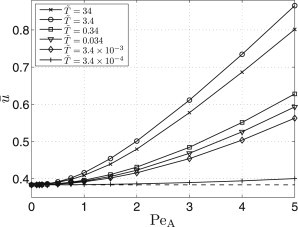
Dependence of the propagation velocity on the amplitude of oscillations: Parameter Set 1. (Dashed line) Propagation velocity in the no-convection regime.
From the above results, we can conclude that the oscillatory convection in the extracellular space can, under certain conditions, lead to a significant acceleration of the signal transmission when compared to the no-convection system. In the following, we explain the observed findings and compare them qualitatively with available experimental results.
Discussion
Lower and upper asymptotes
We will now focus on the lower asymptote of the frequency/period characteristics shown in Fig. 4. When the period of the oscillatory flow is short enough that the characteristic times of all reaction processes are significantly longer (; the protease timescale is 1 and must be also satisfied), the cellular layer cannot respond to these fast flow changes and behaves as if unaffected by the convective transport. The propagation velocity at the lower asymptote is then given by the solution of Eqs. 7–10 with PeA = 0 or alternatively with the use of results given in Přibyl et al. (43). The lower asymptotic value of the velocity is approximately attained when the fastest reaction process is at least 10 times slower than the oscillatory flow period. The fastest process for Set 1 is the ligand kinetics (τS = 0.002) and then the asymptote is attained at (Fig. 4 A). To verify this observation, we computed the frequency characteristics for the other two parameter sets (Fig. 4, B and C). The lower asymptote is attained at and when the timescales of the reaction processes are 1 and 0.01, respectively.
The upper asymptote is attained when the period of the oscillations is significantly longer than the reaction timescales. In all cases in Fig. 4, the characteristic timescale of the slowest reaction processes is equal to 1 and the asymptotic behavior is attained at . In such a case, the propagation velocity at any particular time is equal to the propagation velocity in a system with a constant Péclet number, i.e., we look for solutions of
| (14) |
To evaluate the propagation velocity for a constant Péclet number, we introduce a moving coordinate ξ,
| (15) |
where μ is the dimensionless velocity of the traveling front wave. After the coordinate transformation, we obtain
| (16) |
The dependence of the propagation velocity μ of the traveling front wave connecting the uniform on- and off-steady states on the Péclet number (Fig. 6) can be found by means of the continuation software AUTO-07P (50). We note that Eqs. 8–10 defined on the cellular boundary also have to be transformed into moving coordinates.
Figure 6.
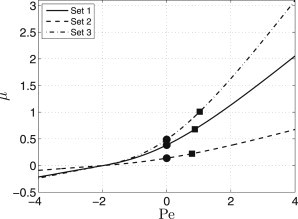
Dependence of the propagation velocity on the Péclet number for nonoscillating regimes. The parameter values are given in Table 2. (Dots and squares) Velocity values at the lower and upper asymptotes in Fig. 4, respectively.
The dependences of the propagation velocity on the Péclet number for the considered parameter sets are plotted in Fig. 6. These dependences are monotonous and convex. They can be used for the evaluation of the upper asymptotic value of the propagation velocity in the oscillatory regime. The time-averaged velocity is
| (17) |
where
| (18) |
The upper asymptotic values plotted in Fig. 4 are indicated as squares in Fig. 6. For the sake of completeness, we also show the lower asymptotic velocity values, which correspond to circles. Clearly, the increase of the propagation velocity under oscillatory convection is a result of nonlinearity of the autocrine signaling in the cellular tissue.
Depending on the period of oscillation, the observed increase of the propagation velocity ranges from 0 to ∼100% in our study. This observation agrees well with many experimental reports, where the increase or decrease of a protein activity or gene expression is several tens of percent or higher (22,27,34,51). Reported experiments also indicate that the effect of the steady convection (time-independent Pe) on cellular cultures can be stronger than that of the oscillatory flow (27,35,52). This is in a good agreement with the data in Fig. 6. However, such findings do not apply to all cases because many experiments show that, when exposed to oscillatory flow, the cells may display completely different responses than those at steady flow (17,23,53).
The above results indicate that the experimentally observed changes in cells due to the oscillatory flow do not necessarily rely on direct mechanotransduction of the extracellular stress into the cell (17). We suggest that the changes can be also induced by classical autocrine signal transmission mediated by extracellular growth factors and their transmembrane receptors. Experimentally observed modifications of the intracellular activities under oscillatory flow thus can be a result of nonlinear coupling between the extracellular growth factor transport and new ligand.
Front width amplitude
To visualize basic properties of the autocrine communication under the influence of oscillatory flow, we plot the front width amplitude as a function of the period for all dependent variables (Fig. 7). Here, the front width amplitude (FWA) is defined as the distance between two most outlying positions of the concentration front observed within one period of a sustained periodic regime (Fig. 3 B). The front position of a particular variable was determined at the concentration value equal to the middle of the maximal concentration range, namely,
Figure 7.
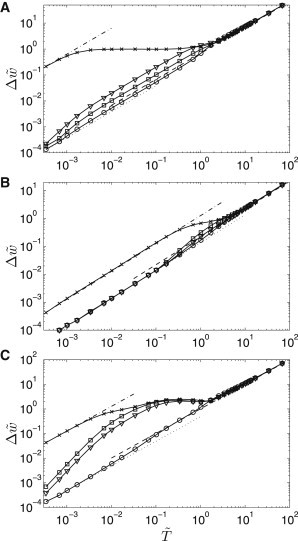
Dependence of the front width amplitude on the period of oscillations. (A) Parameter Set 1; (B) parameter Set 2; (C) parameter Set 3, PeA = 4. (Crosses) Ligand front; (circles) protease front; (squares) receptor front; (triangles) complex front. (Dashed, dotted, and dash-dotted lines) Asymptotic width amplitudes.
FWA of the ligand, receptor, complex concentration, and protease activity generally differ and depend on the period of oscillations. Particular character of these dependences is affected by the timescales of the corresponding reaction kinetics and the extracellular ligand transport. To explain the FWA dependences for the basic Set 1 of the model parameters (Fig. 7 A), we first need to clarify their character for Set 2, where τS = τR = τC = 1 (Fig. 7 B). When the oscillation period is significantly higher than 1, the kinetics of all reaction processes at the cellular layer is faster than the changes of convective flow, i.e., the receptor, complex, and protease concentrations are found in pseudo-steady state and follow the ligand transport in the extracellular medium. This regime corresponds to the upper asymptote in Fig. 4. FWAs of all model variables are then given by the averaged velocity computed from Eq. 17 and its value is calculated using
| (19) |
This asymptotic dependence perfectly fits the FWA values for (Fig. 7 B, dashed line).
In another asymptotic regime, where the reaction kinetics are much slower than changes of the convective velocity , FWAs of the protease, receptor, and complex can be again evaluated with Eq. 19. Because very fast velocity changes do not affect autocrine signaling, as we showed in Fig. 4, the velocities corresponding to no-convection regimes are used in Eq. 19. These values are marked by circles in Fig. 6. One can see that the computed FWA values for perfectly coincide with the asymptotic dependence, i.e., with the dotted line in Fig. 7 B.
The ligand FWA values attain a different asymptotic dependence at low ( Fig. 7 B, dash-dotted line). In high-frequency regimes, the convective transport of the ligand is much faster than either the diffusion transport or the ligand-receptor kinetics. Equation 7 then reduces to the kinematic equation (54)
| (20) |
Due to the harmonic character of the convective oscillations, FWA is attained in one-half of the oscillation period and we can write
| (21) |
Timescales and velocity maxima
The FWA values of the model variables at a particular oscillation period generally differ due to different timescales of the reaction and transport processes. This is clearly demonstrated in Fig. 7 A, where τS < τC < τR < 1. For , the FWA values decrease in the order of ligand, complex, receptor, and protease. For example, the spatial extent of the ligand front oscillations above the cellular layer is wider than that of the complex, as the complex kinetics is so slow that it is unable to fully follow the ligand concentration changes. When the ligand, complex, and receptor timescales are equal to 0.01 (Fig. 7 C), their FWA values coincide for , while the protease FWA value is much smaller due to the unity timescale.
By comparing Figs. 4 and 7, it becomes clear that the complex frequency characteristics (Fig. 4, A and C) result from different timescales of the reaction-transport processes of the involved chemical species. Distinct curvature of the characteristics is typically observed at such oscillation periods where the FWA values of particular chemical species significantly differ. Then nontrivial coupling between the formation of particular reaction species and the ligand transport definitely occurs in the cell culture.
A quite interesting phenomenon is the occurrence of the maximum in the frequency characteristics (Fig. 4, A and C). Here, the maximal value of the propagation velocity exceeds the upper asymptotic value and the FWA values are comparable for all model variables. The maximal velocity is localized at the oscillation period close to 1. It implies that the flow oscillations are slow enough that all chemical species including the protease can respond to the ligand changes in the extracellular medium.
Upon inspection of the concentration fronts in sustained periodic regimes, we discover qualitative changes of the protease activity propagation near to the maximum (Fig. 8). We selected three periods for which the protease fronts are plotted: Fig. 8 A, the propagation velocity maximum at ; Fig. 8 B, regime with a short period ; and Fig. 8 C, regime with a large period . The motion of protease fronts is visualized by taking equidistant snapshots within one period.
Figure 8.
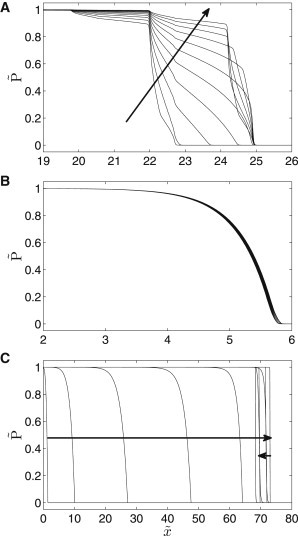
Profiles of the protease activity in stable periodic regimes. Eleven profiles equidistantly calculated through one period are plotted. (A) , (B) , (C) . (Arrows) Direction of the protease activity propagation. Parameter Set 1, PeA = 4.
A short period leads to formation of a narrow slightly pulsatile front (Fig. 8 B). The front shape does not change within one period because the protease kinetics is two orders-of-magnitude slower than the convective oscillations. The other extreme is represented by Fig. 8 C. As indicated by the arrows, the protease front moves forth and back within one period of the oscillations. When the signal propagates forward, the upper edge of the front is rounded and the lower edge is sharp, and vice versa. This finding is in agreement with our previous study (44). The protease front spreads over a large part of the cellular layer within one period because the kinetics are much faster than the flow variations. An interesting characteristic of the protease front was found at the propagation velocity maximum (Fig. 8 A). Here, the usual timescale of the protease kinetics and the oscillation period are comparable. The front is always monotonous; however, several inflection points are detected. There is no obvious front reversal even when the flow becomes negative. In other words, the half-period with negative convective velocity is not long enough to significantly lower the protease activity in the domain where the protease was previously activated, i.e., within the other half-period with positive convective velocity.
In summary, our findings indicate that the propagation velocity of chemical signals under the oscillatory flow can exceed the upper asymptote (Fig. 4) if:
-
1.
The timescales of the oscillatory convective flow and the protease activation/deactivation are comparable; and
-
2.
The kinetic timescales of the other species are smaller than that of protease so that they can follow the protease dynamics.
Conclusions
We have shown that distinct responses of cellular cultures to no-convection, steady-convection, and oscillatory-convection conditions in the extracellular space can result from coupling between the extracellular transport and complex intracellular reaction cascades forming a positive feedback loop of the autocrine signaling. We suggest that this mechanism may apply independently of, or coupled with, direct stress sensing due to mechanotransduction.
Different genes can be expressed and/or other proteins activated in distinct tissue regions due to the autocrine communication. Because the autocrine signaling is slower under oscillatory convection than under properly chosen steady convective flow, related developmental processes can affect a much smaller region of the tissue. In principle, slower autocrine signaling can either suppress or promote atherosclerosis-related gene expression in the endothelium at vessel bifurcations (22,26–28,52). However, the propagation velocity under oscillatory flow may still be significantly higher than that under no flow by as much as twice, as shown in our study. We have shown that the reason for the velocity increase is a nonlinear dependence of the propagation velocity on the Péclet number, particularly the convex character of the dependence.
In general, the dependence of the time-averaged propagation velocity on the period of oscillations is nonlinear and can be quite complex with several inflection points and a distinct maximum. We identified upper and lower asymptotic values of the propagation velocity. The complex character of the frequency/period dependences results from various timescales of the receptor-related reactions. We found corresponding asymptotic relations between the period of oscillations and the front width amplitudes for all model variables. In addition, the velocity maximum was observed only when the protease kinetic timescale was comparable with the period of the convective oscillations while, at the same time, the other kinetic timescales were smaller than that of protease.
Our findings offer an explanation as to why different cellular responses are obtained under different flow conditions. This work together with our previous work (44) form a solid starting point to a future study focused on pulsatile flow because such a flow can be understood as a superposition of steady flow and harmonic oscillatory flow at least in asymptotic regimes. We believe that the presented results will be also useful in the engineering of artificial tissues or in clarifying experimental results on autocrine signaling under oscillatory flow.
Acknowledgments
The authors thank the Ministry of Education, Youth and Sports of the Czech Republic for financial support (KONTAKT project No. ME10036 and Specific University Research No. 20/2013).
Appendix A: Dynamics of The Intracellular and Surface Processes
The receptor and the ligand-receptor complex dynamics and the dynamics of the protease activation are given by
| (22) |
| (23) |
| (24) |
where symbols , , QR, gP, and kP are the kinetic constants of the complex and receptor endocytosis, the rate of formation of new surface receptors, and the kinetic constants of the protease activation and decay, respectively. The nonlinear response of the protease activity to the concentration of the ligand-receptor complexes is described by a sigmoidal function
| (25) |
where CT and δ represent the complex concentration threshold for the protease activation and the sharpness of the sigmoidal function. Typical values of the model parameters can be found in Nebyla et al. (44).
Appendix B: Scaling Factors and Dimensionless Parameters
Following Nebyla et al. (44), the scaling factors for concentrations, time, and space are
| (26) |
and the definitions of eight dimensionless parameters (see Table 1 for their physical meaning) are
| (27) |
The dimensionless amplitude of the Péclet number, the dimensionless frequency, and period of the convective flow oscillations are
| (28) |
We emphasize the different meaning of the symbols PeA and Pe. The Péclet number amplitude (PeA) comes from nondimensionalization of the harmonic function in Eq. 2 and represents the amplitude of the convective flow oscillations. The Péclet number (Pe) accounts for the dimensionless representation of the unidirectional flow velocity.
Supporting Material
References
- 1.Cartwright J.H.E., Piro O., Tuval I. Fluid-dynamical basis of the embryonic development of left-right asymmetry in vertebrates. Proc. Natl. Acad. Sci. USA. 2004;101:7234–7239. doi: 10.1073/pnas.0402001101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ng C.P., Helm C.L.E., Swartz M.A. Interstitial flow differentially stimulates blood and lymphatic endothelial cell morphogenesis in vitro. Microvasc. Res. 2004;68:258–264. doi: 10.1016/j.mvr.2004.08.002. [DOI] [PubMed] [Google Scholar]
- 3.Chang S.F., Chang C.A., Chiu J.J. Tumor cell cycle arrest induced by shear stress: roles of integrins and Smad. Proc. Natl. Acad. Sci. USA. 2008;105:3927–3932. doi: 10.1073/pnas.0712353105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Polacheck W.J., Charest J.L., Kamm R.D. Interstitial flow influences direction of tumor cell migration through competing mechanisms. Proc. Natl. Acad. Sci. USA. 2011;108:11115–11120. doi: 10.1073/pnas.1103581108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Shi Z.-D., Ji X.-Y., Tarbell J.M. Interstitial flow promotes vascular fibroblast, myofibroblast, and smooth muscle cell motility in 3-D collagen I via upregulation of MMP-1. Am. J. Physiol. Heart Circ. Physiol. 2009;297:H1225–H1234. doi: 10.1152/ajpheart.00369.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bruyère F., Noël A. Lymphangiogenesis: in vitro and in vivo models. FASEB J. 2010;24:8–21. doi: 10.1096/fj.09-132852. [DOI] [PubMed] [Google Scholar]
- 7.Tomei A.A., Siegert S., Swartz M.A. Fluid flow regulates stromal cell organization and CCL21 expression in a tissue-engineered lymph node microenvironment. J. Immunol. 2009;183:4273–4283. doi: 10.4049/jimmunol.0900835. [DOI] [PubMed] [Google Scholar]
- 8.Fleury M.E., Boardman K.C., Swartz M.A. Autologous morphogen gradients by subtle interstitial flow and matrix interactions. Biophys. J. 2006;91:113–121. doi: 10.1529/biophysj.105.080192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pedersen J.A., Swartz M.A. Mechanobiology in the third dimension. Ann. Biomed. Eng. 2005;33:1469–1490. doi: 10.1007/s10439-005-8159-4. [DOI] [PubMed] [Google Scholar]
- 10.Helm C.L.E., Fleury M.E., Swartz M.A. Synergy between interstitial flow and VEGF directs capillary morphogenesis in vitro through a gradient amplification mechanism. Proc. Natl. Acad. Sci. USA. 2005;102:15779–15784. doi: 10.1073/pnas.0503681102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hernández V.R., Genové E., Semino C.E. Interstitial fluid flow intensity modulates endothelial sprouting in restricted Src-activated cell clusters during capillary morphogenesis. Tissue Eng. Part A. 2009;15:175–185. doi: 10.1089/ten.tea.2007.0314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shi Z.-D., Tarbell J.M. Fluid flow mechanotransduction in vascular smooth muscle cells and fibroblasts. Ann. Biomed. Eng. 2011;39:1608–1619. doi: 10.1007/s10439-011-0309-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Semino C.E., Kamm R.D., Lauffenburger D.A. Autocrine EGF receptor activation mediates endothelial cell migration and vascular morphogenesis induced by VEGF under interstitial flow. Exp. Cell Res. 2006;312:289–298. doi: 10.1016/j.yexcr.2005.10.029. [DOI] [PubMed] [Google Scholar]
- 14.Rutkowski J.M., Swartz M.A. A driving force for change: interstitial flow as a morphoregulator. Trends Cell Biol. 2007;17:44–50. doi: 10.1016/j.tcb.2006.11.007. [DOI] [PubMed] [Google Scholar]
- 15.Shamloo A., Ma N., Heilshorn S.C. Endothelial cell polarization and chemotaxis in a microfluidic device. Lab Chip. 2008;8:1292–1299. doi: 10.1039/b719788h. [DOI] [PubMed] [Google Scholar]
- 16.Song J.W., Munn L.L. Fluid forces control endothelial sprouting. Proc. Natl. Acad. Sci. USA. 2011;108:15342–15347. doi: 10.1073/pnas.1105316108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Barakat A., Lieu D. Differential responsiveness of vascular endothelial cells to different types of fluid mechanical shear stress. Cell Biochem. Biophys. 2003;38:323–343. doi: 10.1385/cbb:38:3:323. [DOI] [PubMed] [Google Scholar]
- 18.Thoumine O., Nerem R.M., Girard P.R. Oscillatory shear stress and hydrostatic pressure modulate cell-matrix attachment proteins in cultured endothelial cells. In Vitro Cell. Dev. Biol. Anim. 1995;31:45–54. doi: 10.1007/BF02631337. [DOI] [PubMed] [Google Scholar]
- 19.De Keulenaer G.W., Chappell D.C., Griendling K.K. Oscillatory and steady laminar shear stress differentially affect human endothelial redox state: role of a superoxide-producing NADH oxidase. Circ. Res. 1998;82:1094–1101. doi: 10.1161/01.res.82.10.1094. [DOI] [PubMed] [Google Scholar]
- 20.Magid R., Murphy T.J., Galis Z.S. Expression of matrix metalloproteinase-9 in endothelial cells is differentially regulated by shear stress. Role of c-Myc. J. Biol. Chem. 2003;278:32994–32999. doi: 10.1074/jbc.M304799200. [DOI] [PubMed] [Google Scholar]
- 21.Chen X.L., Grey J.Y., Kunsch C. Sphingosine kinase-1 mediates TNF-α-induced MCP-1 gene expression in endothelial cells: upregulation by oscillatory flow. Am. J. Physiol. Heart Circ. Physiol. 2004;287:H1452–H1458. doi: 10.1152/ajpheart.01101.2003. [DOI] [PubMed] [Google Scholar]
- 22.Hahn C., Orr A.W., Schwartz M.A. The subendothelial extracellular matrix modulates JNK activation by flow. Circ. Res. 2009;104:995–1003. doi: 10.1161/CIRCRESAHA.108.186486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Helmlinger G., Berk B.C., Nerem R.M. Calcium responses of endothelial cell monolayers subjected to pulsatile and steady laminar flow differ. Am. J. Physiol. 1995;269:C367–C375. doi: 10.1152/ajpcell.1995.269.2.C367. [DOI] [PubMed] [Google Scholar]
- 24.Silacci P., Formentin K., Hayoz D. Unidirectional and oscillatory shear stress differentially modulate NOSIII gene expression. Nitric Oxide Biol. Chem. 2000;4:47–56. doi: 10.1006/niox.2000.0271. [DOI] [PubMed] [Google Scholar]
- 25.Hosoya T., Maruyama A., Yamamoto M. Differential responses of the Nrf2-Keap1 system to laminar and oscillatory shear stresses in endothelial cells. J. Biol. Chem. 2005;280:27244–27250. doi: 10.1074/jbc.M502551200. [DOI] [PubMed] [Google Scholar]
- 26.Guo D., Chien S., Shyy J.Y.J. Regulation of endothelial cell cycle by laminar versus oscillatory flow: distinct modes of interactions of AMP-activated protein kinase and Akt pathways. Circ. Res. 2007;100:564–571. doi: 10.1161/01.RES.0000259561.23876.c5. [DOI] [PubMed] [Google Scholar]
- 27.Pfenniger A., Wong C., Kwak B.R. Shear stress modulates the expression of the atheroprotective protein Cx37 in endothelial cells. J. Mol. Cell. Cardiol. 2012;53:299–309. doi: 10.1016/j.yjmcc.2012.05.011. [DOI] [PubMed] [Google Scholar]
- 28.Laughlin M.H., Newcomer S.C., Bender S.B. Importance of hemodynamic forces as signals for exercise-induced changes in endothelial cell phenotype. J. Appl. Physiol. 2008;104:588–600. doi: 10.1152/japplphysiol.01096.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.White C.R., Frangos J.A. The shear stress of it all: the cell membrane and mechanochemical transduction. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2007;362:1459–1467. doi: 10.1098/rstb.2007.2128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Du D., Furukawa K., Ushida T. Oscillatory perfusion seeding and culturing of osteoblast-like cells on porous β-tricalcium phosphate scaffolds. J. Biomed. Mater. Res. A. 2008;86:796–803. doi: 10.1002/jbm.a.31641. [DOI] [PubMed] [Google Scholar]
- 31.Lee D.-Y., Li Y.-S.J., Chien S. Oscillatory flow-induced proliferation of osteoblast-like cells is mediated by αvβ3 and β1 integrins through synergistic interactions of focal adhesion kinase and Shc with phosphatidylinositol 3-kinase and the Akt/mTOR/p70S6K pathway. J. Biol. Chem. 2010;285:30–42. doi: 10.1074/jbc.M109.010512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.You J., Reilly G.C., Jacobs C.R. Osteopontin gene regulation by oscillatory fluid flow via intracellular calcium mobilization and activation of mitogen-activated protein kinase in MC3T3-E1 osteoblasts. J. Biol. Chem. 2001;276:13365–13371. doi: 10.1074/jbc.M009846200. [DOI] [PubMed] [Google Scholar]
- 33.Wu C.C., Li Y.S., Chien S. Roles of MAP kinases in the regulation of bone matrix gene expressions in human osteoblasts by oscillatory fluid flow. J. Cell. Biochem. 2006;98:632–641. doi: 10.1002/jcb.20697. [DOI] [PubMed] [Google Scholar]
- 34.Case N., Sen B., Rubin J. Steady and oscillatory fluid flows produce a similar osteogenic phenotype. Calcif. Tissue Int. 2011;88:189–197. doi: 10.1007/s00223-010-9448-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lu X.L., Huo B., Guo X.E. Calcium response in osteocytic networks under steady and oscillatory fluid flow. Bone. 2012;51:466–473. doi: 10.1016/j.bone.2012.05.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Du D., Furukawa K.S., Ushida T. 3D culture of osteoblast-like cells by unidirectional or oscillatory flow for bone tissue engineering. Biotechnol. Bioeng. 2009;102:1670–1678. doi: 10.1002/bit.22214. [DOI] [PubMed] [Google Scholar]
- 37.Alvarez-Barreto J.F., Sikavitsas V.I. Improved mesenchymal stem cell seeding on RGD-modified poly(L-lactic acid) scaffolds using flow perfusion. Macromol. Biosci. 2007;7:579–588. doi: 10.1002/mabi.200600280. [DOI] [PubMed] [Google Scholar]
- 38.Jaasma M.J., O’Brien F.J. Mechanical stimulation of osteoblasts using steady and dynamic fluid flow. Tissue Eng. Part A. 2008;14:1213–1223. doi: 10.1089/ten.tea.2007.0321. [DOI] [PubMed] [Google Scholar]
- 39.Qin K.-R., Xiang C., Cao L.-L. Dynamic modeling for flow-activated chloride-selective membrane current in vascular endothelial cells. Biomech. Model. Mechanobiol. 2011;10:743–754. doi: 10.1007/s10237-010-0270-2. [DOI] [PubMed] [Google Scholar]
- 40.John K., Barakat A.I. Modulation of ATP/ADP concentration at the endothelial surface by shear stress: effect of flow-induced ATP release. Ann. Biomed. Eng. 2001;29:740–751. doi: 10.1114/1.1397792. [DOI] [PubMed] [Google Scholar]
- 41.Barakat A.I. A model for shear stress-induced deformation of a flow sensor on the surface of vascular endothelial cells. J. Theor. Biol. 2001;210:221–236. doi: 10.1006/jtbi.2001.2290. [DOI] [PubMed] [Google Scholar]
- 42.Mazzag B.M., Tamaresis J.S., Barakat A.I. A model for shear stress sensing and transmission in vascular endothelial cells. Biophys. J. 2003;84:4087–4101. doi: 10.1016/S0006-3495(03)75134-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Přibyl M., Muratov C.B., Shvartsman S.Y. Long-range signal transmission in autocrine relays. Biophys. J. 2003;84:883–896. doi: 10.1016/S0006-3495(03)74906-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Nebyla M., Přibyl M., Schreiber I. Effects of convective transport on chemical signal propagation in epithelia. Biophys. J. 2012;102:990–1000. doi: 10.1016/j.bpj.2012.01.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Edwards D.R., Handsley M.M., Pennington C.J. The ADAM metalloproteinases. Mol. Aspects Med. 2008;29:258–289. doi: 10.1016/j.mam.2008.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Ferrell J.E., Jr., Machleder E.M. The biochemical basis of an all-or-none cell fate switch in Xenopus oocytes. Science. 1998;280:895–898. doi: 10.1126/science.280.5365.895. [DOI] [PubMed] [Google Scholar]
- 47.Přibyl M., Muratov C.B., Shvartsman S.Y. Discrete models of autocrine cell communication in epithelial layers. Biophys. J. 2003;84:3624–3635. doi: 10.1016/S0006-3495(03)75093-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Shvartsman S.Y., Wiley H.S., Lauffenburger D.A. Spatial range of autocrine signaling: modeling and computational analysis. Biophys. J. 2001;81:1854–1867. doi: 10.1016/S0006-3495(01)75837-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Deen W.M. Oxford University Press; New York: 1998. Analysis of Transport Phenomena. [Google Scholar]
- 50.Doedel E.J., Oldeman B.E. Concordia University; Montreal, Canada: 2009. AUTO-07P: Continuation and Bifurcation Software for Ordinary Differential Equations. [Google Scholar]
- 51.Hsiai T.K., Cho S.K., Ho C.M. Micro sensors: linking real-time oscillatory shear stress with vascular inflammatory responses. Ann. Biomed. Eng. 2004;32:189–201. doi: 10.1023/b:abme.0000012739.88554.01. [DOI] [PubMed] [Google Scholar]
- 52.Ali F., Zakkar M., Mason J.C. Induction of the cytoprotective enzyme heme oxygenase-1 by statins is enhanced in vascular endothelium exposed to laminar shear stress and impaired by disturbed flow. J. Biol. Chem. 2009;284:18882–18892. doi: 10.1074/jbc.M109.009886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lum R.M., Wiley L.M., Barakat A.I. Influence of different forms of fluid shear stress on vascular endothelial TGF-β1 mRNA expression. Int. J. Mol. Med. 2000;5:635–641. doi: 10.3892/ijmm.5.6.635. [DOI] [PubMed] [Google Scholar]
- 54.Varma A., Morbidelli M. Oxford University Press; New York: 1997. Mathematical Methods in Chemical Engineering. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


