Abstract
Mechanical deformation applied at the joint or tissue level is transmitted through the macroscale extracellular matrix to the microscale local matrix, where it is transduced to cells within these tissues and modulates tissue growth, maintenance, and repair. The objective of this study was to investigate how applied tissue strain is transferred through the local matrix to the cell and nucleus in meniscus, tendon, and the annulus fibrosus, as well as in stem cell-seeded scaffolds engineered to reproduce the organized microstructure of these native tissues. To carry out this study, we developed a custom confocal microscope-mounted tensile testing device and simultaneously monitored strain across multiple length scales. Results showed that mean strain was heterogeneous and significantly attenuated, but coordinated, at the local matrix level in native tissues (35–70% strain attenuation). Conversely, freshly seeded scaffolds exhibited very direct and uniform strain transfer from the tissue to the local matrix level (15–25% strain attenuation). In addition, strain transfer from local matrix to cells and nuclei was dependent on fiber orientation and tissue type. Histological analysis suggested that different domains exist within these fibrous tissues, with most of the tissue being fibrous, characterized by an aligned collagen structure and elongated cells, and other regions being proteoglycan (PG)-rich, characterized by a dense accumulation of PGs and rounder cells. In meniscus, the observed heterogeneity in strain transfer correlated strongly with cellular morphology, where rounder cells located in PG-rich microdomains were shielded from deformation, while elongated cells in fibrous microdomains deformed readily. Collectively, these findings suggest that different tissues utilize distinct strain-attenuating mechanisms according to their unique structure and cellular phenotype, and these differences likely alter the local biologic response of such tissues and constructs in response to mechanical perturbation.
Introduction
Fiber-reinforced soft tissues of the musculoskeletal system, such as meniscus, tendon, and annulus fibrosus (AF), function to transmit large loads and deformations. These tissues are composed of a dense extracellular matrix consisting primarily of collagens and proteoglycans (PG) (1–4), which are structurally organized to support this function. For instance, tendon is mostly composed of type I collagen with fibers that are highly aligned in the loading direction (1). The meniscus is a wedge-shaped fibrocartilage in the knee that has circumferentially aligned fibers with changing alignment and composition through the depth and radial position (2). The AF is an angle-ply laminate structure in the intervertebral disk of the spine. In the AF, collagen fibers are highly aligned and alternate at ±28–40° from the circumferential direction (5). In all of these tissues, fiber content and structure provides mechanical properties that are uniquely designed to support the physiological loading environment.
Cells within these highly structured connective tissues respond to their mechanical environment. Indeed, loads and deformations applied at the joint or tissue level propagate through the tissue hierarchy to produce mechanical perturbations at the cellular level. Cells respond to this mechanical microenvironment to regulate their biologic responses, including proliferation, differentiation, and matrix production (6). The mechanism of strain transfer from the tissue length scale to the cell length scale, defined here as the local matrix, is not well understood. and may differ across tissue types. Quantifying this multiscale strain transfer will be crucial for predicting how signals to cells are transduced into molecular responses. For instance, the local matrix strain fields in meniscus and rat-tail tendon are highly heterogeneous, but on average, the strains are correlated from the tissue scale to the local matrix scale (7,8). On the other hand, the local matrix strain in outer AF tissue subjected to biaxial tension does not correspond with tissue-level strain (9). This indicates a dependence of tissue-type and fiber alignment on strain transfer that has not been fully clarified.
While there have been extensive studies on how mechanical forces alter cellular responses by activating various mechanosensitive, transmembrane receptors and by regulating nuclear structure and trans-nuclear transport of transcription factors (6,10), very little is known regarding strain magnitudes sensed by cells and the consequent alterations in nuclear morphology in situ. For instance, mechanical deformation of cells can activate membrane-associated phospholipases and stimulate various secondary messenger pathways, such as Ca2+ release from intracellular stores and activation of protein kinase C (6). There is also a body of literature demonstrating that nuclear shape and structure plays an important role in regulating cellular phenotype (11–13). Mechanical signal transduction to the nucleus occurs through direct strain transfer from the local matrix, by propagation through integrin receptors and the contractile actin cytoskeleton, to the nuclear and subnuclear compartments (10). While it is clear that applied strains are transferred through the local matrix to the subcellular level, this strain transfer has not been quantified and it is not yet clear where the strain heterogeneity arises in native tissue.
The significance of strain transfer mechanisms on mechanotransduction is also pertinent in tissue-engineered replacements for these load-bearing tissues. Upon implantation, such engineered tissues will be exposed to the same mechanical environment, and will be required to mechanoregulate to function in the host environment. A further complication with these growing tissues is that, as the construct matures, the biochemical content, cell mechanics, and matrix properties change (14,15). As such, the multiscale strain transfer mechanisms operative in such engineered tissues are likely to change with maturation. Ideally, engineered tissues should develop microenvironments that closely resemble their native tissue counterparts to provide physiologically relevant mechanical stimuli to the cells. Previous studies employing nanofibrous scaffolds seeded with mesenchymal stem cells (MSCs) have demonstrated that nuclear orientation, morphology, and deformation changes are dependent on the nanofiber orientation, organization, and loading axis (15–17). In addition, the cellular response in these engineered systems is more predictive than in native tissue, where cell and nuclear deformation appear to be more directly correlated with applied stretch in the engineered tissues. However, it is unknown as of this writing how the multiscale strain transfer mechanism in immature engineered tissues relates to native tissues.
The objective of this study was to quantify multiscale strain transfer from the tissue-level through to the local matrix, the cell, and ultimately to the nucleus in fibrous tissues, including meniscus, tendon, and single lamellar AF, as well as in MSC-seeded scaffolds engineered to reproduce the organized microstructure of the native tissues. Because fiber angle and structural heterogeneity varies across these tissues, we hypothesized that the strain would not directly transfer to the local matrix and the cell for tissues where the fiber angle deviated from the loading direction (as in the AF) and as the structure became less ordered (as in meniscus compared to tendon). We further hypothesized that the local matrix strains would be more heterogeneous for tissues with less-ordered structure. Because immature cell-seeded scaffolds are highly ordered structures, we hypothesized that strain would directly transfer to the local matrix in these constructs. A second objective of this study was to provide an additional mechanism to the previously reported heterogeneity in native tissue local matrix strains; here we hypothesized that discordant strain transfer at the cellular level was the result of distinct local microdomains within these tissues that are either fibrous or PG-rich, with strain transfer being more direct in fibrous tissue domains. To test this hypothesis, we performed histological analyses to identify the existence of such microdomains and computed the cell and nuclear strain based on nuclear shape signatures indicative of their presence in a fibrous or PG-rich microdomain.
Materials and Methods
Preparation of native tissue samples
Juvenile (1–6 months-old) bovine menisci, patellar tendons, and caudal intervertebral disks were harvested within 12 h postmortem (n = 6 each). Meniscus test samples were obtained from the outer region of the tissue. Patellar tendon test samples were acquired from the midsubstance region. Single lamellar AF test samples with a circumferential orientation were harvested from the disk outer region. Each sample was cut with a scalpel to uniform dimension of 12.0 × 3.0 × 0.3–0.8 mm (length × width × thickness). The primary collagen fiber direction of meniscus and tendon samples was parallel to the sample length. The primary collagen fiber direction of AF samples was oriented ∼30° to the sample length, consistent with its anatomic orientation in the spine. After isolation, samples were maintained in culture medium (Dulbecco’s Modified Eagle Medium, DMEM, with 100 U/mL penicillin and 100 μg/mL streptomycin; Life Technologies, Grand Island, NY) for no longer than 4 h before mechanical testing.
Preparation of cell-seeded scaffolds
Aligned nanofibrous poly(ε-caprolactone) (PCL) scaffolds were produced by electrospinning as described previously in Baker and Mauck (18). Briefly, PCL (BrightChina, Hong Kong, China) was dissolved at 14.3% w/v in a 1:1 mixture of tetrahydrofuran and n,n-dimethylformamide (Fisher Chemical, Fairlawn, NJ). This solution was expelled through a charged spinneret (+13 kV) via syringe pump at a rate of 2.5 mL/h. The resulting fiber jet was collected onto a grounded mandrel rotating with a surface velocity of 10 m/s. Scaffold sheets of ∼800-μm thickness were removed from the mandrel and sectioned into rectangles (65 × 5 mm2) with the prevailing fiber direction oriented at 0° or 30° with respect to the sample length (n = 6 each) (16,19). The scaffold was sterilized and hydrated using serial washes with decreasing concentrations of ethanol (100, 70, 50, 30, and 0%) and then soaked overnight in a solution containing fibronectin at 20 μg/mL (20). Before seeding, scaffolds were washed once with phosphate-buffered saline (PBS).
Bovine mesenchymal stem cells (MSCs) were isolated from bone marrow from the femurs and tibiae of 3–6 month-old calves at room temperature, as described previously in Mauck et al. (21). Cells were expanded for two passages on tissue culture plastic in basal medium (high glucose DMEM containing 1% penicillin, streptomycin, fungizone, and 10% fetal bovine serum; Life Technologies). Cells were seeded onto the scaffolds at a density of 600 cells/mm2 and cultured in basal media for 24 h before mechanical testing.
Custom micromechanical test device
For mechanical evaluation, a custom micromechanical test device was used to apply uniaxial tension to each sample (Fig. 1 A). The device was designed to fit on the stage of a high-speed inverted confocal microscope system (LSM 5 LIVE; Carl Zeiss, Jena, Germany). The device consisted of a 10-N load-cell, two linear stepper motors (Zaber LSM025A-MC06; Zaber, Vancouver, Canada), and grips that project from each motor into the sample bath (Fig. 1 A). This setup enables gripping test specimens immediately above the glass coverslip for imaging on the confocal microscope. Precise height adjustment of the grips was achieved by using shim stocks and consistently screwing the grip onto the platforms using a torque wrench. In addition, two motors were used to apply tension in opposite directions, which minimized region-of-interest movement out of the field-of-view. A custom LabView (National Instruments; Austin, TX) program was written to control the motors and acquire data.
Figure 1.
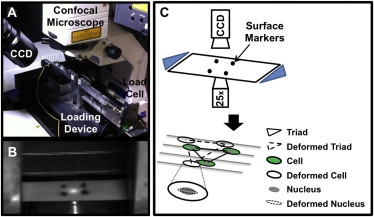
(A) Experimental setup of the custom micromechanical tester situated on confocal imaging system. (B) A representative image of a sample top surface with fiducial markers captured with a CCD camera. (C) Schema of the experimental design, where macroscale and microscale images were simultaneously imaged at each strain level via CCD camera and confocal microscope, respectively. Fiducial surface markers were used to calculate tissue-level strain. Cell nuclear triads were used to calculate local matrix strain. Cell and nuclear strains were also calculated.
Uniaxial tensile testing and confocal imaging
Before testing, cells and/or nuclei within each sample were stained with fluorescent markers to provide fiducial markers for strain analysis and boundaries for quantification of cell and nuclear strain. Native tissue samples were stained with 0.01 μg/mL FM4-64 (Life Technologies) and NucBlue Hoechst 33342 (Life Technologies) in 0.15 M PBS at room temperature for 5 min to visualize cell and nuclear shape, respectively. MSC-seeded scaffolds were stained with 10 μM Calcein AM (Life Technologies) and NucBlue Hoechst 33342 in 0.15-M PBS at room temperature for 15 min to visualize cell and nuclear shape, respectively. After labeling, the samples were washed briefly in PBS to remove residual dye. Four tissue markers were applied on the top side of each sample, using a needle and Verhoeff’s stain. These markers were used to determine tissue-level strain (Fig. 1 B).
Samples were placed into the tensile strain device with the side containing the four tissue markers facing up (Fig. 1, B and C). Samples were kept immersed in culture medium (DMEM with 100 U/mL penicillin and 100 μg/mL streptomycin) at room temperature throughout testing. The tissues may have swelled due to immersion in culture medium, which could alter the multiscale strain transfer. However, because all of the samples were prepared and tested in the same manner, they would be similarly affected by swelling. Samples were preloaded to 0.01 N to remove slack. Subsequently, stepwise grip-to-grip strains of 3, 6, 9, 12, and 15% were applied at a strain rate of 1%/s. In the un-deformed state and 30 s after application of each strain increment, multichannel z-stack confocal images were captured using a water-immersion 25× lens (field of view, 360 × 360 μm2; Hoechst, 405 nm/BP 420–480 nm; FM4-64, 515 nm/LP 650 nm; Calcein AM, 488 nm/LP 505 nm). Our preliminary work and other previous work (9,22) confirmed that no microscopic movements were observed after 30 s, ensuring accurate measurements of immediate strains upon tissue stretch. The same region of interest was visually tracked at each strain increment. Acquisition of z-stack images enabled tracking the same cells moving in and out of plane with applied strain. The position of the tissue fiducial markers on the top surface of each sample was separately captured using a charge-coupled device (CCD) camera during confocal imaging.
Multiscale strain calculation
The four fiducial markers on the sample surface were used to calculate the two-dimensional tissue Lagrangian strains (E11, E22, and E12; n = 6 per group) using a custom MATLAB program (The MathWorks, Natick, MA) that automatically detected and tracked the centroids of each marker. Lagrangian strain was defined as E = 1/2 (C – I), where I is the identity matrix and C is the right Cauchy-Green deformation tensor (C = FT ⋅ F, where F is the deformation gradient). Tissue Lagrangian strain was used instead of applied grip-to-grip strain because sample slipping can occur near the grips, resulting in errors in strain measurements. To calculate local matrix Lagrangian strains, the centroids of three cell nuclei forming a triad were used (Fig. 1 C, n = 20 triads per sample). Maximum tissue and local matrix principal strains (e1) were computed from these measures, using the relationship
Cellular (n = 20) and nuclear (n = 40) long and short axes were measured using a custom MATLAB program (The MathWorks) and the software IMAGEJ (National Institutes of Health, Bethesda, MD), respectively. Using the long and short axis measurements, cellular and nuclear aspect ratios (CAR and NAR, respectively) were calculated by taking the ratio of cell or nuclear long to short axis at each strain increment, where long axis coincided with the direction of prevailing fibers (15–17). Cell and nuclear strains were calculated using the equation
where l and L are deformed and un-deformed long axis lengths, respectively.
Histology
Separate samples were fixed in buffered 10% formalin, and processed for paraffin histology. Processed samples were sectioned and double-stained with Alcian Blue to visualize PGs and with Picrosirius Red to visualize collagen. Samples were also stained with DAPI to visualize nuclear morphology and organization in fibrous and PG-rich regions.
Data analysis
All data are represented as mean ± standard error. Linear regression was performed between Lagrangian tissue versus local matrix strain, local matrix versus cell strain, and cell versus nuclear strain. For tissue versus local matrix strain, linear regression was performed on all matching raw data points. A linear correlation and extra-sum-of-squares F-test was performed to test for significant differences between the slopes of fitted lines against slopes of 0 and 1, which would indicate 0 and 100% strain transmission, respectively. A one-way analysis of variance with Bonferroni posthoc test was performed for initial CAR and NAR data (across sample groups) and normalized CAR and NAR data (within sample groups).
Cell and nuclear strains of meniscus samples were binned into round and elongated NAR determined from histology (round was indicated by an NAR ≤ 2.15 and elongated was indicated by an NAR > 2.15; n = 10), which represent PG-rich and fibrous microdomains respectively. Linear regression was performed between tissue versus cell and tissue versus nucleus for each microdomain. Significance was set at the 95% confidence level.
Results
Cellular and nuclear alignment and morphology
In situ confocal imaging of native tissues revealed that the long axis of both the cell and the nucleus was aligned in the direction of prevailing collagen fibers (Fig. 2, A–C, and E–G). A high degree of cell and nucleus alignment with nanofiber direction was also observed in MSC-seeded scaffolds, consistent with previous results (Fig. 2, D and H) (16). Qualitatively, overall cell and nuclear morphology of tendon cells were more elongated than meniscus and AF cells. In addition, nuclear morphology of MSCs appeared rounder than nuclear morphology of the cells in native tissues.
Figure 2.
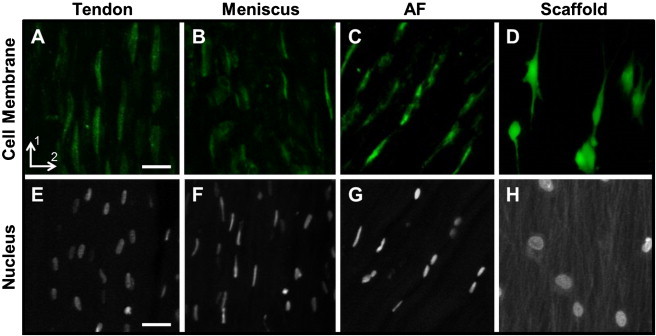
Representative confocal images (25×) of native and engineered tissue cell and nuclei. Fluorescently-labeled cell membrane of (A) tendon, (B) meniscus, (C) AF, and (D) MSC-seeded scaffold; cell nuclei of (E) tendon, (F) meniscus, (G) AF, and (H) MSC-seeded scaffold. Scale bar = 25 μm.
Strain transfer from the tissue to the local matrix
To determine how much of the applied tissue-level strain was transferred to the local matrix (i.e., the intercellular microenvironment at the length scale of cells), Lagrangian tissue and local matrix strains in the direction of loading (E11) were compared via linear correlation (Fig. 3, A and B). Local matrix strain in all native tissues and scaffolds were linearly correlated with their respective tissue-level strains (p < 0.05, 0.2 < r2 < 0.4). Attenuation of the local matrix strain relative to the applied strain was observed in all groups (p < 0.05), defined by the slope of the correlation line, which was <1.0 in each case (Fig. 3, A and B). However, the degree of strain attenuation varied between native tissues and scaffolds. Specifically, local matrix strain transfer was attenuated by 35–70% in all native tissues, whereas local matrix strains were attenuated by only 15–25% in scaffolds (Fig. 3, A and B). Comparison of the maximum principal strains of tissue and local matrix showed a 1:1 relationship (Fig. 3, C and D), where the slopes of correlation lines were not statistically different from a slope of 1.0, demonstrating that the magnitude of tissue strain was conserved and heterogeneity was related to pronounced E12 and E22 strain components at the local matrix level for the native tissue samples.
Figure 3.
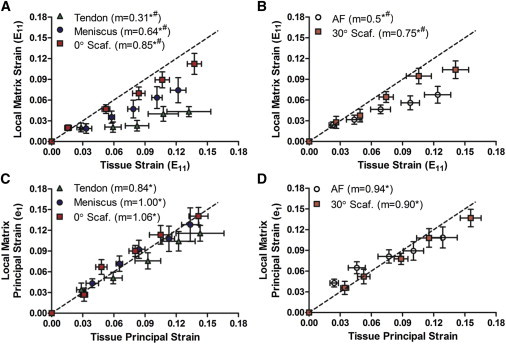
(A) Mean local matrix versus tissue Lagrangian strain (E11) of aligned tissue groups and (B) angled tissue groups. (C) Mean local matrix versus tissue maximum principal strain (e1) of aligned tissue groups and (D) angled tissue groups. (m) Slope; (∗) p < 0.05 compared to slope of 0; (#) p < 0.05 compared to slope of 1; (---) slope of 1.
Strain transfer from local matrix to cell and cell to nucleus
To assess the next level of strain transfer, cell-level strain was measured with respect to the local matrix strain. This analysis showed that local matrix strain (E11) measured in the aligned samples (tendon, meniscus, and 0° scaffold) transferred to the cellular level in a linear fashion (p < 0.05, Fig. 4 A). The degree of attenuation in strain transfer in tendon and 0° scaffold was less than in meniscus (Fig. 4 A), with only 11–15% strain attenuation in tendon and 0° scaffolds compared to 29% attenuation in meniscus (p < 0.05). At the next level, strain transfer from cell to nucleus was highly coordinated in 0° scaffolds, where <10% strain attenuation occurred (p < 0.05, Fig. 4 B). In contrast, only ∼50% of meniscus cell strain was transferred to the nuclei (p < 0.05, Fig. 4 B), and very little cell strain transfer to the nucleus was observed in tendon cells (Fig. 4 B).
Figure 4.
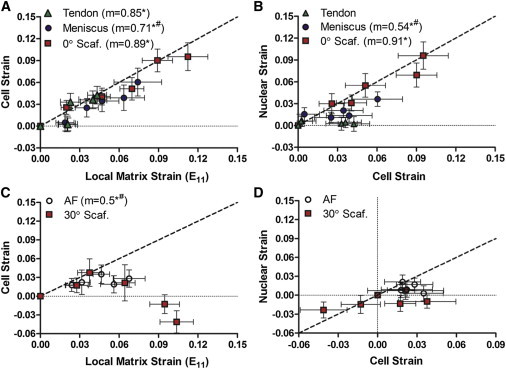
(A) Mean cell versus local matrix Lagrangian strain (E11) and (B) mean nuclear versus cell strain of aligned tissue groups. (C) Mean cell versus local matrix Lagrangian strain (E11) and (D) mean nuclear versus cell strain of angled tissue groups. (m) Slope; (∗) p < 0.05 compared to slope of 0; (#) p < 0.05 compared to slope of 1; (---) slope of 1.
In tissue and scaffold samples whose primary fiber directions were angled with respect to the loading direction (i.e., AF and 30° scaffold), only the AF samples showed strain transfer from the local matrix to the cells, where ∼50% of the local matrix strain was transferred to the cellular level (p < 0.05, Fig. 4 C). No correlation was observed between local matrix and cell strain in 30° scaffolds (Fig. 4 C). Furthermore, no correlations between cell and nuclear strain were observed in either the AF samples or the 30° scaffolds (Fig. 4 D).
Changes in cell and nuclear aspect ratio with strain
Cell aspect ratio (CAR) and nuclear aspect ratio (NAR) was calculated to establish relationships between cellular and nuclear morphology in native and engineered tissues, and their individual responses to applied strain. CARs of all groups ranged from 5 to 8 in the un-deformed state, representing a highly elongated cell shape (Fig. 5 A). Change in CAR with applied tensile strain was most sensitive in the 0° scaffolds, where CAR significantly increased compared to initial CAR, with as little as 9% applied tissue strain (Fig. 5 B, p < 0.05). At high applied tissue strains of 15%, all tissue groups (except for 30° scaffolds) increased in CAR compared to their initial CAR (Fig. 5 B, p < 0.01). In contrast, for the 30° scaffolds, CAR decreased from the initial CAR at 15% applied strain (Fig. 5 B, p < 0.01).
Figure 5.
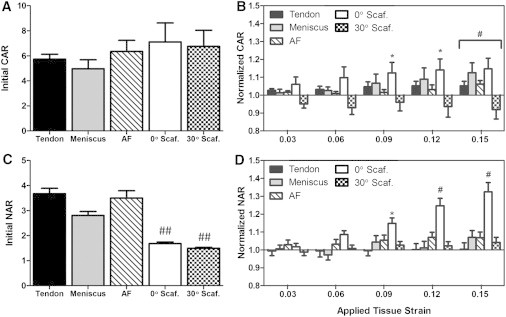
(A) Initial cell aspect ratio (CAR) in tissues and on scaffolds in the un-deformed state. (B) CAR normalized to respective initial CAR with applied tissue-level strain. (C) Initial nuclear aspect ratio (NAR) in tissues and on scaffolds in the un-deformed state. (D) NAR normalized to respective initial NAR with applied tissue-level stain. (∗) p < 0.05 compared to initial aspect ratio within tissue group; (#) p < 0.01 compared to initial aspect ratio within tissue group; (##) p < 0.05 compared to native tissue groups.
The NARs in the initial un-deformed state ranged from ∼3 to 4 in native tissues (Fig. 5 C). In contrast, the initial NAR of MSCs seeded on scaffolds was 1.6, which was significantly less elongated compared to nuclei in native tissue (Fig. 5 C). With applied strain, there was a significant change in NAR only in the 0° scaffolds (significant with >9% applied strain; Fig. 5 D, p < 0.05). The NAR did not change with applied strain for other groups.
Impact of microstructural inhomogeneity in native tissues on local matrix strain heterogeneity and the cellular microenvironment
Given the large degree of heterogeneity we observed in local matrix strain fields (as shown by the error bars in Fig. 3, A and B), we hypothesized that this may be related to inhomogeneity in the tissue microstructure. This would suggest that these tissues are not simply the highly ordered structures that typical schematic illustrations imply. To investigate this, we performed histological analyses on native tissue samples. Alcian Blue staining for PGs revealed that amorphous PG-rich microdomains were present in both the AF and meniscus (Fig. 6 A). Conversely, in tendon, very few PG microdomains were found. Moreover, staining of cell nuclei revealed that the cells residing within the PG-rich microdomains of the meniscus and AF were significantly rounder (NAR ≤ 2.15) than cells residing in fibrous regions (NAR > 2.15), where minimal PG was present (Fig. 6 A). In contrast, the nuclear morphology of tendon cells was homogeneous and uniformly elongated (Fig. 6 A).
Figure 6.
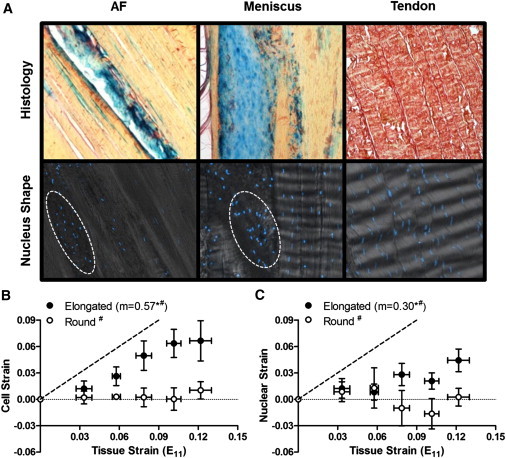
(A) Representative histology (top row) and DAPI-labeled nuclei (bottom row) images of AF, meniscus, and tendon. (Blue) PG-rich and (red) fibrous regions. (B) Mean cell versus tissue strain of elongated and round cells in the meniscus. (C) Mean nuclear versus tissue strain of elongated and round cells in the meniscus. (m) Slope; (∗) p < 0.05 compared to slope of 0; (#) p < 0.05 compared to slope of 1; (---) slope of 1.
Based on the observed structural inhomogeneity described above, we reanalyzed the meniscus strain transfer data from tissue to the local matrix, using the nuclear aspect ratio as an indicator of microstructural domain. That is, based on the coincidence of PG-rich microdomains and rounded meniscus cells, we binned the cells into round (meniscus NAR ≤ 2.15) and elongated (meniscus NAR > 2.15) groups. As hypothesized, in the fibrous regions with elongated cells, strain transfer from tissue to cell in the elongated cell fraction was linearly correlated (57% of tissue strain was transferred), whereas in the rounded cell fraction in PG-rich microdomains, no correlation was observed (Fig. 6 B). Similarly, in fibrous regions, strain transfer to nuclei was linear (30% of tissue strain was transferred), although no correlation was observed in PG-rich domains (Fig. 6 C).
Discussion
The objective of this study was to quantify multiscale strain transfer from the tissue-level through to the local matrix, the cell, and the nucleus in fibrous tissues and in MSC-seeded scaffolds. The results suggest that different tissues utilize distinct strain-attenuating mechanisms according to their unique structures and cellular phenotypes. These findings are significant in mechanobiology studies, where this information will be able to guide application of tissue/cell-specific physiologically relevant matrix, cell, and/or nuclear strains to specific mechanically induced cell signaling pathways. It is often presumed that tissue-level strain is directly transferred and sensed by the residing cells. This study demonstrates that this is not the case. Moreover, strain transfer is dependent on tissue and cell type. From a clinical perspective, these results also serve as foundation for future investigations on fibrous tissue repair and progressive degeneration by establishing how much of the applied strain the cells are able to sense within healthy tissues.
Strain attenuation and inhomogeneity at the local matrix level
The mechanical environment in which fibrous tissues operate dictates the formation, maturation, remodeling, and ultimately degeneration of these tissues. Central to all of these processes is the manner in which cells ensconced within this dense fibrous extracellular matrix sense and interpret mechanical perturbations (at the cell level) and change their behaviors. In carrying out this study, we determined that the strain transfer from the tissue level to the local matrix level was linearly correlated for both fibrous tissues and aligned polymeric nanofibrous scaffolds seeded with mesenchymal stem cells when physiological range of strain (2–15%) was applied. Physiological loading of musculoskeletal tissues remains difficult to measure; however, reported data note that tendon experiences 4–15% axial strain (23–26), outer AF experiences 2–9% circumferential strain (27,28), and outer meniscus experiences 2–6% circumferential strain (29–31). Quite interestingly, we observed that local matrix strain was highly attenuated and heterogeneous in native tissues (Fig. 3, A and B). This finding has important implications for the cells within such fiber-reinforced tissues, which would then be exposed to a highly variable and shielded mechanical microenvironment during physiological loading. Strain attenuation in native tissues may be due to several factors, including collagen fiber sliding (9,22,32,33), fiber uncrimping (34,35), fiber recruitment (36,37), and the presence of structural heterogeneities within these tissues (Fig. 6 A) (38–42), and these findings are consistent with previous work using individual tissue types (7–9,22). Specifically, minimal strain attenuation at low applied strains (3–6%) may be explained by collagen fiber uncrimping and recruitment (Fig. 3, A and B). Higher levels of strain attenuation at high applied strains (6–15%) may be explained by collagen fiber sliding and structural heterogeneities (Fig. 3, A and B), where increased local matrix shear strains were observed.
Another observation of this study was that strain heterogeneity and attenuation was not the same in all fibrous tissues. In fact, we observed discordant strain transmission at different structural length scales and in different locations, depending on tissue type. For instance, in PG-rich microdomains in both the meniscus and the AF (Fig. 6 A), there was minimal strain transfer from the tissue to the cells. This finding suggests that PG-rich microdomains (which potentially lack a dense organized fiber structure) provide a mechanical microenvironment that shields the cells from large mechanical strains (Fig. 7) applied at the tissue level. Indeed, fiber directionality is a key factor for mechanical signal exchange between extracellular matrix and cells (43). In contrast to AF and meniscus, tendon has a more uniform structure with highly aligned fibers, minimal PG-rich microdomains, and few rounded cells (Fig. 6 A). Despite this homogeneous structure, strain transfer in the tendon was also heterogeneous, though the difference between applied strain and transferred strain occurred at a different level of hierarchy and likely arose from different structural mechanisms. For example, it is possible that more prevalent collagen fiber uncrimping, sliding, and recruitment in tendon (22,36) contributed to attenuation and inhomogeneity of applied strain. Additionally, whereas aligned scaffolds and meniscus (to some extent) showed coordinated cell-to-nuclear strain transmission, very little cell-to-nuclear strain transmission occurred in tendon. Collectively, these findings suggest that different tissues utilize dissimilar strain attenuating mechanisms according to their unique structures and cellular phenotypes.
Figure 7.
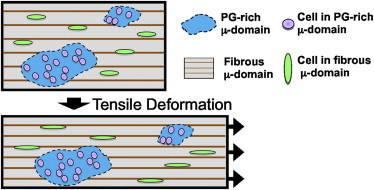
Schema illustrating how cells within a PG-rich microdomain are shielded from applied tissue-level strain, whereas cells residing in fibrous domains experience more direct strain transfer.
In contrast to native tissues, cell-seeded scaffolds transferred nearly all applied tissue strain to the local matrix level with minimal attenuation. This is likely due to the lack of complexity in matrix constitution, in that the aligned PCL nanofibers comprising the scaffold form a regular and simple array that enables direct and uniform strain transmission in these immature scaffolds. Recently, an investigation of microscale mechanics of rat tail tendon and tenocyte-seeded collagen I gels also demonstrated that typical collagen scaffolds do not mimic the highly aligned collagen of the native rat tail tendon (33). This suggests that the hierarchical arrangement of collagen fibrils, in addition to the presence of other proteins, such as collagen cross-links, proteoglycans, minor collagen, and elastin, may play an important role in establishing the mechanical microenvironment guiding strain transmission in native tissues. In our previous work, we have shown that NAR increases as constructs mature and cells infiltrate the fiber matrix and deposit new collagen fibrils in the prevailing scaffold fiber direction (44). These findings suggest that in mature constructs, the mechanical microenvironment will become more similar to native tissues, and perhaps begin to show strain attenuation with increasing matrix deposition. From a tissue engineering perspective, these findings of differential strain transfer in native tissues and immature engineered constructs may be used as a microscale benchmark of native tissues and to guide tissue-specific mechanical culture methods with the goal of accelerating maturation toward native tissue structure and function, and ultimately appropriate biologic response to mechanical loading when implanted in vivo.
Local matrix-to-cell strain transfer and cellular deformation
Although there have been numerous studies detailing how mechanical forces alter cellular responses by activating various mechanosensitive trans-membrane receptors and by regulating nuclear structure and trans-nuclear transport of transcription factors (6,10), very little is known regarding strain magnitudes sensed by cells and the consequent alterations in nuclear morphology in native tissues in situ. In this study, we demonstrated that strain transfer to the cell-level depended on the underlying fiber orientation (aligned versus angled) and on the material (tissue versus cell-seeded scaffold). In aligned samples, the cell strain was uniform and directly correlated with the local matrix strain (Fig. 4 A) and the CAR tended to increase with applied strain (Fig. 5 B). In contrast, in angled samples, strain transfer to the cell level was not directly correlated with local matrix-level strain and was even negative for the cell-seeded scaffold (Fig. 4 C). Thus, there is a strong dependence on fiber orientation for local matrix-to-cell strain transmission (15,16). The unexpected negative cell strains for angled samples may be explained by the incongruity between the directions of the long axis of the cell (aligned in fiber direction), which is at a 30° angle the loading direction. The cell may be compressed as the scaffold deforms and rotates under the uniaxial tensile loading configuration applied in this study (16). This observation is consistent with a recent study where the NAR of MSCs seeded on 30° scaffolds decreased with increasing applied tissue-level strain (16).
We also noted large differences in local matrix-to-cell strain transfer between tissue and cell-seeded scaffolds that were also dependent on fiber orientation. Although strain transfer from local matrix to cells in the 30° scaffolds resulted in negative cell strains at high strain levels, strain transfer from local matrix to cells in the AF tissue samples showed an attenuated, but positive, relationship (Fig. 4 C). It is possible that the microenvironment in which the cells reside may have an effect on their interpretation of these off-axis loading configurations; MSCs are attached on the surface of the PCL fibers while cells in tissue are completely surrounded by matrix proteins. Overall, these findings demonstrate that fiber alignment and the underlying material affects how cells experience strain applied off-axis to their prevailing direction. This differential strain transmission will likely result in discordant mechano-biological consequences in both native and engineered tissues. Indeed, our recent work showed that transcription of matrix molecules with short-term applied deformations was higher for cells on aligned scaffolds loaded in the fiber direction compared to those loaded at 30° with respect to the fiber direction (16).
Cell-to-nucleus strain transfer and nuclear deformation
As the length scale over which strain transfer was analyzed in this study reached the level of the nucleus, effects of fiber orientation and material were accentuated, and the effect of cell type also became prominent. At this level of analysis, strain transfer from the cell to the nucleus was highly correlated only for the 0° scaffold (Fig. 4 B), consistent with previous literature (15,16); in the meniscus, which is also highly aligned, there was only a moderately correlated but attenuated transfer of cell strain to nuclear strain (Fig. 4 B). Interestingly, no correlation was observed in tendon, AF, or 30° scaffold samples (Fig. 4, B and D). Of further note, the initial NAR was significantly higher in tissue specimens compared to immature MSC-seeded scaffolds (Fig. 5 C), likely due to differences in cell type (fibrous tissue cell versus MSC) and three-dimensional fibrous microenvironment (cells atop the surface of fibers compared to within a dense aligned fibrous network).
Collectively, these results show that there may be distinct mechanisms of cell-to-nucleus strain transfer between differentiated and undifferentiated cells, and among different fibroblast-like cell types. The distinct response between MSC and fibrous tissue cells may result from differences in nuclear stiffness and connectivity between undifferentiated and differentiated cells (15). Previous work employing both MSC and fibrochondrocyte-seeded aligned scaffolds have demonstrated that the cytoskeletal networks in both cell types are similar, but that nuclear deformation was greater in MSCs when tensile deformation was applied (15). Indeed, it has been demonstrated that A-type lamins (e.g., lamins A and C), which play a critical role in providing nuclear structure (45–47), shape (46,48,49), stability (50,51), and therefore stiffness, are absent in undifferentiated stem cells but develop as cells undergo differentiation (52). In addition, it has been postulated that density and organization of chromatin also may contribute to the mechanics of the nucleus, and can be altered with differentiation (53).
Mechanobiological implications of PG-rich microdomains in fibrous tissues
One important finding noted above was the heterogeneity of local matrix level strains across the tissue with tensile strain applied at the bulk level. Histological analysis suggested that different domains exist within these fibrous tissues, with most of the tissue being fibrous and characterized by an aligned collagen structure and sparse but elongated cells, and other regions being PG-rich, and characterized by a dense accumulation of PGs and rounder cells at a higher density. These observations are consistent with very recent reports in the literature on tendon in pathologic states, where PG-rich microdomains were primarily characterized by aggrecan (41,42,54,55). In our study, using tissue from juvenile animals, the size and number of these PG-rich microdomains was greater in AF and meniscus tissue samples than in tendon tissue. It is widely accepted that collagen resists tension and proteoglycan resists compression (56–60); however, the greater presence of microdomains in PG-rich fiber-aligned tissues such as meniscus and AF suggests that the role of PG is more complex at the microscale level in these tissues. Moreover, it is unknown whether the cells in different microdomains (e.g., PG-rich versus fibrous microdomains) are subjected to different mechanical microenvironments.
To establish whether these microdomains influence strain transfer locally, we separated the cell strains based on meniscus cell aspect ratio, where the rounded cells were typically located in PG-rich microdomains and the elongated cells were typically located in fibrous microdomains (Fig. 6 A). Interestingly, round cells within PG-rich microdomains did not deform with applied tissue strain, while elongated cells in fibrous microdomain and their nuclei deformed linearly with increasing tissue strain (Fig. 6, B and C). This suggests that the cells within PG-rich microdomains are shielded from tensile strain (Fig. 7). Such diminished strain transfer would likely decrease mechanosensing by these cells, and suggests more generally that cellular response to mechanical stimulation will occur in a domain-dependent manner.
Accumulation of PG-rich microdomains within fibrous regions is commonly observed in injured or degenerated menisci and tendons (38,41,42,54,55). This study established how the applied strain is transferred to the cells within healthy tissues. It remains to be determined whether strain is differentially sensed within damaged tissue, but this is likely the case. It is well known that tissue material properties change with injury and degeneration and that this degradation is cell-mediated. Future investigations on the effects of altered microscale strains on disease onset and on feedback for disease progression will be critical for advancing the treatment of musculoskeletal disorders.
Conclusion
This study investigated multiscale strain transfer behavior and highlighted factors that are involved in governing the strain transfer at different scale levels. Strain transfer from tissue to local matrix level is highly attenuated and heterogeneous in native tissues compared to freshly seeded scaffolds, where direct and uniform strain transfer was observed. It was also determined that meniscus and AF develop PG-rich microdomains that contribute to increased strain transfer heterogeneity, and potentially subject cells within PG-rich microdomains to a different mechanical microenvironment than those in other regions of the tissue. Strain transfer from local matrix to cells depended on the underlying fiber orientation (aligned versus angled) and on the material (tissue versus cell-seeded scaffold). At the subcellular level, these effects were accentuated and the effect of cell type also regulated the final step of strain transfer from the cell level to the nuclear level. To the best of our knowledge, the results demonstrate for the first time that strain transfer from tissue to matrix, cell, and nuclei is tissue-specific and microstructure (i.e., fiber orientation and tissue microdomain)-dependent. In conclusion, these findings shed what we believe to be important new information on the manner in which strain transfer occurs in dense connective tissues as well as tissue-engineered mimics of these native tissues, and will be essential for interpreting the biologic response of such tissues and constructs to their mechanical loading environment.
Acknowledgments
The authors thank Dr. Matthew B. Fisher and Dr. Jeffrey L. Caplan for histology, confocal imaging, and helpful discussions.
Research was funded by the National Institutes of Health grants No. R01EB002425, No. R01AR056624, No. P20RR016458 and No. T32AR007132, and the Penn Center for Musculoskeletal Disorders grant No. P30AR050950.
References
- 1.Vanderby R., Provenzano P.P. Collagen in connective tissue: from tendon to bone. J. Biomech. 2003;36:1523–1527. doi: 10.1016/s0021-9290(03)00132-5. [DOI] [PubMed] [Google Scholar]
- 2.Makris E.A., Hadidi P., Athanasiou K.A. The knee meniscus: structure-function, pathophysiology, current repair techniques, and prospects for regeneration. Biomaterials. 2011;32:7411–7431. doi: 10.1016/j.biomaterials.2011.06.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.McDevitt C.A., Webber R.J. The ultrastructure and biochemistry of meniscal cartilage. Clin. Orthop. Relat. Res. 1990;(252):8–18. [PubMed] [Google Scholar]
- 4.Eyre D.R. Biochemistry of the intervertebral disc. Int. Rev. Connect. Tissue Res. 1979;8:227–291. doi: 10.1016/b978-0-12-363708-6.50012-6. [DOI] [PubMed] [Google Scholar]
- 5.Cassidy J.J., Hiltner A., Baer E. Hierarchical structure of the intervertebral disc. Connect. Tissue Res. 1989;23:75–88. doi: 10.3109/03008208909103905. [DOI] [PubMed] [Google Scholar]
- 6.Mammoto A., Mammoto T., Ingber D.E. Mechanosensitive mechanisms in transcriptional regulation. J. Cell Sci. 2012;125:3061–3073. doi: 10.1242/jcs.093005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Upton M.L., Gilchrist C.L., Setton L.A. Transfer of macroscale tissue strain to microscale cell regions in the deformed meniscus. Biophys. J. 2008;95:2116–2124. doi: 10.1529/biophysj.107.126938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Arnoczky S.P., Lavagnino M., Hoonjan A. In situ cell nucleus deformation in tendons under tensile load; a morphological analysis using confocal laser microscopy. J. Orthop. Res. 2002;20:29–35. doi: 10.1016/S0736-0266(01)00080-8. [DOI] [PubMed] [Google Scholar]
- 9.Bruehlmann S.B., Hulme P.A., Duncan N.A. In situ intercellular mechanics of the bovine outer annulus fibrosus subjected to biaxial strains. J. Biomech. 2004;37:223–231. doi: 10.1016/s0021-9290(03)00244-6. [DOI] [PubMed] [Google Scholar]
- 10.Wang N., Tytell J.D., Ingber D.E. Mechanotransduction at a distance: mechanically coupling the extracellular matrix with the nucleus. Nat. Rev. Mol. Cell Biol. 2009;10:75–82. doi: 10.1038/nrm2594. [DOI] [PubMed] [Google Scholar]
- 11.Thomas C.H., Collier J.H., Healy K.E. Engineering gene expression and protein synthesis by modulation of nuclear shape. Proc. Natl. Acad. Sci. USA. 2002;99:1972–1977. doi: 10.1073/pnas.032668799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lelièvre S.A., Weaver V.M., Bissell M.J. Tissue phenotype depends on reciprocal interactions between the extracellular matrix and the structural organization of the nucleus. Proc. Natl. Acad. Sci. USA. 1998;95:14711–14716. doi: 10.1073/pnas.95.25.14711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Guilak F. Compression-induced changes in the shape and volume of the chondrocyte nucleus. J. Biomech. 1995;28:1529–1541. doi: 10.1016/0021-9290(95)00100-x. [DOI] [PubMed] [Google Scholar]
- 14.Mauck R.L., Baker B.M., Elliott D.M. Engineering on the straight and narrow: the mechanics of nanofibrous assemblies for fiber-reinforced tissue regeneration. Tissue Eng. Part B Rev. 2009;15:171–193. doi: 10.1089/ten.teb.2008.0652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nathan A.S., Baker B.M., Mauck R.L. Mechano-topographic modulation of stem cell nuclear shape on nanofibrous scaffolds. Acta Biomater. 2011;7:57–66. doi: 10.1016/j.actbio.2010.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Heo S.-J., Nerurkar N.L., Mauck R.L. Fiber stretch and reorientation modulates mesenchymal stem cell morphology and fibrous gene expression on oriented nanofibrous microenvironments. Ann. Biomed. Eng. 2011;39:2780–2790. doi: 10.1007/s10439-011-0365-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Stella J.A., Liao J., Sacks M.S. Tissue-to-cellular level deformation coupling in cell micro-integrated elastomeric scaffolds. Biomaterials. 2008;29:3228–3236. doi: 10.1016/j.biomaterials.2008.04.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Baker B.M., Mauck R.L. The effect of nanofiber alignment on the maturation of engineered meniscus constructs. Biomaterials. 2007;28:1967–1977. doi: 10.1016/j.biomaterials.2007.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nerurkar N.L., Elliott D.M., Mauck R.L. Mechanics of oriented electrospun nanofibrous scaffolds for annulus fibrosus tissue engineering. J. Orthop. Res. 2007;25:1018–1028. doi: 10.1002/jor.20384. [DOI] [PubMed] [Google Scholar]
- 20.Nerurkar N.L., Baker B.M., Mauck R.L. Nanofibrous biologic laminates replicate the form and function of the annulus fibrosus. Nat. Mater. 2009;8:986–992. doi: 10.1038/nmat2558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mauck R.L., Yuan X., Tuan R.S. Chondrogenic differentiation and functional maturation of bovine mesenchymal stem cells in long-term agarose culture. Osteoarthritis Cartilage. 2006;14:179–189. doi: 10.1016/j.joca.2005.09.002. [DOI] [PubMed] [Google Scholar]
- 22.Cheng V.W.T., Screen H.R.C. The micro-structural strain response of tendon. J. Mater. Sci. 2007;42:8957–8965. [Google Scholar]
- 23.Lichtwark G.A., Wilson A.M. In vivo mechanical properties of the human Achilles tendon during one-legged hopping. J. Exp. Biol. 2005;208:4715–4725. doi: 10.1242/jeb.01950. [DOI] [PubMed] [Google Scholar]
- 24.Stephens P.R., Nunamaker D.M., Butterweck D.M. Application of a Hall-effect transducer for measurement of tendon strains in horses. Am. J. Vet. Res. 1989;50:1089–1095. [PubMed] [Google Scholar]
- 25.Thorpe C.T., Udeze C.P., Screen H.R. Capacity for sliding between tendon fascicles decreases with aging in injury prone equine tendons: a possible mechanism for age-related tendinopathy? Eur. Cell. Mater. 2013;25:48–60. doi: 10.22203/ecm.v025a04. [DOI] [PubMed] [Google Scholar]
- 26.Carroll C.C., Dickinson J.M., Trappe T.A. Influence of aging on the in vivo properties of human patellar tendon. J. Appl. Physiol. 2008;105:1907–1915. doi: 10.1152/japplphysiol.00059.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Desrochers J., Duncan N.A. Strain transfer in the annulus fibrosus under applied flexion. J. Biomech. 2010;43:2141–2148. doi: 10.1016/j.jbiomech.2010.03.045. [DOI] [PubMed] [Google Scholar]
- 28.Costi J.J., Stokes I.A., Iatridis J.C. Direct measurement of intervertebral disc maximum shear strain in six degrees of freedom: motions that place disc tissue at risk of injury. J. Biomech. 2007;40:2457–2466. doi: 10.1016/j.jbiomech.2006.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Jones R.S., Keene G.C.R., Pearcy M.J. Direct measurement of hoop strains in the intact and torn human medial meniscus. Clin. Biomech. (Bristol, Avon) 1996;11:295–300. doi: 10.1016/0268-0033(96)00003-4. [DOI] [PubMed] [Google Scholar]
- 30.Hollis J.M., Pearsall A.W., 4th, Niciforos P.G. Change in meniscal strain with anterior cruciate ligament injury and after reconstruction. Am. J. Sports Med. 2000;28:700–704. doi: 10.1177/03635465000280051401. [DOI] [PubMed] [Google Scholar]
- 31.Seitz A.M., Lubomierski A., Dürselen L. Effect of partial meniscectomy at the medial posterior horn on tibiofemoral contact mechanics and meniscal hoop strains in human knees. J. Orthop. Res. 2012;30:934–942. doi: 10.1002/jor.22010. [DOI] [PubMed] [Google Scholar]
- 32.Screen H.R.C., Lee D.A., Shelton J.C. An investigation into the effects of the hierarchical structure of tendon fascicles on micromechanical properties. Proc. Inst. Mech. Eng. H. 2004;218:109–119. doi: 10.1243/095441104322984004. [DOI] [PubMed] [Google Scholar]
- 33.Duncan N.A., Bruehlmann S.B., Kelly E.J. In situ cell-matrix mechanics in tendon fascicles and seeded collagen gels: implications for the multiscale design of biomaterials. Comput. Methods Biomech. Biomed. Engin. 2012 doi: 10.1080/10255842.2012.742075. in press. [DOI] [PubMed] [Google Scholar]
- 34.Miller K.S., Connizzo B.K., Soslowsky L.J. Characterizing local collagen fiber re-alignment and crimp behavior throughout mechanical testing in a mature mouse supraspinatus tendon model. J. Biomech. 2012;45:2061–2065. doi: 10.1016/j.jbiomech.2012.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Miller K.S., Connizzo B.K., Soslowsky L.J. Examining differences in local collagen fiber crimp frequency throughout mechanical testing in a developmental mouse supraspinatus tendon model. J. Biomech. Eng. 2012;134:041004. doi: 10.1115/1.4006538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lake S.P., Miller K.S., Soslowsky L.J. Effect of fiber distribution and realignment on the nonlinear and inhomogeneous mechanical properties of human supraspinatus tendon under longitudinal tensile loading. J. Orthop. Res. 2009;27:1596–1602. doi: 10.1002/jor.20938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Guerin H.A.L., Elliott D.M. Degeneration affects the fiber reorientation of human annulus fibrosus under tensile load. J. Biomech. 2006;39:1410–1418. doi: 10.1016/j.jbiomech.2005.04.007. [DOI] [PubMed] [Google Scholar]
- 38.Sun Y., Mauerhan D.R., Gruber H.E. Histological examination of collagen and proteoglycan changes in osteoarthritic menisci. Open Rheumatol. J. 2012;6:24–32. doi: 10.2174/1874312901206010024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Vanderploeg E.J., Wilson C.G., Levenston M.E. Regional variations in the distribution and colocalization of extracellular matrix proteins in the juvenile bovine meniscus. J. Anat. 2012;221:174–186. doi: 10.1111/j.1469-7580.2012.01523.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Melrose J., Ghosh P., Taylor T.K. A comparative analysis of the differential spatial and temporal distributions of the large (aggrecan, versican) and small (decorin, biglycan, fibromodulin) proteoglycans of the intervertebral disc. J. Anat. 2001;198:3–15. doi: 10.1046/j.1469-7580.2001.19810003.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Plaas A., Sandy J.D., Galante J.O. Biochemical identification and immunolocalization of aggrecan, ADAMTS5 and inter-α-trypsin-inhibitor in equine degenerative suspensory ligament desmitis. J. Orthop. Res. 2011;29:900–906. doi: 10.1002/jor.21332. [DOI] [PubMed] [Google Scholar]
- 42.Wang V.M., Bell R.M., Plaas A. Murine tendon function is adversely affected by aggrecan accumulation due to the knockout of ADAMTS5. J. Orthop. Res. 2012;30:620–626. doi: 10.1002/jor.21558. [DOI] [PubMed] [Google Scholar]
- 43.Janmey P.A., Miller R.T. Mechanisms of mechanical signaling in development and disease. J. Cell Sci. 2011;124:9–18. doi: 10.1242/jcs.071001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Baker B.M., Shah R.P., Mauck R.L. Sacrificial nanofibrous composites provide instruction without impediment and enable functional tissue formation. Proc. Natl. Acad. Sci. USA. 2012;109:14176–14181. doi: 10.1073/pnas.1206962109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Broers J.L.V., Kuijpers H.J.H., Ramaekers F.C. Both lamin A and lamin C mutations cause lamina instability as well as loss of internal nuclear lamin organization. Exp. Cell Res. 2005;304:582–592. doi: 10.1016/j.yexcr.2004.11.020. [DOI] [PubMed] [Google Scholar]
- 46.Lammerding J., Fong L.G., Lee R.T. Lamins A and C but not lamin B1 regulate nuclear mechanics. J. Biol. Chem. 2006;281:25768–25780. doi: 10.1074/jbc.M513511200. [DOI] [PubMed] [Google Scholar]
- 47.Stewart C.L., Roux K.J., Burke B. Blurring the boundary: the nuclear envelope extends its reach. Science. 2007;318:1408–1412. doi: 10.1126/science.1142034. [DOI] [PubMed] [Google Scholar]
- 48.Scaffidi P., Misteli T. Lamin A-dependent nuclear defects in human aging. Science. 2006;312:1059–1063. doi: 10.1126/science.1127168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Dahl K.N., Scaffidi P., Misteli T. Distinct structural and mechanical properties of the nuclear lamina in Hutchinson-Gilford progeria syndrome. Proc. Natl. Acad. Sci. USA. 2006;103:10271–10276. doi: 10.1073/pnas.0601058103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lammerding J., Schulze P.C., Lee R.T. Lamin A/C deficiency causes defective nuclear mechanics and mechanotransduction. J. Clin. Invest. 2004;113:370–378. doi: 10.1172/JCI19670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Dahl K.N., Kahn S.M., Discher D.E. The nuclear envelope lamina network has elasticity and a compressibility limit suggestive of a molecular shock absorber. J. Cell Sci. 2004;117:4779–4786. doi: 10.1242/jcs.01357. [DOI] [PubMed] [Google Scholar]
- 52.Constantinescu D., Gray H.L., Csoka A.B. Lamin A/C expression is a marker of mouse and human embryonic stem cell differentiation. Stem Cells. 2006;24:177–185. doi: 10.1634/stemcells.2004-0159. [DOI] [PubMed] [Google Scholar]
- 53.Dahl K.N., Engler A.J., Discher D.E. Power-law rheology of isolated nuclei with deformation mapping of nuclear substructures. Biophys. J. 2005;89:2855–2864. doi: 10.1529/biophysj.105.062554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Bell R., Li J., Wang V.M. Controlled treadmill exercise eliminates chondroid deposits and restores tensile properties in a new murine tendinopathy model. J. Biomech. 2013;46:498–505. doi: 10.1016/j.jbiomech.2012.10.020. [DOI] [PubMed] [Google Scholar]
- 55.Kumagai K., Sakai K., Sakai T. The extent of degeneration of cruciate ligament is associated with chondrogenic differentiation in patients with osteoarthritis of the knee. Osteoarthritis Cartilage. 2012;20:1258–1267. doi: 10.1016/j.joca.2012.07.013. [DOI] [PubMed] [Google Scholar]
- 56.Asanbaeva A., Masuda K., Sah R.L. Mechanisms of cartilage growth: modulation of balance between proteoglycan and collagen in vitro using chondroitinase ABC. Arthritis Rheum. 2007;56:188–198. doi: 10.1002/art.22298. [DOI] [PubMed] [Google Scholar]
- 57.Asanbaeva A., Masuda K., Sah R.L. Cartilage growth and remodeling: modulation of balance between proteoglycan and collagen network in vitro with β-aminopropionitrile. Osteoarthritis Cartilage. 2008;16:1–11. doi: 10.1016/j.joca.2007.05.019. [DOI] [PubMed] [Google Scholar]
- 58.Schmidt M.B., Mow V.C., Eyre D.R. Effects of proteoglycan extraction on the tensile behavior of articular cartilage. J. Orthop. Res. 1990;8:353–363. doi: 10.1002/jor.1100080307. [DOI] [PubMed] [Google Scholar]
- 59.Nerurkar N.L., Sen S., Mauck R.L. Dynamic culture enhances stem cell infiltration and modulates extracellular matrix production on aligned electrospun nanofibrous scaffolds. Acta Biomater. 2011;7:485–491. doi: 10.1016/j.actbio.2010.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Han W.M., Nerurkar N.L., Elliott D.M. Multi-scale structural and tensile mechanical response of annulus fibrosus to osmotic loading. Ann. Biomed. Eng. 2012;40:1610–1621. doi: 10.1007/s10439-012-0525-4. [DOI] [PMC free article] [PubMed] [Google Scholar]


