Estimation of Glomerular Podocyte Number: A Selection of Valid Methods

Abstract

The podocyte depletion hypothesis has emerged as an important unifying concept in glomerular pathology. The estimation of podocyte number is therefore often a critical component of studies of progressive renal diseases. Despite this, there is little uniformity in the biomedical literature with regard to the methods used to estimate this important parameter. Here we review a selection of valid methods for estimating podocyte number: exhaustive enumeration method, Weibel and Gomez method, disector/Cavalieri combination, disector/fractionator combination, and thick-and-thin section method. We propose the use of the disector/fractionator method for studies in which controlled sectioning of tissue is feasible, reserving the Weibel and Gomez method for studies based on archival or routine pathology material.

Podocytes play a key role in the preservation of normal glomerular structure and function.¹ Podocyte loss has been associated with progression of glomerular diseases both in humans^2,3 and in experimental models of glomerular injury.^4–6 The assessment of podocyte number in human renal biopsy samples and in kidney specimens from animal models may therefore be a pivotal component of studies of the pathogenesis and treatment of glomerular disease. Despite this, there is little uniformity in the biomedical literature with regard to the methods used for estimating podocyte number either in experimental models or clinical biopsy specimens. As a result, estimates of podocyte number can vary widely between studies, making meaningful comparisons difficult.

The glomerulus and the cells within it are three-dimensional objects. Quantitative assessment of these structures, on the other hand, has traditionally involved measurements on two-dimensional images from histologic sections. Stereology is a body of mathematical/statistical theory and methods wherein three-dimensional characteristics of objects are estimated from lower-dimensional images of those objects. Although stereology is a well developed field, as with other forms of statistically based reasoning, its results can sometimes seem counterintuitive. At the same time, apparently common-sense approaches to the estimation of quantitative structural variables, such as podocyte number, often lack stereologic validity and, as a result, introduce biologic uncertainty.

In this review we describe five methods for estimating podocyte number, examine their assumptions and limitations, and indicate some of the circumstances under which they may represent appropriate approaches. These methods occupy a range of increasingly general assumptions and corresponding changes in methodologic design. The main body of this paper provides an overview and motivation for these five methods (the Supplemental Material describes the methods with worked examples in more detail). We also present one example of a commonly used but invalid method and illustrate its shortcomings.

A Brief Introduction to Stereology

Stereology is the mathematical/statistical analysis of the structure of three-dimensional objects based on lower-dimensional samples of those objects.^7–9 Its unavoidable use of quite simple equations is often intimidating for biomedical investigators, which may explain the continued use of invalid, apparently common-sense approaches to quantifying structural measures such as podocyte number. However, although the underlying mathematics may seem daunting, stereology as a tool is simple to use. It is essentially based on sampling and counting.

A certain resistance to learning and using more complicated quantitative methods is understandable. However, it would be of great benefit for the research community to embrace the same type of transition in sophistication that was heralded 30 years ago regarding the use of statistics in medicine with the seminal paper by Stanton Glantz¹⁰ on statistical errors in the medical literature. That paper demonstrated a remarkably high frequency of basic statistical errors in articles appearing even in premier biomedical journals and introduced new standards for evaluating and reporting statistical results in the medical literature. The difficulty of making such a transition should not be underestimated, however, inasmuch as common sense and probability seem so often to be at odds.¹¹

In stereologic studies of the kidney, typical samples consist of histologic sections through an entire kidney (as in animal studies) or from a kidney biopsy (as in clinical studies). In classic stereology, measures of the feature of interest (podocyte number) are expressed relative to a reference volume (glomerular volume). In general, cell number is estimated by cell nuclear number because this is a well defined feature of the cell. These classic measures are thus densities, which represent a ratio analogous to the common meaning of density as mass per unit volume. In this case, though, the quantity in the numerator may represent any spatial variable—such as volume, area, length, or number. One of the simplest and oldest stereologic principles is that of Delesse (1847), who demonstrated that fractional volume or volume density of a mineral in rock (V_V, shorthand for volume of mineral per unit volume of rock) may be estimated without bias from the fractional area of the mineral phase in a cut face (section) of the rock (A_A, area of mineral phase per unit cross-sectional area of rock). Here is a case in which the common sense and the stereologic approaches clearly coincide.

All stereologic methods depend on representative sampling of the reference space (the whole kidney, biopsy specimen, or glomerulus). The existence of differences in variability at the different levels of the sampling process means that for any given problem there is an optimal partitioning of effort at the different sampling levels to minimize the total variance of the measurement relative to the time and effort invested, a principle sometimes described as “Do more less well.”¹² Although biologic variation between individuals is often the major source of total variance, the exact inter- and intraindividual variances of the measured variables are in general not known before the study is conducted.

After appropriate unbiased sampling of the tissue, there is a fundamental dichotomy in the subsequent stereologic method between model-based methods and design-based methods.

Model-Based Methods

The earliest stereologic methods for particle counting (in stereology, particles are defined as discrete three-dimensional objects, such as cell nuclei, glomeruli, or other objects) were model-based methods performed on single sections. The model structure, expressed in terms of geometric probability, is the set of assumptions made about the geometric features of the particles in question, such as the assumptions that glomerular tufts are spherical, podocytes are uniformly distributed throughout glomeruli, or podocyte nuclei have a specific shape. To the degree that these assumptions reflect the actual state of affairs, mathematical relationships can be derived relating average values for features measured in the two-dimensional images of sections through the reference space to the desired quantitative structural features of the three-dimensional particles. To the degree that the assumptions systematically deviate from the actual state of affairs, however, the estimates obtained will be biased.

For example, with respect to particle numerical density (number per volume), the likelihood of sampling a particle with a single section through the reference volume is not simply a function of the overall particle density in space but also of the size, shape, and orientation of the particle. This necessitates the introduction of correction factors into the general particle density estimation equation. The simplest such equation (described by Wicksell in 1925) is N_V = N_A/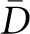, where N_V is the particle numeric density (number of particles per unit volume), N_A is the profile numeric density (number of particle profiles per unit section area), and 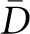is the average caliper diameter of the particles. The average caliper diameter is the average—over all particle orientations—of the maximum extent of the particle between two parallel planes (calipers; Figure 1). More complex forms of estimation equations, such as that of Weibel and Gomez,¹³ contain terms explicitly reflecting particle shape and variation in particle size (see Supplemental Material). It is important to note these methods estimate particle density (N_V) and not absolute particle number (N). Estimation of the latter also requires estimation of the reference volume. For example, estimation of total glomerular podocyte number (N_pod,glom) requires an additional estimate of average glomerular volume (V_glom). The following equation represents stereologic estimation of the total number of podocytes per glomerulus N = N_V × V:

Figure 1.

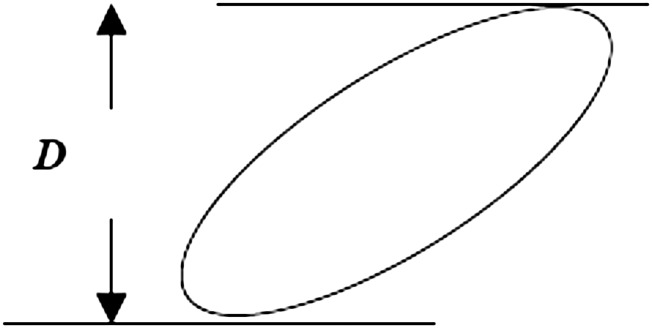
The caliper diameter is the distance D between parallel tangent lines (just touching the object) in any given direction. Note that D will differ depending on the orientation of the tangent lines. The probability of hitting a particle with a single section through a reference space is proportional not only to the density of particles in the space, but to the size of the particle and the thickness of the section. The particle size is quantified by the mean caliper diameter, 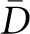, which is the average—over all particle orientations—of the maximum extent of the particle between two parallel planes (calipers).

where N_pod,glom is the number of podocytes per glomerulus, N_Vpod,glom is the number of podocytes per unit glomerular volume, and V_glom is average glomerular volume.

Design-Based (Unbiased) Methods

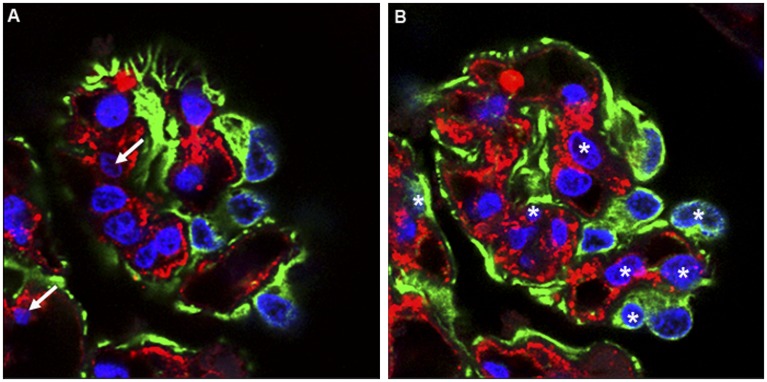
Design-based (unbiased) stereologic methods were developed as a response to the limitations inherent in model-based methods, in particular the bias in sampling introduced by the use of single sections and the difficulty of establishing values for the model (geometric) variables in biologic specimens. The current gold standard for design-based particle number estimation is the disector.¹⁴ As originally described, the physical disector is based on the new appearance of a particle between two physical tissue sections with known separation, implying that the leading point of the particle first occurred within the volume contained between the sections. As long as the specific particle can be identified as present or absent in the two sections, the event of its appearance between the sections is independent of its size or shape and the particle can be unambiguously and uniquely attributed to the volume element in which it first appeared (Figure 2). The disector so described involves two physical tissue sections (called the reference and look-up sections). An optical version of the disector has also been described.¹⁵ In this case, optical sections from bright-field or confocal microscopy are used to count particles at a unique focal point (e.g., when they are first observed) (Figure 3).

Figure 2.

The physical disector is based on the new appearance of a particle between two physical tissue sections with known separation–implying that the leading point of the particle first occurred within the volume contained between the sections. As long as the specific particle can be identified as present or absent in the two sections, the event of its appearance between the sections is independent of its size or shape and the particle can be unambiguously and uniquely attributed to the volume element in which it first appeared. The disector so described involves two physical tissue sections (called the look-up, here A, and reference section, here B). Notice that in the reference section (B) there are seven appearances of podocyte nuclei (blue) not present in the look-up section (A). When counting cell nuclei with physical disectors, section pairs (A, B) are used to count appearing and disappearing nuclei. In this example, 1-µm confocal optical images separated by 4 µm are used. Paraffin sections from a human glomerulus were stained for Wilms tumor 1 (WT-1) antigen to localize podocytes (green cytoplasm), von Willebrand factor (vWF) to localize endothelial cells (red cytoplasm), and DAPI for all nuclei (blue). Nuclei present in the look-up section (A) that were not present in the reference section (B) were counted (white arrows, two nuclei). Then, those nuclei present in the reference section (B) but not in the look-up section (A) were counted (asterisks, seven nuclei).

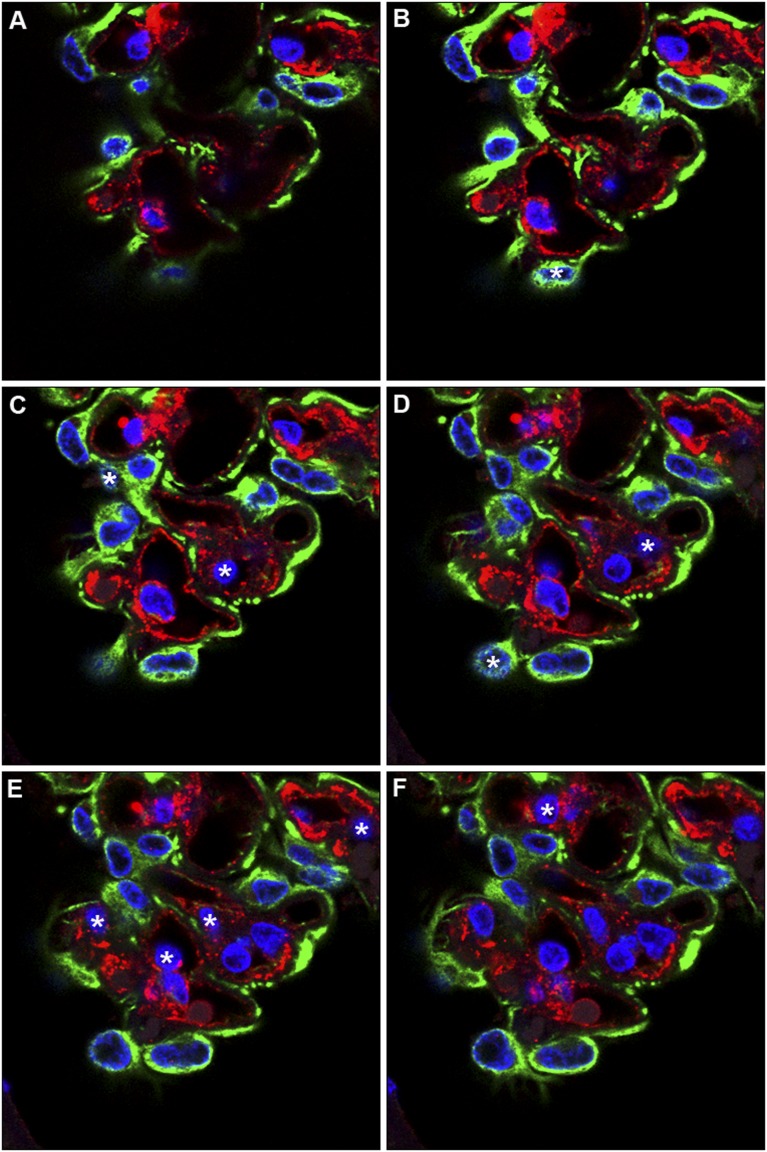
Figure 3.

When cell nuclei are counted with optical disectors, nuclei are counted at a unique moment (e.g., when they first come into focus). In this figure, 14-µm paraffin sections were immunofluorescently stained for Wilms tumor 1 (WT-1) to identify podocytes (green cytoplasm), von Willebrand factor (vWF) to identify endothelial cells (red cytoplasm), and DAPI for all nuclei (blue). Each paraffin section was then optically sectioned using confocal microscopy at 1-µm intervals; six optical sections (A–F) are shown. Nuclei in focus in A were not counted because they did not come into focus. Nuclei that came into focus in sections B–F are indicated by asterisks. The presence of WT-1 and vWF identified which of the counted cells were podocytes (three cells) and which were endothelial cells (seven cells).

Like the above-mentioned model-based methods, the disector by itself does not estimate the absolute number of particles but rather the numeric density of particles within a reference volume (N_V). Estimation of absolute podocyte number (N_pod,glom) thus requires multiplying this density by the average glomerular volume.

Alternatively, the disector can be combined with a hierarchical sampling scheme known as the fractionator to estimate the number of particles directly. This also overcomes the effects of technical artifacts, such as section compression and tissue shrinkage,^16,17 as well as the need for precise estimation of the separation of the tissue sections. Moreover, it is not necessary to estimate glomerular volume when estimating podocyte number using the disector/fractionator combination. Using the fractionator,¹⁷ systematic subsampling of an entire glomerulus or population of entire glomeruli allows an absolute quantity of interest to be determined in a defined fraction of glomerular tissue. Multiplication of the measured quantity by the inverse of the sampling fraction gives the absolute value for the individual glomerulus or an average glomerulus in the population (see Supplemental Material).

Another way to compensate for the effects of particle size and shape on the likelihood of that particle being sampled by a single section was described by Loud and colleagues¹⁸ in 1978 and traced by them to Abercrombie in 1946. This approach uses the fact that for the same actual particle numerical density (N_V), the number of particle profiles per unit area of section (N_A) increases not only with particle caliper diameter (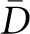) but also with section thickness t (when t is non-negligible compared with 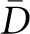): N_A = N_V( 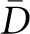+ t) (Figure 4). It can be shown that for varying section thicknesses, the slope of the regression line of the section thickness t on N_A is equal to 1/N_V. A version of this method based on two different section thicknesses has been reintroduced recently under the name thick-and-thin section method.¹⁹

Figure 4.

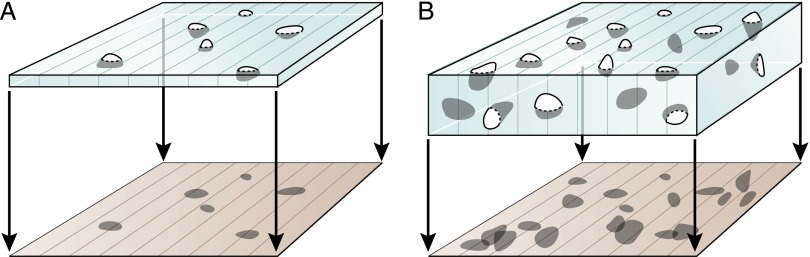
The number of particle profiles per section area (N_A) is a function not only of their density in the reference volume (N_V) but also of their size (caliper diameter, 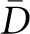) and the section thickness (t): N_A = N_V × ( 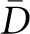+ t). Notice that the thicker section (right) contains more intersection profiles.

Comparing Model-Based and Design-Based Methods

There have been few head-to-head comparisons of model-based and design-based methods to problems of counting in the kidney.^20–22 Basgen et al.²¹ found that in estimating the number of cells (not just podocytes) in the mouse glomerulus, the estimate obtained using the disector/fractionator was not significantly different from that derived from complete enumeration on serial sections, whereas the Weibel and Gomez method yielded an estimate on average about 10% higher than the actual number. Of note, the Weibel and Gomez method showed a considerably greater coefficient of determination (R²) than the disector method and a regression-line slope of approximately 1, illustrating the fact that a method may be characterized by both bias and high precision. White and Bilous,²² on the other hand, found that in 32 renal biopsy specimens from patients with type 1 diabetes and 10 biopsy specimens from controls, the Weibel and Gomez method gave results similar to those of the disector/fractionator method as long as the Weibel and Gomez method was performed on electron microscopic images. In those images, section thickness was negligible compared with the diameter of podocyte nuclei. When section thicknesses of different methods are not comparable, large disparities in podocyte number estimates may be expected.²³

Clearly, additional head-to-head comparisons of podocyte counting methods are needed, especially in studies complemented by the gold standard method of complete enumeration by complete serial sectioning of the glomerulus. It would also be of value to establish shape and size distributions of podocyte nuclei in different species and disease states. Such data could help set limits on the accuracy and applicability of the Weibel and Gomez method.

It is certainly possible that an efficient and precise method with a small bias may be adequate for identifying large differences in podocyte number between groups. If, in fact, the methodologic bias is the same in each experimental group, the statistical evaluation of group differences may even be facilitated with a more precise, biased method compared with a less precise, unbiased method. In that case, problems arising from bias would arise mostly in comparing different studies if they use different methods. Of course, the foregoing approach requires establishing that bias is the same in the various estimates. Establishing this can take longer than performing the study using an unbiased method in the first place. We therefore strongly recommend the latter approach whenever possible.

In addition to considerations of robustness, accuracy, and precision (reproducibility), other characteristics by which estimation methods may be judged include operational efficiency (time invested per measurement and thereby cost), percentage of the overall experimental time spent on measurements, equipment requirements for the measurements, and the nature of the material to which the method is applied. Routine clinical material, not surprisingly, presents rather severe limitations to any method requiring systematic sampling.

Hence, different methods for the estimation of podocyte number may be appropriate depending on the tissue and the laboratory resources available and the need for accuracy and efficiency. Five valid methods currently in use are briefly described below. Please see more detailed descriptions of these methods with worked examples in the Supplemental Material.

Additional Considerations

Estimating Mean Glomerular Volume

Other than the exhaustive enumeration and the disector/fractionator methods, the preceding methods must all be used in conjunction with an estimate of average glomerular volume (V_glom) or individual glomerular volume in order to derive the total number of podocytes per average glomerulus or per individual glomerulus (N_pod,glom). This can easily be performed using the Cavalieri principle,^24,25 which provides an unbiased estimate of V_glom. Division of the volume density of glomeruli by the numeric density of glomeruli also provides an unbiased estimate of V_glom.⁸

Tissue Processing

If tissue used for N_Vpod,glom and V_glom estimates is processed differently (e.g., resin-embedded for the former and paraffin-embedded for the latter), differences in tissue shrinkage between these processing methods can lead to significant errors in the estimate of total podocyte number.

Nonuniform Distribution of Podocytes

A nonuniform distribution of podocyte nuclei through the glomerular tuft may also be a source of bias, at least in the Weibel and Gomez method.²⁶

Podocyte Identification

For the methods described, unambiguous identification of podocyte nuclei is essential. Other than exhaustive enumeration and optical disector approaches, these methods require that podocyte nuclear profiles can be unambiguously identified in single sections.⁹ This is not easy in routine histologic preparations. Therefore, either a very well perfusion-fixed specimen with thin sections and good staining of the glomerular basement membrane must be used, or specific immunostaining (e.g., with antibody against WT-1; see Figures 2 and 3)¹⁹ is needed to identify the podocyte nuclei. Staining of podocytes for light microscopy using anti–WT-1 antibodies may not detect dedifferentiated podocytes, which are present in some diseases.¹⁹ Identifying podocyte nuclei with electron microscopy is generally straightforward but time-consuming.

Binucleate Podocytes

All five methods outlined later are based on equating the number of podocytes with the number of podocyte nuclei. Binucleate podocytes have been described in human biopsy material,²⁷ although their frequency appears to be low. Duplicated nuclei would easily be attributed to a single podocyte in the exhaustive enumeration method and would probably present no significant difficulties to the other methods if images of sufficient resolution were used.

Counting Podocytes in Biopsy Specimens

Clinical biopsy specimens may be archival or of limited volume, effectively excluding the possibility of using podocyte counting methods requiring multiple sections. From the preceding descriptions, it is clear that the Weibel and Gomez method (based on single sections) may be the only feasible option in these cases. Studies based on clinical biopsies would need to be specifically designed to accommodate the use of design-based methods and are likely to exceed the capabilities of any but research-oriented pathology services. The disector or thick-and-thin section methods may be optimal for studies in which whole kidneys are available (largely animal models), especially if the former is used in conjunction with the fractionator.

An Example of an Invalid Method

One example of a commonly used but invalid method of estimation of podocyte number should be mentioned. The number of podocyte nuclear profiles observed in a single glomerular tuft cross-section is often reported as glomerular podocyte number. This is the ultimate common-sense approach to estimating podocyte number—just count the podocytes. But, of course, this approach provides information only on the number of podocyte nuclear fragments seen in a section through the glomerulus and does not provide reliable information on the number of podocytes in the whole glomerulus. In addition, compared with the Weibel and Gomez method as a gold standard, this approach can be shown to have low precision.²⁶ It is subject to several sources of bias. There are often glomerular size changes as a result of natural or experimental renal disease for which this approach does not account. If the volume of the glomerular tuft increases, for example, and the total number of podocytes in the glomerulus remains unchanged, then the number of hits of podocyte nuclei in single sections will decrease (Figure 5). So, to use this approach even comparatively it would be necessary to verify that average glomerular volume does not differ between groups. In addition, if truly random sections through glomeruli are used, there will be a very high variance in the number of nuclear hits. If only the large, central sections are evaluated (to reduce this effect), a bias will be introduced because of the nonuniform distribution of podocytes in the tuft.

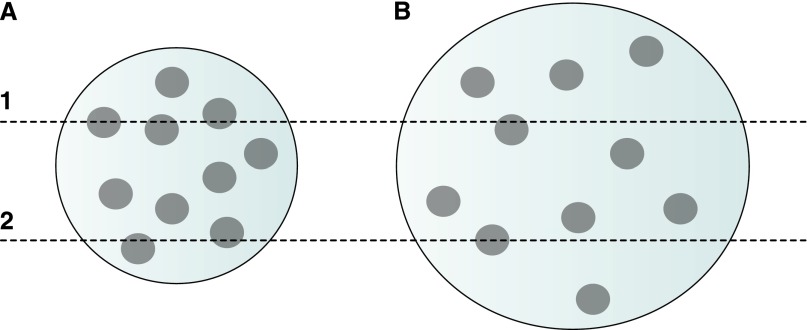
Figure 5.

Changes in the reference space affect podocyte density. This illustrates one source of error in assessing glomerular podocyte number by counting the number of podocyte nuclear hits per glomerular cross section. If the glomerular volume increases, the chances of a single section intersecting a podocyte nucleus will decrease even if the total number of podocytes is unchanged. These two reference spaces (A and B) contain the same number of particles (podocyte nuclei). Because of the larger size of B, single sections through it contain fewer particle profiles per section than sections through space A. In this case, section 1 intersects 3 particles in A and 1 particle in B. Section 2 intersects 2 particles in A and 1 particle in B.

Conclusions

In light of these considerations, we propose that all research studies reporting podocyte number use one of the five methods described below and that particular attention should be paid to satisfying the assumptions of the method used. The Weibel and Gomez method is probably the only practicable method for studies based on routine pathology specimens. The disector-fractionator combination is likely the best method to use in experimental circumstances in which whole kidneys are available. It is imperative that appropriate stereologic expertise be obtained in the review of submitted manuscripts concerning such studies in order to assure the methodologic and biologic validity of the reported results.

Concise Methods

All five methods described below can be used to estimate the total number of podocytes in individual glomeruli (Table 1). With the exception of the exhaustive enumeration method^21,28 (use of which is limited by prohibitive time constraints), all can be used to estimate total podocyte number per average glomerulus.

Table 1.

Overview of five methods

Method	Sectioning	Parameter Estimated	Requires Complete Glomerulus?	Assumptions	Affected by Sample Processing?	Unambiguous Identification of Podocyte Nuclei Required?	Time Consuming?
Exhaustive enumeration	Serial sections	Podocyte number per glomerulus (Npod,glom)	Yes	None	No	Yes	++++
Weibel and Gomez	Single sections. Does not require knowledge of section thickness	Podocyte numerical density (NVpod,glom) Multiplication by Vglom provides Npod,glom	Yes for individual glomeruli; no for average glomerular estimates	Uniform distribution of podocytes in the glomerulus; size and shape of podocyte nuclei known	Only if glomerular volume (Vglom) is estimated from tissue processed in a different manner	Yes (best by electron microscopy; light microscopy may require specific staining)	+/++ (verification of model parameters would add significantly to time required)
Disector/Cavalieri combination	Pairs of physical or optical sections	Podocyte number per glomerulus (Npod,glom)	Yes	None	Only if glomerular volume (Vglom) is estimated from tissue processed in a different manner	Yes; use of multiple sections aids identification	++
Disector/fractionator combination	Pairs of physical sections or optical sections; does not require knowledge of section thickness	Podocyte number per glomerulus (Npod,glom)	Yes for individual glomeruli; no for average glomerular estimates	None	No	Yes; use of multiple sections aids identification	++ for average glomerulus estimates +++ for individual glomerular estimates
Thick-and-thin section method	Multiple sections	Podocyte numerical density (NVpod,glom, number per glomerular volume)	No	None	Yes, if glomerular volume (Vglom) is estimated from tissue processed in a different manner	Yes (using specific stains for light microscopy)	+++

+, little time required to ++++, very time consuming.

1. Exhaustive Enumeration Method

The Basic Idea

• Serial sectioning is performed through the entire reference volume (in this case, a glomerulus).

• Podocyte nuclei are uniquely identified by their appearance in the serial sections.

• No sampling at the level of the glomerulus is required (i.e., every podocyte in the glomerulus is counted).

Principal Measurements

• The number of podocyte nuclei uniquely identified in the sections.

Assumptions of the Method

• Ability to serially section through the whole glomerulus.

• Ability to identify podocyte nuclei.

• Ability to identify profiles as representing the same podocyte nucleus in adjacent sections.

Advantages over Alternative Methods

• Total podocyte number directly determined for a given glomerulus.

• No sampling error at the level of the glomerulus.

• Not affected by changes in tissue dimensions due to processing.

• Adjacent sections can be used to help identify podocyte nuclei.

Disadvantages Compared with Alternative Methods

• Time consuming.

• Only complete glomeruli can be analyzed.

• Because of the time-consuming nature of the technique, unlikely to be used to estimate podocyte number per average glomerulus.

2. Weibel and Gomez Method

The Basic Idea

• The number of podocyte nuclei per unit volume of glomerulus (N_Vpod,glom) can be estimated from the number of podocyte nuclear profiles per unit area of sectioned glomerulus (N_Apod,glom) and the nuclear areal fraction (A_Apod,glom) in a single section through the glomerulus.

• Allowance must be made for the shape of the podocyte nuclei and their variation in size.

Principal Measurements

• The number of profiles of podocyte nuclei (hits) per unit section area of glomerulus (N_Apod,glom) and the areal fraction of the reference (glomerular) area made up by these nuclear profiles (A_Apod,glom).

• Multiplication of N_Vpod,glom by glomerular volume (V_glom, estimated for example using the Cavalieri principle⁸) provides an estimate of the total number of podocytes in the average glomerulus.

Assumptions of the Method

• Podocyte nuclei are uniformly distributed through the glomerulus.

• Podocyte nuclear profiles can be unambiguously identified (even small profiles) in single sections.

• Podocyte nuclei have identical known shapes, random orientations, and known size variation.

• Section thickness is (much) smaller than the mean caliper diameter (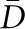) of podocyte nuclei.

Advantages over Alternative Methods

• Can be performed on single sections.

• Does not require knowledge of section thickness.

• Does not require complete glomeruli.

Disadvantages Compared with Alternative Methods

• Requires significant effort to verify model assumptions (shape and size distribution of podocyte nuclei) in each experimental group.

• In most instances requires electron microscopic images to decrease bias due to section thickness.²²

• Also requires estimation of V_glom to obtain N_pod,glom.

3. Disector/Cavalieri Combination

The Basic Idea

• Podocyte nuclei are counted with physical disectors (which use pairs of physical sections; Figure 2) or optical disectors (which use optical sections; Figure 3).

• Podocyte nuclei are counted at a unique point (e.g., when they are sampled by the reference section but not the look-up section, when they are first seen, when they disappear, when they first come into focus).

Principal Measurements

• Obtain physical or optical sections a known distance apart from a random location within the glomerulus.

• Count podocyte nuclei using either physical or optical disectors.

• Measure the area of the glomerular profile in the reference section.

• Determine the separation of the sections (the height of the disector).

• Multiplication of podocyte numerical density (N_Vpod,glom) by glomerular volume (V_glom, estimated using the Cavalieri principle⁸) provides an unbiased estimate of the number of podocytes in the glomerulus.

Assumptions of the Method

• Podocyte nuclear profiles can be recognized and unambiguously assigned as being from the same nucleus in adjacent sections (physical or optical).

• Mean caliper diameter (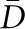) of podocyte nuclei is greater than the distance between sections (most nuclei are hit twice in the paired sections).

Advantages over Alternative Methods

• No assumptions of the shape, orientation, or size of podocyte nuclei are required.

Disadvantages Compared with Alternative Methods

• Time required to obtain two physical sections a known distance apart (cannot rely on microtome settings¹⁹) or obtain optical sections.

• Time required to compare presence or absence of specific podocyte nuclei in reference and look-up sections.

• Requires complete sectioning of glomeruli (for V_glom).

4. Disector/Fractionator Combination

The Basic Idea

• Count podocytes using physical or optical disectors (see above).

• By knowing the fraction of glomerular tissue analyzed (for either a single glomerulus or a population of glomeruli), one can use simple algebra to calculate the total number of podocytes in that individual glomerulus or in an average glomerulus.

Principal Measurements

• Count podocyte nuclei using physical disectors or optical disectors.

• Keep track of the sampling fractions used.

Assumptions of the Method

• Podocyte nuclear profiles can be recognized and unambiguously assigned as being from the same nucleus in adjacent sections (physical or optical).

• The fraction of tissue used to count podocytes is known.

Advantages over Alternative Methods

• No assumptions of the shape, orientation, or size of podocyte nuclei are required.

• Technical artifacts, such as section compression and tissue shrinkage, do not influence estimates.

• Knowledge of section thickness is not required.

• Not necessary to estimate glomerular volume.

• Does not require complete sectioning of glomeruli to obtain average values (i.e., number of podocytes per average glomerulus).

Disadvantages Compared with Alternative Methods

• Time required to obtain two sections a known distance apart (cannot rely on microtome settings¹⁹) or obtain optical sections.

• Time required to compare presence or absence of specific podocyte nuclei in reference and look-up sections.

• Requires complete sectioning of glomeruli to obtain podocyte numbers for individual glomeruli.

5. Thick-and-Thin Section Method

The Basic Idea

• Obtain multiple sections with two or more different specified thicknesses from random locations within the glomerulus.

• The number of podocyte nuclei per unit glomerular volume (N_Vpod,glom) can be estimated from the inverse of the slope of the straight line formed by plotting section thickness t (y axis) against the areal density of podocyte nuclear profiles, N_Apod,glom (x axis).

Principal Measurements

• The number of podocyte nuclear profiles per unit area of glomerular section (N_Apod,glom) for sections of two or more known thicknesses.

Assumptions of the Method

• Podocyte nuclei can be unambiguously identified in any single section.

Advantages over Alternative Methods

• No assumptions about the shape, orientation, size or size distribution of podocyte nuclei are required.

• Unlike the disector, sections are not paired, and nuclear profiles in different sections do not have to be reconciled.

• Does not require a complete glomerulus to obtain average glomerular values (i.e., number of podocytes per average glomerulus).

Disadvantages Compared with Alternative Methods

• Time needed to cut sections of at least two different thicknesses.

• Need to accurately determine the thicknesses of the sections.

• Requires complete sectioning of glomeruli (for V_glom) for estimation of podocyte number in individual glomeruli.

Disclosures

None