Single-Molecule Kinetics Reveal Cation-Promoted DNA Duplex Formation Through Ordering of Single-Stranded Helices

Abstract

In this work, the kinetics of short, fully complementary oligonucleotides are investigated at the single-molecule level. Constructs 6–9 bp in length exhibit single exponential kinetics over 2 orders of magnitude time for both forward (k_on, association) and reverse (k_off, dissociation) processes. Bimolecular rate constants for association are weakly sensitive to the number of basepairs in the duplex, with a 2.5-fold increase between 9 bp (k′_on = 2.1(1) × 10⁶ M⁻¹ s⁻¹) and 6 bp (k′_on = 5.0(1) × 10⁶ M⁻¹ s⁻¹) sequences. In sharp contrast, however, dissociation rate constants prove to be exponentially sensitive to sequence length, varying by nearly 600-fold over the same 9 bp (k_off = 0.024 s⁻¹) to 6 bp (k_off = 14 s⁻¹) range. The 8 bp sequence is explored in more detail, and the NaCl dependence of k_on and k_off is measured. Interestingly, k_onincreases by >40-fold (k_on = 0.10(1) s⁻¹ to 4.0(4) s⁻¹ between [NaCl] = 25 mM and 1 M), whereas in contrast, k_offdecreases by fourfold (0.72(3) s⁻¹ to 0.17(7) s⁻¹) over the same range of conditions. Thus, the equilibrium constant (K_eq) increases by ≈160, largely due to changes in the association rate, k_on. Finally, temperature-dependent measurements reveal that increased [NaCl] reduces the overall exothermicity (ΔΔH° > 0) of duplex formation, albeit by an amount smaller than the reduction in entropic penalty (−TΔΔS° < 0). This reduced entropic cost is attributed to a cation-facilitated preordering of the two single-stranded species, which lowers the association free-energy barrier and in turn accelerates the rate of duplex formation.

Introduction

Since the double-stranded (DS) DNA helix was first discovered more than 50 years ago, its thermodynamic stability has been the subject of much interest (1,2). More recently, DS duplex structural motifs with short complementary regions (6–30 bp) have garnered renewed attention as functional entities in their own right, with kinetics occurring on timescales commensurate with many cellular functions (3,4). As our understanding of nucleic acid’s functionality in regulating cellular processes has grown, so has the number of known duplex-like contacts that guide molecular structure-function relationships. One well-known example is the RNA template in telomerase, which facilitates the addition of telomeric repeats to the 3′ ends of linear eukaryotic chromosomes, where the chemistry is directed by hybridization of the RNA template to the single-stranded (SS) DNA (5). Some other important examples include 1), ribozyme duplex formation (6 bp) for sequence-specific cleavage (3,4); 2), initiation of translation through Shine-Dalgarno/anti-Shine-Dalgarno hybridization (6 bp) in the ribosome (6); and 3), gene silencing through RNA hybridization (20–28 bp) (7,8). This last example, called RNA interference, has been found to play important roles in both plant and animal biology, and is considered to be a critical tool for future biotechnology applications.

Generally, oligonucleotide duplex hybridization is governed by opposing forces. Noncovalent hydrogen-bonding and base-stacking interactions stabilize the duplex, overcoming the electrostatic repulsions of negatively charged backbone phosphate groups. In thermodynamic terms, hydrogen bonding and base stacking provide a large and favorable enthalpy (ΔH° ≪ 0) of formation that competes against a large entropic cost (−TΔS° ≫ 0) of organizing the highly ordered double-helix structure (1). This close fight between thermodynamic properties (i.e., favorable enthalpy versus unfavorable entropy) appears to hold true not only for duplex formation but also for more complex tertiary interactions (9–12). Despite this close balance, the folded and unfolded conformations are typically separated by large free-energy barriers (ΔG^‡), which in turn can result in a rough free-energy landscape. Under such conditions, in which ΔG° ≈ 0 and K_eq ≈ 1, small changes in ΔH° or ΔS° can result in free-energy shifts that significantly influence relative populations of the unfolded and folded states.

Mechanistically, the duplex formation process has traditionally been described as a DS helix/SS random coil (DS helix-SS_RC) equilibrium, where the transition state (TS) is assumed to be the formation of a few native basepairs. It was assumed that once these basepair nucleation seeds were formed, the full duplex could form by means of a rapid zippering mechanism (13–18). These early models were followed by more detailed pictures, including ones that explicitly describe the role of SS, or prehelical, conformations (19–23). In support of this notion, Vesnaver and Breslauer (24) estimated from calorimetry and UV melting experiments that such SS structure could account for upwards of 40% of the total enthalpy release in duplex formation at room temperature. Subsequently, SS base stacking was characterized with a variety of experimental techniques (24–29). These ideas were summarized in a mechanism proposed by Holbrook et al. (25), whereby duplex formation proceeds via a docking type of reaction. In this picture, the extent of vertical base stacking (along the helical axis) does not change appreciably between the SS and DS states, and duplex formation proceeds through the association of two SS helices.

In most of the work described above, duplex equilibria and kinetics were probed in one or a few sets of solution conditions. However, it is well known that the stability of the SS-DS equilibrium can be controlled through the manipulation of solution conditions. In particular, because oligonucleotides are polyanionic, the addition of positive counterions (e.g., Na⁺, K⁺, and Mg²⁺) is known to facilitate secondary and tertiary structure formation (30,31). A simple explanation for this effect is Manning’s counterion condensation theory, in which DS DNA is conceptualized as a rod of regularly spaced negative charges (32–35). However, by its very nature, this treatment does not address cation-induced structural changes within SS oligonucleotides, which clearly must be important in the formation of prehelical structures (24,25). Today, more complex theories about ion-nucleotide interactions have been developed, highlighting the importance of diffuse ions that remain fully solvated in the so-called ion atmosphere (36–39).

In this study, a direct approach is taken to probe duplex formation and dissociation at the single-molecule level. Specifically, DNA/DNA hybridization is observed with the use of single-molecule fluorescence resonance energy transfer (smFRET) methods (40,41). These techniques are particularly valuable because they allow the system of interest to be observed at equilibrium, in contrast to many traditional methods that rely on an externally imposed perturbation and subsequent return to equilibrium to probe kinetic processes (e.g., temperature jump experiments). Here, a synthetic, fluorescently labeled DNA construct is adapted from previous studies of telomerase activity (Fig. 1) (42). The simplicity of the construct permits use of the following bimolecular model to interpret the kinetic data:

$$\text{S}1+\text{S}2\rightleftharpoons \text{DS}$$ (1)

In these experiments, a confocal fluorescence microscope is used to observe single surface-tethered strands of DNA (S1). During the observation, the length of time (τ_dwell) the molecule remains in the hybridized (DS) or unhybridized (S1+S2) states is measured through changes in the FRET efficiency (E_FRET). Thus, the association rate, k_on (S1+S2 → DS) depends on the concentration of the freely diffusing strand (S2), which determines the frequency of interactions between S1 and S2:

$${\text{k}}_{\text{on}}={\text{k}}_{\text{on}}^{’}\left[\text{S}2\right]$$ (2)

Additionally, since S2 is sufficiently dilute (<300 nM), the freely diffusing strands do not interact among themselves and dissociation should simply proceed via pure unimolecular decay kinetics, with a rate constant k_off (DS→ S1+S2) that is independent of the S2 concentration. For a fixed S2 concentration, the bimolecular kinetic model simplifies to a unimolecular equilibrium:

$$\text{SS}\rightleftharpoons \text{DS}$$ (3)

where k_on and k_off rate constants can be used to characterize the equilibrium behavior, i.e.,

$${\text{K}}_{\text{eq}}=\frac{{\text{k}}_{\text{on}}}{{\text{k}}_{\text{off}}}$$ (4)

Figure 1.

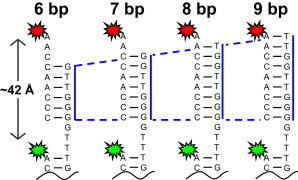
Schematic of the single-molecule construct with a 6–9 bp overhang that is free to hybridize with a complementary Cy5-DNA probe strand.

The major goals of this work are threefold. 1) First of all, we characterize the hybridization kinetics for a model single-molecule DNA duplex construct as a function of strand length and concentration to provide quantitative tests of ensemble trends at the single-molecule level (e.g., additivity of basepairing free energies). 2) Second, we focus on the 8 bp construct and thereby explore the dependence of duplex kinetics on the monovalent cation environment. 3) Finally, we perform extensive temperature-dependent studies of the duplex kinetics, which from van’t Hoff and Eyring analysis provide insights into both the overall and TS barrier free energies, respectively. Most importantly, such temperature-dependent studies enable detailed deconstruction of the corresponding free energies into separate enthalpic and entropic contributions.

A central theme of these combined efforts is that [NaCl] facilitates duplex formation by manipulating the relative magnitudes of enthalpic versus entropic contributions to the free energy. At high [NaCl] concentrations, the enthalpy for duplex formation becomes less exothermic; however, this unfavorable change is counterbalanced by an even larger reduction in the entropic penalty. Such [NaCl]-dependent trends in the thermodynamic parameters are rationalized in part by structural changes in the SS constructs before duplex formation. Specifically, the results provide evidence at the single-molecule level for base stacking and organization of the SS binding partners, i.e., in support of the preordered SS → DS docking mechanism proposed by Holbrook et al. (25).

Materials and Methods

DNA construct and sample preparation

The construct, illustrated in Fig. 1, is prepared as follows: Synthetic dye-labeled DNA oligomers are purchased from Integrated DNA Technologies (Coralville, IA). For all constructs, the same Cy3-labeled surface tethering oligomer is used (Biotin-5′-(CA)₈-3′-Cy3). Unique linker strands, with sequences (S1s) 5′-GTTGGG GTT(TG)₈-3′, 5′-GGTTGGG GTT(TG)₈-3′, 5′-TGGTTGGG GTT(TG)₈-3′, 5′-TTGGTTGGG GTT(TG)₈-3′, are annealed to the tether for the 6–9 bp constructs, respectively (underlined nucleotides are those involved in basepairing). For all measurements, the same Cy5-labeled hybridizing probe (S2, 5′-CCCAACCAA-3′-Cy5) is diluted into the imaging buffer (25–300 nM).

Samples are prepared in Teflon channels enclosed with coverslips glued with RTV adhesive. A 10:1 mixture of bovine serum albumin (BSA; A7638, 5 mg/ml; Sigma, St. Louis, MO) and biotinylated BSA (A8549, 0.5 mg/ml; Sigma) is flowed through the channel and incubated for 10 min, followed by sequential incubations with Streptavidin solution (S4762, 0.1 mg/ml, 10 min; Sigma) and then a 20–80 pM dilution DNA construct (10 min). Just before analysis, the sample is flushed with an imaging buffer containing 1), 2 mM Trolox (9-hydroxy-2,5,7,8-tetramethylchroman-2-carboxylic acid, 238813; Sigma) to suppress triplet blinking; 2), ∼0.1 mg/ml protocatechuate 3,4-dioxygenase (PCD, P8279; Sigma); and 3), ∼10 mM 3,4-dihydroxybenzoic acid (PCA, 37580; Sigma) as a catalytic oxygen scavenger system. All experiments are performed in 50 mM HEPES buffer (H9897; Sigma) at pH 7.5, to which NaCl and the Cy5-labeled strand are added at the desired concentrations. For confocal imaging at all temperatures, the Teflon sample ports are sealed with scotch tape to prevent sample evaporation and any associated changes in concentration of the solution constituents.

Single-molecule fluorescence confocal microscopy

The confocal fluorescence microscope utilizes an inverted base (Olympus IX-70) (43), with samples illuminated by a mode-locked, frequency-doubled Nd:YAG laser (10 ps, 532 nm, LYNX; Time-Bandwidth Products, Zurich Switzerland) operating at 20.6 MHz. The beam is expanded (∼1 cm) to overfill the back aperture of objective and is then focused to a diffraction-limited spot (266 nm) through a 1.2 NA water immersion objective (UPlanApo 60X; Olympus, Center Valley, PA). The laser intensity is attenuated by neutral density filters to deliver 0.05–100 μW at the focal plane. Fluorescence emission is collected by the objective, focused through a 50 μM pin hole and onto four single photon-detecting avalanche photodiodes (APDs, SPCM-AQR-14; Perkin-Elmer Optoelectronics, Fremont, CA). Immediately before the APDs, the photons are separated by a polarizer cube (CVI PBSH-450-1300-100, CVI Laser Optics, Albuquerque, NM) into vertical and horizontal paths, which are further separated into donor (Cy3) and acceptor (Cy5) channels with identical dichroic beam splitters (645DCXR; Chroma Technology, Bellows Falls, VT). The signal from the APDs is recorded on a time-correlated single-photon counting (TCSPC) module (SPC-134; Becker & Hickl, Berlin, Germany) in a time-stamped mode, whereby the arrival time of each photon is recorded relative to both the excitation laser pulse and the start of the observation. With all relevant data stored on a per-photon basis, the photon arrival events are then analyzed with software written in house. To control the temperature and minimize gradients across the sample, the Teflon sample is mounted in a microscope stage heater (HCS60; INSTEC, Boulder, CO). The microscope objective is heated with a resistive collar (Bioptechs, Butler, PA) as previously described (9,44–46). The temperature of both the stage and objective heaters is controlled with proportional, integral, and derivative (PID) servo loops maintaining the sample temperature to within ±0.1°C.

The kinetics of duplex hybridization is characterized from FRET intensity trajectories acquired from immobilized constructs (Fig. 1). Binding and unbinding events are observed as anticorrelated intensity fluctuations between the Cy3 and Cy5 channels (Fig. 2). In the SS state, the count rate on the Cy5 channel notably does not drop identically to zero, due to the presence of multiple freely diffusing Cy5-labeled strands in or near the confocal volume of the objective. From the fluorescence intensities, FRET values (E_FRET) and trajectories are calculated, revealing binary switching between high (E_FRET ∼0.8) and low (E_FRET ∼0) energy transfer efficiency (9). In the high E_FRET state, the Cy3 and Cy5 dyes are ∼43 Å apart, which is entirely consistent with the expected interdye distance of ∼42 Å for dyes separated by 12 bases in a helix (∼3.5 Å/base). Conversely, when no Cy5-label is hybridized to the surface-tethered strand, the dyes are far enough apart (>100 Å) to yield an E_FRET ≈ 0.

Figure 2.

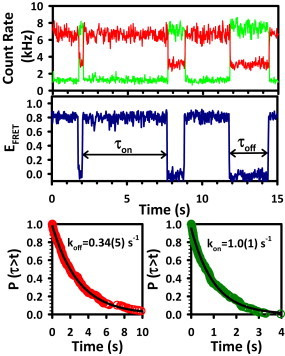
A representative fluorescence intensity trajectory (top panel) and corresponding E_FRET trajectory illustrate anticorrelated fluctuations typical of two-state systems. Crossings between high (E_FRET = 0.8) and low (E_FRET = 0.0) states define the on and off dwell times (τ_on and τ_off), which are then analyzed with CDFs (lower panels) to extract the rate constants for association (k_on) and dissociation (k_off).

Crossings between high and low E_FRET define the time the construct spends in each state, or dwell times (τ_dwell), which are then integrated with cumulative distribution functions (CDFs) that describe the decay out of the respective states (DS or SS) (47). For each rate constant measurement, ∼10–50 individual molecules are observed to collect the 200–500 total switching events. The switching events are randomly sorted into three subdatasets and are least-squares fit to single exponential functions, yielding unimolecular rate constants for dissociation (k_off) and association (k_on) (48,49). The average and standard deviation (SD) of the three independent fits are reported on the plots. Typically, the fractional error on individual data points is ∼10% of its absolute value.

Fluorescence correlation spectroscopy studies

Fluorescence correlation spectroscopy (FCS) is used to measure the diffusion coefficient of the untethered component (S2-Cy5) of the duplex construct. The S2-Cy5 probe is diluted in imaging buffer to a concentration < 200 pM, and as the molecules diffuse through the confocal volume, they are illuminated with a 633 nm pulsed laser diode (∼100 μW, PDL 800B; PicoQuant), resulting in bursts of Cy5 fluorescence that are collected on a pair of APD detectors. Photon arrival times are then cross-correlated using the multi tau algorithm to obtain the FCS decay (50). The correlation function is then fit with a standard diffusional model with a triplet fraction to obtain the half-maximal decay lifetime and 3D diffusion coefficient (51).

Results

Kinetics of association and dissociation as a function of duplex length

Increasing the length of a duplex by 1 bp clearly increases its stability through the formation of an additional two to three hydrogen bonds and two base-stacking contacts. To explore the effects of these interactions, E_FRET trajectories are obtained for the duplexes with 6, 7, 8, and 9 bp (Fig. 3; Table 1). The most striking feature of the data is the large change in the mean on-times, τ_on, with increasing oligo length. At 6 bp, for example, the average τ_on is ≈100 ms, yet with just two additional bp (C-G and A-T), the τ_on values increase ≈100-fold to ≈10 s. In clear contrast with this dramatic behavior in the dissociation times, the corresponding τ_off values remain largely insensitive to the number of basepairs and are indeed all on the order of 1–2 s over the full series of constructs. The trends observed in the dwell times are reflected in the rate constants in Fig. 4, where k_off decreases sharply (i.e., <τ_on> increases) with the addition of basepairs to the duplex. For example, k_off for the 6 bp construct decreases by nearly 600-fold for the 9 bp construct (14(1) s⁻¹ to 0.024(6) s⁻¹). In contrast, however, k_on, is much less sensitive to oligo length, decreasing only from 1.1(1) s⁻¹ to 0.43(3) s⁻¹ for the 6 and 9 bp constructs, respectively (Table 1). The CDFs for all of the association rate constants are summarized in Fig. S1 in the Supporting Material.

Figure 3.

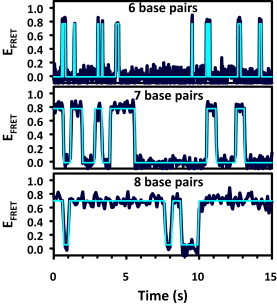
Sample E_FRET trajectories for constructs of different lengths, illustrating the sensitivity to the number of basepairs. The E_FRET trajectory for the 9 bp duplex has average dwell times longer than 30 s and therefore is shown.

Table 1.

Kinetic and thermodynamic data as a function of duplex length measured in 50 mM HEPES buffer at pH 7.5 with 125 mM NaCl

Sequence	koff (s−1)	kon (s−1)	Keq	ΔG°uni (kcal/mol)	k′on (M−1 s−1)	ΔG°bimol (kcal/mol)	ΔG°NN (kcal/mol)
GGGTTG	14(2)	1.1(1)	0.08(1)	1.5(1)	5.0(1) × 106	−7.5(1)	−6.2
GGGTTGG	1.3(1)	0.92(7)	0.71(8)	0.20(6)	4.6(1) × 106	−8.8(6)	−8.1
GGGTTGGT	0.39(8)	0.72(3)	1.8(4)	−0.4(1)	3.5(1) × 106	−9.4(1)	−9.5
GGGTTGGTT	0.024(6)	0.43(3)	18(5)	−1.7(2)	2.1(1) × 106	−10.7(2)	−10.6

All parameters are measured with 200 nM of the freely diffusing complementary strand (Cy5-S2), except for k′_on. ΔG°_NN was calculated using the unified NN parameters, including helix initiation terms for terminal basepairs.

Figure 4.

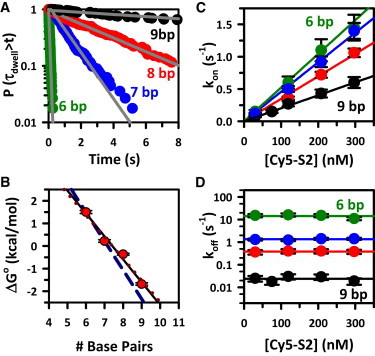
(A) Single-exponential fits to CDFs for 6–9 bp constructs illustrate the dramatic dependence of k_off on duplex length. (B) Hybridization free energy (ΔG°_uni) as a function of duplex length, revealing remarkably linear behavior with a slope giving an average of −1.0(1) kcal/mol/bp. (C) Stern-Volmer plots of k_on for N_bp = 6 (green), 7 (blue), 8 (red), and 9 (black) constructs, illustrating the expected linear dependence of k_on with [S2-Cy5]. The slopes represent k′_on, which decreases systematically with increasing N_bp. (D) In contrast, k_off exhibits no dependence on [S2-Cy5], although the logarithmic axis highlights the extreme sensitivity of k_off to duplex length.

With k_on and k_off well characterized, we can calculate the effective unimolecular equilibrium constants (i.e., for a fixed 200 nM concentration of the freely diffusing single strand) using Eq. 4, and obtain the overall free-energy change for hybridization from ΔG° = −RTln(K_eq) (Table 1). Specifically, for the 6 bp construct, ΔG° is +1.5 kcal/mol, which decreases to −1.7 kcal/mol for the 9 bp construct. A plot of ΔG°_uni versus basepair number is shown in Fig. 4 B, where the slope clearly reveals an approximately linear decrease in free-energy change, corresponding to Δ(ΔG°) ≈ −1.0(1) kcal/mol/bp.

Duplex kinetics versus complementary strand concentration

To validate our assumed model of bimolecular kinetics, we measure k_on and k_off as a function of the concentration of the Cy5-labeled strand. As expected, the k_on data (Fig. 4 C) reveal a simple linear dependence on [Cy5-S2], with the slope yielding the bimolecular rate constant for association, k′_on, as summarized in Table 1. These data also confirm that the bimolecular association rate constants (k′_on) decrease somewhat with increasing duplex length. However, this effect is rather subtle, as k′_on only decreases from 5.0(1) × 10⁶ M⁻¹ s⁻¹ to 2.1(1) × 10⁶ M⁻¹ s⁻¹ with the addition of one G-C and two A-Ts. The corresponding duplex dissociation events, on the other hand, are confirmed in Fig. 4 D to be independent of [Cy5-S2] and therefore purely unimolecular in nature. Specifically, these plots yield data that are always well within the error of the average of all measurements, which is represented by the horizontal lines. However, the need for a logarithmic scale in the y axis once again highlights the enormous sensitivity in k_off to the number of basepairs formed in the duplex.

Fluorescence correlation spectrum of Cy5-S2

In the bimolecular model, k_on is necessarily limited by the frequency of interactions between the hybridizing partners. However, not every collision is successful, and thus the resulting observed k_on may be slower than the diffusion limit. To quantify these constraints, the diffusion coefficient of the freely diffusing Cy5-S2 strand is measured using the FCS capabilities of the microscope. The Cy5-S2 strand is diluted into imaging buffer (∼200 pM) as described in Materials and Methods. The correlation function (G(τ), Fig. 5 B) is calculated from the burst intensity trajectories (Fig. 5 A) and fit with a model that includes both molecular diffusion and triplet blinking terms (red solid line). The diffusional component (blue dashed line) reveals a half-maximal decay time (τ_D) of 0.20(2) ms corresponding to a diffusion coefficient, D_Cy5-S2, of 0.9(1) × 10⁻⁶ cm² s⁻¹. Based on these measurement values, the diffusion-limited rate constant can be predicted from

$${\text{k}}_{\text{diff}}=4{\pi \text{R}}_{\text{DNA}}{\text{D}}_{\text{Cy}5\text{-}\text{S}2}$$ (5)

where R_DNA reflects a sum of the appropriate strand radii and D_Cy5-S2 is the diffusion coefficient of the freely diffusing strand component. For the 8 bp construct, R_DNA is estimated to be 24 Å; the radius of each strand is 4 bases at 3 Å per base in a stacked configuration. These numbers predict a diffusion-limited rate constant of ≈2 × 10⁹ M⁻¹ s⁻¹ at room temperature, i.e., 2–3 orders of magnitude larger than measured values of k′_on, which suggests that only one out of every 100 or 1000 diffusional attempts results in successful formation of a duplex. Such a low efficiency of duplex formation is not unexpected, as many orientations and registrations between the two strands are incapable of hybridization (e.g., parallel instead of antiparallel backbone alignment). Indeed, this observation is consistent with previous ensemble studies in which only one approach in 10⁴ was estimated to be successful (52). To account for the temperature dependence of D_Cy5-S2, k_diff is multiplied by factors of T/295 K and 1 cP/η(T), which at 200 nM [Cy5-S2] results in a rate constant that increases from 400 s⁻¹ at 295 K to 675 s⁻¹ at 335 K (53).

Figure 5.

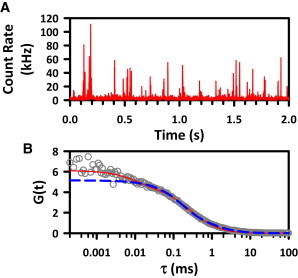
(A) Sample burst trajectory for freely diffusing S2-Cy5. Individual bursts of fluorescence are detected as single molecules traversing the confocal volume. (B) The FCS spectrum is fit with both diffusion and triplet blinking components (red solid line). The blue dashed line represents the diffusive component.

[NaCl] dependence of k_on and k_off

To probe the effect of cosolutes (specifically Na⁺ cations) on the duplex kinetics, we measure k_on and k_off for the 8 bp construct under constant [Cy5-S2] (200 nM) conditions as a function of NaCl in the imaging buffer (Fig. 6 A). In the limit of only Na⁺ from the HEPES buffer (25 mM), k_on is quite low (0.10 (1) s⁻¹). However, as NaCl is added, k_on grows nearly linearly with log([NaCl]), to 4.0 (4) s⁻¹ at 1M [NaCl]. Interestingly, Fig. 6 A also reveals that k_off decreases only from 0.72 (3) s⁻¹ to 0.17 (7) s⁻¹ over the same 40-fold dynamic range in [NaCl].

Figure 6.

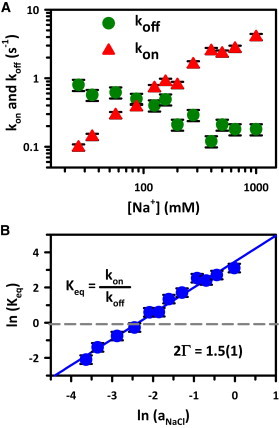
(A) Duplex hybridization and dissociation rates for the N_bp = 8 construct as a function of [NaCl], for 50 mM HEPES buffer at pH 7.5, 0.1 mM EDTA, and 200 nM [S2-Cy5]. Note the logarithmic axes. (B) A plot of ln(K_eq) versus ln(a_NaCl), where the slope (2Γ = 1.5(1)) reflects the net number of ion pair exchanges during duplex formation.

At each [NaCl], K_eq is calculated from the individually measured k_on and k_off values. In particular, K_eq ≈ 0.14 at [NaCl] = 25 mM, which increases to K_eq ≈ 24 for [NaCl] > 1 M (Fig. 6 B), representing an increase of nearly 160-fold. In Fig. 6 B, we use activity coefficients to plot ln[K_eq] versus the natural log of sodium chloride activity, which reveals a surprisingly linear log-log relationship that has been discussed in detail by Leipply et al. (54) This analysis is especially convenient because no assumptions are made about the nature of the ion-nucleic acid interaction, and therefore no model is needed to interpret the data. From this Leipply-type analysis, the unitless slope of ln(K_eq) versus ln(a_NaCl) is 2Γ, where 2Γ reflects a combination of the number of Na⁺ and Cl⁻ ions incorporated from and ejected into the bulk, respectively, upon duplex association. For the present docking partners, [Cy3-S1] and [Cy5-S2], the experimental slope is 2Γ = 1.5(1).

Temperature dependence of K_eq

The effects of cation concentration on the free-energy landscape that give rise to the changes in hybridization kinetics are also explored by measuring the explicit temperature dependences of k_on, k_off, and their ratio K_eq. In particular, experimental control over the temperature as an external parameter allows the free-energy difference (i.e., ΔG° = ΔH° − TΔS°) to be deconstructed from van’t Hoff theory into separate enthalpic (ΔH°) and entropic components (ΔS°). In Fig. 7, ln(K_eq) is plotted against 1/T, and the enthalpy and entropy differences are obtained from the slope (−ΔH°/R) and y-intercept (ΔS°/R), respectively. At all three [NaCl] concentrations, ΔH° is large and negative (ΔH° = −37(5) to −60(6) kcal/mol), indicating a large exothermicity of duplex formation consistent with the formation of multiple Watson-Crick interactions and base stacks. Over the same range of [NaCl], however, ΔS° is also large and negative (−120(16) to −206(21) cal/mol/K). Indeed, at room temperature (295 K) these two thermodynamic contributions largely cancel each other, resulting in substantially more modest free-energy differences ΔG° = +0.77(8) and ΔG° = −1.6(3) kcal/mol at 25 mM and 1 M [NaCl], respectively (Table 2).

Figure 7.

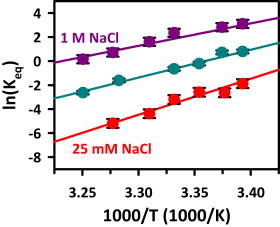
van’t Hoff analysis for the 8 bp single-strand/duplex equilibrium at 25 mM (red), 125 mM (green), and 1 M (purple) [NaCl]. Increasing [NaCl] increases both ΔS° (i.e., smaller increase in order) and ΔH° (i.e., lower exothermicity) with respect to duplex formation. Thermodynamic parameters are listed in Table 2.

Table 2.

NaCl dependence of the standard state and TS enthalpies and entropies of duplex formation

				SS → TS		Duplex → TS
[NaCl] (mM)	ΔH° (kcal/mol)	ΔS° (cal/mol/K)	ΔG°@ 295K (kcal/mol)	ΔH‡ (kcal/mol)	ΔS‡ (cal/mol/K)	ΔH‡ (kcal/mol)	ΔS‡ (cal/mol/K)
25	−60(6)	−206(21)	0.77(8)	−9(3)	−46(10)	51(3)	153(11)
125	−46(2)	−154(7)	−0.57(4)	0(5)	−19(16)	45(3)	133(9)
1000	−37(5)	−120(16)	−1.6(3)	2(1)	−2(3)	39(4)	117(12)

Closer inspection of the dependence of ΔH° and ΔS° on [NaCl] reveals two interesting and counterbalancing trends. First, increasing [NaCl] yields a substantial increase in the enthalpy of formation, i.e., Δ(ΔH°) > 0. Specifically, at 25 mM, the ΔH° of formation is −60(6) kcal/mol, which increases to −37(5) kcal/mol at 1 M [NaCl]. In other words, duplex formation is less exothermic at high [NaCl] than at low [NaCl], which by itself would tend to disfavor association. However, increased [NaCl] also brings with it a greatly reduced entropic cost, i.e., Δ(ΔS° > 0), of duplex formation. At 25 mM [NaCl], the ΔS° is −206(21) cal/mol/K, which decreases to −120(16) cal/mol/K at 1M [NaCl]. Overall, these competing terms combine to yield a modest but significant Δ(ΔG°) < 0, which overall has the well-known effect of favoring the duplex side of the equilibrium with increasing [NaCl].

One can take this type of analysis a step further by examining the temperature dependence of the rate constants from a TS theory (TST) perspective. The Eyring plots of ln(k_on) and ln(k_off) versus 1/T (Fig. S2), as well as a detailed description of the TS parameters as a function of [NaCl], are included in the Supporting Material. The values of the TS parameters are listed in Table 2.

Discussion

In this work, we have taken a direct approach to investigate duplex kinetics at the single-molecule level. Independent of length, CDFs reveal single exponential decay over 2–3 orders of magnitude, as evidenced by a high degree of linearity in the log-linear plots (Fig. 4 and Fig. S1). From a mechanistic perspective, single-exponential CDFs support the notion that duplex formation is an all-or-nothing process that occurs over what appears to be a single, rate-limiting TS barrier. This appears to contrast with early hybridization studies, which suggested a base-by-base zippering and unzippering mechanism as the most probable pathway between SS and DS states (13). It is important to note, however, that these two perspectives are by no means inconsistent. Because individual basepair dynamics likely occur on a submicrosecond timescale, i.e., much faster than the millisecond-to-second timescale for the smFRET experiments, the overall path may be envisioned as a series of rapid equilibria between successive base unzippering events (52). When only a few basepairs remain at the TS, the strands can then dissociate. Based on this mechanism, the population of molecules before the TS is related to the product of equilibrium constants for the multiple fast unzippering steps, with the last and only FRET-detectable dissociation step occurring when the final set of basepairs break. In such a case, the overall dissociation process can still be kinetically well described by unimolecular single-exponential behavior, but with the final dissociation event preceded by many rapid kinetic steps on a much faster timescale (13,15,52,55).

One can further test the validity of such a unimolecular model for SS-DS equilibrium kinetics simply by changing the duplex hybridization length. As a specific example, Fig. 4 displays the dwell-time CDFs for duplex constructs of variable lengths, clearly revealing an order of magnitude decrease in k_off with addition of each subsequent basepair (Table 1). In contrast, k_on proves to be relatively insensitive to the number of basepairs (Fig. S1; Table 1), with a difference of 3 bp resulting in only an ∼2-fold decrease in k_on. Most importantly, however, the association and dissociation rate processes for each construct length are consistently well described by single-exponential kinetics.

Although knowledge about single-molecule kinetics is extremely informative on its own, it is clearly useful to compare such information with results from ensemble studies on duplex formation energetics as a function of length and sequence. For comparison with such thermodynamic data, we measure kinetic rate constants for our series of construct lengths with [Cy5-S2] fixed at 200 nM, which permits direct calculation of unimolecular equilibrium constants and free energies via ΔG° = −RTln(K_eq) (see Table 1). A plot of ΔG° versus the number of basepairs is shown in Fig. 4 B, clearly revealing a nearly linear decrease in free energy with an average slope of m = −1.0(1) kcal/mol/bp. This value compares quite well with ensemble thermodynamic studies in which basepair addition was found to increase overall duplex stability by −0.30 to −1.22 kcal/mol of free energy, with specific values naturally dependent on sequence identity (56–61). An even more direct sequence-specific comparison can be made from Watson-Crick predictions, including modifications due to nearest-neighbor (NN) interactions. Specifically referring back to a bimolecular description of the duplex equilibria, one finds ΔG°_bimol to be −7.5(1), −8.8(1), −9.4(1), and −10.7(2) kcal/mol for the equivalent series of 6–9 bp length constructs, for which the corresponding sequence NN predictions are −6.2, −8.1, −9.5, and −10.6 kcal/mol (see Table 1). Interestingly, the experimental and predicted values clearly agree well for the higher 8 and 9 bp sequences, with perhaps some larger deviations at lower 6 and 7 bp lengths. However, such modest discrepancies for <8 bp duplexes are not unexpected, as the NN parameters have been obtained by fitting to data for larger duplexes with >9 bp.

[NaCl]-dependent equilibrium is dominated by k_on

As mentioned in the Introduction, cosolutes, especially cations, play a critical role in the dynamics of nucleic acid structure formation on both 2° and 3° levels (37,38,62–64). Indeed, cation-nucleic acid interactions are enormously important because the Columbic repulsion of the polyanionic backbone must be reduced and/or eliminated to access the tightly folded structures of native nucleic acids. However, gaining a detailed understanding of the cation-nucleic acid interactions that regulate folding kinetics remains a significant challenge in more complex cationic environments (e.g., the cytosol). In the studies described herein, we greatly simplify this problem of nucleic acid folding by considering only the in vitro dependence on added NaCl. By way of example, Fig. 6 A illustrates a titration of the 8 bp construct, where k_on and k_off increase and decrease, respectively, with [NaCl]. As outlined in the Results section, the plot of ln(K_eq) versus ln(a_NaCl) is remarkably linear, with a slope that defines the preferential interaction coefficient (2Γ) of NaCl uptake during duplex formation (54). The Na titration yields 2Γ = 1.5(1), which is consistent and within error of the value of 1.8(3) reported by Braunlin et al. (65) for a similar 8 bp duplex.

One might expect the dominant effect of NaCl and ionic strength on the duplex formation kinetics to be one of charge shielding, i.e., by reducing interstrand phosphate repulsion within the duplex. From this perspective, increased electrostatic shielding would lower the duplex free energy and thus make dissociation less likely. This is indeed observed in Fig. 6 A, with a gradual fourfold decrease in k_off over the corresponding 50-fold increase in [NaCl] from 20 mM to 1000 mM. Somewhat surprisingly, however, this is clearly not the main reason for such cationic enhancement of duplex formation. Instead, the overall increase in duplex stability and K_eq arises from the much stronger [NaCl] dependence of the association rate constant, k_on, which increases >40-fold over the same change in [NaCl]. Thus, association kinetics (k_on) play a much more pivotal role than dissociation kinetics (k_off) in controlling the SS-DS equilibrium, which is explored further in the temperature-dependent studies described below.

Standard state enthalpy and entropy of duplex formation

Considerably more detailed information about how [NaCl] changes the free-energy landscape of the SS-DS equilibrium can be obtained from temperature-dependent measurements. At the simplest level, van’t Hoff plots of ΔG° versus 1/T are constructed, parsing the overall free energy of duplex hybridization (ΔG°) into enthalpic (ΔH°) and entropic (ΔS°) constituents, from which it is generally observed that nucleic acid folding processes are both enthalpically favored (ΔH° < 0) and entropically costly (TΔS° < 0) (9,45,46,52) (Fig. 7). Interestingly, the two contributions to free energy (ΔH° and −TΔS°) are quite comparable at 300 K. The net result is a ΔG° of ≈0, but one that shifts from spontaneous (ΔG° < 0) to nonspontaneous (ΔG° > 0) with increasing [NaCl] (ΔG° = +0.77 (8) to ΔG° = −1.6 (3) kcal/mol; Table 2).

Two trends are immediately clear from the data in Fig. 7. First of all, the slopes in Fig. 7 decrease but always remain positive as [NaCl] is increased, i.e., duplex formation becomes slightly less exothermic (Δ(ΔH°) > 0) with higher ionic strength. However, this effect is balanced by an even more pronounced increase in the y-axis intercept with increasing [NaCl], indicating a strong increase in entropy (i.e., Δ(ΔS°) > 0) and a corresponding reduction in entropic cost for duplex formation. Thus, even though the net effect of increasing [NaCl] favors duplex formation (Δ(ΔG°) < 0), this is dominated by entropic rather than enthalpic effects, i.e., increasing NaCl reduces the entropic penalty faster than it escalates the enthalpic penalty. These data qualitatively agree with ensemble NMR studies of duplex formation by Braunlin et al. (65), in which increasing [NaCl] resulted in a shift of the van’t Hoff entropy intercept to larger values. Indeed, the fact that cationic enhancement of nucleic acid folding is driven largely by entropy rather than enthalpy is evident in RNA as well, with similar trends observed for the RNA tetraloop-receptor and a three-helix junction motif (45,46,66).

The origins of these cation-based changes to enthalpy and entropy changes have been the subject of significant debate. Early work by Manning (67,68) and Privalov et al. (69), based on a differential cation affinity of SS and DS DNA, provided a model for cation stabilization of the DS state through an exclusively entropic effect. Simply summarized, at higher cation concentrations, more species are available to associate with DS DNA, which reduces the entropic cost of forming the S1 + S2 + n·cation complex. The data presented here clearly show large entropic shifts that favor duplex association, in agreement with the models of Manning and Privalov et al. However, our results also reveal significant shifts in the overall enthalpy change, which was not included in the previous analyses. To account for the observed enthalpy change, charge shielding of interstrand phosphate coulombic repulsion can be considered, which in the absence of any PV work is just the internal potential energy U. The total enthalpy change is then the sum of the molecular interactions, ΔH° = ΔH_H-bond + ΔH_stack + ΔH_p-p, where ΔH_H-bond (hydrogen bonding) and ΔH_stack (base stacking) terms are negative and the ΔH_p-p (phosphate-phosphate repulsion) term is positive. With increasing cation concentration to screen the interstrand phosphate repulsion (i.e., decreasing ΔH_p-p), the overall ΔH° from such a charge-shielding picture would become more negative, which is not consistent with the observed trends (see Table 2).

An alternative explanation is offered by experimental observation of significant changes in both enthalpy (ΔΔH°_25mM→1M = +23 kcal/mol) and entropy (ΔΔS°_25mM→1M = +86 cal/mol·K). In the simplest additive model, the duplex product state is unaffected by [NaCl], and all changes can be attributed to shifts in the SS reactant species from random coil (SS_RC) to a preordered, stacked conformation (SS_stack). In such a model, one can estimate the per-base thermodynamic values (Δh° and Δs°) by scaling the overall changes by the number of stacking interactions, e.g., 14 stacking contacts for the 8 bp construct yield Δh° = 1.6 kcal/mol/bp and Δs° = 6.1 cal/mol·K/bp. These values are close to (albeit somewhat lower than) those reported by Vesnaver and Breslauer (24), (Δh° = 2.3–2.4 kcal/mol/bp and Δs° = 7.2–8.0 cal/mol·K/bp), using a similar stacking model analysis. However, these differences can be easily rationalized, as the previous study used thermal melting to probe thermodynamic parameters for the SS_stack to SS_RC transition, which therefore permits sampling of the fully disordered SS_RC state at high temperature. In contrast, in our measurements there is always residual ionic strength due to the 50 mM HEPES buffer even in the absence of added NaCl. Under such conditions, it is reasonable to assume that the single strands may not yet be fully unstacked, resulting in lower Δh° and Δs° values compared with those expected for complete thermal melting.

Free-energy landscapes

The net thermodynamic effects of [NaCl] on the SS/DS equilibrium and TS are visually summarized in Fig. 8, where for consistency all changes have been referenced to the duplex state. At low [NaCl], duplex formation is a slightly uphill process (ΔG = +1 kcal/mole), with a significant free-energy barrier of ≈5 kcal/mol. With increasing [NaCl], hybridization becomes an overall favorable event (ΔG = −1.7 kcal/mole), with the free-energy barrier also reduced twofold to ≈2.5 kcal/mol. In the reverse direction (DS→SS), the barrier to dissociation is influenced by NaCl to a much smaller degree, increasing only from ≈3.8 to 4.5 kcal/mol. These changes to the forward and reverse barriers in the free-energy profile illustrate the thermodynamic basis for the observed NaCl induced changes to k_on and k_off discussed earlier (Fig. 6), where k_on is responsible for the majority of the cation-dependent changes to K_eq.

Figure 8.

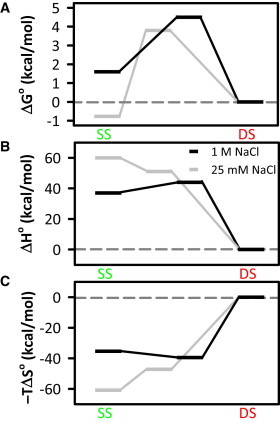
Free-energy profiles are shown for the SS-DS equilibrium at low (25 mM) and high (1M) [NaCl]. The free energy (ΔG^o) as well as the enthalpic (ΔH^o) and entropic (−TΔS^o) components are plotted on the same reaction coordinate. Note that the TSs all shift toward the right at 1 M [NaCl], capturing the observation that single strands adopt a prehelical structure that more closely resembles the duplex under high-cation conditions.

In our proposed picture, in which NaCl primarily impacts the single strand by promoting prehelical structures, we would expect enthalpies and entropies for both the SS state and TS to shift in the direction of the duplex, due to early base stacking and associated heat release. Indeed, this is what is observed in both the enthalpic and entropic profiles (see Fig. 8, B and C), i.e., the SS and TS species lie closer to the duplex (i.e., shift toward zero) at high [NaCl]. Furthermore, in each case the magnitude of the change for the SS state is slightly larger than for the TS. Thus, at high [NaCl] the approach to the TS becomes slightly endothermic, whereas it is exothermic at low [NaCl].

In the context of specific base-base interactions, such an exothermic TS behavior at low NaCl is consistent with a picture in which a few in-register basepairs nucleate the duplex zippering process. At high NaCl, however, if the SS is already highly stacked in a prehelical twist, it is possible to envision a mechanism wherein the single strands have to slightly unstack or straighten (requiring energy) to line up correctly at the TS. Similarly, as [NaCl] increases, the SS state becomes more ordered than the TS, as reflected by a greater increase in −TΔS. At low ionic strength, the system becomes increasingly more ordered with each step from SS→TS→DS. Conversely, however, the data at high [NaCl] actually indicate a small decrease in order on approach to the TS. Again, this is consistent with the picture of an SS_helix having to partially unwind to accommodate a conformational approach of the second strand for duplex formation.

Conclusions

In this work, we present single-molecule constructs that allow investigation of DNA hybridization kinetics under equilibrium conditions. The construct recapitulates all expected kinetic and energetic trends regarding duplex length, strand concentrations, and the diffusion limit. Moreover, monovalent cation stabilization of the duplex state is found to occur largely by accelerating duplex formation and, to a much lesser degree, slowing down duplex dissociation. Recast into thermodynamic terms, although cations actually reduce the favorable exothermicity for duplex formation, they do so by a smaller degree than the corresponding reduction in entropic penalty. Thus, cation-facilitated duplex stabilization in these relatively small DNA constructs appears to be driven, in part, by ordering of base-stacked and/or prehelical SS structures, in support of the mechanisms proposed by Holbrook et al. (25).