Determinants of Maximal Force Transmission in a Motor-Clutch Model of Cell Traction in a Compliant Microenvironment

Abstract

The mechanical stiffness of a cell’s environment exerts a strong, but variable, influence on cell behavior and fate. For example, different cell types cultured on compliant substrates have opposite trends of cell migration and traction as a function of substrate stiffness. Here, we describe how a motor-clutch model of cell traction, which exhibits a maximum in traction force with respect to substrate stiffness, may provide a mechanistic basis for understanding how cells are tuned to sense the stiffness of specific microenvironments. We find that the optimal stiffness is generally more sensitive to clutch parameters than to motor parameters, but that single parameter changes are generally only effective over a small range of values. By contrast, dual parameter changes, such as coordinately increasing the numbers of both motors and clutches offer a larger dynamic range for tuning the optimum. The model exhibits distinct regimes: at high substrate stiffness, clutches quickly build force and fail (so-called frictional slippage), whereas at low substrate stiffness, clutches fail spontaneously before the motors can load the substrate appreciably (a second regime of frictional slippage). Between the two extremes, we find the maximum traction force, which occurs when the substrate load-and-fail cycle time equals the expected time for all clutches to bind. At this stiffness, clutches are used to their fullest extent, and motors are therefore resisted to their fullest extent. The analysis suggests that coordinate parameter shifts, such as increasing the numbers of motors and clutches, could underlie tumor progression and collective cell migration.

Introduction

Cell proliferation, differentiation, migration, and survival are all sensitive to the mechanics of the cell microenvironment (1–3). Several studies have found that cell speed increases with substrate Young’s modulus, including U87 and U373 glioblastoma cells on substrates of 0.08–119 kPa (4), vascular smooth muscle cells on substrates of 8–72 kPa (5), and MCF10A epithelial cells on substrates of 3–35 kPa (6). However, several other studies have found that cell speed decreases with substrate Young’s modulus, including 3T3 fibroblasts on 14–30 kPa (2), T24 carcinoma cells on 1.95–9.9 kPa (7), neutrophils on 10–100 kPa (8), and SNB19 glioblastoma cells on increasingly stiff silicone rubber (9). These apparently opposite results suggest that cell speed may be biphasic with respect to substrate stiffness. The cell speed may rise and then fall, exhibiting maximal migration at some intermediate stiffness depending on the cell type and experimental conditions. Fig. 1 A presents selected monotonic cell migration data with possible biphasic fits to the data and two experimental examples showing biphasic cell migration with respect to substrate Young’s modulus—maximal migration speed of neutrophils at 4–7 kPa (10) and of smooth muscle cells at >300 kPa (11). All of these cell migration studies suggest that the optimum stiffness of cell migration can vary from ≤2 kPa (7) to ≥300 kPa (11).

Figure 1.

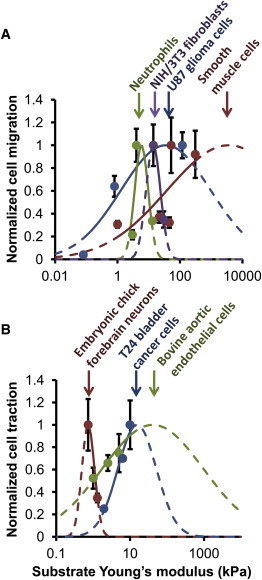
Experimental evidence for shifting stiffness optima. (A) Cell migration data for neutrophils (10), NIH/3T3 fibroblasts (2), U87 glioma cells (4), and smooth muscle cells (11) show varying dependence on stiffness. For U87 glioma cells and smooth muscle cells, experimentally measured migration increases with substrate stiffness. For NIH/3T3 fibroblasts it decreases with stiffness, and for neutrophils it increases and then decreases with stiffness. These results suggest a biphasic dependence of cell migration on substrate stiffness; therefore, Gaussian curves were fit to the data to show potential stiffness optima. (B) Traction force data for embryonic chick forebrain neurons (15), T24 bladder cancer cells (7), and bovine aortic endothelial cells (12) also show varying dependence on substrate stiffness. For embryonic chick forebrain neurons, traction force decreases with stiffness, whereas for T24 bladder cancer cells and bovine aortic endothelial cells it increases with stiffness. This also suggests a biphasic response, and Gaussian curves were fit to the data to show potential stiffness optima. For both A and B, data were normalized to the maximum value for the particular cell type, therefore all data can be shown easily on one plot. Dashed lines indicate extrapolation of the Gaussian curves beyond the given data.

Additionally, cell traction studies have also shown variable dependence on substrate stiffness. For some cells, traction force increases with substrate stiffness (2,7,12–14), although for others it decreases (15). These apparently opposite results suggest a biphasic dependence of cell traction force on substrate Young’s modulus. Fig. 1 B presents select examples of monotonic traction force for different cell types with possible biphasic fits to the data. The possible optimum stiffness for cell traction ranges from ≤1 kPa (15) to ≥30 kPa (2,13). It is unknown why these different cell types have apparently different stiffness optima for both cell migration and traction force.

Several models have been proposed to describe cell migration and force transmission (16). For example, a full description of the keratocyte actomyosin network and force transmission on a stiff substrate has been presented (17). However, this model does not address the stiffness sensing shown in Fig. 1, and the use of a friction coefficient to model traction does not allow for load and fail of adhesions as seen experimentally on soft substrates (15). Another model affords stick-slip properties to the adhesion, allowing load and fail, but imposes empirical stiffness sensitivity (18). Additionally, these models do not include a force-velocity relationship for the driving force on the actin and adhesion. Myosin motors follow this type of relationship (19), as does actin polymerization (20,21), so for either of these sources of force, a force-velocity relationship is obeyed.

Another model for cell traction is the motor-clutch hypothesis, where F-actin self-assembly at the plasma membrane pushes the membrane forward, whereas myosin motors pull F-actin rearward to generate F-actin retrograde flow (22). In this model, cell adhesion molecules act as molecular clutches that transmit force to the extracellular environment, which slows retrograde flow and induces leading edge advance. Recently, we encoded the motor-clutch hypothesis in a stochastic simulation with balanced forces and inclusion of both chemical and mechanical properties of the integrated cell-microenvironment system (15). This model formulation allows for different substrate stiffnesses, load and fail of cellular adhesions, and imposes a force-velocity relationship on the motors. In the model, n_m molecular motors with stall force F_m and unloaded velocity v_u act to transmit loads to the substrate through n_c molecular clutches with on-rate k_on and unloaded off-rate k_off. As the clutches load (having spring constant κ_c), their off-rate increases exponentially in the load (scaled by the characteristic bond rupture force, F_b) (23). Together, the three motor parameters (n_m, F_m, and v_u) and the five clutch parameters (n_c, k_on, k_off, F_b, and κ_c) define the motor-clutch model. If the cell types listed previously adhere to this model, they should possess different parameter values; therefore, we independently varied each parameter to determine the sensitivity of the optimal stiffness with respect to each parameter change. Because single parameter changes resulted in a limited ability to shift the optimum, we went further to examine dual parameter changes, which can extend the range of stiffness sensing over many orders of magnitude.

Materials and Methods

Simulation algorithm

The motor-clutch model was simulated using a stochastic algorithm as previously described (15) with the following modifications (see the Supporting Material for details). The most significant modification was to incorporate a Gillespie stochastic simulation algorithm (SSA) (24), such that the event time for each possible reaction (all clutch binding or unbinding events), t_event,i, was calculated in each iteration by Eq. 1 where URN_i is a uniformly distributed random number between zero and one, and k_i is the kinetic rate for the clutch binding or unbinding

$$t_{event,i}=\frac{-\text{ln}\left(UR{N}_i\right)}{k_i}.$$ (1)

The event with the shortest t_event,i was executed. The Gillespie SSA was computationally faster than the previous fixed time step approach, and guarded against the possibility of two events occurring in a single time step. One might imagine a situation where one clutch is bound, and when using a fixed time step approach, that clutch would unbind and another clutch would bind. If the unbinding event came first, the system should have failed but did not because another clutch was allowed to bind in the same time step. The Gillespie SSA does not allow such instances because one and only one event occurs per variable time step.

Additionally, the order of events was altered so that the force balance was calculated at the end of the time step, which ensured that elastic equilibrium was reached before proceeding to the next iteration. These modifications did not change the conclusions reached in our previous study, and only require modest revision to some of the parameter values previously estimated for embryonic chick forebrain neurons in vitro (i.e., the base parameter set in this study, see the Supporting Material).

Calculation of parameter range values

We define the range of a parameter p with the value R as shown in Eq. 2:

$$R=\text{log}\left(\frac{p_{\mathit{max}}}{p_{\mathit{min}}}\right).$$ (2)

The values p_max and p_min correspond to the maximum and minimum allowable parameter values before resulting in a free flowing or stalled system. The free flowing parameter limit is defined as the parameter value that first results in a minimum F-actin flow rate within 5% of the unloaded velocity, v_u. The stalled parameter limit is defined as the parameter value that first results in a minimum F-actin flow rate within 5% of zero (relative to the unloaded velocity, v_u). An alternative to the stalled limit is the limit where stiffness sensing is lost without stalling. This limit was reached if the difference in the minimum and maximum F-actin flow rates was <5% of the unloaded velocity. The values of p_max and p_min were found by progressively increasing or decreasing the parameter until one of these conditions was reached. Depending on the parameter, p_max may result in either a free flowing or stalled system, with p_min generally resulting in the opposite state. Regardless of the system state, p_max is put in the numerator so the range value is always positive. The R value can be interpreted as the maximum allowable order of magnitude change in the parameter p.

Calculation of parameter sensitivity values

The sensitivity value S of the optimum substrate stiffness κ_s,opt to a parameter p is defined in Eq. 3 (25,26) where p₀ is the base parameter value, and ${\kappa }_{s,opt}^{p_0}$ is the optimum substrate stiffness at the base parameter value:

$$S=\frac{\Delta {\kappa }_{s,opt}{p}_0}{{\kappa }_{s,opt}^{p_0}\Delta p}=\frac{d\text{log}\left({\kappa }_{s,opt}\right)}{d\text{log}\left(p\right)}.$$ (3)

The S value is also equivalent to the slope of κ_s,opt versus p on a log-log scale, and can be interpreted as the fold-change in the optimal stiffness resulting from a fold-change in a parameter value. The S value was calculated by plotting the optimal stiffness at 0.25-, 0.5-, 1-, 2-, and 4-fold changes of the base parameter on a log-log scale. A line was fit to the data points with the slope of the line taken to be the S value. For some parameters, the allowable range did not allow for the extreme fold-changes, so in these cases, the maximum or minimum fold-change of the parameter was used to calculate the sensitivity instead.

Calculation of parameter sensitivity-range values

The sensitivity-range of each parameter was defined as the product of S and R as given in Eq. 4:

$$SR=\frac{d\text{log}\left({\kappa }_{s,opt}\right)}{d\text{log}\left(p\right)}\text{log}\left(\frac{p_{\mathit{max}}}{p_{\mathit{min}}}\right)\approx \frac{\text{log}\left({\kappa }_{s,opt}^{p_{\mathit{max}}}/{\kappa }_{s,opt}^{p_{\mathit{min}}}\right)}{\text{log}\left(p_{\mathit{max}}/p_{\mathit{min}}\right)}\text{log}\left(\frac{p_{\mathit{max}}}{p_{\mathit{min}}}\right)=\text{log}\left(\frac{{\kappa }_{s,opt}^{p_{\mathit{max}}}}{{\kappa }_{s,opt}^{p_{\mathit{min}}}}\right).$$ (4)

This value can be interpreted as the maximum possible order of magnitude change in the optimal stiffness due to parameter p.

Calculation of R, S, and SR for dual parameter changes

For dual parameter changes, S, R, and SR were not calculated for the parameters themselves, but for a multiplier, c, applied to each parameter. Two parameters p_i and p_j can be coordinately changed in two ways: they may both move in the same direction, increasing or decreasing together, or they may move in opposite directions, with one increasing while the other decreases. To coordinately change two parameters in the same direction, the base values of each parameter were both multiplied by the same constant c as in Eqs. 5 and 6:

$$p_i=c{p}_{i,0},$$ (5)

$$p_j=c{p}_{j,0}.$$ (6)

To coordinately change two parameters in opposite directions, the base value of one parameter was multiplied by the constant c and the base value of the other parameter was divided by the constant c as in Eqs. 7 and 8:

$$p_i=c{p}_{i,0},$$ (7)

$$p_j=\frac{p_{j,0}}{c}.$$ (8)

S, R, and SR values were calculated for the constant c as it related to the particular parameter combination of interest.

Catch-slip bonds

To simulate catch-slip bonds, the off-rate of the ith clutch (k_off,i^∗) was modeled as the sum of two exponentials (27) as shown in Eq. 9:

$$k_{off,i}^{\ast }=k_{off}\text{exp}\left(\frac{F_i}{F_b}\right)+k_{off,c}\text{exp}\left(\frac{-F_i}{F_c}\right).$$ (9)

The first term in this equation is identical to the Bell model (23) used in the rest of this study and models the slip portion of the catch-slip bond. As the force on the ith clutch (F_i) increases, the slip bond off-rate increases according to the unloaded off-rate k_off and the characteristic rupture force F_b. The second term models the catch portion of the catch-slip bond and decreases with clutch force according to the unloaded catch off-rate k_off,c and the characteristic catch force F_c. At low clutch force, the catch portion of the model dominates, decreasing the off-rate as force increases. At high clutch force, the slip potion dominates, and off-rate increases as force increases.

Results

Individual parameter changes

To determine which model parameters are the most important in determining substrate stiffness sensing, we first systematically varied the individual motor and clutch parameters of our previously published stochastic model (15) (Fig. 2 A) using an improved model algorithm (see the Supporting Material). New parameter values, summarized in Table 1, were fit to the experimental data from our previous study and were used as the base parameters for the rest of this study. Overall, the new parameters were very similar to our previously published parameters, and do not affect the conclusions that were made previously (see the Supporting Material for additional details). Altering model parameters can change the optimal stiffness and the shape of the modeled F-actin retrograde flow rate. For example, increasing the number of clutches (n_c) causes the maximum traction force to shift to a higher substrate stiffness as shown in Fig. 2 B. Equivalently, the minimum F-actin retrograde flow rate also shifts to a higher stiffness (Fig. 2 C). The optimal stiffness, defined as the substrate stiffness at which traction force is maximal, is also the substrate stiffness at which F-actin retrograde flow is minimal.

Figure 2.

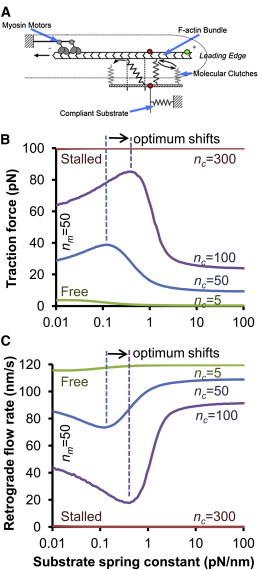
Motor-clutch model for cell traction force. (A) The motor-clutch model describes the adhesion and traction generation of a cellular protrusion (15). Briefly, molecular motors generate forces on the F-actin cytoskeleton that are resisted by molecular clutch bonds that transmit forces to a compliant substrate external to the cell. (B and C) Changing the number of clutches changes the shape of the model output traction force and F-actin retrograde flow rate. Increasing clutches from n_c = 50 to n_c = 100 shifts the traction force maximum and the retrograde flow minimum to the right toward higher stiffness. The traction force maximum corresponds to the retrograde flow minimum. Increasing clutches to n_c = 300 results in a stalled system, whereas decreasing clutches to n_c = 5 results in a free flowing system. (A used with permission of the American Association for the Advancement of Science (AAAS)).

Table 1.

Motor-clutch model base parameter set

	Parameter	Symbol	Value
Motor parameters	Number of motors	nm	50
	Motor stall force	Fm	2 pN
	Motor unloaded velocity	vu	120 nm/s
Clutch parameters	Number of clutches	nc	50
	Clutch bond rupture force	Fb	2 pN
	Clutch on-rate	kon	0.3 s−1
	Clutch unloaded off-rate	koff	0.1 s−1
	Clutch spring constant	κc	0.8 pN/nm

As expected, we also found that further increases in n_c result in a stalled system that is insensitive to stiffness (Fig. 2, B and C). In this situation, there are enough clutches resisting the force of the motors so that the clutches never collectively fail. In this limit, the traction force is constant at the stall force of the motors, and the F-actin retrograde flow rate is very nearly zero at all stiffnesses. Conversely, if the number of clutches is significantly decreased, the system is free flowing. In this opposite extreme case, the motors overpower the clutches and traction force is near zero, whereas the F-actin flow rate is near the unloaded velocity at all substrate stiffnesses. Between these two extremes is a regime where motors and clutches are approximately balanced so that the substrate cyclically loads and fails when the substrate stiffness is near the optimum. In the load-and-fail regime, the time-averaged traction force and retrograde flow rate vary with substrate stiffness and give rise to an optimal stiffness. Animations of these three types of model behavior, stalled, load-and-fail, and free flowing, are shown in Movie S1.

Each model parameter has an effect on the shape of the F-actin retrograde flow rate curve, and most parameters shift the optimal stiffness before resulting in either a free flowing or stalled system. Fig. 3 A depicts the effect of changing any one of the eight parameters. The optimal stiffness is more sensitive to some parameters, such as k_on (clutch on-rate), than to others, such as k_off (clutch unloaded off-rate). Surprisingly, the one parameter that defines a stiffness property of the cell, κ_c (clutch stiffness), does not shift the optimal stiffness, therefore the model optimum is insensitive to changes in κ_c. As with n_c, each parameter also has a limited range before resulting in either a free flowing or stalled system. Some parameters, such as κ_c, have a large range, whereas other parameters, such as n_m (number of motors) have a small one.

Figure 3.

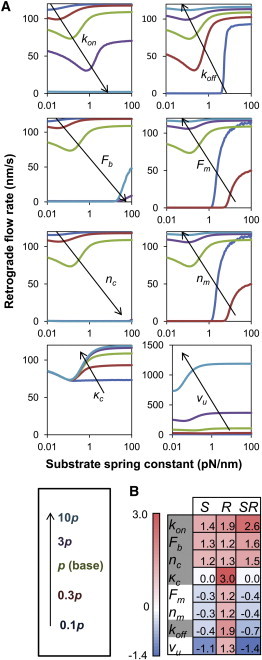
Single-parameter sensitivity. (A) All model parameters affect the shape of the F-actin retrograde flow rate as a function of substrate stiffness. Plots are shown for 0.1, 0.3, 1, 3, and 10 times the base parameter value. (B) The eight parameters have varying sensitivity and range values. The parameters are ranked from strongest positive (red) to strongest negative (blue) sensitivity-range (SR) value. Clutch parameters are highlighted in gray.

The ability of any single parameter to shift the optimal stiffness can be calculated as the product of the sensitivity (S) and range (R) values. This product, which we call the sensitivity-range (SR = S × R), gives the maximum possible order-of-magnitude change in the optimal stiffness due to changes in a particular parameter without entering the stalled or free-flowing regimes. Sensitivity, range, and sensitivity-range values for each parameter are given in Fig. 3 B, which ranks the parameters from those with the greatest ability to positively shift the optimum to those with the greatest ability to negatively shift the optimum (assuming the parameter value is increasing). It should be noted that changes in a model parameter with a high sensitivity may not necessarily result in large changes of the optimal stiffness because the parameter may quickly go out of range. For example, increasing n_c from 50 to 110 clutches causes a stalled system, whereas decreasing it to six clutches causes a free flowing system.

In general, increasing the values of clutch parameters (k_on, F_b, n_c, κ_c, k_off) tended to increase the optimal stiffness, although increasing the values of motor parameters (F_m, n_c, v_u) decreased the optimum. The only exception, the unloaded clutch off-rate k_off, can be explained because an increase in k_off weakens the clutches, whereas an increase in any other clutch parameter strengthens the clutches. Increasing the value of any of the motor parameters strengthens the motors. Therefore, we conclude that any single parameter change that strengthens the clutches will shift the optimum toward higher stiffness, although single parameter changes that strengthen the motors will shift the optimum toward lower stiffness. Importantly, we find that the optimum is generally much more sensitive to changes in the clutches than it is to changes in the motors (Fig. 3 B).

Dual parameter changes

For individual parameter changes, the maximum log-fold-change in the optimal stiffness is 2.6 (Fig. 3 B), which is probably an overestimate considering the dramatic change in the shape of the F-actin retrograde flow curve over this range. Because the optimal stiffness for a cell may vary >2.6 orders of magnitude (10,11,15), we explored dual parameter changes. Chan and Odde (15) showed that model behavior can be rescued by compensating for changes in k_off with changes in n_c. This occurs because an increase in k_off strengthens the motors, whereas an increase in n_c strengthens the clutches. In general, the motor-clutch system can be kept from stalling or free flowing by compensating for one parameter change with another. As seen in Fig. 3 B, clutch parameters generally have positive SR values, whereas motor parameters have negative SR values. To compensate for a change that favors clutches and shifts the system toward stall, a corresponding compensatory change must be made that favors the motors and shifts the system back toward free flowing.

One such example is shown in Fig. 4 A where increases in the clutch number, n_c, are compensated by increases in the motor number, n_m. As a single parameter, an increase in the number of clutches results in a stalled system. However, when coordinately increased with the number of motors, the system maintains its load-and-fail behavior near the optimal stiffness, yet the optimum is shifted to higher substrate stiffness. This happens because the optimum is more positively sensitive to the number of clutches (S = +1.2) than it is negatively sensitive to the number of motors (S = −0.3) as shown in Fig. 3 B, so it shifts positively when both motors and clutches are increased (S = +0.9). The corresponding traction force plot is shown in Fig. 4 B, where average traction forces greater than the 550–1000 pN seen experimentally (28,29) are easily attainable. Because the number of motors is increasing, the magnitude of the traction force also increases as the optimum moves to higher stiffnesses. This is a characteristic feature of compensation for a clutch parameter with a motor parameter: the shape of the F-actin retrograde flow rate remains approximately constant, whereas the magnitude of the traction force increases with increasing motor parameters. We refer to these dual parameter shifts as motor-clutch.

Figure 4.

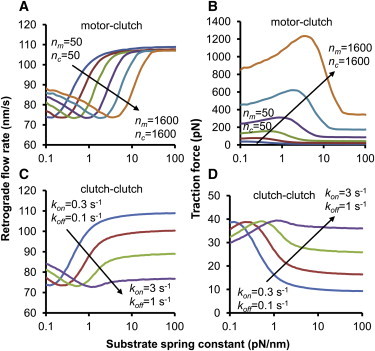
Shifting the optimum by coordinate parameter changes. (A) The minimum in F-actin retrograde flow shifts with coordinate changes in the number of motors and the number of clutches (i.e., motor-clutch parameter changes). (B) The traction force maximum also increases as both motors and clutches increase because the number of motors is increasing. (C) The F-actin retrograde flow rate minimum also shifts with changes in k_on and k_off, but the shape of the curve is not maintained. In this case of coordinate increase in k_on and k_off (i.e., clutch-clutch parameter changes), the maximum traction force remains constant because the number of motors is unchanged.

The optimum can also be shifted by changing two clutch parameters, rather than by changing either a single motor or single clutch parameter. For example, an increase in k_off should counteract the tendency toward stalled behavior produced by increasing k_on. As seen from the individual parameter sensitivities, the single-parameter positive sensitivity of k_on (S = +1.4) should overcome the negative sensitivity of k_off (S = −0.4) and shift the optimal stiffness upward as both increase. Indeed, Fig. 4 C shows this shift for the retrograde flow rate, and Fig. 4 D shows the corresponding traction force dependence. However, the shape of the retrograde flow curve is not maintained, and the minimum becomes less pronounced. In this case of changing two clutch parameters (a clutch-clutch case), the magnitude of the maximum traction force remains constant because it cannot change without a change in either number of motors (n_m) or motor stall force (F_m). This is unlike the case of changing one motor parameter and one clutch parameter (a motor-clutch case).

Given these two examples of dual parameter changes, we performed an exhaustive analysis on all possible pairwise parameter combinations. The S, R, and SR values for all dual parameter changes are given in Fig. 5, A–C. The dual parameter changes that result in the greatest SR values fall into the two categories mentioned previously: motor-clutch changes and clutch-clutch changes. By contrast, motor-motor changes were only weakly effective at shifting the optimum (at most |SR| = 1.0). The five highlighted boxes show parameter combinations that can shift the optimum much more than individual parameter changes (|SR| > 2.6), with the potential to shift the optimum up to five orders of magnitude in some cases (|SR|= 5).

Figure 5.

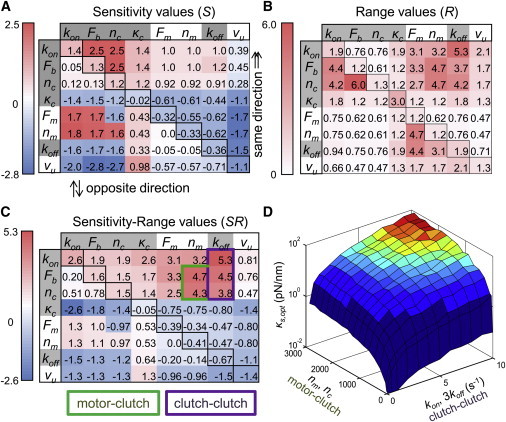
Systematic pairwise parameter sensitivity analysis. (A) Sensitivity values were calculated for each parameter combination. The diagonal corresponds to the single parameter sensitivities, whereas the entries above the diagonal correspond to dual parameter changes in the same direction (i.e., both parameters increase and both parameters decrease). Entries below the diagonal correspond to dual parameter changes in opposite directions (i.e., one parameter increases and the other decreases). Entries are color-coded based on the sensitivity value (S), as previously described by Gaudet et al. (52). (B) The range values (R) of each parameter set were also calculated for all pairwise combinations. Again, the diagonal corresponds to the single parameter ranges, and above and below the diagonal correspond to parameter changes in the same and opposite directions. (C) The product of sensitivity and range, which we call sensitivity-range (SR) is given for all pairwise combinations. The same convention for changes above and below the diagonal is used for SR as for R. Clutch-clutch and motor-clutch parameter changes that shift the optimum to the greatest extent are highlighted. Clutch parameters are highlighted in gray. (D) Combination of the strongest pairwise interactions can extend the SR even further. An example of changing four parameters is shown where the surface signifies the optimal stiffness when changing the numbers of motors and clutches, n_m and n_c, and the kinetic rate constants, k_on and k_off coordinately. The ratios of n_m/n_c and k_on/k_off are maintained at 1 and 3, respectively.

It is possible to change more than two parameters at the same time to gain even more range in the optimal stiffness. The example given in Fig. 5 D shows the change in the optimal stiffness with respect to changes in the number of motors and clutches and the kinetic on- and off-rate constants. By coordinately changing four parameters simultaneously, it is possible to gain more range for the optimal stiffness with smaller parameter changes. Four-parameter changes such as this would be difficult to test experimentally, so the bulk of this analysis was concerned with two-parameter changes, as they can already describe shifting the stiffness optimum over a wide rage.

Deconstruction of model behavior

Although the preceding analysis is informative in terms of which parameter combinations are effective at shifting the optimum, it is not necessarily obvious what determines the optimum generally. For example, as discussed previously, it is necessary for the motors to be approximately balanced by the clutches; otherwise, stiffness sensitivity is lost and the system becomes either stalled or free flowing (Fig. 2, B and C). Therefore, we wished to deconstruct the model, so we could better understand the determinants of optimality at an intuitive level. Through iterative hypothesis testing against computer simulation, we identified three stiffness regimes of the model. On the stiffest substrates, there is no stiffness sensing because the substrate is stiffer than the clutches of the cell. In this regime, clutches load quickly and fail before many clutches may bind, therefore relatively few clutches are engaged at any point in time (15) (Fig. 6 A). We define the ensemble clutch stiffness as the individual clutch stiffness multiplied by the mean number of engaged clutches. The ensemble clutch stiffness is a variable output of the model, whereas the clutch stiffness is a physical property of the individual clutches encoded as an input parameter. In this stiff substrate regime, the ensemble clutch stiffness is the softer of two springs in series, the ensemble clutch spring and substrate spring (Fig. 6 B), so the cell only senses its own stiffness, which is approximately constant, rather than the substrate stiffness. However, as the substrate becomes softer, the ensemble clutch stiffness starts to rise, and there is a point where the ensemble clutch stiffness crosses over the substrate stiffness (Fig. 6 B). To the left of this crossover point, the substrate now becomes the softer of the two springs, and the cell can sense changes in the stiffness of its environment. We call this point the upper limit of stiffness sensing. The region to the right of this point is not stiffness sensitive and is characterized by frictional slippage of the module. The region to the left is characterized by load-and-fail dynamics (15).

Figure 6.

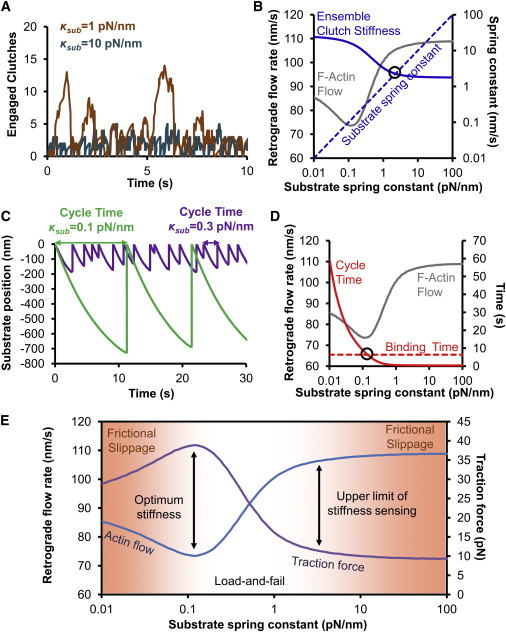
Key determinants of stiffness sensitivity and the optimal stiffness. (A) The number of clutches engaged increases with decreasing substrate stiffness. On soft substrates, it takes longer for forces to build on the clutch bonds, thereby decreasing the rate at which clutch bonds break. The result is an increased number of clutches engaged on average on softer substrates. (B) The upper limit of stiffness sensing occurs when the ensemble clutch stiffness (mean number of engaged clutches multiplied by the individual clutch stiffness) equals the substrate stiffness. At substrate stiffness greater than this crossover point, the ensemble clutch stiffness is the softer of the two springs in series, and the system is insensitive to stiffness changes in the environment. At substrate stiffness below this crossover point, the ensemble clutch stiffness exceeds the substrate stiffness, and the system responds to mechanical changes in the environment. (C) The load-and-fail cycle time near the optimal stiffness increases with decreasing substrate stiffness. On soft substrates, it takes longer to reach the load required to ensure collective failure of the clutch bonds. (D) The optimal stiffness occurs when the clutch binding time (see Eq. 10) equals the load-and-fail cycle time. At substrate stiffness above this crossover point, it is expected that not all of the clutches will engage during one loading cycle, whereas at substrate stiffness below this crossover point, all clutches can engage. Further decreases of substrate stiffness lead to even longer cycle times, and spontaneous low-load individual clutch failure before collective failure leads to a regime of frictional slippage at low substrate stiffness. (E) The model predicts three regimes of stiffness sensing. There are two regions of frictional slippage, one below the optimal stiffness on soft substrates, and one above the upper limit of stiffness sensing on stiff substrates. Between these two regimes, the cycle time is long enough for load-and-fail to occur, but short enough to prevent spontaneous bond rupture. This is the regime of load-and-fail without frictional slippage.

The second regime transition occurs at the optimum stiffness. Below the upper limit of stiffness sensing the system exhibits load-and-fail dynamics, which are characterized by a quasiperiodic cycle time required to reach failure as shown in Fig. 6 C. The softer the substrate, the longer it takes for the motors to reach sufficiently large forces to cause failure (i.e., the longer the cycle time), as shown in Figs. 6, C and D. To use the entire ensemble of clutches, the cycle time must be sufficiently long to allow all clutches to bind at least once during loading. The ensemble binding time (t_binding) does not depend on any system variables, and can be calculated analytically (Eq. 10) by considering the clutches binding as a set of n_c parallel reactions each occurring at rate k_on:

$$t_{binding}=\sum _{i=0}^{n_c-1}\frac{1}{k_{on}\left(n_c-i\right)}.$$ (10)

The binding time does not depend on stiffness, and is therefore constant at all stiffnesses, as shown in Fig. 6 D. On a sufficiently soft substrate, the cycle time equals the binding time, and clutches are used to the maximum extent possible. To the right of this point (i.e., substrate stiffness above the optimum), the cycle time is too short for all of the clutches to bind, so the maximum resistance to flow cannot be achieved. To the left of that point (i.e., substrate stiffness below the optimum), the cycle time is longer than the binding time, and clutches begin to spontaneously unbind before failure even under relatively low load. This is another region of frictional slippage, where clutch turnover again results in less than maximal resistance to flow. Fig. 6 E depicts the three motor-clutch model regimes. At high substrate stiffness, bonds break quickly after they are formed, leading to frictional slippage and poor force transmission. Once substrate stiffness falls below the ensemble clutch stiffness, the upper limit of stiffness sensing is reached and the second regime, characterized by load-and-fail dynamics, is entered. As the substrate becomes softer still, the cycle time eventually equals the binding time, and the maximum in force transmission is reached. Below this substrate stiffness, the third regime is entered, where the cycle time is longer than the binding time. In this regime, the bonds fail spontaneously before failure is reached, leading to a second regime of frictional slippage.

Model validation against previous experiments

The model was tested against previously published experimental results of studies of cellular adhesion and traction. First, the model was used to reproduce the results of stable and fluctuating traction dynamics observed on different substrate stiffnesses and under different experimental conditions as reported by Plotnikov et al. (30). For the parameter set used, mean traction force decreased with stiffness (Fig. 7 A). Traction fluctuated at the low stiffness of 8 pN/nm, although it remained stable at the high stiffness of 32 pN/nm. To mimic the expression of defective paxilin, the number of clutches on 8 pN/nm was decreased resulting in a shift from fluctuating to stable traction. To mimic the addition of blebbistatin, the number of motors on 32 pN/nm was decreased, and the system regained fluctuating traction. A decrease in the force generating capability actually resulted in an increase in the traction force as suggested by Plotnikov et al. (30).

Figure 7.

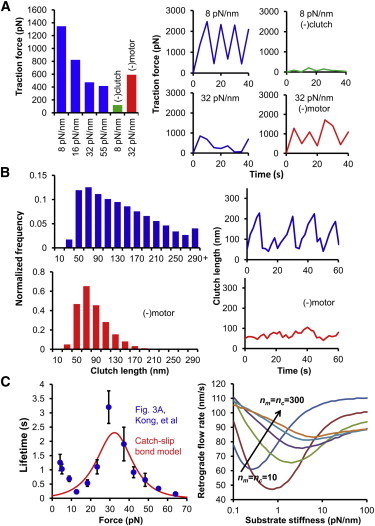
Experimental validation of the motor-clutch model. (A) As in Plotnikov et al. (30), the motor-clutch model produces either fluctuating or stable traction forces depending on the conditions. Parameters were adjusted to show decreasing traction force on substrate stiffnesses ranging from 8 to 55 pN/nm. Over this range the traction dynamics also shifted from fluctuating traction to stable traction (blue). Reduction of the number of clutches on 8 pN/nm resulted in stable traction (green), whereas reduction of the number of motors on 32 pN/nm resulted in fluctuating traction (red). (B) Clutch extension histograms and dynamics show behavior similar to that seen in Margadant et al. (31). Clutch length shows a broad distribution from 10 to >290 nm, whereas individual clutch length cycles through time (blue). Reduction of the number of motors shifts the length distribution to lower values, and the individual clutch length remains relatively constant (red). (C) A catch-slip bond model was fit to integrin catch bond data from Kong et al. (32). The fitted catch-slip bond model was incorporated into the motor-clutch model to produce qualitatively similar results to the simplified slip bond motor-clutch model. The catch-slip bond model produces a minimum in actin retrograde flow with respect to substrate stiffness, and this minimum can be shifted by coordinately changing the number of motors and clutches.

The model was also tested against the talin stretching results of Margadant et al. (31). Assuming the talin length changes are manifested as clutch length changes in the model, the motor-clutch model was able to reproduce the length distribution of talin molecules, as well as the dynamic fluctuations in length (Fig. 7 B). To model the addition of blebbistatin or Y-27632, the number of motors was decreased resulting in a shift of the length distribution to lower values, and less fluctuation in talin molecule length, consistent with the findings of Margadant et al. (31).

Finally, catch-slip bonds were added to the model. The catch-slip off-rate model was fit to integrin catch bond data from Kong, et al. (32) (Fig. 7 C), and the fitted parameters were used to test the model results with catch-slip bonds. The model maintained its qualitative behavior exhibiting a minimum in actin retrograde flow corresponding to a maximum in traction force. Additionally, the coordinate increase of motors and clutches shifted the optimum stiffness higher. The exact relationship between the numbers of motors and clutches and the optimum stiffness seems to be more complicated than with slip bonds, but the qualitative behavior is maintained. This suggests that catch bonds may be important for external cellular forces such as shear flows (33,34) but less important for internally generated cellular forces. Parameter values for all experimental validations are given in the Supporting Material, Table S1.

Discussion

Our simulations show that the optimal stiffness in a motor-clutch model for cell traction can be shifted by coordinately changing a parameter that strengthens the clutches and a parameter that either strengthens the motors or weakens the clutches. By contrast, the optimum is only weakly sensitive to single parameter changes or to two coordinate changes in motor parameters. This provides complementary insight into other clutch analyses (35) by specifically examining the consequences of environmental mechanics. Because the optimal stiffness is generally more sensitive to the clutches than the motors, increasing both will move the optimum toward higher substrate stiffness. The changes do not cancel out because the strong positive sensitivity to the clutch parameters is greater than the weak negative sensitivity to the motor parameters.

We identified five parameter combinations that can cause the greatest change in the optimal stiffness. These involve two motor-clutch combinations, n_m and n_c, and n_m and F_b. They also involve three clutch-clutch combinations: k_on and k_off, F_b and k_off, and n_c and k_off. Each combination involves an increase in a parameter that strengthens the clutches that is compensated by an increase in a parameter that strengthens the motors. We suggest that these coordinate parameter shifts may explain the differences seen in cell traction force and migration with respect to substrate stiffness, where different cells operate at different points in parameter space of the motor-clutch model. Such shifting of the optimal stiffness may then explain why several studies have reported increasing cell traction with substrate stiffness on deformable two-dimensional gels (2,7,12–14) and micropost arrays (36–38), yet others have seen decreasing cell traction (15). The biphasic nature of traction force in the motor-clutch model could explain these conflicting results. The neurons used by Chan and Odde (15) may have a traction maximum at a stiffness below the lowest one observed, although the other cell types may have a traction maximum at a stiffness above the highest one observed. Traction is difficult to measure on surfaces of high stiffness because deflections or deformations become vanishingly small even at high forces. In some cases, it may not be possible to record the decrease in traction to the right of the optimum because the deformations or deflections are below the detection limit.

The shifting optimum of cell migration may also be explained by this model. Although the model was originally tested against neuron filopodia, the behavior of the model is consistent with experimental results for other cell and protrusion types. Depending on the parameter sets, the model can produce both fluctuating and stable traction forces as seen with fibroblast focal adhesions on polyacrylamide gels (30) (Fig. 7 A). Molecular clutch length may also fluctuate or remain stable as seen with talin in CV1 kidney cells (31) (Fig. 7 B). We should note that the model makes no assumption about the identity of the clutch molecules or the location of clutch failure. The clutch failure will occur at the weakest point along the adhesion, whether inside or outside the cell. Experiments have shown failure to occur between integrins and their extracellular matrix ligands (39), which is also consistent with the model because it is only the existence of a failure point, and not its position, that is important to the model. An inverse relationship between actin speed and traction stress has been shown at the edge of kidney epithelial cells (40), and the same relationship is seen in this model. However, to conserve mass, F-actin must undergo net depolymerization as it approaches the convergence zone of anterograde and retrograde flow located between the lamellum and cell body (41). Net depolymerization, which is presumably preceded by severing (42), would result in decreased mean F-actin flow and traction stress. This would produce a direct relationship between F-actin flow and traction stress in the lamellum, as observed experimentally (40).

This convergence zone could be modeled by coupling two motor-clutch modules to one another pointing in opposite directions, one toward the leading edge and one toward the cell center. Larger actin network behavior could be modeled by coupling several motor-clutch modules together with flexible linkages giving compliance to the actin network. The current inextensible actin in the model is accurate when the substrate is softer than the cell, but even in situations where the substrate is stiffer than the cell, the actin compliance can be lumped together with the substrate compliance because the model does not specify the location of this compliance. Greater insight may be gained by including actin polymerization, depolymerization, severing, and capping, as well as membrane mechanics and adhesion maturation (43). Further insight into cell migration could be gained by linking opposing motor-clutch modules together into a whole-cell model. The traction dynamics, stiffness sensitivity, and extension and retraction of the modules should determine the migration behavior of the modeled cell. The whole-cell model could also provide insight into cell morphology (17) and its relationship to the motor-clutch mechanism and environmental mechanics.

It is unclear exactly how this motor-clutch model translates into cell migration, but the stiffness sensitivity of the model traction likely plays a role in the stiffness sensitivity of cell migration. Different cell types have different parameter sets that will result in different stiffness optima. The maximum in cell migration may not necessarily coincide with the maximum in traction force. However, it seems that it should closely correlate with the region of stiffness sensitivity. Studies have shown that short load-and-fail cycle time correlates with fast cell migration (44). However, the fastest cycle times in the model correspond to a frictional slippage regime where little traction force is generated. Therefore, we suspect that the optimum in cell migration will occur to the right of the maximum traction force because the cycle times are shorter, but to the left of the limit of stiffness sensitivity because little traction force is generated beyond that limit. Model parameter changes shift these two points and could therefore shift the optimum migration stiffness.

The shifting of the migration optimum may have important biological consequences. For example, rodent models of glioblastoma exhibit up-regulated myosin II (45), the molecular motor most associated with actin contractility. Several integrins, adhesion molecules associated with molecular clutches (46), are also up-regulated in glioblastoma cells (47). Given that the increased myosin must be active, and noting that several other molecules make up the cellular adhesions, this coordinate increase in motor and clutch molecules may suggest that glioblastoma cells are tuned to a higher stiffness than normal glial cells. This could cause them to migrate quickly along stiff areas of the brain.

The motor-clutch model may also be applicable to collective cell migration such as that observed by border cells in the ovaries of Drosophila melanogaster (48) or in collective tumor cell migration (49). In both cases, cells effectively increase their motors and clutches by teaming together with other cells. Cadherins involved in cell-cell interaction have been shown to transmit actomyosin forces across the cell membrane (50), and cadherin-linked cells have been shown to transmit more force to their substrates than isolated cells (51). Through the mechanical coupling of cadherins, a group of cells working together may effectively tune themselves to a high stiffness and migrate differently than the individual cells. In fact, studies of epithelial cell sheets show that sheets of cells are sensitive at higher stiffnesses than individual epithelial cells (6).

The predictions of this model can be tested through multiple experiments. Model parameters can be perturbed through the addition of inhibitory molecules to cells in culture. Actin retrograde flow and traction stress can be measured for unperturbed cells over a range of substrate stiffness. The actin flow should show a minimum with respect to substrate stiffness corresponding to a maximum in traction stress. A molecule such as blebbistatin could then be added to inhibit the myosin motors of the cells. This should result in a stalled motor-clutch system, and actin flow should approach zero. If the experiment is performed near the optimum substrate stiffness, load-and-fail cycles should cease, resulting in a stable low traction stress. Additionally, a clutch inhibitor such as a soluble RGD compound could be added. This should result in a free flowing motor-clutch system with actin flow consistently near the unloaded velocity. Again, load-and-fail cycles would cease and traction would be stably low. Finally, both molecules could be added to inhibit both the motors and clutches of the cell. The same measurements could be made on the doubly perturbed cells, and the minimum actin flow and maximum traction stress should shift to a lower stiffness. At the correct stiffness below the optimum, addition of soluble RGD would decrease traction stress, but the subsequent addition of the contractile inhibitor blebbistatin would actually increase the traction stress from the clutch inhibited state. This would result because the optimum stiffness was shifted down to the experimental stiffness.

Conclusion

The motor-clutch model provides a possible explanation for the differing results found for cell migration and traction force dependence on substrate stiffness. These experimental results suggest an optimum substrate stiffness that differs with cell type. Although individual parameter changes in the motor-clutch model cannot sufficiently account for the shifting optimum, coordinate parameter changes in the model can shift the optimum substrate stiffness over several orders of magnitude. A coordinate change in motors and clutches is of particular interest because it may apply to collective cell migration as well as individual tumor cell migration. The results of this study suggest that targeting tumor cells to decrease their motor and clutch numbers may slow their migration by shifting their optimum stiffness away from the stiffness of their microenvironment.