The electrostatics of VDAC: implications for selectivity and gating

Abstract

The voltage-dependent anion channel (VDAC) is the major pathway mediating the transfer of metabolites and ions across the mitochondrial outer membrane. Two hallmarks of the channel in the open state are high metabolite flux and anion selectivity, while the partially closed state blocks metabolites and is cation selective. Here we report the results from electrostatics calculations carried out on the recently determined high-resolution structure of murine VDAC1 (mVDAC1). Poisson-Boltzmann (PB) calculations show that the ion transfer free energy through the channel is favorable for anions, suggesting that mVDAC1 represents the open state. This claim is buttressed by Poisson-Nernst-Planck (PNP) calculations that predict a high single-channel conductance indicative of the open state and an anion selectivity of 1.75 – nearly a 2-fold selectivity for anions over cations. These calculations were repeated on mutant channels and gave selectivity changes in accord with experimental observations. We were then able to engineer an in silico mutant channel with three point mutations that converted mVDAC1 into a channel with a preference for cations. Finally, we investigated two proposals for how the channel gates between the open and closed state. Both models involve the movement of the N-terminal helix, but neither motion produced the observed voltage sensitivity, nor did either model result in a cation selective channel, which is observed experimentally. Thus, we were able to rule out certain models for channel gating, but the true motion has yet to be determined.

Introduction

Voltage-dependent anion channels (VDAC) are the dominant protein in the mitochondrial outer membrane (MOM), where they facilitate the flow of adenosine triphosphate (ATP), adenosine diphosphate (ADP), and other metabolites between the cytosol and the intermembrane space^{1; 2}. The efficient flow of materials into and out of the mitochondria is critical to cell survival in all eukaryotic systems, and it is not surprising that VDAC exhibits a large conductance, 0.45-0.58 nS in 0.1 M KCl, compatible with this task³. Experiments in reconstituted bilayers have shown that the channel is maximally open at 0 mV and that it enters a lower-conductance state above +30 mV and below -30 mV resulting in a bell shaped current-voltage relationship¹. Here, we refer to the high-conductance state as the open state and the lower-conductance state, or possibly states, as the partially closed state. While the open state facilitates the flux of ~ 2×10⁶ ATP molecules per second, this value drops to near zero in the partially closed state despite the persistent flow of small ions². Additionally, as the name implies, VDAC is weakly anion selective in the open state, but switches to weakly cation selective in the partially closed state³.

In addition to its energetic role, VDAC appears to have a more complex purpose, serving as a scaffold for proteins and molecules that modulate mitochondria permeability, and thereby its function^{4; 5}. This cell death/survival role has implicated VDAC in the metabolic stresses of cancer and cardiovascular disease specifically as well as mitochondrial-dependent apoptotic cell death in general⁶. Thus, the ability to manipulate VDAC’s function in a rational manner will have important implications for novel therapeutics to modulate cell survival in different diseases.

In mammals, there are three VDAC isoforms (VDAC1, VDAC2, and VDAC3) with VDAC1 being the prototypical channel common to all eukaryotes. These three isoforms share greater than 80% sequence homology, yet they have distinct physiological roles, electrophysiological properties, relative abundance and distribution between cell types^{7; 8; 9}. VDAC2 is the dominant isoform expressed in the brain¹⁰ displaying normal gating patterns relative to VDAC1, but there is an additional population with lower conductance⁹. VDAC3 is less well characterized but appears to have distinct gating properties and reduced metabolite permeability⁹. VDAC1 is by far the most well-studied isoform in the family, and many of the fundamental electrophysiological properties including single-channel conductance, selectivity, and voltage dependence, are remarkably conserved across different organisms ranging from yeast to mammals^{3; 11}. In spite of this basic conservation, there are species related differences resulting in some variations when reconstituted in planar phospholipid membranes^{3; 11}.

Up until now, direct structural insight into the operation of VDAC has come from low-resolution electron microscopy (EM)^{12; 13} and atomic force microscopy (AFM)¹⁴; however, recently three mammalian structures have been reported^{15; 16; 17}, making it possible to ask unprecedented questions concerning VDAC1’s molecular workings. All three structures show that VDAC1 is a β-barrel formed by 19 β-strands with an ~ 3 nm pore diameter in excellent agreement with previous EM^{12; 13} and AFM¹⁴. Mouse VDAC1 (mVDAC1) is the highest resolution structure (2.3Å) revealing an N-terminal helix situated in the pore domain where it adheres to the wall of the barrel¹⁵. At both mouths, the pore is ~ 27 Å wide, but it narrows to 14 Å near the center of the channel at the helix. The long dimension of ATP is also about 14 Å, which would allow metabolites to pass through the channel sterically unhindered. This observation suggests that mVDAC1 may represent the open state of the channel. However, it is possible that permeation is not controlled through steric interactions, but rather by the electrostatic field in the channel created by the ~ 30 charged residues that line the pore. Structural changes could alter this field thereby drastically altering the permeation properties of ATP and ADP, which carry a formal charge of -4 and -3, respectively. With regard to gating, the helix is flanked by two proline residues on the N-terminal side and three glycine residues at the C-terminal end, making it ideally suited to be a mobile element. The helix position was not resolved in the NMR structure, which is consistent with a high degree of mobility^{13; 17; 18}. Therefore, it is quite possible that the N-terminal helix, which has four basic and two acidic residues, is the voltage sensor and metabolite gate as suggested by past work^{19; 20}.

Despite this windfall of structural information, there are still numerous outstanding questions concerning the mechanism by which VDAC1 differentiates between ions, how it conducts ATP at high rates, and how the membrane voltage regulates its conduction state. The most pressing question is whether the latest high-resolution structure represents the open state or the partially closed state of the channel. To better understand VDAC1’s biophysical properties, we have carried out a number of continuum electrostatics calculations on mVDAC1. As we describe below, the channel is anion selective, and it has a large single-channel conductance that is most consistent with the open state. A key aspect of any computational model is the ability to address a wide range of experimental data. Continuum electrostatic calculations provide a rapid means to compute the current-voltage characteristics for a number of mutant channels, and our results are in good agreement with experimental trends. The molecular rearrangements that accompany voltage gating are not known. We examined two hypothetical models that involve motions of the N-terminal helix, and our calculations indicate that neither motion fully accounts for the channel’s observed voltage sensitivity. Thus, we were able to rule out some of the proposed molecular motions, but to gain an understanding of the true mechanism will require extensive probing by a number of different techniques.

Results

Cation and anion energy profiles suggest that the mVDAC1 structure is open

The mVDAC1 structure has been proposed to be in an open conformation¹⁵, which is known to be anion selective. We wanted to quantitatively probe this claim by determining if ion passage through the channel was more conducive to anions or cations. Poisson-Boltzmann (PB) electrostatic calculations are a fast, effective way of calculating such ion transfer free energies and for understanding the role of the protein architecture in the process^{21; 22}. We computed the energy required to transfer a chloride-sized monovalent anion from bulk water through the central pore of mVDAC1. The total free energy of transfer consists of a Born solvation term, which corresponds to stripping waters away from the ion as it passes through the channel, and an electrostatic term, which corresponds to the interaction of charges on the channel with the charge on the ion. The proximity of the ion to the low dielectric of the membrane could drastically affect the permeation energetics, so we embedded the channel in a water-impermeable, uniform slab of dielectric 2, which closely mimics the properties of the membrane.

The geometry of the system is depicted in Fig. 1C,D. The ion (green sphere) was translated from -40 Å to +40 Å, and the total electrostatic energy was calculated every 1 Å. The channel was centered at the origin, and z = 0 and ±20 Å are indicated by arrows in panel C. While included in all of the calculations, the membrane is not pictured but its extent is indicated by grey bars in Fig. 1C. Our choice of orientation along the z-axis is arbitrary since the orientation of VDAC in the membrane is still under debate (see below). For consistency, we define the negative direction to be the side of the membrane that contains the N and C-termini. This convention is held throughout. We see from the set of curves in Fig. 1A that the transfer free energy is energetically favorable resulting in a ~ 2.5 k_BT stabilization of the anion when it is at z = -7.5 Å (1 k_BT ~ 0.6 kcal/mol at room temperature). Interestingly, the profile is not symmetric with respect to the center of the channel. The N-terminal helix occupies the lower half of the channel very close to the energy minima. It is generally thought that the dielectric constant of protein ranges from 2 to 20²³, but it is also understood that proteins are heterogeneous²⁴. We explored the affect of the choice of protein dielectric constant, ε_p, on our results by varying it from 2 to 10. Paradoxically, increasing the protein dielectric value destabilizes the negative ion by 0.5 k_BT (red curve compared to green curve in panel A). While this is only a small change, it results from the decreased electric field in the center of the channel that accompanies increasing the protein dielectric value. In Fig. 2A, we show that the membrane has very little effect on the permeation energetics since the ion remains surrounded by a significant amount of water during penetration due to the large pore size.

Fig. 1.

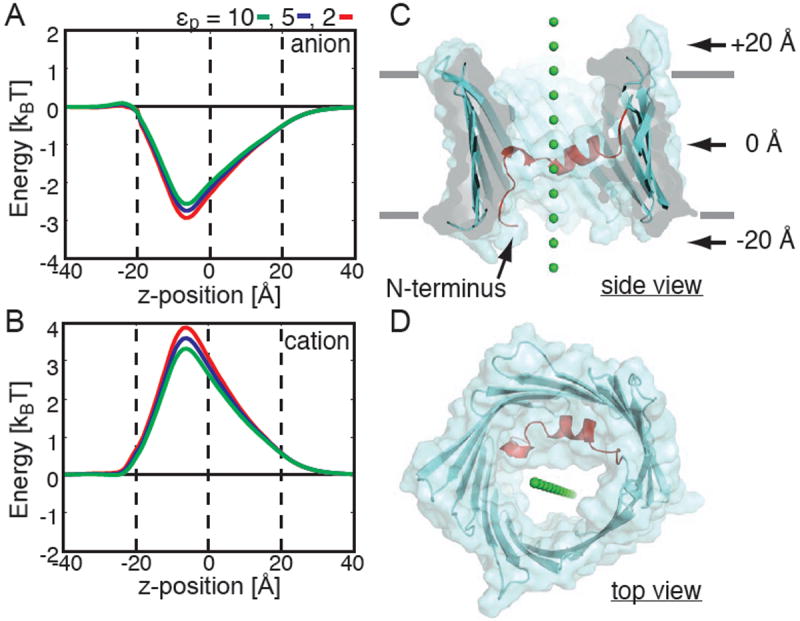
mVDAC1 is selective for anions. Ion transfer free energies calculated through mVDAC1 for a chloride-sized anion (A) and a potassium-sized cation (B). Energies were calculated using the Poisson-Boltzmann equation after embedding mVDAC1 in a low dielectric, ε_m= 2, slab corresponding to the membrane. The path for both ions through the channel is pictured in panels C (side view) and D (top view). Varying the protein dielectric constant, ε_p, had little effect on the free energy profiles. For all calculations, z = 0 corresponds to the center of the channel, and the channel extends from -20 to +20 Å. These positions are indicated by dashed lines in panels A and B.

Fig. 2.

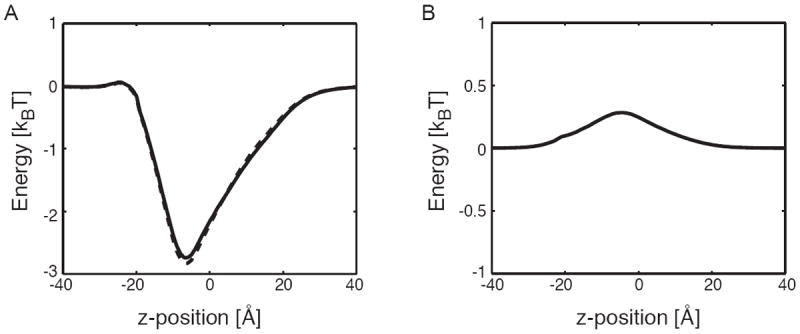
Protein charges dominate the ion transfer free energy. (A) Ion transfer free energy profiles through mVDAC1 for a chloride-sized anion in the absence (dashed curve) and presence (solid curve) of the membrane. The membrane has very little effect on the permeation energetics. (B) Born solvation energy for anion permeation. The energy peaks near the N-terminal helix (-7.5 Å) at 0.25 k_BT. Such a small value indicates that ions remain largely solvated during the transfer from one side of the pore to the other. Panels A and B indicate that the electrostatic interactions of the permeant ions with the permanent charges on mVDAC1 dominate the ion transfer free energy. In both panels that protein dielectric, ε_p, was set to 5.

Next, we carried out all of the free energy calculations using a potassium-sized monovalent cation. Interestingly, the channel presents a free energy barrier to cation movement (Fig. 1B). The maximum energy difference between the curves in panel A and B is 5.5-7 k_BT, which is energetically significant and shows that the channel is selective for anions. This result corroborates the claim that the x-ray structure is indeed the open state¹⁵, and that it is not the cation-selective partially closed state. The anion and cation energy profiles in panels A and B are nearly mirror opposites of each other suggesting that the Born solvation energy is very small, which we verified in separate calculations in Fig. 2B. Therefore, the free energy profile is dominated by the electrostatic interaction with charged groups on the channel. For a narrow pore like the KcsA potassium channel, the Born solvation term is very important since all the water molecules are essentially stripped away during translocation²¹. In our case, the pore is large enough that ions can retain their hydration shell as they move through the channel resulting in a negligible Born energy.

The permeation energetics of mutant channels is in accord with experimentally measured changes to selectivity

VDAC has an open-state chloride to potassium ion selectivity ratio of 1.7-1.9 in a 1.0 M to 0.1 M asymmetric salt gradient³. These selectivity values are modest compared to ion channels like the Shaker voltage-gated potassium channel (1000:1)²⁵, which has a selectivity filter – a narrow stretch made up of a handful of residues responsible for selecting one ion over another via interactions of the carbonyl backbone with the permeating ion²⁶. Blachly-Dyson and co-workers showed that mutations throughout the primary sequence of VDAC from Saccharomyces cerevisiae (scVDAC1) could affect channel selectivity and the largest changes involved charge mutations (such as lysine to glutamic acid)²⁷. Additionally, the effects from multiple mutations were additive, which is suggestive of an electrostatic mechanism in which the electric fields from multiple residues add linearly at the site of the permeating ion. This mechanism is in stark contrast to those of potassium channels, which are believed to depend on the details of packing geometry and fluctuations of the channel around the ion^{28; 29}.

We investigated those residues that were previously shown to contribute to anion selectivity. Blachly-Dyson et al. carried out site directed mutagenesis and identified 14 sites that affect selectivity and 12 that, when mutated, showed little or no change in selectivity²⁷. We aligned mVDAC1 to scVDAC1 and found that 11 of the 14 residues implicated in selectivity are on the bottom half of the channel (the overall sequence identity is 25% and the sequence similarity is 51%). Interestingly, the bottom half of the channel is the most favorable location for anions in the pore as shown by the energy minimum in Fig. 1A. As can be seen in Fig. 3C, we made in silico mutations to some of the homologous residues in mouse VDAC1 using VMD³⁰, and then we recalculated the free energy of ion transfer to compare against calculations on the wild-type structure.

Fig. 3.

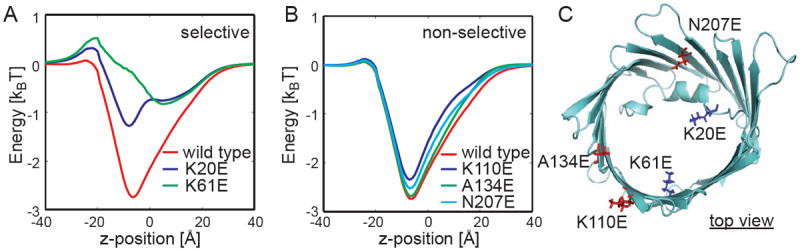
Altered ion transfer free energies through mVDAC1 match measured changes to selectivity. (A) Free energy profile for a chloride anion moving through the wild-type (red) and two mutant channels: K20E (blue) and K61E (green). K20E and K61E significantly destabilize the anion in the channel, and this is consistent with experimental measurements. (B) Mutations K110E, A134E, and N207E have little effect on the free energy profile, which is in excellent agreement with experiment. (C) All residues are pictured. The selective positions (blue) are much closer to the permeation pathway, while the nonselective positions (red) are farther away.

Experimentally, mutating scVDAC1 residues K19E or K61E elicits changes in the reversal potential, which is directly related to a decrease in the channel’s selectivity (see Table). We mutated the corresponding residues in mVDAC1, K20E, and K61E, and plotted the change in the free energy profile compared to wild type (Fig. 3A). The changes in the free energy profile are striking. The free energy minimum near -7.5 Å is decreased by 1.5 and 2.5 k_BT relative to the wild-type curve (red) for K20E (blue) and K61E (green), respectively. Moreover, both mutations present a slight barrier to permeation along the chosen path at z = -20 Å.

Table.

Summary of mutant channel properties.

Mutation (S. cerevisiae)	Mutation (Mouse)	ΔVrev [mV] (ref. (27))	ΔVrev [mV] (Fig. 5A)	ΔVrev [mV] (Fig. 5B)	ΔΔG [kBT] (Fig. 3)
K19E	K20E	-12.3	-6.4	-7.0	1.5
K61E	K61E	-8.4	-4.1	-5.5	2.6
K19E/K61E/K95E	K20E/K61E/K96E	NA	-13.4	-19.0	NA
K108E	K110E	-0.8	-2.5	-0.8	0.4
K132E	A134E	-0.1	-1.4	~ 0.0	0.2
K205E	N207E	-1.0	-1.8	-0.3	0.05

We considered 3 mutations that affected selectivity (green) and 3 that did not (blue). The original mutagenesis was carried out on scVDAC1, and we present the homologous mouse VDAC1 residues mutated for the present study. The change in reversal potential, ΔV_rev, under 1.0 M to 0.1 M KCl conditions are based on experiments from ref. ²⁷, PNP calculations with the channel orientation in Fig. 5A, and PNP calculations with the orientation in Fig. 5B. While ref.²⁷ studied K19E, K61E, and K95E separately, the triple mutant was not studied; hence, this value is listed as not available (NA). The final column is the change in the minimum energy for the mutant channels compared to the wild-type channel based on the transfer free energies in Fig. 3.

Blachly-Dyson and co-workers also reported 12 non-selective sites where mutating basic residues to acidic ones, or vice versa, had little affect on the channel’s selectivity. Our electrostatic calculations on a few of the corresponding mouse mutants (K110E, A134E, and N207E) resulted in very small changes to the free energy profile, less than 0.4 k_BT in each case (see Table). All of the ion transfer free energies in Fig. 3B are very similar to the wild-type curve indicating that these mutations do not alter the biophysical properties of the channel. Thus, our calculations, like the experiments, show that these residues play a minor role in VDAC1 selectivity.

Electrostatic calculations identify anion and cation pathways through the channel

The ion paths shown in Fig. 1 were chosen as straight lines that passed approximately through the middle of the channel. However, the pore is wide, and it is likely that the local electric fields guide anions and cations along different paths that are not straight. PB calculations were used to determine the electric field in the pore, and in Fig. 4, the potential contours were plotted at different heights along the channel: z = +10 Å (panel A), 0 Å (panel B), and -10 Å (panel C). Contours were drawn in 35 mV intervals between -35 mV and 70 mV. At all levels, the pore is dominated by positive potentials showing that the respective anion and cation transfer free energies along single paths in Fig. 1 are representative of the true energetics of ion permeation. For instance, at z = -10 Å the potential is 70 mV or greater throughout 90% of the pore indicating that the anion minimum and cation maximum in Fig. 1 are present for nearly all paths through the channel. For reference, a 60-75 mV potential corresponds to a 2-3 k_BT energy for a monovalent anion at room temperature, in excellent accord with the values in Figs. 1-3. Interestingly, panels A and B indicate that cations will flow along the side of the channel opposite the helix (negative y values), while anions will occupy a larger space closer to the helix (positive y values). The 0 mV contour forms the dividing line between favorable and non-favorable positions for both types of ions.

Fig. 4.

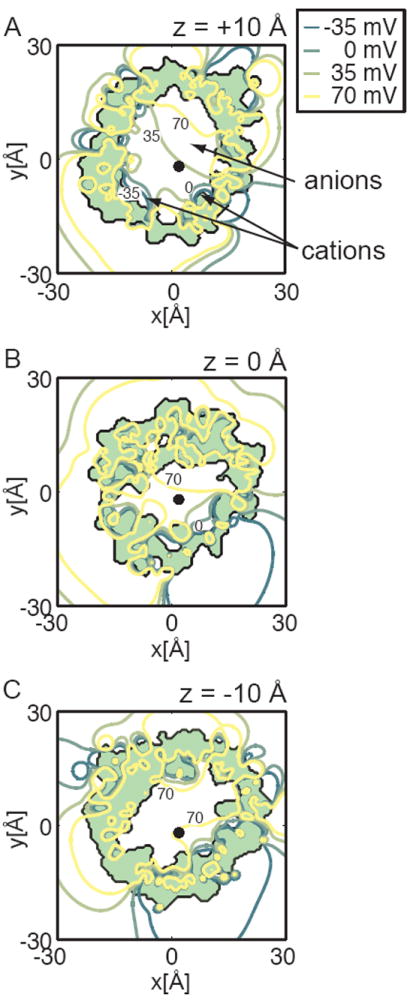
The electrostatic potential at three different heights in the pore. The potential contours due to the protein charges were calculated as in Fig. 1 and then plotted at z = +10 Å (A), z = 0 Å (B) and z = -10 Å (C). Each view is along the pore’s long axis, and the protein interior is shaded light green. The ion path used for all calculations in Figs. 1-3 is indicated by a black dot in each panel. Five equally spaced isocontours were chosen with the blue representing negative potential values and the red values representing more positive values. The contour at 0 mV is indicated in panels A and B, while the +70 mV contour is shown in each. The 0 mV contour divides the region favorable to anions (positive values at positive y values) and cations (negative values at negative y values). The pore is dominated by positive potential values at all heights, especially at z = -10 Å. The ion path falls along contour values that are representative of the average value at each height. At z = +10 Å the value is ~ +30 mV, near the middle of the full range of values. In panel B, the positive potentials occupy more of the cross-sectional area, and the electrostatic potential at the ion pathway increases to +50 mV. In panel C, close to the N-terminal helix, the potential is entirely positive. This is in accord with the anion free energy minimum and cation barrier observed in Fig. 1A,B.

PNP theory suggests a large single-channel conductance most compatible with the open state

Relating our calculated changes in ion free energy profiles to changes in selectivity is not straightforward; however, a change of more than 1 k_BT should bring about a macroscopic change in measured currents. To probe aspects of conductance and selectivity more deeply, we turned to a related continuum approach known as Poisson-Nernst-Planck (PNP) theory. PNP computes the steady state concentration profiles of each ionic species based on the net electrical potential distribution, which depends in a self-consistent manner on the ion concentration profiles. From the computed concentration profiles, the ionic flux through the channel in different physiological conditions can be calculated³¹. Since the ionic concentration profiles are 3-dimensional densities, these calculations do not suffer from picking a single arbitrary pathway, but rather the ions occupy the most favorable positions in the pore during permeation.

We first calculated the ionic flux through wild-type mVDAC1 for a wide range of voltages in symmetric salt conditions corresponding to a 0.1 M KCl solution. Throughout this work, all membrane voltages refer to the value in the lower bath with respect to the upper bath. The current-voltage relation predicted a single-channel conductance of 1.06 nS, and the experimental open-state value is 0.45-0.58 nS in 0.1 M KCl³. It has been found from previous studies that PNP theory yields conductance values that are typically 1.5-2 times higher than experimental values for large pores^{32; 33}. Therefore, given the limitations of this theory, our calculations again suggest that mVDAC1 resides in the open state.

A closer look at VDAC1 selectivity

Next, we solved the PNP equations under asymmetric conditions with the 0.1 M KCl in the upper bath and 1.0 M KCl in the lower bath. In this situation, a net current will result if the channel selects one ion type over the other. The applied voltage required to oppose this current is termed the reversal potential, and it is a direct measure of the channel’s selectivity²⁵. The solid black curve in Fig. 5A shows that mVDAC1 is indeed anion selective as suggested by the curves in Fig. 1. The reversal potential is 11.9 mV, and the ratio of the anion to cation conductance is about 1.75. This is in excellent agreement with the experimental value of 10.2 mV determined for scVDAC1²⁷. Since the charges on the channel are asymmetric, it is possible that the channel’s selectivity could depend on its orientation in the membrane. This concern is particularly relevant since the orientation of the channel in the MOM is debated^{18; 34; 35}. We flipped the channel in the membrane and recalculated the current-voltage curve (solid black curve in Fig. 5B). In this configuration, the reversal potential increases to 14.1 mV indicating a slight gain in anion selectivity. Thus, mVDAC1 is more selective when the energy minimum in Fig. 1A is facing the low concentration bath, but what this means for channel function in the MOM is difficult to say at this time.

Fig. 5.

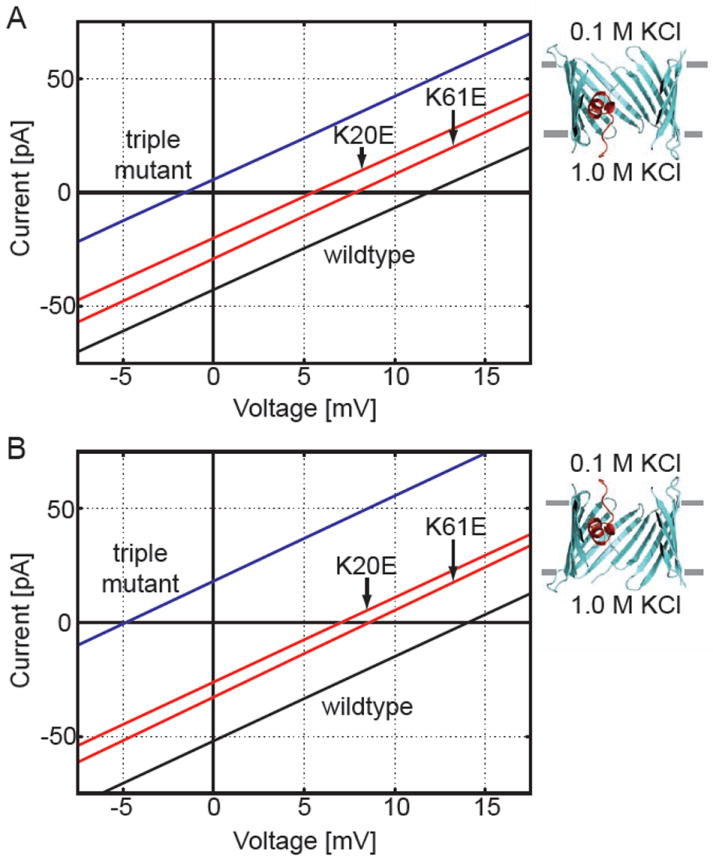
Wild-type and mutant current-voltage curves calculated using PNP theory. The upper bath was held at 0.1 M KCl and the lower bath at 1.0 KCl. The applied voltage is the value in the lower bath relative to the upper bath. Under these conditions, positive reversal potentials indicate that the channel is anion selective. (A) The channel was embedded in a dielectric slab with the N and C-termini facing the lower solution. The black line is the wild-type curve, and the red curves correspond to K20E and K61E. The leftward shift of both red curves indicates that both mutants reduce the anion selectivity of mVDAC1. The blue curve corresponds to the K20E/K61E/K96E triple mutant. This curve has a negative reversal potential indicating that the channel has been engineered to be cation selective. (B) The orientation of the channels in the membrane were reversed compared to panel A. In this case, the N and C-termini face the upper bath. Interestingly, the reversal potentials are all shifted compared to those in panel A demonstrating that the channel’s selectivity depends on its orientation in the membrane.

We also calculated the current-voltage curves for the point mutants investigated in Fig. 3 using both channel orientations. These curves are plotted on the respective panels in Fig. 5. Both K20E and K61E produced a leftward shift in the reversal potential indicating that they reduce the channel’s anion selectivity (red curves in both panels); however, these changes are more pronounced for the orientation in panel B. Our calculations predict that K20E evokes a shift 1.5 times larger than K61E, and this is exactly what is observed experimentally²⁷. In general, K110E and A134E produced small changes in the reversal potential, as observed experimentally, but there are orientation dependent differences (see Table). One should note that the homologous sites for A134 and N207 in scVDAC1 are K132 and K205, so acidic substitution results in an overall change in charge of -2, but only -1 for the present calculations. This difference will have very little affect on the reversal potential shifts reported using the orientation in Fig. 5B, but it would make the shifts calculated using the configuration in Fig. 5A even larger. Finally, we wanted to convert mVDAC1 into a cation-selective channel. We created a triple mutant channel, K20E/K61E/K96E, based on three of the highest impact mutations identified by Blachly-Dyson and co-workers²⁷. As can be seen from the blue curves in Fig. 5A,B, this hypothetical channel has a negative reversal potential showing that we were able to convert the anion channel into a cation channel through electrostatic manipulation of the pore residues. An obvious test of our modeling efforts would be to create and experimentally measure the reversal potential of this mVDAC1 mutant channel.

What is VDAC1’s voltage sensor and how does it move?

Next, we hoped to gain deeper insight into the operation of mVDAC1 by considering the gating motion and its dependence on membrane voltage. Voltage biases VDAC between an open state that allows ATP passage and a partially closed state that does not². Moreover, the channel becomes slightly cation selective in the closed state³. Several studies imply that VDAC1’s voltage sensor is the N-terminal helix^{13; 19; 20}, while other studies indicate that the residues involved in gating are distributed throughout the primary sequence³⁶. Our work above suggests that the mVDAC1 structure represents the open state. If this is true, how does the channel rearrange to occlude ATP passage? To our knowledge, the most specific gating models involve movement of the N-terminal helix, but even within this subclass of models, the degree of motion and exact molecular position of the helix is highly debated^{13; 15; 37}. We used computational methods to ask whether N-terminal helix movement could account for the channel’s voltage sensitivity and changes in ion selectivity.

A signature of the closing motion is the ‘gating charge’ or ‘sensor valence’ associated with the movement. The sensor valence is equal to the fraction of the membrane electric field that the charges on the voltage sensor pass through during gating. 1 charge moving through the entire membrane electric field would contribute a valence of 1, but since the voltage-sensor charges need not pass through the entire field this value often takes on non-integer values. The voltage dependence of the channel is directly proportional to its valence, with a high sensor valence corresponding to a steeply voltage-dependent protein. The valence of the VDAC voltage sensor varies slightly with the subtype, but it is estimated to be between 2.5 and 4.5 charge units based on single-channel recordings^{3; 17} compared to 12-14 for Shaker voltage-gated potassium channels³⁸.

We considered two hypothetical gating motions that have been suggested in the literature. First, looking at the surface representation of mVDAC1 along the channel axis, as in Fig. 1D, it is clear that an ATP molecule can pass through the channel sterically unhindered^{15; 39}. However, moving the N-terminal helix into the center of the pore would obstruct this pathway. Ujwal and co-workers proposed a hypothetical partially closed state model in which the N-terminal helix was rigidly rotated by pivoting about the C-terminus of the helix just before the beginning of the first β-strand¹⁵. While this movement is speculative, electrostatic interactions between the N-terminal helix and charged residues on the wall of the β-barrel opposite the helix might account for such a rearrangement. These two states can be seen in Fig. 6A. The theory for using continuum electrostatic calculations to determine the voltage-dependence of such movements was developed previously⁴⁰. Briefly, a modified PB equation is solved to account for the transmembrane potential, and a series of calculations are carried out to isolate the interaction energy of the charges on the protein with this field⁴⁰. Several studies have applied this theory to particular channels^{41; 42; 43}, and here we implement the procedure using the electrostatics package APBS⁴⁴ to determine the sensor valance of this motion (gating motion 1). Fig. 6C shows the energy difference between the hypothetical state and the starting x-ray structure, ΔE = E_{hypo. state} − E_mVDAC1. This is only the energy difference due to the interaction of the protein charges with the membrane electric field. The switch between the states in panel A shows absolutely no voltage dependence (blue curve in Fig. 6C). The slope of this line determines the corresponding voltage-sensor valence, which is ~ 0 in this case. This strongly supports the notion that gating motion 1 is not correct. Second, N-terminal antibody studies on native MOM indicate that gating involves the helix exiting the β-barrel^{13; 37}, so we considered a second motion (gating motion 2) in which the helix moves into the upper bath as pictured on the right side of Fig. 6B. This situation is equivalent to removing the helix from mVDAC1 since the electrostatic potential of the outer bath is nearly zero everywhere. Fig. 6C shows that positive potentials stabilize the helix in the outer bath whereas decreasing the membrane potential stabilizes the x-ray crystal structure (red curve). This happens because the helix has a net charge of +2. Decreasing the membrane potential from +50 to -50 mV results in a 6 k_BT stabilization of the x-ray structure compared to the hypothetical state. The sensor valence of gating motion 2 is only 1.5, which is again too weak to be the true motion, but it could form part of the motion as discussed below^{3; 17}.

Fig. 6.

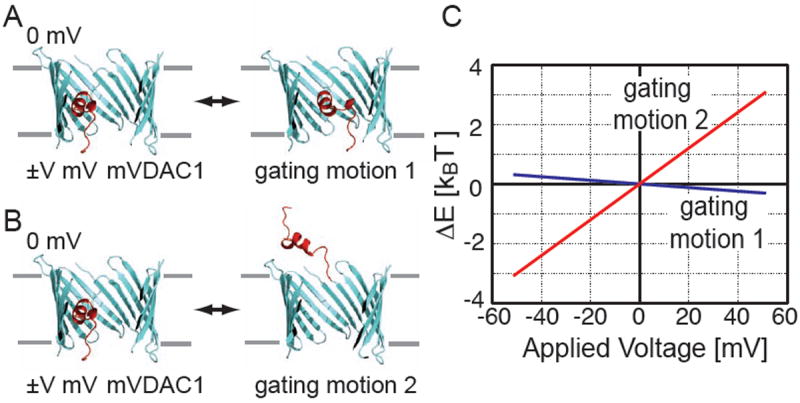
Voltage dependence of the mVDAC1 x-ray structure compared to two hypothetical gating motions. (A) mVDAC1 is pictured on the left and a hypothetical partially closed state suggested by Ujwal et al. (ref. ¹⁵) is on the right (gating motion 1). (B) mVDAC1 is pictured on the left and the N-terminal helix (red) has been removed from the pore on the right (gating motion 2). (C) Poisson-Boltzmann calculations were carried out to determine the membrane potential’s contribution to the energy difference between these sets of structures (ΔE = E_{hypo. state} − E_mVDAC1). The outer bath was held at 0 mV and the inner bath was varied from -50 to +50 mV. To represent the hypothetical state in panel B, the helix was deleted from mVDAC1 as discussed in the text. The energy difference between the states in A is represented by the blue curve, and the difference between the states in B is represented by the red curve. Gating motion 1 shows no voltage dependence, while gating motion 2 has a voltage-sensor valence of 1.5.

The hypothetical closed states are still anion selective

We showed in Fig. 6 that the hypothetical gating motions do not generate the observed gating charge; however, a second additional property of the closed state is whether it is cation selective. To determine this, we computed the electrostatic potential in the pores at two different z values (-3 and +10 Å). Fig. 7A,B show that the protein interior (light green) is identical for both models at the outer slice; however, the pore of hypothetical closed state 1 is noticeably more positive (left panel) suggesting that it would be more anion selective. At the inner slices, we can see that the helix occupies the pore in the Ujwal model (panel C), but that the pore is less obstructed in hypothetical closed state 2 (panel D). As with the x-ray structure, positive potentials dominate at the inner slices for both models. These positive values are due in part to the preponderance of basic residues lining the inner half of the β-barrel.

Fig. 7.

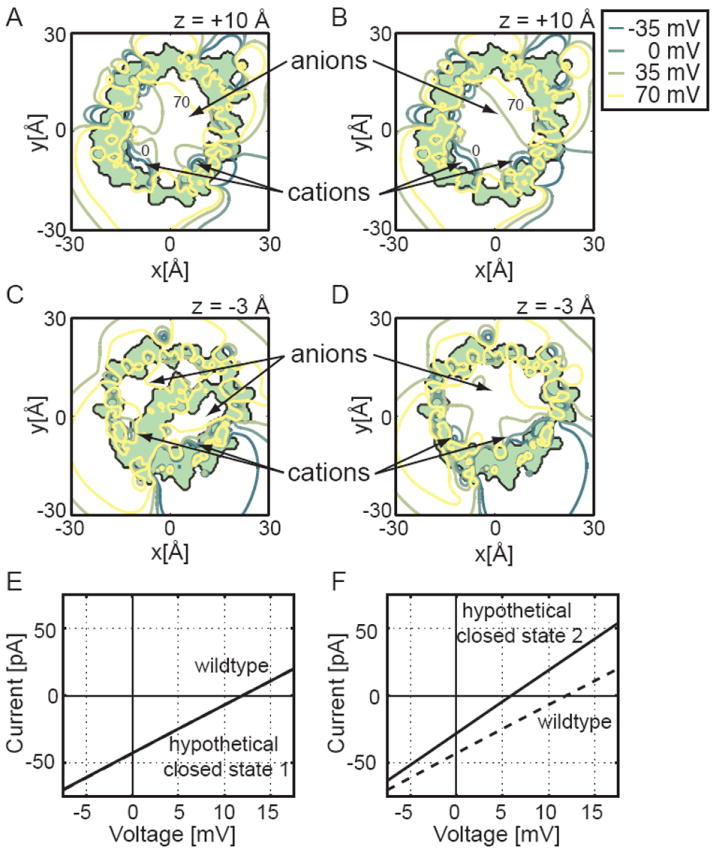
Biophysical properties of the two hypothetical closed states. The electrostatic potential of hypothetical closed state 1 was calculated and plotted at z = +10 Å (A) and z = -3 Å (C), and the isocontours for hypothetical closed state 2 were plotted at z = +10 Å (B) and z = -3 Å (D). Each channel is viewed along the pore’s long axis, and the protein interior is shaded light green. We see in panel C that the N-terminal helix occludes the middle of the pore of hypothetical closed state 1, but panels B and D show that hypothetical closed state 2 has an unobstructed pore at all levels. As in Fig. 4, four equally spaced isocontours are depicted with dark green curves representing negative potentials and yellow curves representing more positive potentials. From panel C we see that closed model 1 has only a very small portion of the pore favorable to cation passage. Current-voltage curves for closed state 1 (E) and closed state 2 (F) were also carried out using PNP calculations. The conductance of hypothetical closed state 1 (solid) is so similar to wild type (dashed) that it is hard to distinguish both curves. Due to the larger pore diameter, hypothetical closed state 2 has an increased conductance, indicated by a steeper slope (solid curve) compared to the wild type (dashed). Since the current-voltage curve in panel F crosses the x-axis at a positive potential, the channel is anion selective as is the wild-type channel.

PNP calculations carried out on the hypothetical closed states show that they are both anion selective (solid lines require positive voltages to stop ion flow in Fig. 7E,F). In accord with the electrostatic potentials, hypothetical closed state 2 is less anion selective than state 1 and the mVDAC1 x-ray structure. Moreover, the conductance of state 2 is greater than hypothetical closed state 1 and the mVDAC1 structure as indicated by the steeper current-voltage curve. This is to be expected since model 2 no longer has the helix occupying the pore domain. Thus, these hypothetical models fail to reproduce the selectivity, voltage-dependence, and conductance changes required for the closed state.

Discussion

Both the PB and PNP electrostatic calculations show that the mVDAC1 x-ray structure is anion selective suggesting that the structure is open. While the transfer free energy profile in Fig. 1A has a clear minimum in the electrostatic component of the free energy, its depth is very weak, ~2.5 k_BT. However, this might be exactly what we would expect of a channel whose primary role is to quickly shuttle high-valence negatively charged metabolites across the membrane. An ATP molecule, with a charge of -4, will experience a well depth 4 times deeper than a chloride anion implying that a shallow minimum for chloride would be a much deeper for ATP. Close coordination by magnesium or other cations could reduce this well, but if too deep, it could lead to increased ATP dwell times and decrease the channel conductance. The true test of the channel’s conduction state will come from a detailed study of ATP and ADP permeation energetics. Unfortunately, due to the increased complexity and conformational flexibility, continuum approaches are not appropriate for studying ATP’s interactions with the channel. Fully atomistic simulations will be required to properly address this question.

The theoretical conductance values presented here are larger than those predicted by experiment for the open channel. PNP is a mean field theory that neglects dynamical ion-ion correlations, and it is generally thought that this can lead to a larger current flux through the pore^{32; 45}. Despite being inflated with respect to experiment, our calculations are in good agreement with other researchers’ findings that PNP theory overestimates the experimental values. For instance Im and Roux calculated a conductance value for OmpF that was 1.8 times higher than experiments carried out in 0.2 M KCl³², while our value is 1.8-2.3 times higher than values reported for VDAC in 0.1 M KCl³. Nevertheless, such a large conductance value is even more incompatible with the partially closed-state conductance found to be 0.22 nS in 0.1 M KCl⁴⁶. If the mVDAC1 structure truly represents the partially closed state, this would imply that our PNP calculations are off by a factor of 5, and to our knowledge, such a large discrepancy between theory and experiment has never been reported. Thus, we feel that our conductance calculations suggest that mVDAC1 represents the open structure. Interestingly, while PNP overestimates the flux, it appears to do a better job of determining the relative ratio of the anion to cation flux. In our case, we predict reversal potentials within 2 to 4 mV of the value reported for scVDAC1, and Im and Roux determined a value within 2 mV of the recorded value for OmpF³².

Our analysis illustrates that not all pore-facing residues contribute equally to channel selectivity. This was first apparent from our observation that most residues that affect selectivity in the Blachley-Dyson et al. study²⁷ are on the lower half of the channel. From Fig. 3C one can see that A134 and N207 are both pore-facing residues, but they are at the outer mouth of the channel near the upper solution. Acidic substitution of these residues has a modest affect on the reversal potential when the channel is in the configuration in Fig. 5A, but it has almost no effect on selectivity when the channel is in the opposite orientation. Meanwhile, K20E and K61E impact selectivity regardless of the orientation of the channel. We believe that these results can be explained by the proximity of the mutated residue to the channel’s natural energy minima at -7.5 Å (Fig. 1A). Residues that increase or decrease the depth of this minimum appear to have the largest effect on selectivity. Interestingly, the calculated reversal potential shifts elicited by point mutations found to affect selectivity, while significant, are still smaller than the experimental shifts (see Table). We feel that there are two primary reasons for this inconsistency. First, the charged, pore-facing residues on scVDAC1 and mVDAC1 are not strictly conserved, which could lead to a different electrostatic profile in the pore of mVDAC1. Second, we do not know the true, predominant rotamer conformations of the point mutants, and incorrectly modeled side chains could heavily influence the electrostatics along the permeation pathway. Additionally, non-mutated residues may adopt new rotamer conformations in response to a point mutant, and this could not be accounted for. All of these effects could explain the differences between theory and experiment. Nonetheless, there is a clear delineation between the selective mutants and the non-selective ones, especially when considering the channel orientation in Fig. 5B.

Our results show that VDAC1 selectivity depends on the orientation of the channel in the membrane. The channel is slightly less selective when the N and C-termini face the high concentration bath (equivalent to ~ 2 mV shift in reversal potential compared to both termini facing the low-concentration bath). Since the orientation of VDAC1 in the mitochondria is currently debated^{18; 34; 35; 47}, the physiological relevance of this result is unclear. However, it is obvious that our calculated reversal potential shifts correspond most closely to the experimental results when the N and C-termini face the low-concentration bath (see Table). We believe that this finding could have consequences for our understanding of VDAC’s topology in the MOM. Theory could be used to predict mutant channels that produce large shifts in the reversal potential when the N and C-termini are presented to the cytoplasm and very little shift when presented to the inner membrane space. Conversely, a set of mutant channels could be engineered that have the opposite property. Expressing and carefully recording these mutants directly from the mitochondrial outer membrane may provide a means to test the channel’s orientation in vivo. Experimentally, we would expect large reversal potential shifts for one orientation and negligible shifts for the opposite arrangement. The control experiments would come from the point mutations that predict the opposite result.

Finally, we investigated two hypothetical gating motions in an attempt to better understand the molecular determinants of VDAC1’s voltage dependence. In both cases, the motions resulted in a sensor valence below experimentally reported values. With regard to motion 1, it is attractive to imagine that the N-terminal helix moves into the middle of the channel to block metabolite passage; however, this motion has no voltage dependence. Nonetheless, it is possible that a similar final state does result in channel closure. The N-terminal helix is amphipathic due to a distribution of both basic and acidic residues along its length, and therefore, simply rotating the helix in the membrane electric field could produce a sizable gating charge. Thus, the true motion could involve swinging the helix out into the pore and rotating it. Meanwhile, gating motion 2 also has some very attractive features despite producing only about half of the observed sensor valence. The reactivity of antibodies to the N-terminus increases with the lysis of the outer membrane indicating that the N-terminus is exposed or accessible from the inner surface of the MOM³⁴. Therefore, a model of gating has been suggested that involves the helix leaving the pore prior to entering the partially closed state³⁷. The helix may then associate with the lipid bilayer as suggested by immuno-electron microscopy¹³. This second step would require the helix to move partially through the membrane electric field, and it may produce enough charge movement to account for the missing 1-2 fundamental charge units in gating motion 2. As further confirmation that both of these motions are not correct, we calculated the electrostatic properties of the end configurations in Fig. 7. Both models are still anion selective, while the true partially closed state is cation selective. This suggests that neither of the proposed structural models is correct.

Lastly, VDAC1’s voltage dependence is more complicated than our analysis has suggested because the channel closes at both negative and positive membrane potentials. Energetically, it seems unlikely that both partially closed states are the same since the membrane potential would bias the channel in different states at different voltages. It is entirely possible that the closed state(s) involve a more complex rearrangement than simply moving the N-terminal helix, as suggested by functional work^{36; 48}. Computationally, it is more difficult to determine these alternate conformations if they involve rearrangements of the β-barrel itself, but such a scenario cannot be ruled out. Moreover, if gating involves the N-terminal helix, it is doubtful that it moves as a rigid body. All of these factors complicate the determination of the partially closed states from the known mVDAC1 structure. Fortunately, the partially closed and open states exhibit different selectivities and conductances, so future studies can judge the likelihood of any given hypothetical state based on sensor valence calculations as well as selectivity calculations using PNP theory as we have done in Fig. 7.

Materials and Methods

Poisson-Boltzmann calculations

We used the program APBS⁴⁴ to carry out continuum electrostatic calculations on the mVDAC1 structure (PDB ID 3EMN). Calculations were carried out using the Poisson-Boltzmann (PB) equation in the linearized limit in the presence of 100 mM salt concentration. The equation was solved using a finite difference method on a 161 × 161 × 161 grid with two levels of focusing. The grid spacing at the finest level of focusing was 0.56 Å. The PARSE parameter set was used to assign partial charges to the protein⁴⁹ using the PDB2PQR web server with standard protonation states for all residues⁵⁰. The influence of the membrane was included as a low-dielectric slab of dielectric value ε_m = 2⁴². Water was assigned a dielectric value of ε_w = 80, and the protein dielectric constant was assigned values of ε_p = 2, 5, and 10 in separate calculations. Based on the structure, a suitable path for the ion through the pore was selected (see green path in Fig. 1C,D). We have adopted the convention that the N and C-termini face the lower bath; this is represented by negative z values in Fig. 1. The center of the channel is always positioned near z = 0 Å. Ion transfer free energies are calculated by first computing the total energy of the ion plus protein system and then subtracting off the energy of the solo ion in bulk solution and the energy of the channel without the ion^{21; 22}.

The voltage dependence of the hypothetical gating motions in Fig. 6 was calculated using the same setup described above; however, the far-field boundary conditions were manipulated to impose an applied membrane potential in the program APBS as described previously in reference⁴². The interaction energy of the protein charges with the field due to the membrane potential is calculated as follows. First, the electrostatic potential profile across the membrane-protein system is determined in the absence of any protein charges by calculating the PB equation with all of the protein charges set to zero. In this case, a uniform charge density is added to the lower bath to give rise to the desired membrane potential. Second, the protein charges are reintroduced and overlaid on the calculated electrostatic map. The interaction energy is given by the sum over all of the protein partial charges multiplied by the local membrane potential value calculated from APBS.

Poisson-Nernst-Planck calculations

We used PNP calculations to compute the steady-state ionic flux through mVDAC1 using code written in the Coalson lab^{31; 51}. Current-voltage curves were computed under bi-ionic conditions with the upper bath and lower bath maintained at 0.1 M and 1.0 M KCl, respectively, and curves were also computed under symmetric 1.0 M KCl solutions. The PNP equations were solved on a 135 × 135 × 185 grid with a grid spacing of 0.83 Å. The channel structures and spatial orientations were identical to those used in the PB calculations; however, the channels were flipped 180° to simulate the insertion with the opposite topology. As with the PB calculations, a low-dielectric slab representing the membrane extended from -14 to +14 Å along the z-axis, and it was assigned a dielectric value of 2. The protein dielectric value was set to 5. A membrane potential was imposed across the membrane, and the value was varied from -5 mV to +15 mV to construct the current-voltage relation. The bulk diffusion coefficient for potassium and chloride ions was set to 19.5×10^-6 cm²/s, and the value in the channel was reduced by 40% based on our MD results. The zone of reduced diffusion was defined by a cylinder of radius 18.5 Å centered on the channel and extending 36 Å along the axis of the channel from z = -19 to +17 Å. For each imposed membrane potential value, the PNP equations were solved via relaxation methods using anywhere from 36,000-47,000 iterations. Solutions under both symmetric and asymmetric conditions exhibited excellent convergence.

Molecular dynamics simulations

We used the CHARMM-GUI to align mVDAC1 along the z-axis, embed the protein in a DMPC lipid bilayer, and then solvate the entire system in a hexagonal cell⁵². We enforced electroneutrality by adding 0.15 M KCl (14 positive ions and 17 negative ions). The approximate system size is 75 Å × 75 Å × 66 Å, and it consists of 34,228 atoms. Simulations were carried out using NAMD with the CHARMM27 parameter set and TIP3P water molecules⁵³. Initially, a conjugate gradient minimization was carried out for 3,000 steps on the full system. During equilibration, the temperature was increased every 50 steps by 1 K until it reached 303 K using Langevin dynamics. The time step was 2 fs, and a 10 Å cut-off was used for van der Waals interactions. All electrostatic energies were calculated using the Particle Mesh Ewald summation. After reaching 303 K, an additional 1 ns of simulation was carried out using the NPT ensemble with a Langevin piston set to 1 bar. We equilibrated a chloride ion in the channel pore at two positions: z = 0 and z = +2. From each set up we ran a 2 ns simulation and recorded positions every 100 fs. For both simulations, the ion remained in the channel. For each ion trajectory we calculated R²(t) = (r(t) − r(t=0))² for t = 0 to 1 ns, where r is the chloride ions vector position in time. We then stepped through the time series data and recalculated R²(t) to arrive at an average squared displacement <R²(t)>. The slope of this curve was set equal to 6D to estimate the chloride diffusion coefficient in the channel, D (data not shown). We repeated this process for a potassium-chloride ion pair in a cubic water box of length 20 Å to estimate D in bulk solution. Our calculations in the channel were ~ 40% smaller than our estimate of the bulk value, and this 40% reduction was used to model the diffusion coefficient of the ions in the channel for the PNP calculations. This amount of reduction is very close to the value used by Im and Roux in their study of porins³².