Nonfixed Retirement Age for University Professors: Modeling Its Effects on New Faculty Hires

Abstract

We model the set of tenure-track faculty members at a university as a queue, where “customers” in queue are faculty members in active careers. Arrivals to the queue are usually young, untenured assistant professors, and departures from the queue are primarily those who do not pass a promotion or tenure hurdle and those who retire. There are other less-often-used ways to enter and leave the queue. Our focus is on system effects of the elimination of mandatory retirement age. In particular, we are concerned with estimating the number of assistant professor slots that annually are no longer available because of the elimination of mandatory retirement. We start with steady-state assumptions that require use of Little’s Law of Queueing, and we progress to a transient model using system dynamics. We apply these simple models using available data from our home university, the Massachusetts Institute of Technology.

Introduction

Education represents one of our most important service sectors, with approximately 10% of the U.S. gross domestic product devoted to education. Effective management of faculty and staff is a key element of successful education service systems. In this paper our focus is on university faculties and on one very specific topic: retirement. Our analysis brings to this problem a classic tool of service systems analysis, queueing theory, born approximately 100 years ago in Denmark.

Faculty members at universities and colleges enjoy a rare job benefit: tenure. Academic tenure in higher education was established in the late 1800s as a measure of protection for faculty against dismissal for exercising freedom of speech and inquiry (Keast 1973). If they successfully navigate the professional hurdles of reappointment and promotion leading to the granting of tenure, faculty members enjoy job security until they retire. Federal rules regarding the age of retirement have been prescribed over the past 45 years by the Age Discrimination in Employment Act of 1967 (Pub. L. 90-202) (ADEA), as amended from time to time. Until 1982, retirement of faculty members at many universities was mandatory at age 65. Because of amendments to the ADEA, in 1982 the minimum allowable mandatory retirement age was increased to age 70. In 1986 Congress made additional amendments to the ADEA, prohibiting any mandatory retirement ages for most workers in the United States.

The philosophy behind these amendments was that individuals should be judged not for their age but for their skills and knowledge (Hammond 1991). Such legislation raised important questions in the field of higher education and particularly in research universities, where mandatory retirement was an integral component of human resource policy for academic personnel (Clark 2001). As a result, the issue was put out for analysis, and ending mandatory retirement ages for university faculty members was delayed. Then in 1994 mandatory retirement for faculty members was finally prohibited in all U.S. colleges and universities.

Previous studies have demonstrated an increase in the expected age at which faculty retire after the ADEA amendments came into force (Ashenfelter 2002). In this paper we estimate the first-order effects of nonmandatory retirement age on the number of new faculty slots available in a typical research institution. The first step will be to outline and model a simple “back-of-the-envelope” procedure, which will then serve as the basis for more detailed and complex models.

Background

Given the restrictions that arise from tenure, mandatory retirement provided universities with flexibility to hire new faculty in developing fields. To better understand the implications of the 1986 ADEA amendments, Congress postponed their implementation in higher education and commissioned a study to determine their broader effects in academia. This permitted colleges and universities to continue requiring tenured faculty members to retire at age 70 until 1994, when the final decision was to be made in light of the study’s recommendations. The study, carried out by the Committee on Mandatory Retirement in Higher Education at the National Research Council (NRC), concluded that at most colleges and universities, few tenured professors would continue working past age 70 if mandatory retirement were to be eliminated (Hammond 1991). Consequently, the main recommendation to Congress was that mandatory retirement of tenured faculty should be allowed to expire at the end of 1993. The NRC committee also recommended that Congress and regulatory agencies assist research universities in minimizing the potential adverse effects of eliminating mandatory retirement for tenured faculty.

For research universities, the committee pointed out that if mandatory retirement were to be eliminated, a high proportion of tenured faculty would choose to work past age 70 (Hammond 1991). This analysis concluded that research-oriented faculty who enjoyed inspiring students and had light teaching loads were more likely to work past age 70. This outcome was also foreseen by Rees and Smith (1991) and later confirmed by Ashenfelter (2002). The NRC report argued that abolishing mandatory retirement would reduce faculty turnover, reducing the continual faculty reinvigoration that helps these institutions maintain the cutting edge of American science. Lower retiring rates would limit hiring and promotion of new faculty with new views and new areas of research. In addition, continued employment of older and usually higher-salaried professors could result in increased costs and financial difficulties.

Confirming the committee’s forecasts, Ashenfelter (2002) found that after 1994, the fraction nationally of 60-year-olds who worked until 73 had risen to about 10% and to 30% and higher at some private research universities. While analyzing the University of North Carolina (UNC), Clark and Ghent (2008) found that its two research institutions had lower retirement rates than the other types of institutions in the UNC system. Regarding the impact of institutions’ overall academic quality on retirement patterns, Rees and Smith, in 1991, concluded that retirement age tended to be higher with higher SAT scores of entering students. Subsequent to Rees and Smith’s work and the abolishment of mandatory retirement age, the national percentage of tenured professors age 70 years and older increased threefold to 2.1% between 1992 and 2006. At the Harvard University Faculty of Arts and Sciences, the increase during the same period was from 0% to 9.1% (Bombardieri 2006). Despite the lack of recent data regarding the current average age of retiring faculty at leading research universities, the available studies suggest that it has indeed increased significantly.

In light of the impacts of the ADEA amendments, the following analysis will implement simple modeling techniques to describe how new faculty slots are reduced after the elimination of mandatory retirement. Any college or university can use the modeling methods to obtain first-order back-of-the-envelope estimates of the effect of no mandatory retirement age. To illustrate, we apply them with limited available data to our institution—the Massachusetts Institute of Technology (MIT).

Intuition

At first glance, one might think that ending mandatory retirement results only in a transient effect, where the number of new faculty slots available is reduced until the system returns to steady state. Steady state requires that the total number of faculty members remains approximately fixed over time, and that has been the case at MIT for at least three decades—with approximately 1,000 tenure-track faculty members across the university’s five schools. In addition, steady state requires that the number of departures from the faculty balances the number of new faculty hires in any given year. Suddenly terminating mandatory retirement at age 65 or at age 70 would indeed create strong transient effects, as older faculty members who had been scheduled to retire decide not to do so, thereby reducing the near-term number of new faculty slots available for assistant professors. However, as our analysis will show, once steady state sets in, the number of new faculty hires is permanently reduced by the cessation of a mandatory retirement age.

Applying Little’s Law

To understand the effects of nonmandatory retirement age on new faculty hiring, we apply Little’s Law of Queueing from operations research:

$$L=\lambda W,$$ (1)

where

• L = the time-average number of “customers” in the queueing system,

• λ = average rate at which new customers enter the system, and

• W = the average time spent in the system by a random customer who enters.

Little’s Law applies to any queueing system operating in steady state (Little 1961). The relationship does not require Markovian or other simplifying structural assumptions and is valid independent of probability distributions involved. It has stood the test of time, as discussed in a recent historical overview article celebrating its 50th anniversary (Little 2011). In application to university faculties, we have the following correspondences:

• L = the time-average number of tenure-track faculty members employed by the university,

• λ = average annual rate at which new tenure-track faculty members join the faculty, and

• W = the average number of years spent on the faculty by a newly hired assistant professor.

For this initial analysis, we focus only on tenure-track appointments and ignore more senior faculty appointments above rank of assistant professor. We believe that ours is the first application of Little’s Law to college and university faculties.

To apply Equation (1), we need to estimate W, the average number of years spent on the faculty by a typical new assistant professor. To do this, we think of the key decision points made for and by this faculty member as she or he proceeds through her or his career. A typical career trajectory involves the following milestones:

1. At the end of year 2, reappointment as assistant professor without tenure.

2. At the end of year 4, appointment as associate professor without tenure.

3. At the end of year 7, appointment as associate professor with tenure.

4. Remaining on the faculty until retirement, not voluntarily departing from the university at some preretirement time, most often associated with a faculty or business appointment elsewhere.

5. Retirement from the faculty.

Milestone 4 is not really a specific time-marked event. It is included to account for those faculty, typically in their 40s or 50s, who voluntarily leave to become deans, provosts, and presidents at other universities or to engage full time in some business activity. At MIT, an example is Dr. Robert Brown, once provost of MIT, who left in 2005 at age 54 to become president of Boston University. Another example is Dr. Lawrence Bacow, once chancellor at MIT, who in 2001 at age 49 became president of Tufts University.

Let us denote

$$P_i=\text{conditional probability that milestone}i\text{is achieved},\text{given that milestone}(i-1)\text{is achieved},i=1,2,3,4,5.$$

Then, of course, (1 − P_i) is the conditional probability that milestone i is not achieved, given that milestone (i − 1) is achieved. We assume that if any reappointment, promotion, or tenure decision (milestone 1, 2, or 3, respectively) is unsuccessful, institutions allow the affected faculty member to remain on the faculty for one more year after that negative decision to allow time for that individual to identify and solidify alternative career paths. We assume that the new faculty slot created by such a negative decision opens up only after the individual has left the institution’s faculty. For the sake of simplicity, we will also assume that P₅ = 1, meaning that any tenured professor who does not voluntarily leave the faculty eventually retires with probability 1.

For the times associated with milestones, we define for i = 1, 2, 3, 4, 5,

$$Y_i\equiv \text{time from first appointment as assistant professor until milestone}i\text{is achieved}.$$

Table 1 provides estimates of the milestone probabilities using available data from a select research institution in the United States (MIT 2010). Initially, mortality rates are not taken into account. In Table 1, we show the estimated numerical values for P₁ and P₄ with an asterisk because MIT does not possess reliable university-averaged data for these parameters. They represent best estimates at this time and may be subject to correction at some future point. The rightmost column of Table 1 displays numerical values for the Y_is, the number of years from appointment as assistant professor to the achievement of each respective milestone, assuming first hire at age 30 and mandatory retirement at age 65.

Table 1.

Illustrative Milestone Probabilities and Career Durations

Milestone	Probability	Years
1	P1 = 0.9*	Y1 = 2
2	P2 = 0.74	Y2 = 4
3	P3 = 0.62	Y3 = 7
4	P4 = 0.95*	Y4 = 20
5	P5 = 1	Y5 = 35

The general equation for W, the mean time spent on the faculty by a randomly hired assistant professor, is given by

$$W=Y_1+P_1(Y_2-Y_1)+P_1{P}_2(Y_3-Y_2)+P_1{P}_2{P}_3(Y_4-Y_3)+P_1{P}_2{P}_3{P}_4(Y_5-Y_4)+(1-P_1{P}_2{P}_3).$$ (2)

The intuition is as follows: The first term reflects the fact that each new faculty hire will, with probability 1, spend at least Y₁ years on the faculty. The second term accounts for those faculty who are reappointed as assistant professor and as a result spend a time at least equal to (Y₂ − Y₁) additional years on the faculty. Similar milestone arguments support the third, fourth, and fifth terms. The sixth and final term corresponds to those faculty members who do not obtain tenure and who drop out at any of the first three milestone points. Because the fraction of faculty members who do obtain tenure is the product of the success probabilities associated with the first three milestones—that is, P₁P₂P₃—the fraction who do not obtain tenure is (1 − P₁P₂P₃). Each such individual spends one additional year on the faculty after failure to achieve the milestone, that year devoted to career planning. So, in effect, the sixth term is multiplied by “one year.”

Now let us compute W with the data described above, and assume that each new faculty member hired is 30 years old and that mandatory retirement occurs at age 65. Using the numbers from Table 1 and Equation (2), we can write

$$\begin{array}{cc}\hfill W=& 2+0.9(4-2)+\left(0.9\right)\left(0.74\right)(7-4)+\left(0.9\right)\left(0.74\right)\left(0.62\right)(20-7)\hfill \\ \hfill & +\left(0.9\right)\left(0.74\right)\left(0.62\right)\left(0.95\right)(35-20)+(1-(0.9\left)\right(0.74\left)\right(0.62\left)\right),\hfill \end{array}$$

or

$$W=17.64\text{years}.$$

These calculations suggest that, with a mandatory retirement age of 65, and given all of the assumptions regarding milestone probabilities, the average career time spent on the faculty by a random newly hired 30-year-old assistant professor is 17.64 years.

We now substitute this number into Little’s Law and obtain the average new assistant professor faculty hires per year:

$$\lambda =L∕W=1,000∕17.64\approx 57\text{new assistant professor faculty hires per year}.$$

Now suppose that we abolish mandatory retirement at age 65. This affects the fifth term in Equation (2). As mentioned previously, there is widespread evidence that the average age of faculty at leading research universities has increased markedly since 1994, suggesting an increase in the average retirement age. Even though there are no recent data on this statistic, 75 years is likely to be an upper bound at most universities. Let us assume then, for the sake of illustration, that the average age of retirement increases from 65 to 75 after the abolishment of mandatory retirement. This increase changes Y₅ in the fifth term from 35 to 45, yielding an average career time spent on faculty of 21.56 years.

That is, given the model’s assumptions, termination of mandatory retirement at age 65 increases the mean number of years that a newly hired assistant professor spends on the MIT faculty from 17.64 to 21.56 years, an increase of about 22%. We now substitute this into Little’s Law, retaining 1,000 total faculty members as constant, and we obtain for the revised annual rate of new faculty hires

$$\lambda =L∕W=1,000∕21.56\approx 46.$$

The figure of 46 new assistant professor faculty hires per year represents a reduction of about 19% compared to the retire-at-65 policy with 57 new hires per year. That is, about 11 would-be new appointments, over all of MIT, would not be made because of the increase in retirement age. This is a steady-state result, indicating that effects far beyond transient effects are at play here.

The equation “λW = constant” implies that an X% increase in W (mean length of a faculty career) requires a compensating reduction in λ, the rate of annual hires of assistant professors. This demonstrates that our initial intuition was quite incorrect.

To improve our intuition, let us move to an extreme. Suppose there exists a university whose faculty could only be faculty members for one year. If the total number of faculty members were 1,000, then 1,000 new hires would be made each year because there would be 1,000 departures each year. But now suppose that the length of a faculty career were doubled to two years. Then, on average, only half of the 1,000 faculty members would depart each year, so the number of new hires would correspondently halve to 500. Although this is an extreme and unrealistic example, the same logic applies in more realistic settings: an X percentage increase in faculty career length requires a compensating reduction in the rate of new faculty hires.

More formally, suppose that we have for a given mandatory retirement age

$$L={\lambda }^0{W}^0.$$

Now we increase W⁰ by X%. We can write

$$L={\lambda }^{\prime }{W}^0(1+X∕100),$$

where λ′ is the new steady-state hiring rate for junior faculty members. Solving for λ′, we find

$${\lambda }^{\prime }=L∕\left[W^0\right(1+X∕100\left)\right]={\lambda }^0∕[1+X∕100].$$ (3)

Equation (3) confirms that if W is doubled, λ is halved. If X = 22%, as in our numerical example, Equation (3) reaffirms that λ is reduced by a factor 1/[1 + 0.22] = 1/1.22 ≈ 0.82, or 18%. Equation (3) can be used by university administrators to obtain a first-order approximation to the effect on new faculty hiring of increased age at retirement. Generalizing the arguments leading to Equation (3), one can, in a straightforward manner, add lateral entries of faculty hires and other complexities. These computations can be applied to subsets of university faculties, such as faculty members in individual schools or academic departments. And they can be applied by gender and/or demographic attributes. But we must recall that application of these simple arguments requires a steady state or equilibrium in numbers. When that is not the case, the time-dependent modeling of system dynamics is more appropriate.

Accounting for Mortality and Lateral Hires

Two major omissions in the simple procedure previously outlined are impacts of mortality rates and lateral hires. Death is an event that can occur prior to a retirement decision and therefore is important to include in the analysis. Similarly, lateral hires will reduce the availability of new assistant professor hires per year.

Research shows that on average, people with higher education attainment live longer lives in the United States. Given that professors at research universities have attained the highest levels of education, using aggregate U.S.-wide mortality rates is not appropriate for this analysis. Instead, we use average mortality rates for highly educated individuals taken from the Social Security Administration (2007), weighted by college-educated averages from Brown et al. (2002).

In an expanded version of our model, we find that the addition of mortality rates reduces the average length of time W spent as a tenured professor, assuming a mandatory retirement age of 65, from 17.6 years to 17.3 years. This equates roughly to one additional new hire per year—from 57 hires per year to 58 hires per year. When the mandatory retirement age is abolished and we use an average retirement age of 75, the mortality tables suggest that, on average, about two preretirement faculty members will pass away each year. The effect would be to change λ from 46 to about 48 new hires per year.

Although MIT does not track the number of faculty that depart yearly from death, these figures seem reasonably consistent with general estimates of the number of faculty members passing away per year. Not surprisingly, as the average retirement age increases, increased mortality rates in the older population have a greater effect on the number of new faculty hires.

Adding lateral hires to our analysis is straightforward. One basically thinks of two queues or pools of faculty members: those hired as new assistant professors and those brought to the university at a later stage in their careers, some with and some without tenure. In that case Equation (1) is expanded to have two terms on the right-hand side of the equation, λ₁W₁ and λ₂W₂L/W, the first representing new assistant professor hires and the second representing lateral hires. These terms are added, and the analysis proceeds in a straightforward way. In this paper we do not attempt to expand our illustrative numerical results to include lateral hires due primarily to data limitations of our home university, MIT. Although some lateral hires do occur at MIT, the great preponderance of faculty hires is new assistant professors. Finally, depending on details, a few moments of thought will reveal that lateral hires may increase or decrease W, the mean time that a random faculty member remains on the faculty. In either case, the effect on the hiring rate of new assistant professors is that of a net reduction.

System Dynamics Modeling

The previous analysis was focused on a steady-state condition, estimating changes in the faculty-hiring rate as a result of retirement age policy change after a sufficiently long time period when system inputs and outputs are in balance. In this section, we take a further step by analyzing what will happen during the transition to a new steady-state level, and how the number of faculty members and the hiring rate change after implementing a new retirement policy. For such a purpose, we develop a model using system dynamics.

System dynamics is a computer-aided deterministic simulation technique that can be used to analyze the behavior of a complex social system over time (Sterman 2000, Forrester 1968). The “stock and flow” structure that serves as the basic construct in system dynamics provides an appropriate platform to model the behavior of faculty hiring and retirement while accounting for the delays in each of these processes. In addition, system dynamics models are framed graphically—aiding intuition—and produce visual output, showing how changes in retirement policies affect the behavior of the system over time.

Figure 1 represents the model structure built for this analysis. This simple model consists of a single stock, employed professors (L), with two explicit inflows and two explicit outflows. The two inflows are incoming assistant professors (I₁) and lateral hires (I₂), and the two outflows are exit (O₁) and death (O₂). The dropout rate for professors who voluntarily leave before retirement is embedded in W, the average number of years that faculty remain employed.

Figure 1.

The System Dynamics Model

The model uses Little’s Law to determine the rate of retirement (O₁), and the death rate (O₂) is estimated to be at 0.1% of the employed professor pool. Equations (4) and (5) represent the outflows:

$$O_1=L∕W,$$ (4)

$$O_2=0.001L.$$ (5)

The average number of years that faculty members remain employed (W) is calculated using the same probability model outlined previously. The number of employed professors (L) at any given time changes by hiring and exiting rates. Mathematically, we have a first-order differential equation:

$$dL∕dt=I_1+I_2-O_1-O_2.$$ (6)

In this equation, assistant professor hiring (I₁) is the main inflow. In equilibrium, where a university has the desired number of professors, a university’s normal yearly hiring rate (N) should be equal to what it expects the net exit rate will be (O₁ + O₂ − I₂). In other words, to ensure that the total number of faculty members remains constant, the university’s normal hire rate (N) should be equal to its net exit rate (O₁ + O₂ − I₂). We define N as a lagged variable of the exit rate (with delay of τ), to represent the fact that it takes time for a university to observe a sudden change in the exit rate:

$$N_t={(O_1+O_2-I_2)}_{t-\tau }.$$ (7)

The subscripts represent time.¹ A hiring rate of I₁ = N will balance the hiring with the exit rate and eventually bring the number of faculty members to a steady-state level. However, when a university decides to grow, it needs to hire an additional number of faculty members to fill the gap between the number of current faculty members (L) and the desired number of faculty members (L*). The rate of additional hiring depends on the time that it takes to implement the development policy and equals (L* − L)/τ. Therefore, the total yearly hiring rate that accounts for both the normal exit rate and the desired level of-professors is as follows:

$$I_1=N+(L^{\ast }-L)∕\tau ,$$ (8)

where I₁ is nonnegative (I₁ ≥ 0).²

The remaining inflow, yearly lateral hiring rate (I₂), is estimated according to the available data at 0.1% of the employed faculty pool:

$$I_2=0.001L.$$ (9)

Preliminary Model Validation

The model was calibrated using historical data on the number of faculty employed at the Massachusetts Institute of Technology between 1980 and 2010. There were two major shocks to the system during this period. The first was in 1994, when federal law lifted mandatory retirement. The second shock happened in 1996, when a special, one-time early retirement incentive program was offered to MIT employees (MIT 1995). Many higher-education institutions have implemented similar programs to address the mentioned drawbacks of removing mandatory retirement (Kim 2003). By 2007, institutions offering retirement incentives had increased to 57% from 35% in 1987 (Chronister and Kepple 1987).

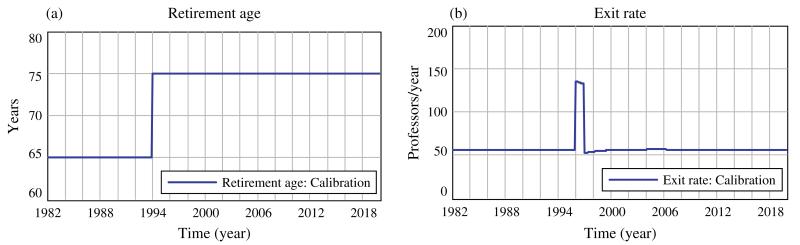
Inserting a step function in the retirement age variable at time t = 1994 reflects the sudden removal of mandatory retirement by permanently increasing retirement age from 65 to a modeled 75. We use the age of 75 for modeling purposes, recognizing that there is in fact no mandatory retirement age. Similarly, inserting a pulse function in the exit rate at t = 1996 reflects the sudden retirement of faculty members who accepted the incentive offered during that year. It is worth noting that even though both of these shocks are immediate, the built-in delays and the exponential smoothing structures in the model allow the system to respond gradually, as it would in reality. In other words, the stepwise increase in retirement age does not result in a stepwise increase in the average duration of the fifth milestone, or in the average time that faculty remain employed. Figures 2(a) and 2(b) illustrate these two shocks.

Figure 2.

Operationalization of Policy Shocks in Retirement Age and Exit Rate: (a) Change as a Result of Removing Mandatory Retirement, and (b) Effect of 1996 Retirement Incentives

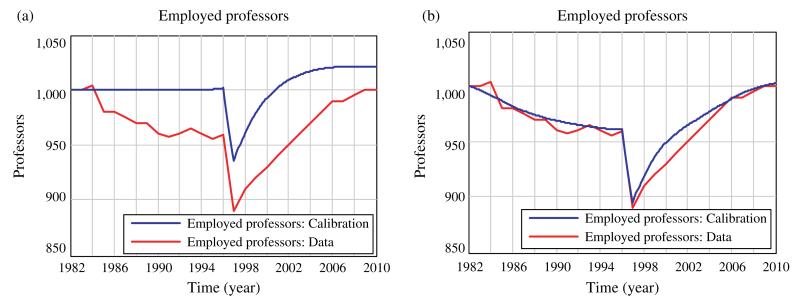
To calibrate multiple variables such as the time to hire new faculty and the retirement adaptation delay, a Powell hill-climbing algorithm is used for optimization. This optimization engine is integrated into the system dynamics software package used to build the model.³ Using this optimization algorithm in conjunction with manual tuning provides satisfactory outcomes, as shown in Figure 3.

Figure 3.

Graphs for Employed Professors Comparing Model Results (Blue) with Historical Data in MIT (Red) Under Two Scenarios: with Constant (a) and with Nonconstant (b) Desired Faculty Size

Figure 3(a) illustrates the behavior of the model (blue) compared to actual data (red) if the target faculty size is held constant at 1,000 throughout the simulation period. Figure 3(b) shows the same comparison, relaxing the assumption that the desired faculty size at MIT remains constant. Table 2 summarizes the fitted parameters along with their R-squared measure of goodness of fit. These results provide an initial validation of the model’s integrity.

Table 2.

Goodness-of-Fit Measures Using the Calibrated Values for Employed Professors

Delay because of faulty hiring processes	Delay in professors’ adaptation to policy changes	R-squared
		Constant desired faculty size	Variable desired faculty size
5.7 years	8 years	0.57	0.94

Simulation Results

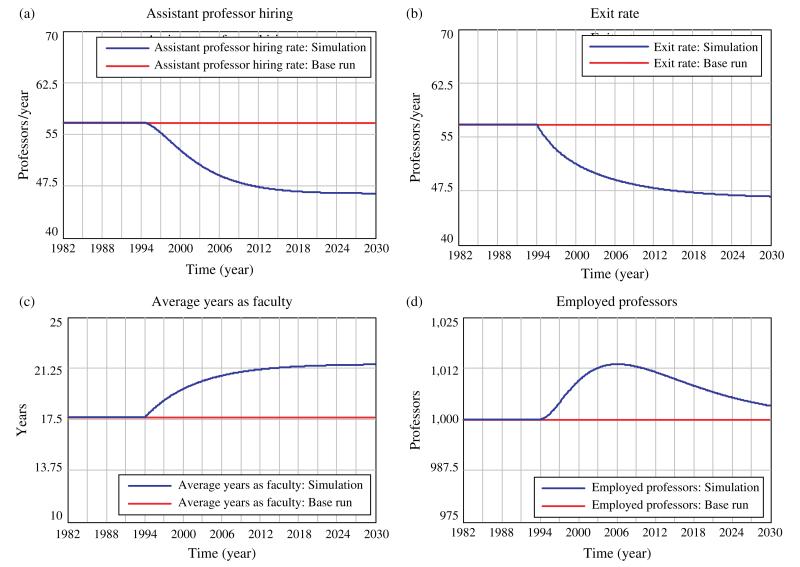
Now we can run the model and examine the isolated effects of removing mandatory retirement in 1994. The policy is operationalized in a similar way that was explained in the previous section: by changing the retirement age at 1994 from 65 to 75.

Figure 4 shows the simulation results. In this figure we can compare variables in the simulation run, which includes the change in policy, with a counterfactual base run. The base run represents a situation with no change in retirement policy and an employed professor pool remaining constant at 1,000. We can see from Figure 4(a) that the number of new assistant professor hires per year starts declining in 1994 from 57 until reaching a new equilibrium at around 46 almost two decades later. This hiring behavior reflects what happens with the faculty exit rate (see Figure 4(b)). The number of years that individuals remain in the employed professors stock starts to increase from 17.64 years in 1994 until reaching a new equilibrium point at around 21 years, approximately two decades after the restriction is lifted (see Figure 4(c)). Finally, in Figure 4(d), we see that the pool of employed professors starts to increase once the policy is implemented and then starts to decrease gradually until it eventually returns to its target size. This increase in faculty size is what would have taken place at MIT had the early retirement incentive program not been implemented.

Figure 4.

Simulation Results: Impact of Policy vs. Counterfactual

The results from the system dynamics simulation provide insight on the time required by similar systems to reach new equilibrium levels. We see that these adjustment periods are nontrivial, and accounting for their duration provides a more complete model to understand the impact of changes in retirement policies.

Discussion

Quantitative models such as the ones described in this paper hold the potential to assist human resources departments when determining hiring and retirement policies in academic institutions. Being able to forecast the time it takes for specific academic workforce systems to recover from sudden changes is critical when determining these policies. External shocks, such as legislation that prohibits mandatory retirement, should be accompanied by internal policies targeted at smoothing the effects of these disruptions.

MIT responded to the ADEA amendments first enforced in 1994 in part through the 1996 retirement incentive program. This program resulted in the departure of a considerable number of faculty in a relatively short time, causing a sharp drop in the number of employed faculty from which it took MIT several years to recover. In contrast, MIT’s most recent retirement incentive program, known as the Faculty Renewal Program, spans a three-year period (Pfeiffer 2009). By spreading out the time period during which participants become eligible, this program addresses the shortcomings encountered after 1996 as illustrated in our system dynamics model. This recent initiative also offers flexibility regarding the actual date of retirement, further reducing the potential for sudden shocks to the system.

The system dynamics model developed for this examination is relatively simple. It is the first version of more complex models that we are currrently developing. Our plan is to expand this model beyond MIT, using this initial approach as a proof of concept. In terms of the model’s structure, the current version lumps together all employed faculty in a single stock, failing to account for the dynamics at play between three clearly defined stocks in the faculty pipeline: assistant, associate, and full professors. Furthermore, stocks can be separated by academic specialty. Although the total number of faculty members may remain constant (1,000 in the case of MIT), there can be wide compensating swings up and down by academic department. Including and examining these stocks is one of the next steps in our analysis. The applicability of Little’s Law for these future analyses remains relevant, as it provides a coherent and correct framework for increasingly complex models.

Finally, future models will take into account the impacts that changes in the faculty pipeline have in variables such as Ph.D. production and average duration of postdoc appointments—factors that are critical for the continued availability of a motivated and trained higher-education workforce. Gaining insight into these broader dynamics could ultimately assist policy makers in understanding the possible outcomes of levers ranging from reaearch funding to retirement laws, providing an analytical grounding before policies are implemented.

Biographies

Richard C. Larson is the Mitsui Professor in the Engineering Systems Division at MIT. He has focused on operations research as applied to services industries, primarily in the fields of criminal justice, technology-enabled education, urban service systems, queueing, logistics, and workforce planning. He is founding director of Learning International Networks Consortium (LINC), (http://linc.mit.edu), an MIT-based international project that has held five international symposia and sponsored a number of initiatives in Africa, China, and the Middle East. With Elizabeth Murray, he leads LINC’s newest and largest initiative, Blended Learning Open Source Science or Math Studies (BLOSSOMS), (http://blossoms.mit.edu), sponsored by the Hewlett Foundation and other foundations and companies. He has active research projects focused on education as a complex system. He is past president of INFORMS, a member of the National Academy of Engineering, an INFORMS founding fellow, and a recipient of the INFORMS President’s Award, Lanchester Prize, and Kimball Medal.

Mauricio Gomez Diaz is a second-year master’s student and research assistant at MIT’s Engineering Systems Division. He holds undergraduate degrees in computer science and Japanese, with a minor in political science. His current research at MIT, sponsored by the National Institutes of Health, focuses on the dynamics of the biological and medical sciences workforce in the United States. Mauricio is interested in modeling and simulation, particularly using system dynamics, as tools for decision makers to understand the impacts and unforeseen effects of particular policies.