POWER ANALYSIS FOR COMPLEX MEDIATIONAL DESIGNS USING MONTE CARLO METHODS

Abstract

Applied researchers often include mediation effects in applications of advanced methods such as latent variable models and linear growth curve models. Guidance on how to estimate statistical power to detect mediation for these models has not yet been addressed in the literature. We describe a general framework for power analyses for complex mediational models. The approach is based on the well known technique of generating a large number of samples in a Monte Carlo study, and estimating power as the percentage of cases in which an estimate of interest is significantly different from zero. Examples of power calculation for commonly used mediational models are provided. Power analyses for the single mediator, multiple mediators, three-path mediation, mediation with latent variables, moderated mediation, and mediation in longitudinal designs are described. Annotated sample syntax for Mplus is appended and tabled values of required sample sizes are shown for some models.

Why Mediation?

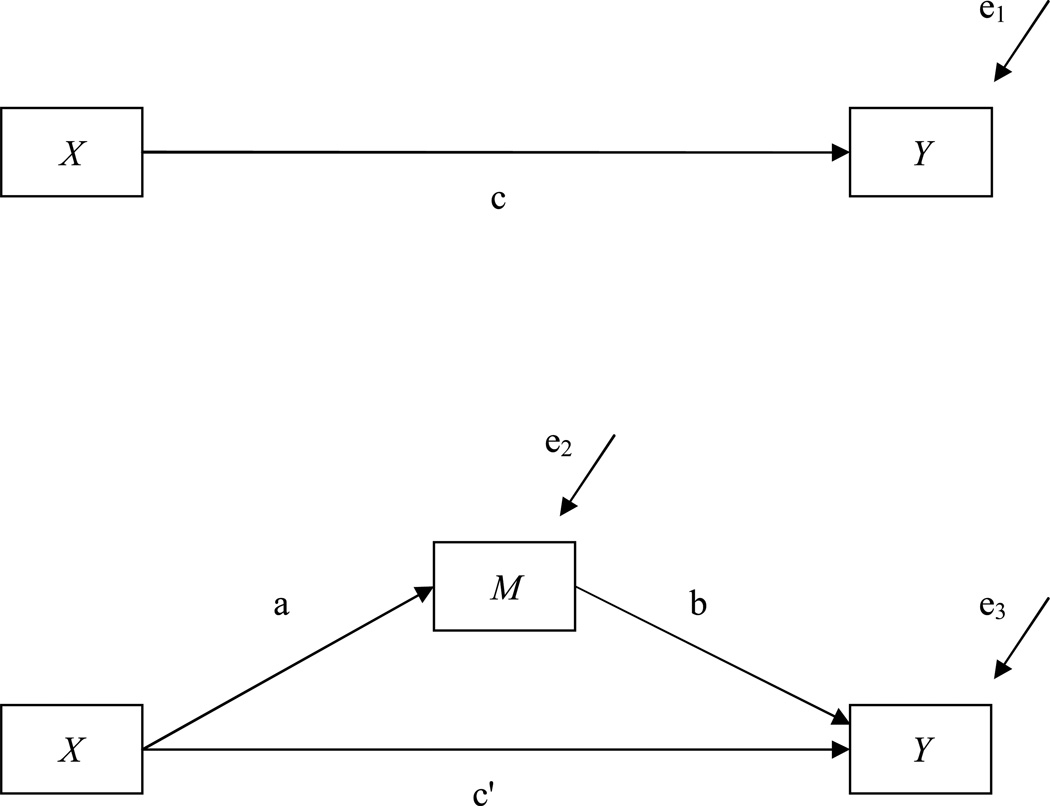
The use of mediation analysis is widespread in the social sciences and other disciplines (MacKinnon, Lockwood, Hoffman, West, & Sheets, 2002). One of the original papers on mediation analysis by Baron and Kenny (1986) has now been cited over 10,000 times, indicating interest in this method. Mediation analysis is a useful statistical tool for researchers who want to answer substantive questions about how an independent variable affects a dependent variable (MacKinnon, 2008). In the simplest mediation model one variable causes an intervening variable, the mediator, which then causes the outcome as shown in Figure 1 below (Baron & Kenny, 1986; MacKinnon, 2008).

Figure 1.

A single mediator model.

In the top panel of Figure 1 an independent variable X is related to an outcome Y. Coefficient c describes the total effect of X on Y. The bottom panel of Figure 1 adds a mediating variable relating X to Y. The path relating X and the mediator M is labeled a, the path relating M to Y is labeled b. Under certain assumptions (including an accurately specified model) (Holland, 1988; Mackinnon, 2008), the product, ab, is the mediated or indirect effect. The path labeled c’ is the direct effect. The sum of the indirect and direct effect is the total effect and is equal to c.

This single mediator model in Figure 1 can be expressed in three regression equations.

$$Y=i_i+cX+e_1$$ (1a)

$$Y=i_2+c\text{'}X+\mathit{\text{bM}}+e_2$$ (1b)

$$M=i_3+\mathit{\text{aX}}+e_3$$ (1c)

The single mediator model described in the equations and Figure 1 has been extensively studied including assumptions, power, and Type I error rates (e.g. MacKinnon, 2008). However, most applications of mediation analysis involve much more complex models, including multiple mediators, longitudinal mediation, and categorical variables.

Power Analysis

Statistical power is the probability of rejecting a false null hypothesis (1 – probability of a Type II error) and is generally recognized as a critical part of research (Cohen, 1988; Sedlmaier & Gigerenzer, 1989). One important use of statistical power analysis is to calculate required sample sizes to achieve at least .80 probability to reject a false null hypothesis (in some circumstances even higher levels of power might be desirable, e.g. Topol et al., 1997, cited in Maxwell, 2000). As a result, power analysis is an important aspect of designing any study. Without proper power analysis, sample sizes for a study might be too low to find a real effect of small magnitude. On the other hand, a sample size that is too large is also undesirable because it is usually wasteful to spend additional resources on larger samples with only marginal benefits.

Power analyses for “traditional” statistical methods have been advocated in psychology and other social sciences for some time (e.g. Cohen, 1988) and are now routinely required by some of the major grant agencies, e.g. the National Institute of Health (NIH). Guidelines have been established and some great practical resources have been published in numerous outlets (e.g. Lenth, 2001). Furthermore, statistical software for the calculation of power is now readily and in some cases freely available (e.g. Faul, Erdfelder, Lang, & Buchner, 2007; Lenth, 2006)

Power in mediational models was recently explored by Fritz and MacKinnon (2007), who provided researchers with sample size requirements for various sizes of the a and b path in the single mediator model in Figure 1. Fritz and MacKinnon (2007) showed that sample size requirements can be very large, especially if small mediated effects are to be detected. They also suggested using asymmetric confidence intervals or resampling methods like the bootstrap for testing the mediated effect to increase statistical power. No existing literature provides sufficient information on how to calculate power for more complex mediational models and there are several aspects of the single mediator model not yet described – such as power to detect mediation with categorical variables. Substantive researchers, however, often deal with models that are much more complex than the single mediator model. This paper describes how researchers can estimate power for complex mediational analyses, such as multiple mediators, three-path mediation, mediation with latent variables, moderated mediation, and mediation in longitudinal designs. Several examples of complex structural equation models and a general framework for the estimation of power for a very wide variety of models are described.

Power Analysis in Structural Equation Models (SEM)

The estimation of power in SEM usually requires the researcher to specify the relation among all variables in the model. In a complex model this might involve a large number of parameters, which makes it inherently more challenging than estimating power for a t-test or an ANOVA model. Predicting expected effect sizes is probably the hardest part of any power analysis. Once these predictions are made, the power analysis consists of formalized steps that are well laid out or are implemented in software packages. For SEM the process is more complex because no specialized software exists, and the power analysis has to be performed using general purpose SEM software (e.g., see Miles, 2003).

There are at least three different methods that have been proposed in the literature to assess power in SEM. All three are described briefly below.

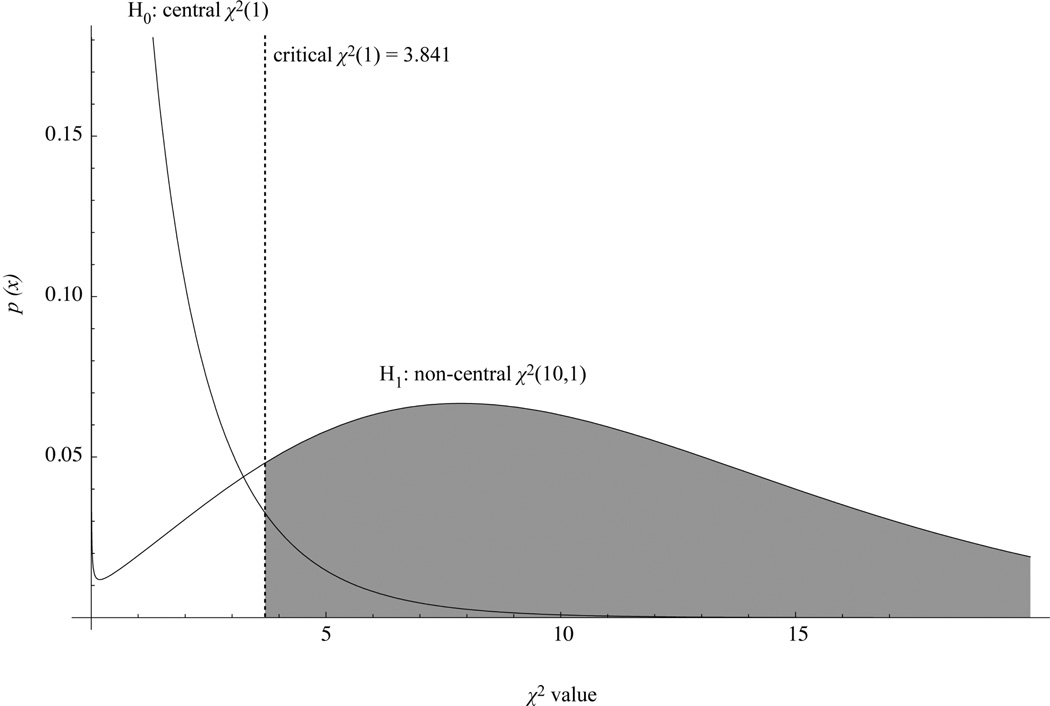
Satorra and Saris (1985) introduced one of the first methods to estimate power in SEM. Their approach can be summarized in three steps. In a first step, researchers define each parameter in an SEM based on past research, pilot studies or theoretical considerations. For example, in the single mediator model described earlier, researchers would have to provide a value for the magnitude of the a, b, and c’ paths, and furthermore the variances of each of the three variables X, M, and Y. This resulting model contains the best available values for all required parameters. This step is important, as inaccurate parameter values will lead to power estimates that are based on the wrong population model. For example, if a parameter is specified to be of large magnitude but in reality this parameter is only small in magnitude, power will be overestimated. Likewise, guesses for parameters that are too small, will yield needed sample sizes that are too large. In a second step a covariance matrix is generated from the parameters chosen for the population model. If this covariance matrix would be analyzed under the original model, the exact same parameter values that were defined in the first step would be recovered. In a third step, this generated covariance matrix is analyzed under a model in which the researcher fixes one or more parameters at a value different from the first step (usually, but not always, the value is fixed at zero). The parameters that are fixed are the ones for which a power analysis is desired. The resulting likelihood ratio statistic from this constrained model is used as an estimate of the non-centrality parameter, λ, in a power analysis. Power is then calculated as the probability of obtaining a χ² value from a non-central χ² (df,λ) distribution that is larger than the critical value of a central χ² (df) distribution, where df is the number of parameters with different values in the second model. Figure 2 below illustrates this point and depicts, as an example, a central χ² (1) distribution with an α= .05 cutoff at 3.841 and a non-central χ² (1, 10) distribution with a non-centrality parameter λ equal to 10. The shaded area represents power to detect that the parameter of interest is significantly different from zero.

Figure 2.

Central and non-central χ²distributions with area representing power shaded gray.

The Satorra and Saris method may be used to determine power for testing one specific parameter, e.g. the a path, or joint power for more than one parameter. An advantage of the method is that these steps only have to be performed one time for each parameter given a certain sample size. If the χ² value for one sample size condition is known, then power values for other sample sizes can be easily computed because the non-centrality parameters are perfectly linearly related to sample size. In addition, the Satorra and Saris method allows estimation of power for hypotheses that posit that parameter values are significantly different from any value of interest, and not just zero, as in the case of the classic null hypothesis.

One drawback of this method is that certain characteristics of the data (e.g. non-normality, missing data, etc) cannot be easily accounted for. Another potentially more severe drawback is that the definition of a non-centrality parameter becomes difficult in the context of a mediation analysis. If it is of main interest to assess that a mediated effect (the ab product term) is adequately powered, a non-centrality parameter could be derived by either setting the a path, the b path, or both to zero. All three constraints would result in the ab product term to be zero. However, if the magnitude of a and b differs substantially, power estimates can vary greatly and it is unclear which estimate would actually best represent power to detect the mediated effect. The so-called “phantom variable” approach (Rindskopf, 1984) in which a single variable that represents the product term ab is added to the model (e.g. Cheung, 2007) does not solve this problem. An example of this issue is presented later for the single mediator model.

The second approach to test power in SEM, proposed by MacCallum, Browne, & Sugawara (1995) is also based on using a χ² value (or more technically a value based upon a χ² value) as a non-centrality parameter. In this approach the value of the RMSEA can be used to estimate power for a comprehensive test of an entire SEM against a generic alternative. The RMSEA itself is a function of both the χ² value and the degrees of freedom for a model, expressed as:

$$\mathit{\text{RMSEA}}=\sqrt{\frac{{\chi }^2/(\mathit{\text{df}}-1)}{N-1}}$$ (4)

MacCallum et al. (1995) proposed to test the power of rejecting the null hypothesis of not-close fit (H₀: RMSEA > .05). This type of power analysis has several advantages. First, it is a general calculation that gives the researcher information about which sample size to choose based on a whole model. The MacCallum et al. (1995) approach does not require the researcher to guess any specific parameter values of the model. The power analysis pertains only to the model as a whole not to single parameters. This strength is also a weakness, because the researcher does not know whether a crucial parameter of the model, e.g. the mediated effect, is adequately powered. Maxwell (2004) makes this point in a more general context and notes that in many models that include multiple hypothesis tests (virtually every SEM), any particular hypothesis test might be under-, over-, or adequately powered. It should also be noted that the MacCallum et al. (1995) and the Satorra and Saris (1985) method can yield identical results if certain values for the RMSEA in the MacCallum et al. (1995) approach are chosen.¹

A third approach that is computationally more demanding but similar to the logic of Satorra and Saris (1985) is the Monte Carlo approach described by Muthén & Muthén (2002). The Monte Carlo approach is used in this manuscript because of its flexibility and ease of implementation. Similar to Satorra and Saris (1985) the first step of this approach is to define a model in which all parameters are fixed to values based on prior research or theory. This model represents the best guess of the true population model. Based on this model specification, a population is defined, and a large number of samples are drawn from this population. In other words, a population is created in which the postulated model is true and subsequently, many samples of a specific and constant size are drawn from this population. Each sample is fitted to the postulated model, and parameters are estimated and recorded. Like in a real sampling process, the parameter estimates of each sample will vary around the specified true parameter value. Some of the parameter estimates in some samples will be significant, while other estimates in other samples will not. Given enough replications (at least several hundred - higher numbers are more desirable, because they give more stable estimates and precise confidence intervals) the empirical rate of statistical significance averaged across all replications is the power estimate. For example, imagine that a parameter in a given SEM has the value of 0.5 in the population, and 1000 samples of size n=200 are drawn from this population. Now imagine further that in 800 of the 1000 samples this parameter is deemed statistically significant. The empirical power to reject the hypothesis that this coefficient is equal to zero given a sample size of 200 is equal to 800 / 1000 or simply 80%. The Monte Carlo approach is intuitive, because it mimics the sampling process that occurs during data collection, but repeats it many more times. The repeated draws of samples of specific size from a defined population yield a probability statement about how often one would expect to find a significant result.

The Monte Carlo approach has other advantages as well. First, like Satorra and Saris (1985) it is possible to estimate the power of a test for each individual parameter of the model and make specific decisions about sample size based on these considerations. This includes the mediated effect (product term ab), which is impossible to unambiguously define in the other approaches. Second, the Monte Carlo approach can account for specific data characteristics, e.g., missing data on some variables, non-normality on other variables, model misspecifications, or incorrect dichotomization of continuous variables can be modeled into the population. Also, the Monte Carlo approach may produce more accurate results for power than other methods when the sample size under consideration is small. A drawback of the Monte Carlo approach is that it is computationally more intensive, and since an easy transformation of non-centrality parameters is not available, power for different sample sizes has to be estimated separately.

Power Estimation using the Monte Carlo method

In this section, several examples of how to estimate power for complex mediational models are described. Syntax and steps for power estimation are described for each example. The software program of choice in this article is Mplus, but the Monte Carlo approach can also be conducted in other programs that have simulation capabilities, e.g. SAS, LISREL, or EQS.

In all following examples X, the independent variable, is considered to be dichotomous and randomly assigned to participants. Furthermore, a balanced distribution is assumed. This mimics a situation of a randomly assigned intervention with two possible treatments. All other variables, including the mediator variable, M, and the outcome variable, Y, are generated to be continuous variables. For simplicity all continuous variables are generated to have a mean of 0 and a variance of 1.

To express effect sizes in the mediation model we chose Cohen’s guidelines (1988) for R², the amount of explained variance in the outcome. Cohen (1988) defined a small, medium, and large effect on the R² metric as .02, .13, and .26. For the a path, relating the dichotomous variable X to the continuous mediator M unstandardized path coefficients of .28, .72, and 1.02, were used to represent small, medium, and large effect sizes. These path coefficients yield the precise amount of explained variance that was defined as small, medium, and large. For the b path relating the mediator M to the outcome Y the values .14, .36, and .51 as the size for the path coefficient were chosen. The residual variances of the dependent variables were fixed so that the total variance of all variables was 1.0. The exact covariance algebra that was used to determine the residual variance is presented in Appendix A. The direct path, c’, relating X to Y while controlling for the mediator, does not influence the size of the mediated effect (ab), so this path was kept constant at a value of .28, which expresses a small effect size in terms of R². In applied settings, researchers should try to obtain estimates of parameters based on previous research or theory and should try to avoid the small, medium, and large categorization (see Lenth, 2001) when more information is available.

Statistical Significance of the mediated effect

In the following Monte Carlo simulations the significance of the mediated effect for each sample is automatically assessed by Mplus. Mplus computes a test statistic by dividing the mediated effect (product term of ab) by a standard error developed by Sobel (1982). This standard error is defined as:

$${\mathit{\text{SE}}}_{\mathit{\text{ab}}}=\sqrt{a^2{\mathit{\text{SE}}}_b^2+b^2{\mathit{\text{SE}}}_a^2}$$ (5)

where SE_a and SE_b are the standard errors of the effects a and b, respectively. The resulting test statistic is compared to a critical value from a normal distribution (1.96 is the critical value for a two-tailed significance test with α=.05).

Comparing the test statistic to a normal distribution assumes that the distribution of the mediated effect is in fact normally distributed. However, the distribution of the product term ab can only under few circumstances be approximated by a normal distribution. For many values of a and b the distribution of the product is different from a normal distribution. Using normal theory standard errors will therefore produce confidence intervals that do not cover the actual 95% of plausible values. MacKinnon, Lockwood, and Williams (2004) and Shrout and Bolger (2002) suggest employing the methods of bias corrected bootstrap to test the significance of the mediated effect. Mplus can provide bias corrected bootstrap standard errors, but unfortunately not in conjunction with Monte Carlo simulations. Another approach to assess significance of the mediated effect has been proposed by MacKinnon, Fritz, Williams, and Lockwood (2007). They suggest computing critical values based on numerical integration of the actual distribution of the product and show that 95% confidence limits based on critical values derived from the distribution of the product are able to capture the true 95% of values of the distribution better than confidence intervals based on normal theory standard errors. MacKinnon, Fritz, Williams, and Lockwood (2007) provide a stand-alone software (PRODCLIN) and macros for common statistical packages that compute the critical values and confidence intervals based on a numerical integration algorithm developed originally by Meeker and Escobar (1994). It is possible to post-process results of a Monte Carlo simulation in Mplus with a SAS macro (see Appendix B) that computes a 95% confidence interval of the mediated effect.

Example 1: Single Mediator Model with dichotomous X

The first example that we consider is the same single mediator model for which Fritz and MacKinnon, 2007, provided power tables. However, here X is a dichotomous variable, such as assignment to either a treatment or control group. For this first example, a more detailed explanation of how to set up the Mplus syntax is provided. For all subsequent models example code is simply appended. The syntax for the first example is provided in Appendix C.

Using the MONTECARLO command in Mplus invokes the simulation mode in which samples are drawn repeatedly from a population. The NAMES command lists all variables in the population. Note that these do not refer to any real existing datafile and are only used to define variables in the population that is being created. The CUTPOINT option creates a dichotomous variable X that defines treatment assignment. Dichotomization at the value of 0 on the X variables is requested. The NOBS command is an important aspect in this simulation. This defines the size of sample that is repeatedly drawn from the population and essentially defines for which sample size power is estimated. In an applied setting, it is recommended to begin a power analysis with the maximum number of participants that the researcher believes can be realistically achieved and then adjust this number in subsequent runs to approximate power of .80 for the desired parameter estimate. The NREPS command defines the number of iterations of the simulation study. Generally speaking the more replications are being conducted, the more precise results are going to be; however the returns are diminishing with increased number of replications. Depending on model complexity, several hundred replications might give relatively precise estimates, but given modern computing power most of these simulations of simple models will be finished in few minutes, even for thousands of replications. In the provided examples the number of replications was set to 10,000.

The MODEL POPULATION command fixes all parameter estimates of the model to values that are believed to be true in the population, e.g. based on pilot studies. In Mplus, the variable means are fixed by putting square brackets around parameter estimates as in “[x@0]”, variances are fixed without the square brackets as in “x@0.25”. Note that this fixes the total variance of independent variables, but fixes the residual variance of dependent variables. Some covariance algebra (as presented in Appendix A) is usually necessary to determine proper values for the residual variance. It is usually desirable to have a total variance of 1.0 to easily translate unstandardized path coefficients into meaningful effect sizes. Path coefficients that define relationships between variables are defined using the ON statement, as in “m on x@0.28” which defines a path coefficient from X to M with the value of .28. The MODEL command along with all path coefficients in the model estimates means and variances of dependent variables and paths that were defined in the population. The * symbol defines the start value and should be equal to the true parameter value to ensure fast convergence of the mode. Finally, the MODEL INDIRECT command estimates the direct and the indirect (i.e. mediated effect) from X to Y. This example is set up that the program will provide power estimates for each path in the model and the mediated effect given the path coefficients defined in the MODEL POPULATION command. In this example we use an overall sample size of n=275, as evidenced in the NOBS statement. Furthermore, both the a and b path are set to be of small magnitude, as defined by the amount of explained variance in the outcome variables M and Y. The Monte Carlo simulation will cycle 10000 times, as defined in the NREPS statement.

Running this syntax yields power estimates for each path. These are presented in the output under MODEL RESULTS in the column labeled “% Sig Coeff”. The value denotes the proportion across the 10,000 replications that the path coefficient reached significance at the .05 level. This is the empirical power estimate. Table 1 partially reproduces the information from Mplus using the same notation as used in the output file.

Table 1. Partially reproduced output from Mplus, highlighting the power estimate of the mediated effect.

TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS

	ESTIMATES			% Sig
	Population	Average	Std. Dev.	Coeff
Effects from X to Y
Total	.323	.3219	.1179	.774
Total Indirect	.040	.0403	.0250	.209
Specific Indirect
Y M X	.040	.0403	.0250	.209
Direct
Y X	.283	.2816	.1177	.661

Running the model from Appendix C yields power for the direct path from treatment assignment X to the mediator M (the a path) of .67, which indicates insufficient power. The path from the mediator to the outcome variable (the b path) has power of .66 and is therefore also underpowered. The mediated effect (ab) is underpowered with power equal to .21. In this situation the researchers would need to increase the sample size if the main interest was to have .80 power to detect the mediated effect. For the single mediator model with a dichotomous treatment variable X, required sample sizes to achieve .80 power to detect the mediated effect are presented in Table 2. This particular example requires a total sample size of at least 640 to have .80 power to detect significant mediation.²

Table 2.

Required sample size to detect a mediated effect with power of .80 in a single mediator model with dichotomous treatment assignment

	b path
a path	small (.14)	medium (.39)	large (.59)
small (.2)	640	404	394
medium (.5)	450	92	66
large (.8)	512	76	42

Note. c’ path is held constant at .28, because it does not influence the power of the mediated effect (ab)

To highlight the difference of the Monte Carlo approach and the Satorra and Saris method to detect power for the mediated effect, power was calculated for one condition (medium a path and small b path) for several sample sizes. In the Satorra and Saris approach the only way to estimate power of the mediated effect is to set either the a path or the b path to zero. By setting one of those paths to zero it is ensured that the product term is zero as well. However, the assessment of power then pertains to the individual paths and not the product term. Hence this analysis is not informative if power for the mediated effect is desired. As can be seen in Table 2, the Satorra and Saris method, overstates power to detect the mediated effect when either setting the a or the b path to zero. Both of these individual paths are larger in value than the product of the two paths and therefore have larger power estimates.

Example 2a. Three-Path Mediation Model

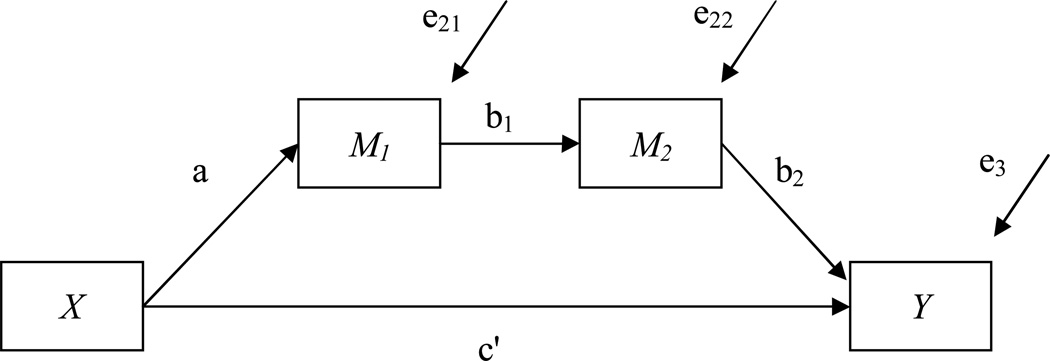
It is not uncommon that the mediated relationship is assumed to be a part of a larger sequence or process in which several variables cause each other to cause a final outcome of interest. The following example considers the simplest case of meditational chains by adding a second intermediary variable between the outcome and the mediator (see Figure 3).

Figure 3.

A three-path mediation model.

The mediated effect can now be expressed as the product of the three paths relating the treatment to the first mediator, the first mediator to the second mediator, and the second mediator to the outcome (Taylor, MacKinnon, & Tein, 2008). The product term of the three paths can in many circumstances be very small making it harder to detect a true mediated relation. Appendix D describes how to set up the three path mediation model and examine power for the mediated effect. Even though the model setup changes, the general logic of conducting the power analysis that was explained in Example 1 remains the same. In this example the a path is defined to be of medium magnitude (R² =.13, unstandardized path coefficient =0.721). The paths b₁ and b₂ are also defined to be of medium magnitude (R² =.13, unstandardized path coefficient =0.39). Given a sample size of 90 yields power for the a path to be 0.96. Both the b₁ and b₂ path are also adequately powered with power of .95. The mediated effect (ab₁b₂) on the other hand has only power of .53. It is interesting to note that although all individual paths have very high power, the mediated effect can still fail to be adequately powered.

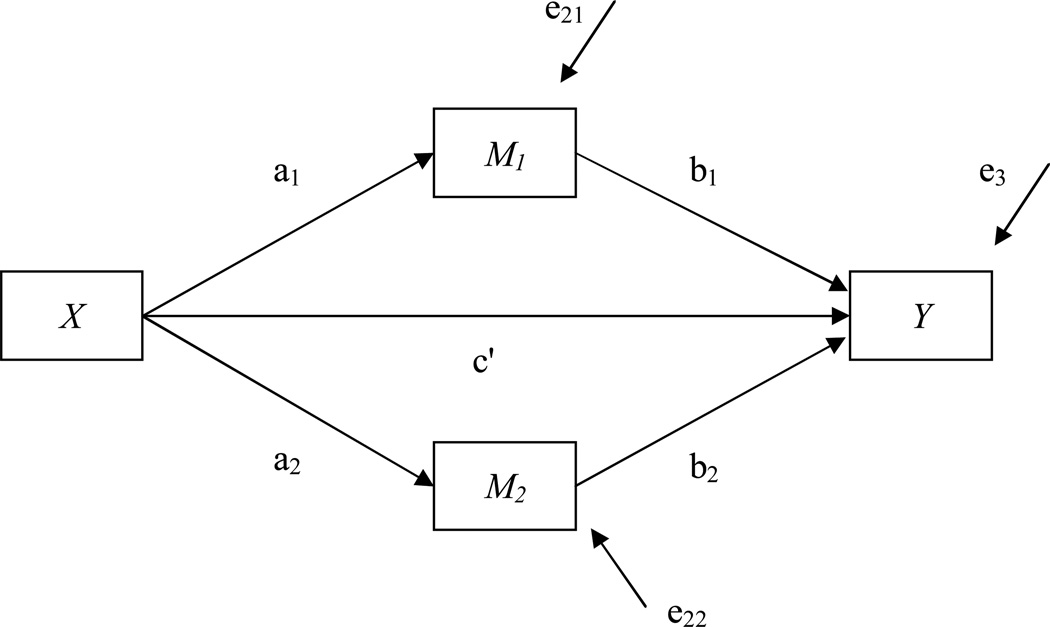
Example 2b. Mediation Models with Two Mediating Variables

Often researchers are interested in more than just one focal mediating variable, as seen in Example 2a. Several variables might be considered as potential mediators in a more complex model (e.g. Hansen, 1999; Hansen & Graham, 1991) in which multiple pathways from the treatment to the outcome exist. Note that the difference to the previous example is that here the second mediator is hypothesized to be caused by only the treatment and not the other mediator. In this particular example, two mediating variables are considered that are both caused by the treatment and are both causing the outcome. In general, these multiple mediators can have positive or negative relations to the treatment assignment or the outcome (MacKinnnon, 2008). In the example presented here, both mediators have positive relations (see Figure 4). Syntax on how to set up this model is provided in Appendix E. In the example the a₁ path, relating the treatment assignment to the first mediator, was set at a small value of 0.283. The b₁ path was also set at a small value of 0.14, therefore the mediated effect a₁b₁ was estimated to be 0.04. On the other hand, the a₂ path was set to a medium value of 0.721, and the b₂ path was set to a medium value of 0.36, therefore the mediated effect a₂b₂ was 0.26. The Monte Carlo power analysis was run for a sample size of 110. The simulation yields power estimates to detect either mediated effect, but also the total mediated effect, which is simply the sum of the two product terms a₁b₁ and a₂b₂. In this example, power to detect the mediated effect a₁b₁ was very low at .10, whereas power to detect the mediated effect a₂b₂ was extremely high at .99. The power to detect the total mediated effect was also .99. This example shows that different mediated pathways in one model can have quite different power estimates.

Figure 4.

A mediation model with two mediators.

Example 3. Mediation and Moderation with Latent Variables

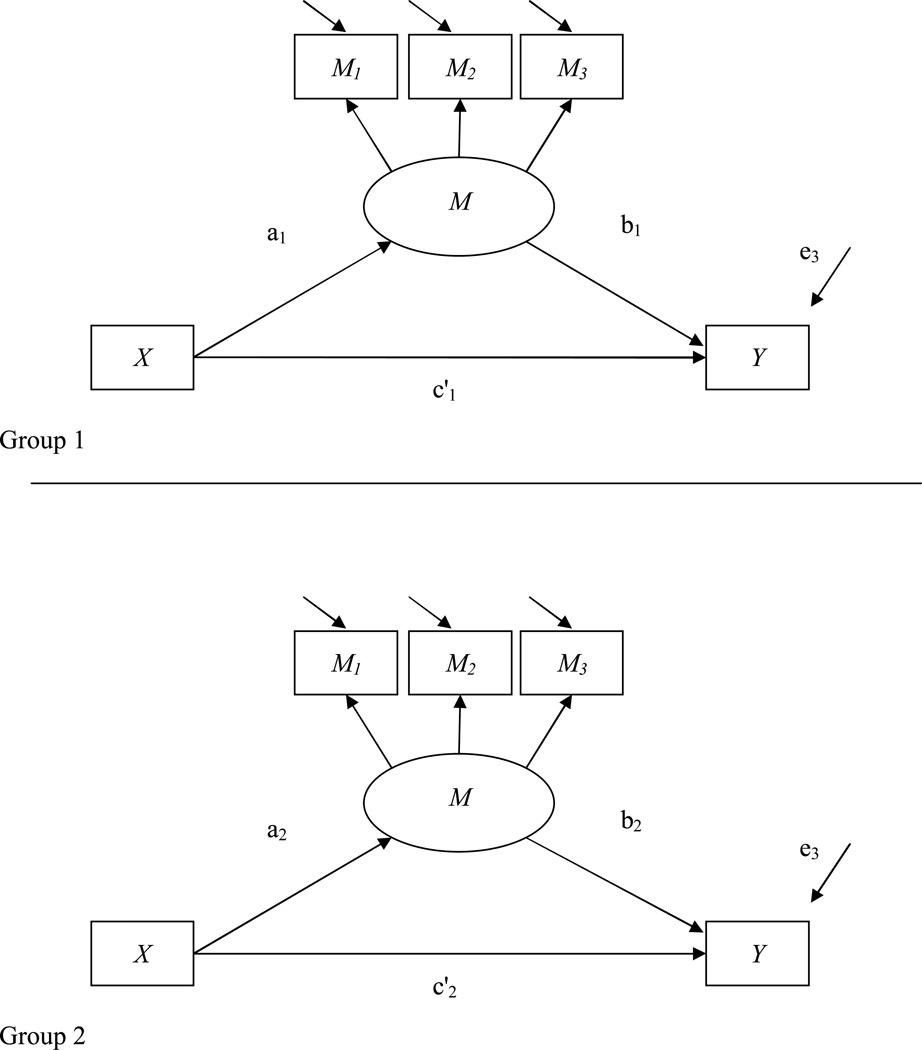
In this example two additional concepts are considered: the use of latent variables and moderated mediation with categorical variables (see Figure 5). For this example, more details about setting up Mplus syntax are provided because some lesser known features of the software are used.

Figure 5.

Mediation with latent variable and multiple groups.

Note. Labels for residual terms for indicator variables M₁-M₃ are omitted in the graph.

In Appendix F syntax is provided for a model in which the mediator is a latent variable that is composed of three manifest variables. The estimation of the mediated effect is however still identical to previous examples (product term of a and b path). In addition, a moderated mediation effect is examined (Baron & Kenny, 1986; Kraemer, Wilson, Fairburn, & Agras, 2002; MacKinnon, Weber, & Pentz, 1989), in which the moderator variable is categorical. Moderated mediation can be present in different ways. The path relating the treatment to the mediator (a path) can differ across groups of the categorical moderator variable, the path relating the mediator and the outcome (b path) can differ between the groups, or both paths can differ. In addition, it is possible to test whether the mediated effect (ab product term) is significantly different across groups. The provided syntax estimates whether moderation exists for the a or b path, but also whether the mediated effect is significantly different across the groups defined by the categorical moderator and provides thus the most thorough examination of moderated mediation. In particular the syntax demonstrates how to set up two groups and define parameters for each. In this example it is assumed that only the b path differs across the groups and that the a path and the c’ path are identical to each other. Note that parameters are defined for each group using separate MODEL POPULATION statements and that paths in the groups are labeled using parentheses at the end of the command line. The labels are needed to define new quantities that are needed to investigate moderation effects. The actual power to detect moderated mediation can be examined using the MODEL CONSTRAINT statement. In a first step, new variables that define the mediated effect in each group and differences in the a path, b path, and the product term ab, are initialized. Start values behind the * symbol should be given to ensure convergence of the simulation. In a second step, these new variables are mathematically defined as either product terms or differences between paths. For example, the difference in the mediated effect, labeled “diffmed”, is defined as the difference of the quantities “med1” and “med2”, which in turn were defined earlier as product terms of the a and b path in each group. The labels that were assigned earlier in parentheses have to be used to clearly define each quantity. Of special interest is how often the difference terms reach significance across all iterations of the simulation. This quantity can then (similar to previous examples) be used as an empirical power estimate to detect moderated mediation. In the example at hand, the first group is defined to have the following parameters: the a path is assumed to be 0.721, and the b path is assumed to be of size 0.36. The latent factor is identified by setting the loading of the first item to be 1.0; the other two loadings are set at 0.8. The total variance of the factor is set to be 1.0. The second group only differs on the b path which is now assumed to be of size 0.14. Furthermore, the sample size for the first group is 400, whereas the sample size for the second group is 200. This mimics a situation in which one group might be underrepresented in the overall population. The power to detect a mediated effect in the first group is very high at .99, whereas power to detect the mediated effect in the second group is only .37. Power (or actually Type I error rate, because the population a path was equal in the two groups) to detect differences in the a path is .054, which is very close to the expected Type I error rate of .05. Power to detect differences in the b path is .61. Finally, power to detect a significant difference between the two mediated effects is .53. If the main purpose of the study was to examine differences in the mediated effect, the study would be underpowered.

Example 4. Mediation in Longitudinal Designs – Latent Growth Curve Models

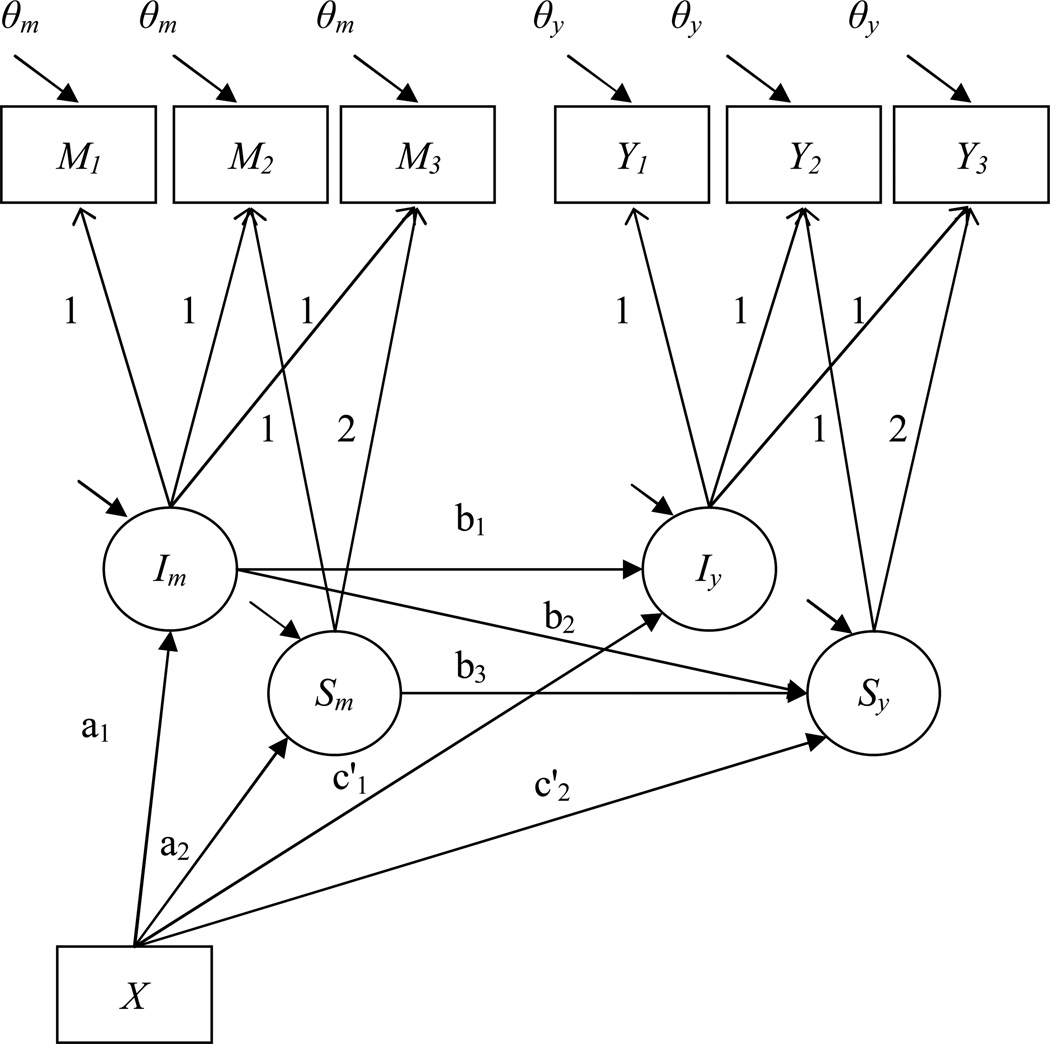
The last example considers mediation in a longitudinal design. Although longitudinal mediation can be expressed in several models (e.g. autoregressive models, Gollob & Reichardt, 1991; Cole & Maxwell, 2003), this example considers in particular the latent growth curve model (Cheong, MacKinnon, & Khoo, 2003; Muthén & Curran, 1997). Briefly explained, a latent growth curve model is characterized by the estimation of latent factors that characterize average initial status of a variable and average growth over time. The functional form of growth can be modeled in complex ways, but is in most circumstances assumed to be linear. The latent growth curve example at hand assumes the presence of one binary treatment indicator, and three waves of measurement of both the mediator and the outcome. The measurement waves are modeled with a latent intercept and a latent slope as depicted in Figure 6. The mediation effect is defined by the path relating the treatment assignment to the latent growth of the mediator and in turn to the latent growth of the outcome. This type of model is sometimes referred to as a parallel process model of mediation (Cheong, MacKinnon, & Khoo, 2003). Syntax on how to set this model up in Mplus is provided in Appendix G.

Figure 6.

Mediation in longitudinal designs – Latent growth curve models.

Note. Labels of residual terms for latent variables are omitted in the graph.

Defining reasonable parameter values for a power analysis is more difficult for latent growth curve models. Feingold (2009) describes how to use Cohen’s d metric in the context of latent growth curve models. Hertzog, von Oerten, Ghisletta, and Lindenberger (2008) also give an overview of conducting power analyses in latent growth curve models. They also provide information on implied covariance of the observed variables as a function of the latent growth parameters, which can be helpful in defining effect sizes.

In the example presented here, three waves of measurement of the mediator and the outcome variable are considered. The first measurement is a baseline measure that is measured at the same time of treatment assignment. Treatment assignment is denoted by X and is assumed to be random and balanced. The average initial status of the control group for both the mediator and outcome (the latent intercepts I_m and I_y) are set to be 0, while the average growth of the control group is set to be 0.1 (the latent growth factors S_m and S_y). This implies that the control group will have model implied means on the mediator of 0, 0.1, and 0.2, at wave 1, 2, and 3 respectively. As simplifying assumptions the covariance between latent intercepts and slopes is set to be 0, and the error variance of the observed mediators and outcomes is set to be equal across waves of measurements. Also, the variance of the latent intercept factors are set to be 1.0, and the variance of the latent slope factors are set to a value of 0.1, which is realistic for many substantive contexts. The residual variances of the observed variable M₁ and Y₁ are set to 0.25. This implies an average reliability of the variables at baseline of .80, because the total model implied variance of M₁ (which is equal to the variance of I_m and the residual variance of M) will be 1.25. To simplify the model, all residual variances will be constrained to be equal.

The initial difference on the mediator variable between the control and the treatment group at the onset of the study is set to be 0, as would be expected in a randomized trial. This initial difference is represented by path a₁ in the model. Also, the initial difference between the two groups on the outcome variable Y is set to be 0. This is represented by path c’₁.

The a₂ path is the difference in growth trajectories on the mediator between the control and treatment group. In this example it is set at a value of .4. This implies that the treatment group will have model implied means of 0 at time 1, 0.5 at time 2, and 1.0 at time 3. The same difference of 0.4 in growth trajectories (represented by path coefficient c’₂) will be used for the outcome variable Y.

The three structural paths of the model b₁, b₂, and b₃, represent the relation between the latent intercept of the mediator to the latent intercept of the outcome variable (b₁), the relation between the latent intercept of the mediator to the latent slope of the outcome (b₂), and the relation between the latent slope of the mediator to the latent slope of the outcome (b₃). The mediated effect that is usually of greatest interest is the indirect effect of the treatment assignment to the latent growth of the outcome via the latent growth of the mediator (path a₂b₃). This effect examines whether the independent variable X affects the growth of the mediator, which in turn affects the growth of the outcome variable.

In this example path b₁ is set to small value of .14, the path b₂ is set to .05, and the path relating the two growth factors, b₃, is set to .4.

This results in model implied means that are displayed in Table 4.

Table 4.

Model implied means of outcome variables.

		Time 1	Time 2	Time 3
Mediator (M)	Control group	0	.1	.2
	Treatment group	0	.5	1.0
Outcome (Y)	Control group	0	.15	.3
	Treatment group	0	.75	1.5

The power of the mediated effect a₂b₃ with a sample size of 750, as in this example, is estimated to be .97, indicating sufficient power to detect the mediated effect.

Summary

The purpose of this paper was to introduce the flexible Monte Carlo approach to estimate power with particular focus on mediational models. As outlined above, the Monte Carlo approach has many desirable features, most notably the ease at which the power estimation is conducted and the flexibility with which many different models and data situations can be accommodated. In this paper Mplus was used throughout, but it is also possible to use other software packages with simulation capabilities.

The special focus on mediation analysis was chosen because of the current interest in the method and the lack of available resources on how to calculate power for these complex and interesting models. The paper described power estimation for the single mediator model, mediation with multiple mediators, mediation models with latent variables and moderated mediation, and mediation in latent growth curve models. Additional models could have been considered, e.g. mediation in autoregressive models. We do however hope that the presented examples strike a balance between conciseness and pedagogical value. Ultimately, we hope that this paper contributes to the more widespread use of power analysis, even in models that are as complex as the ones we considered.

Table 3.

Comparison of estimated power of the mediated effect between the Monte Carlo approach and the Satorra and Saris approach using constraints on either the a or the b path.

	Method
Sample size	Monte Carlo	S&S – a path	S&S – b path
10	.02	.20	.07
100	.17	.94	.29
250	.52	.99	.60
500	.84	>.99	.87
1000	.99	>.99	.99

Note. S&S stands for Satorra & Saris method. The a path in this example is held constant at .721, the b path is held constant at .14, and the c’ path is held constant at .283

Appendix A

Covariance Algebra to determine effect sizes in Mplus

The three variances in the simple mediation model can be expressed as (see MacKinnon, 2008; Chapter 4.10):

$$\mathit{\text{Var}}(X)=.25\mathit{\text{Var}}(M)=a^2·\mathit{\text{Var}}(X)+\mathit{\text{Var}}(e_M)\mathit{\text{Var}}(Y)=c{\text{'}}^2·\mathit{\text{Var}}(X)+b^2·\mathit{\text{Var}}(M)+2·\mathit{\text{bc}}\text{'}·\mathit{\text{Cov}}(X,M)+\mathit{\text{Var}}(e_Y)$$

where Var is a variance of a variable, a, b, and c’, are unstandardized path coefficients, Cov is a covariance, and Var(e) is a residual or unexplained variance term.

The variance of the binary independent variable X is .25 in the population, because variances of binary variables are defined as, where p and q are proportions of possible values of the binary variable. In the case of an even split pq = .5² = .25.

The variance of the dependent variable M is a function of the relationship of X to M and the residual variance term, and the variance of the dependent variable Y is a function of the relationship of X to Y, M to Y, and the covariance between X and M.

To achieve a desired R² each formula above can be solved by substituting known values and solving for the remaining unknowns. For example if the desired R² effect size for the relationship between X and M (the a path) is set to be .13 (medium effect size), we can set the total variance of M to be 1.0 and the residual variance to be (1− R²), or simply .87.In a next step we can set the variance of X to be .25 and then solve for a, the unstandardized path coefficient. This yields a = .721, which is the value for the unstandardized path coefficient in Mplus that will result in an R² effect size of .13. Note that the residual variance in Mplus needs to be fixed to .87, so that the overall variance of M is exactly 1.0.

$$\mathit{\text{Var}}(M)=a^2·\mathit{\text{Var}}(X)+\mathit{\text{Var}}(e_M)1=a^2·\mathit{\text{Var}}(X)+[1-.13]1=a^2·\mathit{\text{Var}}(X)+.871=a^2·(.25)+.87\frac{1-.87}{.25}=a^2=.52a=.721$$

Similarly, we can solve for the path coefficients and residual variance of Y. Assuming it is of interest to achieve an R² effect size of .13 for the relationship of M to Y (b path), and an R² effect size of .02, for the relationship between X and Y (c’ path), the following values can be substituted. Note that the covariance between X and M is defined through the previous equation. In the case of a binary independent variable the unstandardized path coefficient a can be transformed into a covariance using the following formula:

$$a·\mathit{\text{Var}}(X)=\mathit{\text{Cov}}(X,M)(.721)·(.25)=.18=\mathit{\text{Cov}}(X,M)$$

This covariance can be substituted along other known values into the following equation.

$$\mathit{\text{Var}}(Y)=c{\text{'}}^2·\mathit{\text{Var}}(X)+b^2·\mathit{\text{Var}}(M)+2·bc\text{'}·\mathit{\text{Cov}}(X,M)+\mathit{\text{Var}}(e_Y)1=c{\text{'}}^2·\mathit{\text{Var}}(X)+b^2·\mathit{\text{Var}}(M)+2·bc\text{'}·\mathit{\text{Cov}}(X,M)+\mathit{\text{Var}}(e_Y)1=c{\text{'}}^2·\mathit{\text{Var}}(X)+b^2·\mathit{\text{Var}}(M)+2·\mathit{\text{bc}}\text{'}·\mathit{\text{Cov}}(X,M)+\mathit{\text{Var}}(e_Y)1=c{\text{'}}^2·(.25)+b^2·1+2·\mathit{\text{bc}}\text{'}·(.18)\mathit{\text{Var}}(e_Y)$$

To uniquely solve the equation above, additional information has to be entered. Based on the example, it is known that the unique explained variance of the c’ path is .02, and .13 for the b path. Therefore these two additional equations can be set up.

$$c{\text{'}}^2·(.25)=.02b^2=.13$$

Solving for both c’ and b yields:

$$c=\sqrt{\frac{.02}{.25}}=.283b=\sqrt{.13}=.36$$

This finally allows solving for the residual variance of Y, by substituting known values of the path coefficients.

$$1=c{\text{'}}^2·(.25)+b^2·1+2·\mathit{\text{bc}}\text{'}·(.18)+\mathit{\text{Var}}(e_Y)1={(.283)}^2·(.25)+{(.36)}^2+2·(.36)·(.283)·(.18)+\mathit{\text{Var}}(e_Y)1=.02+.13+.037+\mathit{\text{Var}}(e_Y)1-.02-.13-.037=\mathit{\text{Var}}(e_Y)=.813$$

Appendix B

SAS Syntax to perform Monte Carlo simulation with PRODCLIN asymmetric confidence intervals

ods html close;
options nomprint noxwait;

data data1;
/*Change file address to match the location of the results from Mplus*/;
infile "C:\results.dat"
/* Change number and order of variables in dataset
/* according to Mplus technical output 1
/* In this example only quantities of interest get unique labels
/* Other quantities in the Mplus output file
/* are simply labeled p1-p7 and se1-se7*/;
input rep p1-p2 a b cprime p6-p7
se1-se2 sea seb secprime se6-se7
chi1 chidf chip ll0 ll1 df aic bic cbic rmsea srmr;
rho = 0;
alpha = .05;
drop p1-p2 p6-p7 se1-se2 se6-se7
chi1 chidf chip ll0 ll1 df aic bic cbic rmsea srmr;
da=a/sea;
db=b/seb;
sedadb=sqrt(da*da+db*db+1);
dadb=da*db;
ab=a*b;
sobelse=sqrt(a*a*seb*seb+b*b*sea*sea);
run;

data temp;
format rep 8.0 lcrit 16.8 ucrit 16.8;
run;

%macro prodclinmc(i);
%do i = 1 %to &i;

data _null_;
set data1;
if rep = &i;
*Change file address to match the location of the file prodclin.exe;
file "C:\prodclin\raw.txt";
put a @; put sea @; put b @; put seb @; put rho @; put alpha @;
run;

*Change file address to match the location of the file prodclin.exe;
X cd C:\prodclin;
*Change file address to match the location of the file prodclin.exe;
X call "C:\prodclin\prodclin.exe";

data data2;
*Change file address to match the location of the file prodclin.exe;
infile "C:\prodclin\critval.txt";
input lcrit ucrit;
rep = &i;
run;

proc append base=temp data=data2 force;
run;
%end;

data results;
merge data1 temp;
by rep;
low=(lcrit-dadb)/(sedadb);
high=(ucrit-dadb)/(sedadb);
prodlow=ab+low*sobelSE;
produp=ab+high*sobelSE;
if lcrit=99999 then prodlow=99999;
if ucrit=99999 then produp=99999;
if produp < 0 then power = 1;
if prodlow > 0 then power = 1;
if produp = . then power = .;
if prodlow = . then power = .;
run;
%mend;

/*Change the value of i to match the number or replications*/;
%prodclinmc(i=1000);
run;

proc means data=results;
var power;
run;

Appendix C

Single mediator model

TITLE: MONTE CARLO POWER EXAMPLE 1 - MEDIATION PATH MODEL

MONTECARLO:
        names are x m y;                 !Define variable names;
        cutpoints = x (0);               !Define cutpoint to generate binary treatment;

        nobs = 275;                      !Power is estimated for this sample size;

        nreps = 10000;                   !Number of replications;
       seed = 2222;                      !Seed value for random number generator;

ANALYSIS: TYPE=meanstructure;

MODEL POPULATION:

          [x @ 0];                       !mean of x set to 0;
          x @ .25;                       !total variance of x set to .25;
          [m -y @ 0];                    !mean of m and y set to 0;
          m @ .98;                       !residual variance of m set to .98;
          y @ .954;                      !residual variance of y set to .954;
          m on x @ .283;                 !a path;
          y on m @ .141 x @ .283;        !b path, c’ path;

MODEL:                                   !MODEL statement repeats all paths;
          [m -y * 0];                    !and mean and variances;
          m @ .98;                       !of endogenous (dependent) variables;
          y @ .954;
          m on x * .283;
          y on m * .141 x * .283;

MODEL INDIRECT:                          !MODEL INDIRECT statement to obtain mediated effect;
          y IND x;                       !Start and endpoint of mediation model defined here;

Appendix D

Three path mediation

TITLE: MONTE CARLO POWER EXAMPLE 2a – THREE PATH MEDIATION

MONTECARLO:
        names are x m1 m2 y;
        cutpoints = x(0);

        nobs = 90;

        nreps = 10000;
        seed = 2222;

ANALYSIS: TYPE=meanstructure;

MODEL POPULATION:

          [x @ 0];                               !mean of x set to 0;
          x @ .25;                               !variance of x set to .25;
          [m1 -y @ 0];
          m1 @ .87;                              !residual variance of m1 set to .87;
          m2 @ .868;                             !residual variance of m2 set to .868;
          y @ .844;                              !residual variance of y set to .844;

          m1 on x @ .721;                        !a path;
          m2 on m1 @ .36;                        !b1 path;
          y on m2 @ .36 x @ .283;                !b2 path, c’ path;

MODEL:
          m1 * .87;
          m2 * .868;
          y * .844
          m1 on x * .721;
          m2 on m1 * .36;
          y on m2 * .36 x * .283;

MODEL INDIRECT:
          y IND x;

OUTPUT:

Appendix E

Mediation model with two mediators

TITLE: MONTE CARLO POWER EXAMPLE 2b - MEDIATION MODEL WITH TWO MEDIATORS

MONTECARLO:
        names are x m1 m2 y;
        cutpoints = x(0);

        nobs = 180;

        nreps = 10000;
        seed = 2222;

ANALYSIS: TYPE=meanstructure;

MODEL POPULATION:

          [x @ 0];
          x @ .25;
          [m1 -y @ 0];
          m1 @ .98;
          m2 @ .87;
          y @ .78;

          m1 on x @ .238;                     !a1 path;
          m2 on x @ .721;                     !a2 path;
          y on m1 @ .14 m2 @ .36 x @ .283;    !b1 path, b2 path, c’ path;

MODEL:

          [m1 -y * 0];
          m1 * .98;
          m2 * .87;
          y * .78;
          m1 on x * .238;
          m2 on x * .721;
          y on m1 * .14 m2 * .36 x * .283;

MODEL INDIRECT:
          y IND x;

OUTPUT:

Appendix F

Mediation and moderation with latent variables

TITLE: MONTE CARLO POWER EXAMPLE 3 - LATENT MULTIGROUP;

MONTECARLO:

           names are x
           m1 m2 m3 y;
           cutpoints = x (0) | x (0);
           ngroups = 2;

           nobs = 400 200;     !Sample sizes for each group;

           nreps = 10000;
           seed = 2222;

ANALYSIS: TYPE = MEANSTRUCTURE;

MODEL POPULATION:
          [x @ 0];
          x @ .25;
          [y @ 0];
          y @ .81;
          [m1 -m3 @ 0];
          m1 - m3 @ .36;
          m by m1 @1.0 m2 @.80 m3 @.80;
          m @ .87;
          [m @ 0];
          m on x @ .721;                    !a1 path;
          y on m @ .36 x @.283;             !b1 path, c’1 path;

MODEL POPULATION-G1:

MODEL POPULATION-G2:
          y @ .95;
          y on m @ .14 x @ .283;            !b2 path, c’2 path;

MODEL:
          m * .87;
          [m @ 0];
          m by m1@1 m2*.8 m3*.8;
          m on x * .721;
          y on m * .36 x * .283;

MODEL G1:
          m @ 1;
          [m @ 0];
          m by m1 - m3 * .80;
          m on x * .721 (a1);
          y on m * .36 (b1) x * .283;

MODEL G2:
          m @ 1;
          [m @ 0];
          m by m1 - m3 * .80;
          m on x * .721 (a2);
          y on m * .14 (b2) x * .283;

MODEL INDIRECT:
        y IND x;

MODEL CONSTRAINT:
NEW(med1*.26 med2*.10 diffa*0 diffb*.22 diffmed*.16);    !New parameters and start values;
med1 = a1 * b1;                                          !Mediated effect for group 1;
med2 = a2 * b2;                                          !Mediated effect for group 2;
diffa = a1 - a2;                                         !Difference in a paths;
diffb = b1 - b2;                                         !Difference in b paths;
diffmed = med1 - med2;                                   !Difference in mediated effects;

OUTPUT:

Appendix G

Longitudinal mediation using latent growth curves

TITLE: MONTE CARLO POWER EXAMPLE 5 - LGC;

MONTECARLO:

            names are x
            m1 m2 m3
            y1 y2 y3;
            cutpoints = x (0);

!The number of observations is the
!sample size that we want power to
!be estimated for!

            nobs = 750;
            nreps = 10000;
            seed = 2222;

MODEL POPULATION:
            [x @ 0];
             x @ .25;

            im sm | m1@0 m2@1 m3@2;    !Definition of latent growth curve for mediator;
            [im@0 sm@.1];              !Variance of latent factors;
            im@1; sm@.1;               !Means of latent factors;

            iy sy | y1@0 y2@1 y3@2;    !Definition of latent growth curve for outcome;
            [iy@0 sy@.1];              !Variance of latent factors;
            iy@1; sy@.1;               !Means of latent factors;

            im with sm @ 0;                            !Covariance between latent factors;
            iy with sy @ 0;                            !Covariance between latent factors;

            im on x @ 0;                               !a1 path;
            sm on x @ .4;                              !a2 path;

            iy on im @ .14 x @ 0;                      !b1 path, c’1 path;
            sy on im @ .05 sm @ .5 x @ .4;             !b2 path, b3 path, c’2 path;

            [m1 - y3 @ 0];                             !Means of observed variables;
            m1 @ .25; m2 @ .25; m3 @ .25;              !Residual variances of observed variables;
            y1 @ .25; y2 @ .25; y3 @ .25;              !Residual variances of observed variables;

MODEL:

            im sm | m1@0 m2@1 m3@2;

            iy sy | y1@0 y2@1 y3@2;

            im with sm * 0;
            iy with sy * 0;

            im on x * 0;
            sm on x * .4;

            iy on im * .14 x * 0;
            sy on im * .05 sm * .5 x * .4;

MODEL INDIRECT:

            sy IND x;

OUTPUT: