Analysis of repeated measurement data in the clinical trials

Abstract

Statistics is an integral part of Clinical Trials. Elements of statistics span Clinical Trial design, data monitoring, analyses and reporting. A solid understanding of statistical concepts by clinicians improves the comprehension and the resulting quality of Clinical Trials. In biomedical research it has been seen that researcher frequently use t-test and ANOVA to compare means between the groups of interest irrespective of the nature of the data. In Clinical Trials we record the data on the patients more than two times. In such a situation using the standard ANOVA procedures is not appropriate as it does not consider dependencies between observations within subjects in the analysis. To deal with such types of study data Repeated Measure ANOVA should be used. In this article the application of One-way Repeated Measure ANOVA has been demonstrated by using the software SPSS (Statistical Package for Social Sciences) Version 15.0 on the data collected at four time points 0 day, 15^th day, 30^th day, and 45^th day of multicentre clinical trial conducted on Pandu Roga (~Iron Deficiency Anemia) with an Ayurvedic formulation Dhatrilauha.

INTRODUCTION

Clinical research involves investigating proposed medical treatments, assessing the relative benefits of competing therapies, and establishing optimal treatment combinations. Before the widespread use of experimental trials, clinicians attempted to answer the medical questions by generalizing from the experiences of individual patients to the population at large. Clinical judgment and reasoning were applied to reports of interesting cases in pursuit of medical progress. The concepts of variability among individuals and its sources may have been noted, but were not formally addressed.

In the twentieth century, the field of statistics developed and was applied to clinical research. Statistics is the “theoretical science or formal study of the inferential process, especially the planning and analysis of experiments, surveys, and observational studies” (Piantadosi 2005). The accurate use of statistics in biomedical research plays a significant role in enhancing the quality of research and observing research ethics. The misuse of statistics is unethical and can have serious clinical consequences in medical research. ICH Harmonized Tripartite Guideline on Statistical Principles for Clinical Trials also emphasizes on the correct use of statistics in the clinical research.[1]

In general, the independent sample t-test is used to compare observations from two populations. It tests if they have equal means or if the means of observations from two groups from one population are the same. When we deal with more than two populations or groups, we use Analysis of Variance (ANOVA). Similarly, paired t-test is used when a single sample of participant is measured twice on the same dependent variable. However, when the measurements are made more than two times repeatedly over a period of time on the same dependent variable repeated measure ANOVA should be used. The use of standard ANOVA method to compare group means is inappropriate in this kind of study design, as it does not consider dependencies between observations within subjects in the analysis.

Repeated measures analysis deals with response outcomes measured on the same experimental unit at different times or under different conditions. Longitudinal data is a common form of repeated measures in which measurements are recorded on individual subjects over a period of time.[2,3,4,5]

Since last few decades in the field of Ayurveda longitudinal studies are becoming increasingly popular whether they are in the form of RCTs, parallel group studies or single arm interventional studies. A longitudinal study is a study in which the subjects are followed over time to see their progress and change in the status. This means, in longitudinal studies we take repeated measurements of the same individual over a time span long enough to encompass a detectable change in their developmental status. An example of a repeated measurement data in a longitudinal study is the measurement of blood pressure of the patients after every week in a study in which patients are followed at an interval of 1 week for 3 months.

Assessment of the effectiveness of treatments is more sensitive in repeated measure study designs because they make it possible to measure how the treatment affects each individual. When control and treatment groups consist of different individuals the changes brought about by the treatment may be masked by the variability between subjects. By contrast, in repeated measures designs each subject serves as own control.[6] So in repeated-measures designs the variability between subjects can be isolated, and analysis can focus more precisely on treatment effects. A repeated-measures ANOVA puts each individual on an equal footing, and simply looks at how scores change with alternative treatments, or over time. The modification required to the standard method of performing analysis of variance is through partitioning of the total variation.

The present work intends to bring to the attention of applied researchers the latest developments in data analysis strategies of longitudinal studies.[7] This article demonstrates the use of repeated measure ANOVA with the help of the Statistical Software SPSS 15.0 by using the data of 423 patients assessed at four different time points viz. 0 day, 15^th day, 30^th day and 45^th day from a multicentre clinical study on Pandu Roga (~Iron Deficiency Anemia) with an Ayurvedic formulation, Dhatrilauha.

ONE-WAY REPEATED MEASURE DESIGN-ASSUMPTIONS

Repeated-measure design is a research design in which subjects are measured two or more times on the dependent variable. Rather than using different participants for each level of treatment, the participants are given more than one treatment and are measured after each. This means that each participant will be its own control.[8] In repeated-measures analysis, scores for the same Individual are dependent, whereas the scores for different individuals are independent. The following are the assumptions underlying this type of study design:

• The dependent variable is measured on interval or ratio scale (dependent variable is continuous)

• The sample was randomly selected from the population. The cases represent a random sample from the population, and there is no dependency in the scores between participants

• The dependent variable is normally distributed in the population for each level of the within-subjects factor

• The population variances for the test occasions are equal. The population correlation coefficients between pairs of test occasion scores are equal. The population variance of difference scores computed between any two levels of a within-subjects factor is the same value regardless of which two levels are chosen. This assumption is sometimes referred to as the sphericity assumption or as the homogeneity-of-variance-of-differences assumption. The sphericity assumption is meaningful only if there are more than two levels of a within-subjects factor.

Basically, sphericity refers to the equality of the variances of the differences between levels of the repeated measures factor. In other words, we calculate the differences between each pair of levels of the repeated measures factor and then calculate the variance of these difference scores. Sphericity requires that the variances for each set of difference scores be equal. When this assumption is not met, the Type I error rate can be seriously affected. However, an appropriate correction can be made by changing the degrees of freedom from K – 1 and (n – 1)(K –1) to 1 and n – 1, respectively.

Normally for checking the condition of Sphericity, Mauchly's test is used as the violation of sphericity assumption leads to inflated F-value and hence inflated Type I error. However, the power of Mauchly's test of sphericity depends on the sample size. For large sample size, even small violations of sphericity can produce significant results, and in case of small sample size, the Mauchly's test often does not have the power to detect large violations of sphericity. There are three common corrections for violation of sphericity:

• Greenhouse-Geisser correction

• Huynh-Feldt correction

• Lower Bound correction.

All these three methods adjust the degrees of freedom using a correction factor called Epsilon. Epsilon lies between 1/k-1 and 1, where k is the number of levels in the within subject factor.

LIMITATIONS OF REPEATED-MEASURE DESIGNS

As in repeated-measure designs the same group of participants are measured on multiple occasions, therefore sometimes the order of measurements have a differential effect on participants responses as some experiments involve repeated exposure to the same task. These differential effects can be broadly explained as:

• Practice effect or learning effect-As participants complete the measures after each condition, they may get better practice, or they may get bored or tired. As a result of which participants change as they are repeatedly tested

• Latency effect-refers to a situation in which the effect of a treatment is not evident until a subsequent level of the treatment is introduced. A latency effect may predispose a researcher to erroneously contend that the administered treatment had little to no effect on the monitored behavior when, in actuality, the effect of the treatment was not evidenced until an additional condition had been implemented

• Carry-over effect-refers to the influence of a previous level of treatment on the observed behavior in a subsequent level of the same treatment condition.

Carry-over, latency, and practice effects tend to skew results by influencing the responses of participants and can be both either positive or negative in nature. Counterbalancing should be done in order to eliminate the bias in results caused by these effects. It involves presenting levels of a treatment condition so that each level occurs equally often at each stage of practice and so that each level precedes another level as many times as it follows the level.

ONE-WAY REPEATED MEASURE ANOVA IN SPSS-PROCEDURE AND OUTPUT

One-way repeated-measures ANOVA can be undergone in SPSS by going under the “Analyze” menu > “General Linear Model” > “Repeated Measures”.

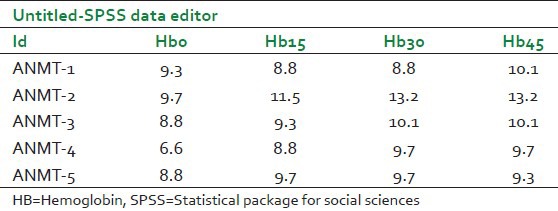
The data for repeated measure design in SPSS data editor is entered differently from the way data are entered for one-way between-subjects ANOVA. In the repeated-measures case, each level of the independent variable is represented as a separate column. Table 1 shows the data pattern for the variable hemoglobin as entered in the SPSS data editor.

Table 1.

Format for entering data in SPSS

The syntax for the analysis in SPSS is:

GLM

Hb0 Hb15 Hb30 Hb45

/WSFACTOR = time 4 Simple (1)

/METHOD = SSTYPE (3)

/PLOT = PROFILE (time)

/PRINT = DESCRIPTIVE ETASQ OPOWER PARAMETER

/CRITERIA = ALPHA (0.05)

/WSDESIGN = time

The procedure on running in SPSS will generate a great number of tables in the output window. But in this article a few tables have been explained that are relevant for interpreting the results of One-Way Repeated Measure Anova undergone in SPSS. For simplicity we have taken the variable hemoglobin for explaining the output.

The first table [Table 2] generated in output window tells about the levels of independent variable (within subject factor) and labels the time points 1, 2, 3, and 4. The column labeled as dependent variable tells that the dependent variable “Hemoglobin” is measured at four time points 0 day, 15^th day, 30^th day, and 45^th day.

Table 2.

Within subject factor levels for hemoglobin

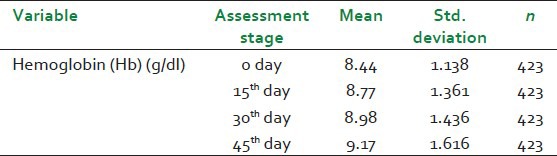
The second table [Table 3] simply illustrates the Mean and Standard deviation of dependent variable hemoglobin (Hb) at different time points i.e., 0 day, 15^th day, 30^th day, and 45^th day.

Table 3.

Descriptive statistics for hemoglobin

The another table [Table 4] which is of real interest is the one showing the result of the Mauchly's test of Sphericity which tests for one of the assumption of the Repeated Measure ANOVA, namely Sphericity. The approximate Chi-Square value and its associated P value tells that the significance level is below 0.05 (it is <0.0001). This significant value for Mauchly's test of Sphericity indicates that the assumption of Sphericity has been violated. In this situation the test would proceed by using the different correctional adjustment namely Greenhouse-Geisser, Huynh-Fedlt and Lower-Bound. This table also tells us the epsilon values for the three different correctional adjustments. It is evident from this table also that epsilon is lying between 1/(4-1) to 1, where 4 is the number of levels (0 day, 15^th day, 30^th day, and 45^th day) on which our dependent variable hemoglobin has been measured.

Table 4.

Result of Mauchly's test of sphericity

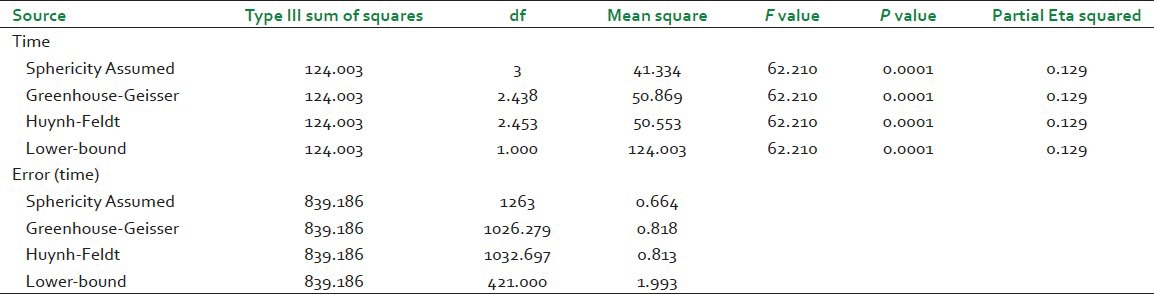
The next table [Table 5] provides the information that there was an overall significant difference between the means at the different time points. This table demonstrates the F-value for the “Time” factor, its associated significance level and effect size (Partial Eta squared). As the data has violated the assumption of sphericity, therefore, the results presented in the row labeled as Greenhouse-Geisser will be interpreted. Had sphericity not been violated the results under the Sphericity Assumed row would have been interpreted. It can be seen that for preceding the test with Greenhouse-Geisser correction SPSS has adjusted the degrees of freedom by multiplying the corresponding epsilon value with the degrees of freedom for the sphericity assumed condition. In our case the corresponding epsilon value for Greenhouse-Geisser correction is 0.813. Therefore, the adjusted degrees of freedom for Greenhouse-Geisser correction are obtained as 0.813 multiplied by 3 the corresponding degree of freedom for sphericity assumed condition, which gives 2.439, similarly error degrees of freedom are calculated by multiplying the corresponding error degree of freedom for sphericity assumed condition with the epsilon value for Greenhouse-Geisser correction. That is 0.813 multiplied by 1263 which gives 1026.819.

Table 5.

Test of within subject effects for hemoglobin

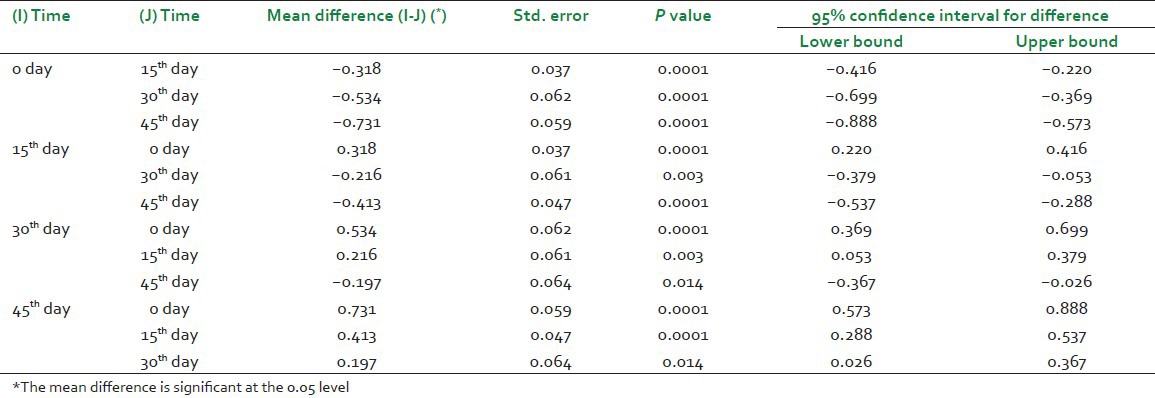
The last table [Table 6] gives the result of post hoc comparisons which depict that where exactly the differences occurred if an overall significant difference has been achieved. This table presents the result of Bonferroni post hoc test, which allows to discover which specified means differed.[9] It can be seen from this table that the significant difference has been observed at all time points from 15^th day onwards as compared to baseline visit (0 day). Moreover, this table also tells that a significant difference has been observed between the level of hemoglobin at 15^th day and 30^th day, 15^th day and 45^th day and also between 30^th day and 45^th day.

Table 6.

Result of post hoc comparisons for hemoglobin

INTERPRETATION OF THE RESULTS

The output generated from the application of One-Way Repeated Measure Analysis of Variance on the Parameter Hemoglobin (Hb) can be summarized as: A repeated measure ANOVA with a Greenhouse-Geisser correction determined the mean value of hemoglobin has been statistically significant between assessment stages (0 day, 15^th day, 30^th day, and 45^th day) (F (2.438, 1026.279) =62.210, P < 0.0001). Post hoc test using the Bonferroni correction revealed a slight increase in the value of hemoglobin at all assessment stages [8.44 ± 1.13, 8.77 ± 1.36, 8.98 ± 1.436 and 9.17 ± 1.616 (g/dl), respectively] P < 0.0001. It can be concluded that the formulation Dhatrilauha has been able to increase the hemoglobin level by 0.73 g/dl over a period of 45 days as compared to baseline.

DISCUSSION

It is common in medical research for methods of statistical analysis to become standard for particular types of data. Their use widely becomes accepted and little thought is given to whether they are truly appropriate for the clinical question being posed.[10,11] Mean difference comparison procedures are widely used in most biological and medical research as well as other life and social sciences. The inappropriate uses of such methods may lead to wrong conclusions about the nature of differences and the relationship of factors for the outcome of interest under the comparison. Aside from the widely used procedures, such as one or two sample t-tests and some non-parametric tests, the standard ANOVA and repeated measures ANOVA have been of concern to researchers with their uses and interpretation of results, since researchers feel confused with the use of these two methods. Researchers should think about their studies carefully before they perform statistical analysis in terms of the method of measuring responses, independence among observations, and the use of appropriate models. In this article, an attempt has been made to demonstrate the use of repeated measures ANOVA on serial measurement data in clinical trials.