Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Aug 8;3:2383. doi: 10.1038/srep02383

Multiscale distribution of oxygen puddles in 1/8 doped YBa2Cu3O6.67

Alessandro Ricci 1,2, Nicola Poccia 2,3, Gaetano Campi 4, Francesco Coneri 3, Alessandra Stella Caporale 2, Davide Innocenti 2, Manfred Burghammer 5, Martin v Zimmermann 1, Antonio Bianconi 2,a
PMCID: PMC3737503  PMID: 23924946

Abstract

Despite intensive research a physical explanation of high Tc superconductors remains elusive. One reason for this is that these materials have generally a very complex structure making useless theoretical models for a homogeneous system. Little is known on the control of the critical temperature by the space disposition of defects because of lack of suitable experimental probes. X-ray diffraction and neutron scattering experiments used to investigate y oxygen dopants in YBa2Cu3O6+y lack of spatial resolution. Here we report the spatial imaging of dopants distribution inhomogeneity in YBa2Cu3O6.67 using scanning nano X-ray diffraction. By changing the X-ray beam size from 1 micron to 300 nm of diameter, the lattice inhomogeneity increases. The ordered oxygen puddles size distribution vary between 6–8 nm using 1 × 1 μm2 beam, while it is between 5–12 nm with a fat tail using the 300 × 300 nm2 beam. The increased inhomogeneity at the nanoscale points toward a network of superconducting puddles made of ordered oxygen interstitials.

While the layered heterostructure at atomic limit is accepted as a universal feature for the lattice of high temperature superconductors, little is known on the control of the critical temperature by the space disposition of defects in the spacer layers1,2,3,4,5,6,7. Defects, as mobile oxygen interstitials, can control electronic inhomogeneity8,9,10,11,12,13,14 and complex multi-scale phase separation15,16,17,18,19,20,21,22,23,24. Furthermore, inhomogeneity in the form of stripes have been shown to induce “shape resonances”22,23 in the superconducting gaps in a multi-band superconductor24, which are type of Fano-Feshbach resonances at a BEC-BCS crossover.

The advances in control of atomic defects and their spatial self-organization is needed for the engineering of new electronic devices at atomic level11. Imaging is needed to control defects organization at the nanoscale in novel quantum functional superconducting materials and it is the first step for unveiling the structure–property relation. Several spatial length scales are involved, which creates strongly intermingled defects structures. In high temperature superconductors (HTS), these networks of defects can influence essential properties such as the Fermi surface, pseudogap energy, spin density waves, charge density waves, and even the superconducting critical temperature. The strong tendency towards complex phase separation14,15,16,17,18,19,20,21,22,23,24 can be used as advantage for developing new electronic devices. In fact, in some circumstances, defects order can be manipulated by scanning tunneling microscopy (STM)11, and/or by continuously exposing the sample to a UV or X-ray beam6,7,10. Developing techniques for imaging the nanoscale heterogeneity of defects organization is the first step to open new opportunities for their manipulation.

YBa2Cu3O6+y (YBCO) high temperature superconductor is one of the most studied HTS material because of its superconducting transition above the nitrogen liquid evaporation temperature. From high resolution hard X-ray diffraction and neutron scattering experiments it is known that the y oxygen dopants form one-dimensional oxygen-compositional stripes that segregate in short-range puddles25,26,27,28,29,30 but few information exist on their spatial distribution. Here we report a spatial imaging using scanning nano X-ray diffraction5,6,7,8,9 of the spatial distribution of the puddles made of compositional oxygens stripes (Ortho-VIII puddles) in the basal plane of YBa2Cu3O6.67 at hole doping p≈1/831,32,33,34.

In particular high quality untwined single crystals of YBCO with doping set at 6.67 corresponding to 1/8 holes per Cu site in the Y(CuO2)2 bilayer, have become available in these last years26. These new crystals have allowed the identification of the Fermi surface reconstruction with the appearance of a new electron-pocket32, the anomalous Nerst effect32, the proximity to a critical hole doping regime33, the unusual magnetic orders34 and broken symmetries35. Although the observation of all these effects is certainly due to the high quality of the samples, understanding the disposition in real space of the YBCO structural components could be a difficult task, as we may expect form the variety of its oxygen phases in the phase diagram26,27,28,29. Of course, as the oxygen ions and the charged vacancies order, a corresponding charge density wave (CWD) and orbital density wave are generated as well.

The key result of this experiment is to unveil the intrinsic inhomogeneity of oxygen puddles distribution. We have recorded images with different spatial resolution by changing the X-ray beam size from 1 micron to 300 nm of diameter. The Ortho-VIII puddles size normal distribution is in the range 6–8 nm for the 1 × 1 μm2 beam while it is much broader (in the range 5–12 nm) with a fat tail using the 300 × 300 nm2 beam. The increased inhomogeneity at the nanoscale points toward an intrinsic granular complexity of puddles at 1/8 doping. This is confirmed by the correlation lengths of the spatial correlation function of the maps that show a dramatic reduction decreasing the beam size.

Results

Synchrotron radiation x-ray diffraction shows the high quality of the YBa2Cu3O6.67 single crystal with P4/m spatial symmetry, unit cell dimensions a = 3.807(11) Å, b = 3.864(12) Å, c = 11.52(2) Å and volume of 169.5(8) Å3. The diffuse streaks of the superlattice reflections have no well-defined peaks along l and the streaks shown in Fig. 1A and B provide direct evidence for nanoscale puddles in the basal a–b plane with Ortho-VIII modulation with a substantial disorder in the stacking of full and empty chains along the c direction. The nanoscale size of Ortho-VIII puddles embedded in a disordered medium is shown as pictorial view in Fig. 1C representing the basal Cu-O plane of YBCO. The Ortho-VIII puddles are made of alternated 5 filled and 3 empty oxygen wires every 8 rows. The number of oxygen ions per unit in the puddles is 6.625 = 6.5 + 0.125 that gives exactly 1/8 holes per Cu site in the Y(CuO2 )2 bi-layers with Cu2+ ions in the chains of the basal plane. Since the average oxygen concentration is 6.67 = 6.5 + 1/6 the hole doping in the disordered background is larger than 1/8.

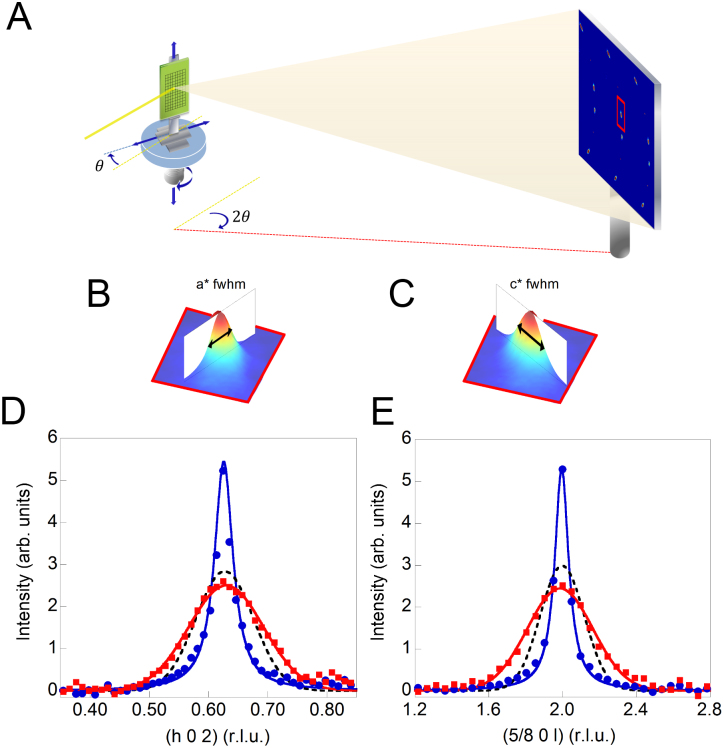
Figure 1. YBa2Cu3O6.67 single crystal diffraction pattern at room temperature.

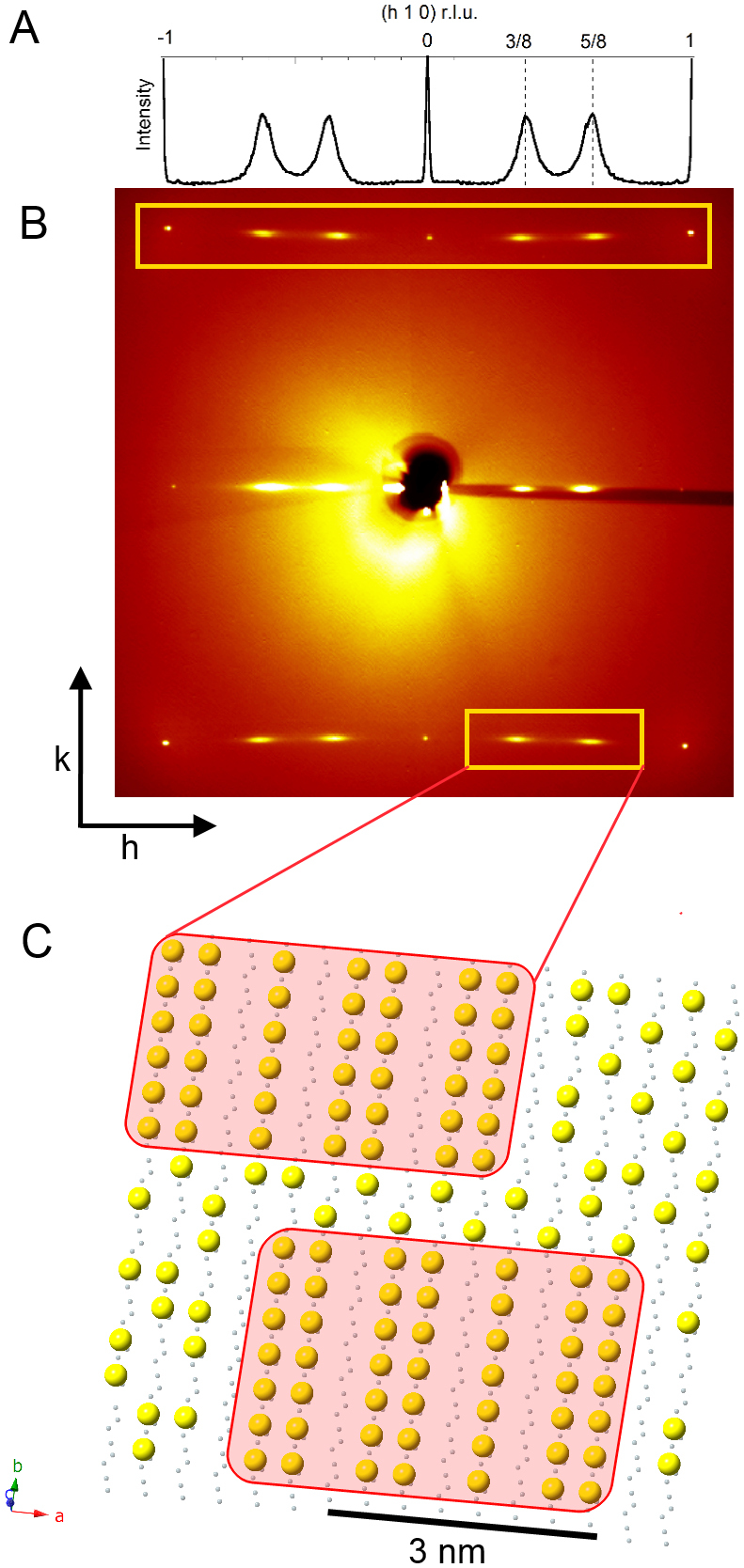
Figure 1

Open in a new tab

(A) The X-ray diffraction pattern shows diffuse superstructure satellites at 3/8 and 5/8 positions, their profile along h is plotted. (B) Room temperature diffraction pattern collected using a transmission geometry. The CuO chains superlattice reflections qOrtho-VIII(a*) = (3/8,k,0) and qOrtho-VIII(a*) = (5/8,k,0) are highlighted in the empty yellow box. (C) Pictorial view of the basal Cu-Oiy plane of YBCO. The small grey dots are the Cu(1) sites and the large yellow dots are the oxygen ions Oiy in defective basal plane. The pictorial view of oxygen ordered metamorphic phases called Ortho-VIII, with formal oxygen content ypuddle = 0.625 shown in the pink filled rectangles, are embedded in the disordered background with an oxygen content slightly larger than the average oxygen content yaver = 0.67.

In order to understand the real space disposition of the Ortho-VIII puddles, and to avoid the transmission electron microscopy (TEM) complications due to electron beam damage of the sample, we have used scanning micro/nano X-ray diffraction (μXRD/nXRD) developed at the ID13 beam-line of the European Synchrotron Radiation Facility in Grenoble (France) (see supplementary info). μXRD and nXRD techniques have been already successfully applied on La2145,6,7, Bi22128 cuprates and on iron-based superconductors9. In this work by scanning micro areas, this technique gives a mixed information of the k- and r-space of the bulk structure inhomogeneities and it has never been applied on a YBa2Cu3O6.67 single crystal. A 1 × 1 μm2 and 300 × 300 nm2 beam size, have been employed for our measurements at room temperature.

The integrated intensity of the observed superstructure in Fig. 2A and the peak position of satellites in different spot of the crystal are quite homogenous, qortho-VIII = 0.625 with a standard deviation of 0.001. This indicates that the nanoscale oxygen puddles have the Ortho-VIII periodicity and confirms the high quality of the crystal. On the contrary, the FWHM along a* (Fig. 2B) and along c* (Fig. 2C) of diffraction profiles, measured at each point (x,y) of the sample reached by the x-y translator with micron resolution, clearly show a spatial variation. The diffraction profiles (Fig. 2D, 2E) show the position dependence of the domain size, derived from the measured full width half maximum (FWHM) of the superstructure reflections via standard methods of diffraction. The spatial variation of the domain size in the a and c crystallographic directions is showed for three spots of the sample corresponding respectively to a narrow, average and a broad superstructure reflection. Although the micro X-ray diffraction profiles give a rough picture on the size variations of the Ortho-VIII puddles, three spots cannot give enough information to construct a real space image of the organization of the Ortho-VIII puddles.

Figure 2.

Figure 2

Open in a new tab

(A) Scanning micro X-ray diffraction experimental set-up at the ID13 beamline of the European Synchrotron Radiation Facility (ESRF) of Grenoble. Full width half maximum (FWHM) of the superlattice reflections along h qOrtho-VIII(a*) = (h,0,2) (B) and along l qOrtho-VIII(c*) = (5/8,0,l) (C). The (h 0 2) and the (5/8 0 l) superlattice peak profile respectively along a* (D) and along c* (E). The blue filled dots, the black dotted lines and the red squares correspond respectively to the profile of a narrow, an average and a broad reflection. Using therefore a micron and sub-micron X-ray beam we are able to resolve the peaks FWHM fluctuations from one spot to the other in the sample.

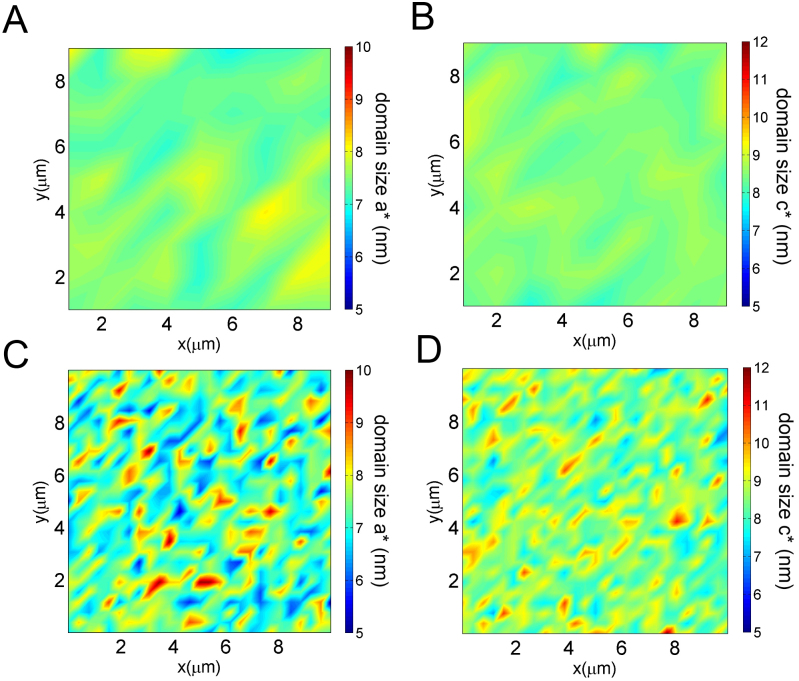
To solve this issue, we have collected 10000 images of μXRD diffraction patterns, scanning the sample with a 1 micron step along both the real space direction x–y (a–c plane). Fig. 3A and Fig. 3B show the maps of the Ortho-VIII domain size along a* and along c*. Although the color bar of the maps extends from dark blue to dark red and is associated to 5 nm to 12 nm sizes respectively, actually the observed color are green and yellow, which indicate a smooth variation of the puddles size in the system within a range of 6.5 nm to 8.5 nm. The average size of this interval is in agreement with the average size of the Ortho-VIII puddles investigated with hard X-ray diffraction at ELETTRA using a 200 × 200 μm2 beamsize. To test if the observed size variation of the Ortho-VIII puddles is an intrinsic aspect of the YBCO system or it is a sample dependent property, we have increased the spatial resolution of the X-ray beam, by diminishing the beam size and performed the same experiment in a similar area. Using a monochromatic X-ray beam of photon energy 14 KeV (ΔE/E = 10−4), the beam has been focused by Kirkpatrick Baez (KB) mirrors down to a 300 nm spot size on the sample (full width at half maximum). We collected other 20000 diffraction images in the reflection geometry using a Fast Readout Low Noise charged coupled device (FReLoN CCD) detector. We constructed the 2D maps from the collected nXRD diffraction patterns, each one for a different spatial x–y position (a–c plane) of the sample. Figure 3C and 3D show respectively the 2D plots of the domains size variation along a and c crystallographic directions. Visual inspection of the maps show a more inhomogeneous spatial distribution of the Ortho-VIII puddles respect that measured delivering a 1 × 1 μm2 beam on the sample (μXRD case). Here the color extends from dark blue to dark red, respectively associated to 5 and 12 nm. The broad distribution of sizes shown in the map indicates an intrinsic and incommensurate nanoscopic order in the system. In addition, the heterogeneous granular structure of the dopants, unveiled by the employ of a nanobeam, shows the relevance of the spatial resolution of the probe on the sample.

Figure 3.

Figure 3

Open in a new tab

The position dependence of the Ortho-VIII domain size along a*(A) and along c* (B), obtained from data measured by scanning micro X-ray diffraction, using a 1 micron incident beam on the sample.The Ortho-VIII domain size do have variations which range from light blue to yellow in a region of about 9 micron squares. The same region size has been investigated, using a 300 nm incidence beam on the sample. The Ortho-VIII mapping of the domain size along a* (D) and along c* (E) are shown. Here the variation is more pronounced, indeed, the intense red–yellow peaks in the two-dimensional color map represent locations in the sample with high strength of Ortho-VIII ordering, and dark blue indicates spots of disordered Ortho-VIII domains.

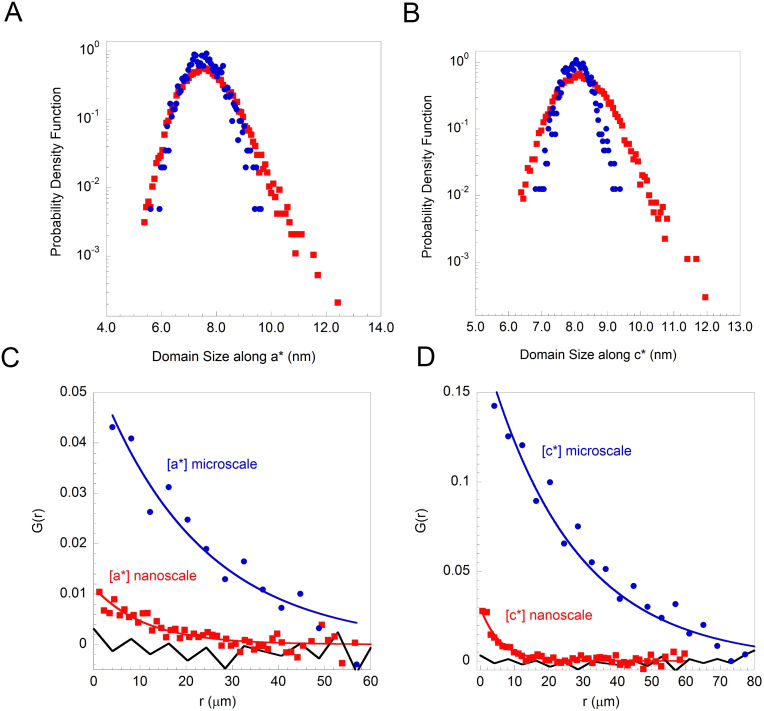
Statistical analysis is used to quantify the size distributions of the Ortho-VIII puddles as seen by scanning micro and nano X-ray diffraction experiments. Figure 4A shows the probability density function (PDF) of the Ortho-VIII puddles sizes along the crystallographic a-axis, observed using a beam of 1 μm and 300 nm of diameter. The distribution of the puddles is nearly symmetric as seen with a resolution of 1 micron while with 300 nm X-ray beam it shows a remarkable asymmetric fat tail, although the average value of 7.5 ± 0.2 nm is comparable. Figure 4B shows the probability density function of the Ortho-VIII puddles sizes along the c crystallographic direction. Also in the size of the puddles in the transversal direction from the CuO2 planes is nearly symmetric however the distribution of sizes measured by the 300 nm nXRD probe, shows a remarkable fat tail. Also in this case the maps obtained by μXRD and the nXRD are in agreement for the average size of domains which is 8.0 ± 0.2 nm. The standard deviation is 0.4 nm for the 1 micron X-ray probe and 0.6 nm for the 300 nm X-ray probe. The fat tails, observed in the maps, have been quantified by the evaluation of the higher statistical moments (see supplementary info). The third moment called Skewness γ gave γa = 0.47 and γc = 0.34 for the Ortho-VIII domain size along the a and c direction, respectively. Their positive values indicate a larger weight of the tails in both distributions; in the maps measured with the 1 micron X-ray probe, the Skewness values γa = 0.23 and γc = 0.09 result quite smaller (see Tab. 1). Similar situation is evidenced evaluating the fourth statistical moment, the Kurtosis κ, that is an indication of the distribution sharpness respect to the Gaussian shape that has κ = 0. Like is summarized in Tab. 1 κa = 0.61 and κc = 0.64 for the Ortho-VIII domain size measured by nXRD and κa = 0.03 and κc = 0.05 for μXRD results. In all the cases, the Skewness and the Kurtosis parameters, result to deviate from the Gaussian distribution characteristic 0 values. The more symmetric distribution observed by the μXRD can be easily explained by the fact that the X-ray beam probes a sample volume of the order of μm3, since the effective X-ray penetration depth is in the micron range, that contains about 106 puddles, on the contrary using the nXRD the number of Ortho-VIII puddles decreases by a factor higher than 10. Although the number of 105 puddles, in each illuminated spot of the nXRD, is still quite large, it allows to unveil the fat tails of the Ortho-VIII puddles quite clearly.

Figure 4.

Figure 4

Open in a new tab

Probability density function of the domain size along a-axis (A) and along c-axis (B) obtained by the microbeam (filled circles) and the nanobeam (filled squares) measurements. Radial correlation function G(r) calculated on domain size map along a-axis (C) and c-axis (D). The blue circles and the red filled squares correspond to the μXRD and nXRD measurements. A comparison between the G(r) behaviors is shown.

Table 1. Statistical moments of the Ortho-VIII domain size PDF along a and c direction. PDFs are calculated from the intensity maps measured by μXRD (beamsize of 1 × 1 μm2) and nXRD (beamsize of 300 × 300 nm2). Both PDFs from μXRD and nXRD show compatible mean values, but variance increased a lot going from the first to second case. The third and the fourth statistical moments deviate from the nominal 0 value for a Gaussian distribution. In particular it is evident that the Skewness and Kurtosis parameters increase a lot decreasing the dimension of the incident beam. In addition, the coherence length ξ, calculated from G(r), is shown in the last row, going from micro-beam to nano-beam it shows a dramatic reduction indicating the intrinsic inhomogeneity of cuprates.

  Nano-beam Micro-beam  
  300 × 300 nm2 1 × 1 μm2  
PDF(x) Moments Size-a Size-c Size-a Size-c Gaussian case
III Skewness (γ) 0.47(1) 0.34(1) 0.23(1) 0.09(1) 0
IV Excess of Kurtosis (κ) 0.61 (1) 0.64(1) 0.03(1) 0.05(1) 0
coherence length ξ (μm) 11.0(2) 5.1(2) 22.0(2) 25.0(2)  
Open in a new tab

Looking at the distance-dependent intensity correlations in Fig. 4C and 4D measured with a 1 micron and 300 nm X-ray beam, it is clear that along both the directions a* and c* the size of the beam unveils different level of spatial organization. Although the G(r) measured by μXRD and nXRD show that the spatial correlations are more extended out-of-plane than in-plane, the G(r) appears different by comparing the result from different beam sizes. For the domain sizes distribution along the a directions, the correlation length of 22 micron measured by μXRD, is reduced of about the half (to 11 micron) using a 300 nm X-ray beam (nXRD). Along the c directions, the reduction is even more dramatic, in fact, from about 25 micron measured with the 1 micron X-ray beam, the correlation length of the scanned area with a 300 nm X-ray beam is 5 micron.

Discussion

We have shown that the intrinsic granular organization of mobile oxygen defects can be unveiled by scaling the size of the X-ray beam in the specific case of YBa2Cu3O6.67 single crystal. If we were seeing a narrowing in the size distributions and a broadening in the correlation length of the puddles, this would have mean that the inhomogeneity observed with the 1 micron beam was due to the sample preparation procedure. Instead, what we measure is a broader and asymmetric distribution of the puddles sizes which show a range of 5–12 nm and a shorter correlation length both along a and c-direction, by scaling the X-ray beam from 1 micron to 300 nm. So far, the defects self-organization and the related nanoscale phase separation controlled by thermal treatments have been well established in high temperature superconductors, like super-oxygenated La2CuO4+y5,6,7, Bi2Sr2CaCuO8+y8 and electron doped iron-chalcogenides9. Therefore, the present results support the idea that each high temperature superconductor displays different and specific realizations of a granular and spatially inhomogeneous lattice, controlled by misfit strain36,37,38. Moreover, high temperature superconductivity resists to the complex lattice broken symmetry that is the characteristic feature of the superstripes scenario39,40. These results show that also broken symmetry observed in the pseu dogap phase35 could be triggered by a lattice broken symmetry in nanoscale grains and in the domain walls at the interface between the nano-puddles.

We have investigated the spatial arrangement of Ortho-VIII puddles in YBa2Cu3O6.67, using scanning micro and nano X-ray diffraction for measuring superstructure reflections with unprecedented real space resolution up to 300 nm. Nevertheless the crystal is clearly of high quality, intrinsic inhomogeneities are found in the Ortho-VIII puddles size distributions. In particular, comparing maps obtained from measurements at different spatial scale (1 × 1 μm2 vs. 300 × 300 nm2), we are able to show how the inhomogeneities appears more clearly at smaller scale, indicating such local structural inhomogeneities as an intrinsic property in these materials.

Methods

The high-quality untwined YBCO crystals were grown in a nonreactive BaZrO3 crucible from high-purity starting materials26. The oxygen content was set at y = 0.67. The hole concentration (doping) p = 0.12 was determined from the c-axis lattice constant. The diamagnetic response across the superconductive transition of the YBa2Cu3O6.67 single crystal has been characterized by means of the Vibrating Sample Magnetometer (VSM) option in a Physical Properties Measurement System (PPMS 6000) from Quantum Design (see supplementary info). After cooling down the sample from room temperature to 10 K in zero applied field (Zero Field Cooling, ZFC) the diamagnetic response upon application of H = 20 Oe has been observed during the warm up across the transition, spanning the 10 K to 80 K temperature range at a rate of 0.5 K/min K. The superconducting transition temperature results to be Tc = 66 K. To study the superlattice reflections due to the oxygen ions (Oi) ordering in the basal plane Ortho-VIII superstructure we performed x-ray diffraction measurements in transmission geometry at the XRD1 beamline of ELETTRA in Trieste (Italy) (see supplementary info) with an energy of 20 KeV and a 200 × 200 μm2 beamsize. We recorded the x-rays scattered by the sample in the a*b* diffraction plane using a charged coupled device (CCD) and results are in agreement with the hard X-ray diffraction data26. Scanning micro/nano X-ray diffraction patterns were collected in the reflection geometry with a CCD that records the X-rays scattered from the sample in the a*c* diffraction plane, showing the Ortho-VIII oxygen chains superlattices qOrtho-VIII(a*) = (3/8,k,0) and qOrtho-VIII(a*) = (5/8,k,0).

Author Contributions

A.R., N.P., G.C., M.B. performed the experiment. A.R., G.C., N.P., D.I., A.S.C., A.B. performed the analysis of the data. N.P., F.C. performed the vibrating sample magnetometer measurements. A.R., N.P., G.C., A.B. have conceived and planned the experiment. N.P., A.R., G.C., A.B., M.v.Z. have written the paper.

Supplementary Material

Supplementary Information

Multiscale distribution of oxygen puddles in 1/8 doped YBa2Cu3O6.67

srep02383-s1.doc (193.5KB, doc)

Acknowledgments

We thank Ruixing Liang, D. A. Bonn, and Walter N. Hardy of the Department of Physics of the University of British Columbia for providing us with the crystals and for helpful discussions. We thank the ID13 beamline staff of ESRF and the XRD1 beamline staff of ELETTRA, especially G. Arrighetti, L. Barba, G. Bais and M. Polentarutti. For financial support we are grateful to superstripes onlus (Via dei Sabelli 119A, 00185 Roma, www.ricmass.eu).

References

  1. Littlewood P. Superconductivity: An x-ray oxygen regulator. Nat. Mater. 10, 726–727 (2011). [DOI] [PubMed] [Google Scholar]
  2. Geballe T. H. & Marezio M. Enhanced superconductivity in Sr2CuO4−v. Phys. C Supercond. 469, 680–684 (2009). [Google Scholar]
  3. Ksenofontov V. et al. Phase separation in superconducting and antiferromagnetic K0.8Fe1.6Se2 probed by mössbauer spectroscopy. Phys. Rev. B 84, 180508+ (2011). [Google Scholar]
  4. Zeljkovic I. et al. Imaging the impact of single oxygen atoms on superconducting Bi2+ySr2–yCaCu2O8+x. Science 337, 320–323 (2012). [DOI] [PubMed] [Google Scholar]
  5. Fratini M. et al. Scale-free structural organization of oxygen interstitials in La2CuO4+y. Nature 466, 841–844 (2010). [DOI] [PubMed] [Google Scholar]
  6. Poccia N. et al. Optimum inhomogeneity of local lattice distortions in La2CuO4+y. Proc. Natl. Acad. Sci. U.S.A. 109 (39), 15685–15690 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Poccia N. et al. Evolution and control of oxygen order in a cuprate superconductor. Nat. Mater. 10, 733–736 (2011). [DOI] [PubMed] [Google Scholar]
  8. Poccia N. et al. Spatial inhomogeneity and planar symmetry breaking of the lattice incommensurate supermodulation in the high-temperature superconductor Bi2Sr2CaCu2O8+y. Phys. Rev. B 84, 100504+ (2011). [Google Scholar]
  9. Ricci A. et al. Nanoscale phase separation in the iron chalcogenide superconductor K0.8Fe1.6Se2 as seen via scanning nanofocused x-ray diffraction. Phys. Rev. B 84, 060511+ (2011). [Google Scholar]
  10. Poccia N., Bianconi A., Campi G., Fratini M. & Ricci A. Size evolution of the oxygen interstitial nanowires in La2CuO4+y by thermal treatments and x-ray continuous illumination. Supercond. Sci. Tech. 25, 124004+ (2012). [Google Scholar]
  11. Bryant B., Renner C., Tokunaga Y., Tokura Y. & Aeppli G. Imaging oxygen defects and their motion at a manganite surface. Nat. Comm. 2, 212 (2011). [DOI] [PubMed] [Google Scholar]
  12. Zaanen J. High-temperature superconductivity: The benefit of fractal dirt. Nature 466, 825–827 (2010). [DOI] [PubMed] [Google Scholar]
  13. Bishop A. R. HTC oxides: a collusion of spin, charge and lattice. J. Phys: Conf. Ser. 108, 012027+ (2008). [Google Scholar]
  14. Dagotto E. Complexity in strongly correlated electronic systems. Science 309, 257–262 (2005). [DOI] [PubMed] [Google Scholar]
  15. Bianconi G. Superconductor-insulator transition on annealed complex networks. Phys. Rev. E 85, 061113 (2012). [DOI] [PubMed] [Google Scholar]
  16. Gor'kov L. P. & Teitel'baum G. B. Spatial inhomogeneities in iron pnictide superconductors: The formation of charge stripes. Phys. Rev. B 82, 020510+ (2010). [Google Scholar]
  17. Kugel K. I., Rakhmanov A. L., Sboychakov A. O., Poccia N. & Bianconi A. Model for phase separation controlled by doping and the internal chemical pressure in different cuprate superconductors. Phys. Rev. B 78, 165124+ (2008). [Google Scholar]
  18. Innocenti D. et al. A model for Liquid-Striped liquid phase separation in liquids of anisotropic polarons. J. Supercond. Nov. Magn. 22, 529–533 (2009). [Google Scholar]
  19. Kresin V., Ovchinnikov Y. & Wolf S. Inhomogeneous superconductivity and the ” pseudogap” state of novel superconductors. Phys. Rep. 431, 231–259 (2006). [Google Scholar]
  20. Bianconi G. Superconductor-insulator transition in a network of 2d percolation clusters. Europhys. Lett. 101, 26003 (2013). [Google Scholar]
  21. de Mello E. V. L. Description and connection between the oxygen order evolution and the superconducting transition in La2CuO4+y Europhys. Lett. 98, 57008 (2012). [Google Scholar]
  22. Bianconi A., Valletta A., Perali A. & Saini N. L. Superconductivity of a striped phase at the atomic limit. Phys. C: Supercond. 296, 269–280 (1998). [Google Scholar]
  23. Perali A., Bianconi A., Lanzara A. & Saini N. L. The gap amplification at a shape resonance in a superlattice of quantum stripes: A mechanism for high Tc. Solid State Comm. 100, 181–186 (1996). [Google Scholar]
  24. Jarlborg T. & Bianconi A. Fermi surface reconstruction of superoxygenated La2CuO4 superconductors with ordered oxygen interstitials. Phys. Rev. B 87, 054514 (2013). [Google Scholar]
  25. Jorgensen J. D. Defects and Superconductivity in the Copper Oxides. Physics Today 44, 34 (1994). [Google Scholar]
  26. Zimmermann V. et al. Oxygen-ordering superstructures in underdoped YBa2Cu3O6+x studied by hard x-ray diffraction. Phys. Rev. B 68, 104515 (2003). [Google Scholar]
  27. Liang R. et al. Preparation and characterization of homogeneous YBCO single crystals with doping level near the SC-AFM boundary. Phys. C: Supercond. 383, 1–7 (2002). [Google Scholar]
  28. de Fontaine D., Ozolins V., Islam Z. & Moss S. C. Origin of modulated structures in YBa2Cu3O6.63 A first-principles approach. Phys. Rev. B 71, 212504 (2005). [Google Scholar]
  29. Campi G. et al. Scanning micro-x-ray diffraction unveils the distribution of oxygen chain nanoscale puddles in YBa2Cu3O6.33. Physical Review B 87, 014517 (2013). [Google Scholar]
  30. Liang R., Bonn D. A. & Hardy W. N. Growth of YBCO single crystals by the self-flux technique. Philosophical Magazine 92, 2563–2581 (2012). [Google Scholar]
  31. LeBoeuf D. et al. Lifshitz critical point in the cuprate superconductor Y123 from high-field hall effect measurements. Phys. Rev. B 83, 054506 (2011). [Google Scholar]
  32. Chang J. et al. Nernst and seebeck coefficients of the cuprate superconductor YBa2Cu3O6.67: a study of fermi surface reconstruction. Phys. Rev. Lett. 104, 057005 (2010). [DOI] [PubMed] [Google Scholar]
  33. Baek S. H. et al. Evidence of a critical hole concentration in underdoped YBa2Cu3OY single crystals revealed by 63Cu NMR. Phys. Rev. B 86, 220504 (2012). [Google Scholar]
  34. Sonier J. E. et al. Detection of the unusual magnetic orders in the pseudogap region of a high-temperature superconducting YBa2Cu3O6.6 crystal by muon-spin relaxation. Phys. Rev. Lett. 103, 167002+ (2009). [DOI] [PubMed] [Google Scholar]
  35. Daou R. et al. Broken rotational symmetry in the pseudogap phase of a high-Tc superconductor. Nature 463, 519–522 (2010). [DOI] [PubMed] [Google Scholar]
  36. Bianconi A., Saini N. L., Agrestini S., Di Castro D. & Bianconi G. The strain quantum critical point for superstripes in the phase diagram of all cuprate perovskites. Int. J. Mod. Phys. B 14, 3342–3355 (2000). [Google Scholar]
  37. Poccia N., Ricci A. & Bianconi A. Misfit strain in superlattices controlling the Electron-Lattice interaction via microstrain in active layers. Adv. Cond. Matt. Phys. 2010, 261849-1-261849-7 (2010). [Google Scholar]
  38. Ricci A., Poccia N., Ciasca G., Fratini M. & Bianconi A. The Microstrain-Doping phase diagram of the iron pnictides: Heterostructures at atomic limit. J. Supercond. Nov. Magn. 22, 589–593 (2009). [Google Scholar]
  39. Bianconi A. Superstripes. Int. J. Mod. Phys. B 14, 3289–3297 (2000). [Google Scholar]
  40. Innocenti D. et al. Resonant and crossover phenomena in a multiband superconductor: Tuning the chemical potential near a band edge. Phys. Rev. B 82, 184528+ (2010). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Multiscale distribution of oxygen puddles in 1/8 doped YBa2Cu3O6.67

srep02383-s1.doc (193.5KB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES