Evaluating the Diffusion Coefficient of Dopamine at the Cell Surface During Amperometric Detection: Disk vs. Ring Microelectrodes

Abstract

During exocytosis, small quantities of neurotransmitters are released by the cell. These neurotransmitters can be detected quantitatively using electrochemical methods, principally with disk carbon fiber microelectrode amperometry. An exocytotic event then results in the recording of a current peak whose characteristic features are directly related to the mechanisms of exocytosis. We have compared two exocytotic peak populations obtained from PC12 cells with a disk carbon fiber microelectrode and with a pyrolyzed carbon ring microelectrode array, with a 500 nm ring thickness. The specific shape of the ring electrode allows for precise analysis of diffusion processes at the vicinity of the cell membrane. Peaks obtained with a ring microelectrode array show a distorted average shape, owing to increased diffusion pathways. This result has been used to evaluate the diffusion coefficient of dopamine at the surface of a cell, which is up to an order of magnitude smaller than that measured in free buffer. The lower rate of diffusion is discussed as resulting from interactions with the glycocalyx.

Exocytosis, the fundamental process of inter-neuronal communication, is based on the vesicular release of neurotransmitters, such as dopamine. During this event, nanometer sized vesicles, stored in the presynaptic neuron and packed with neurotransmitters, fuse with the cell membrane, thus allowing their content to diffuse through the synaptic cleft.¹ These released neurotransmitters eventually reach some postsynaptic receptors and activate the postsynaptic neuron. Adrenal cells, such as chromaffin cells or PC12 cells (from rat pheochromocytomas of the adrenal medulla) are relatively easy to use and often preferred as a model for exocytosis.^2,3

Owing to the limited magnitude of these exocytotic events (about 100,000 molecules released over few milliseconds)⁴ and the small typical size of this system (a PC12 vesicle is about 150 nm in diameter), studying exocytotic release is problematic. Electrochemical methods offer the opportunity of performing quantitative analyses of exocytotic events by placing a carbon disk microelectrode at the surface of the cell, thus creating an artificial synapse, and performing continuous oxidation (some neurotransmitters, such as dopamine in the case of K⁺ stimulated PC12,^5,6 are easily oxidized at a carbon surface).^7–11 Typically, a current spike is obtained as the released material is oxidized, and this peak contains quantitative as well as kinetic information about the different steps and mechanisms of the exocytotic event.¹² A wealth of studies have been focused on the effects of pharmacological or physico-chemical parameters on the characteristics of these peaks to attempt to further our knowledge about exocytosis.^13–16

In this report, amperometric traces obtained PC12 cells using ring and disk microelectrodes are compared. The specific geometry of the ring electrode is used as a complement to the traditional disk electrode to estimate the diffusion parameters controlling these diffusive events. We find that the differences in diffusion profiles at the surface of these electrodes distort the peaks simply because of longer diffusive pathways in the case of the ring geometry. The ring electrode is indeed characterized by a very long edge in relation to its surface, when compared to the disk. The contribution of this edge is expected to lead to higher diffusive pathways, and therefore to dispersed peaks. From this result, it has been possible to evaluate the diffusion coefficient of dopamine at the surface of the cell, in the glycocalyx.

Experimental Section

Electrodes

The radius of the disk microelectrodes was 2.5 µm. The inner and outer radii of a typical ring microelectrode were measured as 1.5 µm and 2.0 µm (see Supplemental Figure S1).¹⁷ Electrodes were beveled at 45°, hence, the electrode surface is actually an ellipse, and their surface area can be obtained by multiplying the surface area of the electrode, considered as a disk or a perfect ring, by √2.

Data processing

The amperometric traces were processed using Igor Pro 6.21 software (Wavemetrics, USA) originating from David Sulzer’s group.¹² The filters for the current and differentiated current traces were 2 and 1 kHz, respectively. The threshold for peak detection on the differentiated trace was four times the standard deviation of the noise. The traces were carefully inspected after peak detection and false positives were manually rejected. All the peaks larger than 2 pA (about four times the noise of the smoothed signal, between 0.5 and 0.7 pA in our experiments, based on 5- to 10-s baseline acquisitions at the beginning of the trace) were collected. All the data processing routines were performed with Igor Pro 6.21.

The exocytotic data presented in this article were obtained from a population of 5 cells (total number of events = 2209) with an 8-ring microelectrode array for the ring geometry and from 14 cells (total number of events = 962) for the disk. A higher number of cells had to be tested for the disk geometry to account for the higher number of events measured, for one cell, with the ring arrays, as 8 traces are obtained simultaneously. The exocytotic parameters were pooled, and the median of the data was calculated. The distribution of the sample was evaluated using the 1^st quartile-3^rd quartile (or 25 %-75 %) interval. The distribution of the exocytotic parameters is asymmetric and strongly deviates from normality, hence motivating the use of the median in place of the mean.^12,18–20 Additionally, the use of the median was found to minimize the impact of the cell-to-cell variations, as the value is less sensitive to outliers. Pairs of datasets were compared with the two-tailed Wilcoxon-Mann-Whitney rank-sum test, ***: p<0.001; **: p<0.01.²¹

In the analysis of the distributions, the data is fitted with a sum of Gaussians, and the data is reported as mean ± standard deviation (SD), where applicable. The measurement errors were propagated along the successive steps of the calculations as a component of the SD.

Supporting information

Details about chemicals and solutions, fabrication of the disk and ring microelectrodes, cell culture, single cell experiment procedures and transmission electron microscopy (TEM) of PC12 cells are presented as Supporting Information.

Results and Discussion

The exocytotic peaks measured with carbon ring microelectrodes are broader and provide new information

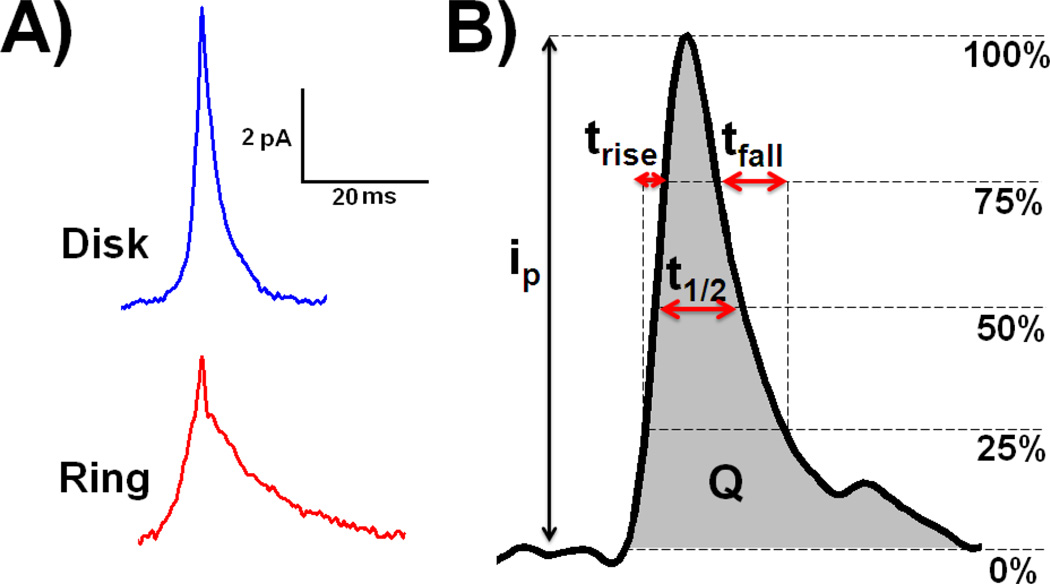
Amperometric traces obtained at ring and disk microelectrodes both show exocytotic spikes. However, when comparing the average spikes obtained for the ring and disk microelectrodes (Figure 1A), it appears that the spikes measured with the ring geometry are much broader in shape. Several parameters were obtained from the analysis of these peaks, compared for the disk and ring geometries and are presented in Table 1. The rise time, t_rise (the time separating 25 % of the maximum from 75 % of the maximum on the ascending part of the spike), the half peak width, t_1/2 (the width of the exocytotic event at half of its magnitude), the fall time, t_fall (the time separating 75 % of the maximum from 25 % of the maximum on the descending part of the spike), and the number of molecules released, Q (obtained by integrating the area under the peak and dividing the result by n × e where n is the number of electrons exchanged by a single molecule, and e is the elemental charge 1.6 10⁻¹⁹ C) as shown on Figure 1B. All these parameters are significantly different comparing the disk and ring geometries apart from the peak current, i_p.

Figure 1.

A) Average exocytotic spikes obtained at disk (blue line) and ring (red line) microelectrodes from a single typical amperometric trace; B) definition of the peak characteristics i_p, t_rise, t_1/2, t_fall and Q. The number of molecules released Q is represented by the gray area under the curve.

Table 1.

Experimental results for t_rise t_1/2, t_fall, i_p and Q, for ring and disk geometries.^a

Geometry	trise/ ms	t1/2/ ms	tfall/ ms	ip/ pA	Q/ 103 molecules
Disk (14 cell, 962 peaks)	1.0 (0.5–2.4)	3.5 (2.4–4.9)	3.1 (2.1–4.8)	4.3 (3.1–7.2)	83 (54–132)
Ring (5 cells, 2209 peaks)	1.1 (0.7–3.4)	5.0 (3.3–6.8)	4.7 (3.2–.4)	4.2 (3.2–6.1)	108 (75–162)
Variations	+10%**	+43%***	+52%***	−2%	+30%***

^athe data are presented as median (1^st quartile-3^rd quartile). The pairs of datasets were compared using a two-tailed Wilcoxon-Mann-Whitney rank-sum test

^***p < 0.001;

^**p < 0.01. The variations of the median between the two geometries are also reported.

These discrepancies are understood as owing to the different electrode geometries. As reducing the diameter of the electrode has been reported to result in no significant effect on t_1/2,²² this indicates the role of the characteristic shape of the ring, where the contribution of the edge is larger when compared to a disk electrode.

Relationships between Q, t_1/2 and t_fall

The number of molecules released, Q, is related to the fraction of the vesicular neurotransmitter content released during the exocytosis event.⁴ The value of t_1/2 is a marker of diffusion, as it relates to the movement of the exocytotic bolus across the artificial synapse.¹⁸ Finally, the fall time, t_fall, is characteristic of the vesicular efflux of dopamine at the end of the event. Whether this value is indicative of the closing of the fusion pore^4,23 or of the depletion of the vesicular store²⁴ is still under discussion, but it is nevertheless strongly controlled by diffusion. During in vivo experiments, the decaying section of the event is usually associated with the reuptake of the neurotransmitters by the dopamine transporter (DAT).^25,26 Reuptake has been observed in PC12 cells, but this phenomenon is limited compared to the rate of release. Assuming Michaelis-Menten kinetics, a V_max of 3.2 pmol min⁻¹ for 2 10⁵ cells has been measured.²⁷ If the DAT is functioning in saturated mode, about 1,600 molecules will be absorbed during a 10 ms event by a cell. However, this value assumes that the reuptake occurs over the total cell surface. In the case of exocytosis, a high concentration of dopamine compatible with a high uptake rate is located only at the vicinity of the release site. The concentration of the exocytotic bolus quickly decays after release because of diffusion, probably over 1 µm (vide infra), as indicated by electrochemical imaging with an electrode array.¹⁷ Assuming that the PC12 has a radius of 10 µm and a height of 2 µm,²⁸ and that only a disk of radius 2 µm centered of the release site is exposed to dopamine during a single exocytotic event, only 3.6% of the cell surface contributes to the reuptake. Hence, about 60 molecules should be reabsorbed by the cell during the event, and 100,000 molecules are usually detected at the electrode. The contribution of the DAT is therefore not taken into account in our analysis, and t_fall is considered to be principally diffusion controlled.

The population correlation coefficient ρ_{A, B} between 2 variables A and B describes how the relative variations of these variables are correlated. The output is a number between −1 and 1, with −1 and 1 respectively indicating negative and positive perfect correlations, and 0 a complete absence of correlation between the variables. This value is calculated using the formula ρ_A,B = cov(A, B)/(σ_Aσ_B) where cov is the covariance, and σ is the standard deviation. The population correlation coefficients between i_p, t_rise, t_1/2, t_fall and Q were calculated and are shown on Table 2. For both the disk and the ring, the highest correlation is found between t_1/2 and t_fall. This is consistent with exocytotic peaks being partially controlled by diffusion between the cell and the electrode, as these times are characteristic of diffusion, and they therefore change in the same manner.

Table 2.

Population correlation coefficients between t_1/2, t_rise, t_fall, i_p and Q, for ring and disk geometries.

Geometry	t1/2 vs. trise	t1/2 vs. tfall	t1/2 vs. ip	t1/2 vs Q	trise vs. tfall	trise vs. ip	trise vs. Q	tfall vs. ip	tfall vs. Q
Disk	0.24	0.58	−0.07	0.52	0.14	−0.14	0.10	−0.13	0.44
Ring	0.26	0.58	0.08	0.41	0.15	−0.12	0.07	−0.01	0.32

The value of Q shows a high coefficient of correlation with t_1/2 and t_fall. It has been reported that exocytotic events occurring up to 1–2 µm beyond the edge of the electrode can be detected.²⁹ The molecules released during these events then must diffuse over a further distance to reach the carbon surface of the electrode. In the case of large released amounts, this additional diffusion pathway induces diffusional broadening of the peak, and in this case, the released charge is therefore correlated to t_1/2 and t_fall, which are also controlled by diffusion. This diffusional broadening also induces the rejection of smaller spikes, as only large events can induce a recorded current high enough to overcome the detection threshold. Therefore, the peak recording at the edge of the carbon surface will induce a positive bias towards taller, larger peaks. The fact that a higher Q is recorded for the ring geometry is in good agreement with this phenomenon, as the contribution of the edge of the electrode is comparatively more important in the case of this geometry. A decrease in i_p would have been expected in this case. However, the limit of detection is unchanged between the two experimental setups and this value (2 pA) is close to the median reported for i_p. This is expected to limit the effect of a decrease in i_p on the measured median. Additionnaly, a greater prevalence of taller peaks could be observed for the disk geometry, as indicated by the higher 3^rd quartile reported for i_p. This is also revealed by the higher current of the average peak obtained for the disk on Figure 1A. This is therefore still in good agreement with a diffusional hindrance due to the shape of the ring electrode.

There are two peak populations, and using a ring instead of a disk changes their relative importance

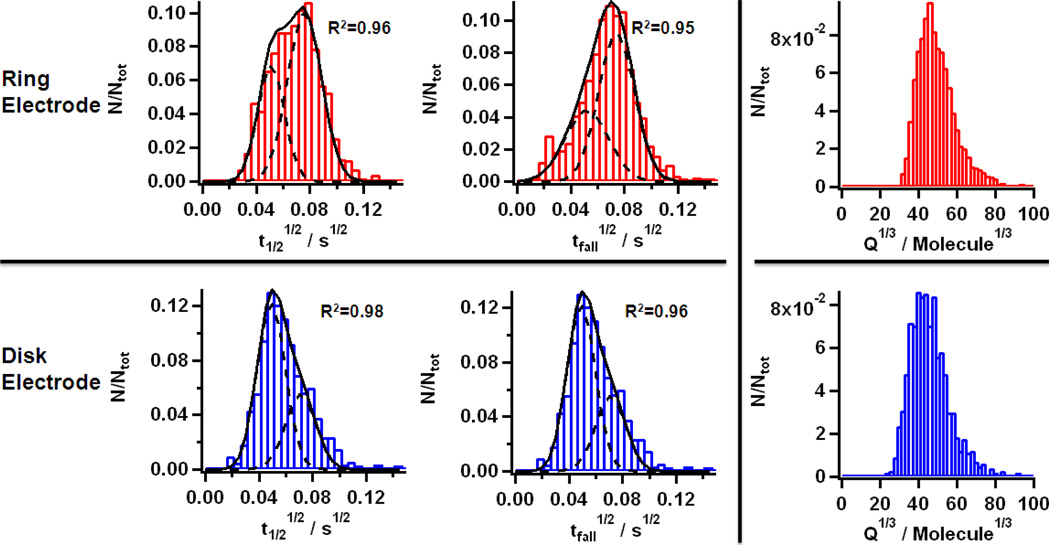
To investigate the effect of diffusion and the possible variations in repartition of the peak characteristic values for different electrode geometries, t_1/2, t_fall and Q were analyzed by plotting histograms, where the cube root of the charge was plotted to obtain a quasi-normal distribution (Figure 2).⁴ The distributions of the data obtained with the ring and the disk geometries are largely similar for Q. For t_1/2 and t_fall, the distributions obtained with the ring microelectrode array are skewed towards higher values. These time variations are assumed to be mostly diffusion dependent and therefore to be determined by the relative positions of the different elements of the system (i.e. the electrode and the vesicle).

Figure 2.

Histograms (30 bins, width: 0.005 s^1/2) for the half peak width (t_1/2)^1/2 (left) and the 75%–25% decrease time (t_fall)^1/2 (center) obtained for the ring (upper row) and disk (bottom row) geometries. The R² values obtained for the Gaussian fitting are shown on each panel. The histograms for Q^1/3 (50 bins, width: 20 molecules^1/3) obtained for the ring (upper row) and disk (bottom row) geometries are also shown on the right side of the figure.

Owing to the cylindrical geometry of the problem, this position can be reduced to the distance from the center of the pore to the center of the electrode. Vesicle exocytosis is equivalent to a random set of points on a 2D plane, and points leading to similar responses are localized on circles centered over the center of the electrode. Consequently, as the distance is linearly related to the square root of the time required to diffuse over this distance, the square roots of t_1/2 and t_fall were used to relate these characteristic times to the geometry of the system.

The histograms were fitted with double Gaussians. For each parameter, and the data obtained for ring and disk microelectrodes, the Gaussians are located at similar positions (Table 3), but their relative heights vary. This was interpreted as evidence for the larger contribution from diffusion at the edge for the ring compared to the disk, inducing a higher probability to obtain diffusion distorted peaks, as indicated on Figure 3. Two distinct populations are observed: ‘fast’ peaks (low t_1/2 and low t_fall) and ‘slow’ peaks (large t_1/2 and large t_fall).

Table 3.

Characteristic values for the Gaussian fitting.^a

Parameter	Type of electrode	Center of the fast Gaussian/ ms	Center of the slow Gaussian/ ms	Ratio areaslow/areafast	w/ nm	D/ cm2s−1
t1/2	Ring	2.6	5.8	1.86	655 ± 179	6.3 ± 0.7×10−7
	Disk	2.7	5.2	0.46	614	8.3 ×10−7
t fall	Ring	2.7	5.5	1.72	607 ± 166	6.6 ± 0.7×10−7
	Disk	2.4	5.0	0.48	646	7.8 ×10−7

^aThe central values associated to the different Gaussians shown on Figure 2, defined as fast (low t_1/2, low t_fall) and slow (high t_1/2, high t_fall) Gaussians, and the ratios of their areas, assumed to be equal to area_crown/ area_{projection of the electrode}, are presented. For the sake of clarity, the centers of the Gaussians were expressed in ms, not in ms^1/2, even though the fitting was performed on the distributions of the square roots of t_1/2 and t_fall. Finally, the crown thickness w and the diffusion coefficient D, calculated for each case, are reported. In the case of the ring geometry, w is reported with the standard deviation accounting for the variability in the thickness of the pyrolyzed carbon surface.¹⁷

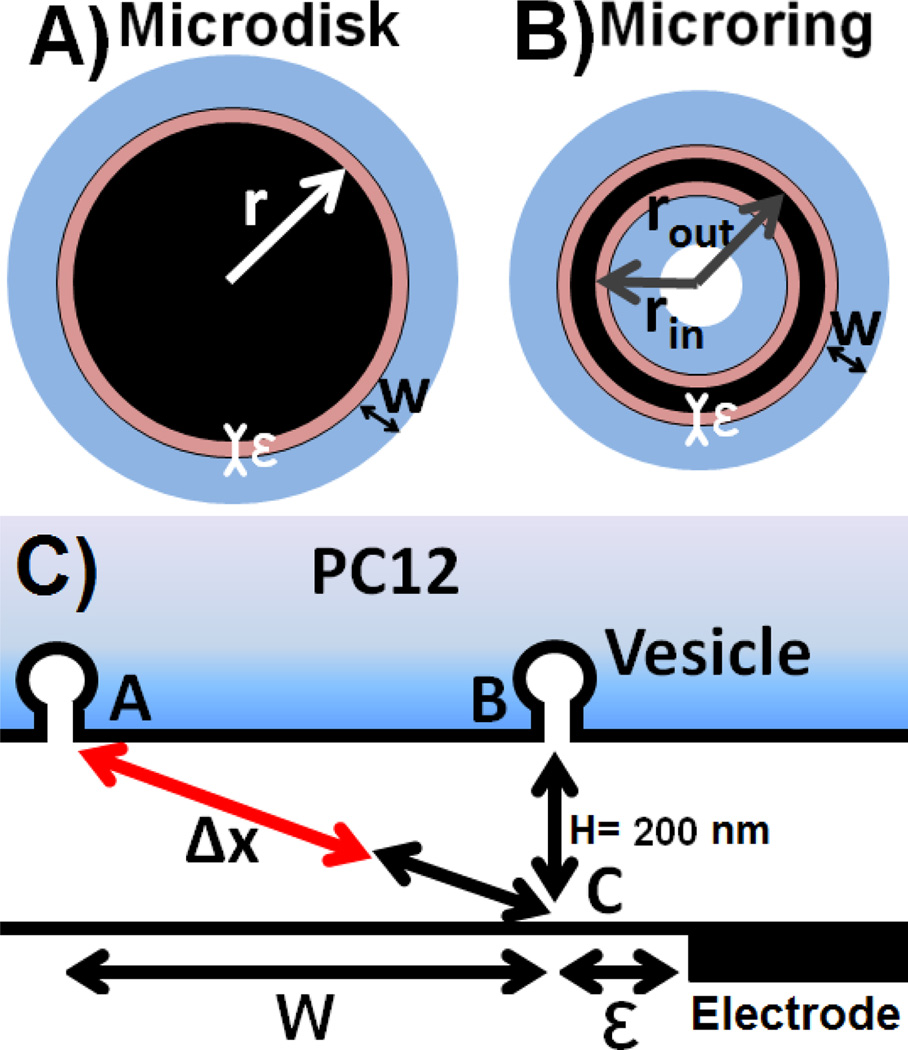
Figure 3.

Geometry of the system. Definition of the different parameters for A) a disk and B) a ring: r is the disk radius, r_out and r_in are respectively the outer and inner radii of the ring electrode. An additional distance, ε, at the edge of the carbon surface, is contributing to the formation of fast spikes and is drawn in red. The crown, i.e. the area generating diffusion distorted peaks, characterized by its thickness w, is shown in light blue (note that for the sake of clarity, the electrodes are here assumed to be circular, but they are actually elliptical because of the 45° beveling); C) scheme showing two vesicles fusing at the two limit locations of the cell surface described in the text (vesicles A and B produce slow and fast peaks, respectively) and the additional diffusion pathway Δx inducing the diffusional broadening at the edge of the electrode.

As the relative distribution between slow and fast peaks appears to be dependent on the geometry of the electrode, it was assumed that the slow peaks were generated by exocytosis occurring outside the projection of the carbon surface on the cell membrane (Figure 3), therefore leading to longer diffusion pathways and peak distortion. The portion of the system leading to these peaks is then referred to here as the crown.

Increased diffusion pathways can explain these variations in peak characteristics

By assuming that there are 2 discrete regions, and that the projection of the electrode surface on the cell surface is the area generating fast peaks, it is possible to arrive at an approximation of the width of the crown associated to the slow peaks (Figure 3). We can assume that the increased diffusion pathway is the only factor resulting in the two populations for t_1/2 and t_fall, all the other factors being the same, as only the electrode geometry is changed.

Finally, as shown on Figure 3C, vesicles positioned at the limit positions (i.e. edge of the section of the cell producing fast peaks, vide infra, and portion of the crown related to the maximum of the slow peak Gaussian) define a right triangle ABC, where AB = w, BC = 200 nm and AC = Δx + 200 nm with AC² = BC² + AB². The thickness H of the artificial synapse was fixed at 200 nm, as this distance is in good agreement with values previously published.^21,30,31 This point is discussed in more detail later. If the number of events recorded is sufficient to assume that the exocytotic activity is uniformly distributed over the cell surface, the time distribution of the population is controlled by the geometry of the system. If a vesicle fuses directly accross from the carbon surface, the distance to the electrode is short and the event is fast. On the contrary, if the vesicle fuses far from the carbon surface, the event will be slow. Hence, the probability of obtaining a slow peak or a fast peak is directly related to the area of the electrode and to the area of the crown (in blue on Figure 3). The histograms presented in Figure 2 are the probability density functions of events occurring at random points at the surface of the plane, thus modifying their distance to the electrode and the characteristic times of the exocytotic peak. Using these assumptions, and by calculating the area of each (i.e. slow or fast) Gaussian and considering α, the ratio area_{slow Gaussian}/area_{fast Gaussian}, it is possible to calculate the thickness w of the crown using the geometry of the system, as α is equal to area_crown/area_{projection of the electrode}. A correction factor, ε, was added in the model, to take into account the fact that a vesicle fusing not exactly over the carbon electrode, but at a very short distance of its edge, might still be considered as producing a fast peak. Hence, because of the very short additional diffusion distance observed for spikes arising from vesicles fusing slightly away from the edge of the projection of the carbon surface, the radius of the section of the cell surface associated to fast peak kinetics was the electrode radius extended by a short distance, ε, as detailed on Figure 3.

The calculations are detailed in the Supporting Information. In the case of the disk microelectrode,

$$w=\frac{\sqrt{\Delta }-\left(\right(1+\sqrt{2})r+2\epsilon )}{2}$$ (1)

with

$$\Delta ={\left(\right(1+\sqrt{2})r+2\epsilon )}^2+4\alpha (r+\epsilon )(\sqrt{2}r+\epsilon )$$ (2)

and in the case of the ring microelectrode,

$$w=\sqrt{2}\alpha \frac{t_c+2\epsilon }{1+\sqrt{2}}$$ (3)

where t_c = r_out − r_in is the thickness of the deposited pyrolytic carbon ring. This value was measured as 520 ± 84 nm.¹⁷ Interestingly, in the case of the ring, w is independent of the radius of the ring, but depends only on the thickness of the carbon layer. The width of the crown, w, was calculated for each of the four cases (i.e. for t_1/2 and t_fall measured at ring and disk microelectrodes), for values of e varying from 0 nm to 300 nm, and the standard deviation for the four calculated w was obtained. As w should not depend on the geometry of the sensor, i.e. the ring or the disk, but only on the diffusion properties of the system, the e minimizing the standard deviation (110 nm) was chosen. The 4 different w were then calculated for this evaluation of e and reported on Table 3. This value, defining the sensing region of the electrode, was found to be in the 600 nm −700 nm range. From the SEM images presented as Supporting Information, the distance between the carbon edges in the array is usually above 2 µm. So, even though there is strong electrochemical crosstalk between the electrodes in homogeneous solution,¹⁷ in the case of the limited release observed during exocytosis this phenomenon is limited.

Evaluation of the diffusion coefficient of dopamine at the surface of a single cell

The histogram analysis and the w calculation relate a time delay to a distance. Therefore, by considering the extreme cases, as shown on Figure 3C, the diffusion length is related to the diffusion time through the equation (in three dimensions):²⁹

$${\sigma }_x=\sqrt{6Dt}$$ (4)

where σ_x is the standard deviation of the diffusing population, D is the diffusion coefficient, and t is the time elapsed since the bolus was allowed to start diffusing. If x₀ is the pathway leading to a fast peak and x the one leading to a slow peak, and t₀ and t are the characteristic times (t_1/2 or t_fall) for the fast and slow peaks, the following equation is obtained:

$$\Delta x=x-x_0=\sqrt{6Dt}-{\sqrt{6Dt}}_0=\sqrt{6D}(\sqrt{t}-\sqrt{t_0})$$ (5)

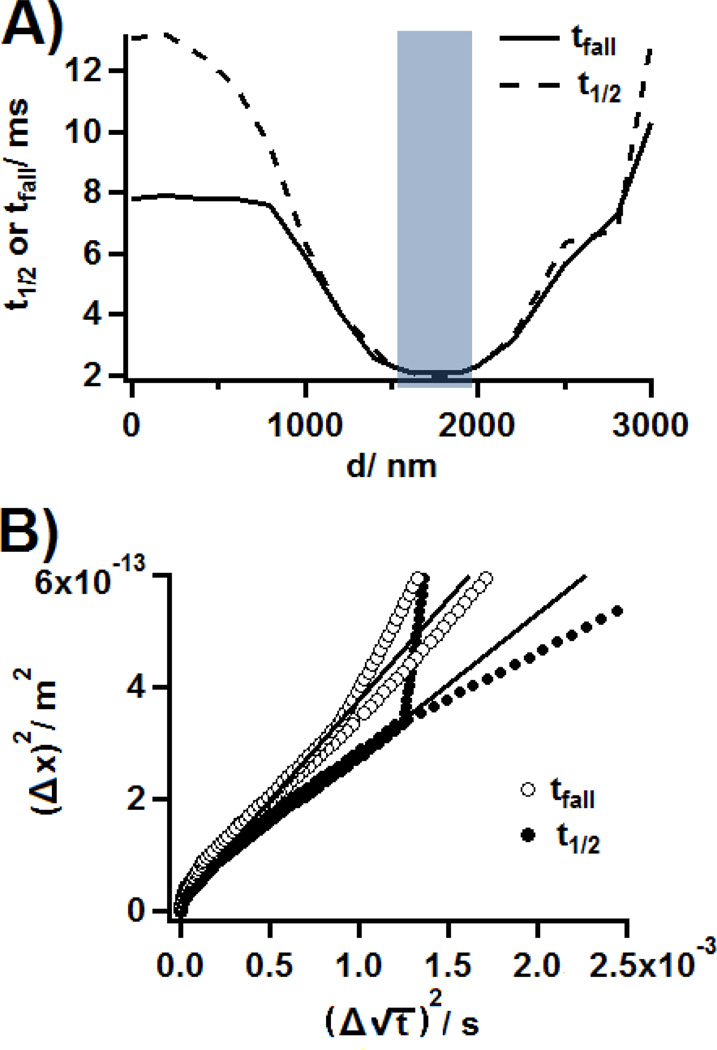
The validity of this equation was assessed with finite element simulations. A model of an artificial synapse was established (see Supporting Information), for a ring electrode, and a low diffusion coefficient (6 10⁻⁷ cm²s⁻¹) was used, as suggested by previous work reporting a lower diffusion coefficient for neurotransmitters at the cell surface.³² Simulated exocytotic peaks were obtained for increasing distances d between the center of the electrode and the fusion pore. Figure 4A shows the relationship between d and t_1/2 or t_fall. From this set of simulations, the square of the difference in diffusion pathway (Δx)² could be calculated and compared to ${(\Delta \sqrt{t})}^2={(\sqrt{t}-\sqrt{t_0})}^2$ as shown on Figure 4B (the initial values x₀ and t₀ were the values obtained at the center of the carbon ring (d = 1750 nm)). A clear linear relationship appears for the values obtained for vesicles located at up to 700 nm away from the electrode (i.e. still located in the crown). From Equation 5, D could be calculated from the slope of this line and was found to be 6.3 10⁻⁷ cm²s⁻¹ (t_fall) and 4.5 10⁻⁷ cm²s⁻¹ (t_1/2), in very good agreement with the input value used for the simulations. This model therefore supports the use of Equation 5 as a method to calculate D from t_1/2 or t_fall.

Figure 4.

Simulation of the kinetics of exocytosis for different vesicle to center of the electrode distances, d, in the case of a ring electrode (I.D.: 1.5 µm, O.D.: 2.0 µm). A) Characteristic times t_1/2 or t_fall computed for different values of d (0, 200, 400, 600, 800, 1000, 1200, 1400, 1600, 1700, 1800, 1900, 2000, 2200, 2500, 2800, and 3000 nm). The light blue section indicates the position of the carbon ring. B) Plots of (Δx)² as a function of ${(\Delta \sqrt{t})}^2={(\sqrt{t}-\sqrt{t_0})}^2$, where t can be t_1/2 or t_fall (see text). The thin lines show the linear regressions for values of t_1/2 or t_fall associated to vesicles located into the crown.

Using the width w of the halo obtained from each case, Δx, as defined from Figure 3, was calculated. This system can be used to approximate the diffusion coefficient of dopamine at the surface of a cell. The diffusion coefficient was calculated for different values of w obtained previously using a synaptic width H of 200 nm as shown in Table 3. The mean ± SD of these four values is 7.3 ± 1.1 10⁻⁷ cm²s⁻¹. This value is smaller than the diffusion coefficient of dopamine in water, 6.0 10⁻⁶ cm²s⁻¹,³³ usually used to model these events and indicates diffusional hindrance. Interestingly, as previously mentioned, Lindau and coworkers have reported that the diffusion coefficient of dopamine at the surface of an adrenal cell is one-tenth that in water. This was based on microelectrode array experiments, and their lower value is in good agreement with the result we present here.³²

Diffusion in tissue^43,44 or in solutions containing biological macromolecules⁴⁵ is known to be hindered by tortuosity and charge interactions. The Mackie-Meares model⁴⁶ can be used to evaluate the diffusion hindrance in a partially blocked solution, like a polymer or cartilage.^{47Equation 6} describes the variations in diffusion coefficients in partially blocked solutions:

$$\frac{D}{D_0}={\left(\frac{1-\varphi }{1+\varphi }\right)}^2$$ (6)

where D is the apparent diffusion coefficient, D₀ is the diffusion coefficient in the buffer (here 6.0 10⁻⁶ cm²s⁻¹) in the free buffer and ϕ is the excluded volume fraction. Assuming an 88 % decrease in diffusion coefficient, a matrix occupancy of ≈48% is found. This model, however, does not account for the possible electrostatic interactions, but nevertheless indicates the presence of a densely packed matrix between the cell and the electrode.

This decrease in apparent diffusion coefficient is probably due to the presence of glycocalyx and extracellular matrix around the cell.⁴⁸ Indeed, every cell is surrounded by the glycocalyx, a matrix mostly composed of proteins and polysaccharides.^40,49 This layer plays a crucial role in cell adhesion, cell physiology and immune recognition.^49–53 As this matrix actually acts as a glue holding the cells together, it has been shown to possess a significant mechanical strength, and is therefore densely packed (above 30,000 molecules per µm²).^40,54 Furthermore, the presence of numerous charged polymers is expected to slow down the diffusion of charged molecules.⁴⁸

The value calculated for the diffusion coefficient was found to be dependent of H, the width of the artificial synapse, as this increase in pathway length can induce peak broadening.⁵⁵ To facilitate the previous calculations, H was assumed to be equal to 200 nm, as suggested in the literature, but 300 nm has also been reported for real²¹ or artificial³⁰ cell models. The calculations for D were carried out for H values up to 1 µm (see Figure S3 in the Supporting Information). For H = 1 µm, D was found to be 60 times lower than in free buffer. This value is much lower than expected for a diffusion hindrance due to a charged polymer, hence indicating that H is actually much lower than 1 µm.

Practically, the distance between the electrode and the cell is expected to be highly dependent on the experimental setup (accuracy of the electrode positioning, roughness of the electrode surface, quality of the electrode polishing …) and on the thickness of the glycocalyx. Measuring the thickness of this layer is challenging as it is below the limit of axial resolution of most optical methods, such as confocal scanning microscopy (typically 0.5 µm).^56,57 The axial resolution is indeed limited by the axial dimension of the point spread function, which is convoluted to the geometry of the sample to obtain the fluorescent image. ^58–60 However, using other methods, such as near-field microscopy, a cell-substrate distance in the 10 – 160 nm range has been reported.^35–42 These measurements take into account the geometry of the cell membrane as well as the thickness of the glycocalyx. This distance is however expected to be at least 60 % higher in the case of apical recording of exocytosis, as i_p is found to be higher when exocytosis is analyzed from the bottom of the cell, in comparison to the traditional single cell amperometry.⁶¹

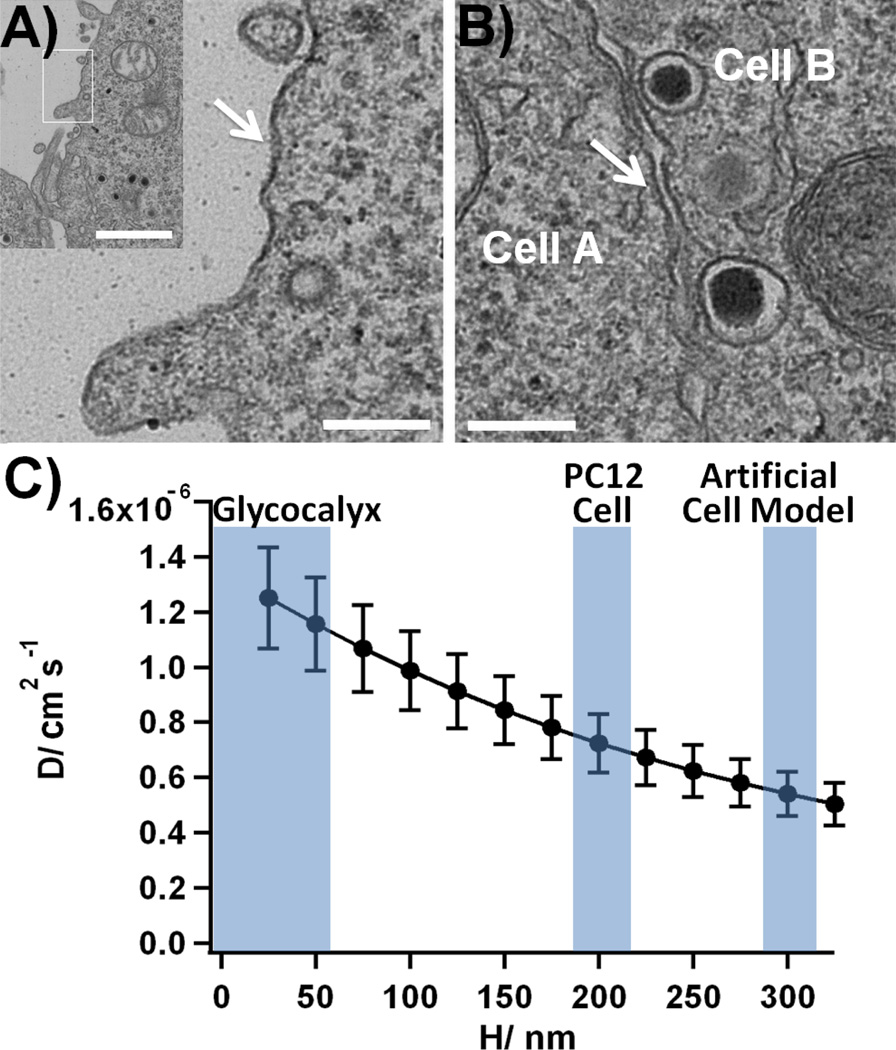
Figure 5A shows a typical TEM image of a PC12 cell. The surface of the cell is covered by a very thin (17 ± 5 nm, mean ± SD from 5 random measurements at different sites of the image) fuzzy, dark layer. This image is very similar to TEM images of monocyte glycocalyx published by others.³⁴ Furthermore, as presented on Figure 5B, some images showed that individual PC12 cells are separated by a very thin (24 ± 9 nm, mean ± SD from 5 random measurements at different sites of the image) gap. Despite the denaturation of the glycocalyx during the sample preparation leading to structural alterations,⁶² our micrographs nevertheless emphasize the small thickness of the glycocalyx.

Figure 5.

TEM imaging of PC12 cells. A) The imaging of the membrane of a single PC12 cell shows the presence of a stained fuzzy layer (thickness: 17 ± 5 nm, mean ± SD from 5 random measurements at different sites of the image), in good agreement with TEM imaging of glycocalyx layer in monocytic cells³⁴ (the white bar indicates 200 nm and 1 µm on the insert); B) TEM images showing the gap separating two PC12 cells, the thickness of the gap was measured as 24 ± 9 nm (mean ± SD from 5 random measurements at different sites of the image, the white bar indicates 200 nm). C) Variations of the calculated diffusion coefficient of dopamine at the surface of a PC12 cell D as a function of H, the width of the artificial synapse (average over the 4 values obtained for the ring and the disk electrodes, for t_1/2 and t_fall, ± SD). The blue areas indicate the reported thickness ranges for the extracellular matrix,^35–42 the artificial synapses at a PC12 cell³¹ and at an artificial cell model.³⁰ See Figure S3 in the Supporting Information for a plot of D for H values varying from 25 nm to 1 µm.

From these indications, we can therefore assume that the thickness of the extracellular matrix is between few tens to few hundreds of nanometers, which is in the range of the synaptic width (200 nm) used in the exocytotic model. From this result and the indications obtained from the literature (vide supra), the variations of D were computed for values of H varying from 25 nm to 325 nm, as presented on Figure 5C. This distance accounts for the glycocalyx thickness and the experimental setup (electrode roughness, accuracy of the positioning …).

Conclusions

Using two different shapes of electrodes, it was possible to show that recordings of exocytotic peaks can be distorted by diffusion because of longer diffusive pathways at the edge of the system. This phenomenon was used to evaluate the diffusion coefficient of dopamine in the extracellular matrix surrounding the cell. Our results suggest that the diffusion coefficient of dopamine is 6 to 10 times lower at the vicinity of the cell surface than in free solution. We suggest that a good approximation of the diffusion coefficient of dopamine at the cell surface is the mean +/− SD of the values calculated over this range, i.e. 8.2 ± 1.3 10⁻⁷ cm²s⁻¹. This average value still indicates that the diffusion coefficient of dopamine is decreased by almost an order of magnitude at the vicinity of the cell membrane. Some of the results for exocytotic events recording with varying physico-chemical conditions may also be reconsidered as the extracellular matrix plays a critical role in the kinetics of exocytosis. Changes in osmolarity, pH or temperature might indeed affect the cross-linking of that matrix and consequently change the diffusion characteristics of the problem.