Kinematic Analysis of Line-Out Throwing in Elite International Rugby Union

Abstract

The rugby union line-out is a key aspect of game play and involves players from both teams contesting for the ball after it has been thrown in from the side line. Successful lines-out throws require the ball to be delivered accurately to the hands of a jumping and/or lifted team mate (approximately 3-3.5 m off the ground) over distances of between 5- 18 m. Previous research has suggested considerable inter and intra-individual differences in the throwing techniques of international level players. Accordingly, this project investigated the interrelationships between accuracy and the line-out throwing characteristics of three elite international rugby players, and then analyzed whether these changed for throws over increasing length. Three-dimensional (3D) data were developed from video footage (50 Hz) of three elite international subjects for 30 throws over three distances (6 m, 10 m, and 15 m). Results showed notable differences between subjects in many variables at each of the key throw phases. However, several variables such as the degree of trunk flexion at the end of the backswing and at ball release, coupled with elbow flexion angle at ball release remained constant as throw length increased. All subjects exhibited high levels of consistency in movement patterns across all throw lengths. Findings indicated that these high performance line-out throwers shared several common characteristics that will provide useful guides in the development of training programs.

Key points.

• A key aspect of this research was the assessment of throwing accuracy using a functional throwing task that mimicked normal performance.

• Although individual differences in throwing technique occurred, several technical aspects of the throw were common to each of these elite international players.

• Subjects tended to be extremely consistent in the way they positioned the ball at the end of the backswing, and had very consistent elbow (flexion) and shoulder (flexion and abduction) angles at both the end of the backswing and at ball release.

• In addition, throwers kept the trunk close to upright during the throw with minimal trunk flexion or extension regardless of throw distance.

• To throw for longer distances participants tended to increase the involvement of the legs.

Introduction

In rugby union (rugby) the line-out is an aspect of play that is unique to the sport. It occurs when the ball is thrown back into the field of play after it has crossed the side-line. Although the International Rugby Board (IRB) rules of the game allow for numerous variations, a standard line-out formation involves at least two players from both teams standing in two lines perpendicular to the sideline, 2 m apart with the first player 5 m from the sideline. A single player then throws the ball down the gap between the two rows. The line-out throwing action adopted by most players is a two handed overhead delivery with the ball being spun about its longitudinal axis during flight (unlike soccer, the rules of rugby do not regulate throwing technique). A throw is deemed legal if the ball travels a minimum of 5 m and is thrown without biasing either team (IRB, 2010).

The need to throw the ball down the middle of the line-out has resulted in teams using a variety of techniques and tactics to out manoeuvre the opposition and gain possession. One of the most common methods involves one or two players (Lifters) clasping a Jumper by his thighs and hoisting him high into the air to intercept the ball. This has resulted in most line-out throws being caught approximately 3-3.5 m above the ground, although this height varies in relation to the height of the Jumper and the stature and ability of the Lifters. Throws to the front of a rugby line-out travel typically 5-7 m, while throws to the back of the line-out travel approximately 15-18 m.

In international level rugby there are approximately 34 line-outs per game, although the exact number varies considerably between matches (IRB, 2007). Despite the importance of the line-out in rugby union game play, biomechanical analyses of line-out throwing have been reported infrequently. Indeed, only recently have biomechanical analyses of line-out throwing been presented in the scientific literature (Griffiths and Hughes, 2005; Sayers, 2005; Trewartha et al., 2008). The first published project that reported the kinematics of line-out throwing involved six international level players throwing to the front, middle and back of a line-out (Sayers, 2005). In addition to identifying numerous visual differences in throwing techniques of these players, this researcher highlighted the importance of increasing the involvement of the lower limb when throwing for greater distance. However, this paper neglected to include a measure of throwing accuracy in the analysis making it difficult to draw conclusions on throwing effectiveness.

In a later study, Trewartha et al., 2008 attempted to address this issue by including a simple measure of throw accuracy to a thorough kinematic analysis of three players of varying ability (club, junior and senior international). A key finding of this research concerned the high level of consistency in several spatiotemporal variables for the senior international competitor. These researchers suggested that consistent upper limb movement patterns (both in timing and range of motion), particularly at the shoulder and elbow, were key elements for improving the accuracy of the throwing action. The use of only one international level competitor by these researchers represented a clear limitation for this project, as it is questionable whether these data can be applied across all high performance line- out throwers.

The throwing accuracy measure used by Trewartha et al., 2008 was calculated by recording the distance of the ball from the target - a mark on a basketball backboard. While an accepted method for assessing accuracy in traditional target sports (e.g. archery, shooting) this is not a functional method for line-out throwing as it gives equal weighting to accuracy regardless of the relative position to the target. For example, throws cannot be caught if they are only marginally higher than the Jumper’s hands, while throws that are 0.4 m too low have the potential to be intercepted by the opposition. Clearly a more functional measure of line-out throwing accuracy is required that considers the specific requirements of the sport and includes a line-out Jumper with Lifters.

Accordingly, the aim of this project was to determine which body positions and movement patterns constitute the key elements of the line-out throwing action in a group of international line-out throwers. To address this question this study first examined whether elite line-out throwers share any similarities in throwing technique during a match specific throwing accuracy task. Next, analyses focused on determining whether throwing accuracy and technique were influenced by throwing to the front, middle and back of the line-out.

Methods

Three high profile international level players from an IRB world ranked (top 2) rugby team served as subjects (age = 26.3 ± 2.9 years, body mass = 103.3 ± 5.0 kg, height = 1.82 ± 0.07 m, throwing hand = right). Each of the subjects had 10, 52 and 33 international caps respectively at the time of testing. The test protocols required subjects to complete 30 throws (5 sets of 6 throws) to a Jumper being held by two Lifters over three marked distances (6m - Front, 10 m - Middle, 15 m - Back) with the order randomized both between and within trials. There were no opposition Jumpers for any of the trials. Participants were given a traditional warm-up (e.g. light jogging and upper body mobility exercises) and several minutes of practice drills prior to commencing data acquisition.

Throw accuracy was quantified at the completion of the testing using a five point scale: (1) Ball was not caught, or would have required the Jumper to move his hands the equivalent of 4 ball diameters; (2) Jumper caught the ball having to move his hands the equivalent of 3 ball diameters; (3) Jumper caught the ball having to move his hands the equivalent of 2 ball diameters; (4) Jumper caught the ball having to move his hands the equivalent of 1 ball diameter; and (5) Jumper caught the ball without having to move his hands. To improve the reliability of this system images were created from individual video frames of each ball catch. A scaled bull’s-eye like target was then superimposed over the Jumper’s hands using standard photo editing software (Figure 1). The bull’s- eye like target was distorted to make the accuracy scores more functional, as throws that were only one ball diameter too high were not catchable by the Jumper.

Figure 1.

Example image (single digital video frame) that shows a ball being caught by a line-out Jumper with the accuracy scoring system included as an overlay.

Kinematic data

Twenty-two body landmarks were marked with reflective tape prior to testing to create a simple 14 segment model of the body. Landmark locations were limited to the proximal and distal ends of the limbs with additional markers attached to the pelvis, head and spine. Specific sites on the left and right limbs were the distal ends of the boot adjacent to the 1^st and 5^th metatarsals, lateral malleoli, lateral femoral epicondyles, greater trochanters, lateral margins of the acromion processes, lateral humeral epicondyles and the radial styloid processes. Additional sites were the two anterior superior iliac spines, spinous processes of the 7^th cervical (C7) and 2^nd sacral (S2) vertebrae, and the base and apex of the skull. Two landmarks were attached at either end of the ball along its longitudinal axis. A model of the pelvis was created based on the markers located on the anterior superior iliac spines, S2 and the greater trochanters. The spine was modelled from the C7 and S2 markers, together with those on the acromion processes. The simple end-point modelling of the upper and lower limbs limited the description and these segments to 4 degrees of freedom.

Data were collected using three JVC digital camcorders (GR-DV900) operating at 50 Hz. One camera was situated directly behind the throwers, while the other two cameras were positioned approximately 8 m in front of the thrower and 5 meters either side of the throw path. Each camera was synchronized from the point of ball release. Following data capture, all landmarked points were digitized using APAS motion analysis software (Ariel Dynamics Inc. USA) for every frame from the start of the throwing action until ball release. To allow for potential end-points errors, 10 additional frames were digitized either side of the throwing action with these data being deleted after the smoothing process. The APAS software has been shown to develop both accurate and reliable linear and angular kinematic data (Klein and DeHaven, 1995; Wilson et al., 1997). Transformed three-dimensional data were smoothed using a 7 Hz digital low-pass Butterworth filter. A global coordinate system was then established with its origin on the sideline the Y-axis in the direction of ball travel, the X-axis to the right and the Z-axis oriented vertically.

The orientation of the pelvis and trunk was recorded with anterior tilt, lateral tilt and axial rotations defined using Euler angle calculations as angular rotations about the global coordinate system’s X, Y and Z axes. Analyses of angular displacement and velocity data for the upper and lower limbs were limited to movements in flexion/extension (about X-axis) and abduction/adduction (about Y-axis). Flexion and adduction were defined as positive rotations of the distal segment about the proximal segment’s x and y axes respectively. Linear displacement and velocity data for the centre of mass (CoM) were calculated relative to the three planes of motion (CoM_x, CoM_y, CoM_z) at each of the key throw phases. Resultant ball release velocity was calculated as the vector resolution from two frames before and after ball release.

The throw was divided into two phases - backswing and forward throw. The start of the backswing was defined as occurring at initiation of backward ball movement from the thrower’s set position, with this phase ending when the ball stopped moving backwards (0 m.s^-1 in Y direction). The forward throw commenced at the completion of the backswing and continued through until ball release. Linear and angular kinematic data were identified at each event and maximum and minimum linear and angular velocity data were calculated for each phase. For the purposes of this research no data after ball release have been analyzed.

Statistical analyses

Descriptive statistics were calculated for each kinematic variable using standard procedures. The standard deviations (SD) for each throw were used as a measure of movement consistency and were normalized via log transformation prior to analysis. Effect Size (ES) statistics (confidence level of 95%) were used to determine differences between throwers and throw distances, as the relatively small sample sizes precluded the use of standard comparative statistical tools (Cohen, 1988). Descriptors of the magnitude of ES differences were based on those suggested by Hopkins, 2002. The multiple comparisons used in this analysis meant that analysis was limited to those variables that reported large ES differences.

Results

Throw accuracy and ball kinematics

Results showed that Thrower 3 (T3) was the most accurate thrower followed by Thrower 2 (T2), then Thrower 1 (T1). ES analyses indicated that accuracy scores did not differ markedly between throw distances (ES<0.2). Analysis of accuracy SD data showed that T3 was also the most consistent thrower and T1 was the least consistent. Regardless, the mean accuracy scores for each subject indicated that they were able to deliver the ball within two ball diameters of the target irrespective of throw distance.

Ball release velocities not only differed considerably by subject (ES>1.2) but also by throw length (ES>3.0). Throws to the Front of the line-out had slower release velocities (8.31 m·s^-1 ± 0.32) than those recorded for throws to the Middle (9.31 m·s^-1 ± 0.59), which was slower again than throws to the Back of the line-out (10.36 m·s^-1 ± 0.66). Analysis also showed differences in the lateral and vertical position of the ball (relative to the CoM) at the end of the backswing between throwers (ES>2.7). All players displayed high levels of consistency with this variable, with SD values ranging from 0.01 m to 0.03 m for the most and least accurate throwers respectively.

Throwing arm kinematics

Results showed marked differences between throwers in the way they oriented the arm segments at both the end of the backswing phase and at ball release (Table 1). Notably, shoulder and elbow flexion angles varied significantly between throwers at both these positions, but did not change significantly at ball release for throws of increasing length. Conversely, significant differences in shoulder orientation at these throw positions were found between both throwers and throw length. Regardless of the orientation of the arm at each of the key throw positions, throwers displayed high levels of movement consistency. For example, shoulder flexion angles at the end of the backswing were 154 deg (± 2) for T1 and 143 deg (± 3) and 148 deg (± 5) for T2 and T3 respectively. Similarly, despite differences in mean elbow angles between throwers, the SD in elbow angles at both the end of the backswing and at ball release varied between participants by only 1 to 6 degs.

Table 1.

Summary of the results of Effect Size (ES) analyses for selected angular kinematic data at the end of the backswing and at ball release. Data were summarized so that only comparisons that recorded Large or Very Large (Hopkins 2002) ES are listed, with those that recorded Trivial, Small or Medium ES left blank.

Variable	Comparison by Thrower			Comparison by Length
	T1-T2	T1-T3	T2-T3	Front-Middle	Front-Back	Middle-Back
At the end of the backswing
Pelvic rotation angle					L
Trunk flexion angle		VL
Upper trunk rotation		VL		VL	VL	L
Shoulder flexion angle	VL	VL		-L	-VL	-L
Shoulder abduction angle	VL	VL	-L
Elbow flexion angle	-VL	-VL	VL	-L	-VL	-L
At ball release
Pelvic rotation angle	-L	-VL	-L
Trunk flexion angle		VL	VL
Upper trunk rotation		VL	VL
Shoulder flexion angle	VL	VL	VL	-VL	-VL
Shoulder abduction angle	L	L	L	-L
Elbow flexion angle	L	VL	VL

L = Large VL = Very Large.

^* Negative values indicate that the first group is smaller than the second (e.g. the values for T2 are small than for T3)

Analysis of the maximum angular velocities during the forward throw phase also showed clear differences between participants for all arm variables (Table 2). The differences in throwing kinematics between participants are also typified in the maximum angular velocity data during the forward throw (Table 2). Figure 2 presents maximum elbow extension velocities during the forward throw for each thrower across all distances and shows that T3 typically extended this joint slower during the forward throw than the other two participants. Analysis by throw distance revealed that elbow extension velocities typically decreased for longer throws. Conversely shoulder extension velocities were greater for throws to the Back of the line-out compared to those to the Front.

Table 2.

Summary of the results of Effect Size (ES) analyses for maximal linear and angular kinematic data during the forward throw phase. Data is summarized so that only comparisons that recorded Large or Very Large (Hopkins 2002) ES are listed, with those that recorded Trivial, Small or Medium ES values left blank.

Variable	Comparison by Thrower			Comparison by Length
	T1-T2	T1-T3	T2-T3	Front-Middle	Front-Back	Middle-Back
Linear velocities
CoMx
CoMy	VL		-VL*	-VL	-VL	-VL
CoMz	L	VL	VL		-L
Angular velocities
Ankle plantar flexion	-VL	-VL		-VL	-VL	-VL
Knee extension	VL	VL			-VL	-VL
Hip extension				-VL	-VL	-L
Pelvic rotation	-L	VL	VL	L
Trunk flexion		VL
Upper trunk rotation
Shoulder extension	-VL		VL		-L
Shoulder adduction	-L		L
Elbow extension	VL	VL	VL	-VL	-L

L = Large, VL = Very Large.

^* Negative values indicate that the first group is smaller than the second (e.g. the values for T2 are small than for T3)

Figure 2.

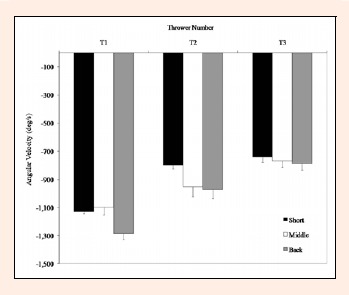
Mean throwing arm maximum elbow extension velocities for the three participants at each throw distance. ES analyses indicated Very Large to Large differences in mean values between participants and between throw distances.

Pelvis, trunk and CoM kinematics

In contrast to the findings for the arm segments several non-significant differences were noted for pelvis and trunk orientation for throws of increasing length, particularly at ball release (Table 1). Notably, the orientation of the trunk about the X and Z axes varied markedly between participants at both the end of the backswing phase and at ball release. Conversely, the degree of axial pelvic rotation (about Z-axis) was similar between throwers at the end of the backswing, but differed considerably at ball release. The most accurate thrower had the pelvis close to neutral at ball release, while the other throwers had rotated the pelvis forward nearly 40 deg. The degree of trunk and pelvis rotation at the end of the backswing were both affected by throw distance, with the right side of the pelvis and trunk being rotated further back for longer throws. None of the pelvis or trunk variables at ball release were influenced by throw distance. Regardless of the differences, each thrower varied their trunk flexion angle by less than 3 deg at ball release over the course of the 30 throws, with throwers flexing the trunk through less than 10 deg during the forward throw phase.

Maximum axial upper trunk rotation velocities did not differ notably between throwers or for each throw distance. Similarly, maximum trunk flexion velocity only differed between T1 (202 ± 23 deg·s^-1) and T3 (92 ± 20 deg·s^-1). However, maximal pelvic rotation velocities differed between throwers and increased markedly between throws to the Front and Middle of the line-out. The relative stability of the trunk orientation for throws of increasing length is also reflected in the consistent CoM_x velocities at ball release across all throws. Analyses indicated that both CoM_y and CoM_z velocities at ball release tended to increase with greater throw length. Regardless, these velocities were less than 0.5 m/s for CoM_y and less than 0.05 m/s for CoM_z velocities indicating that the CoM was kept relatively still throughout the throwing action.

Lower limb kinematics

Lower limb angular velocity data reflected a trend towards an increase in the rate of extension at each of the key leg joints for each subsequent increase in throw distance (Table 2). Marked differences were noted for between throwers for maximum ankle plantar flexion and knee extension velocities, while the rate of maximum hip flexion remained relatively consistent between participants (ES < 0.4).

Discussion

Maximum ball release velocities reported here are at least 10% slower than the release velocities recorded when participants have been required to throw at a fixed target (Trewartha et al., 2008). This simple finding suggests that the use of static targets in the training of line-out throwing may be counterproductive to effective performance. It is hypothesized that the accuracy assessment protocols used in this project are more applicable to on-field performance than traditional target testing, and once subjected to reliability analyses should be adopted uniformly by both coaches and scientists.

The numerous significant differences in the throwing techniques adopting by the three throwers concurs with previous research that has found considerable inter-individual differences between international level players (Sayers, 2005; Trewartha et al., 2008). However, the high levels of movement consistency displayed by these throwers meant that even slight differences in limb orientation between participants resulted in statistically significant findings. Regardless, several functional similarities existed in the throwing actions of these high performance line-out throwers that could be used to form a model of performance. For example, although each thrower positioned the ball in a slightly different position (relative to the COM) at the end of the backswing there was minimal variation in this position between throws. Similarly, all throwers achieved very consistent elbow (flexion) and shoulder (flexion and abduction) angles at both the end of the backswing and at ball release. In addition, the trunk was kept close to upright during the throw, with any transverse plane rotation occurring with minimal trunk flexion or extension. This is not the case for throwing in other football codes such as the quarterback pass in American football (Rash and Shapiro, 1996), or the soccer throw-in (Kollath and Schwirtz, 1988; Lees et al., 2005).

Interestingly basketball players have also been shown to adopt an upright and consistent trunk angle at ball release regardless of shooting distance (Elliott, 1992; Miller and Bartlett, 1996). There are several key advantages in achieving a consistent and trunk relatively upright trunk position at ball release in these sports. First, a stable upright trunk will assist with focusing on the target by helping to minimize head movements. Next, consistency in trunk orientation at release means that the movements at the shoulder and elbow can also be held consistent. For example, if the trunk flexion increases at release for a particular throw there would need to be compensatory flexion and abduction movements at the shoulders to achieve the same ball release angle (assuming similar elbow positioning). Although it has been the topic of some debate (Bartlett et al., 2007), consistency of movement patterns is common in accuracy based throwing sports (Etnyre, 1998) and also appears to be a key factor in determining line-out throwing proficiency.

An area of great interest in this project concerned the methods adopted by these high performance line-out throwers to deliver the ball accurately over the three different throw lengths. For example, at the end of the backswing numerous variables were changed with increases in throw length, but at ball release only shoulder flexion and abduction angles showed significant changes. Similarly, for the longer throws participants rotated the upper trunk further back at the end of the backswing but still released the ball with the trunk relatively square to the target. The net result of these actions is the maintenance of the crucial release position with an increase in the range of motion over which the ball can be accelerated to achieve faster release velocities. The changes in shoulder orientation at ball release may be a function of slight increases in ball release angle, which are known to occur over longer line-out throws (Trewartha et al., 2008). The process of increasing transverse plane trunk movements for longer line-out throws has the potential to result in accuracy problems and should be regarded with caution by coaches.

This study concurred with previous research that has suggested line-out throwers tend to increase throwing distance by increasing the involvement of the lower limb (Sayers, 2005; Trewartha et al., 2008). There are clear advantages in using the legs and trunk to develop ball velocity for longer throws, leaving the more distal segments to focus on accuracy. The most accurate thrower (T3) had relatively large increases in shoulder extension velocities during the forward throw at each throw distance, with proportionally smaller increases in elbow extension velocities. Conversely, the least accurate thrower (T1) had exactly the opposite profile, relying heavily on increases in elbow extension velocity for the longer line-out throws. Similarly, T1 tended to increase the rate of ankle plantar flexion for the longer throws, while the most accurate thrower (T3) had the slowest plantar flexion velocities and tended to increase knee extension velocity for the longer throws. The strategy of increasing the involvement of the legs to increase throwing distance is similar to the techniques involved in basketball shooting (Elliott, 1992; Miller and Bartlett, 1996). Therefore, although the arm action for line-out throwing appears somewhat unique to the sport, the rest of the throwing action has strong similarities with basketball shooting and should be trained as such.

Conclusion

This study compared the complex 3D kinematics of three elite international rugby players during a new sports specific line-out throwing accuracy task. The assessment of line-out throwing accuracy using the methodologies reported in this study provided a functional measure of performance that was simple to administer. Results of the kinematic analyses showed that several technical aspects were common to each of the line-out throwers and appeared to be determinants of proficient throwing technique. An important aspect of this research concerned the small intra-individual differences in body orientation demonstrated by each thrower at each of the key throw phases regardless of throw distance. The results from this study can assist coaches in the designing of training programs by providing a simple model of performance. However, this project would need to be extended to include a larger population of high performance line-out throwers before a more definitive model can be created.

Biography

Mark G.L. Sayers

Employment

Head of Discipline, Sport and Exercise Science, School of Health and Sport Science, University of the Sunshine Coast, Australia.

Degree

PhD.

Research interests

Sports biomechanics, analysis of the key skills from each of the main football codes.

E-mail: msayers@usc.edu.au