RNA Challenges for Computational Chemists

Abstract

Some experimental results for the thermodynamics of RNA folding cannot be explained by simple pairwise hydrogen-bonding models. Such effects include the stabilities of isoguanosine–isocytidine (iG–iC) base pairs and of various 2 × 2 nucleotide internal loops. Presumably, these results can be explained by base stacking effects, which can be partitioned into Coulombic and overlap effects. We review experimental measurements that provide benchmarks for testing the approximations and theories used for modeling nucleic acids. Quantitative agreement between experiment and theory will indicate understanding of the interactions determining RNA stability and structure.

An understanding of the physical–chemical interactions underlying RNA folding would allow predictions of structure and perhaps function from sequence. The large number of atoms in an RNA molecule necessitates the use of approximate methods, rather than the rigorous equations of quantum mechanics. Many approaches are possible, including coarse-grained potentials (1), which use residue-centered force fields; molecular mechanics, which uses atom-centered force fields such as AMBER (2), CHARMM (3, 4), and GROMOS (5, 6); approximate quantum mechanics, which considers interactions of electrons and nuclei (7, 8); and QM/MM, which combines quantum mechanics with molecular mechanics (9–16). Depending on the property to be predicted, the size of the RNA, and the domain of interest, different approaches will provide acceptable approximations.

The secondary structure of RNA can sometimes be deduced by sequence comparison, which relies on the Watson–Crick rules for base pairing and the assumption that secondary structures are more conserved than sequences for function (17). Often, however, there are not enough sequences to determine a definitive secondary structure. For these cases, free-energy minimization with a nearest neighbor model is the most popular method for predicting secondary structures (18–38). In this method, possible secondary structure motifs are assigned free-energy parameters, and these values are added to predict the total free energy of forming a secondary structure. The structure with the lowest free energy is assumed to dominate in solution. Rigorously, however, the concentrations of the various possible structures are predicted to be weighted by a Boltzmann factor, exp(−ΔG°/RT), where ΔG° is the free energy change for folding, R is the gas constant, 1.987 cal K⁻¹mol⁻¹, and T is the temperature in kelvins. Understanding intermolecular interactions such as hydrogen bonding, stacking, and so forth would allow accurate prediction of ΔG° and therefore secondary structure for an RNA.

Watson–Crick base pairs are the most common and most extensively studied motif in RNA structures. Configurations with the same base compositions but different permutations of base pairs generally have different free energies. For example, the duplexes (5′CGCG3′)₂ and (5′GGCC3′)₂ both have four GC base pairs, but have free-energy changes of duplex formation in 1 M NaCl at 37 °C of −3.7 and −5.4 kcal/mol, respectively (33). Presently, nearest-neighbor models are the best approximate methods to predict thermodynamic properties of RNA and DNA duplexes containing only Watson–Crick pairs (18–22, 28–31, 33). Figure 1 illustrates how the INN-HB¹ (individual nearest neighbor-hydrogen bonding) model (33) is used to calculate the free-energy change for folding the duplexes 5′iGCGCiG/3′iCGCGiC and 5′GCiGCG/3′CGiCGC and the hairpin 5′GGCAAAAGCC3′.

Figure 1.

Application of INN-HB model (33) to duplex formation by 5′iGCGCiG/3′iCGCGiC and 5′GCiGCG/3′CGiCGC (a and b) and to intramolecular folding by 5′GGCAAAAGCC3′ (26) (c) at 37 °C. Additional examples are given elsewhere (31, 33, 93). In this model, ΔG°_init is the free-energy change for forming the first base pair and is assumed to depend on the free energy for hydrogen bonding within a GC pair and the free-energy penalty for either bringing two strands together (a and b) or forming a loop (c). ΔG°_sym is a symmetry correction that is only applied when two strands of identical sequence form a duplex, ΣΔG°_NN is the sum of nearest neighbor free-energy parameters (33, 76), each of which contains a contribution from half of the hydrogen bonds in the nearest neighbor base pairs and from the stacking of the nearest neighbor base pairs; ΔG°_{term–iG–iC} is half the difference in hydrogen bonding free energy between an iGiC and GC pair (76). This term accounts for the possibility that two helices may contain the same nearest neighbors but different base pair compositions. For example, the duplexes (a) and (b) have the same nearest neighbors but (a) has two iG-iC pairs while (b) has only one. For natural sequences, ΔG°_{term–iG–iC} is replaced by ΔG°_term–A–U. For the hairpin, ΔG°_{First Mismatch} is the free energy for stacking of the first mismatch on the stem helix and ΔG°_{Bonus/Penalty} is applied to loop sequences with unusual stability.

Free-energy minimization with a nearest neighbor model is a useful approximation for predicting RNA secondary structure, but on average, predicts only 73% of known base pairs (25). One major limitation is that most algorithms do not include pseudoknots. In a pseudoknot, a nucleotide between paired nucleotides i and j forms a base pair with a nucleotide not between i and j. Complete inclusion of pseudoknots is an NP-complete problem, that is, one for which there is no known polynomial time solution (35). Algorithms that allow many types of pseudoknots are available, however, and able to run in time that scales as N⁵ (36, 37) or N⁶ (38), where N is the number of nucleotides. The algorithm of Rivas and Eddy (38) is able to handle 90% of the pseudoknots found in a database of 486 structures (39). Good parameters for predicting the stabilities of pseudoknots are not available, however, due to lack of experimental data on model systems. This lack of experimentally measured parameters is also a problem for other types of loops, especially multibranch loops (40, 41). The parameters used in most algorithms (25, 33) have been measured in 1 M NaCl, which usually mimics well typical intracellular ionic conditions, for example, 0.15 M KCl and several millimolar Mg²⁺ (42–44). Motifs have been discovered, however, where Mg²⁺ or K⁺ increase stability by several kilocalories per mole (45–47). The limited knowledge of such effects also limits the accuracy of structure prediction.

Secondary structures may also be perturbed by other interactions not included in prediction algorithms. For example, tertiary interactions and/or interactions with proteins may be important. Both types of interactions are expected to be relatively weak compared to base pairing, however. A single GC pair can stabilize a helix by 3 kcal/mol at 37 °C. In contrast, the entire folding free energy for proteins having molecular weights of about 10 000 averages about 9 kcal/mol (48).

Of course, free-energy minimization methods assume that the RNA is in equilibrium. This may not be true for all RNAs. The very favorable free energy associated with a canonically paired helix can kinetically trap an RNA secondary structure. Such kinetic trapping is often observed when RNA is renatured (49). The reasonable success of free-energy minimization despite the limitations discussed above, however, suggests that kinetics does not usually play a dominant role in determining secondary structure.

Some of the above limitations can be overcome by combining free-energy minimization with sequence comparison and/or constraints derived from experiments (23–27, 32, 34). These enhancements, however, do not compensate well for pseudoknots. For example, when predictions are constrained by chemical modification data in an algorithm that does not allow pseudoknots, the average accuracy of secondary structure predictions is only 60% for five sequences having 7–10% of base pairs in pseudoknots. In contrast, the average accuracy is 84% for 11 sequences with ≤5% of base pairs in pseudoknots (25).

In principle, if the intermolecular interactions in RNA were understood, then it should be possible to predict secondary structure and subsequently local and global three-dimensional structure. This review discusses some considerations for theoretical approaches and then presents some experimental benchmarks for testing these approaches.

THEORY

Theories for important interactions are required to rationalize experimental results and predict the secondary and three-dimensional structures of RNA molecules. Quantum mechanics is the best theory for describing the interactions in atomic systems. Unfortunately, even the simplest RNA systems have hundreds of atoms. As a result, direct application of ab initio quantum mechanics is not yet possible. Improvement in computer power and algorithms may allow the direct use of quantum mechanics on these complicated systems in the future, however.

Quantum mechanics cannot be applied directly to even small RNAs, but it can be applied to individual components such as guanine, adenine, uracil, and cytosine, and those results can be used to build models to predict experimental observables. These models are called force fields. Most of the popular force fields (2–6) include an atom-centered point-charge model. Therefore, these simulation methods need a set of point charges for all of the atoms in the system. Methods to determine the charges include CHELP (50), CHELPG (51), RESP (52), and the Merz–Kollman scheme (53, 54). The best method for finding charges depends on the system of interest (55). Starting with an initial structure and using a force field, properties such as stability and dynamics can be predicted for complicated RNA configurations. The initial structure can be obtained from X-ray crystallography or NMR spectroscopy or can be homology-modeled from X-ray and NMR structures.

Theoretical simulations are done using molecular mechanics (56). In these simulations, the initial structure is varied in order to minimize the energy. Molecular mechanics is combined with molecular dynamics and Monte Carlo methods to predict properties. Molecular dynamics uses Newtonian mechanics (57–61). A molecular simulation is created by changing the positions and velocities of the initial configuration as a function of time. A configuration will be reached, which corresponds to a local or global energy minimum. In the Monte Carlo method (62–64), the initial configuration is changed randomly, and configurations are retained if they lower energy or pass a Boltzmann-weighted probability test (Metropolis Criterion).

The crucial point in molecular mechanics is to find a force field that provides a good description of the system. The potential functions used in force fields can include electrostatic, exchange repulsion, and dispersion (induced dipole–induced dipole) terms, among others. Adding more terms and better parameters to the potential functions will improve predictions. For example, there is a correlation between stacking free energies, melting temperatures, and polarizabilities of DNA bases (65, 66), which suggests that a polarizable force field might improve predictions of RNA thermodynamics and conformations.

RNA and DNA molecules have polyelectrolyte character because of the phosphate group at each residue. This highly negative charge character of RNA and DNA opposes folding. Positive counterions such as Mg²⁺, K⁺, and Na⁺ stabilize nucleic acid structures by reducing the Coulombic interactions between the phosphate groups. The positive ions accumulate around the RNA molecule, as described by polyelectrolyte theory (67–69). This “counterion condensation” reduces the effective charge of RNA and DNA molecules.

Ion–RNA interactions are not restricted to counterion condensation along the RNA backbone. Some ions, such as Mg²⁺ and K⁺, stabilize tertiary structures better than other ions (45, 47, 70, 71). Such stabilization is not well-understood. Because the cell environment of living organisms is ionic, ionic effects must be included in models for predicting stability and structure. Approaches to this include nonlinear Poisson–Boltzmann theory (72) and Ewald summation of Coulombic interactions (73, 74).

EXPERIMENT

A variety of experimental results are required to test the effectiveness of the various approximations and parameters used to predict the properties of RNAs. Some possible benchmarks are described below.

iG–iC versus G–C

A relatively straightforward challenge for computational methods is the description of isoguanosine (iG) and isocytidine (iC). As shown in Figure 2, they form an unnatural base pair, iG–iC, in which the amino and carbonyl groups of G and C are transposed (75). Table 1 lists thermodynamic parameters measured for several RNA duplexes containing G–C or iG–iC base pairs. Table 2 lists nearest neighbor thermodynamic parameters for G–C and iG–iC base pairs, as derived from experimental data such as that listed in Table 1 (76). Within experimental error, the stability of only the 5′GC/3′CG nearest neighbor is affected by iG-iC substitution. In particular, the duplex stability of 5′GC/3′CG is increased by 0.6 kcal/mol for each iG–iC substitution.

Figure 2.

GC (a) and iGiC (b) base pairs with their RESP charges. Guanosine and cytidine are natural nucleosides, while isoguanosine and isocytidine are unnatural nucleosides. The GC pair was extracted from the crystal structure of 1QC0 (94). Transposing the carbonyl and amino groups of G and C creates iG and iC, respectively. The RESP charges (52, 95) were calculated by following the R.E.D. procedure (96). Calculations were done on the nucleosides, but only the C1′ of the ribose is shown.

Table 1.

Thermodynamics of Formation of RNA Duplexes in 1 M NaCl

sequence (5′ → 3′)	1/TM vs ln(CT) parameters
	ΔG°37 (kcal/mol)	ΔH° (kcal/mol)	ΔS° (eu)	Tm (°C)
GCGCa	−4.6 ± 0.1	−30.5 ± 1.5	−83.4 ± 4.8	26.6
iGiCiGiCb	−7.0 ± 0.1	−50.6 ± 5.4	−140.6 ± 17.1	45.2
CCGGc	−4.6 ± 0.2	−34.2 ± 0.2	−95.6 ± 0.8	27.2
iCiCiGiGb	−4.8 ± 0.1	−39.8 ± 1.1	−112.9 ± 3.6	30.5

^aRef 86.

^bRef 76.

^cRef 87.

Table 2.

Nearest-Neighbor Parameters for RNA Duplexes Containing iG–iC and G–C Pairs in 1 M NaCl (33, 76)^a

	ΔG°37 (kcal/mol)	ΔH° (kcal/mol)	ΔS° (eu)
$\begin{array}{c}{5}^{\prime }\text{CG}{3}^{\prime }\\ 3^{\prime }\text{GC}{5}^{\prime }\end{array}$	−2.36 ± 0.09	−10.64 ± 1.65	−26.70 ± 5.0
$\begin{array}{c}{5}^{\prime }\text{iCG}{3}^{\prime }\\ 3^{\prime }\text{iGC}{5}^{\prime }\end{array}$	−2.46 ± 0.08	−10.80 ± 1.12	−27.01 ± 3.13
$\begin{array}{c}{5}^{\prime }\text{iCiG}{3}^{\prime }\\ 3^{\prime }\text{iGiC}{5}^{\prime }\end{array}$	−2.45 ± 0.17	−12.69 ± 2.23	−33.28 ± 6.29
$\begin{array}{c}{5}^{\prime }\text{GG}{3}^{\prime }\\ 3^{\prime }\text{CC}{5}^{\prime }\end{array}$	−3.26 ± 0.07	−13.39 ± 1.24	−32.70 ± 3.8
$\begin{array}{c}{5}^{\prime }\text{iGG}{3}^{\prime }\\ 3^{\prime }\text{iCC}{5}^{\prime }\end{array}$	−3.46 ± 0.11	−14.94 ± 1.44	−36.80 ± 4.04
$\begin{array}{c}{5}^{\prime }\text{GiG}{3}^{\prime }\\ 3^{\prime }\text{CiC}{5}^{\prime }\end{array}$	−3.07 ± 0.11	−14.67 ± 1.48	−37.34 ± 4.20
$\begin{array}{c}{5}^{\prime }\text{iGiG}{3}^{\prime }\\ 3^{\prime }\text{iCiC}{5}^{\prime }\end{array}$	−3.30 ± 0.17	−14.01 ± 2.26	−34.58 ± 6.35
$\begin{array}{c}{5}^{\prime }\text{GC}{3}^{\prime }\\ 3^{\prime }\text{CG}{5}^{\prime }\end{array}$	−3.42 ± 0.08	−14.88 ± 1.58	−36.90 ± 4.9
$\begin{array}{c}{5}^{\prime }\text{iGC}{3}^{\prime }\\ 3^{\prime }\text{iCG}{5}^{\prime }\end{array}$	−4.00 ± 0.09	−16.90 ± 1.19	−41.32 ± 3.33
$\begin{array}{c}{5}^{\prime }\text{iGiC}{3}^{\prime }\\ 3^{\prime }\text{iCiG}{5}^{\prime }\end{array}$	−4.61 ± 0.17	−19.98 ± 2.31	−49.36 ± 6.53
per terminal iG–iCa	−0.19 ± 0.07	−1.00 ± 0.98	−2.54 ± 2.77

^aSee caption to Figure 1 for molecular interpretation.

Because only the carbonyl and amino groups of the G and C are transposed to generate iG and iC, iG–iC and G–C pairs are isosteric. The electron density, however, is different (Figures 2 and 3). Therefore, the iG–iC pair is a good system to test predictions of the effects of different electron distributions.

Figure 3.

The calculated electrostatic potential surfaces of 5′CG/3′GC vs 5′iCiG/3′iGiC (top), 5′GC/3′CG vs 5′iGiC/3′iCiG (middle), and 5′GG/3′CC vs 5′iGiG/3′iCiC (bottom). Structures for 5′CG/3′GC, 5′GC/3′CG, and 5′GG/3′CC were extracted from the crystal structure of 1QC0 (94), and the iso structures were created using the program Insight II (Biosym Technologies, San Diego, CA) by transposing the amino and carbonyl groups. The potential surfaces were created with the program GRASP (77). To create these surfaces, the RESP charges (52, 95) for G, C, iG, and iC nucleosides were calculated using R.E.D. (96), and only the charges on the base rings were used in order to focus on the Coulombic effects. These surfaces were created around the bottom base pairs with a probe radius of 1.4 Å. The red regions represent negative potential, while the blue regions represent positive potential. The red-blue color spectrum runs from −20 to +20 kT/e, respectively. Namely, it shows the potential of a positive unit charge on these surfaces when the charges on the base rings are present. Below each structure, the experimental free energies are presented. To compare the stacking interactions between the G–C and iG–iC pairs, the hydrogen bond strength enhancement of the iG–iC pairs is excluded, and these hydrogen-bond-corrected free energies are shown in parentheses. The top parts of the structures are in the major groove, while the bottom parts are in the minor groove.

One likely factor determining the stabilities of iG–iC base pairs is increased strength of the hydrogen bonds relative to G–C pairs. This is expected from the increased and decreased electron densities on hydrogen bonding acceptors and donors, respectively (Figure 2). An experimental estimate of the free-energy contribution from these stronger hydrogen bonds can be deduced from the terminal iG–iC term of −0.19 kcal/mol in Table 2 (76). This term effectively accounts for the different base compositions of sequences with the same nearest neighbors, but different terminal base pairs. For example, as illustrated in Figure 1, if two duplexes have the same nearest neighbors, but one has two terminal G–C pairs, while the other has two terminal iG–iC pairs, then the one with the iG–iC terminal pairs will have one more iG–iC pair than the duplex with two terminal G–C pairs. Because the nearest neighbors and therefore presumably stacking interactions in the two duplexes are the same, the difference in hydrogen bonding within an iG–iC and G–C pair is estimated as 2 × (−0.19) = −0.38 kcal/mol. Because a single nearest neighbor interaction accounts for half of the hydrogen bonds in the two neighboring base pairs, the difference in hydrogen bonding strength between iG–iC and G–C accounts for about 0.4 kcal/mol of the 1.2 kcal/mol enhanced stability of 5′iGiC/3′iCiG relative to 5′GC/3′CG.

The remaining 0.8 kcal/mol of increased stability for 5′iGiC/3′iCiG compared to 5′GC/3′CG is likely due to the stacking interactions for the iG–iC pairs. The stacking interaction can be partitioned into Coulombic and overlap effects. Coulombic effects are due to interactions between effective permanent partial charges on each atom. Overlap effects will include other electrostatic interactions between bases, for example, dispersion interactions, and may also include effects due to burial of bases away from water.

Figure 3 shows electrostatic potential surfaces calculated by the program GRASP (77) for the nearest neighbors 5′CG/3′GC versus 5′iCiG/3′iGiC (top), 5′GC/3′CG versus 5′iGiC/3′iCiG (middle), and 5′GG/3′CC versus 5′iGiG/3′iCiC (bottom) in A-form RNA. Only the charges on the base part of the structures were used in the calculations in order to focus on the stacking interactions. Thus, Figure 3 provides a qualitative picture of the Coulombic effect in these nearest neighbor base pairs. For example, there is a big difference between 5′GC/3′CG and 5′iGiC/3′iCiG potential surfaces. In contrast, the differences between potential surfaces are modest for 5′CG/3′GC versus 5′iCiG/3′iGiC and 5′GG/3′CC versus 5′iGiG/3′iCiC. This suggests that the Coulombic interaction is the dominant factor when 5′GC/3′CG is compared to 5′iGiC/3′iCiG.

A qualitative comparison can be made between the pictures in Figure 3 and the experimental results in Table 2. The red-blue color spectrum reflects the value of the electrostatic potential on the surface created around the bottom base pair. The most favorable stacking would place opposite charges on top of each other, producing a neutral (white) potential halfway between the charges. The least favorable stacking would place identical charges on top of each other, producing a large positive (blue) or negative (red) potential halfway between the charges. Qualitatively, the potential surface of 5′iGiC/3′iCiG is smaller in magnitude than 5′GC/3′CG, suggesting more favorable Coulombic interactions. This is consistent with 5′iGiC/3′iCiG being more stable than 5′GC/3′CG even after correction for differences in hydrogen bond strength. Conversely, the electrostatic potential of 5′GG/3′CC is smaller in magnitude than that of 5′iGiG/3′iCiC, suggesting more favorable Coulombic interactions. After correction for differences in hydrogen bonding, 5′GG/3′CC is more stable than 5′iGiG/3′iCiC, although the difference is within experimental error. For 5′iCiG/3′iGiC and 5′CG/3′GC, there is little difference in the electrostatic potential or stability. It is likely that Figure 3 does not capture all the important physics and chemistry. For example, the minor groove is more accessible to water than the major groove, so that the local dielectric constants may not be identical. Consideration of only duplex geometries also neglects any differential stacking in the single strands.

Another determinant of stability that can be seen in Figure 3 is the base overlap. The base rings of 5′GC/3′CG and 5′iGiC/3′iCiG helices have more overlap than the other nearest neighbors. This overlap will enhance dispersion interactions and thus the stability of the structure. Burial of surface area away from water may also be important (78). Interestingly, at 37 °C, 5′GC/3′CG is −0.16 kcal/mol more favorable than 5′GG/3′CC, even though the electrostatic potential surface of 5′GG/3′CC appears more favorable than that of 5′GC/3′CG. This suggests that 5′GC/3′CG gains stability because of overlap effects and that the free-energy gain from overlap effects in 5′GC/3′CG compensates for the less favorable Coulombic interactions relative to 5′GG/3′CC. Consistent with this speculation is that 5′iGiG/3′iCiC appears to have less favorable Coulombic interactions than 5′GG/3′CC and is thermodynamically less stable than 5′GC/3′CG. As another example, comparison of 5′CG/3′GC with 5′GC/3′CG reveals that the base overlap in 5′CG/3′GC is less than in 5′GC/3′CG, and the Coulombic interactions in 5′CG/3′GC are similar to those in 5′GC/3′CG. Thus, qualitatively, 5′GC/3′CG is expected to be more stable than 5′CG/3′GC, and this is the case (Table 2).

The qualitative comparisons above suggest that much of the sequence dependence of base pair stability in RNA can be rationalized by current force fields. Quantitative calculations are required, however, to test this hypothesis.

G•U Closure of 2 × 2 Internal Loops: $\begin{array}{c}{5}^{\prime }{G}^{NM}C{3}^{\prime }\\ 3^{\prime }{C}_{MN}G{5}^{\prime }\end{array}$ versus $\begin{array}{c}{5}^{\prime }{G}^{NM}U{3}^{\prime }\\ 3^{\prime }{U}_{MN}G{5}^{\prime }\end{array}$

Internal loops with G•U closing pairs are often involved in tertiary and quaternary interactions that are important for structural and functional roles (79, 80). As a result, a good understanding of the thermodynamics of internal loops will help predict both secondary and tertiary structures of RNA. Table 3 lists experimental free-energy parameters for symmetric 2 × 2 purine internal loops with different closing pairs.

Table 3.

Free-Energy Increments (kcal/mol at 37 °C) for Symmetric 2 × 2 Purine Loops (88)^a

closing base pairs	loops
	$\begin{array}{c}\text{GA}\\ \text{AG}\end{array}$	$\begin{array}{c}\text{AG}\\ \text{GA}\end{array}$	$\begin{array}{c}\text{AA}\\ \text{AA}\end{array}$
$\begin{array}{c}{5}^{\prime }\text{G}\\ 3^{\prime }\text{C}\end{array}$	−2.6	−1.3	1.5
$\begin{array}{c}{5}^{\prime }\text{C}\\ 3^{\prime }\text{G}\end{array}$	−0.7	−0.7	1.3
$\begin{array}{c}{5}^{\prime }\text{A}\\ 3^{\prime }\text{U}\end{array}$	0.3	1.7	2.8
$\begin{array}{c}{5}^{\prime }\text{U}\\ 3^{\prime }\text{A}\end{array}$	0.7	0.9	2.8
$\begin{array}{c}{5}^{\prime }\text{G}\\ 3^{\prime }\text{U}\end{array}$	1.8	2.6	4.1
$\begin{array}{c}{5}^{\prime }\text{U}\\ 3^{\prime }\text{G}\end{array}$	0.1	3.4	2.1

^aAll motifs are symmetric. Thus, a closing base pair of $\begin{array}{c}{5}^{\prime }\text{G}\\ 3^{\prime }\text{C}\end{array}$ and a loop of $\begin{array}{c}\text{GA}\\ \text{AG}\end{array}$ represent the motif $\begin{array}{c}{5}^{\prime }\text{G}\underset{\_}{\mathbf{GA}}\text{C}{3}^{\prime }\\ 3^{\prime }\text{C}\mathbf{AG}\text{G}{5}^{\prime }\end{array}$. Values are from refs 26 and 88, and based on the experimental data from refs 88–92.

Internal loops closed by GC rather than AU pairs are more stable by 1.3 kcal/mol on average, and this difference has been attributed to the different number of hydrogen bonds in GC and AU pairs (44). AU and GU pairs both have two hydrogen bonds, but the predicted increment of 1.3 kcal/mol relative to loop closure by GC pairs cannot rationalize some of the results listed in Table 3, especially for closure by GU pairs. In particular, when the internal loops 5′GA/3′AG, 5′AG/3′GA, and 5′AA/3′AA are closed by GC rather than GU pairs, the stabilities are enhanced by 4.4, 3.9, and 2.6 kcal/mol, respectively. The same trend is seen when 5′GGAC/3′CAGG and 5′GAGC/3′CGAG are compared with 5′AGAU/3′UAGA and 5′AAGU/3′UGAA, respectively. When 5′GA/3′AG and 5′AG/3′GA loops are closed with GC base pairs, the stabilities are enhanced by 2.9 and 3.0 kcal/mol, respectively, compared to the same loops closed with AU base pairs. Because the shapes and electronic structures of GU, GC, and AU pairs differ, the Coulombic and overlap interactions between closing base pairs and loop must be different. Thus, calculations of these effects should provide another test of the ability of theory to rationalize experimental results.

GC ersus CG Closure of Tandem G•A Pairs: $\begin{array}{c}{5}^{\prime }{G}^{GA}C{3}^{\prime }\\ 3^{\prime }{C}_{AG}G{5}^{\prime }\end{array}$ versus $\begin{array}{c}{5}^{\prime }{C}^{GA}G{3}^{\prime }\\ 3^{\prime }{G}_{AG}C{5}^{\prime }\end{array}$

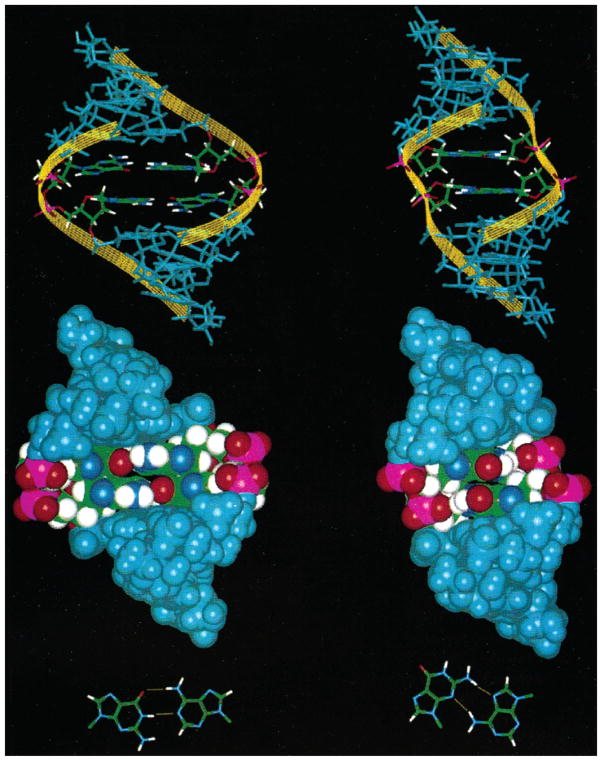
According to Table 3, the free energy of the GC closure of the 5′GA/3′AG internal loop is enhanced by 1.9 kcal/mol compared to CG closure of the 5′GA/3′AG internal loop. Moreover, NMR structures of these two motifs are different, as shown in Figure 4 (81). This, again, suggests that Coulombic and overlap interactions between bases are important. Moreover, nonplanar guanine amino groups might be important, too (82). Thus, this system presents a challenge to theoretical methods to predict both the stabilities and structures as a function of sequence in these motifs.

Figure 4.

Stacking interactions (Coulombic and overlap effects) can change local 3D structures (81). The NMR structures of 1MIS, $\begin{array}{c}{5}^{\prime }\text{GCG}\underset{\_}{\mathbf{GA}}\text{CGC}{3}^{\prime }\\ 3^{\prime }\text{CGC}\mathbf{AG}\text{GCG}{5}^{\prime }\end{array}$, (left (81)) and 1YFV, $\begin{array}{c}{5}^{\prime }\text{GGC}\underset{\_}{\mathbf{GA}}\text{GCC}{3}^{\prime }\\ 3^{\prime }\text{CCG}\mathbf{AG}\text{CGG}{5}^{\prime }\end{array}$, (right (97)) are shown in stick (top two) and space-filling (center two) representations, viewed from major grooves. Imino hydrogen-bonded (bottom left) and sheared (bottom right) GA mismatches are shown in stick representations. Yellow ribbons follow the sugar–phosphate backbone. Because of the electronic structure differences of these two motifs, the local 3D structures are different.

Tandem G•U Pairs

Table 4 lists the free-energy increments for symmetric tandem G•U, I•U, and A–U motifs closed by GC and CG base pairs. One interesting result is that the free energy of 5′CAUG/3′GUAC is 4.2 kcal/mol more favorable than that of 5′CGUG/3′GUGC. The only difference between these two structures is that 5′CGUG/3′GUGC has two adjacent G•U base pairs, while 5′CAUG/3′GUAC has two adjacent A–U base pairs. It is likely that this difference is also due to differences in Coulombic and overlap interactions because the simple hydrogen-bond model cannot rationalize this difference. Interestingly, NMR and chemical substitution effects suggest that not all adjacent G•U pairs form two hydrogen bonds (83), and molecular dynamics calculations reproduce this interpretation (84).

Table 4.

Comparison of Free-Energy Increments (kcal/mol at 37 °C) for Symmetric Tandem G•U, I•U, and A–U Motifs

adjacent base pairs	$\begin{array}{c}\text{UG}\\ \text{GU}\end{array}$	$\begin{array}{c}\text{UI}\\ \text{IU}\end{array}$	$\begin{array}{c}\text{UA}\\ \text{AU}\end{array}$	(UG–UI)	(UG–UA)
$\begin{array}{c}{5}^{\prime }\text{G}\\ 3^{\prime }\text{C}\end{array}$	−4.9a	-	−5.8a	-	0.9
$\begin{array}{c}{5}^{\prime }\text{C}\\ 3^{\prime }\text{G}\end{array}$	−4.2a	+0.5b	−5.5a	−4.7	1.3

adjacent base pairs	$\begin{array}{c}\text{GU}\\ \text{UG}\end{array}$	$\begin{array}{c}\text{IU}\\ \text{UI}\end{array}$	$\begin{array}{c}\text{AU}\\ \text{UA}\end{array}$	(GU–IU)	(GU–AU)
$\begin{array}{c}{5}^{\prime }\text{G}\\ 3^{\prime }\text{C}\end{array}$	−4.1a	-	−5.8a	-	1.7
$\begin{array}{c}{5}^{\prime }\text{C}\\ 3^{\prime }\text{G}\end{array}$	−1.1a	+2.1b	−5.3a	−3.2	4.2

^aRef 83.

^bRef 85.

Replacement of guanine by inosine produces other interesting results. The only structural difference between guanine and inosine is replacement by a hydrogen atom (−H) of an amino group (−NH₂) that is not involved in base–base hydrogen bonding. The free energies of 5′CUGG/3′GGUC and 5′CGUG/3′GUGC are 4.7 and 3.2 kcal/mol more favorable than 5′CUIG/3′GIUC and 5′CIUG/3′GUIC, respectively (85). Presumably, this is due to the electronic structure differences between guanine and inosine. A quantitative analysis of these two structures would provide another test of our understanding of Coulombic and overlap effects in RNA molecules.

CONCLUSION

A sufficient understanding of intermolecular interactions in RNA would permit prediction of RNA structure. In this review, some experimental results for RNA thermodynamics and structures are presented, which can serve as benchmarks for theoretical calculations. Generally, these structures have non-Watson–Crick base pairs, such as G•U, I•U, G•A, A•A, and iG–iC. Qualitative comparison between G–C and iG–iC base pairs suggests that stability differences may be rationalized with current force fields by decomposing the effects into Coulombic and overlap effects. Quantitative calculations on a variety of systems are required to test this and other approaches.