What Is the Significance of Difference in Phenotypic Variability across SNP Genotypes?

Abstract

We studied the general problem of interpreting and detecting differences in phenotypic variability among the genotypes at a locus, from both a biological and a statistical point of view. The scales on which we measure interval-scale quantitative traits are man-made and have little intrinsic biological relevance. Before claiming a biological interpretation for genotype differences in variance, we should be sure that no monotonic transformation of the data can reduce or eliminate these differences. We show theoretically that for an autosomal diallelic SNP, when the three corresponding means are distinct so that the variance can be expressed as a quadratic function of the mean, there implicitly exists a transformation that will tend to equalize the three variances; we also demonstrate how to find a transformation that will do this. We investigate the validity of Bartlett’s test, Box’s modification of it, and a modified Levene’s test to test for differences in variances when normality does not hold. We find that, although they may detect differences in variability, these tests do not necessarily detect differences in variance. The same is true for permutation tests that use these three statistics.

Main Text

Motivated by a recent report¹ of significant differences in the variance of body mass index (BMI) across the three genotypes of a SNP in the FTO locus [MIM 610966], we consider here the general problem of interpreting and detecting differences in phenotype variability and, more specifically, variances among SNP-specific genotypes. By restricting our consideration to an autosomal diallelic SNP, and hence to only three genotypes, we can examine the problem comprehensively, both from a biological and a statistical point of view.

There are many measures that can be used to describe the phenotype distribution of a quantitative trait, and these can be broadly classified into measures of location (e.g., the mean and the median) and measures of variability. We shall use the word variability here to indicate all the aspects of a distribution other than its location. The measures of variability include measures of spread (e.g., the variance and the interquartile distance) and shape (e.g., skewness and kurtosis). In general, the complete distribution can be identified by all its moments, provided they exist. Although the commonest measures used for describing the genotype-specific distribution of a quantitative trait are measures of location, it has sometimes been suggested that measures of variability be used to both describe and infer particular biological phenomena. For example, genetic segregation underlying a trait will induce platykurtosis, positive skewness, and/or an increase in sibship variance as a function of the sibship mean,^2,3 and differences in the genotypic variances of a trait of interest result if the “reaction norm”^4,5 of each genotype is different, suggesting the possibility of a genotype × environment or genotype × genotype interaction. In this last case the environment or genotypes at other loci could be acting at the cellular, organ, or individual level; at some point, a metabolic process that results in trait variability, and variance in particular, that differs from genotype to genotype might be involved. However, whereas in each of these cases the phenomenon would result in differences in the variability of the phenotype distribution, as indicated in the references cited, this does not necessarily imply that such differences, when found, must be due to that phenomenon.

In this report we argue that, for an autosomal diallelic SNP in particular, it is difficult to make valid biological inferences about a quantitative trait on the basis of variance heterogeneity among the genotype-specific distributions unless the locations (in particular, the means) of the three distributions are equal. We first argue that, when the means are not all equal, the variance heterogeneity might in fact be explained by a distribution in which the variance is a function of the mean. To highlight this fact, we argue that there exists a transformation of the data that will tend to make the variances equal and describe a standard method that will at a minimum decrease the variance heterogeneity. We then consider the difficulty of even testing specifically for differences among variances. In order to demonstrate our argument, we illustrate these points by using statistics that have been reported elsewhere.¹

The first thing to note is that, for the purpose of statistical analysis, the informational content of a set of data points remains the same if each is transformed by a strictly monotonic function, which amounts to a change in the scale of measurement in the sense that, if we know all the data values on one scale, we can determine them on the other. Clearly, whenever we measure a quantitative trait the scale units used must be taken into account, whether for clinical purposes or merely for their magnitudes to be generally understood; and some scales help us better understand physical processes. Nevertheless, the scales on which we measure quantitative (interval-scale) traits are man made and have little intrinsic biological relevance. Figure 1 illustrates four different changes in scale, each of which corresponds to a nonlinear transformation. In each case the transformation is a strictly monotonic function, so that the ranks of the measurements are identical on the two scales, the original and the transformed, as indicated by the fact that the lines connecting the two scales never cross. Furthermore, arbitrary scales of measurement can induce a variety of relationships between the mean and variance of any distribution. It follows that making any biological inferences on the basis of the fact that genotype-specific variances are different is highly questionable when a simple monotonic transformation could remove the observed differences. At the very least, we should attempt to show that no such transformation of the data can drastically reduce, or even eliminate, any differences in the variances that are found.

Figure 1.

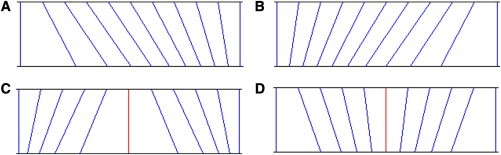
Pictorial Representation of Four Different Nonlinear Changes in the Scale of Measurement Representing Four Different Classes of Monotonic Transformations

In each panel, equal intervals on the original scale of measurement (top line) become different, unequal intervals on the transformed scale (bottom line). In panel (A) the transformation leads to decreasing intervals with increasing values on the original scale; in panel (B), the transformation leads to increasing intervals. In the lower panels, the red line is the point at which there is a change from increasing to decreasing (C) or from decreasing to increasing (D) intervals, corresponding to a zero second derivative of the transformation function.

As explained above, there are many different measures of variability for a quantitative trait, and hence, as opposed to the distribution means, these various distribution measures can differ from SNP genotype to SNP genotype in many different ways. If the genotype-specific distributions differ in any specific measure of variability, this could be a hint that we should seek an underlying cause for the differences. Here we concentrate on the variance and show that, provided the three means are different, there is always a monotonic transformation that will tend to equalize the three variances. Finding a transformation that will do this is often simple when we assume there are only three phenotypic distributions, so that the variance, V, can always be expressed as a quadratic function, f, of the mean, m:

$$V=f\left(m\right)=a{m}^2+bm+c.$$ (Equation 1)

If we can express the variance of a trait x as a function of its mean m_x, f(m_x), then a standard way of seeking a transformation y that will tend to make the variances approximately equal is given by Bartlett:⁶

$$y=g\left(x\right)\propto \int \frac{dx}{\sqrt{f\left(x\right)}}.$$ (Equation 2)

This is based on approximating the variance of a function of a random variable by the first few terms of a Taylor series; the more terms taken in the series, the more equal we would expect the variances to be, so that with enough terms the variances would be equal; however, with more terms we would arrive at an integral equation with no analytical solution.

Provided this integral equation can be solved, it gives us an approximate variance-equalizing transformation. Because it is always possible to fit a quadratic polynomial to three points on the plane, we consider this as the functional relationship between the variance and the mean. Note that if the three means are equal, the three variances, unless all equal, cannot be the same function of the means.

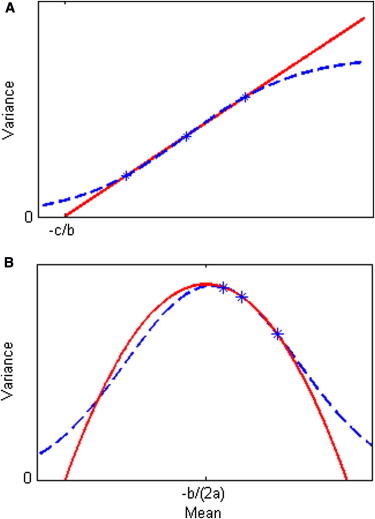
Because a variance must be positive, there are four possible situations, as illustrated in Figure 2. In this figure, panels A and B illustrate the special situation when a = 0, so that f is a linear function that meets the x axis at –c/b. The corresponding transformations, shown in Figures 3A and 3B, result in the changes of scale seen in Figures 1A and 1B, respectively. (Once transformed, any further linear transformation applied to all the data does not change the homogeneity or heterogeneity of the variances, so there are no vertical scales shown in Figure 3). Figures 2C and 2D illustrate the two types of quadratic function possible; for the integral in Equation 2 to be solvable (in the sense of having a real solution) for these quadratic functions, we must either have a > 0 and b² − 4ac ≤ 0 or have a < 0 and b² − 4ac > 0. The corresponding transformations, shown in Figures 3C and 3D, result in the changes of scale seen in Figures 1C and 1D, respectively (mathematical expressions for all these transformations are given in Appendix A). Note that if the minimum of the curve in Figure 2C touches the x axis, which occurs at the point –b/(2a), this would indicate a point where the variance would be 0; in this case the transformation would be monotonic only if the values of x lie either all below or all above that minimum point; if the minimum is below the x axis (when b² − 4ac > 0), the variance is positive only below L₁ and above L₂. Conversely, the curve in Figure 2D meets the x axis at two points, L₂ and L₁, and as seen in Figure 3D, only values of x between these two points could be transformed by the corresponding transformation.

Figure 2.

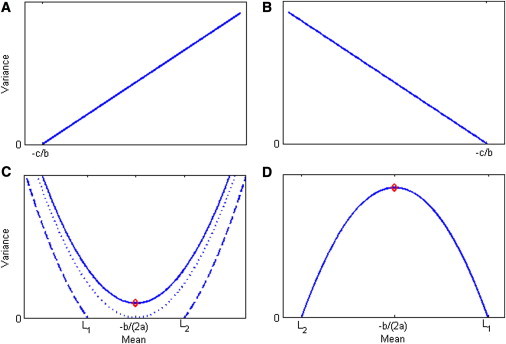
Functional Relationship between the Variance and the Mean, V = am²+ bm +c, Fitted to Three Points, which Are SNP Genotypes

(A and B) Linear functions (a = 0) with b > 0 and b < 0, respectively.

(C and D) Quadratic functions. (C) a > 0: the solid curve is for b² − 4ac < 0; the dotted curve is for b² − 4ac = 0; the dashed curve is for b² − 4ac > 0. (D) a < 0 and b² − 4ac > 0. The red points in (C) and (D) correspond to the red lines in Figures 1C and 1D. L₁ = $(-b-\sqrt{b^2-4ac})/2a$ and L₂ = $(-b+\sqrt{b^2-4ac})/2a$.

Figure 3.

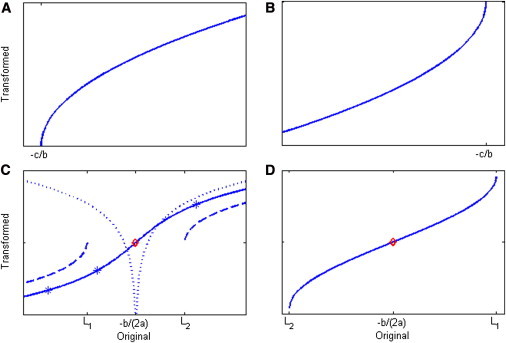
The Four Classes of Monotonic Transformation Functions

(A, B, C, and D) These panels correspond, respectively, to Figures 2A, 2B, 2C, and 2D. In each panel the abscissa (x axis) is the original value, and the ordinate (y axis) is the transformed value. (C and D) Red points correspond to the red points in Figure 2 and to the red lines in Figure 1. (C) The solid line is the transformation for b² − 4ac < 0; the dotted one is for b²− 4ac = 0 and is monotonic only on each side of x = −b/(2a); the dashed line is the transformation for b² − 4ac > 0. L₁ = $(-b-\sqrt{b^2-4ac})/2a$ and L₂ = $(-b+\sqrt{b^2-4ac})/2a$.

Thus, a first step should be to fit a quadratic equation to the SNP data: the three pairs of values (variance, mean). There are the four possibilities, illustrated in Figures 1–3 and summarized as follows:

• Panel A: a = 0, b > 0; the transformation can only be applied to values of x > −c/b

• Panel B: a = 0, b < 0; the transformation can only be applied to values of x < −c/b.

• Panel C: a > 0; if b² − 4ac < 0, all values of x can be transformed; if b² − 4ac = 0, we obtain a monotonic transformation only when all x lie to one side of −b/(2a); if b² − 4ac > 0, we obtain a monotonic transformation only when all x < L₁ or > L₂.

• Panel D: a < 0, b² − 4ac > 0; the transformation can only be applied to values of x in the interval (L₂, L₁).

We now illustrate the above procedure with the data in Table 1, which we adapted from the bottom six entries in the first column of Table 2 in Yang et al.¹ This adaptation gave BMI estimates corresponding to the SNP rs7202116 (we arbitrarily added 25 to the mean values they report; doing this puts into perspective the mean differences that were found but has no effect on the final results we give below). Although Yang et al. considered various transformations to reduce the variance heterogeneity among the genotype groups, they did not use a transformation designed specifically for this purpose, so it is of interest, as an illustration, to see what their particular result might have been. From the data in Table 1 we find the quadratic equation

$$V=f\left(m\right)=2.101m^2-104.123m+\mathrm{1290.918.}$$ (Equation 3)

Table 1.

Estimated Means and Variances of BMI for the Three Genotypes at FTO SNP rs7202116

	AA	AB	BB
Variance (V)	0.93	0.99	1.14
Mean (m)	24.929	25.005	25.129

Adapted from Yang et al.¹

Table 2.

Parameters Used for Data Generation in the Simulation Experiments

	Group 1	Group 2	Group 3
Normal Distribution, Variance 1
Mean	1	2	3
Excess kurtosis	0	0	0
Normal Distribution, Variance 100
Mean	1	2	3
Excess kurtosis	0	0	0
Log-Normal Distribution, Variance 1
Mean	2.8777	7.4552	20.1104
Excess kurtosis	2.1616	0.2928	0.0397
Log-Normal Distribution, Variance 100
Mean	5.5792	10.2991	22.0539
Excess kurtosis	511.6796	34.2338	3.9777

We note that b² − 4ac = −7.419 < 0 and a = 2.101 > 0. We are therefore in the situation illustrated in panel C of Figures 1–3, so that all values of x can be transformed. Figure 4 shows that all the means are to the right of the red cutoff in those figures, so for these data the transformed intervals always decrease as BMI increases.

Figure 4.

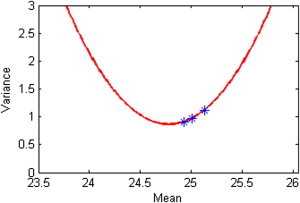
The Quadratic Function Fitted by the Three Genotypes at SNP rs7202116 in the FTO Locus with the Means and Variances in Table 1

The question now arises as to how well this transformation performs in equalizing the three variances, which could be examined in the data. Without the data, however, given the values in Table 1 we can estimate the three variances after transformation if we make assumptions about the form of the distribution. We did this for two situations: assuming three normal distributions and assuming three log-normal distributions (details are given in Appendix B). We note in Table 1 that the largest variance divided by the smallest variance is 1.226; the corresponding ratio after the transformation is 1.106 when we assume normal distributions and 1.103 when we assume log-normal distributions. Thus, in either case there is more than a 50% reduction in the difference between the largest and smallest variance.

Before we seek a variance-equalizing transformation of the data, it would be reasonable to test whether the data at hand exhibit significantly different variances between genotype groups. One way this might be done is to use Bartlett’s test.⁷ Let $s^2$ be the pooled variance estimated from the three groups corresponding to the three genotypes, let $s_t^2$ be that from the t-th group, with ${\varphi }_t$ being the number of degrees of freedom, and let $\text{Φ}={\sum }_t{\varphi }_t$. Then, if we let M = $\text{Φ}\ln s^2-{\sum }_t{\varphi }_t\ln s_t^2$, Batlett’s test statistic is

$${\mathit{M}}_1=\frac{\mathit{M}}{\left(\mathit{1+A}\right)}\text{where}\mathit{A}=\frac{1}{3\left(k-1\right)}\left(\sum _t\frac{1}{{\varphi }_t}-\frac{1}{\text{Φ}}\right)\text{and}\mathit{k}=3\text{,}\text{the}\text{number}\text{of}\text{groups}\text{.}$$

Under the assumption of normality and equal variances, in large samples this is distributed as ${\chi }_{k-1}^2$ (i.e., chi-square with k − 1 degrees of freedom [df]). However, even when one uses permutations to evaluate the p value, this test is not robust to non-normality, so a significant result could indicate either non-normality or differences in variability among the three distributions. If we are specifically interested in testing variances, it might be possible to use Bartlett’s test statistic as modified by Box.⁸ Let ${\gamma }_2$ denote the standardized fourth cumulant, i.e., the excess kurtosis (the coefficient of kurtosis − 3). Then, for large samples, Box showed that if ${\gamma }_2$ is the same in all groups, we might expect M to be distributed as (1 + ${\gamma }_2/2$) ${\chi }_2^2$; that is, M₂ = M/(1 + ${\gamma }_2/2$) should be distributed as ${\chi }_2^2$. Alternatively, we might consider using either M₁ or M₂ in a permutation test. We attach the genotype as a label to each observation and obtain a replicate sample by shuffling the labels. From each of N replicates we calculate the test statistic and compare the N values with our observed statistic M^∗. The permutation p value of the observed statistic M^∗ is then estimated to be:

$$\text{p}\text{value}=\frac{\text{number}\text{of}\text{statistics}\text{from}\text{replicates}\ge M^{\text{∗}}}{N}.$$ (Equation 4)

However, centering the observations—as required in the calculation of M₁ and M₂—must be performed prior to shuffling the labels when one obtains each permutation replicate, rather than after shuffling. To the extent that we can equate all measures of spread of a distribution, a better way to test whether variances are different might be to use a modification of Levene’s test, which has been reported to be robust to many types of non-normality provided it is used with a bootstrapping approach.⁹

Because bootstrapping and a permutation test could be computationally intensive, and because there is no underlying theoretical result for conducting the modification that Box made to Bartlett’s test for variance homogeneity when there is different excess kurtosis in the groups being tested, we conducted small simulation experiments to determine to what extent the asymptotic distributions are good approximations for a test of variances when we substitute for ${\gamma }_2$ a pooled estimate obtained from the three groups. For each experiment we simulated 1,000 data sets each of 1,000 individuals under the assumption that the 1,000 individuals are from three different marker genotype distributions. We assumed that the minor allele frequency (MAF), q, is 0.5 or 0.1 and that the genotype frequencies follow Hardy-Weinberg proportions, q², 2q(1 − q), and (1 − q).² Within each marker group, we assumed normal or log-normal trait distributions. In each simulation, the three distributions had the same variance, but different means and (in the case of log-normal distributions) different excess kurtosis, as detailed in Table 2. We considered two different common variances, 1 and 100; in the latter case the additive effect of an allele is 1/10 of a standard deviation, which corresponds approximately to what was found for the FTO locus SNP.¹ Estimating ${\gamma }_2$ as indicated in Appendix C, we calculated the statistics M₁ and M₂ = M/(1 + ${\gamma }_2/2$); the former should asymptotically follow ${\chi }_2^2$ if the data in each group are normally distributed, and the latter should follow the same distribution if the excess kurtosis is the same in each group. We also performed Levene’s test, modified to use the median instead of the mean because, for this test also, there are no underlying theoretical results and only simulation results have been reported. The left half of Table 3 shows the fractions of the data sets for which the statistics reached or exceeded the 0.95 and 0.99 fractiles of the ${\chi }_2^2$ distribution (respectively, 5.991465 and 9.21034). It can be seen that the type I error is reasonably well controlled when the data in each group are normally distributed but that it is inflated when they are log-normally distributed —especially when the variance is large compared to the mean (which leads to more excess kurtosis).

Table 3.

Type I Error Studied by Simulation Experiments with the Parameters Described in Table 2

Allele Freqency qa	Variance	As χ22Testsb						As Permutation Tests
		α = 0.05			α = 0.01			α = 0.05			α = 0.01
		M1	M2	L	M1	M2	L	M1	M2	L	M1	M2	L
Normal Distribution
0.1	1	0.054	0.060	0.042	0.013	0.015	0.008	0.057	0.056	0.043	0.012	0.012	0.010
	100	0.052	0.056	0.042	0.010	0.011	0.008	0.055	0.055	0.043	0.011	0.012	0.010
0.5	1	0.059	0.056	0.049	0.009	0.008	0.008	0.052	0.054	0.049	0.008	0.008	0.008
	100	0.055	0.060	0.049	0.009	0.011	0.008	0.062	0.059	0.049	0.010	0.009	0.008
Log-Normal Distribution
0.1	1	0.095	0.092	0.058	0.025	0.024	0.011	0.084	0.085	0.068	0.019	0.021	0.014
	100	0.781	0.325	0.688	0.663	0.159	0.470	0.373	0.328	0.700	0.169	0.132	0.441
0.5	1	0.122	0.072	0.094	0.048	0.019	0.023	0.070	0.063	0.097	0.019	0.016	0.027
	100	0.818	0.231	0.936	0.722	0.119	0.850	0.213	0.154	0.940	0.115	0.060	0.864

Bartlett’s statistic (M₁), Box’s modification of Bartlett’s statistic (M₂), and Levene’s test statistic based on the median (L) are compared to fractiles of the χ₂² distribution (left half of table); permutation tests using these three statistics are compared to estimated fractiles of the corresponding null distributions (right half of table).

^aThe proportions of the three groups are respectively q², 2q(1 − q), (1 − q)².

^bLevene’s statistic L asymptotically follows $(1/2){\chi }_2^2$.

Furthermore, we investigated whether the same statistics, when used in a permutation test, could serve as tests for variance homogeneity. To do this, we subtracted the group means for each generated data set and then obtained 1,000 replicate permutation samples. From each of these we calculated the permutation p value as in Equation 4; this value should follow a uniform distribution in [0,1] under the null distribution. We then determined the type I error of the permutation test as the fraction of the 1,000 data sets for which the permutation p value was less than or equal to 0.05 or 0.01. In the case of Levene’s test, this should be equivalent to bootstrapping. The results of these simulations are presented in the right half of Table 3. It is seen that, if the data in each of the three groups are normally distributed, the corresponding permutation tests are reasonably valid for testing differences in variance; however, this does not hold when the three groups are log-normally distributed. Note that although these tests might detect differences in variability, they are not valid for specifically testing differences in variance. (It is well known that Batlett’s test without permutation can also detect departure from normality, even when all the central moments are the same in the three groups⁷).

Finally, several things should be noted. First, had the three means in Figure 4 spanned both sides of the minimum on the curve, this would imply that, with increasing values of the trait (see Figure 1C), on the transformed scale intervals first increase and then decrease. Because it is not unnatural for traits to have both a floor and a ceiling (this is always true for a proportion, which must lie between 0 and 1), this would not be a reason to disqualify the transformation.

Second, when we fit a quadratic polynomial to the data on three genotypes, the resulting integral in Equation 1 does not have a real solution when the variance is negative, which is of course impossible. However, it could happen that some extreme data points lie to the right of L₁ or to the left of L₂ (see Figure 2) and that they thus correspond to no real solutions and cannot be transformed. Unless such data points are too numerous (which is unlikely to happen when the data are normally distributed within groups), they could be trimmed or winsorized. It is also possible that a different function that would always lead to a real solution to Equation 1 and that fits three points perfectly (Figure 5) could be found. In fact, it is always possible to find a polynomial that it will fit any number of points and is of high enough degree that it will always lie above 0. In particular, this is true if the three points that fit a quadratic polynomial lie on the dashed line illustrated in Figure 2C, for the case b² – 4ac > 0. Thus we can always find a transformation that will tend to equalize the variances, both in this case and more generally, when there are more than three genotypic groups with different means. But a transformation that changes intervals as the trait increases in value from increasing to decreasing, and then back to increasing (and this occurs multiple times), would hardly be acceptable.

Figure 5.

Different Functions that Can Be Fitted to Three (Mean, Variance) Points

The solid curves are the functions shown in Figure 2. Panels (A) and (B) correspond to Figures 2A and 2D, respectively. The dashed curves are a cumulative logistic function in (A) and an exponentiated quadratic in (B). Because these functions are always positive, a corresponding approximate variance-stabilizing transformation is theoretically available for all x (an analytical solution to the integral is possible for the function in [B], but not for that in [A]).

Third, a reviewer asked whether the reduction in variance heterogeneity obtained by using the transformation given by Equation 1, which necessarily would not be expected to eliminate all the variance heterogeneity, would reduce the statistical significance of the differences among the variances. We showed in our example that the ratio of the largest to the smallest variance is reduced, but interestingly, that is not sufficient to show that the statistical significance of the variance heterogeneity is reduced. We therefore simulated 1,000 samples, each comprising 1,000 individuals for whom BMI values mimicked values in Table 1, by assuming Hardy-Weinberg proportions and using genotypic fractions based on one of the reported allele frequencies:¹ 173 were simulated to have values from N(24.929,0.93), 486 from N(25.005,0.99), and 341 from N(25.129,1.14). We applied the six tests indicated in Table 3 before and after transformation and found that the distribution of p values increased after transformation. For example, before transformation the proportion of tests significant at the 5% level (whether the p values were nominal or obtained from a permutation test) ranged from 0.308 to 0.341; after transformation, that proportion ranged from 0.015 (the original Bartlett’s test) to 0.188 (Box’s modification of Bartlett’s test, by permutation). That the p value is expected to increase is not necessarily a general result, however, because it can be shown (specifically in the case of Levene’s test) that it is possible to find a small part of the parameter space (i.e., values of the means and proportions in each genotype group) where this result would not hold. Of course, what level of significance to use for such a test depends on both the purpose of the test and how many such tests are performed. We argue that in any case it is difficult to make valid biological inferences from such a test alone. If we wish to use such a test as a screen to seek specific biological phenomena, to be tested by other means, we might be ready to allow for a relatively large type I error, especially in view of the fact that much larger samples are required to detect differences in measures of variability than differences in measures of location. But then we might be more interested in other measures of variability than simply the variance because in principle, specifically for three distributions, it should be possible to transform the data to make the estimated variances equal if the means are different.

Fourth, it might be thought that one can always make the data virtually normally distributed within groups by applying the inverse normal transformation to the ranks of the data within each group. But if we transform the data this way, then their ranks in the total sample, across all three groups, no longer stay the same and the transformation is thus not monotonic.

Fifth, it is of interest to note that any change of scale that eliminates variance heterogeneity must also eliminate any interaction caused by this heterogeneity. This implies that the recent enthusiasm for using tests of variance heterogeneity as a screen to find interactions with diallelic SNPs^10–12 should be tempered by the knowledge that, unless the genotype means are virtually equal, such a screen might serve no useful purpose. Because more parsimonious statistical models without interaction terms tend to lead to more precise parameter estimates,^13,14 scale transformation should generally be considered for statistical modeling purposes, but the results should be transformed back to the original scale for ease of interpretation.

In conclusion, we might always expect there to be small differences among the genotype groups, either in their means or in their variances. In large enough samples, we are virtually certain to find statistically significant differences. The biological and/or clinical significance of such differences will always need to be determined on nonstatistical grounds. It is well appreciated that statistically significant differences among genotype means require a plausible mechanism to be biologically significant. The same is true for any measure of variability. In the absence of genotypic mean differences, we can hardly infer that differences in variances are per se of biological interest. We have demonstrated how when the means are different a relatively simple change of scale can diminish any variance heterogeneity, and from a theoretical point of view, as we have indicated, there implicitly exists a scale that would remove all the variance heterogeneity – although that scale might have undesirable properties, especially if there are more than three genotypes. In addition, it is not clear how we can even test for differences in variance. We have shown by simulation that Bartlett’s test, Box’s modification of it, and Levene’s test, as well as permutation tests based on the same statistics, are generally applicable to testing for variance differences only when the data are normally distributed in each genotype group. For non-normal cases, they might detect statistically significant variability differences, which could well have biological significance, but not necessarily significant variance differences.

Appendix A

We give here the mathematical expressions for the transformations in the four panels of Figures 1–3.

Panel A

$$y=g\left(x\right)\propto \int \frac{dx}{\sqrt{bx+c}}=\frac{2\sqrt{bx+c}}{b}\text{,}\text{where}b>0,x>-\frac{c}{b}\text{.}$$

Panel B

$$y=g\left(x\right)\propto \int \frac{dx}{\sqrt{bx+c}}=\frac{2\sqrt{bx+c}}{b}\text{,}\text{where}b<0,x<-\frac{c}{b}.$$

Panel C

• (1)If b² − 4ac < 0,

$$y=g\left(x\right)\propto \int \frac{dx}{\sqrt{a{x}^2+bx+c}}=\frac{1}{\sqrt{a}}{\sinh }^{-1}\frac{2ax+b}{\sqrt{4ac-b^2}};$$

• (2)If b² − 4ac = 0,

$$y=g\left(x\right)\propto \int \frac{dx}{\sqrt{a{x}^2+bx+c}}=\frac{1}{\sqrt{a}}\ln \left|2ax+b\right|:$$

in this case, if all the x > −b/(2a), the transformation is a monotonic increasing function; if all the x < −b/(2a), the transformation is a monotonic decreasing function; if the x values are on both side of −b/(2a), the transformation is not monotonic;

• (3)If b² – 4ac > 0,

$$y=g\left(x\right)\propto \int \frac{dx}{\sqrt{a{x}^2+bx+c}}=\frac{1}{\sqrt{a}}\ln \left|2\sqrt{a\left(a{x}^2+bx+c\right)}+2ax+b\right|,$$

$$x<\frac{-b-\sqrt{b^2-4ac}}{2a}\text{or}x>\frac{-b+\sqrt{b^2-4ac}}{2a}.$$

Panel D

$$y=g\left(x\right)\propto \int \frac{dx}{\sqrt{a{x}^2+bx+c}}=\frac{-1}{\sqrt{-a}}{\sin }^{-1}\frac{2ax+b}{\sqrt{b^2-4ac}},$$

$$\frac{-b+\sqrt{b^2-4ac}}{2a}<x<\frac{-b-\sqrt{b^2-4ac}}{2a};$$

in the above expression, y takes on the principal values of the inverse sine function between $-\pi /2$ and $\pi /2$.

Appendix B

If we take the transformation $y=g\left(x\right)=(1/\sqrt{a}){\sinh }^{-1}\left(\right[2ax+b]/\sqrt{4ac-b^2})$, where x is the variable on the original scale and y is on the transformed scale, and if a = 2.101, b = −104.123, and c = 1290.918 (see Equation 3), within each genotype group the variance on the transformed scale is E(y²) − [E(y)]² = E[g(x)]² − {E[g(x)]}² = $\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}{\left(g\left(x\right)\right)}^{2}f\left(x\right)dx-{\left[\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}g\left(x\right)f\left(x\right)dx\right]}^2$, where f(x) is the probability density function of x on the original scale. If BMI is normally distributed, then f(x) = $(1/\sigma \sqrt{2\pi })e^{-{(x-\mu )}^2/2{\sigma }^2}$, where μ and σ² were taken to be the means and variances in Table 1. If BMI is log-normally distributed with mean μ and variance σ², then f(x) = $(1/x\nu \sqrt{2\pi })e^{-{(\ln x-\tau )}^2/2{\nu }^2}$(x > 0), where ν² = $\text{ln}\left({\sigma }^2/e^{2\ln \mu }+1\right)$ and τ = $\ln \mu -{\nu }^2/2$. The integrals were calculated with the R function “integrate” and a requested accuracy of 10⁻⁶.

Appendix C

We estimated the excess kurtosis for the t-th genotype group by

$$G_{2t}=\frac{k_4}{k_2^2}=\frac{\left(n_t+1\right)n_t\left(n_t-1\right)}{\left(n_t-2\right)\left(n_t-3\right)}\frac{\sum _{i=1}^n{\left(x_{it}-{\overline{x}}_t\right)}^4}{{\left(\sum _{i=1}^n{\left(x_{it}-{\overline{x}}_t\right)}^2\right)}^2}-3\frac{{\left(n_t-1\right)}^2}{\left(n_t-2\right)\left(n_t-3\right)}\text{,}t=1\text{,}2\text{,}3\text{,}$$

where x_it is the i-th observations in the t-th group, which has sample mean ${\overline{x}}_t$.

Then we took the pooled estimate of ${\gamma }_2$ for the whole data set to be $G_{2pool}={\sum }_{t=1}^k{\psi }_t{G}_{2t}/{\sum }_{t=1}^k{\psi }_t$, where ${\psi }_t=\left(n_t+1\right)n_t\left(n_t-1\right)/\left(n_t-2\right)\left(n_t-3\right)$, t = 1, 2, 3.

Web Resources

The URL for data presented herein is as follows:

• Online Mendelian Inheritance in Man (OMIM), http://www.omim.org/