Meta-analysis of Gene-Level Associations for Rare Variants Based on Single-Variant Statistics

Abstract

Meta-analysis of genome-wide association studies (GWASs) has led to the discoveries of many common variants associated with complex human diseases. There is a growing recognition that identifying “causal” rare variants also requires large-scale meta-analysis. The fact that association tests with rare variants are performed at the gene level rather than at the variant level poses unprecedented challenges in the meta-analysis. First, different studies may adopt different gene-level tests, so the results are not compatible. Second, gene-level tests require multivariate statistics (i.e., components of the test statistic and their covariance matrix), which are difficult to obtain. To overcome these challenges, we propose to perform gene-level tests for rare variants by combining the results of single-variant analysis (i.e., p values of association tests and effect estimates) from participating studies. This simple strategy is possible because of an insight that multivariate statistics can be recovered from single-variant statistics, together with the correlation matrix of the single-variant test statistics, which can be estimated from one of the participating studies or from a publicly available database. We show both theoretically and numerically that the proposed meta-analysis approach provides accurate control of the type I error and is as powerful as joint analysis of individual participant data. This approach accommodates any disease phenotype and any study design and produces all commonly used gene-level tests. An application to the GWAS summary results of the Genetic Investigation of ANthropometric Traits (GIANT) consortium reveals rare and low-frequency variants associated with human height. The relevant software is freely available.

Introduction

Meta-analysis, which combines summary statistics from a series of independent studies, plays an increasingly important role in human genetics research.^1–3 Obtaining summary statistics is much more appealing than collecting individual participant data because it protects the privacy of study participants, avoids cumbersome integration of genotype and phenotype data from different studies, and increases the number of available studies. In addition, meta-analysis of summary statistics is statistically as efficient as joint analysis of individual participant data.^4,5 Thus, meta-analysis has become a norm in GWASs, resulting in the discoveries of numerous common variants associated with complex human diseases.

Recent advances in next-generation sequencing technologies have made it possible to extend association studies to rare variants, which are expected to have larger effects on complex human diseases than common variants.^6,7 To enrich association signals and reduce the penalty of multiple testing, investigators typically perform gene-level association tests by aggregating the mutation information of the rare variants within a gene. The simplest approach is the burden test, which calculates a single burden score for each subject by taking a weighted sum of the mutation counts over the variant sites with weights dependent on minor allele frequencies (MAFs) and assesses the disease association with the burden score.^8–12 A second approach is the variable threshold (VT) method, which performs a burden test by aggregating the variants whose MAFs are lower than a threshold and minimizes the p value over observed MAF thresholds.^11,12 A third approach is the variance-component testing, which is aimed at detecting the presence of both deleterious and protective variants in the same gene.^13–15 Gene-level tests for rare variants have limited power because only a small fraction of study subjects carry any mutation within a gene and there are high background rates of neutral variation even in “causal” genes. Thus, there is a growing recognition that identifying “causal” rare variants would require large-scale meta-analysis.

It is much more challenging to perform meta-analysis of rare variants than to do so with common variants. First, different studies may adopt different types of gene-level tests, so the test results are not compatible. Second, even if the same type of test is adopted, different studies may use different gene annotations, different classes of variants, or different MAFs. Third, meta-analysis is restricted to the specific gene-level test results provided by the participating studies and there is no flexibility to perform other tests. Fourth, VT and variance-component tests are multivariate in nature, so the meta-analysis requires multivariate summary statistics (i.e., the components of the test statistic and their covariance matrix); combining the p values of multivariate tests would lose power. Although these difficulties may be alleviated by following a common protocol in a well-organized consortium, the tremendous effort required to execute such a protocol will seriously limit the use of meta-analysis.

To circumvent these problems, we propose to collate only the results of single-variant analysis from participating studies and leave the choices of the gene-level test, annotation, variant class, and MAFs to the discretion of the meta-analyst. This attractive strategy is possible because of two important insights. First, all commonly used gene-level test statistics can be constructed from the score vector and the corresponding information matrix for testing the global null hypothesis that none of the variants in the gene is associated with the disease phenotype. Second, the score vector and information matrix can be recovered from the single-variant results, namely the p values based on Wald, score, or likelihood-ratio (LR) tests and the effect estimates, together with the correlation matrix of the single-variant test statistics. The correlation matrix can be estimated from one of the participating studies, perhaps the study that the meta-analyst is directly involved with. If such a study is not available, the correlation matrix can be approximated by the correlation matrix of the genotypes from a publicly available database, such as the 1000 Genomes, HapMap, or NHLBI Exome Sequencing Project (ESP).^16–18 We show both theoretically and numerically that the proposed meta-analysis approach provides accurate control of the type I error and is as powerful as joint analysis of individual participant data. This approach can accommodate any disease phenotype and any study design and produce all commonly used gene-level tests.

The proposed approach not only greatly facilitates meta-analysis of sequencing studies but also provides a way to exploit the massive GWAS data. Many GWASs have focused on common variants but have also produced single-variant results for rare and low-frequency variants, which have seldom been exploited. Our approach can be used to combine such single-variant results and perform gene-level association tests. Single-variant results are available in NCBI’s database of Genotypes and Phenotypes (dbGaP) and can be freely accessed without applying for controlled access to individual participant data. Thus, the proposed approach is far more useful than any methods that require multivariate summary statistics or individual participant data.

This work was motivated by the GIANT project.^19,20 The GIANT consortium successfully identified a number of common variants for anthropometric traits.^19,20 It also collected single-variant summary results for rare and low-frequency variants. Single-variant meta-analysis of those results would have little power. Therefore, we wished to conduct gene-based meta-analysis for those variants. Because the consortium involved a very large number of cohorts, it would not be feasible to ask individual investigators to perform gene-level association tests and provide multivariate summary statistics. Therefore, we applied the proposed methods to the existing single-variant summary results by using one of the participating cohorts, the Atherosclerosis Risk in Communities (ARIC) Study,²¹ as the internal reference. We identified several genes containing variants for extreme height that were not detectable by single-variant meta-analysis.

Material and Methods

Suppose that we are interested in m rare variants within a gene. (We use the term “rare variants” to encompass both low-frequency and truly rare variants.) The genotypes are represented by $G={\left(G_1,\dots ,G_m\right)}^{\text{T}}$, where G_j is the number of minor alleles at the j^th variant site. Let Y denote the trait of interest, which can be continuous or discrete, and let X denote a set of covariates (e.g., demographical variables and principal components for ancestry) plus the unit component. We relate Y to G and X through a generalized linear model by specifying the conditional density function of Y given G and X as

$$\text{exp}\left\{\frac{y\left({\beta }^{\text{T}}G+{\gamma }^{\text{T}}X\right)-b\left({\beta }^{\text{T}}G+{\gamma }^{\text{T}}X\right)}{a\left(\varphi \right)}+c\left(y,\varphi \right)\right\},$$ (Equation 1)

where $\beta ={\left({\beta }_1,\dots ,{\beta }_m\right)}^{\text{T}}$ and γ are regression parameters, ϕ is a dispersion parameter, and a, b, and c are specific functions. Denote $b^{\prime }\left(z\right)=db\left(z\right)/dz$ and $b^{″}\left(z\right)=d^{2}b\left(z\right)/d{z}^2$. For the linear model, $a\left(\varphi \right)={\sigma }^2$, $b\left(z\right)=\left(1/2\right)z^2$, $b^{\prime }\left(z\right)=z$, and $b^{″}\left(z\right)=1$. For the logistic regression model, $a\left(\varphi \right)=1$, $b\left(z\right)=\text{log}\left(1+e^z\right)$, $b^{\prime }\left(z\right)=e^z/\left(1+e^z\right)$, and $b^{″}\left(z\right)=e^z/{\left(1+e^z\right)}^2$.

For a study with n unrelated subjects, the data consist of $\left(Y_i,G_i,X_i\right)$ $\left(i=1,\dots ,n\right)$. The score statistic for testing the null hypothesis $H_0:\beta =0$ is

$$U=a{\left(\hat{\varphi }\right)}^{-1}\sum _{i=1}^n\left\{Y_i-b^{\prime }\left({\hat{\gamma }}^{\text{T}}{X}_i\right)\right\}{G}_i,$$

where $\hat{\gamma }$ and $\hat{\varphi }$ are the restricted maximum likelihood estimators (MLEs) of γ and ϕ under H₀. For the linear model, $\hat{\gamma }={\left({\sum }_{i=1}^n{X}_i{X}_i^{\text{T}}\right)}^{-1}{\sum }_{i=1}^n{Y}_i{X}_i$ and $a\left(\hat{\varphi }\right)={\hat{\sigma }}^2=n^{-1}{\sum }_{i=1}^n{\left(Y_i-{\hat{\gamma }}^{\text{T}}{X}_i\right)}^2$. Under H₀, U is asymptotically m-variate normal with mean 0 and covariance matrix

$$V=a{\left(\hat{\varphi }\right)}^{-1}\left[\sum _{i=1}^n{b}^{″}\left({\hat{\gamma }}^{\text{T}}{X}_i\right)G_i{G}_i^{\text{T}}-\left\{\sum _{i=1}^n{b}^{″}\left({\hat{\gamma }}^{\text{T}}{X}_i\right)G_i{X}_i^{\text{T}}\right\}{\left\{\sum _{i=1}^n{b}^{″}\left({\hat{\gamma }}^{\text{T}}{X}_i\right)X_i{X}_i^{\text{T}}\right\}}^{-1}\left\{\sum _{i=1}^n{b}^{″}\left({\hat{\gamma }}^{\text{T}}{X}_i\right)X_i{G}_i^{\text{T}}\right\}\right],$$ (Equation 2)

which is the information matrix evaluated at $\beta =0$, $\gamma =\hat{\gamma }$, and $\varphi =\hat{\varphi }$.

Suppose that we wish to combine the results of L independent studies. For $l=1,\dots ,L$, let $U^{\left(l\right)}$ and $V^{\left(l\right)}$ denote the values of U and V from the l^th study. It is not necessary for all m variants to be present in all studies. If the l^th study contains no mutation at a particular variant site, we simply set the corresponding entries in $U^{\left(l\right)}$ and $V^{\left(l\right)}$ to 0. Define

$$\overline{U}=\sum _{l=1}^L{U}^{\left(l\right)},\overline{V}=\sum _{l=1}^L{V}^{\left(l\right)}.$$

Under H₀, $\overline{U}$ is asymptotically m-variate normal with mean 0 and covariance matrix $\overline{V}$. If we allow γ and ϕ of Equation 1 to be different among the L studies, then $\overline{U}$ is exactly the score statistic for testing H₀ in the joint likelihood of the individual participant data of the L studies.⁵ Thus, meta-analysis based on score statistics is equivalent to joint analysis of individual participant data.

Given $\overline{U}$ and $\overline{V}$, we can construct all commonly used gene-based association tests for rare variants. Specifically, define the (weighted) burden score ${\xi }^{\text{T}}G$, where ξ is an m-vector of weights that depend on the MAFs.^8–12 The score statistic for testing the disease association with the burden score can be expressed as $\tilde{U}={\xi }^{\text{T}}\overline{U}$, whose variance is $\tilde{V}={\xi }^{\text{T}}\overline{V}\xi$.¹² The test statistic $T=\tilde{U}/{\tilde{V}}^{1/2}$ is referred to the standard normal distribution. If we are interested in K burden scores with vectors of weights ${\xi }_1,\dots ,{\xi }_K$, then we calculate ${\tilde{U}}_k={\xi }_k^{\text{T}}\overline{U}\left(k=1,\dots ,K\right)$. Under the null hypothesis of no association, ${\left({\tilde{U}}_1,\dots ,{\tilde{U}}_K\right)}^{\text{T}}$ is asymptotically K-variate normal with mean 0 and covariance matrix $\left\{{\tilde{V}}_{kl};k,l=1,\dots ,K\right\}$, where ${\tilde{V}}_{kl}={\xi }_k^{\text{T}}\overline{V}{\xi }_l$. The p value for the maximum statistic $T_{\text{max}}={\text{max}}_{k=1,\dots ,K}\left|{\tilde{U}}_k\right|/{\tilde{V}}_{kk}^{1/2}$ is determined by the multivariate normal distribution of ${\left({\tilde{U}}_1,\dots ,{\tilde{U}}_K\right)}^{\text{T}}$.¹² The SKAT statistic can be written as $Q={\overline{U}}^{\text{T}}W\overline{U},$ where W is a diagonal weight matrix that depends on the MAFs through a beta function.¹⁵ The null distribution of Q is determined by ${\sum }_{j=1}^m{\lambda }_j{\chi }_{1,j}^2,$ where ${\lambda }_1,\dots ,{\lambda }_m$ are the eigenvalues of ${\overline{V}}^{1/2}W{\overline{V}}^{1/2}$ and ${\chi }_{1,1}^2,\dots ,{\chi }_{1,m}^2$ are independent ${\chi }_1^2$ random variables.

The above meta-analysis approach is predicated on the availability of U and V for each study. Note that U is an m × 1 vector and V is an m × m matrix. Such multivariate summary statistics are not available in published papers or public databases. Even for a well-organized consortium, it is logistically difficult to generate such multivariate summary statistics. We show below that it is possible to recover U and V for each study from the (univariate) single-variant statistics provided that the correlation matrix of U can be estimated from an internal or external reference panel.

For each study, let U_j denote the j^th component of U and $V_{jl}$ denote the ${\left(j,l\right)}^{\text{th}}$ element of V. Let Z_j denote the standard-normal statistic for testing the null hypothesis $H_j:{\beta }_j=0$ under Equation 1 with ${\beta }^{\text{T}}G$ replaced by ${\beta }_j{G}_j$. For the score, Wald, and LR tests, Z_j takes the forms of $U_j/V_{jj}^{1/2}$, ${\hat{\beta }}_j/s{e}_j$, and $\text{sign}\left({\hat{\beta }}_j\right)\sqrt{LR}$, respectively, where ${\hat{\beta }}_j$ is the MLE of β_j, $s{e}_j$ is the standard error of ${\hat{\beta }}_j$, and LR is the likelihood ratio statistic. The three forms of Z_j are asymptotically equivalent. When U_j is not available but Z_j is, we approximate U_j by

$${\hat{U}}_j=w_j{Z}_j,$$

where $w_j$ is an approximation to $V_{jj}^{1/2}$. Write $\hat{U}={\left({\hat{U}}_1,\dots ,{\hat{U}}_m\right)}^{\text{T}}$, which is asymptotically m-variate normal with mean 0 and covariance matrix $\hat{V}=\left\{{\hat{V}}_{jl};j,l=1,\dots ,m\right\}$, where

$${\hat{V}}_{jl}=w_j{R}_{jl}{w}_l,$$

and $R=\left\{R_{jl};j,l=1,\dots ,m\right\}$ is the covariance or correlation matrix of ${\left(Z_1,\dots ,Z_m\right)}^{\text{T}}$. We substitute $\hat{U}$ and $\hat{V}$ for U and V in each study and perform the aforementioned gene-based association tests. If Z_j is the score test and $w_j=V_{jj}^{1/2}$, then ${\hat{U}}_j=U_j$. If Z_j is the Wald or LR test or $w_j\ne V_{jj}^{1/2}$, then ${\hat{U}}_j\ne U_j$; however, meta-analysis based on $\hat{U}$ and $\hat{V}$ will still have correct type I error as long as the correlation matrix R is correctly estimated for each study.

We show in Appendix A that the correlation matrix R is determined primarily by the correlation matrix of G. Specifically, two studies with the same correlation matrix of G will have the same R if covariates are absent or independent of genotypes and will have approximately the same R even if covariates are correlated with genotypes. Thus, we can use the value of R from one study to approximate the values of R in other studies with similar linkage disequilibrium (LD) structures. We refer to such a study as the internal reference. If no internal reference is available, we resort to an external reference panel such as the HapMap, 1000 Genomes, or ESP.^16–18 It is desirable to use an internal or external reference panel that has the same ancestry as the target study to ensure similar LD structures.

We assume that the summary statistics that are available for meta-analysis contain the parameter estimates and p values of individual variants, i.e., $\left({\hat{\beta }}_j,p_j\right)\left(j=1,\dots ,m\right)$, for each study, where p_j is the (two-sided) p value based on the Wald, score, or LR test. We recover the test statistic Z_j by $\text{sign}\left({\hat{\beta }}_j\right){\text{Φ}}^{-1}\left(1-p_j/2\right)$, where Φ is the standard-normal distribution function. (We replace $p_j/2$ by p_j in the formula if the p value is based on a one-sided test.)

The standard error estimates $s{e}_j$s are usually contained in the summary results. If not, we recover $s{e}_j$ by ${\hat{\beta }}_j/Z_j$. This approximation is exact if Z_j is the Wald statistic and is accurate if Z_j is the score or LR statistic. Recall that $s{e}_j$ is the standard error estimate of ${\hat{\beta }}_j$ and that $V_{jj}$ is the variance estimate of U_j. It is reasonable to set $w_j=1/s{e}_j$ because $1/s{e}_j$ is the same as $V_{jj}^{1/2}$ except that the information matrix used to calculate $s{e}_j$ is evaluated at the MLEs of β_j, γ, and ϕ whereas the information matrix used to calculate $V_{jj}$ is evaluated at $\beta =0$ and the restricted MLEs of γ and ϕ. For rare variants, the $s{e}_j$s may be unstable. If an internal reference study is available, we may set $w_j={\left\{\left(n/n^{\text{∗}}\right)V_{jj}^{\text{∗}}\right\}}^{1/2}$, where $n^{\text{∗}}$ and $V_{jj}^{\text{∗}}$ are the values of n and $V_{jj}$ for the reference study, the reason being that $V_{jj}$ is approximately proportional to the sample size when the trait variance (for continuous Y) or the case-control ratio (for binary Y) is fixed. If the trait variances or the case-control ratios are possibly different between the reference and target studies, we replace ${\left(n/n^{\text{∗}}\right)}^{1/2}$ by the median of $\left\{\left(s{e}_l^{\text{∗}}/s{e}_l\right);l=1,\dots ,M\right\}$, where M is the total number of variants that are genotyped and $s{e}_l^{\text{∗}}$ is the value of $s{e}_l$ in the reference study. The median provides a stable estimate for the ratio of the two standard errors, allowing the trait variances or the case-control ratios to be different between studies. If no internal reference is available, we set $w_j={\left(s{e}_j^{†}\right)}^{-1}\times {\text{median}}_{l=1,\dots ,M}\left(s{e}_l^{†}/s{e}_l\right)$, where $s{e}_l^{†}$ is the value of $s{e}_l$ in the largest study of the meta-analysis.

In short, the summary results contain minimally the p values and effect estimates, from which we recover the standard-normal statistics. The standard error estimates are optional. When they are not available, we set $s{e}_j={\hat{\beta }}_j/Z_j$. If an internal reference is available, we set $w_j=V_{jj}^{{\text{∗}}^{1/2}}\times {\text{median}}_{l=1,\dots ,M}\left(s{e}_l^{\text{∗}}/s{e}_l\right)$ and estimate R by the correlation matrix of the score statistics in the internal reference; otherwise, we set $w_j={\left(s{e}_j^{†}\right)}^{-1}\times {\text{median}}_{l=1,\dots ,M}\left(s{e}_l^{†}/s{e}_l\right)$ and estimate R by the correlation matrix of the SNP genotypes in the external reference.

Results

Simulation Studies

We carried out extensive simulation studies to evaluate the performance of the proposed methods in realistic settings. To cover different MAF and LD spectrums, we chose two genes on chromosome 1 (OR2T29 and LDLRAD1) and focused on SNPs with MAFs <5%. According to the WHI African-American data from the ESP,¹⁸ there are seven SNPs in OR2T29, with MAFs of 0.003, 0.030, 0.003, 0.036, 0.017, 0.017, and 0.036 for rs142202454, rs199706827, rs200777722, rs200169450, rs201345491, rs200919674, and rs201896684 and genotype correlations shown in the upper block of Table 1. This gene contains a few relatively common SNPs that are in modest LD. There are eight SNPs in LDLRAD1, with MAFs of 0.021, 0.001, 0.001, 0.017, 0.001, 0.007, 0.007, and 0.001 for rs143619888, rs150468103, rs141759859, rs149768061, rs147345740, rs145889899, rs142900519, and rs149114405 and genotype correlations shown in the upper block of Table 2. This gene contains mostly rare SNPs, the correlations being very low except for one pair. We generated the SNP genotypes of the two genes via GWAsimulator²² to mimic the MAFs and LD patterns observed in the ESP WHI data.

Table 1.

Correlation Matrices for OR2T29

Correlation Matrix of Genotypes
	rs142202454	rs199706827	rs200777722	rs200169450	rs201345491	rs200919674	rs201896684
rs142202454	1	0.141	−0.003	0.129	0.109	0.110	0.120
rs199706827		1	0.292	0.656	0.541	0.523	0.581
rs200777722			1	0.128	−0.007	−0.007	0.025
rs200169450				1	0.496	0.555	0.799
rs201345491					1	0.829	0.613
rs200919674						1	0.672
rs201896684							1
Correlation Matrix of Test Statistics with Case-Control Ratio of 1
	rs142202454	rs199706827	rs200777722	rs200169450	rs201345491	rs200919674	rs201896684
rs142202454	1	0.136	−0.004	0.124	0.104	0.104	0.115
rs199706827		1	0.293	0.646	0.531	0.511	0.568
rs200777722			1	0.125	−0.012	−0.012	0.020
rs200169450				1	0.483	0.543	0.793
rs201345491					1	0.825	0.602
rs200919674						1	0.663
rs201896684							1
Correlation Matrix of Test Statistics with Case-Control Ratio of 2
	rs142202454	rs199706827	rs200777722	rs200169450	rs201345491	rs200919674	rs201896684
rs142202454	1	0.132	−0.004	0.120	0.101	0.101	0.111
rs199706827		1	0.292	0.640	0.524	0.504	0.562
rs200777722			1	0.124	−0.011	−0.012	0.020
rs200169450				1	0.476	0.537	0.790
rs201345491					1	0.822	0.597
rs200919674						1	0.658
rs201896684							1

Table 2.

Correlation Matrices for LDLRAD1

Correlation Matrix of Genotypes
	rs143619888	rs150468103	rs141759859	rs149768061	rs147345740	rs145889899	rs142900519	rs149114405
rs143619888	1	0.005	0.005	0.019	0.005	0.012	0	0
rs150468103		1	0.001	0.005	0.001	0.003	0	0
rs141759859			1	0.005	0.002	0.003	0.003	0
rs149768061				1	0.005	0.639	0.011	0
rs147345740					1	0.003	0.003	0
rs145889899						1	0.007	0
rs142900519							1	0
rs149114405								1
Correlation Matrix of Test Statistics with Case-Control Ratio of 1
	rs143619888	rs150468103	rs141759859	rs149768061	rs147345740	rs145889899	rs142900519	rs149114405
rs143619888	1	0.005	0.005	0.021	0.005	0.014	0.001	0.001
rs150468103		1	0.001	0.005	0.001	0.003	0	0
rs141759859			1	0.005	0.001	0.003	0.003	0
rs149768061				1	0.005	0.641	0.012	0
rs147345740					1	0.003	0.003	0
rs145889899						1	0.008	0
rs142900519							1	0
rs149114405								1
Correlation Matrix of Test Statistics with Case-Control Ratio of 2
	rs143619888	rs150468103	rs141759859	rs149768061	rs147345740	rs145889899	rs142900519	rs149114405
rs143619888	1	0.006	0.006	0.021	0.006	0.014	0.001	0.001
rs150468103		1	0.001	0.005	0.001	0.003	0	0
rs141759859			1	0.005	0.001	0.003	0.003	0
rs149768061				1	0.005	0.636	0.011	0
rs147345740					1	0.004	0.003	0
rs145889899						1	0.008	0
rs142900519							1	0
rs149114405								1

We conducted meta-analysis of three studies with 2,000, 1,500, and 1,000 subjects, referred to as study 1, study 2, and study 3, respectively. We considered the situations both with and without an internal reference. For the former, study 1 was treated as the internal reference. For the latter, we generated an “external” reference panel with 1,000 subjects (mimicking the ESP WHI data). We simulated quantitative traits from the linear regression model $Y=\beta S+0.2X+\mathit{ϵ}$ and binary traits from the logistic regression model $\text{log}\left\{P\left(Y=1\right)/P\left(Y=0\right)\right\}=\beta S+0.2X$, where S is the total number of mutations the subject carries in the gene, X is a normal random variable with mean 0.2S and variance one, and ε is zero-mean normal with variance σ². Note that X is correlated with S and may represent a principal component for ancestry. To allow the possibilities of both equal and unequal error variances among studies, we set ${\sigma }^2=1.0$ in study 1 and varied the values of σ² in the other two studies. For binary traits, we obtained an equal number of cases and controls for study 1 and varied the case-control ratios for the other two studies. As shown in Tables 1 and 2, the correlation matrices of the test statistics are highly similar between the case-control ratios of 1 and 2 (middle and bottom blocks) and are also very similar to the correlation matrix of the genotypes in the external reference panel (upper block). These results corroborate the theoretical results given in Appendix A.

We evaluated the proposed methods based on single-variant statistics with an internal or external reference, denoted as SV-I and SV-E, respectively. As a benchmark, we included the meta-analysis method based on multivariate statistics (i.e., U and V), referred to as MV, which is a gold standard because it is equivalent to joint analysis of original data. We also included a naive method that sets $w_j$ to $1/s{e}_j$ and R to the identity matrix; the naive method assumes independence among variants and thus does not use any reference data to estimate the LD. We constructed the burden, VT, and SKAT tests. For the burden test, we adopted the MAF threshold of 5%, which is commonly called T5. For SKAT, we used the default weighted linear kernel function. We considered the p values from the Wald, score, and LR tests.

The type I error rates for quantitative and binary traits when the summary statistics contain the standard error estimates are shown in Tables 3 and 4, respectively. The corresponding results when the summary statistics do not contain the standard error estimates are shown in Tables S1 and S2 available online. The two sets of results are highly similar. For quantitative traits, both SV-I and SV-E with the score, LR, or Wald test are as accurate as MV. For binary traits, SV-I tends to be more accurate than SV-E and the Wald test tends to be more conservative than the score and LR tests, especially for LDLRAD1. The naive method has severe inflation of the type I error, even for LDLRAD1, which has only one pair of correlated SNPs.

Table 3.

Type I Error Divided by the Nominal Significance Level for Quantitative Traits

Gene	Test	σ2	MV	SV-I			SV-E			Naive
				Score	LR	Wald	Score	LR	Wald	Score	LR	Wald
OR2T29	T5	0.5	0.97	0.98	0.99	1.00	0.96	0.97	0.98	75.83	75.98	76.15
		1.0	1.00	1.01	1.01	1.02	0.98	0.98	1.00	75.69	75.85	76.00
	VT	0.5	0.98	1.00	1.01	1.02	0.97	0.99	1.00	53.67	53.82	53.94
		1.0	1.00	1.00	1.00	1.01	1.01	1.02	1.03	53.45	53.60	53.75
	SKAT	0.5	0.97	0.95	0.97	0.98	0.95	0.96	0.98	19.27	19.38	19.49
		1.0	1.00	1.01	1.01	1.02	0.99	1.00	1.01	19.20	19.29	19.37
LDLRAD1	T5	0.5	0.99	0.98	0.99	1.00	0.97	0.98	1.00	2.89	2.91	2.92
		1.0	1.00	0.98	0.98	0.98	0.97	0.97	0.98	2.84	2.85	2.87
	VT	0.5	1.01	1.04	1.04	1.05	1.02	1.03	1.04	2.94	2.97	2.99
		1.0	1.02	1.05	1.06	1.06	1.01	1.02	1.02	2.99	3.01	3.02
	SKAT	0.5	1.01	1.02	1.03	1.04	1.01	1.03	1.04	2.42	2.45	2.48
		1.0	1.01	1.00	1.01	1.02	1.04	1.05	1.06	2.40	2.42	2.45

The summary statistics include the standard error estimates. The nominal significance level α = 0.001. σ² pertains to the error variance in studies 2 and 3. MV is the gold standard. Each entry is based on 1,000,000 replicates.

Table 4.

Type I Error Divided by the Nominal Significance Level for Binary Traits

Gene	Test	Ratio	MV	SV-I			SV-E			Naive
				Score	LR	Wald	Score	LR	Wald	Score	LR	Wald
OR2T29	T5	1.0	0.93	0.86	0.91	0.79	0.83	0.89	0.72	72.00	73.05	69.90
		2.0	1.03	0.97	0.98	0.90	0.92	0.94	0.81	72.33	72.47	70.05
	VT	1.0	0.93	0.87	0.93	0.77	0.81	0.90	0.66	50.14	51.01	48.18
		2.0	1.04	1.01	1.00	0.88	0.95	0.95	0.75	50.78	50.82	48.67
	SKAT	1.0	0.92	0.88	0.92	0.79	0.82	0.89	0.66	17.06	17.67	15.90
		2.0	1.00	0.97	0.96	0.85	0.90	0.92	0.73	17.44	17.58	16.10
LDLRAD1	T5	1.0	0.88	0.81	0.88	0.70	0.75	0.84	0.58	1.97	2.13	1.62
		2.0	1.03	1.05	0.99	0.88	0.96	0.94	0.74	2.81	2.60	2.32
	VT	1.0	0.95	0.76	0.83	0.59	0.62	0.75	0.40	1.80	2.03	1.40
		2.0	1.04	1.06	0.98	0.84	0.85	0.82	0.56	2.84	2.59	2.16
	SKAT	1.0	0.90	0.81	0.92	0.63	0.68	0.81	0.43	1.31	1.52	0.96
		2.0	0.93	0.91	0.93	0.68	0.73	0.81	0.48	1.67	1.63	1.25

The summary statistics include the standard error estimates. The nominal significance level $\alpha =0.001$. Ratio is the case-control ratio in studies 2 and 3. MV is the gold standard. Each entry is based on 1,000,000 replicates.

Figures 1 and 2 compare the powers of SV-I, SV-E, and MV for quantitative and binary traits, respectively. The results of the naive method are not shown because it has inflated type I error and thus would not make a fair power comparison. For quantitative traits, both SV-I and SV-E are as powerful as MV. For binary traits, SV-I and SV-E tend to be slightly less powerful than MV; SV-E loses a little more power than does SV-I because the $w_j$s in SV-E are not as stable as in SV-I. However, all the power differences are very small. The results for SV-I and SV-E shown in Figures 1 and 2 pertain to the score test. For quantitative traits, the results based on the Wald and LR tests are virtually identical to those of the score test (data not shown). For binary traits, the LR test yields slightly higher power than the score test whereas the Wald test yields slightly lower power; see Figures S1 and S2.

Figure 1.

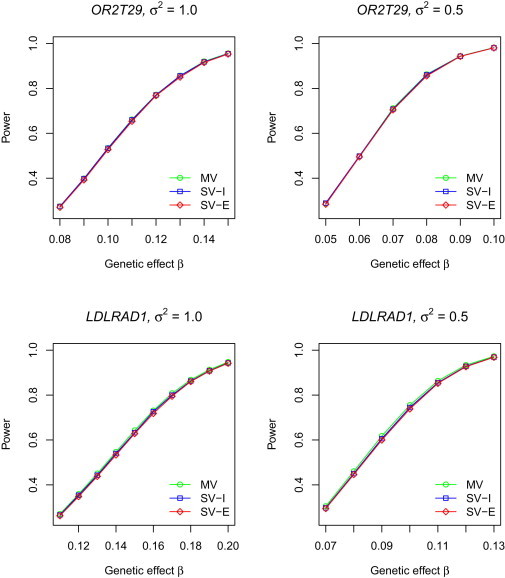
Power of T5 at the Nominal Significance Level α of 0.001 for Quantitative Traits

σ² is the error variance for studies 2 and 3. For SV-I and SV-E, single-variant p values are based on the score test. Each power estimate is based on 10,000 replicates.

Figure 2.

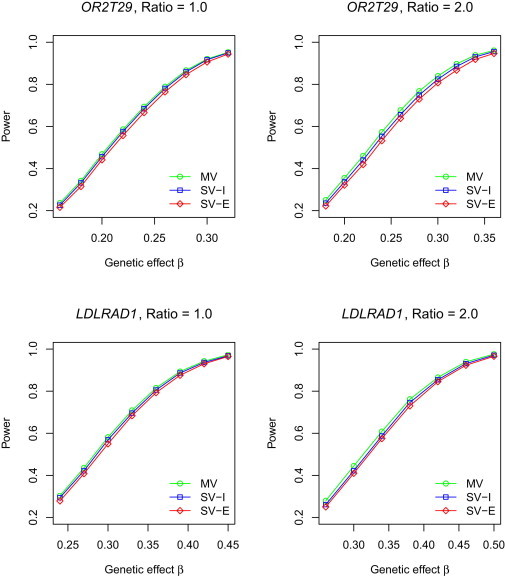
Power of T5 at the Nominal Significance Level α of 0.001 for Binary Traits

Ratio is the case-control ratio for studies 2 and 3. For SV-I and SV-E, single-variant p values are based on the score test. Each power estimate is based on 10,000 replicates.

We also compared our methods to Fisher’s method of combining p values. As shown in Figure S3, our methods are substantially more powerful than Fisher’s method.

Finally, we examined the robustness of the proposed methods to misspecification of the reference. We simulated an external reference mimicking the HeartGO African-American data from the ESP while still simulating studies 1–3 from the ESP WHI data. In the HeartGO data, the eight SNPs in LDLRAD1 have MAFs of 0.011, 0, 0.001, 0.016, 0, 0.01, 0.001, and 0 and genotype correlations shown in Table S3. Clearly, the MAFs and LD patterns differ considerably between the WHI and HeartGO data. The simulation results for the proposed method based on single-variant statistics with the misspecified external reference, denoted by SV-E′, are shown in Table S4 and Figure S4. Evidently, SV-E′ has reasonable control of the type I error and is slightly less powerful than SV-E (using the correct external reference).

GIANT Data

The GIANT consortium is an international collaboration that seeks to discover genetic loci that modulate human body size and shape, including height and measures of obesity.¹⁹ The consortium was recently interested in identifying genetic loci associated with the extremes of height, body mass index (BMI), and waist-hip ratio adjusted by BMI.²⁰ The investigators from 50 GWASs were asked to perform case-control comparisons, treating individuals in the highest 5^th percentile of the age- and sex-adjusted distribution as cases and those in the lowest 5^th percentile as controls, for a total of ∼2.8 million SNPs (genotyped or imputed by the HapMap CEU population); the analysis was stratified by sex and disease status and adjusted by age and principal components for ancestry. The summary results submitted to the consortium contain the effect estimates, the standard error estimates, and the two-sided p values of the association tests for individual SNPs. The associations with common SNPs had been assessed by single-variant meta-analysis; however, the information on rare variants had not yet been exploited because of the lack of proper analysis methods. With the proposed methods, we conducted gene-level association tests of rare variants through meta-analysis of the single-variant summary results, focusing on the binary trait of extreme height.

The 50 studies involved ∼160,000 cohort members of the European ancestry, among whom ∼14,600 subjects were selected as cases or controls for extreme height. The sample sizes ranged from 812 to 14,594, with a median of 13,413. We had access to the original data from one of the cohorts, the ARIC study,²¹ which contains 8,108 cohort members and 812 subjects with extreme height. Because the subjects from the 50 studies are all of the same ancestry, we used the ARIC study as the internal reference. We annotated the genes in PLINK and filtered out SNPs with MAFs >5% to end up with 10,851 genes containing at least one SNP. Thus, the genome-wide significance threshold based on the Bonferroni correction would be ∼5 × 10⁻⁶. The qq-plots for the SV-I and naive methods are displayed in Figure 3. The naive method yielded excessive positive findings and failed to identify some of the genes identified by the SV-I method. Although the values of the genomic control λ were ∼1.1 for the SV-I tests, the modest inflation is unlikely attributed to the proposed methods because the value of λ was ∼1.08 in the single-variant meta-analysis (data not shown).

Figure 3.

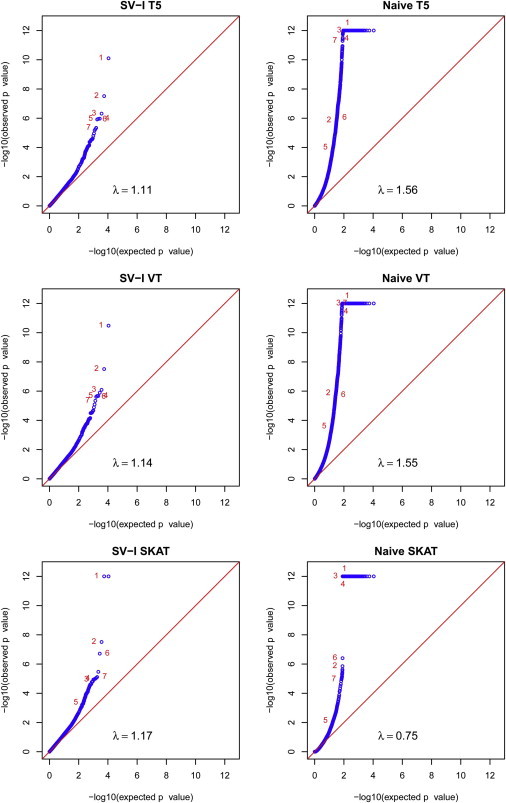
Quantile-Quantile Plots of −log₁₀(p Values) in the Meta-analysis of the GIANT Extreme Height Studies

The genes that pass the genome-wide significance threshold by the SV-I T5 tests are marked. The p values <10⁻¹² are truncated.

The SV-I T5 tests identified seven genes that pass the genome-wide significance threshold of 5 × 10⁻⁶. The results for those genes are shown in Table 5. One of the genes (SNRPC [MIM 603522]) contains only one SNP, so the gene-level and single-variant tests are the same. A second gene (CRYBB1 [MIM 600929]) contains three SNPs, one of which has a p value that is the same as the gene-based p value and two of which have very large p values. A third gene (SPEF2 [MIM 610172]) contains 15 SNPs, 9 of which have p values similar to the gene-based p value and the rest of which have large p values. For the remaining four genes (ACAN [MIM 155760], CPNE1 [MIM 604205], RBM12 [MIM 607179], and FAM134A), the gene-level p values are smaller than the single-variant p values. Among those four genes, only two have single-variant p values that are less than 5 × 10⁻⁶. The foregoing results show that the proposed method may boost the association signals.

Table 5.

Top Genes Identified by T5 in the SV-I Meta-analysis

Gene/SNP	Chr	Position	MAF	Effect	SE	p Value
ACAN						8.0 × 10−11
rs16942341	15	87189909	0.026	−0.508	0.082	3.7 × 10−10
rs16942383	15	87206056	0.034	−0.437	0.070	1.3 × 10−9
rs12385976	15	87205096	0.042	−0.358	0.060	2.6 × 10−9
rs8024016	15	87209085	0.038	−0.356	0.060	8.0 × 10−9
rs3784757	15	87204408	0.031	−0.430	0.071	1.5 × 10−8
SNRPC						3.1 × 10−8
rs9462016	6	34847768	0.046	0.263	0.055	3.1 × 10−8
CPNE1						4.9 × 10−7
rs6060540	20	33711263	0.048	0.216	0.054	7.0 × 10−5
rs17426738	20	33701348	0.047	0.219	0.055	7.0 × 10−5
rs6060536	20	33700401	0.047	0.219	0.055	7.1 × 10−5
rs926994	20	33684437	0.048	0.215	0.055	7.6 × 10−5
rs2230219	20	33682894	0.048	0.215	0.055	7.6 × 10−5
rs6121021	20	33715852	0.048	0.216	0.055	7.9 × 10−5
rs17427233	20	33709531	0.047	0.217	0.055	7.9 × 10−5
rs6058292	20	33712183	0.048	0.217	0.055	8.0 × 10−5
rs17426419	20	33693059	0.047	0.208	0.054	1.1 × 10−4
rs6121019	20	33714062	0.048	0.210	0.055	1.2 × 10−4
rs17092957	20	33715359	0.033	0.201	0.071	4.2 × 10−3
rs7272885	20	33690567	0.033	0.203	0.071	4.9 × 10−3
rs17092885	20	33693038	0.033	0.198	0.071	6.0 × 10−3
rs17092937	20	33707024	0.033	0.193	0.071	6.7 × 10−3
rs17092945	20	33708972	0.033	0.198	0.071	6.9 × 10−3
rs8050	20	33700638	0.033	0.197	0.071	7.4 × 10−3
rs17092915	20	33702884	0.033	0.196	0.071	7.4 × 10−3
rs17092869	20	33687762	0.046	0.190	0.090	1.4 × 10−2
rs2425068	20	33678137	0.045	−0.048	0.080	4.3 × 10−1
RBM12						1.1 × 10−6
Subset of CPNE1 SNPs
CRYBB1						1.1 × 10−6
rs2301439	22	25327383	0.019	−0.789	0.184	1.1 × 10−6
rs5752354	22	25332648	0.007	−0.231	0.172	4.6 × 10−2
rs7290642	22	25331364	0.010	−0.176	0.110	8.1 × 10−2
FAM134A						1.2 × 10−6
rs2293072	2	219753698	0.041	0.299	0.063	1.7 × 10−6
rs2385393	2	219757631	0.003	0.908	0.608	3.3 × 10−1
SPEF2						4.6 × 10−6
rs6862961	5	35736129	0.021	−0.392	0.088	4.3 × 10−6
rs7714298	5	35760267	0.021	−0.385	0.088	5.4 × 10−6
rs10061088	5	35759618	0.021	−0.386	0.088	5.5 × 10−6
rs10058394	5	35757834	0.021	−0.384	0.088	6.0 × 10−6
rs10051352	5	35757747	0.021	−0.383	0.088	6.8 × 10−6
rs10071847	5	35757450	0.021	−0.383	0.088	7.6 × 10−6
rs7703587	5	35756245	0.021	−0.382	0.088	7.6 × 10−6
rs7703605	5	35756281	0.021	−0.383	0.088	8.2 × 10−6
rs6891096	5	35733720	0.021	−0.387	0.089	1.2 × 10−5
rs2361394	5	35836304	0.044	−0.013	0.017	8.7 × 10−2
rs11742689	5	35841905	0.041	−0.099	0.067	1.8 × 10−1
rs11740118	5	35714128	0.047	−0.094	0.060	2.0 × 10−1
rs7725710	5	35732941	0.023	0.117	0.174	3.3 × 10−1
rs286441	5	35673325	0.036	0.022	0.060	9.7 × 10−1
rs12514911	5	35662699	0.036	0.022	0.060	9.7 × 10−1

The top gene in our analysis, ACAN, was previously identified by the GIANT consortium through the single-variant meta-analysis for the full height distribution and the extreme height;^19,20 only SNP rs16942341 in this gene was reported.¹⁹ None of the other genes in Table 5 have previously been identified to be associated with human height. All the SNPs identified by previous single-variant meta-analysis²⁰ are relatively common, i.e., MAFs $\ge 0.15$, so those SNPs were not included in the current gene-level analysis.

For further comparisons, we performed the single-variant meta-analysis of all the ∼126,000 rare variants that were included in the gene-level analysis. We found that 19 of them pass the Bonferroni threshold of $0.05/126,000\approx 4\times {10}^{-7}$. Those 19 SNPs belong to five genes (ACAN, DIS3L2 [MIM 614184], SNRPC, UQCC [MIM 611797], and PLAG1 [MIM 603026]), only two of which (ACAN and SNRPC) were identified by the gene-level meta-analysis. Thus, the proposed approach is complementary to single-variant meta-analysis and can facilitate discoveries of rare variants for complex human traits.

Discussion

We presented a simple strategy to perform meta-analysis of association results for rare variants in GWASs and sequencing studies. Our approach is very convenient and versatile because it requires only univariate statistics from standard single-variant analysis and accommodates any type of study and any type of trait. Our algorithms are very fast. It took ∼2 hr on an IBM HS22 machine to perform the meta-analysis of the GIANT data. The proposed methods are implemented in the software MAGA: Meta-Analysis of Gene-level Associations.

Alternative methods are being pursued independently by other research groups. To our knowledge, those methods all require multivariate statistics (i.e., the score vector U and the information matrix V). It is more challenging, both theoretically and computationally, to develop meta-analysis methods based on univariate statistics. We made a key observation that multivariate statistics can be recovered from univariate statistics provided that the correlation matrix of the single-variant test statistics can be determined. We rigorously justified the use of an internal or external reference to estimate the correlation matrix and derived statistically optimal and numerically stable weighting schemes. From a practical point of view, multivariate statistics can be collected only prospectively in well-organized consortia. By contrast, our approach requires only readily available univariate results from single-variant analysis and is particularly attractive in the retrospective analysis of existing studies.

Our approach requires a good estimate for the correlation matrix of the single-variant test statistics. We showed both theoretically and numerically that the correlation matrix of the test statistics is determined primarily by the correlation matrix of the genotypes and is not sensitive to the trait variance, the case-control ratio, or the distribution of covariates. The studies to be combined need not to be drawn from a single ancestral population. If the studies involve both European and African ancestries, then race-specific (internal or external) references can be used. It is preferable to use an internal than an external reference and to use a large reference panel.

Our methods allow variants to be polymorphic in only some of the participating studies by setting the entries in the score vector and information matrix corresponding to a nonpolymorphic variant to zero. In our current implementation, we disregard the variants that are not polymorphic in the reference panel. An alternative strategy is to assume that such rare variants are independent of others so that the corresponding entries in the correlation matrix R can be set to zero.

Meta-analysis based on score tests performs better than that of LR or Wald tests, especially for binary traits with rare variants. We make use of the standardized test statistics or p values rather than the score statistics (i.e., components of U) and their variances (i.e., diagonal elements of V). The latter, together with the correlation matrix, would completely recover the multivariate statistics. We do not require score statistics and their variances because they are not available in standard software packages such as SAS and R. However, score statistics and their variances can be obtained from special computer programs, such as SCORE-Seq¹² and SCORE-SeqTDS.²³ We recommend that such information be included in the summary results of single-variant analysis in the future, which will lead to more accurate meta-analysis.

In the current practice, a variant that does not have a valid effect estimate is excluded from the summary results file. For a case-control study, the log odds ratio cannot be estimated if there are no mutations in either the case group or the control group. However, such a study contains valuable information about the association. To solve this dilemma, we again recommend that researchers include the score statistics and their variances in the summary results, which can be combined efficiently in meta-analysis. Another (less attractive) solution would be to report the p value of an asymptotic or exact test and the direction of the association. These two pieces of information can be used to construct an approximate standard-normal statistic, and the sample size and MAF can be used to estimate the variance for the weighting scheme.

Although we have focused on studies of unrelated individuals with quantitative and binary traits, the proposed methods are applicable to other study designs and other traits, such as family studies, extreme-trait sampling, ordinal traits, and (potentially censored) ages at disease onset. In addition, the proposed methods can be extended to incorporate heterogeneous effects among studies by defining the burden statistic as ${\sum }_{l=1}^L{\left({\xi }^{\left(l\right)\text{T}}{U}^{\left(l\right)}\right)}^2$ and the SKAT statistic as ${\sum }_{l=1}^L{U}^{\left(l\right)\text{T}}{W}^{\left(l\right)}{U}^{\left(l\right)}$, where ${\xi }^{\left(l\right)}$ and $W^{\left(l\right)}$ pertain to the l^th study.

In summary, we developed a simple and practical tool to perform meta-analysis of rare variants based on single-variant statistics. We showed both theoretically and numerically that the proposed approach has correct type I error and is as powerful as joint analysis of individual participant data (provided that an appropriate reference panel is available). With the GIANT data, we demonstrated that the proposed approach can facilitate the discoveries of rare variants associated with complex human traits.

Appendix A

The joint distributions of ${\left(Z_1,\dots ,Z_m\right)}^{\text{T}}$ for the Wald, score, and LR tests are asymptotically the same.²⁴ Thus, it suffices to evaluate the covariance matrix of ${\left(Z_1,\dots ,Z_m\right)}^{\text{T}}$ in terms of the correlation matrix of U. Without loss of generality, we center the $G_i$s at their sample mean.

In the absence of covariates, Equation 2 reduces to

$$V=a{\left(\hat{\varphi }\right)}^{-1}{b}^{″}\left(\hat{\gamma }\right)\sum _{i=1}^n{G}_i{G}_i^{\text{T}},$$

so the corresponding R is equal to the sample correlation matrix of G. If there exist covariates but they are independent of or weakly correlated with genetic variables, then

$$\begin{array}{c}V\approx a{\left(\hat{\varphi }\right)}^{-1}\left[n^{-1}\sum _{i=1}^n{b}^{″}\left({\hat{\gamma }}^{\text{T}}{X}_i\right)\sum _{i=1}^n{G}_i{G}_i^{\text{T}}-\left\{n^{-1}\sum _{i=1}^n{G}_i\sum _{i=1}^n{b}^{″}\left({\hat{\gamma }}^{\text{T}}{X}_i\right)X_i^{\text{T}}\right\}{\left\{\sum _{i=1}^n{b}^{″}\left({\hat{\gamma }}^{\text{T}}{X}_i\right)X_i{X}_i^{\text{T}}\right\}}^{-1}\left\{n^{-1}\sum _{i=1}^n{b}^{″}\left({\hat{\gamma }}^{\text{T}}{X}_i\right)X_i\sum _{i=1}^n{G}_i^{\text{T}}\right\}\right],\\ =a{\left(\hat{\varphi }\right)}^{-1}{n}^{-1}\sum _{i=1}^n{b}^{″}\left({\hat{\gamma }}^{\text{T}}{X}_i\right)\sum _{i=1}^n{G}_i{G}_i^{\text{T}},\end{array}$$

where the second equality follows from the centering of the genotype values. Thus, the corresponding R is approximately equal to the correlation matrix of G. In conclusion, two studies with the same LD structure will have essentially the same correlation matrix R if there are no covariates or if the covariates and genetic variables are independent or weakly correlated.

We now consider the uncommon situation in which covariates are strongly correlated with genetic variables. For the linear regression analysis of quantitative traits, $a\left(\varphi \right)={\sigma }^2$ and $b^{″}\left(z\right)=1$. Thus,

$$V={\hat{\sigma }}^{-2}\left\{\sum _{i=1}^n{G}_i{G}_i^{\text{T}}-\left(\sum _{i=1}^n{G}_i{X}_i^{\text{T}}\right){\left(\sum _{i=1}^n{X}_i{X}_i^{\text{T}}\right)}^{-1}\left(\sum _{i=1}^n{X}_i{G}_i^{\text{T}}\right)\right\}.$$

This implies that two studies with the same joint distribution of $\left(G,X\right)$ will have the same R even when their trait variances $\left({\sigma }^2\right)$ are different. For the logistic regression analysis of case-control data,

$$V=\sum _{i=1}^{n}v\left({\hat{\gamma }}^{\text{T}}{X}_i\right)G_i{G}_i^{\text{T}}-\left\{\sum _{i=1}^{n}v\left({\hat{\gamma }}^{\text{T}}{X}_i\right)G_i{X}_i^{\text{T}}\right\}{\left\{\sum _{i=1}^{n}v\left({\hat{\gamma }}^{\text{T}}{X}_i\right)X_i{X}_i^{\text{T}}\right\}}^{-1}\left\{\sum _{i=1}^{n}v\left({\hat{\gamma }}^{\text{T}}{X}_i\right)X_i{G}_i^{\text{T}}\right\},$$

where $v\left(z\right)=e^z/{\left(1+e^z\right)}^2$. Thus, two studies with the same value of γ and same joint distribution of $\left(G,X\right)$ will have the same R. Note that the value of $v\left({\hat{\gamma }}^{\text{T}}{X}_i\right)$ does not depend strongly on the covariate values provided that the case-control ratio is not close to 0 or 1. Thus, $v\left({\hat{\gamma }}^{\text{T}}{X}_i\right)\approx v\left({\hat{\gamma }}_0\right)$, where ${\hat{\gamma }}_0$ is the intercept component of $\hat{\gamma }$. Therefore,

$$V\approx v\left({\hat{\gamma }}_0\right)\left\{\sum _{i=1}^n{G}_i{G}_i^{\text{T}}-\sum _{i=1}^n{G}_i{X}_i^{\text{T}}{\left(\sum _{i=1}^n{X}_i{X}_i^{\text{T}}\right)}^{-1}\sum _{i=1}^n{X}_i{G}_i^{\text{T}}\right\},$$

which implies that two studies with the same joint distribution of $\left(G,X\right)$ will have approximately the same R even when their case-control ratios are different.

Web Resources

The URLs for data presented herein are as follows:

• dbGaP, http://www.ncbi.nlm.nih.gov/gap

• International HapMap Project, http://hapmap.ncbi.nlm.nih.gov/

• MAGA, http://userwww.service.emory.edu/∼yhu30/software.html

• NHLBI Exome Sequencing Project (ESP) Exome Variant Server, http://evs.gs.washington.edu/EVS/

• Online Mendelian Inheritance in Man (OMIM), http://www.omim.org/

Consortium

Genetic Investigation of ANthropometric Traits (GIANT) Consortium members: Sonja I. Berndt, Stefan Gustafsson, Reedik Mägi, Andrea Ganna, Eleanor Wheeler, Mary F. Feitosa, Anne E. Justice, Keri L. Monda, Damien C. Croteau-Chonka, Felix R. Day, Tõnu Esko, Tove Fall, Teresa Ferreira, Davide Gentilini, Anne U. Jackson, Jian’an Luan, Joshua C. Randall, Sailaja Vedantam, Cristen J. Willer, Thomas W. Winkler, Andrew R. Wood, Tsegaselassie Workalemahu, Yi-Juan Hu, Sang Hong Lee, Liming Liang, Dan-Yu Lin, Josine L. Min, Benjamin M. Neale, Gudmar Thorleifsson, Jian Yang, Eva Albrecht, Najaf Amin, Jennifer L. Bragg-Gresham, Gemma Cadby, Martin den Heijer, Niina Eklund, Krista Fischer, Anuj Goel, Jouke-Jan Hottenga, Jennifer E. Huffman, Ivonne Jarick, Åsa Johansson, Toby Johnson, Stavroula Kanoni, Marcus E. Kleber, Inke R. König, Kati Kristiansson, Zoltán Kutalik, Claudia Lamina, Cecile Lecoeur, Guo Li, Massimo Mangino, Wendy L. McArdle, Carolina Medina-Gomez, Martina Müller-Nurasyid, Julius S. Ngwa, Ilja M. Nolte, Lavinia Paternoster, Sonali Pechlivanis, Markus Perola, Marjolein J. Peters, Michael Preuss, Lynda M. Rose, Jianxin Shi, Dmitry Shungin, Albert Vernon Smith, Rona J. Strawbridge, Ida Surakka, Alexander Teumer, Mieke D. Trip, Jonathan Tyrer, Jana V. Van Vliet-Ostaptchouk, Liesbeth Vandenput, Lindsay L. Waite, Jing Hua Zhao, Devin Absher, Folkert W. Asselbergs, Mustafa Atalay, Antony P. Attwood, Anthony J. Balmforth, Hanneke Basart, John Beilby, Lori L. Bonnycastle, Paolo Brambilla, Marcel Bruinenberg, Harry Campbell, Daniel I. Chasman, Peter S. Chines, Francis S. Collins, John M. Connell, William Cookson, Ulf de Faire, Femmie de Vegt, Mariano Dei, Maria Dimitriou, Sarah Edkins, Karol Estrada, David M. Evans, Martin Farrall, Marco M. Ferrario, Jean Ferrières, Lude Franke, Francesca Frau, Pablo V. Gejman, Harald Grallert, Henrik Grönberg, Vilmundur Gudnason, Alistair S. Hall, Per Hall, Anna-Liisa Hartikainen, Caroline Hayward, Nancy L. Heard-Costa, Andrew C. Heath, Johannes Hebebrand, Georg Homuth, Frank B. Hu, Sarah E. Hunt, Elina Hyppönen, Carlos Iribarren, Kevin B. Jacobs, John-Olov Jansson, Antti Jula, Mika Kähönen, Sekar Kathiresan, Frank Kee, Kay-Tee Khaw, Mika Kivimaki, Wolfgang Koenig, Aldi T. Kraja, Meena Kumari, Kari Kuulasmaa, Johanna Kuusisto, Jaana H. Laitinen, Timo A. Lakka, Claudia Langenberg, Lenore J. Launer, Lars Lind, Jaana Lindström, Jianjun Liu, Antonio Liuzzi, Marja-Liisa Lokki, Mattias Lorentzon, Pamela A. Madden,Patrik K. Magnusson, Paolo Manunta, Diana Marek, Winfried März, Irene Mateo Leach, Barbara McKnight, Sarah E. Medland, Evelin Mihailov, Lili Milani, Grant W. Montgomery, Vincent Mooser, Thomas W. Mühleisen, Patricia B. Munroe, Arthur W. Musk, Narisu Narisu, Gerjan Navis, George Nicholson, Ellen A. Nohr, Ken K. Ong, Ben A. Oostra, Colin N.A. Palmer, Aarno Palotie, John F. Peden, Nancy Pedersen, Annette Peters, Ozren Polasek, Anneli Pouta, Peter P. Pramstaller, Inga Prokopenko, Carolin Pütter, Aparna Radhakrishnan, Olli Raitakari, Augusto Rendon, Fernando Rivadeneira, Igor Rudan, Timo E. Saaristo, Jennifer G. Sambrook, Alan R. Sanders, Serena Sanna, Jouko Saramies, Sabine Schipf, Stefan Schreiber, Heribert Schunkert, So-Youn Shin, Stefano Signorini, Juha Sinisalo, Boris Skrobek, Nicole Soranzo, Alena Stančáková, Klaus Stark, Jonathan C. Stephens, Kathleen Stirrups, Ronald P. Stolk, Michael Stumvoll, Amy J. Swift, Eirini V. Theodoraki, Barbara Thorand, David-Alexandre Tregouet, Elena Tremoli, Melanie M. Van der Klauw, Joyce B.J. van Meurs, Sita H. Vermeulen, Jorma Viikari, Jarmo Virtamo, Veronique Vitart, Gérard Waeber, Zhaoming Wang, Elisabeth Widén, Sarah H. Wild, Gonneke Willemsen, Bernhard R. Winkelmann, Jacqueline C.M. Witteman, Bruce H.R. Wolffenbuttel, Andrew Wong, Alan F. Wright, M. Carola Zillikens, Philippe Amouyel, Bernhard O. Boehm, Eric Boerwinkle, Dorret I. Boomsma, Mark J. Caulfield, Stephen J. Chanock, L. Adrienne Cupples, Daniele Cusi, George V. Dedoussis, Jeanette Erdmann, Johan G. Eriksson, Paul W. Franks, Philippe Froguel, Christian Gieger, Ulf Gyllensten, Anders Hamsten, Tamara B. Harris, Christian Hengstenberg, Andrew A. Hicks, Aroon Hingorani, Anke Hinney, Albert Hofman, Kees G. Hovingh, Kristian Hveem, Thomas Illig, Marjo-Riitta Jarvelin, Karl-Heinz Jöckel, Sirkka M. Keinanen-Kiukaanniemi, Lambertus A. Kiemeney, Diana Kuh, Markku Laakso, Terho Lehtimäki, Douglas F. Levinson, Nicholas G. Martin, Andres Metspalu, Andrew D. Morris, Markku S. Nieminen, Inger Njølstad, Claes Ohlsson, Albertine J. Oldehinkel, Willem H. Ouwehand, Lyle J. Palmer, Brenda Penninx, Chris Power, Michael A. Province, Bruce M. Psaty, Lu Qi, Rainer Rauramaa, Paul M. Ridker, Samuli Ripatti, Veikko Salomaa, Nilesh J. Samani, Harold Snieder, Thorkild I.A. Sørensen, Timothy D. Spector, Kari Stefansson, Anke Tönjes, Jaakko Tuomilehto, André G. Uitterlinden, Matti Uusitupa, Pim van der Harst, Peter Vollenweider, Henri Wallaschofski, Nicholas J. Wareham, Hugh Watkins, H.-Erich Wichmann, James F. Wilson, Goncalo R. Abecasis, Themistocles L. Assimes, Inês Barroso, Michael Boehnke, Ingrid B. Borecki, Panos Deloukas, Caroline S. Fox, Timothy Frayling, Leif C. Groop, Talin Haritunian, Iris M. Heid, David Hunter, Robert C. Kaplan, Fredrik Karpe, Miriam Moffatt, Karen L. Mohlke, Jeffrey R. O’Connell, Yudi Pawitan, Eric E. Schadt, David Schlessinger, Valgerdur Steinthorsdottir, David P. Strachan, Unnur Thorsteinsdottir, Cornelia M. van Duijn, Peter M. Visscher, Anna Maria Di Blasio, Joel N. Hirschhorn, Cecilia M. Lindgren, Andrew P. Morris, David Meyre, André Scherag, Mark I. McCarthy, Elizabeth K. Speliotes, Kari E. North, Ruth J.F. Loos, Erik Ingelsson