Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Aug 9;3:2404. doi: 10.1038/srep02404

Noise induced oscillations and coherence resonance in a generic model of the nonisothermal chemical oscillator

David S A Simakov 1,a, Juan Pérez-Mercader 1,2
PMCID: PMC3738947  PMID: 23929212

Abstract

Oscillating chemical reactions are common in biological systems and they also occur in artificial non-biological systems. Generally, these reactions are subject to random fluctuations in environmental conditions which translate into fluctuations in the values of physical variables, for example, temperature. We formulate a mathematical model for a nonisothermal minimal chemical oscillator containing a single negative feedback loop and study numerically the effects of stochastic fluctuations in temperature in the absence of any deterministic limit cycle or periodic forcing. We show that noise in temperature can induce sustained limit cycle oscillations with a relatively narrow frequency distribution and some characteristic frequency. These properties differ significantly depending on the noise correlation. Here, we have explored white and colored (correlated) noise. A plot of the characteristic frequency of the noise induced oscillations as a function of the correlation exponent shows a maximum, therefore indicating the existence of autonomous stochastic resonance, i.e. coherence resonance.

Chemical oscillators, which are the canonical example for non-equilibrium chemical dynamics, are found in many natural and synthetic systems (notable examples are the Krebs cycle1, the circadian clock2, the cell cycle3,4, and the Belousov-Zhabotinsky reaction5). Such systems are unavoidably subject to stochastic fluctuations in the values of some environmental physical variables, such as pressure or temperature. These fluctuations can generically be classified as noise, and can potentially affect system behavior by modifying its parameters, for example of the kinetic coefficients of a chemical reaction. Since its first introduction in the realm of science, noise and its effects have been intensively studied in many different fields6 including chemistry and biochemistry. For example, it has been suggested that noise could have played a significant role in the emergence of bistability in regulatory feedback circuits7 and played a role in the origin of life8. Another remarkable noise-induced phenomenon, originally proposed to explain the periodicity in the Earth's ice ages, is stochastic resonance9. In fact, stochastic resonance has been experimentally observed in a number of biological and chemical systems (e.g. sensory neurons10, ion channels11, mechanoreceptors12, Belousov-Zhabotinsky reaction13). It has also been extensively studied theoretically14,15,16,17,18,19.

In general, oscillations in nonlinear chemical systems may arise around unstable steady states (such as unstable focuses or multiple stable attractors separated by unstable saddle points), which can arise due to feedback interactions such as autocatalysis and positive or negative feedback loops20. These interactions are being considered as fundamental mechanisms maintaining functionality of living systems and could have played a significant role in the course of prebiotic evolution21. Notable examples of mathematical models of oscillators include the Sel'kov model of self-oscillations in glycolysis22, the “Brusselator”23, and the “Oregonator”5 that models the Belousov-Zhabotinsky reaction. In fact, sustained limit cycle oscillations can be generated by a single negative feedback loop. This mechanism was first suggested to describe enzymatic regulation of gene expression24,25,26. Importantly, a strong nonlinearity of the inhibition is necessary in this model20,26. In biochemistry, two fundamental phenomena that can lead to strong nonlinearities are allosteric cooperativity27,28 and covalent modification of proteins29. In inorganic chemistry, highly nonlinear reaction kinetics can arise in heterogeneous catalysis30,31, including in some cases sigmoidal kinetics32. In fact, recently, heterogeneous catalysis has been considered as one of the prerequisites for the emergence of life33.

Any chemical or biological system depends on temperature, which affects it in a very nonlinear way because of the Arrhenius dependence (remarkably, recent studies showed measurable gradients of temperature within a single living cell, due to heat generation in mitochondria34). However, nonisothermal effects are commonly not considered in studies of chemical and biological oscillators. For example, it has been suggested that the oscillatory Belousov-Zhabotinsky reaction could have some temperature compensation mechanism35. Effects of temperature on this system were studied both experimentally and theoretically36,37,38. However, a common feature of these studies is that temperature was considered as a parameter, not a variable. A notable example from biology is temperature compensation in the circadian clock, which has been studied theoretically employing the Goodwin oscillator model39,40,41 but, again, using isothermal formulation (temperature is a parameter).

In this paper, we explore the effects of temperature dependence explicitly by formulating a mathematical model of a minimal nonisothermal chemical oscillatory system, whose dynamics is governed by a single, threshold-controlled, negative feedback loop. We study numerically the effects of stochastic fluctuations in the system's environment temperature in the absence of a deterministic limit cycle. We intentionally do not refer to any particular system, but study a generic scheme of a minimal oscillator and trying to understand the basic mechanism of the system response to noise. Our results show that due to the nonisothermal character of the model, fluctuations in temperature can induce sustained limit cycle oscillations. These noise-induced oscillations turn out to have a characteristic frequency and a magnitude that depend on both the noise amplitude and its correlation. We also observe and characterize the phenomenon of autonomous stochastic resonance, which can be parametrically described as a function of the correlation exponent of the colored noise.

Results

We now describe the mathematical formulation of our idealized model, its main characteristics and the specific features related to noise-induced behavior.

Model formulation

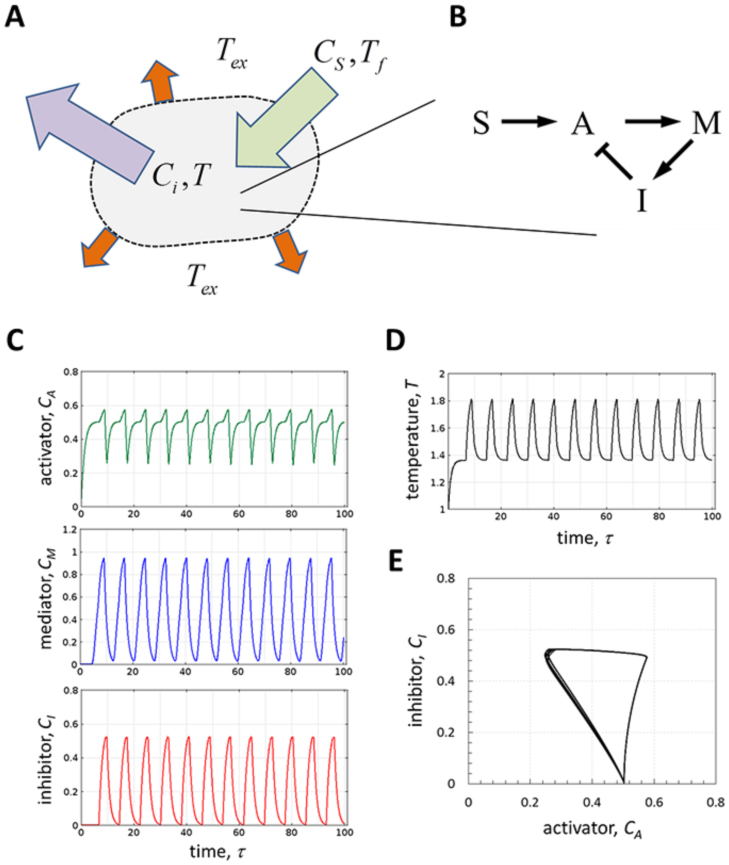
Let us consider a hypothetical enclosed chemical system subject to a constant flow of matter (for example through a semipermeable membrane) with temperature Tf and substrate concentration CS. For an exothermic system, heat will be generated and dissipated to the environment whose temperature is Tex (Fig. 1A). The state of this nonisothermal system is described by the concentrations of i compounds (Ci) and its temperature (T). Now, let us assume that the system is oscillatory and that its dynamics can be described well enough by an elementary network of limiting interactions shown in Fig. 1B (in doing this we assume that other interactions are very fast and that intermediates are sufficiently abundant): a negative feedback loop with an input (assumed to be constant). When there are no internal gradients of concentrations or temperature (e.g., due to small system size and fast homogeneous mixing) the system can be described using the formalism of an ideal continuously stirred tank reactor (CSTR)42. Then, the equations for this system (we are using a dimensionless formulation) are

graphic file with name srep02404-m1.jpg
graphic file with name srep02404-m2.jpg
graphic file with name srep02404-m3.jpg
graphic file with name srep02404-m4.jpg
graphic file with name srep02404-m5.jpg

In the above equations, the dynamics for each variable (Ci and T) is governed by the sum of a nonlinear generation term (gi) and a linear decay term (which represents the continuous removal of matter, Fig. 1A); τ and ε denote dimensionless time and time constant, respectively. For generality, we have included an additional term in the heat balance, to account for heat dissipation (Fig. 1A). An Arrhenius temperature dependence of kinetic rates (gi) is assumed, and βi and αi stand for the dimensionless activation energy and reaction enthalpy, respectively. We assume that heat dissipation follows Newton's law of cooling, with an effective heat transfer coefficient ϕ. The network of interactions (Fig. 1B) is composed of an activator (A), a mediator (M), and an inhibitor (I), with a constant input S (gA0 = const in equation (3)). This configuration ensures the existence of sustained limit cycle oscillations which, according to Bendixon's criterion20,26,43, cannot exist with only two intermediates. An additional requirement for oscillatory behavior in our model is nonlinearity of reaction rates20,26. To be taken as an asymptotic approximation, we represent such nonlinearities through a step function44, an idealization, which is frequently used in mathematical models of biochemical regulation45. This is realized in our model by using the Heaviside step function H(x). Since in equations (3–5) H(x) is equal to 0 when its argument is negative and 1 otherwise and, the production of A, M, and I switches on and off at their corresponding thresholds θAI, θMA, and θIM. We point out the resemblance between our model without temperature dependence and the Goodwin oscillator model25.

Figure 1. Minimal nonisothermal chemical oscillator.

Figure 1

Open in a new tab

(A) A hypothetical oscillatory chemical system subject to a constant flow of matter and heat. The heat is dissipated to the external environment, which is at temperature Tex; (B) A network of chemical interactions – a negative feedback loop with an input; (C) Time series of concentrations of the activator (CA), mediator (CM), and inhibitor (CI); (D) Corresponding time series of temperature (T); (E) The phase plane portrait showing a deterministic limit cycle. Parameters: εi = εT = 1, θMA = θIM = θAI = 0.5, αM = βM = 0, αA = αI = βA = βI = 1, gA0 = 1.05, ϕ = 0.35, Tf = 1, Tex = 0.95, Cif = 0, CA(0) = CM(0) = CI(0) = 0, T(0) = 1.

Deterministic oscillations

Typical simulation results are shown in Fig. 1C–E. We set the reactions of production of A and I to be exothermic (αA > 0 and αI > 0 in equation (2)) and, for simplicity, assume that the activation energy and reaction enthalpy of production of M are negligibly small, as compared to corresponding parameters for A and I (values of all parameters are listed in the figure caption). We select exothermic reactions rather than endothermic, because endothermic effects are expected to suppress the system by reducing its temperature due to the heat consumption in chemical reactions, as an opposite to exothermic effects leading to heat generation. For simplicity, we assume that production of both the activator and the inhibitor is exothermic. It should be pointed out at this point that exothermic chemical oscillators have been extensively studied in heterogeneous catalytic systems, e.g. CO and NH3 oxidation on Pt and Pd46,47,48.

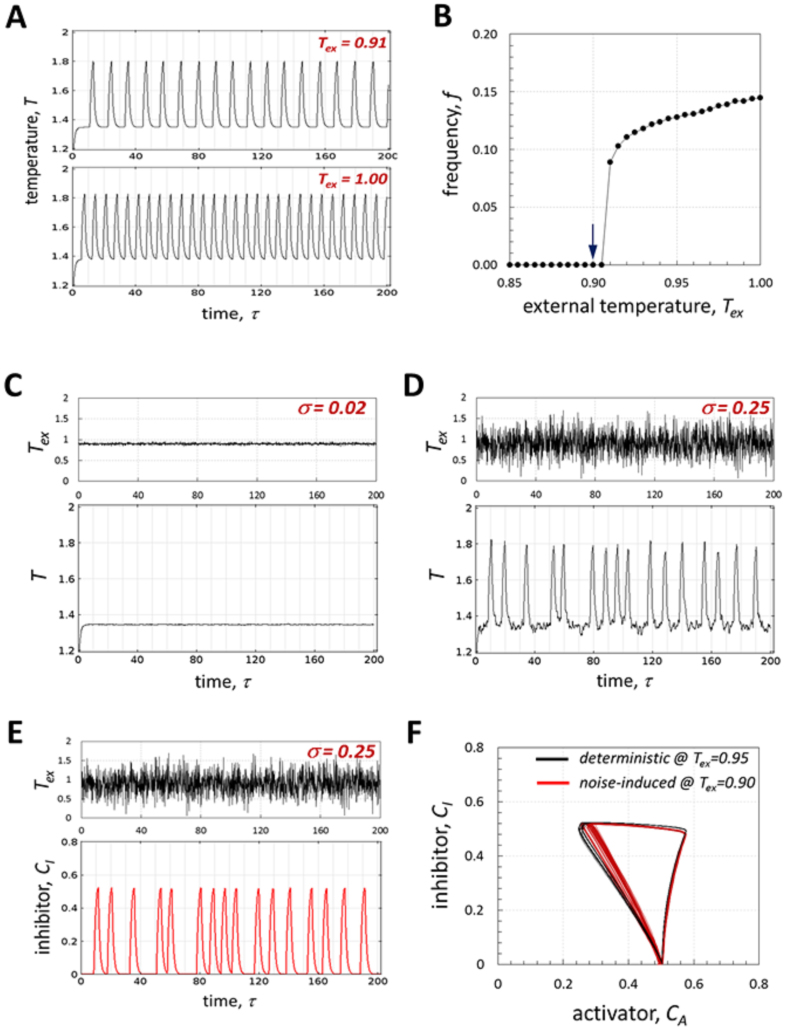
In the absence of any fluctuations, the system generates sustained limit cycle periodic oscillations in concentrations and temperature, independently on initial conditions and in a wide range of parameters (as it was confirmed by numerical simulations). Note that limit cycle oscillations are also generated in the isothermal version of our model, i.e. T = const, due to the inherent ability of the negative feedback loop to generate periodic solutions20. Indeed, accumulation of A switches on the production of M, which starts accumulating and, eventually, activates the production of I, which then suppresses the production of A. However, as we demonstrate in the next section, mutual interactions between chemical and thermal dynamics, i.e. nonisothermal effects, are necessary for generation of noise-induced limit cycle in the absence of deterministic oscillations (Fig. 3). The oscillation frequency increases with Tex (Fig. 2A), which is expected, because higher T results in faster accumulation of A due to exothermic effects. Because of this, we have selected the external temperature (Tex) as a bifurcation parameter and identified the bifurcation point (Fig. 2B).

Figure 2. Noise-induced sustained limit cycle oscillations.

Figure 2

Open in a new tab

(A, B) Deterministic oscillations: effect of external temperature (Tex) on oscillation frequency (A) and bifurcation point (B) are shown; (C–F) Noise-induced oscillations: no oscillations are observed for low noise amplitude, σ = 0.02 (C), while for large noise amplitude (σ = 0.25) oscillations are induced (D, E) and a limit cycle is created (F). Other parameters are as in Figure 1, except for Tex in A and B and Tex = 0.9 + ηw(τ) in (C–F).

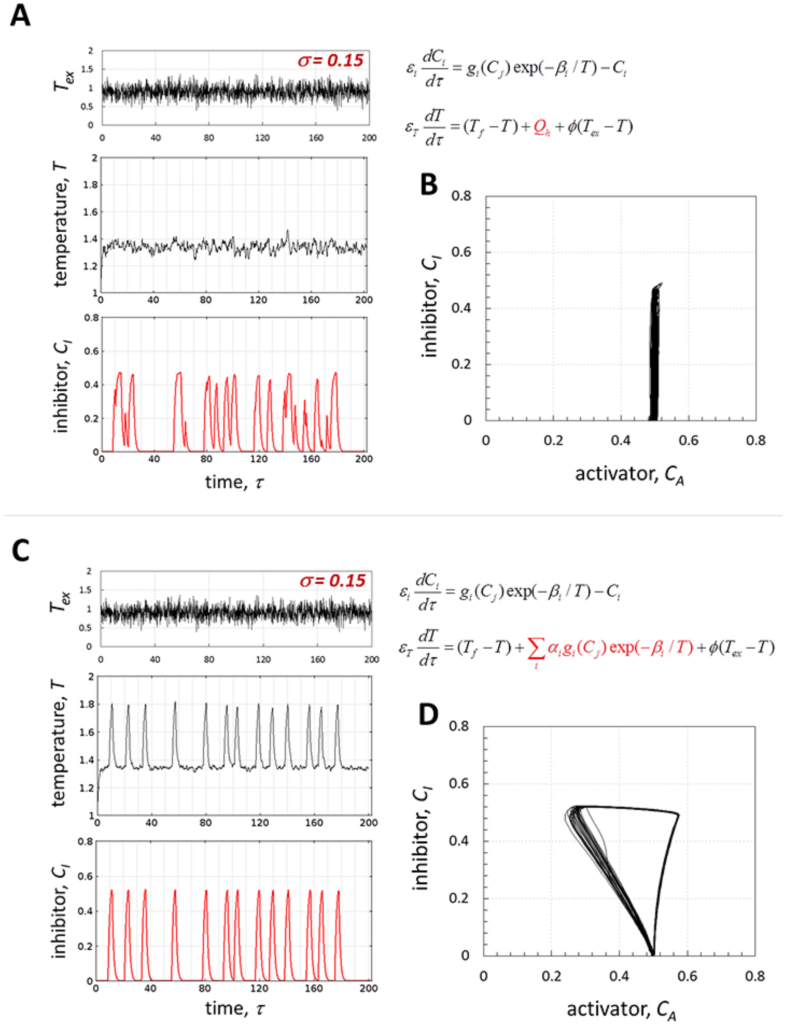
Figure 3. Noise-induced limit cycle is due to nonisothermal effects.

Figure 3

Open in a new tab

(A) Time series of the applied noise (σ = 0.15) and of the resulting temperature and inhibitor concentration with constant heat generation (Qh = 0.5) – the system responds randomly and no limit cycle is generated (B); (C) Time series of the applied noise (σ = 0.15) and the resulting temperature and inhibitor concentration, with the heat generation term dependent on concentrations (nonisothermal system); (D) corresponding noise-induced limit cycle. Other parameters are as in Figure 2.

Noise-induced oscillations

In order to study the system response to fluctuations in temperature, we selected Tex = 0.9, the point where no deterministic limit cycle exists (Fig. 2B), and applied noise in the vicinity of this value, by setting Tex = 0.9 + ηw(τ), where ηw(τ) is a zero-mean Gaussian distributed white noise with standard deviation σ and amplitude modulation frequency of 10 (in all simulations value of ηw changes every 0.1 unit of dimensionless time). While small amplitude perturbations have no effect (Fig. 2C), increasing the noise amplitude leads to oscillations in temperature and concentrations (Fig. 2D, E). Interestingly and surprisingly, noise with amplitude of σ = 0.25 recovers almost completely the deterministic limit cycle obtained at Tex = 0.95 (Fig. 2F, other parameters are identical).

The ability of the system to generate the noise-induced limit cycle, which is very similar to the deterministic cycle, can be therefore attributed to the nonisothermal effects, as it is shown in Fig. 3. A typical example of the numerical simulation with constant heat generation (Qh = 0.5), which was adjusted in such a way that the mean value of temperature was equal to the mean baseline value for the temperature in Fig. 2D (T ≈ 1.35), is shown in Fig. 3A, B (note that in such formulation temperature does not depend on concentrations, while reaction rates still depend on temperature). As expected for the system near the bifurcation point and subject to noise, there are excursions in concentration, but they are random (Fig. 3A) and no limit cycle is generated (Fig. 3B). With the same noise amplitude and mean baseline temperature, but including nonisothermal effects due to the heat generation dependence on the reaction rates, noise-induced limit cycle oscillations are generated (Fig. 3C, D).

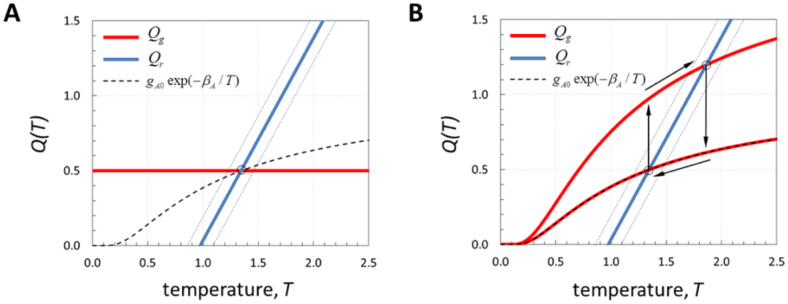
A mechanism to account for this phenomenon could be as follows. For constant heat generation, equation (2) has a single stable steady state (Fig. 4A, where Qg and Qr stand for heat generation and removal respectively). For a particular set of parameters used in Fig. 3 and as long as CI ≤ θAI (no repression of A), this solution corresponds to CA = gA0exp(−βA/T) = 0.5 (Fig. 4A), which is the threshold for M activation (parameter values are listed in figure captions). Fluctuations in the heat removal caused by noise in Tex (these fluctuations are bounded as indicated by dashed blue lines in Fig. 4A) induce random fluctuations in the term gA0exp(−βA/T) (production rate of CA, equations (1,3)) around the stable steady state. This can only lead to random initiation and termination of production of M and, consequently, I (Fig. 3A). In the nonisothermal case, the heat generation term is nonlinear and depends on the production of both A and I (equation (2)). This results in two solutions, depending on whether only A, or both A and I are produced (Fig. 4B). The upper state (T ≈ 1.85) is unstable: when both A and I are produced, eventually I unavoidably represses production of A, leading to a transition to the lower state (T ≈ 1.32). This state is stable to weak noise (Fig. 2C), but unstable to large perturbations which can induce a positive feedback on heat generation due to the exothermicity (equations (1,2)), leading to production of both A and I again. Therefore, fast transitions between the states may occur (Fig. 4B), generating a limit cycle that resembles the deterministic limit cycle. Note that the values of the temperature for two solutions (Fig. 4B) correspond to the baseline and peak temperatures in Fig. 3C.

Figure 4. Noise-induced limit cycle generation mechanism.

Figure 4

Open in a new tab

Steady state solution of temperature balance (equation (2)) with (A) constant heat source (Qg = 0.5) and (B) with the heat generation function dependent on kinetic terms (Qg = αAgA0exp(−βA/T) + αIexp(−βI/T)). The heat removal function is Qr = (T − Tf) + ϕ(T − Tex) in both cases. Dashed blue lines correspond to the range of Qr fluctuations for σ = 0.15; gA0exp(−βA/T) corresponds to the production term of A (when the concentration of I is below repression threshold). Other parameters are as in Figure 3.

This mechanism of noise-induced limit cycle generation is expected to apply for exothermic negative feedback loop oscillators in general. The only requirement for reaction rates is the existence of a sharp transition between virtually no production and production at nearly maximal rate. An additional requirement is that this transition should result in a significant change in the rate of heat generation. In such a system, after the transition from the lower state to the upper curve of heat generation takes place (as shown by the up-pointing arrow in Fig. 4B), the heat generation rate is higher than the rate of heat removal. As a result, temperature will increase and the system will tend to the upper state. The transition from the upper state to the lower curve of heat generation (as shown by the down-pointing arrow in Fig. 4B) results in the heat generation rate, which is lower than the rate of heat removal. In this case, due to decreasing temperature the system will tend to the lower state. Examples of noise-induced sustained limit cycle oscillations obtained in our model with Heaviside function in the reaction rates replaced by a more realistic Hill function dependence are shown in Supplementary Information (see Supplementary Figs. S1–S4 online). Since oscillations occur in the isothermal version of our model (see section Deterministic oscillations), the endothermic version is also expected to generate deterministic periodic orbits (see Supplementary Fig. S5 online). However, due to absence of the accelerating effect of the exothermic reaction the response of the endothermic system to noise is irregular (see Supplementary Figs. S5 and S6 online).

Characteristic frequency of noise-induced oscillations and effect of colored noise

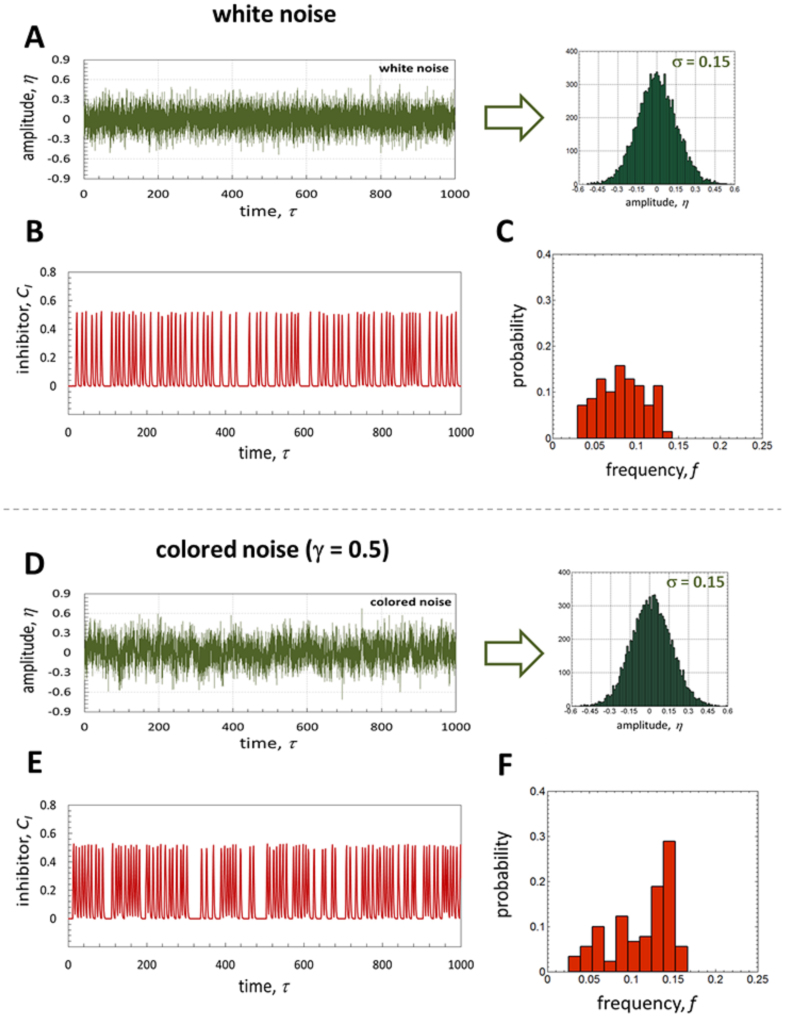
The obtained noise-induced oscillations have a relatively narrow frequency distribution with some characteristic frequency, as it is shown in Fig. 5A–C. A typical example of the numerical simulation, performed with Tex = 0.9 + ηw(τ) for 1000 dimensionless units of time, is shown in Fig. 5B. The corresponding time series of stochastic input (Tex) are shown in Fig. 5A (note high frequency of amplitude variation: ηw changes every 0.1 unit of dimensionless time). The frequency distribution (Fig. 5C) is calculated as the reciprocal of the distribution of the inter-spike intervals calculated from Fig. 5B. Some characteristic frequency can be recognized in Fig. 5C.

Figure 5. Noise-induced frequency distribution.

Figure 5

Open in a new tab

(A–C) Frequency distribution of white noise-induced oscillations, showing the time series of the applied noise (Tex = 0.9 + ηw(τ)) with corresponding random sequence distribution (A), the induced oscillations (B), and the corresponding frequency distribution (C); (D–F) Frequency distribution of colored noise-induced oscillations (Tex = 0.9 + ηc(τ)), showing the time series of the applied correlated noise (correlation exponent is y = 0.5) with corresponding random sequence distribution (D), the induced oscillations (E), and the corresponding frequency distribution (F). Noise amplitude is σ = 0.15 in both cases; other parameters are as in Figure 1.

The shape of the frequency distribution and the location of the characteristic frequency change significantly when colored (correlated) noise is applied instead of white noise. A typical example is shown in Fig. 5D-F (note that in both cases random sequences are Gaussian–distributed with the same standard deviation). We use the same procedure for numerical simulations as for the white noise, i.e. using Tex = 0.9 + ηc(τ), except that now ηc(τ) is zero-mean power-law correlated noise, which is, in addition to the Gaussian distribution standard deviation σ, characterized with a correlation exponent γ:

graphic file with name srep02404-m6.jpg

To generate correlated sequences, we used an algorithm, which is based on the modified Fourier filtering method49 (see the Methods section for details). For colored noise, the frequency distribution is left-skewed and there is a very significant shift of the characteristic frequency towards higher values. Note that Fig. 5 shows typical examples of 20 repeated simulations for each type of noise (each one for 1000 units of time), and the characteristic trend of the left-skewed distribution with higher characteristic frequency for colored noise was obtained in all cases. Importantly, these substantial dissimilarities in system response to white and correlated noise are not a consequence of the idealized and rather artificial reaction rates we used in our formulation (Heaviside function), since similar differences are observed with more realistic reaction rates (see Supplementary Fig. S4 online). These differences can be therefore attributed to noise correlation (we discuss this point in the next section).

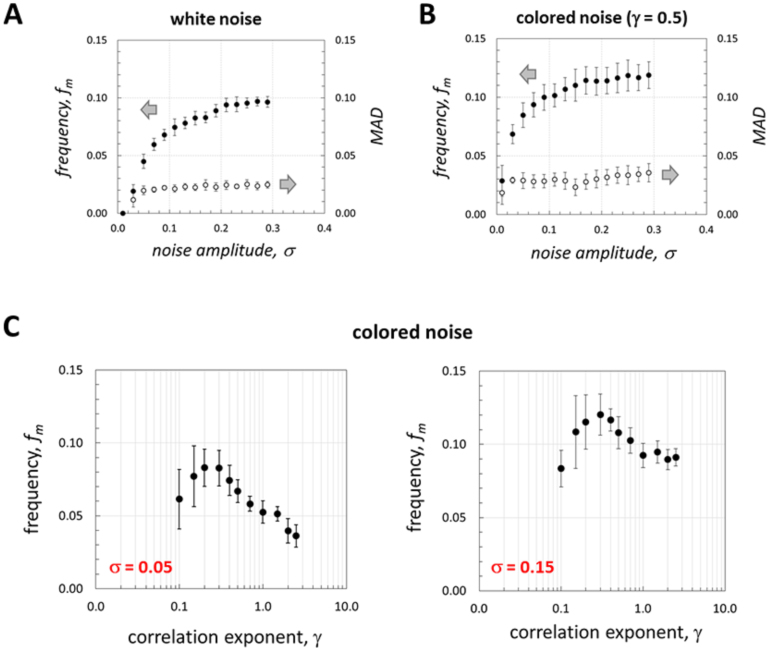
Figures 6A and 6B show the averaged results of repeated simulations for different noise amplitudes (the error bars show standard deviation between measurements). Numerical simulations (each run is for 1000 dimensionless units of time, as in Fig. 5B, E) were performed until there was no further significant change (more than 10%) in accumulated standard deviation error between the measurements, although at least 10 runs were performed for each type of noise and each value of the noise amplitude. We calculated the characteristic frequency as the median of the frequency distribution (such as shown in Fig. 5C, F), denoted as fm in Fig. 6A, B, where the median absolute deviation (MAD) is also shown. It can be seen that the frequency distribution is relatively narrow, while the MAD magnitude is slightly higher for colored noise. Furthermore, the characteristic frequency increases with increasing noise amplitude, and attains a relatively constant value for intermediate noise amplitudes. We verified that there is no optimum in the fm vs. σ plots even for very large noise amplitudes (as high as σ = 1), for a range of the correlation exponent of 0.1 ≤ γ ≤ 2.5. We restrict our representation, however, for σ ≤ 0.3 since for σ > 0.3, temperature (Tex) attains negative values. Interestingly enough, the characteristic frequency was significantly higher for colored noise (compare Fig. 6A and B).

Figure 6. Frequency dependence and coherence resonance.

Figure 6

Open in a new tab

(A, B) The dependence of the characteristic frequency of noise-induced oscillations (calculated as the median of the frequency distribution) on the noise amplitude for white (A) and colored noise (B); error bars show standard deviation between the measurements and MAD is the median absolute deviation; (C) Plots of the characteristic frequency vs. correlation exponent for two different noise amplitudes; error bars show standard deviation between the measurements. Parameters are as in Figure 1, except for Tex = 0.9 + ηw(τ) and Tex = 0.9 + ηc(τ) for white and colored noise, respectively.

Coherence resonance

A plot of the characteristic frequency as a function of the correlation exponent (γ) showed a pronounced maximum for different values of noise amplitude; typical examples are shown in Fig. 6C (error bars show standard deviation between the measurements). This indicates the existence of stochastic resonance, occurring in the absence of any periodic forcing, therefore, such phenomenon can be classified as autonomous stochastic resonance, also known in the literature as coherence resonance17,50. Note that (not surprisingly) for high values of the correlation exponent (poorly correlated noise) the characteristic frequency magnitude tends to that induced by white (uncorrelated) noise (compare Figs. 6C and 6A). The occurrence of coherence resonance as a function of correlation exponent can be attributed to dissimilarities in spectral densities of noise with different correlation. For white noise (and for large values of γ) spectral density is equally distributed over the frequency spectrum. In contrast and depending on its correlation, colored noise has enhanced spectral density for certain ranges of frequencies (see Supplementary Figs. S7 and S8 online). Overlap between these enhanced frequencies and the natural frequency of the oscillator can result in an optimum in the plot of the characteristic noise-induced frequency versus the correlation exponent.

In its classical formulation, stochastic resonance is recognized in a dynamical system subject to both weak periodic forcing and random perturbation, as the emergence of periodic behavior, which is absent when either the forcing or the perturbation are absent9. Such systems are commonly bistable, with the probability of occupation of a certain stable state being affected by noise, while some "optimal" noise may lead to quasiperiodic switching between these two states. In the model presented here we have found that sustained limit cycle oscillations are created by stochastic fluctuations in temperature in the absence of any periodic forcing in the oscillatory system which does not have multiple stable states. These noise-induced oscillations are due to the presence of the negative feedback loop in the kinetic terms (equations (3–5) and Fig. 1B) and the mutual interaction between the chemical and thermal dynamics. That is, they are due to nonisothermal effects, while coherence resonance is observed as a function of the amplitude of colored noise-correlated temperature fluctuations.

Discussion

Motivated by the ubiquitous presence of oscillatory behavior in the chemistry of complex systems and by their natural exposure to various sources of noise, we have formulated a nonisothermal mathematical model of a minimal chemical oscillator subject to noise in the form of temperature fluctuations. We performed a numerical analysis for this system using the formalism of an ideal continuously stirred flow reactor (CSTR), which promotes the temperature into a system variable. Temperature variations affect the reaction rate constants via the highly non-linear Arrhenius factor, leading to interplay between thermal and chemical dynamics. In order to discard potential built-in causes for our results, we have studied the effects of stochastic fluctuations in temperature in the absence of any periodic forcing. We have found that noise in temperature can induce sustained oscillations in the absence of any deterministic limit cycle. Furthermore, temperature fluctuations can recover deterministic limit cycles.

For white noise, the noise-induced oscillations that set in have a relatively narrow frequency distribution and a characteristic frequency that increases with noise amplitude, although no optimum is observed. Instead, the characteristic frequency reaches a relatively constant value. Because the idealization to white noise (with zero correlation) is unlikely to be realized in the real world where stochastic fluctuations are expected to have at least some degree of correlation, we have also considered colored (power-law correlated) noise. Colored noise is defined by some fixed scale called "correlation length" and by the "correlation exponent", which is essentially a logarithmic measure of the preponderance of scales in relation to the correlation length. Not surprisingly, we have discovered that there exist marked differences in both the induced frequency distribution and characteristic frequency magnitude depending on whether the noise is white or colored.

Our calculations show that given identical noise amplitude and random sequence distribution, colored noise fluctuations can result in a significantly higher characteristic frequency than what is induced for white noise temperature fluctuations. This underscores the role of the noise correlation and points to its use as a "control knob" for the selection of induced phenomenological behaviors via noise correlation. When we plotted the characteristic frequency of the colored noise induced oscillations as a function of the colored noise correlation exponent, we found a pronounced maximum with an optimal range that results in the highest frequency for the noise induced oscillations. Because this resonance appears in the absence of any periodic forcing, we interpret it in terms of the existence of autonomous stochastic resonance also known as coherence resonance17. The coherence resonance observed in our study is very different from the stochastic resonance in its classical formulation9, which refers to a bistable system subject to a weak subthreshold periodic signal and stochastic fluctuations, for which the probability of the occupancy of a certain state may be affected by noise. In our model, sustained limit cycle oscillations are induced in the absence of any form of periodic forcing, purely by stochastic fluctuations in temperature.

Our findings highlight the importance of the mutual interplay between chemical and thermal dynamics, which is frequently omitted in models of chemical and biological oscillators. To the best of our knowledge, this is the first numerical study showing sustained limit cycle oscillations induced by temperature fluctuations in the nonisothermal chemical oscillator. Our results are clearly a consequence of the nonisothermal character of our model: when reaction heat dependence on reaction rates is not accounted for the system simply responds in a random manner and no limit cycle is created (Fig. 3).

We believe that the results presented here could be useful for a fundamental understanding of noise-induced phenomena in oscillatory systems. Newly emerging fields, such as synthesis of artificial metabolic cycles and transcriptional networks51,52,53 can benefit from studies of minimal mathematical models, such as the one we present here. Such studies could provide new ideas or illuminate new strategies for experimental investigations. Understanding the dynamics of simple chemical oscillators, while accounting for reaction heat and external noise (both of which are always present in natural environments), may help to understand the emergence of prebiotic metabolic cycles, as well as the pervasive presence of metabolic oscillators in biological systems.

Methods

We use a dimensionless form of equations (Eqs 1–5) in order to reduce a number of parameters. In the dimensionless representation, time is scaled by a typical decay rate of the problem, while time constants (εi and εT) compare the decay rate of each model variable to the typical decay rate. Model variables (Ci and T) and kinetic rates (gi) are normalized to their maximum values and kinetic thresholds (θij) vary from 0 to 1. Parameters βi, αi and ϕ stand for dimensionless activation energy, reaction enthalpy and heat transfer coefficient, respectively. The set of ODEs given by Eqs 1 and 2 was integrated using a standard integration routine (COMSOL Multiphysics) with adaptive time stepping, with initial conditions Ci(0) = 0 and T(0) = 1. The following values of parameters were used in all the simulations: εi = εT = 1, θMA = θIM = θAJ = 0.5, αM = βM = 0, αA = αI = βA = βI = 1, gA0 = 1.05, ϕ = 0.35, Tf = 1. Correlated noise was generated using an algorithm based on the modified Fourier filtering method49. Briefly, a sequence of random numbers with power-low correlation is generated by filtering the Fourier components of an uncorrelated sequence of random numbers (Gaussian-distributed).

Author Contributions

D.S.A.S. performed the numerical simulations and prepared the figures. D.S.A.S. and J.P.-M. wrote the main text and reviewed the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information

srep02404-s1.doc (1.7MB, doc)

Acknowledgments

We thank Michael Rudenko for help with the implementation of the correlated noise generation procedure. This work was funded by Repsol, S.A. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

References

  1. Bertram R., Budu-Grajdeanu P. & Jafri M. S. Using phase relations to identify potentialmechanisms for metabolic oscillations in isolated β-cell mitochondria. Islets 1, 87–94 (2009). [DOI] [PubMed] [Google Scholar]
  2. Novák B. & Tyson J. J. Design principles of biochemical oscillators. Nature Review 9, 981–991 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Goldbeter A. A minimal cascade model for the mitotic oscillator involving cyclin and cdc2 kinase. PNAS 88, 9107–9111 (1991). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Murray A. W. Recycling the cell cycle: cyclins revisited. Cell 116, 221–234 (2004). [DOI] [PubMed] [Google Scholar]
  5. Field R. J. & Noyes R. M. Mechanisms of chemical oscillators: conceptual bases. Acc. Chem. Res. 10, 214–221 (1977). [Google Scholar]
  6. Cohen L. The hystory of noise. IEEE Signal Processing Magazine 22, 20–45 (2005). [Google Scholar]
  7. Kuwahara H. & Soyer O. S. Bistability in feedback circuits as a byproduct of evolution of evolvability. Mol. Syst. Biol. 8, 564 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Krakauer D. C. & Sasaki A. Noisy clues to the origin of life. Proc. R. Soc. Lond. B 269, 2423–2428 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Benzi R., Sutera A. & Vulpiani A. The mechanism of stochastic resonance. J. Phys. A: Math. Gen. 14, L453–L457 (1981). [Google Scholar]
  10. Nozaki D., Mar D. J., Grigg P. & Collins J. J. Effects of colored noise on stochastic resonance in sensory neurons. Phys. Rev. Lett. 82, 2401–2405 (1999). [Google Scholar]
  11. Bezrukov S. M. & Vodyanoy I. Noise-induced enhancement of signal trunsduction across voltage-dependent ion channels. Nature 378, 362–364 (1995). [DOI] [PubMed] [Google Scholar]
  12. Douglass J. K., Wilkens L., Pantazelou E. & Moss F. Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance. Nature 365, 337–340 (1993). [DOI] [PubMed] [Google Scholar]
  13. Guderian A., Dechert G., Zeyer K.-P. & Schneider F. W. Stochastic resonance in chemistry. 1. The Belousov-Zhabotinsky reaction. J. Phys. Chem. 100, 4437–4441 (1996). [Google Scholar]
  14. Bezrukov S. M. & Vodyanoy I. Stochastic resonance in non-dynamical systems without response thresholds. Nature 385, 319–321 (1997). [DOI] [PubMed] [Google Scholar]
  15. Parc Y. W., Koh D.-S. & Sung W. Stochastic resonance in an ion channel following the non-Arrhenius gating rate. Eur. Phys. J. B. 69, 127–131 (2009). [Google Scholar]
  16. Song H., Smolen P., Av-Ron E., Baxter D. A. & Byrne J. H. Dynamics of a minimal model of iInterlocked positive and negative feedback loops of transcriptional regulation by cAMP-response element binding proteins. Biophys. J. 92, 3407–3424 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Muratov C. B., Vanden-Eijnden E. & Weinan E. Self-induced stochastic resonance in excitable systems. Physica D 210, 227–240 (2005). [Google Scholar]
  18. Amemiya T., Ohmori T., Nakaiwa M. & Yamaguchi T. Two-parameter stochastic resonance in a model of the photosensitive Belousov-Zhabotinsky reaction in a flow system. J. Phys. Chem. A 102, 4537–4542 (1998). [Google Scholar]
  19. Zhong S. & Xin H. Internal signal stochastic resonance in a modified flow Oregonator model driven by colored noise. J. Phys. Chem. A 104, 297–300 (2000). [Google Scholar]
  20. Tyson J. J. Classification of instabilities in chemical reaction systems. J. Chem. Phys. 62, 1010–1015 (1975). [Google Scholar]
  21. Deamer D. On the origin of systems. EMBO Rep. 10, S1–S4 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Sel'kov E. E. Self-oscillations in glycolysis. European J. Biochem. 4, 79–86 (1968). [DOI] [PubMed] [Google Scholar]
  23. Prigogine I. & Lefever R. Symmetry breaking instabilities in dissipative systems. II. J. Chem. Phys. 48, 1695–1700 (1965). [Google Scholar]
  24. Goodwin B. C. Oscillatory behavior in enzymatic control processes. Advances in Enzyme Regulation 3, 425–428 (1965). [DOI] [PubMed] [Google Scholar]
  25. Goodwin B. C. An entrainment model for timed enzyme synthesis in bacteria. Nature 209, 479–481 (1966). [DOI] [PubMed] [Google Scholar]
  26. Griffith J. S. Mathematics of cellular control processes I. Negative feedback to one gene. J. Theoret. Biol. 20, 202–208 (1968). [DOI] [PubMed] [Google Scholar]
  27. Goldbeter A. Kinetic cooperativity in the concerted model for allosteric enzymes. Biophysical Chemistry 4, 159–169 (1976). [DOI] [PubMed] [Google Scholar]
  28. Changeux J.-P. Allostery and the Monod-Wyman-Changeux model after 50 years. Annu. Rev. Biophys. 41, 103–133 (2012). [DOI] [PubMed] [Google Scholar]
  29. Goldbeter A. & Koshland D. E. Jr An amplified sensitivity arising from covalent modification in biological systems. PNAS 78, 6840–6844 (1981). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Xu W., Kong J. S. & Chen P. Single-molecule kinetic theory of heterogeneous and enzyme catalysis. J. Phys. Chem. C 113, 2393–2404 (2009). [Google Scholar]
  31. Xu W., Shen H., Liu G. & Chen P. Single-molecule kinetics of nanoparticle catalysis. Nano Res. 2, 911–922 (2009). [Google Scholar]
  32. Caliskan S., Zahmakiran M., Durapc F. & Özkara S. Hydrogen liberation from the hydrolytic dehydrogenation of dimethylamine–borane at room temperature by using a novel ruthenium nanocatalyst. Dalton Trans. 41, 4976–4984 (2012). [DOI] [PubMed] [Google Scholar]
  33. Cleaves II H. J., Michalkova Scott A., Hill F. C., Leszczynski J., Sahai N. & Hazen R. Mineral–organic interfacial processes: potential roles in the origins of life. Chem. Soc. Rev. 41, 5502–5525 (2012). [DOI] [PubMed] [Google Scholar]
  34. Okabe K., Inada N., Gota C., Harada Y., Funatsu T. & Uchiyama S. Intracellular temperature mapping with a fluorescent polymeric thermometer and fluorescence lifetime imaging microscopy. Nat. Commun. 3, 705 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Ruoff P. Antagonistic balance in the Oregonator: about the possibility of temperature-compensation in the Belousov-Zhabotinsky reaction. Physica D 84, 204–211 (1995). [Google Scholar]
  36. Masia M., Marchettini N., Zambrano V. & Rustici M. Effect of temperature in a closed unstirred Belousov-Zhabotinsky system. Chem. Phys. Lett. 341, 285–291 (2001). [Google Scholar]
  37. Bansagi T. Jr, Leda M., Toiya M., Zhabotinsky A. M. & Epstein I. R. High-frequency oscillations in the Belousov-Zhabotinsky reaction. J. Phys. Chem. A 113, 5644–5648 (2009). [DOI] [PubMed] [Google Scholar]
  38. Novak J., Thompson B. W., Wilson M. C. T., Taylor A. F. & Britton M. M. Low frequency temperature forcing of chemical oscillations. Phys. Chem. Chem. Phys. 13, 12321–12327 (2011). [DOI] [PubMed] [Google Scholar]
  39. Ruoff P., Vinsjevik M., Monnerjahn C. & Rensing L. The Goodwin oscillator: On the importance of degradation reactions in the circadian clock. J. Biol. Rhythms 14, 469–479 (1999). [DOI] [PubMed] [Google Scholar]
  40. Francois P., Despierre N. & Siggia E. D. Adaptive temperature compensation in circadian oscillations. PLoS Comput. Biol. 8, e1002585 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Bodenstein C., Heiland I. & Schuster S. Temperature compensation and entrainment in circadian rhythms. Phys. Biol. 9, 036011 (2012). [DOI] [PubMed] [Google Scholar]
  42. Schmidt L. D. The Engineering of Chemical Reactions. (Oxford University Press, 1998). [Google Scholar]
  43. Andronov A. A., Vitt A. A. & Khaikin S. E. Theory of Oscillators (Pergamon Press, Oxford, 1966). [Google Scholar]
  44. Tyson J. J. & Othmer H. G. The dynamics of feedback control circuits in biochemical pathways. Prog. Theor. Biol. 5, 1–62 (1978). [Google Scholar]
  45. Simakov D. S. A., Cheung L. S., Pismen L. M. & Shvartsman S. Y. EGFR-dependent network interactions that pattern Drosophila eggshell appendages. Development 139, 2814–2820 (2012). [DOI] [PubMed] [Google Scholar]
  46. Flytzani-Stephanopoulos M., Schmidt L. D. & Caretta R. Steady state and transient oscillations in NH3 oxidation on Pt. J. Catal. 64, 346–355 (1980). [Google Scholar]
  47. Sheintuch M. Oscillatory states in the oxidation of carbon-monoxide on Platinum. AIChE Journal 27, 20–25 (1981). [Google Scholar]
  48. Liauw M. A., Somani M., Annamalai J. & Luss D. Oscillating temperature pulses during CO oxidation on a Pd/AI2O3 ring. AIChE Journal 43, 1519–1528 (1997). [Google Scholar]
  49. Makse H. A., Havlin S., Schwartz M. & Stanley H. E. Method for generating long-range correlations for large systems. Phys. Rev. E 53, 5445–5449 (1996). [DOI] [PubMed] [Google Scholar]
  50. Yang L., Hou Z. & Xin H. Stochastic resonance in the absence and presence of external signals for a chemical reaction. J. Chem. Phys. 10, 3591–3595 (1999). [Google Scholar]
  51. Zhang X. V. & Martin S. T. Driving parts of Krebs cycle in reverse through mineral photochemistry. J. Am. Chem. Soc. 128, 16032–16033 (2006). [DOI] [PubMed] [Google Scholar]
  52. Kim J. & Winfree E. Synthetic in vitro transcriptional oscillators. Mol. Syst. Biol. 7, 465 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Fung E. et al. A synthetic gene–metabolic oscillator. Nature 435, 118–122 (2005). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep02404-s1.doc (1.7MB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES