A method for energy window optimization for quantitative tasks that includes the effects of model-mismatch on bias: application to ⁹⁰Y bremsstrahlung SPECT imaging

Abstract

Quantitative Yttrium-90 (⁹⁰Y) bremsstrahlung SPECT imaging has shown great potential to provide reliable estimates of⁹⁰Y activity distribution for targeted radionuclide therapy (TRT) dosimetry applications. One factor that potentially affects the reliability of the activity estimates is the choice of the acquisition energy window. In contrast to imaging conventional gamma photon emitters where the acquisition energy windows are usually placed around photopeaks, there has been great variation in the choice of the acquisition energy window for⁹⁰Y imaging due to the continuous and broad energy distribution of the bremsstrahlung photons. In quantitative imaging of conventional gamma photon emitters, previous methods for optimizing the acquisition energy window assumed unbiased estimators and used the variance in the estimates as a figure-of-merit (FOM). However, for situations, such as⁹⁰Y imaging, where there are errors in the modeling of the image formation process used in the reconstruction there will be bias in the activity estimates. In⁹⁰Y bremsstrahlung imaging this will be especially important due to the high levels of scatter, multiple scatter, and collimator septal penetration and scatter. Thus variance will not be a complete measure of reliability of the estimates and thus is not a complete FOM. To address this, we first aimed to develop a new method to optimize the energy window that accounts for both the bias due to model-mismatch and the variance of the activity estimates. We applied this method to optimize the acquisition energy window for quantitative⁹⁰Y bremsstrahlung SPECT imaging in microsphere brachytherapy. Since absorbed dose is defined as the absorbed energy from the radiation per unit mass of tissues, in this new method we proposed a mass-weighted root mean squared error (RMSE) of the volume of interest (VOI) activity estimates as the FOM. To calculate this FOM, two analytical expressions were derived for calculating the bias due to model-mismatch and the variance of the VOI activity estimates, respectively. To obtain the optimal acquisition energy window for general situations of interest in clinical⁹⁰Y microsphere imaging, we generated phantoms with multiple tumors of various sizes and various tumor-to-normal activity concentration ratios using a digital phantom that realistically simulates human anatomy, simulated⁹⁰Y microsphere imaging with a clinical SPECT system and typical imaging parameters using a previously validated Monte Carlo (MC) simulation code, and used a previously-proposed method for modeling the image degrading effects in quantitative SPECT reconstruction. The obtained optimal acquisition energy window was 100–160 keV. The values of the proposed FOM were much larger than the FOM taking into account only the variance of the activity estimates, thus demonstrating in our experiment that the bias of the activity estimates due to model-mismatch was a more important factor than the variance in terms of limiting the reliability of activity estimates.

1. Introduction

Because of its chemistry, the half life of its radioactive decay, and the energy of β-particles emitted during its decay, Yttrium-90 (⁹⁰Y) has been widely used in targeted radionuclide therapy (TRT) for treatment of non-Hodgkin’s lymphoma (⁹⁰Y labeled antibodies) and unresectable liver cancer (⁹⁰Y radioactive microspheres) (Stigbrand et al., 2008; Nag et al., 2007). To achieve optimal tumor response and avoid normal tissue toxicity, pre-therapy dosimetry using a surrogate radionuclide or imaging agent is usually performed to determine the prescribed administered activity. Since these surrogates may not accurately predict the⁹⁰Y distribution, post-therapy dosimetry based on quantitative⁹⁰Y bremsstrahlung single photon emission computed tomography (SPECT) imaging is potentially useful to confirm absorbed dose delivery and allow planning for adjuvant therapy.

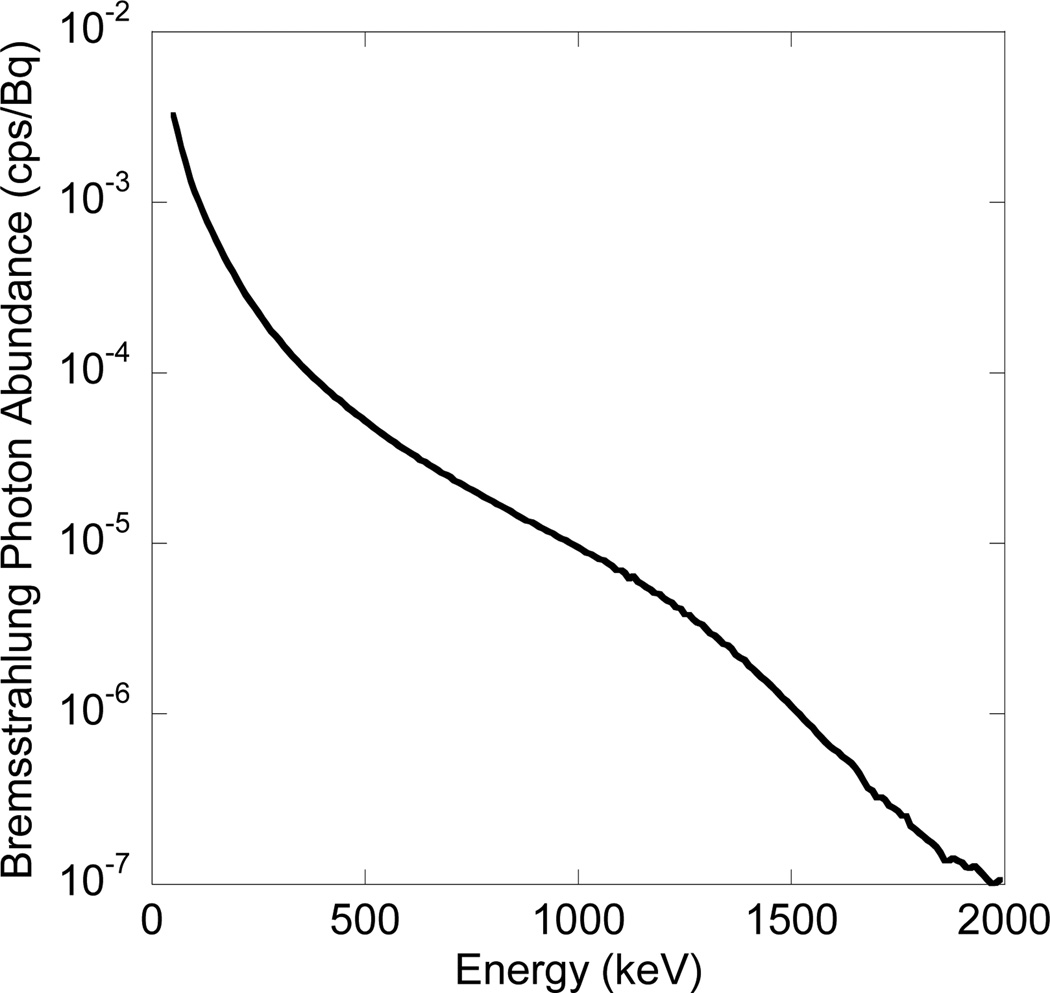
Reliable dosimetry is founded on reliable estimation of the 3D activity distribution (Sgouros et al., 2008). One factor that potentially affects the reliability of the activity estimates is the choice of the acquisition energy window. For conventional gamma photon emitters, the choice of acquisition energy windows is usually straightforward: relatively narrow windows are placed around photopeaks to accept the majority of primary photons and reject scattered photons. However, bremsstrahlung radiation, literally ‘braking radiation’, results from the interaction of β-particles with atomic nuclei in the object. As a result, the energies of bremsstrahlung photons range continuously from the highest β-particle energy down to zero. Thus for⁹⁰Y bremsstrahlung imaging, where the β-particles can have energies up to 2.28 MeV, there has been great variability in the choice of the acquisition energy window due to the continuous and broad energy distribution of bremsstrahlung photons and lack of a well-defined photopeak (See Figure 1).

Figure 1.

Energy spectrum (50–2000 keV, 10 keV interval) of ⁹⁰Y bremsstrahlung photons in water.

For other quantitative radionuclide imaging applications it has been recognized that the choice of acquisition energy window impacts the variance of the activity estimates. As a result, some of the previous efforts to optimize acquisition energy windows for quantitative tasks using conventional gamma-emitting radionuclides used the Cramer-Rao lower bound on the variance as the figure of merit (FOM) for optimization (El Fakhri et al., 2002). This implicitly assumes that the quantitative estimates are unbiased, or at least that the bias is independent of energy window.

However, for some applications, including⁹⁰Y bremsstrahlung imaging, the bias of the activity estimates may be an important factor limiting the reliability of the activity estimates. One potential source of bias is lack of full compensation for attenuation, scatter, and collimator-detector response. In statistically based iterative reconstruction methods, the quantitative accuracy of the reconstructed image strongly depends on how accurately the image formation process is modeled in the projector; modeling errors in the system matrix, which defines the mapping from the reconstructed image space to the projection data space, will cause errors in the reconstructed image, and thus bias in the quantitative estimates of the activity distribution (Qi and Huesman, 2005). In this paper we refer to these modeling errors – the discrepancies between the model and the actual image formation process – as model-mismatch.

The amount of model-mismatch depends both on the magnitude of the various image degrading effects and on the difficulty of accurately incorporating them in the system matrix. For example, high levels of scatter will likely result in a larger amount of model-mismatch than lower levels. Similarly, multiple scatter or backscatter from structures behind the crystal will be harder to model than single scatter in the patient. Since the relative amounts of different categories of photons change as a function of energy, the bias due to model-mismatch will vary with energy window.

In particular,⁹⁰Y bremsstrahlung photons have a continuous and broad energy distribution, and the highest energy is more than 2 MeV. This imposes substantial challenges on accurate modeling of the image formation process, even for detailed Monte Carlo simulation methods. First, since there are a significant number of detected scattered photons at all energies below 2 MeV, the scatter-to-primary ratio will be very large in any energy window. Second, high-energy photons can result in image degrading effects in lower energy windows via mechanisms including down-scatter (i.e., photons with energies above a particular energy window that are scattered and detected in that window), collimator scatter and penetration, partial deposition in the crystal, and backscatter from structures behind the crystal. Some of these effects can be difficult to model. In addition, beam hardening (i.e., depth-dependent changes in energy spectrum) is much more serious over a broad energy range than a narrow one. Because of these challenges, model-mismatch may be large; since the model-mismatch has a great impact on the bias of the activity estimates, the bias may also be large and should not be ignored in optimizing various acquisition parameters.

Of particular relevance to⁹⁰Y bremsstrahlung imaging, the bias of the activity estimates will be affected by the choice of acquisition energy window. The fraction of photons carrying good positional information about the activity distribution may be quite different for different acquisition energy windows. For instance, the fraction of geometrically collimated primary photons (i.e., photons that exited the body without interaction and passed through the collimator holes without touching the septa) – the photons providing the highest quality spatial information about the activity distribution – in a 100–120 keV window is much larger than in a 500–520 keV window. Thus in different acquisition energy windows, the amount of model-mismatch may differ for a given modeling method, leading to different bias of the activity estimates obtained with different energy windows.

In cases where bias of the activity estimates can be large and the choice of acquisition energy window may have a great impact on both the bias and the variance of the activity estimates, applying a variance-only FOM may result in sub-optimal activity estimates. As discussed above and shown in detail below, this is the case for⁹⁰Y bremsstrahlung imaging.

To the best of our knowledge, to date only ad hoc arguments about the numbers of various kinds of photons have been proposed to optimize the acquisition energy window for⁹⁰Y bremsstrahlung imaging (Heard et al., 2004; Shen et al., 1994). Thus it is both necessary and innovative to develop an optimization method that takes into account both the bias and the variance of the activity estimates for optimizing acquisition energy window for quantitative⁹⁰Y bremsstrahlung SPECT imaging. We propose the weighted root mean squared error (RMSE) of volume of interest (VOI) activity estimates, which takes into account both the bias due to model-mismatch and the variance of the VOI activity estimates, as the figure of merit for optimization. We have derived analytical expressions for calculating this figure of merit. We applied this method to optimize the acquisition energy window for quantitative⁹⁰Y bremsstrahlung SPECT imaging in clinical microsphere brachytherapy. A digital phantom simulating realistic human anatomy was used to simulate an object relevant to⁹⁰Y microsphere imaging for absorbed dose estimation.

In this work we used the SIMIND Monte Carlo (MC) simulation code to simulate scintillation camera imaging (Ljungberg and Strand, 1989). In previous work, we have improved and validated SIMIND simulation of⁹⁰Y bremsstrahlung imaging (Rong et al., 2012). We used a bremsstrahlung emission energy spectrum previously estimated from experimental measurements by Rault et al. (Rault et al., 2010) and incorporated a model of the distance between⁹⁰Y decay location and bremsstrahlung emission location into the SIMIND bremsstrahlung simulation. We validated this improved SIMIND bremsstrahlung simulation by comparison to experimentally measured projection data of a⁹⁰Y line source.

Because both the acquisition energy window and the modeling method used in reconstruction affect the model-mismatch, and thus the bias of the activity estimates, the optimal acquisition energy window depends on the modeling method. To make the optimization results more general, we used a modeling method developed previously for quantitative⁹⁰Y bremsstrahlung SPECT (Minarik et al., 2008), which is based on methods applied to conventional gamma-emitting radionuclides (He et al., 2005). This method includes models for all the effects in the image formation process including object scatter, attenuation and the full collimator-detector response (CDR).

2. Materials and methods

2.1. Figure of merit

Since the goal of quantitative⁹⁰Y bremsstrahlung SPECT imaging is to provide reliable activity estimates as input information for dosimetry, the proposed figure of merit should reflect the reliability of the activity estimates related to absorbed dose calculation. Since the absorbed dose is the absorbed energy from the radiation per unit mass of tissue, we propose a figure of merit (FOM) for optimizing the acquisition energy window as follows:

$$\text{FOM}=\frac{1}{N}\sum _{i=1}^N\frac{\text{RMSE}(A_i)}{m_i}=\frac{1}{N}\sum _{i=1}^N\frac{\sqrt{\text{Variance}(A_i)+{(\text{Bias}(A_i))}^2}}{m_i},$$ (1)

(1) where N is the number of volumes of interest (VOI); RMSE stands for root mean squared error; A_i and m_i denote the estimated activity and the mass of the ith VOI, respectively. Assuming that the estimated absorbed dose is proportional to the estimated activity per unit mass in each VOI, this FOM is proportional to the RMSE of the absorbed dose for all the VOIs of interest. An acquisition energy window giving the smallest value of this FOM is considered optimal.

Rather than estimate the activities in individual voxels and then sum them over each VOI to calculate the total activity in each VOI, we directly estimated the activities in the VOIs. This was done to reduce the number of the estimated parameters considering that the voxel activities were nuisance parameters for VOI activity estimation.

We now derive expressions for the FOM. Denote the measured projection data by y = [y₁, y₂ ,…,y_M]^T ∈ℕ^{M× 1}, where the elements of y follow an independent Poisson distribution and M is the number of projection bins. Let a_t ∈ℝ^N×1 be a vector defining the true expected number of decays in the VOIs, where the jth element of a_t is the true expected number of decays in the jth VOI and the subscript “t” denotes the “true” number of decays. The mean projection data is given by

$$\mathrm{E}[\mathit{y}]={\mathit{P}}_{\mathrm{t}}{\mathit{a}}_{\mathrm{t}},$$ (2)

(2) where E[·] denotes ensemble mean and P_t ∈ℝ^M×N denotes the true system matrix. The element in the ith row and the jth column of the true system matrix is the probability that a photon is detected in projection bin i for a single decay in the jth VOI. Thus the true system matrix exactly represents all the effects in the image formation process including photon abundance, system sensitivity, object-scatter and attenuation, and collimator-detector interactions.

Estimating the vector of activities requires an estimate of the system matrix. In practice the system matrix is not known exactly and a model of the image formation process is incorporated into a forward projection code to compensate for various image-degrading effects. This forward projection process implicitly involves a system matrix, P_e (the subscript “e” stands for “estimated”), which is termed the model-estimated system matrix. Since the image degrading effects are very complicated, the model of these effects is, in all likelihood, not perfectly accurate. Also, because computation time is of concern in practice, some approximations and simplifications are typically made in the model and the forward projection code to speed up the computation. Thus, in practice it is almost impossible that P_e = P_t. As a result, we define the model-mismatch between the true and estimated system matrix by Δ P = P_e − P_t. In the following we will investigate how this model-mismatch affects the activity estimates.

Suppose a∈ℝ^{N× 1} denotes the expected number of decays in the VOIs, the maximum likelihood estimate of a is found by maximizing the log-likelihood function:

$${\mathit{a}}_{\mathrm{e}}=\underset{\mathit{a}\ge 0}{\text{argmax}}\{\mathrm{l}\mathrm{n}[\mathrm{P}\mathrm{r}(\mathit{y}|\mathit{a})]\}.$$ (3)

(3) Since the projection data, y, follow independent Poisson distributions, we have:

$$\mathrm{l}\mathrm{n}[\mathrm{P}\mathrm{r}(\mathit{y}|\mathit{a})]=\sum _{j=1}^M\{y_j\mathrm{l}\mathrm{n}[{({\mathit{P}}_{\mathrm{e}}\mathit{a})}_j]-{({\mathit{P}}_{\mathrm{e}}\mathit{a})}_j-\mathrm{l}\mathrm{n}(y_j!)\},$$ (4)

(4) where y_j and (P_ea)_j denote the jth element of y and P_ea, respectively. Here note that we use the model-estimated system matrix, P_e, in the estimation process.

Unfortunately a closed form solution to equation (4) is not available. However, when the number of photon counts per projection data bin is larger than 10, it is an excellent approximation that y follows a Gaussian distribution. This is usually the case for⁹⁰Y microsphere imaging due to the large activities used in brachytherapy. Thus, finding the maximum likelihood estimator is equivalent to solving a weighted least-squares problem (Barrett and Myers, 2004; Kadrmas et al., 1997):

$${\mathit{P}}_{\mathrm{e}}^T\mathit{B}{\mathit{P}}_{\mathrm{e}}{\mathit{a}}_{\mathrm{e}}={\mathit{P}}_{\mathrm{e}}^T\mathit{B}\mathit{y},$$ (5)

(5) where the diagonal matrix B = diag {1 / E[y_j]} ∈ ℝ^M×M is the inverse of the covariance matrix of the projection data. To avoid division by a small number, we set 1 / E[y_j]to be 0 when E[y_j] <1.

Note that, by definition and the linearity of the projection process, E[y] = P_ta_t. We can use this with equation (5) to derive equations for calculating the bias and the covariance matrix of a_e as follows:

$$\text{Bias}({\mathit{a}}_{\mathrm{e}})\equiv \mathrm{E}[{\mathit{a}}_{\mathrm{e}}]-{\mathit{a}}_{\mathrm{t}}={({\mathit{P}}_{\mathrm{e}}^T\mathit{B}{\mathit{P}}_{\mathrm{e}})}^{-1}·{\mathit{P}}_{\mathrm{e}}^T\mathit{B}·\mathrm{E}[\mathit{y}]-{\mathit{a}}_{\mathrm{t}}={({\mathit{P}}_{\mathrm{e}}^T\mathit{B}{\mathit{P}}_{\mathrm{e}})}^{-1}·{\mathit{P}}_{\mathrm{e}}^T\mathit{B}·{\mathit{P}}_{\mathrm{t}}{\mathit{a}}_{\mathrm{t}}-{\mathit{a}}_{\mathrm{t}}={({\mathit{P}}_{\mathrm{e}}^T\mathit{B}{\mathit{P}}_{\mathrm{e}})}^{-1}·{\mathit{P}}_{\mathrm{e}}^T\mathit{B}·{\mathit{P}}_{\mathrm{t}}{\mathit{a}}_{\mathrm{t}}-{({\mathit{P}}_{\mathrm{e}}^T\mathit{B}{\mathit{P}}_{\mathrm{e}})}^{-1}·{\mathit{P}}_{\mathrm{e}}^T\mathit{B}·{\mathit{P}}_{\mathrm{e}}{\mathit{a}}_{\mathrm{t}}={({\mathit{P}}_{\mathrm{e}}^T\mathit{B}{\mathit{P}}_{\mathrm{e}})}^{-1}·{\mathit{P}}_{\mathrm{e}}^T\mathit{B}·({\mathit{P}}_{\mathrm{t}}-{\mathit{P}}_{\mathrm{e}}){\mathit{a}}_{\mathrm{t}}=-{({\mathit{P}}_{\mathrm{e}}^T\mathit{B}{\mathit{P}}_{\mathrm{e}})}^{-1}·{\mathit{P}}_{\mathrm{e}}^T\mathit{B}·\mathit{\Delta }\mathit{P}{\mathit{a}}_{\mathrm{t}},$$ (6)

(6)

$$\text{Cov}({\mathit{a}}_{\mathrm{e}})\equiv \mathrm{E}[({\mathit{a}}_{\mathrm{e}}-\mathrm{E}[{\mathit{a}}_{\mathrm{e}}]){({\mathit{a}}_{\mathrm{e}}-\mathrm{E}[{\mathit{a}}_{\mathrm{e}}])}^T]={({\mathit{P}}_{\mathrm{e}}^T\mathit{B}{\mathit{P}}_{\mathrm{e}})}^{-1}·{\mathit{P}}_{\mathrm{e}}^T\mathit{B}·\text{Cov}(\mathit{y})·\mathit{B}{\mathit{P}}_{\mathrm{e}}{({\mathit{P}}_{\mathrm{e}}^T\mathit{B}{\mathit{P}}_{\mathrm{e}})}^{-1}={({\mathit{P}}_{\mathrm{e}}^T\mathit{B}{\mathit{P}}_{\mathrm{e}})}^{-1}·{\mathit{P}}_{\mathrm{e}}^T\mathit{B}·{\mathit{B}}^{-1}·\mathit{B}{\mathit{P}}_{\mathrm{e}}{({\mathit{P}}_{\mathrm{e}}^T\mathit{B}{\mathit{P}}_{\mathrm{e}})}^{-1}={({\mathit{P}}_{\mathrm{e}}^T\mathit{B}{\mathit{P}}_{\mathrm{e}})}^{-1},$$ (7)

(7) Note the direct effect of the model-mismatch, ΔP, on the bias of the estimates. In general, ${\mathit{P}}_{\mathrm{e}}^T\mathit{B}{\mathit{P}}_{\mathrm{e}}$ is invertible for the VOI activity estimation problem due to the fact that the number of the projection data bins is much larger than the number of VOIs (M ≫ N). When ${\mathit{P}}_{\mathrm{e}}^T\mathit{B}{\mathit{P}}_{\mathrm{e}}$ is not invertible, singular value decomposition (SVD) can be used to calculate its pseudoinverse. However, we did not encounter this situation in optimization of the acquisition energy window for⁹⁰Y imaging. Noting thata_e = [A_i·t]∈ℝ^N×1, where t is the imaging time per projection view, we have:

$$\text{Bias}(A_i)=\frac{1}{t}·{[\text{Bias}({\mathit{a}}_{\mathrm{e}})]}_i,$$ (8)

(8)

$$\text{Variance}(A_i)=\frac{1}{t^2}·{[\text{Cov}({\mathit{a}}_{\mathrm{e}})]}_{ii},$$ (9)

(9) where [Bias(a_e)]_i is the ith element of Bias(a_e) and [Cov(a_e)]_ii is the ith diagonal element of Cov(a_e). From equations (6) and (7) we can see that the choice of acquisition energy window affects both the bias and the variance of the activity estimates due to its effects on P_e, B and ΔP.

2.2. Experimental design

We used the proposed FOM to optimize the acquisition energy window for quantitative⁹⁰Y bremsstrahlung SPECT imaging in microsphere brachytherapy. To make our optimization results more general, we simulated realistic human anatomy, various tumor sizes and various tumor-to-normal activity concentration ratios using a digital phantom that realistically simulates human anatomy; the true system matrices were generated by simulating a clinical SPECT system with typical imaging parameters using a previously validated MC simulation code; the model-estimated system matrices were generated using a forward projection code that incorporated a model of all image degrading factors, which produced model-mismatch typical of that obtained using conventional quantitative SPECT methods. During the optimization process, windows within the energy range 60–500 keV were considered. Details of the windows investigated will be described below. This energy range was chosen because most photons with energies lower than 60 keV will be attenuated in the body and most detected photons with energies higher than 500 keV have penetrated through or been scattered by the collimator septa. As a result, it is highly unlikely that the optimal acquisition energy window is outside this range, which will be confirmed later by the experimental results.

2.2.1. Generation of the phantom

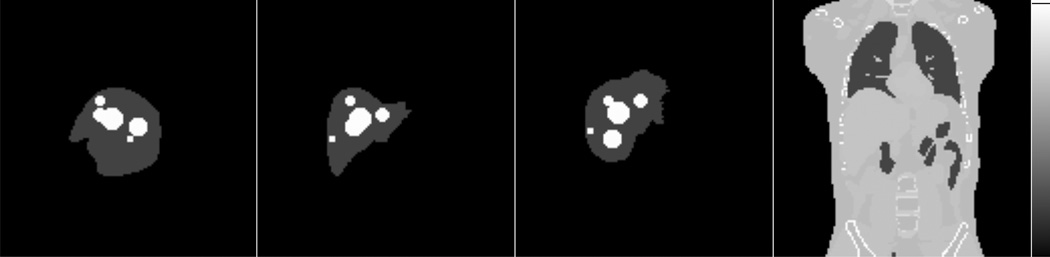
The XCAT phantom code, a computer program for generating a digital phantom realistically simulating human anatomy, was used to generate both the activity distribution and the mass density map (Segars et al., 2010). To make our optimization results more general, we simulated multiple tumors of various sizes and various tumor-to-normal activity concentration ratios. The values of these sizes and ratios were chosen based on the typical values from clinical situations. In particular, we simulated 9 VOIs in the liver including 5 spheres of diameters ranging from 1.5 to 5.5 cm representing 5 tumors of different sizes and 4 VOIs spanning the normal liver. The 9 VOIs did not overlap in 3D space. This implies that regions inside the liver that were part of a tumor VOI were not part of any normal liver VOI. The activity concentration was assumed constant inside each VOI. The 5 tumors had the same activity concentration and the 4 VOIs representing normal liver tissue had the same activity concentration as each other but different from that of the tumors. We simulated three tumor-to-normal activity concentration ratios (5:1, 7.5:1, 10:1) and a total activity of 1.5 GBq, which was a typical activity during⁹⁰Y microsphere imaging. It was assumed there was no activity outside the liver, a reasonable assumption for microsphere brachytherapy. Table 1 gives the activities and volumes of individual VOIs in the liver when the tumor-to-normal activity concentration ratio was 5:1. Figure 2 illustrates the positions of the 5 spheres.

Table 1.

Activities (MBq) and volumes (cm³) of individual VOIs in the liver when the tumor-to-normal activity concentration ratio was 5:1.

	Tumor1	Tumor2	Tumor3	Tumor4	Tumor5	Normal1	Normal2	Normal3	Normal4
Activity	4.77	20.34	44.95	97.69	185.59	253.35	231.70	275.75	385.85
Volume	1.93	8.22	18.16	39.47	74.98	511.74	468.01	556.99	779.38

Figure 2.

Maximum intensity projections of the activity distribution along lateral, anterior-posterior and superior-inferior directions, and a sample slice of the mass density map generated using the XCAT phantom (left to right). Note that the 5 tumors did not overlap in 3D space.

2.2.2. Generation of true system matrices and mean projection vectors

We first generated 9 VOI-maps; the ith VOI-map (i=1,2…9) represented the decay distribution where the sum of the voxel values in the ith VOI was 1 and the voxel values in other VOIs were 0, and the voxel values were constant in the ith VOI. Since the ith column (i=1,2…9) of the true system matrix P_t ∈ ℝ^{M× 9} is the ensemble mean of the projection data when the sum of the voxel values in the ith VOI is 1 and the voxel values in other VOIs are 0, we used an MC simulation code to generate low-noise projection data with the ith VOI-map as the input decay distribution and then arranged the projection data to form the ith column of the true system matrix.

In this work, the low-noise projection data were generated using a SIMIND MC simulation of a Philips Precedence SPECT/CT system with a high-energy general-purpose (HEGP) collimator and a 9.525 mm thick NaI(Tl) crystal. The compartments behind the crystal were simulated as a slab of SiO₂ with density of 2.6 g/cm³ and thickness of 6 cm. We simulated an energy resolution of 9.5% full width at half maximum (FWHM) at 140 keV and an intrinsic spatial resolution of 3.4 mm, both with an energy dependence of $1/\sqrt{E}$ , where E was the energy imparted. We simulated 64 projection views over 360° and a total imaging time of 30 min with a single camera. The projection image size at each view was 128×128 and the pixel size was 4.664 mm. We simulated a body-contouring noncircular orbit by adjusting the radius of rotation for each view based on the attenuation map so that the camera face was close to the body surface.

We divided the energy range 60–500 keV into 18 non-overlapping acquisition energy windows and simulated the projection data for each of the 18 windows. The dividing energies were 70, 80, 90, 100, 120, 140, 160, 180, 200, 220, 240, 260, 280, 300, 350, 400 and 450 keV. At lower energies we used narrower windows because of the larger numbers of detected photons. A total of 10¹² emitted photons were simulated with various variance reduction techniques to generate low-noise data. During the optimization process, only contiguous windows that could be represented by combining the above-mentioned 18 windows were considered; in other words, the set of true system matrices for the considered windows was obtained from ${\mathit{P}}_{\mathrm{t}}=\sum _{j=j_1}^{j_2}{\mathit{P}}_{\mathrm{t},j}$ (j₁,j₂=1,2…18, and j₁ ≤ j₂), where P_t,j ∈ℝ^M×9 (j = 1,2…18) denotes the true system matrix for the jth window generated from the above-mentioned SIMIND simulation. For example, the true system matrix for a 60–70 keV window was P_t,1, and the true system matrix for a 80–120 keV window was P_t,3 + P_t,4 + P_t,5. Thus a total of 171 windows were investigated during the optimization process. Figure 3 shows the anterior projection view of the 9 VOI-maps for an acquisition energy window of 60–180 keV.

Figure 3.

Anterior projection view of the 9 VOI-maps for the acquisition energy window 60–180 keV (Left to right: tumor 1–5, normal 1–4). The normal liver VOIs divided the liver into 4 non-overlapping volumes. In particular, normal liver VOIs 1 and 2 were anterior to the normal liver VOIs 3 and 4, and normal liver VOIs 1 and 3 were superior to normal liver VOIs 2 and 4.

The equations for variance and bias require the mean projection, y, which were calculated for each energy window using equation 2 with the true system matrices described above and the vector of the true expected number of decays in the VOIs for each tumor-to-normal activity concentration ratio investigated.

2.2.3. Generation of model-estimated system matrices

We first generated P_e,j (j=1,2…18) for the above-mentioned 18 windows using a forward projection code (Zeng et al., 1994; Frey et al., 1993; Frey and Tsui, 1996; Wang et al., 2002) incorporating models of various image degrading factors as described below. We then modeled the estimated system matrices as ${\mathit{P}}_{\mathrm{e}}=\sum _{j=j_1}^{j_2}{\mathit{P}}_{\mathrm{e},j}$ (j₁,j₂=1,2…18, and j₁ ≤ j₂) for the other windows investigated in the optimization. All the effects in the image formation process including object scatter, attenuation and the full collimator-detector response (CDR) – including geometric response, collimator penetration and scatter, lead characteristic X-ray, partial deposition in the crystal, intrinsic resolution, as well as backscatter from compartments behind the crystal – were modeled in P_e,j.

In the attenuation modeling, we used a different effective attenuation coefficient for each of the 18 windows (in this context, the effective attenuation coefficient refers to the attenuation coefficient that would have predicted the observed transmitted fraction of a polychromatic radiation beam based on the monochromatic Beer-Lambert exponential attenuation equation). We chose 15 cm as a reasonable representative source depth for the use in the effective attenuation coefficient calculations. To take into account the important and complicated effects of detector interactions on the detection probability in these calculations, we used simulations of a point source at the center of a 15 cm radius cylindrical water phantom and in air to compute the effective attenuation coefficient. In these simulations we recorded the number of geometrically collimated primary photons detected in each of the 18 windows. The effective mass attenuation coefficient for water was given by (ln(C_air/C_phan))/15 cm⁻¹, where C_air and C_phan were the numbers of the detected geometrically collimated primary photons in air and in the phantom, respectively. Then we multiplied the voxel values in the mass density map generated from the XCAT phantom by the obtained effective mass attenuation coefficient to generate the attenuation map for each of the 18 windows.

Scatter was modeled using the Effective Source Scatter Estimation (ESSE) method (Frey and Tsui, 1996). Kernels used in ESSE were generated from a SIMIND simulation of a point source in the center of a water slab of size 100×80×80 cm³ for each of the 18 windows.

In the CDR modeling (Wang et al., 2002), the CDR tables were generated from a SIMIND simulation of a point source in air at various distances from the camera face for each of the 18 windows.

Forward projection incorporating all the above-mentioned modeling was performed for each of the 9 VOI-maps to generate the model-estimated projection data, which were then arranged to form the corresponding columns of P_e,j.

2.2.4. Calculation of FOM

In the calculation of the FOM, we assumed that the mass density inside the liver and tumor VOIs was constant and equal to the density of water. For each of the windows, P_t and P_e were calculated as $\sum _{j=j_1}^{j_2}{\mathit{P}}_{\mathrm{t},j}$ and $\sum _{j=j_1}^{j_2}{\mathit{P}}_{\mathrm{e},j}$ , respectively, by choosing appropriate j₁ and j₂. Next, Bias(A_i) and Variance(A_i) were calculated for each VOI using equations (6) (8) and equations (7) (9), respectively. The FOM was calculated using equation (1). The window with the smallest FOM value was deemed optimal.

3. Results

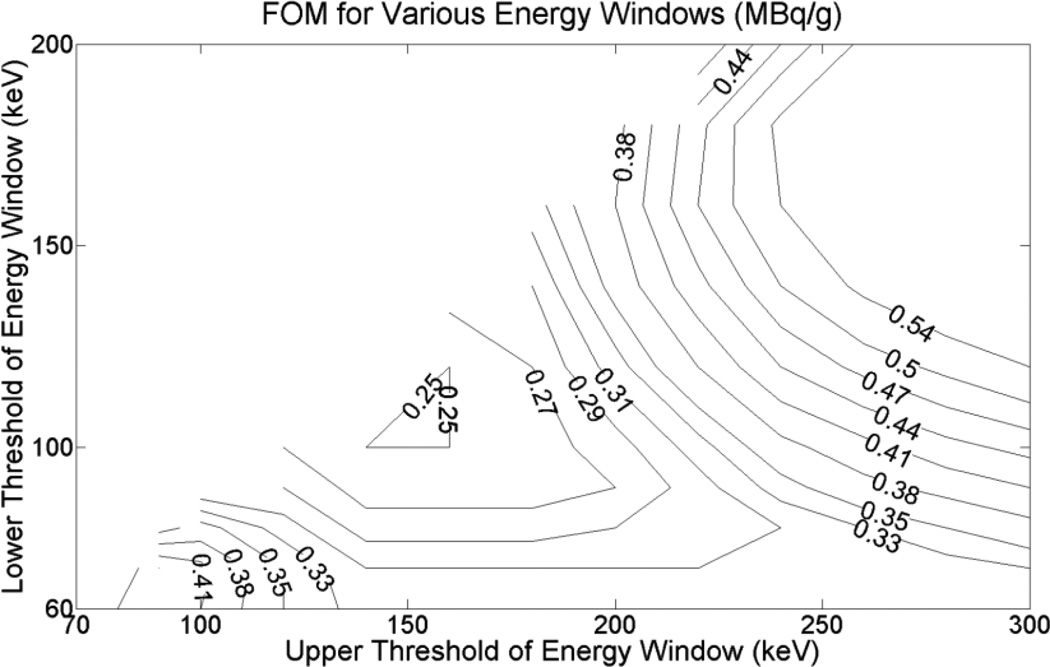
For all the three tumor-to-normal activity concentration ratios (5:1, 7.5:1 and 10:1) the optimal energy window was 100–160 keV and the corresponding FOM values were 0.25, 0.23 and 0.22 MBq/g, respectively. We can see that the optimal window was independent of the activity concentration ratios investigated. Figure 4 shows a 2D contour plot of the FOM values as a function of the lower and upper threshold of the energy window when the tumor-to-normal activity concentration ratio was 5:1. To show the optimal region more clearly, energies above 300 keV, which had larger FOM values, are not shown. Note that the FOM is defined only when the lower threshold is smaller than the upper threshold, so the upper left corner of Figure 4 contains no contours.

Figure 4.

2D contour plot of the FOM values as a function of the lower and upper threshold of the energy window for the case of a tumor-to-normal activity concentration ratio of 5:1. The energy window with the smallest FOM value was deemed optimal.

To provide insight into why the 100–160 keV was the optimal acquisition energy window we investigated the fraction of detected photons that underwent various processes during their propagation for four acquisition energy windows (60–100, 100–160, 160–300 and 300–2000 keV). We simulated the same phantom and imaging parameters used in the above-mentioned experiment. The tumor-to-normal activity concentration ratio was 5:1. The results are shown in Table 2. Note that a photon could belong to multiple categories, e.g., a photon could be scattered in the body, then penetrate the septa, then be backscattered from the compartments behind the crystal, and then be detected in the crystal. Compared to the other three windows, the 100–160 keV window had a larger proportion of geometrically collimated primary photons, which were the photons providing the highest quality spatial information about the activity distribution compared to photons in other categories. The 60–100 keV window had a larger proportion of body-scattered photons. More important, it had much larger proportion of photons with high scatter orders (see Table 3). The photons with high scatter orders are a major source of modeling errors for this energy window since photons with higher scatter orders are more difficult to accurately model than ones with lower scatter orders. Collimator lead characteristic X-rays could also contribute to the modeling errors for this energy window. Some previous studies have suggested using acquisition energy windows having a lower threshold less than 100 keV because of the large number of detected photons (Dezarn et al., 2011; Shen et al., 1994; Heard et al., 2004). However, according to the analysis above, this appears not to be a good choice for accurate quantitative imaging unless the high order scatter can be modeled accurately in the projector. The 160–300 keV window had the largest proportion of photons backscattered from the compartments behind the crystal among the four windows. Since these photons are difficult to model, there will be larger model-mismatch, which would contribute to bias in the activity estimates. In the 300–2000 keV window, most detected photons have penetrated through or scattered in the collimator septa. These photons provide low-quality spatial information about the activity distribution and could result in both larger bias and variance in the activity estimates.

Table 2.

Fraction of detected photons that underwent various processes during their propagation.

	GeoPri a	ScaInBody b	PenScaCol c	X-ray d	Bck e
60–100 keV	9.4%	66.4%	27.1%	9.3%	22.7%
100–160 keV	9.9%	49.2%	51.9%	0.01%	50.6%
160–300 keV	5.1%	30.3%	83.1%	0.00%	72.6%
300–2000 keV	1.2%	21.7%	97.5%	0.00%	31.9%

^aGeometrically collimated primary photons.

^bBody-scattered photons.

^cCollimator scatter and penetration.

^dCollimator lead characteristic X-ray.

^eBackscatter from compartments behind the crystal.

Table 3.

Fraction of body-scattered photons with various scatter orders.

Scatter order a	1	2	3	4	5	> 5
60–100 keV	29.3%	20.3%	16.6%	13.0%	9.2%	11.6%
100–160 keV	47.4%	24.7%	14.6%	7.8%	3.5%	1.9%

^aScatter order: the number of times a photon has been scattered.

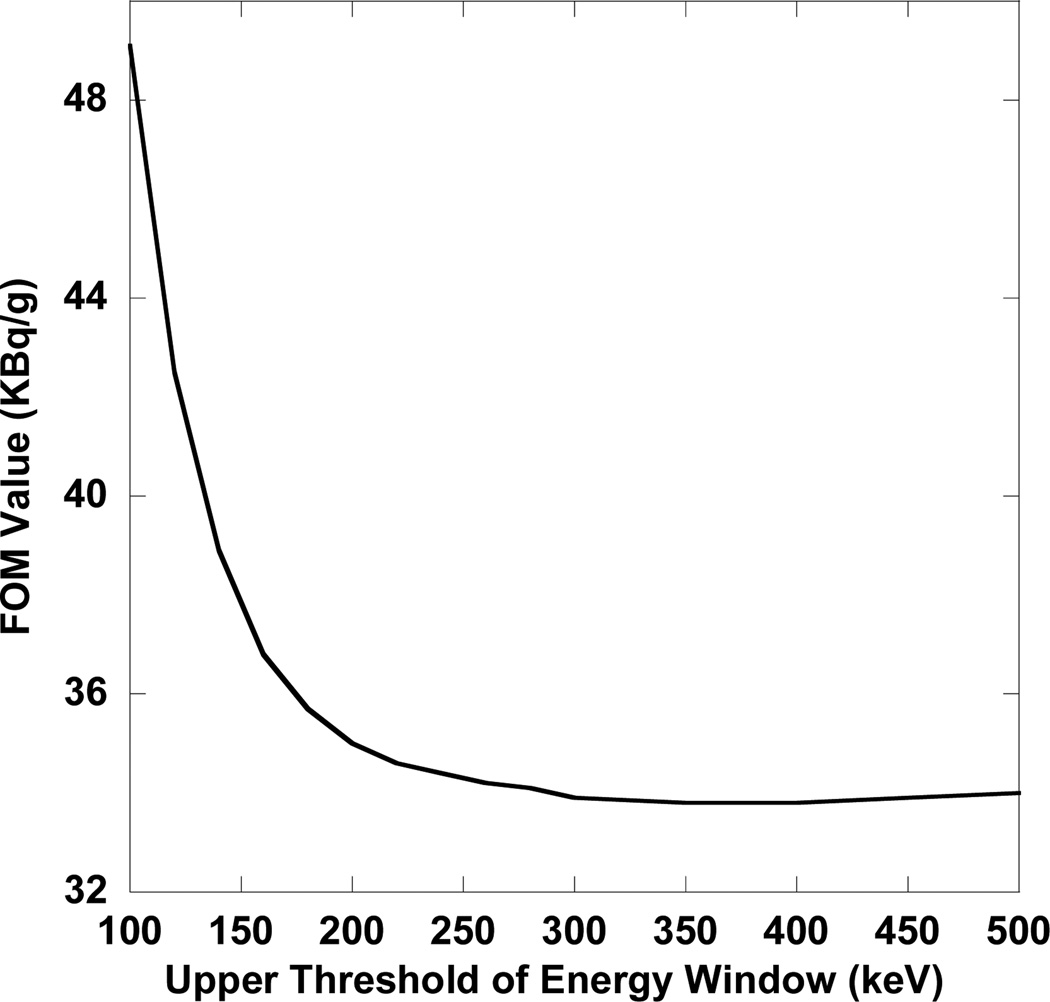
To demonstrate the importance of taking into account the bias of the activity estimates for optimization, we calculated the FOM values assuming the bias was zero in the equation (1) for the above-mentioned experiment when tumor-to-normal activity concentration ratio was 5:1. Under this assumption, the FOM becomes the sum of mass-weighted standard deviations of the activity estimates and is thus related to a Cramer-Rao variance bound FOM. Figure 5 shows the FOM as a function of the upper threshold with a lower threshold of 60 keV. Without bias in the FOM, in general, energy windows with larger numbers of detected photons had smaller FOM values, and lower energy windows had smaller FOM values than higher energy windows. The 60–400 keV window had the smallest FOM value. This is consistent with a larger number of detected photons resulting in smaller variance and thus smaller FOM values with the exception that the very high energy photons increased the variance due to large tails increasing the noise sensitivity of the matrix inverse. Also, the FOM values calculated assuming zero bias were much smaller than when the actual bias was included (e.g., in the 100–160 keV window the FOM values were 0.056 MBq/g vs. 0.25 MBq/g), which means that the bias of the activity estimates was a more important factor than the variance in terms of limiting the reliability. As a result, the optimal energy window obtained using the proposed method (100–160 keV) should produce more reliable activity estimates than the result obtained by taking into account only the variance (60–400 keV).

Figure 5.

FOM values assuming unbiased estimates as a function of the upper threshold of the acquisition energy window with a lower threshold of 60 keV when the tumor-to-normal activity concentration ratio was 5:1. The optimal energy window was 60–400 keV, which was different from the optimal one when taking into account the bias (100–160 keV).

4. Discussion

In the proposed method, the true VOI activities λ = [λ₁,λ₂,…,λ _N]^T ∈ ℝ^{N× 1} were deterministic variables (λ did not appear in the proposed method explicitly; for a given λ, the vector of true expected number of decays in each VOI is a_t = [λ₁·t,λ₂,·t,…,λ _N·t]^T∈ ℝ^{N× 1}, where t is the imaging time per projection view). Since the activity distributions vary from patient to patient, it is more general to treat λ as random variables instead of deterministic ones. The proposed FOM could be modified to incorporate the variations in λ:

$$\text{FOM}=\frac{1}{N}\sum _{i=1}^N\frac{\text{RMSE}(A_i)}{m_i}=\frac{1}{N}\sum _{i=1}^N\frac{\sqrt{{\mathrm{E}}_{\mathbf{\lambda }}{[\text{Variance}(A_i|\mathbf{\lambda })+(\text{Bias}(A_i|\mathbf{\lambda }))]}^2}}{m_i},$$ (10)

(10) where Bias(A_i|λ) and Variance(A_i|λ) denote the conditional bias and conditional variance with respect to λ, respectively, and E_λ [∙] denotes the ensemble mean with respect to λ. Thus Bias(A_i|λ) can be calculated using equations (6) and (8), and Variance((A_i|λ)) can be calculated using equations (7) and (9). E_λ [∙] can be calculated numerically based on sampling a probability density function (PDF) of λ predefined for a specific application. By choosing an appropriate PDF, more general optimization results could have been obtained for⁹⁰Y microsphere imaging that take into account not only the quantum noise but also the variation in⁹⁰Y activity concentration in the various compartments. However, we did not implement this for two reasons. First, we obtained the same optimal energy window (100–160 keV) for all the three tumor-to normal activity concentration ratios; since these three ratios and the various sizes of tumors simulated in our experiment represent general situations of interest in clinical⁹⁰Y microsphere imaging, it is reasonable to believe that the 100–160 keV window is near-optimal even when taking into account variations in⁹⁰Y activity concentration. Second, VOI analysis of the variations in tumor and normal liver activity concentration using sufficient clinical data is required to obtain a realistic estimate of the PDF of λ. We currently do not have sufficient clinical data to conduct this study.

In addition to incorporating variations in VOI activities into the proposed method, a further step to increase the generality of the method would be incorporation of variations in the number, volume and position of VOIs. However, this would make both the mathematical derivation and the implementation of the method much more complicated. As a result, we did not pursue this topic. However, to make the results more general, we did divide the liver into several sub-VOIs (allowing for the possibility that they had different activity concentrations, as might result from the case where the microspheres were delivered to only a part of the liver) and include multiple tumors having a range of sizes (diameters ranging from 1.5 to 5.5 cm). These provide a more, though certainly not completely, general representation of the situations in clinical microsphere brachytherapy.

Since the proposed method is based on the assumption that the projection data follow a Gaussian distribution, in cases where the number of photon counts per projection bin is very small, the accuracy of the proposed method may be limited. This could occur in applications where the activities in VOIs are very low or the acquisition time is very short such as dynamic studies.

Although Monte Carlo simulation was used to generate the true system matrix in this work, it is not necessarily a prerequisite for the application of the proposed method. In principle, the information required for calculating the FOM such as E[y] and a_t could be measured experimentally instead of obtained using Monte Carlo simulation. In practice, however, there are several difficulties involved in this kind of experiment. First, since the system matrix not only includes the effects of the imaging system, but also the patient anatomy (image degrading effects such as attenuation and scatter are closely related to patient anatomy), it is desirable to simulate realistically the relevant human anatomy in the experiment. In many cases, available physical phantoms may be too simple to achieve this goal. Second, to obtain accurate measurements of required information such as E[y], the noise in the projection data needs to be very low. In optimization of energy window, these information need to be measured for many energy windows with narrow widths. Since the widths of these windows are very narrow, the acquisition time needs to be relatively long to obtain low-noise data from multiple projection views. For scanners without list-mode acquisition capability, the overall experimental time might be very long due to the large number of energy windows investigated. In addition, in physical experiments some important information such as a_t may not be measured accurately. The errors in these measurements could affect the accuracy of the optimization results.

When applying the proposed method to optimize the energy window for⁹⁰Y bremsstrahlung imaging, we used the SIMIND simulated system sensitivity in both the true and the model-estimated system matrices. In clinical situations, there may be errors in measuring the geometric system sensitivity due to difficulty in separating geometrically collimated primary photons from photons that have been scattered in the calibration phantom or penetrated the collimator septa. These errors will likely be energy dependent and could affect the amount of model-mismatch. Since the amount of these errors strongly depends on the specific method used in the calibration process, we did not investigate their effects in this study and these effects are not reflected in the optimal energy window. However, it is likely that the bias in the sensitivity measurement would be large in energy windows where the model-mismatch is large. Thus we believe that neglecting this effect has relatively small impact on the optimal energy window.

It should be noted that the obtained optimal energy window is a function of the imaging system parameters such as the crystal thickness and the collimator. How these parameters affect the optimal energy window is a topic for future study.

5. Conclusions

In this work, we have developed a new method for optimizing the acquisition energy window for quantitative imaging when bias is an important factor limiting reliability. We applied this method to optimizing the energy windows in quantitative⁹⁰Y bremsstrahlung SPECT as applied to⁹⁰Y microsphere brachytherapy for liver cancer. In contrast to previous methods for conventional gamma photon emitters that only take into account the variance of the activity estimates and implicitly assume unbiased estimates, the proposed method takes into account both the bias due to model-mismatch and the variance of the activity estimates. We observed that the bias due to model-mismatch was a more important factor limiting the reliability of the activity estimates than the variance, and that the amount of bias due to model-mismatch varied with energy. We found the optimal energy window for an object consisting of multiple tumors of various sizes and various tumor-to-normal activity concentration ratios in the anatomically realistic XCAT phantom. Model-mismatch was represented by the difference between detailed Monte Carlo simulation and a projector modeling attenuation, scatter, and the collimator-detector response previously validated for quantitative⁹⁰Y bremsstrahlung SPECT. For this combination of object and imaging model the optimal acquisition energy window was 100–160 keV.