Cost-effectiveness of bone densitometry among Caucasian women and men without a prior fracture according to age and body weight

Abstract

Summary

We used a microsimulation model to estimate the threshold body weights at which screening bone densitometry is cost-effective. Among women aged 55–65 years and men aged 55–75 years without a prior fracture, body weight can be used to identify those for whom bone densitometry is cost-effective.

Introduction

Bone densitometry may be more cost-effective for those with lower body weight since the prevalence of osteoporosis is higher for those with low body weight. Our purpose was to estimate weight thresholds below which bone densitometry is cost-effective for women and men without a prior clinical fracture at ages 55, 60, 65, 75, and 80 years.

Methods

We used a microsimulation model to estimate the costs and health benefits of bone densitometry and 5 years of fracture prevention therapy for those without prior fracture but with femoral neck osteoporosis (T-score≤−2.5) and a 10-year hip fracture risk of ≥3%. Threshold pre-test probabilities of low BMD warranting drug therapy at which bone densitometry is cost-effective were calculated. Corresponding body weight thresholds were estimated using data from the Study of Osteoporotic Fractures (SOF), the Osteoporotic Fractures in Men (MrOS) study, and the National Health and Nutrition Examination Survey (NHANES) for 2005–2006.

Results

Assuming a willingness to pay of $75,000 per quality adjusted life year (QALY) and drug cost of $500/year, body weight thresholds below which bone densitometry is cost-effective for those without a prior fracture were 74, 90, and 100 kg, respectively, for women aged 55, 65, and 80 years; and were 67, 101, and 108 kg, respectively, for men aged 55, 75, and 80 years.

Conclusions

For women aged 55–65 years and men aged 55–75 years without a prior fracture, body weight can be used to select those for whom bone densitometry is cost-effective.

Introduction

Fractures related to osteoporosis are projected to occur in 3 million US women and men at a cost of $25 billion by 2025 [1]. Clinical efforts to reduce this burden rely in part on bone densitometry to select those for whom pharmacologic fracture prevention therapy is indicated [2]. Most economic modeling studies have focused on the cost-effectiveness of fracture reduction therapy, but have not considered the upfront cost of screening to estimate fracture risk. Previous studies show that bone densitometry followed by 5 years of pharmacologic therapy is cost-effective among women aged ≥65 years [3–5] and in the USA for men ≥70 years [6]. However, they generally have not considered other factors that affect the pre-test probability of osteoporosis and therefore the cost of screening, nor have they addressed appropriate screening strategies at ages less than 65 years. The US Preventive Services Task Force (USPSTF) estimated that in women without previous vertebral fracture, the number needed to screen to prevent one hip fracture in 5 years was 1667 in women aged 55–59 years, compared to 556 in women aged 65–69 years [7]. Strategies that screen subsets of middle-aged individuals with a higher pre-test probability of very low BMD and high fracture risk are more likely to be cost-effective.

Several validated clinical decision rules can help select those for whom the pre-test probability of osteoporosis is raised. The Osteoporosis Self-Assessment Tool (OST) uses only age and body weight to estimate pre-test probability of osteoporosis [8] and performs as well as other clinical decision rules that incorporate other risk factors [9, 10]. Particularly for those without a history of fracture, body weight might influence the cost-effectiveness of bone densitometry. Our objective was to estimate the body weights below which bone densitometry is cost-effective for US Caucasian women and men aged 55–80 years without a prior clinical fracture.

Methods

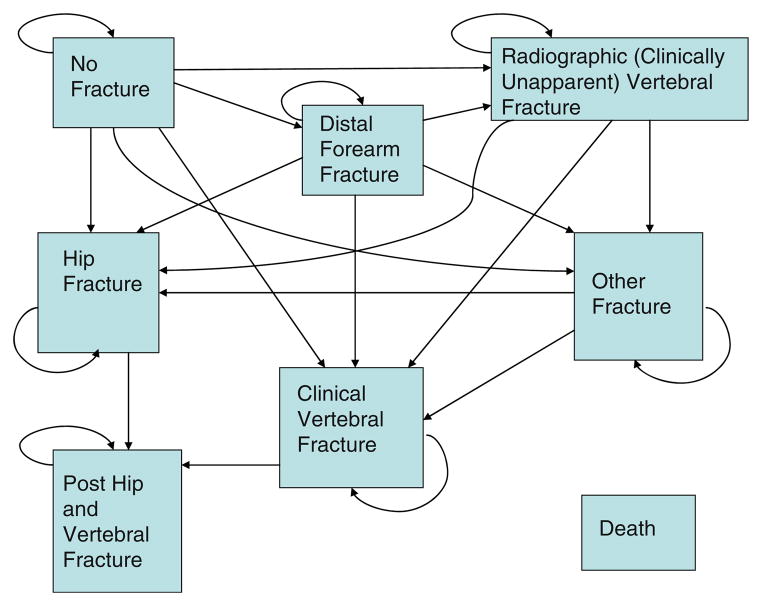
The validated Markov microsimulation model (Data Pro Healthcare software [Williamstown, MA]) used for this study is thoroughly described in prior publications [3, 6, 11–14]. Our analyses apply to older Caucasian US women and men who have not had a prior clinical fracture since age 50 years, and assume a national health payer perspective. The model health states were no fracture, post-distal forearm fracture, post-clinical vertebral fracture, post-radiographic vertebral fracture (i.e., not recognized clinically at onset), post-hip fracture, post-other fractures (i.e., of the proximal forearm, humerus, scapula, clavicle, sternum, ribs, pelvis, distal femur, patella, tibia, or proximal fibula), post-both hip and clinical vertebral fracture, and death (Fig. 1). Individuals could transition to a different state once every 3 months. Individuals aged 55, 60, 65, 70, 75, and 80 years were screened at baseline and followed until age 100 years or death in order to capture all long-term costs and disutility from fractures. Models were run as Monte Carlo simulations with 100,000 trials each, assuming a 3% annual discount rate for costs and health benefits.

Fig. 1.

State diagram of Markov model. Transition to death may also occur from any state (not shown with arrows)

Based on a recent cost-effectiveness study [15], most current guidelines in the USA recommend pharmacologic treatment if the estimated 10-year risks of hip or major osteoporotic fractures exceed, respectively, 3% or 20% [16]. We used the FRAX fracture risk calculator [17] to estimate the BMD T-score threshold at which the risk of hip or major osteoporotic fractures exceeded one of these thresholds for US Caucasian men and women of average height and weight for their age and sex with no additional fracture risks other than low BMD. However, the fracture reduction benefit of drug therapy for those with neither a prevalent vertebral fracture nor a femoral neck BMD T-score ≤−2.5 remains unproven [18]. Hence, we postulated that drug therapy would be indicated for those with both a femoral neck T-score ≤−2.5 and either a 10-year estimated hip fracture risk of ≥3% or major osteoporotic fracture risk of 20% (Table 1). For men, we calculated T-scores using young male norms.

Table 1.

Parameters for determining fracture risk attributable to low BMD among those with bone density femoral neck T-score below treatment cutpoint

Age (years)	Femoral neck T-scorea Rx cutpoint		Mean Z-score below Rx cutpointa		Prevalence of prior clinical fracture (%)
	Women	Men	Women	Men	Women	Men
55	−2.95	−2.65	−2.69	−2.42	21.9	11.4
60	−2.8	−2.55	−2.30	−2.30	26.6	12.6
65	−2.6	−2.5	−2.11	−2.09	29.5	14.3
70	−2.5	−2.5	−1.85	−1.90	34.2	16.3
75	−2.5	−2.5	−1.57	−1.84	40.9	18.0
80	−2.5	−2.5	−1.42	−1.72	46.3	19.8

^aCutpoint set to either (whichever is lower) −2.5 or BMD T-score where the 10-year risk of hip fracture by FRAX with BMD for US Caucasians with no additional risk factors for fracture is 3.0%

We assumed a willingness to pay (WTP) threshold of $75,000 per quality adjusted life year (QALY) gained for the primary analyses, which is roughly twice the per capita gross domestic product (GDP) of the USA. We based this on the WHO Commission of Macroeconomics and Health suggesting that a reasonable willingness to pay threshold for a given country may be one to three times the per capita GDP [19], and on cost-effectiveness work by Borgstrom and colleagues assuming a societal WTP equal to twice per capita GDP [20]. However, we also performed analyses assuming WTP thresholds of $50,000 and $100,000.

Overall analytic strategy

We first used our microsimulation model to estimate the costs per QALY gained for the intervention strategy compared to no intervention across a wide range of assumed pre-test probabilities of low BMD warranting drug therapy for each age and sex. Second, we calculated the pre-test probability threshold for each age and sex at which the cost per QALY gained would be equal to each of the three WTP thresholds by linear interpolation between those pre-test probabilities associated with the costs per QALY gained just above and below each WTP threshold.

Third, for each subset defined by age and sex, we calculated the body weights at which the pre-test probability of low BMD warranting drug therapy is equal to the pre-test probability threshold of low BMD below which bone densitometry is cost-effective. The weight thresholds were calculated from a) the mean body weight for that subset; b) the mean pre-test probability of low BMD warranting drug therapy for that subset; c) the pre-test probability of low BMD at which the intervention strategy is cost-effective; and d) the association between body weight and the pre-test probability of low BMD. This association allowed us to translate how much weight change from the mean would correspond to the change in pre-test probability of low BMD from the mean to the cost-effective threshold pre-test probability (described in detail in “ Appendix”). We then calculated the body weight threshold at which bone densitometry is cost-effective by adding or subtracting the weight change from the mean body weight for that that subset defined by age and sex. Fourth, the proportion of the population within each subset defined by age and sex below these body weight thresholds were then calculated using NHANES 2005–2006 data.

We estimated the association of low BMD warranting drug therapy and body weight among women and men without prior fracture using unpublished data from the second SOF study visit (7,927 women, mean age 73.7 years) and the baseline MrOS study visit (5,993 men, mean age 73.7 years). The derivations of the separate logistic regression models for each treatment cutpoint are described in the technical “Appendix”. Earlier publications have detailed the recruitment and characteristics of the SOF population attending the second SOF visit and the MrOS population at the first MrOS visit [21–23].

Model parameters

Mortality rates

Background mortality rates for Caucasian women and men were estimated from 2004 US vital statistics [24]. The mortality for the first year after hip fracture attributable to the fracture was estimated to be 0.375 times the background rate [25].

Fracture probabilities

Fracture rate equations for hip and clinical vertebral fractures as a function of age for each sex were developed from recent data for the US Caucasian population [26]. We assumed that only 25% of all radiographically detected vertebral fractures would be clinically recognized at the time of their occurrence and that the rate of radiographic (but clinically unapparent) vertebral fractures is three times the rate of clinical vertebral fractures [22]. Fracture rate equations for wrist and other fractures were constructed from published data [27, 28] as previously described [3, 6, 11]. Since these fracture rate equations are for all individuals regardless of BMD or prior clinical fracture status, these rates were adjusted for the absence of a prior clinical fracture and the presence of BMD below the treatment cutpoint (described in detail in the technical “Appendix”), based on the relative risks of fracture attributable to low BMD and prior clinical fracture noted in Table 2. The relative risks of fractures on bisphosphonate therapy based on published randomized controlled trials [29–34] are shown in Table 2. After a 5-year treatment course, a gradual linear loss of fracture reduction benefit was assumed to occur over the subsequent 5 years.

Table 2.

Model parameters

Parameter	Value	References
Disutility per year*
No fracture state	0	Peasgood [43]
Post-distal forearm fracture	0.04 (1st year), then 0
Post-hip fracture	0.20 1st year, then 0.131 years 2–5
Post-clinical vertebral fracture	0.23 1st year), then 0.064 years 2–5
Post-radiographic vertebral fracture	0.126 1st year, then 0.06 years 2–5	Kanis [44]
Post-hip and clinical vertebral fracture	0.36 (1st year), then 0.20 years 2–10	Tosteson [45]
Post-“other” fracture	0.073 (1st year), then 0.023 years 2–5	Kanis [44]
Direct medical costs
Acute hip fracture	$35,322
Direct medical costs	$23,455	Gabriel [39]
1st year long-term care	$11,867	Leibson [40]
Acute clinical vertebral fracture	$9,244	Gabriel [39]
Acute radiographic (clinically unapparent) vertebral fracture	$0	Gabriel [39]
Acute distal forearm fracture	$5,017	Gabriel [39]
Acute other fracture	$7,264	Gabriel [37]
Annual long-term care>1 year after hip fracture	$9,057	Leibson [40]
Relative risk of fractures on bisphosphonate therapy	Men: non-spine fractures 0.73, spine fractures 0.36. Women: vertebral 0.5; hip, wrist 0.60; other 0.80	Orwoll [61], Ringe [62], Sawka [34], Black [30]
Relative risks fractures due to low BMDa	Men	Women
Hip
Age 55	3.92	3.29
Age 60	3.59	3.01
Age 65	3.38	2.83
Age 70	3.25	2.73
Age 75	3.02	2.53
Age 80	2.67	2.24
Age 85	2.26	1.89
Wrist and other	1.34	1.40
Vertebral	1.80	1.90
Relative risks fractures prior clinical fracture vs no prior fracture	Men	Women
Hip
Age 55	4.84	3.83
Age 60	3.84	3.04
Age 65	2.77	2.20
Age 70	2.31	1.83
Age 75	1.99	1.58
Age 80	1.71	1.36
Age 85	1.61	1.27
Wrist and other	2.01	1.73
∘Vertebral	2.40	1.32

^aPer SD decrease of femoral neck BMD

^*QALY value for health state is 0.84 for those age <75 years and 0.82 age 75 and older. Disutilities are represent difference in QALY value between healthy and other states

Relative risk of fractures associated with obesity in men

The age-adjusted and BMD-adjusted relative risks of hip and non-spine fractures in men have been estimated to be 1.76 and 1.29 [35], respectively, for men who are obese (body mass index [BMI] ≥30 kg/m²) compared to men with BMI ≤25. Hence, for male age groups where the weight below which bone densitometry is cost-effective is higher than the average weight, the cost-effectiveness of bone densitometry followed by drug therapy may be underestimated without taking these increased fracture risks into account. Therefore, models for those male age groups were re-run with hip and non-hip, non-spine fracture rates raised, respectively, 1.76 and 1.29-fold.

Costs

The cost of bone density screening per person being treated was calculated as the mean Medicare reimbursement for the first half of 2010 ($97.41) [36] divided by the prevalence of BMD below the treatment cutpoint in that subset defined by age and sex. The prevalence of those with femoral neck BMD below the treatment cutpoint for each starting age for US Caucasian females and males, regardless of prior clinical fracture status, was estimated from NHANES 2005–2006 data [37]. However, those without a prior clinical fracture have higher BMD, and hence these prevalences were adjusted for the absence of a prior clinical fracture (Table 1). The details of these calculations are given in the technical “Appendix”.

For the primary and secondary analyses, respectively, we assumed bisphosphonate costs of $500 and $250 per year. Although the cost of generic alendronate is as low as $100 per year, in clinical practice some individuals will be switched to other, more expensive agents (most of which have an average 2010 wholesale drug cost of $1400 to $1600 per year) [38] based on patient preference or intolerance to alendronate. Assuming a drug cost equal to generic alendronate is invalid because this implies that patients known to have osteoporosis after having a bone density test would go untreated if they could not tolerate alendronate. An aggregate cost of $500 per year would correspond to 70% being treated with generic alendronate and 30% with other medications, whereas a cost of $250 per year would correspond to 89% being treated with generic alendronate and 11% with other medications.

The direct medical costs of acute hip, clinical vertebral, distal forearm, and “other” fractures are expressed in 2010 US dollars (Table 2) [39]. As detailed in previous publications [6, 11], the proportion of those with an incident hip fracture who are community dwelling before their hip fracture and require permanent long-term care after their hip fracture was estimated to be 12.2%, costing $9,055 per year until death averaged over all hip fracture patients (2010 US dollars, Table 2) [40, 41].

Quality adjusted life years (QALYs) associated with each health state

Based on age-specific US population based values, we assumed a QALY value of 0.84 for those younger than age 75 years and 0.82 for those aged 75 years and older for the “no fracture” state [42]. The disutilities for the first and subsequent years after hip, distal forearm, and clinical vertebral fractures [43], for the first year following other fractures [44], for all fractures more than 1 year after their occurrence [44], and for those who have had both a hip and a clinical vertebral fracture [45] are shown in Table 2.

Medication adherence

We assumed that 85% of prescribed medication is purchased and taken in the first 3 months and that this percentage drops to 65% by the end of 1 year, 60% by the end of the second year, and 55% by the start of the fifth (and final) year of drug therapy [46]. Medication costs and fracture reduction efficacy were assumed to be proportional to adherence [47, 48].

Sensitivity analyses

Univariate sensitivity analyses were done varying fracture costs, rates, and disutility, bone densitometry cost, and the association between weight and odds of low BMD warranting drug therapy. Since drug therapy may not be acceptable to many patients unless they are at higher fracture risk than currently accepted treatment thresholds, we also did sensitivity analyses assuming initiation of treatment only if the 10-year hip fracture risk is ≥6% (corresponding to femoral neck T-scores of −3.26 and −3.15, respectively, for 65-year-old Caucasian women and men without prior fracture or other risk factors). For parameters derived from SOF and MrOS (association between weight and odds of low BMD warranting drug therapy, proportion with a prior clinical fracture, and odds of low BMD warranting treatment in those with compared to those without prior clinical fracture), sensitivity analyses varying these over wide ranges were also performed for 55-year-old men and women.

To capture the effect of simultaneous changes of multiple parameters, probabilistic sensitivity analyses were done (see details of parameter distributions in the technical “Appendix”).

Results

The mean body weights, the prevalence of femoral neck BMD below the treatment cutpoint for each age, and the threshold pre-DXA test probability of femoral neck BMD being below the treatment cutpoint for each age and sex are shown in Table 3 for women and Table 4 for men, assuming a WTP threshold per QALY gained of $75,000. The pre-test probability of BMD sufficiently low to warrant pharmacologic therapy such that bone densitometry followed by pharmacologic therapy would be cost-effective ranged from 1.6% for women aged 55 years to 1.1% for women aged 70 years and from 15.7% for men aged 55 years to 1.3% for men aged 80 years. The body weight thresholds corresponding to these pre-test probabilities of low BMD ranged from 73.8 kg for women aged 55 years to 100.2 kg for women aged 80 years and from 67.2 kg for men aged 55 years to 108.2 kg for men age 80 years.

Table 3.

Prevalence of bone density below treatment T-score cutpoint and corresponding threshold weights for screen and treat strategy to be cost-effective for women without prior clinical fracture (societal WTP=$75,000 per QALY gained)

Age (years)	Mean weight (kg)*	Prevalence BMD below Rx threshold (%)**	Drug cost $500 per year		Drug cost $250 year
			Cost-effective pre-test probability (%)^	Threshold weight (kg)^^	Cost-effective pre-test probability (%)	Threshold weight (kg)
55	78.5	0.93	1.62	73.8	1.45	74.7
60	79.1	2.76	1.49	84.9	1.35	85.8
65	76.6	4.42	1.23	90.5	1.16	91.1
70	74.0	8.16	1.13	97.6	1.04	98.5
75	68.7	14.59	1.15	99.4	1.09	100.1
80	66.4	19.21	1.23	100.2	1.15	101.0

^*Ten-year hip fracture risk treatment threshold varied from 6 to 3%

^**Odds ratio of femoral neck osteoporosis per 10-kg increase body weight varied from 0.22 to 0.65

^***Fracture disutility varied from 50 to 150% of base case value

^{^}Fracture costs varied from 70 to 130% of base case value

^{^^}Fracture rates varied from 80 to 120% of base case value

Table 4.

Pre-test probability of bone density below treatment T-score cutpoint and corresponding threshold weights for screen and treat strategy to be cost-effective for men without prior clinical fracture (societal WTP=$75,000 per QALY gained)

Age (years)	Mean weight (kg)a	Prevalence BMD below Rx cutpoint (%)b	Drug cost $500 per year		Drug cost $250 year
			Cost-effective pre-test probability (%)c	Threshold weight (kg)d	Cost-effective pre-test probability (%)	Threshold weight (kg)
55	91.0	2.03	15.2	67.2	7.14	76.5
60	92.7	2.77	7.87	80.6	4.87	86.2
65	90.5	4.65	4.46	91.0	3.40	94.4
70	88.7	7.23	2.68	101.2	2.24	103.4
75	86.9	8.38	2.44	102.5	1.65	107.3
80	81.6	10.74	1.30	108.3	1.19	109.4

^aMean for US age-matched and sex-matched Caucasians (from NHANES 2005–2006 [20])

^bPrevalence of BMD below femoral neck T-score treatment cutpoint

^cPre-test probability of low BMD warranting drug therapy at which bone densitometry is cost-effective

^dBody weight threshold corresponding to cost-effective pre-test probability of low BMD warranting drug therapy

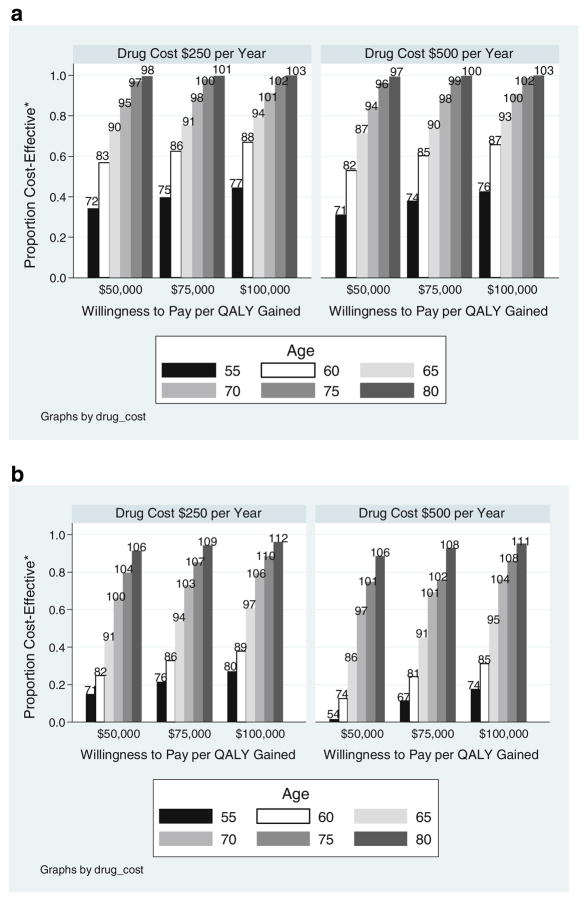
Assuming a willingness to pay per QALY gained of $75,000 and yearly drug cost of $500, the proportions of women without a prior clinical fracture aged 55, 65, and 75 at or below the body weight thresholds such that bone densitometry followed by fracture prevention therapy was cost-effective were, respectively, 41, 76, and 98% (Fig. 2a). Similarly, bone densitometry was cost-effective for 10, 51, and 83%, respectively, of men without a prior clinical fracture at ages 55, 65, and 75 (Fig. 2b). These proportions change modestly under the assumptions of willingness to pay thresholds of either $50,000 or $100,000 per QALY gained, or yearly fracture prevention drug cost of $250 per year.

Fig. 2.

Proportion of women (a) and men (b) without prior fracture for whom bone densitometry followed by fracture prevention therapy is cost-effective. *Proportion cost-effective is the proportion with a body weight below the threshold weight in kilogram (label at top of bars)

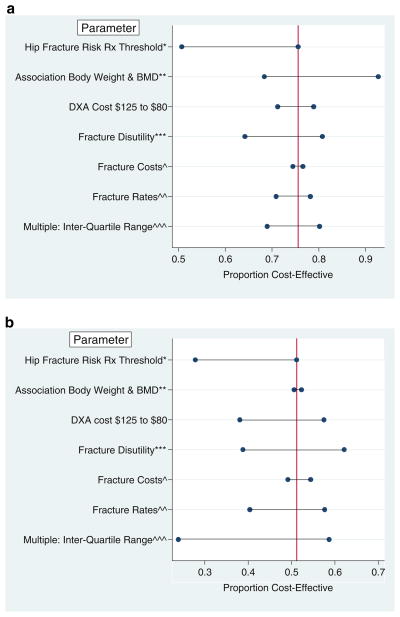
Importantly, the proportion of men and women for whom bone densitometry is cost-effective is sensitive to changes in treatment threshold. For example, if treatment is offered (or accepted) only if the 10-year risk of hip fracture is 6%, then the treatment T-score thresholds for 65-year-old women and men, respectively, are −3.26 and −3.1, and the proportions for whom bone densitometry is cost-effective fall to 51% and 28% (Fig. 3a, b). These results are also somewhat sensitive to DXA cost, fracture rates, and fracture disutility. However, the proportions of men and women aged 55 for whom bone densitometry is cost-effective change little (<5%) with changes of the prevalence of prior clinical fracture and of the odds of low BMD warranting treatment. Changes in the association of body weight and bone mineral density also have little effect on these proportions if the base case estimated cost-effective body weight threshold is very close to the mean body weight (as for men aged 65, Fig. 3a), but have a larger influence on the estimated body weight threshold if the base case estimated body weight threshold is quite different from the mean body weight (Fig. 3b). Varying multiple parameters simultaneously has a greater effect on the estimated proportions of men for whom bone densitometry is cost-effective than for women, largely because of greater uncertainty regarding the fracture reduction efficacy of bisphosphonates in men compared to women.

Fig. 3.

Sensitivity analyses: effect of parameter changes on proportions of women (a) and men (b) aged 65 without prior fracture for whom bone densitometry is cost-effective. *Ten-year hip fracture risk treatment threshold varied from 6 to 3%; **Odds ratio of femoral neck osteoporosis per 10kg increase body weight varied from 0.22 to 0.65; ***Fracture disutility varied from 50 to 150% of base case value; ^Fracture costs varied from 70 to 130% of base case value; ^^Fracture rates varied from 80 to 120% of base case value; ^^^From probabilistic sensitivity analyses (see “Appendix”). Vertical line represents base vase proportion for whom bone densitometry is cost-effective

Discussion

Bone densitometry in the USA is widely recommended at least once for all women aged 65 and older [2, 49, 50] and all men aged 70 and older [2, 50]. Cost-effectiveness evaluations have lent support to these recommendations [3, 4, 6], consistently showing modest cost relative to the health benefits gained for these older individuals. With few exceptions [6, 51], these studies have not considered the costs and potential health benefits of bone densitometry for subgroups stratified on risk factors for low bone mass other than age and sex.

Among Caucasian women between the ages of 55 and 65 and men between the ages of 55 and 75 without a history of a clinical fracture after age 50, our data show that body weight can aid selection of those for whom it is cost-effective to perform bone densitometry. However, bone densitometry is cost-effective for virtually all women aged 70 and older and for men aged 80 years regardless of body weight. Incorporating body weight into electronic decision tools (embedded in the medical record) as to whether or not a bone density test is indicated for a specific individual is likely to be feasible. This could reduce the frequency of measuring BMD on those younger post-menopausal women and men whose likelihood of having bone mass below a reasonable treatment threshold is very low. While our results are modestly changed by varying assumptions regarding drug cost and the willingness to pay threshold per QALY gained, they hold up well under reasonable changes in these assumptions.

Our suggested body weight thresholds for bone densitometry among women younger than age 65 years old are somewhat more liberal than levels recommended by the US Preventive Services Task Force [49]. The USPSTF recommended that bone densitometry be offered to women younger than age 65 if the pre-test estimated risk of major osteoporosis fracture was 9.3% (calculated using FRAX without BMD), since this is the average risk of 65-year-old Caucasian women. At the body weight thresholds derived from our analyses for women aged 55 and 60 of average height and with no other risk factors, the 10-year major osteoporotic fracture risk is, respectively, 5.3% and 6.3%. Our recommendations are derived explicitly using cost-effectiveness criteria, whereas those of USPSTF are not.

We chose not to do these analyses within the context of the complete FRAX calculator for two reasons. First, among all of the FRAX risk factors, age, sex, BMD, and prior fracture explain the majority of fracture risk in populations where the other risk factors (e.g., current smoking, parental history of hip fracture, glucocorticoid use, rheumatoid arthritis, heavy alcohol use) are of low prevalence [52]. Hence, at the population level, for younger post-menopausal women and men without a prior clinical fracture, subsequent fracture risk will be driven largely by BMD. Second, the benefit of currently available therapies for preventing non-vertebral fractures among those with neither osteoporosis by BMD criteria nor a prevalent vertebral fracture remains unproven. Our results and conclusions would differ if we assumed that the fracture reduction benefit of drug therapy is unrelated to BMD. In that instance, there will be subsets with clinical fracture risk factors sufficient to warrant therapy regardless of BMD [51].

There are limitations to our study. Our results do not apply to individuals who have additional risk factors for fractures such as current smoking, glucocorticoid use, or chronic diseases such as COPD or rheumatoid arthritis. Our results are applicable only to Caucasian women and men who have men not had a prior bone density test, and therefore cannot be used to estimate when bone densitometry should be repeated. We derived some of our model parameters from SOF and MrOS which enrolled individuals aged 65 and older, and from these data estimated these parameters for women and men aged 55–65 by extrapolation. Our models assume that individuals with a BMD value that correlates with a 10-year hip fracture risk of 3% or more will at least initially accept a prescription for a fracture prevention medication. If the majority of such individuals would not accept such treatment, then bone densitometry may be inappropriate. The estimated thresholds of body weight below which bone densitometry is cost-effective are lower if treatment was offered and accepted only at higher levels of fracture risk.

Finally, our results do not imply that individuals above the body weight thresholds in our analysis are never at risk of fracture [53]. Bone densitometry may be cost-effective for many of those heavier than our proposed thresholds if therapies at some point are shown to reduce fractures significantly in those with neither prevalent vertebral fracture nor osteoporosis by BMD criteria.

In summary, the cost-effectiveness of bone densitometry for women and men without a history of fracture is influenced by body weight, largely by its effect on the pre-test probability of BMD being sufficiently low to warrant drug therapy. Our results suggest that considering body weight can help identify women between ages 55 and 65 and men between ages 55 and 75 without additional fracture risk factors for whom a bone densitometry likely to be cost-effective.

Appendix

This technical appendix describes in detail the derivation of a) the relative risks of fractures attributable to the absence of prior clinical fracture; b) the proportion of those without clinical fracture who have low bone mass warranting drug therapy; c) the relative risks of fractures attributable to low BMD warranting drug therapy; d) the pre-test probability cutpoints of low BMD below which bone densitometry followed by fracture prevention therapy is cost-effective; and e) the body weight thresholds below which the pretest probability of low BMD warranting drug therapy is high enough such that bone densitometry is cost-effective.

Relative risk of fracture in those without prior fracture (RR_{NoPriorFracture vs All})

This relative risk is calculated from the following equation:

$${\text{RR}}_{\text{NoPriorFracture}\text{vs}\text{All}}=1/[1+({\text{RR}}_{\text{PriorFx}\text{vs}\text{NoPrior}\text{Fx}}-1)\ast {\mathrm{Prev}}_{\text{PriorFx}}]$$ (1)

[12]

We assumed the relative risk of incident clinical fracture in those with compared to those without prior fracture (RR_{PriorFx vs NoPrior Fx}) to be 1.73 and 2.04, respectively, for women and men [54].

The prevalence of prior clinical fracture at each age for each sex (Prev_PriorFx) was determined in three steps using unpublished second study visit data from the Study of Osteoporotic Fractures and baseline visit data from the Osteoporotic Fractures in Men (MrOS). First, prediction equations for the odds of prior clinical fracture as a function of age and BMD were derived using logistic regression, as described in a previous publication [6]. We used these same equations to extrapolate estimated prevalences of prior clinical fracture for those under age 65. Since SOF and MrOS only included women and men aged 65 and older, we did sensitivity analyses for 55-year-old men and women assuming prevalences of prior clinical fracture only half that predicted by these equations.

Second, the mean BMD for each age were obtained for Caucasian men and women from public use NHANES 2005–2006 data files [37]. Third, these mean BMD values were then entered into the prediction equations to obtain the estimated odds of a prior clinical fracture for each group defined by age and sex. These odds were converted to prevalences (Table 1) by the equation:

$$\text{Prevalence}=\text{Odds}/(\text{1}+\text{Odds})\text{.}$$ (2)

Proportions of those without prior clinical fracture with bone density below treatment cutpoints

The prevalence of femoral neck BMD below the treatment cutpoints for each starting age in the female and male Caucasian US population was estimated from NHANES 2005–2006 data (labeled Prev_{BMD≤Cutpoint, All} in Eq. 3) [37]. This is then converted to an odds by the following equation:

$${\text{Odds}}_{\text{BMD}\le \text{Cutpoint},\text{All}}={\text{Prev}}_{\text{BMD}\le \text{Cutpoint},\text{All}}/(1-{\text{Prev}}_{\text{BMD}\le \text{Cutpoint},\text{All}}).$$ (3)

To estimate these proportions for the subsets without prior clinical fracture, we first estimated (using logistic regression models) the age-adjusted odds of femoral neck BMD below the treatment cutpoints in those with compared to those without prior clinical fracture (OR_{BMD≤Cutpoint, PriorFx vs NoPriorFx}) for women and men using unpublished second study visit data from SOF (7,927 women, mean age 73.7 years) and baseline visit data from MrOS (5,993 men, mean age 73.7 years).

The odds ratio (OR) for low BMD in those without prior clinical fracture compared to the entire subset of same age and sex is then

$${\text{OR}}_{\text{BMD}<\text{Cutpoint},\text{NO}\text{prior}\text{fracture}\text{vs}\text{all}}=1/[1+({\text{OR}}_{\text{BMD}\le \text{Cutpoint},\text{PriorFx}\text{vs}\text{NoPriorFx}}-1)\ast {\text{Prev}}_{\text{PriorFx}}],$$ (4)

where Prev_PriorFx is the prevalence of prior clinical fracture since age 50 for that age and sex, and OR_{BMD≤Cutpoint, PriorFx vs NoPriorFx} is 1.91 for men, 1.97 for women when the BMD T-score cutpoint is −2.5, and 2.10 for women when the BMD T-score cutpoint is −2.6 or lower.

The odds of BMD sufficiently low to warrant drug therapy is then given by the equation:

$${\text{Odds}}_{\text{BMD}\le \text{Cutpoint},\text{NoPriorFx}}={\text{Odds}}_{\text{BMD}\le \text{Cutpoint},\text{All}}\ast {\text{OR}}_{\text{BMD}<\text{Cutpoint},\text{NO}\text{prior}\text{fracture}\text{vs}\text{all}}.$$ (5)

The prevalence of femoral neck BMD below the treatment cutpoints for those in each subset defined by age and sex without prior clinical fracture (Prev_{BMD≤Cutpoint, NoPriorFx}) is then calculated from the odds (Odds_{BMD≤Cutpoint, NoPriorFx}) using Eq. 2.

The Z-score cutpoint of low BMD (Z_cut) corresponding to this prevalence is then calculated from the normal distribution function.

Fracture risks attributable to low bone density

The mean Z-scores of those below the Z-score cutpoints were then calculated using the inverse Mills ratio (Table 1):

$$\text{Mean}\text{Z}-\text{score}=-exp[-{\left({Z_{\text{cut}}}^2\right)}^{\ast }0.5]/\left[\text{Normal}{\left(Z_{\text{cut}}\right)}^{\ast }{(2^{\ast }\text{pi})}^{0.5}\right]$$ (6)

For each fracture type, the relative risk of incident fracture in those with a femoral neck BMD T-score below the treatment cutpoint was equal to a^−Z, where Z is the mean Z-score for those with BMD below the treatment cutpoint (Table 1), and a is the relative risk of fracture per standard deviation (SD) decrease in femoral neck Z-score.

The relative risks of hip fracture for each SD decrease in femoral neck BMD, derived from a large meta-analysis of hip fracture predictors [55], were assumed to decrease with age from 3.29 and 3.92, respectively, for women and men aged 55 years to 2.24 and 2.67, respectively, for women and men aged 80 years (Table 2). The relative risks of hip fracture in those with compared to those without prior clinical fracture were assumed to decrease with age from 3.83 and 4.84 for women and men aged 55 years to 1.36 and 1.71 for women and men aged 80 years [54]. For women, we assumed relative risks for incident vertebral fracture of 1.32 in those with compared to those without prior fracture [56] and 1.9 per SD decrease in femoral neck BMD [57]. The relative risks of non-vertebral non-hip fractures per SD decrease in femoral neck BMD were assumed to be 1.34 and 1.44, respectively, in men [58] and women [57]. Using Rotterdam study data, for men we assumed relative risks for incident vertebral fractures of 1.8 per SD decrease of femoral neck BMD and 2.4 in those with compared to those without prior clinical fracture [59].

Estimation of weight thresholds below which bone densitometry is cost-effective

To calculate the weight threshold below which bone densitometry is cost-effective, we start with the prevalence (pre-test probability) of low bone density warranting drug therapy for the age-specific and sex-specific subgroup without prior fracture, and the threshold pre-test prevalence of low bone density at which bone densitometry becomes cost-effective for that subgroup (columns 2 and 3, Table 5 [women] and Table 6 [men]). These prevalences are converted to odds (columns 4 and 6) by the equation:

$$\text{Odds}=\text{Prevalence}/(\text{1}-\text{Prevalence})$$ (7)

Table 5.

Calculation of weight threshold at which bone densitometry becomes cost-effective for women

Age (years)	Age- and sex-specific prevalence low BMD (%)	Cost-effective pre-test probability of low BMD (%)	Age- and sex-specific odds low BMD		Threshold odds low BMD		Change in log [Odds]	Odds low BMD per 10 kg increase in weight (log [Odds])	Weight change from mean to reach threshold weight (kg)
			Odds	Log (Odds)	Odds	Log (Odds)
55	0.93	1.62	0.0094	−4.671	0.0164	−4.108	0.563	0.30 (−1.204)	−4.7
60	2.76	1.49	0.0284	−3.560	0.0151	−4.192	−0.632	0.33 (−1.109)	5.7
65	4.42	1.23	0.0462	−3.073	0.0125	−4.383	−1.310	0.39 (−0.942)	13.9
70	8.16	1.13	0.0888	−2.421	0.0115	−4.469	−2.048	0.42 (−0.867)	23.5
75	14.59	1.15	0.1708	−1.767	0.0116	−4.453	−2.396	0.42 (−0.867)	27.5
80	19.21	1.23	0.2378	−1.436	0.0124	−4.389	−2.953	0.42 (−0.867)	30.8

Table 6.

Calculation of weight threshold at which bone densitometry becomes cost-effective for men

Age (years)	Age- and sex-specific prevalence low BMD (%)	Cost-effective pre-test probability of low BMD (%)	Age- and sex-specific odds low BMD		Threshold odds low BMD		Change in log [Odds]	Odds low BMD per 10 kg increase in weight (log [Odds])	Weight change from mean to reach threshold
			Odds	Log (Odds)	Odds	Log (Odds)
55	2.03	15.2	0.0207	−3.878	0.1789	−1.721	2.158	0.40 (−0.916)	−23.8
60	2.77	8.87	0.0285	−3.558	0.0855	−2.460	1.228	0.40 (−0.916)	−12.1
65	4.65	4.46	0.0487	−3.021	0.0467	−3.063	−0.042	0.44 (−0.821)	0.5
70	7.23	2.68	0.0780	−2.551	0.0275	−3.592	−1.041	0.44 (−0.821)	12.5
75	8.38	2.44	0.0915	−2.392	0.0250	−3.687	−1.296	0.44 (−0.821)	15.6
80	10.74	1.30	0.1203	−2.118	0.0215	−4.327	−2.118	0.44 (−0.821)	26.6

Since the change of the odds of low BMD warranting drug therapy per change in body weight is linear in the natural logarithm scale, we then take the logs of these odds (columns 5 and 7). The difference in log(Odds) between these two=[log(Odds_threshold)−log(Odds_{age, sex})] (column 8).

The age-adjusted association between body weight and odds of femoral neck BMD below the treatment cutpoint among Caucasians (OR_{per10 kg weight change}) was estimated using unpublished data from the baseline visit of the MrOS study (for men) and the second study visit of the SOF visit (for women) with separate logistic regression models for each treatment cutpoint (column 9, Tables 5 and 6). These odds ratios were 0.30, 0.33, 0.39, and 0.42, respectively, for women aged 55, 60, 65, and 70 years and older, and were 0.40 and 0.44, respectively, for men younger than age 60 and age 65 and older (column 6, Tables 5 and 6).

The weight change (in kilogram, column 10) required for the odds of low bone density warranting drug therapy to change from the mean for that age-specific and sex-specific subgroup to the threshold for cost-effectiveness is equal to the difference in log-odds (column 8) times ten divided by the change in log(Odds) per 10-kg change in body weight (column 9):

$${\text{WeightChange}}_{\text{age},\text{sex}}={[\text{difference}\text{in}\text{log}(\text{Odds})]}^{\ast }10/[ln({\text{OR}}_{\text{per10}\text{kg}\text{weight}\text{change}})],$$ (9)

and

$$\text{Threshold}\text{Weight}={\text{MeanWeight}}_{\text{age},\text{sex}}+{\text{WeightChange}}_{\text{age},\text{sex}}.$$ (10)

Probabilistic sensitivity analyses: distributions

Fracture costs were assumed to follow a log-normal distribution (Table 7), based on the distribution from the study of Gabriel and colleagues [39]. The proportion of individuals requiring long-term care beyond the first year after hip fracture was estimated to be 12% (38 out of 312 individuals), and this was assumed to follow a binomial distribution. A normal approximation to this yields a point estimate for long-term care costs of $9,057 (2010 US dollars) per year with a standard deviation of $1,103.

Table 7.

Distributions for parameters allowed to vary in probabilistic sensitivity analyses

Parameter	Distribution	Mean (95% CI or range)
Cost of hip fracture	Log normal	$35,320 (22,010–56,678)
Cost of spine fracture	Log normal	$9,244 (2,230–38,318)
Cost of distal forearm fracture	Log normal	$4,928 (692–35,102)
Cost of other fractures	Log normal	$7,264 (1,707–30,901)
Long-term care costs	Normal	$9,057 (6,556–11,558)
Disutility of fractures	Uniform	50–150% of base case values
Fracture rates	Normal	Standard deviation 22% of mean rate
Vertebral fracture drug efficacy	Log normal	Men: 0.36 (0.22–0.59); women: 0.40 (0.20–0.80)
Non-vertebral fracture drug efficacy	Log normal	Men: 0.73 (0.53–0.99)
Hip fracture drug efficacy	Log normal	Women: 0.60 (0.38–0.94)
Wrist fracture drug efficacy	Log normal	Women: 0.6 (0.44–0.81)
Other fracture drug efficacy	Log normal	Women: 0.8 (0.65–0.99)
Association of hip fracture with prior fracture (logHR)	Log normal	Men: 2.77 (2.22–3.46); women: 2.20 (1.47–3.29)
Association of Hip Fracture with 1 SD change of BMD (logHR)	Log normal	Men: 3.38 (2.65–4.30); women: 2.83 (2.34–3.43)
Association of vertebral fracture with prior fracture (logOR)	Log normal	Men: 2.40 (1.20–4.80); women: 1.32 (1.00–1.78)
Association of vertebral fracture with 1 SD change of BMD (logOR)	Log normal	Men: 1.80 (1.28–2.54); women: 1.90 (1.48–2.45)
Association of Wrist/Other Fracture with Prior Fracture (logHR)	Log normal	Men: 2.04 (1.61–2.59); women: 1.73 (1.57–1.91)
Association of wrist/other fracture with 1 SD change of BMD (logHR)	Log normal	Men: 1.34 (1.17–1.53); women: 1.44 (1.39–1.49)

We constructed distributions for fracture rates by first assuming that the distributions of the proportions of individuals at risk who have a first distal forearm, clinical vertebral, or hip fracture within each specified age range [27] are binomial. The 95% confidence intervals can be calculated using an exact method appropriate for proportions close to zero [60]. If a normal approximation to these distributions is then assumed, the standard deviation for these proportions ranges from 30% for vertebral fracture between ages 65 and 69 to 10.9% for hip fracture after age 85. For the probabilistic sensitivity analysis, an additional normally distributed variable was created with mean value of 1.0 and standard deviation equal to 0.22. This is then multiplied by all of the fracture rates, so that fracture rates vary together over a normal distribution with the means equal to the point estimates rendered by the fracture risk equations.

Because of significant uncertainty regarding disutility from fractures, we assumed a uniform distribution for these to vary from between 50% and 150% of the base case disutility. The relative risks for hip, non-spine non-hip, and vertebral fractures attributable to osteoporosis or prior clinical fracture were assumed to be log-normal (since hazard ratios and odds ratios are linear in the logarithmic scale), as were the relative risks of fractures on oral bisphosphonates compared to no drug therapy.

Performance of probabilistic sensitivity analyses

The analyses were done with 500 simulations, with 10,000 trials per simulation. For each simulation, the parameter values are selected randomly from the above distributions. These analyses were repeated over a wide range of assumed prevalences of low bone density warranting drug therapy. We then determined, by linear interpolation, the threshold cost-effective low BMD prevalences (assuming a willingness to pay of $75,000 per QALY gained and a yearly drug cost of $500) using the 25th and 75th percentiles of costs per QALY gained. The corresponding weight thresholds were calculated for each of these two prevalences, and the proportion of the population of that age and sex below each of the two weight thresholds calculated as shown previously. The difference between these weight thresholds represents the interquartile range for the body weights at which bone densitometry is cost-effective for subgroup without prior fracture defined by age and sex.