Label-free viscosity measurement of complex fluids using reversal flow switching manipulation in a microfluidic channel

Abstract

The accurate viscosity measurement of complex fluids is essential for characterizing fluidic behaviors in blood vessels and in microfluidic channels of lab-on-a-chip devices. A microfluidic platform that accurately identifies biophysical properties of blood can be used as a promising tool for the early detections of cardiovascular and microcirculation diseases. In this study, a flow-switching phenomenon depending on hydrodynamic balancing in a microfluidic channel was adopted to conduct viscosity measurement of complex fluids with label-free operation. A microfluidic device for demonstrating this proposed method was designed to have two inlets for supplying the test and reference fluids, two side channels in parallel, and a junction channel connected to the midpoint of the two side channels. According to this proposed method, viscosities of various fluids with different phases (aqueous, oil, and blood) in relation to that of reference fluid were accurately determined by measuring the switching flow-rate ratio between the test and reference fluids, when a reverse flow of the test or reference fluid occurs in the junction channel. An analytical viscosity formula was derived to measure the viscosity of a test fluid in relation to that of the corresponding reference fluid using a discrete circuit model for the microfluidic device. The experimental analysis for evaluating the effects of various parameters on the performance of the proposed method revealed that the fluidic resistance ratio (R_JL/R_L, fluidic resistance in the junction channel (R_JL) to fluidic resistance in the side channel (R_L)) strongly affects the measurement accuracy. The microfluidic device with smaller R_JL/R_L values is helpful to measure accurately the viscosity of the test fluid. The proposed method accurately measured the viscosities of various fluids, including single-phase (Glycerin and plasma) and oil-water phase (oil vs. deionized water) fluids, compared with conventional methods. The proposed method was also successfully applied to measure viscosities of blood with varying hematocrits, chemically fixed RBC_S, and channel sizes. Based on these experimental results, the proposed method can be effectively used to measure the viscosities of various fluids easily, without any fluorescent labeling and tedious calibration procedures.

INTRODUCTION

The biophysical properties of blood are impaired by the pathophysiological processes of diseases such as malaria,^{1, 2, 3, 4} sepsis,^{5, 6} and sickle-cell diseases.⁷ Several biophysical properties of blood, including haematocrit,⁸ blood viscosity,^{9, 10, 11} viscoelasticity,^{12, 13, 14, 15} deformability,^{16, 17, 18} and aggregation,^{19, 20, 21} are measured to effectively diagnose or monitor patients with cardiovascular diseases (CVDs). Among these properties, blood viscosity has been considered as an appropriate index for monitoring the changes in blood plasma protein resulting from acute or chronic tissue damages. This property is also key parameter for estimating shear stress which mechanically stimulates the endothelium cells of blood vessels.^{22, 23} Information on blood viscosity has been clinically applied to diagnose hyper-viscosity syndromes, such as hypertension, diabetes mellitus, and several heart diseases.^{24, 25, 26} Therefore, the accurate measurement of blood viscosity is necessary for the early detection of CVDs and microcirculation diseases.²⁷

Conventional bulky viscometers, such as cone-and-plate, capillary type,¹⁰ and Oswald,^{9, 28} are used to measure viscosity of complex fluid in various biomedical fields. However, these viscometers have several drawbacks, such as large volume consumptions due to repetitive tests, unexpected measurement errors resulting from surface tension of air-liquid interfaces, tedious and time-consuming cleaning procedures that might come in direct contact with the patient's blood, and routine calibrations.²⁸

Recently, microfluidic devices with distinctive advantages, including small sample volume, high sensitivity, and point of care feasibility, have been introduced to effectively manipulate small amounts of fluids in microfluidic channels for biomedical applications. For example, several microfluidic platforms have been applied to measure fluid properties such as surface tension,^{29, 30} density,^{31, 32, 33} pressure drop,^{34, 35, 36} flow rate,^{37, 38} and fluid resistance.^{39, 40} Microfluidic platforms have also been adopted to measure fluid viscosity instead of conventional bulky platforms.^{32, 33} These fluid viscosity measurement methods can be classified into two groups, depending on flow conditions. Under quasi-static flow conditions, fluid viscosity in a microfluidic channel can be determined using laser-induced capillary waves,⁴¹ acoustic-propagated waves,⁴² and resonance frequency with a micro-cantilever.^{31, 33} Alternatively, the viscosity of moving fluids can be measured by a comparator using parallel flow,^{34, 43, 44} fluidic Wheatstone-bridges using pressure sensors,⁴⁵ and droplet-based movements.⁴⁶ However, these methods still have technological limitations on accurate fluid viscosity measurements because they require calibration procedures using a standard fluid as reference. As the viscosities of complex fluids containing particles or cells vary depending on flow conditions, additional imaging procedures using complex mathematical models are required.⁴⁴ To resolve these problems, a flow-compartment method using microfluidic channel array (MCA) has been proposed to measure complex fluid viscosity without calibration procedures.⁴⁷ However, this method still remains difficult in measuring the viscosity of oil, under oil-water phase flow conditions. Additionally, this method requires labeling by adding either fluorescent particles or dyes to visualize the interface between a test fluid and a corresponding reference fluid.

In this study, we adopt a fluid-switching phenomenon based on hydrodynamic balancing in microfluidic channels. In measuring complex fluid viscosity without labeling, the proposed method has four distinctive advantages compared with conventional methods. First, instead of interface movement in a single channel, the flow switching phenomenon (left or right movement) in the junction channel of the reference or test fluid is used to identify the viscosity ratio between the two fluids. Thus, this method does not need additional image processing procedures that use complex mathematical models. Second, this method determines the viscosities of test fluids by comparing it with a corresponding reference fluid under various phases (aqueous vs. aqueous, oil vs. aqueous, and blood vs. aqueous). Third, this method is precise and serves as an easy means to measure the viscosities of test fluids, especially without labeling. Thus, this method does not require labeling through the addition of fluorescent particles or dyes to visualize the interface between two fluids. Lastly, this method measures fluid viscosities consistently by installing a flow stabilizer to supply constant flow rates into the microfluidic device. In this study, the flow stabilizers using air compression in cavity volume (0.1 ml) are installed between a syringe pump and the microfluidic device for each fluid. To demonstrate the feasibility and usefulness of the proposed method, a discrete parameter model was established for the microfluidic device to derive an analytical viscosity formula. Using this analytical formula, we conducted experiments on several parameters that affect the performances of this method. The performance of the proposed method was evaluated for three different test fluids, namely, glycerin, plasma, and oil, and the results were compared with those of a conventional method. Finally, the proposed method was applied to measure viscosities of blood with varying hematocrits, chemical fixation of red blood cells, and channel size.

FLOW-SWITCHING MANIPULATION BASED ON HYDRODYNAMIC BALANCING

Principle of the proposed method

Fluid flow-switching in a microfluidic channel occurs based on hydrodynamic force balancing. In this study, this phenomenon is used to measure complex fluid viscosity with label-free operation. Controlling flow rate ratio between the test fluid (test) and reference fluid (ref) induces a reverse flow in a microfluidic channel. The viscosity of test fluid then can be determined using the given value of the corresponding reference fluid. This method can be applied to various combinations of different fluids such as (a) aqueous vs. aqueous, (b) oil vs. aqueous, and (c) blood vs. aqueous. Therefore, this measurement method does not require tedious labelling techniques to detect the interface between two fluids in microfluidic channels.

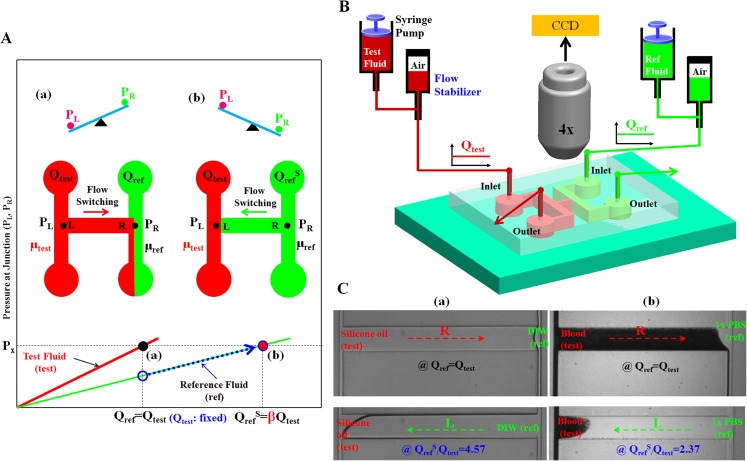
Fig. 1A shows a schematic diagram of the principle of the proposed method. If the viscosity of a test fluid (μ_test) is greater than that of the reference fluid (μ_ref) at the same flow rate (Q_test = Q_ref), the pressure (P_L) at left end side of the junction channel is greater than that (P_R) at the right side (P_L > P_R). Thus, the test fluid generally moves toward the right direction in the junction channel (Fig. 1AA). When the pressures at both junctions (L, R) reach the hydrodynamic balancing state (P_x = P_L = P_R) by increasing the flow rate of the reference fluid to a specific condition (Q_ref^S = βQ_test), the reference fluid immediately moves toward the left direction because of the flow instability in the junction channel (Fig. 1AB). In other words, the interface between two fluids is not positioned within the junction channel of our carefully designed device, compared with the previous work.⁴⁴ However, using this interesting fluid flow-switching phenomenon of the test fluid in the junction channel, the viscosity (or resistance) of the test fluid can be easily and accurately determined by measuring the flow rates (Q_ref^S, Q_test) of the test fluid and reference fluid.

Figure 1.

Proposed viscosity measurement method using fluidic flow switching in microfluidic channels based on hydrodynamic balancing with a label-free operation. (A) Schematic diagram of the proposed method using a simple microfluidic device which consists of two inlets and two outlets, two side channels for guiding two fluids, and one junction channel connecting the two parallel side channels for detecting flow direction depending on the flow-rate ratio (Q_ref/Q_test). (a) When the viscosity of a test fluid is larger than that of reference fluid (μ_test > μ_ref), the test fluid moves toward the right direction in the junction channel due to higher pressure at the left junction rather than the right junction (P_L > P_R). (b) The reference fluid reversely moves toward the left direction in the junction channel, at a specific flow-rate ratio (Q_ref^S/Q_test). The viscosity of the test fluid to that of the reference fluid can be identified by monitoring the specific flow-rate ratio, at which fluidic flow-switching phenomenon occurs in the junction channel. (B) The microfluidic system which is composed of two syringe pumps for delivering the sample and reference fluids, two flow stabilizers for regulated fluidic flows, and the microfluidic device for fluid viscosity identification. The flow switching in the junction channel was monitored using an optical microscopy with a CCD camera. (C) Viscosity measurements of (a) silicone oil (test) in relation to DIW (ref), and (b) blood (test) in relation to 1 × PBS solution (ref). The test fluid reversely flows from the right direction (Q_ref = Q_test) to the left direction in the junction channel, at a specific switching flow rate (Q_ref^S/Q_test).

Similarly, if the viscosity (μ_test) of the test fluid is less than that (μ_ref) of the reference fluid at the same flow rate (Q_test = Q_ref), the reference fluid moves toward the left direction in the junction channel (P_L < P_R). The viscosity of the test fluid is also determined by measuring the flow rates (Q_ref^S, Q_test) of the test fluid and the reference fluid, by which the moving direction of the test or reference fluid switches in the junction channel.

Fig. 1B shows the microfluidic platform used for demonstrating the proposed method. The platform is composed of a microfluidic device for measuring fluid viscosity, flow stabilizers for regulating fluidic flow in the microfluidic channels, and syringe pumps for supplying two fluids. The microfluidic device has (a) two inlets for supplying two fluids, (b) an H-shaped channel composed of two parallel side channels and a junction channel for detecting the flow direction depending on hydrodynamic balancing, and (c) two outlets for removing the two fluids. The test and reference fluids are correspondingly co-infused into inlet (A) and inlet (B) at given flow rates (Q_ref and Q_test), respectively. The reference fluid should be a Newtonian fluid and suitable for label-free operation. Thus, in the experiments, deionized water (DIW) was used as the reference fluid, except for blood, in which 1 × PBS phosphate-buffered saline (PBS) solution was used. The flow stabilizers were adopted to minimize flow fluctuations in the microfluidic channels for a stable measurement. The fluidic flow in the junction channel was monitored with an image acquisition system comprising an optical microscope with a charge-coupled device (CCD) camera.

Fig. 1C illustrates how to measure the viscosities of (a) silicone oil with respect to DIW, and of (b) blood with respect to 1 × PBS solution. The silicone oil flows from the right direction (Q_ref = Q_test) to the left direction in the junction channel, at a specific flow-rate ratio of Q_ref^S/Q_test = 4.57. For the blood with a hematocrit of H_ct = 50%, RBCs moved from the right direction (Q_ref = Q_test) to the left direction, at a flow-rate ratio of Q_ref^S/Q_test = 2.37. In these preliminary experiments, flow-switching phenomenon occurs in the junction channel at a specific flow-rate ratio: this ratio depends on the ratio of the viscosities of the test and reference fluids.

Analytical formula for a fluidic circuit model

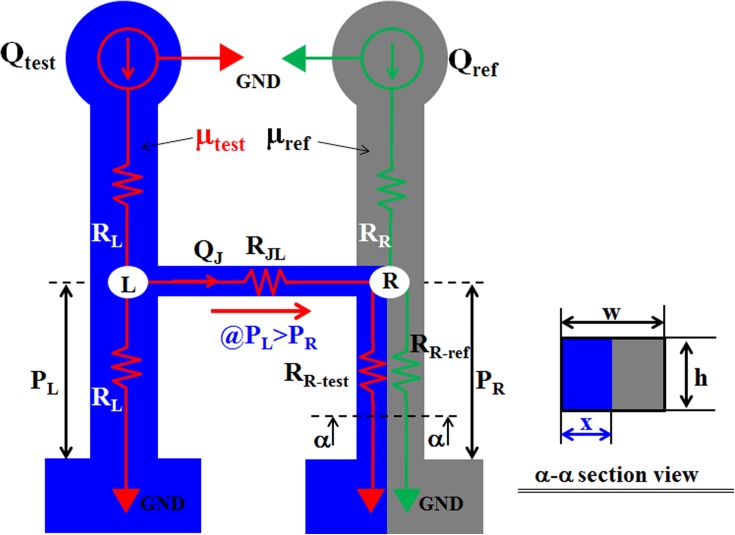
Fig. 2 illustrates a discrete fluidic circuit model used to derive an analytical formula for the viscosity of a test fluid in a microfluidic device. For mathematical representation of our proposed device as simple as possible, we have assumed that both compliance effect of the microfluidic channels and the capillary force in the junction channels are negligible.

Figure 2.

Discrete circuit model for the proposed microfluidic system. The governing parameters include the flow rates (Q_test, Q_ref) for the test and reference fluids, the fluidic resistances (R_L, R_R, R_R-test, R_R-ref, R_JA) for the two side channels and the junction channel, and the fluidic pressures (P_L, P_R) at the junction points (L, R) under a negligible compliance effect in the microfluidic device.

Based on the analogy between electric circuits and fluidic networks, the flow rate of each fluid and the fluidic resistance in a fluid-filled channel are modeled as current (Q) and resistance (R), respectively. The flow rates of the reference and sample fluids are represented as Q_ref and Q_test, respectively. Their viscosities are denoted by μ_ref and μ_test, respectively. If the viscosity of a test fluid (μ_test) is greater than that of the reference fluid (μ_ref), the pressure (P_L) at the junction L is greater than that (P_R) at the junction R. Therefore, the test fluid moves toward the right direction in the junction channel. The upper and lower side channels on the left side and the junction channel are filled with the test fluid. The upper side channel on the right side is only filled with the reference fluid. However, the lower side channel on the right side is partially filled with the reference and test fluids. The width of the test fluid in the side channel with a rectangular cross-section (width = W and depth = H) is expressed as X. In the discrete fluidic circuit model, the fluidic resistances in the upper side channel filled with the test and reference fluids are modeled as R_L (test) and R_R (ref), respectively. The fluidic resistance in the junction channel filled with the test fluid is denoted by R_JL (test). The fluidic resistances in the lower right side channel filled with the test and reference fluids connected in parallel are expressed as R_R-test (test) and R_R-ref (ref). Fig. 2 shows the discrete fluidic circuit model that is applied to derive the analytical formula for the viscosity of the test fluid (μ_test). The mass conservation law at junctions L and R provides the following equations:

$${\mathrm{Q}}_{\text{test}}=\frac{{\mathrm{P}}_{\mathrm{L}}}{{\mathrm{R}}_{\mathrm{L}}}+\frac{{\mathrm{P}}_{\mathrm{L}}-{\mathrm{P}}_{\mathrm{R}}}{{\mathrm{R}}_{\text{JL}}},$$ (1)

and

$${\mathrm{Q}}_{\text{ref}}+{\mathrm{Q}}_{\mathrm{J}}=\frac{{\mathrm{P}}_{\mathrm{R}}}{{\mathrm{R}}_{\mathrm{R}-\text{test}}}+\frac{{\mathrm{P}}_{\mathrm{R}}}{{\mathrm{R}}_{\mathrm{R}-\text{ref}}}.$$ (2)

In Eq. 2, Q_J indicates flow rate of test fluid in the junction channel, which can be expressed as

$${\mathrm{Q}}_{\mathrm{J}}=\frac{{\mathrm{P}}_{\mathrm{L}}-{\mathrm{P}}_{\mathrm{R}}}{{\mathrm{R}}_{\text{JL}}}.$$ (3)

In addition, the flow rate of a test fluid (Q_J) invades into the lower right side channel. Thus, the lower right side channel is partially filled with the test fluid and reference fluid. Since both fluids have the same pressure as P_R at the right junction (R), the same pressure condition for each fluid is analytically described as

$${\mathrm{P}}_{\mathrm{R}}={\mathrm{Q}}_{\mathrm{J}}\cdot {\mathrm{R}}_{\mathrm{R}-\text{test}}={\mathrm{Q}}_{\text{ref}}\cdot {\mathrm{R}}_{\mathrm{R}-\text{ref}}.$$ (4)

Using Eqs. 3 and4, the following relationship is established:

$$\left(\frac{{\mathrm{P}}_{\mathrm{L}}-{\mathrm{P}}_{\mathrm{R}}}{{\mathrm{R}}_{\text{JL}}}\right)\hspace{0.17em}{\mathrm{R}}_{\mathrm{R}-\text{test}}={\mathrm{R}}_{\mathrm{R}-\text{ref}}{\mathrm{Q}}_{\text{ref}}.$$ (5)

Using Eqs. 1, 2, 3, 4, 5, the ratio of the flow rate of the reference fluid to that of the test fluid can be expressed as follows:

$$\frac{{\mathrm{Q}}_{\text{ref}}}{{\mathrm{Q}}_{\text{test}}}=\frac{\frac{1}{{\mathrm{R}}_{\mathrm{R}-\text{ref}}}+\frac{1}{{\mathrm{R}}_{\mathrm{R}-\text{test}}}}{\frac{1}{{\mathrm{R}}_{\mathrm{L}}}+\mathrm{D}\cdot \frac{{\mathrm{R}}_{\mathrm{R}-\text{ref}}}{{\mathrm{R}}_{\mathrm{R}-\text{test}}}\cdot {\mathrm{R}}_{\text{JL}}},$$ (6)

here D is defined as

$$\mathrm{D}=\left(\frac{1}{{\mathrm{R}}_{\text{JL}}}+\frac{1}{{\mathrm{R}}_{\mathrm{R}-\text{test}}}+\frac{1}{{\mathrm{R}}_{\mathrm{R}-\text{ref}}}\right)\cdot \left(\frac{1}{{\mathrm{R}}_{\mathrm{L}}}+\frac{1}{{\mathrm{R}}_{\text{JL}}}\right)-{\left(\frac{1}{{\mathrm{R}}_{\text{JL}}}\right)}^2.$$ (7)

When flow-switching occurs in the junction channel by suitably controlling the flow-rate ratio between the reference and test fluids (Q_ref^S/Q_test), the width (X) in the lower right side channel approaches to zero. In this case, R_R-test and R_R-ref become

$$\underset{\mathrm{X}\to 0}{\text{Lim}}{\hspace{0.17em}\mathrm{R}}_{\mathrm{R}-\text{test}}(\mathrm{x})=\infty ,\hspace{1em}\text{and}\hspace{1em}\hspace{0.17em}\underset{\mathrm{X}\to 0}{\text{Lim}}{\hspace{0.17em}\mathrm{R}}_{\mathrm{R}-\text{ref}}(\mathrm{x})={\mathrm{R}}_{\mathrm{R}}.$$ (8)

Therefore, the flow-rate ratio is simplified as

$$\frac{{\mathrm{R}}_{\mathrm{L}}}{{\mathrm{R}}_{\mathrm{R}}}=\frac{{{\mathrm{Q}}_{\text{ref}}}^S}{{\mathrm{Q}}_{\text{test}}}.$$ (9)

According to Eq. 9, the fluidic resistance of the test fluid is directly related to that of the reference fluid by identifying flow-rate ratio (Q_ref^S/Q_test), at which a reverse flow is induced in the junction channel. If both side channels have the same dimensions (width, depth, and length), the fluidic resistance ratio (R_L/R_R) in Eq. 9 is then expressed as

$$\frac{{\mathrm{R}}_{\mathrm{L}}}{{\mathrm{R}}_{\mathrm{R}}}=\frac{{\mu }_{\text{test}}}{{\mu }_{\text{ref}}}.$$ (10)

From Eqs. 9, 10, the viscosity formula for the test fluid is simply related to that of the reference fluid as follows:

$${\mu }_{\text{test}}={\mu }_{\text{ref}}\frac{{{\mathrm{Q}}_{\text{ref}}}^S}{{\mathrm{Q}}_{\text{test}}}.$$ (11)

Therefore, the viscosity (μ_test) of the test fluid can be measured by using the known viscosity (μ_ref) of the reference fluid and the flow-rate ratio (Q_ref^S/Q_test), at which the direction of fluidic flow in the junction channel is changed, depending on the hydrodynamic balancing in both side channels.

On the other hand, at the condition of hydrodynamic balancing, most of the lower left side channel with a rectangular shape (width = w, depth = h) is filled with test fluid. Using definition of a hydraulic diameter (i.e., D) for a rectangular channel, a shear rate formula for viscosity of test fluid is approximately estimated as,

$$\dot{\gamma }=\frac{32Q_{\mathit{t}\mathit{e}\mathit{s}\mathit{t}}}{\pi D^3}.$$ (12)

In Eq. 12, Q_test denotes flow rate of test fluid which was delivered by a syringe pump.

EXPERIMENTAL

Microfluidic device and sample preparation

All microfluidic devices were carefully designed to examine the effects of various design parameters. The channel depth was fixed at 50 μm. The design parameters include the fluidic resistance ratio (R_JL/R_L) between the junction channel and the side channel, the length (L_J) of the junction channel, and the width ratio (W/W_JL) between the side channel and the junction channel. After fabricating a silicon molder using typical MEMS technologies of photolithography and deep reactive-ion etching, Polydimethylsiloxane (Sylgard 184, Dow Corning, USA) was used to construct a microfluidic device using a conventional soft lithography technique. Microfluidic channels inside the microfluidic device were sealed by bonding these channels with a glass substrate using oxygen plasma (CUTE, Femto Science, Korea).

Various volume-based concentrations of Glycerin (SAMCHUN Chemical Co., Korea) (10%, 20%, 30%, 40%, and 60%) using 1 × PBS, and plasma (50% and 100%) were prepared as test fluids to demonstrate the proposed method for various complex fluids (aqueous, oil, and bloods). Two different oils, namely, silicone oil (XIAMETER PMX-200 [5 CS], Dow Corning, USA) and mineral oil (M5310-1 L, Sigma-Aldrich, USA) were tested to demonstrate the performance for oil-water phase flows (oil [test]) vs. DIW [ref]). Blood samples provided by a blood bank (Daegu-Kyeongbuk Blood Bank, Korea) with varying haematocrits ranging from 20% to 50% were also tested using 1 × PBS (pH 7.4, Bio Solution, Korea) as a reference fluid. The blood sample was chemically fixed using glutaraldehyde (GA) with concentration of 0.5% and 1% (Junsei Chemical Co., JAPAN) to examine the variations of viscosity resulting from the hardening of RBC membrane. For this test, 1 × PBS solution was used as the reference fluid to avoid rupture of the RBC membrane due to osmotic pressure difference induced when a DIW solution is used as the reference fluid.

Experimental setup and viscosity measurement procedure

The microfluidic device was mounted on an optical microscope (Nikon, Tokyo, Japan) equipped with a CCD camera (PCO, Germany). The reference and test fluids were supplied into the microfluidic channels using a syringe pump (neMESYS, Centoni Gmbh, Germany). All experiments were conducted at room temperature (25 °C). The change of flow direction in the junction channel was continuously monitored with the CCD camera.

Under the fixed flow rate of test fluid, the flow rate of reference fluid was appropriately controlled to find out reversal flow of test or reference fluid in the junction channel. After setting the flow rate each time, reversal flow in the junction had been monitored for at least 10 s, which indicates time delay of the fluidic system. As the first step, flow rate of reference fluid was increased to estimate a switching flow rate roughly, while monitoring interface in the right side. Then, to switch back flow direction in the junction channel, flow rate of reference fluid was sufficiently reduced to 80% of the switching flow rate which depends on hysteresis behaviors. As the second step, the flow rate of reference fluid was precisely controlled to evaluate the flow switching in the junction channel. Through these two steps, the viscosity of the test fluid was measured by identifying the switching flow-rate ratio (Q_ref^S/Q_test), at which the fluidic flow direction of the test or reference fluid in the junction channel tends to change. Furthermore, to quantitatively evaluate measurement accuracy of the proposed method, the viscosities obtained by the proposed method were compared with those measured by a commercial viscometer (DV-II, Brookfield, USA) equipped with a fluid- temperature controller, at the shear rates ranges from 85 s⁻¹ to 128 s⁻¹.

RESULTS AND DISCUSSIONS

Performance test

In this study, a simple viscosity formula (Eq. 11) of test fluid using a discrete model in steady flow condition was derived by assuming that reversal flow occurs in the junction channel when hydrodynamic balancing at both junctions (P_L≈P_R) is established. Practically, to induce reversal flow in the junction, the pressure at the right junction (P_R) should be greater than the sum of the pressure at the left junction (P_L) and the dynamic friction loss in the junction channel (ΔP_J). The dynamic friction loss which is negligible in this study would be influenced by several factors such as fluidic resistance (R_JL), and channel dimensions (W_J, L_J). In this study, instead of including the dynamic friction loss which is difficult to evaluate, we have derived a simple viscosity formula using a discrete fluidic circuit model in steady flow condition. To satisfy the assumption that the dynamic friction loss in the junction channel is negligible, and does not have an influence on performances, the performances of the proposed method were evaluated depending on three design parameters including (a) the fluidic resistance ratio between the junction channel and the side channel (R_JL/R_L), (b) the length of the junction channel (L_J), and (c) the width ratio between the side channel and the junction channel (W/W_JL).

A 40% Glycerin solution, which is diluted with DIW, was tested as the test fluid to examine the effects of each parameter on the performance of the proposed method. DIW, which behaves as a Newtonian fluid, was used as the reference fluid.

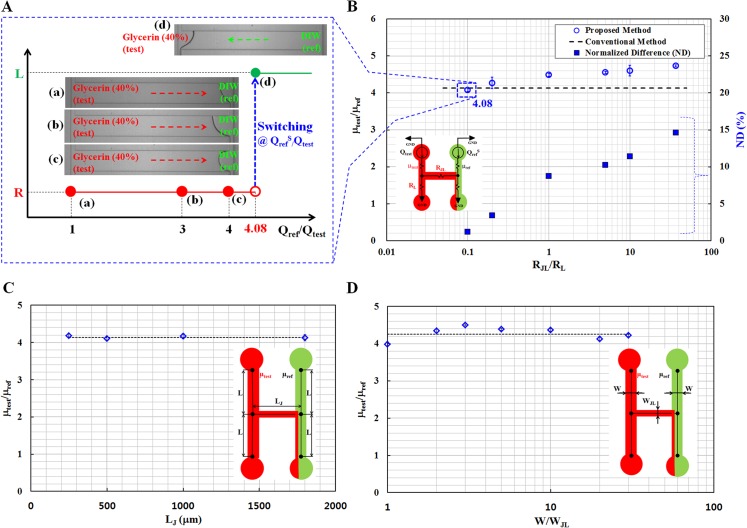
Fig. 3A shows typical images captured by the optical microscope for four different flow-rate ratios ((a) Q_ref/Q_test = 1, (b) Q_ref/Q_test = 3, (c) Q_ref/Q_test = 4, and (d) Q_ref^S/Q_test = 4.08). When the flow rate is the same (Q_ref = Q_test), the test fluid moves toward the right direction (R) in the junction channel because of the higher viscosity of the fluid compared with that of the reference fluid (μ_test > μ_ref) as shown in Fig. 3AA. The flow rate of the reference fluid was increased to change the fluidic flow direction in the junction channel. For convenience, the flow rate of the test fluid was fixed at 1 ml/h. When the flow rate of the reference fluid was set to approximately 4.08 ml/h, the flow direction in the junction channel was switched. That is, the fluidic flow direction of the Glycerin as the test fluid in the junction channel was reversed from the right direction (R) to the left direction (L), at a specific flow-rate ratio of Q_ref^S/Q_test = 4.08. Therefore, using Eq. 11, the viscosity of the test fluid was found to be 4.08 (μ_test/μ_ref = 4.08) at a fluidic resistance ratio of 0.1 (R_JB/R_B = 0.1).

Figure 3.

Performance evaluation results of the proposed method for various design parameters, including the fluidic resistance ratio (R_JL/R_L), the length of the junction channel (L_J), and the width ratio between the side channel and the junction channel (W/W_JL). (A) Microscopic images showing fluidic flow direction in the junction channel depending on flow-rate ratio ((a) Q_ref/Q_test = 1, (b) Q_ref/Q_test = 3, (c) Q_ref/Q_test = 4, and (d) Q_ref/Q_test = 4.08) for the 40% Glycerin solution as the test fluid and DIW as the reference fluid. The fluidic flow of the Glycerin was reversely moved in the junction channel from right direction (R) to left direction (L), at a specific flow rate ratio of Q_ref^S/Q_test = 4.08). (B) Variation of viscosity ratios (μ_test/μ_ref) identified using the proposed method with respect to the fluidic resistance ratios (R_JL/R_L) between the junction channel and the side channel. The normalized differences (NDs) compare the results obtained by the proposed method and the conventional method. (C) Variations of viscosity ratios identified by the proposed method with respect to various lengths (L_J) of the junction channel ranging from 250 μm to 1800 μm. (D) Variations of viscosity ratios measured by the proposed method with respect to different width ratios (W/W_JL) between the side channel and the junction channel.

Following the measurement procedure proposed in this study, the viscosity ratio (μ_test/μ_ref) was determined depending on the fluidic resistance ratio between the junction channel and the side channel (R_JL/R_L). The fluidic resistance ratio was theoretically estimated using a fluidic resistance formula for a rectangular channel (width = w, depth = h).⁴⁷ Additionally, it was only determined from channel dimensions, because both channels were filled with the same fluid. Fig. 3B shows the variation of viscosity rates (μ_test/μ_ref) with respect to the fluidic resistance ratios ranging from 0.1 to 36.6, whose values were theoretically calculated using a fluidic resistance formula for the rectangular channel.⁴⁷ The viscosity ratio of the test fluid in relation to the reference fluid is strongly influenced by the fluidic resistance ratio. The viscosity ratio gradually increases as the fluidic resistance ratio increases. This behavior indicates that the junction channel filled with test fluid would contribute to the overall fluidic resistance of left side channel, especially at higher fluidic resistances. Thus, the identified viscosity of test fluid tends to increase compared with reference value of fluid viscosity. Compared with the viscosity ratios measured by the conventional method (Brookfield viscometer), measurement performance becomes better at lower fluidic resistance ratios. In other words, for smaller fluidic resistance ratios ranging from 0.1 to 0.2, the normalized difference (ND) between the proposed method and the conventional method is less than 5%. This result indicates that the dynamic effect in the junction channel is negligible, and does not have any influence on performances. However, when fluidic resistance ratio is greater than 1 (i.e., R_JL/R_L > 1), viscosity of test fluid is overestimated owing to dynamic friction loss which is neglected in the viscosity formula (Eq. 11). Thus, ND significantly increases at the higher fluidic resistance ratios. Therefore, this proposed method can measure fluid viscosities with reasonable accuracy, particularly at smaller fluidic resistance ratios (R_JL/R_L < 1).

The effects of the length (L_J) of the junction channel on the measurement accuracy of the proposed method were also investigated. The viscosity ratio was measured by varying the channel lengths from 250 μm to 1800 μm. This range was selected in considering the constant fluidic resistance ratio (R_JL/R_L = 0.1). As shown in Fig. 3C, the viscosity of the test fluid has a consistent value of μ_test/μ_ref = 4.09 ± 0.04, regardless of the lengths of the junction channel. This result implies that the length of the junction channel does not play a significant role in the measurement accuracy of the proposed method.

The effect of the width ratio between the side channel and the junction channel (W/W_JL) on the measurement accuracy was also examined. The width ratios were properly designed to have a constant fluidic resistance ratio of R_JL/R_L = 0.1. As shown in Fig. 3D, the viscosity ratio of the test fluid to that of the reference fluid (μ_test/μ_ref) is consistently identified to be 4.26 ± 0.17 for various width ratios ranging from 1 to 30.6. Therefore, channel width ratios have little effect on the measurement accuracy of the proposed method.

Viscosity of various pure liquids

The feasibility and measurement accuracy of the proposed method were examined for various pure liquids including five different concentrations of Glycerin, as well as two different concentrations of plasma, silicone oil, and mineral oil. To validate the measurement accuracy, the conventional technique was also used for measuring viscosities of the various test fluids. In these experiments, DIW was used as the reference fluid.

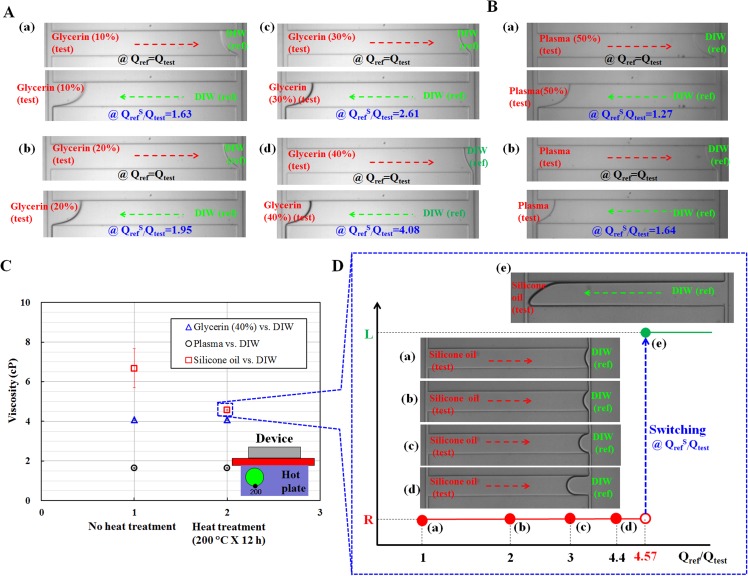
First, the experiment was conducted for Glycerin solutions with five different concentrations ((a) C_Glycerin = 10%, (b) C_Glycerin = 20%, (c) C_Glycerin = 30%, and (d) C_Glycerin = 40%, and (e) C_Glycerin = 60%). Fig. 4A shows four microscopic images of the fluidic flows in the junction channel at the same flow rate (Q_test = Q_ref) and switching flow-rate ratio (Q_ref^S/Q_test), at which the flow in the junction channel is reversed.

Figure 4.

Typical microscopic images captured by the optical microscope for illustrating the performance of the proposed device (W = 50 μm) for various fluids, including Glycerin, plasma, and oil, respectively. In this experiment, DIW was applied as the reference fluid. (A) Microscopic images captured for measuring viscosity of different concentrations of Glycerin ((a) C_Glycerin = 10%, (b) C_Glycerin = 20%, (c) C_Glycerin = 30%, and (d) C_Glycerin = 40%). (B) Microscopic snapshots captured for identifying fluid viscosity for two different concentrations of plasma ((a) C_plasma = 50%, and (b) C_plasma = 100%). (C) Viscosity variations of test fluids ((a) Glycerin (40%) vs. DIW, (b) Plasma vs. DIW, and (c) Silicon oil vs. DIW) depending on heat treatment (200 °C for 12 h) of the microfluidic device. (D) Microscopic images showing change of flow direction of the silicone oil in the junction channel depending on flow-rate ratio ((a) Q_ref/Q_test = 1, (b) Q_ref/Q_test = 2, (c) Q_ref/Q_test = 3, (d) Q_ref/Q_test = 4.4, and (e) Q_ref^S/Q_test = 4.57).

The corresponding switching flow-rate ratio (Q_ref^S/Q_test) for each concentration of the glycerin was found to be (a) Q_ref^S/Q_test = 1.63 for C_Glycerin = 10%, (b) Q_ref^S/Q_test = 1.95 for C_Glycerin = 20%, (c) Q_ref^S/Q_test = 2.61 for C_Glycerin = 30%, (d) Q_ref^S/Q_test = 4.08 for C_Glycerin = 40%, and (e) Q_ref^S/Q_test = 13.8 for C_Glycerin = 60%. Using Eq. 11, the viscosity ratio (μ_test/μ_ref) for each concentration of the Glycerin is identified as (a) μ_test/μ_ref = 1.63 for C_Glycerin = 10%, (b) μ_test/μ_ref = 1.95 for C_Glycerin = 20%, (c) μ_test/μ_ref = 2.61 for C_Glycerin = 30%, (d) μ_test/μ_ref = 4.08 for C_Glycerin = 40%, and (e) μ_test/μ_ref = 13.8 for C_Glycerin = 60%. To verify the measurement accuracy of these results identified by the proposed method, the conventional method was applied to the same test fluids for comparison. Each experiment was repeated five times (n = 5).

As listed in Table TABLE I., the viscosity ratios of the test fluids measured by the proposed method are consistent with those obtained by the conventional method. This result indicates that the proposed method can be effectively used to determine the viscosity of a test fluid with a reliable accuracy.

TABLE I.

Quantitative comparison of the viscosity ratios determined by the proposed method (W = 50 μm, R_JL/R_L = 0.1) and by the conventional methods for several pure liquids and different phases (single phase and oil–water phase).

Test fluid (test)	Reference fluid (ref)	Proposed method (n = 5)			Conventional method (n = 5) a	ND (%) c	Phase
		Qtest (ml/h)	QrefS (ml/h) b	(μtest/μref)pm	(μtest/μref)cm
Glycerin (10%)	DI-water (DIW)	1	1.63 ± 0.05	1.63 ± 0.05	1.53 ± 0.02	6.5	DIW vs. DIW
Glycerin (20%)		1	1.95 ± 0.03	1.95 ± 0.03	1.93 ± 0.05	1.0
Glycerin (30%)		1	2.61 ± 0.02	2.61 ± 0.02	2.73 ± 0.05	4.3
Glycerin (40%)		1	4.08 ± 0.04	4.08 ± 0.04	4.13 ± 0.06	1.2
Glycerin (60%)		1	13.8 ± 0.23	13.8 ± 0.23	13.95 ± 0.26	1.1
Plasma (50%)		1	1.27 ± 0.03	1.27 ± 0.03	1.35 ± 0.03	6.2
Plasma (100%)		1	1.64 ± 0.05	1.64 ± 0.05	1.54 ± 0.04	6.3
Silicone oil		1	4.57 ± 0.06	4.57 ± 0.06	4.76 ± 0.05	4.0	Oil vs. DIW
Mineral oil		1	29.2 ± 0.66	29.2 ± 0.66	30.0 ± 0.52	2.7

^aConventional method refers to the viscosity measurements using the Brookfield viscometer.

^bFlow-rate data are expressed as average ± standard deviation.

^cND is abbreviated words of normalized difference between the viscosity ratios (μ_test/μ_ref) determined by the proposed and conventional methods. It is calculated using the formula, |(μ_test/μ_ref)^pm/(μ_test/μ_ref)^cm − 1| × 100. Here, superscripts pm and cm denote the proposed method and the conventional method, respectively.

Next, we applied the proposed method to measure the viscosity of plasma which is the liquid component of blood, even under the osmotic pressure difference between plasma and DIW. Two different concentrations of plasma ((a) C_Plasma = 50% and (b) C_Plasma = 100%) were prepared using 1 × PBS, which has the same osmotic pressure as the plasma. In other words, 50% plasma denotes that blood plasma was diluted to 50% (vol./vol.), using PBS solution. In addition, 100% plasma represents pure plasma without addition of PBS solution. For the two different concentrations of plasma, Fig. 4B shows microscopic images, at the same fluid rate (Q_test = Q_ref) and switching flow-rate ratio (Q_ref^S/Q_test). In this experiment, we have assessed carefully several problems including contaminations, stacking of debris, and clogging in the microfluidic channels. As showed in Figs. and 4BA, 4BB, the present method which does not require label operation using fluorescent particles, does not undergo performance degradation due to those problems. The corresponding viscosity ratios of the plasma (test) in relation to that of DIW (ref) are as follows: (a) μ_test/μ_ref = 1.27 for C_Plasma = 50%, (b) μ_test/μ_ref = 1.64 for C_Plasma = 100% from the corresponding switching flow-rate ratio for each concentration of the plasma. The conventional method was also applied to evaluate the measurement accuracy. As summarized in Table TABLE I., the viscosities of the plasma as test fluid, which were identified by the proposed method, are consistent with those measured by the conventional method. Therefore, the proposed method can be used to measure plasma viscosities with sufficient accuracy.

The comparator method using a parallel flow in the single microfluidic channel was developed to measure oil viscosities by selecting an appropriate reference fluid.^{48, 49} However, the unstable fluidic behaviors of oil-water phase flows, such as oil vs. DIW, make it difficult to measure oil viscosities using the microfluidic device. For the present microfluidic device, similar unstable fluidic behaviors, including co-laminar, transition, and dripping occur, even in one channel of both side channels with respect to the flow rate of each fluid. However, among the two fluids, only one fluid passes in the junction channel, which allows the measurement of oil viscosities without any flow rate dependency, in contrast to the comparator. Two different oils, namely, silicone oil and mineral oil, were tested to demonstrate the feasibility and measurement accuracy of the proposed method. For this test, DIW was selected as the reference fluid. When oil and water are supplied in the microfluidic channels, an interface developed by oil-water phase might induce capillary force in the junction channel. This capillary force would influence pressure (or fluidic resistance) and flow behaviors. Thus, to evaluate the effect of capillary force in the junction channel, viscosity measurements were conducted using test fluids ((a) Glycerin (40%), (b) plasma, and (c) silicon oil), under two different hydrophobicity. To enhance hydrophobicity of the microfluidic channel, the microfluidic device had been exposed to high temperature (200 °C) using a hot-plate for 12 h. By using a contact angle measurement system, a contact angle of DIW on PDMS substrate was increased from 104° to 112° through the heat treatment. However, a contact angle of the Glycerin and plasma solutions on the PDMS substrate remained constant as 102°, without respect to heat treatment. In addition, silicon oil was completely spread on the PDMS substrate (i.e., hydrophilic), which makes it difficult to measure contact angle of the silicon oil. As depicted in Fig. 4C, the viscosities of the Glycerin (40%) and plasma solutions are remained consistently, without respect to different hydrophobicity. However, the viscosity of silicon oil strongly depends on hydrophobicity. In other words, under no heat treatment of the microfluidic device, the viscosity of silicon oil shows large deviations. This result indicates that capillary force in the junction channel would influence fluidic behaviors severely. For consistent viscosity measurement of test fluids, the microfluidic device was prepared using the heat treatment, especially for oil-water phase fluid (oil vs. DIW). Fig. 4D shows images illustrating the flow direction in the junction channels of the silicone oil as test fluid, for four different flow-rate ratios ((a) Q_ref/Q_test = 1, (b) Q_ref/Q_test = 2, (c) Q_ref/Q_test = 3, (d) Q_ref/Q_test = 4.4, and (e) Q_ref^S/Q_test = 4.57). When the flow rate ratio (Q_ref/Q_test) is less than the switching flow rate ratio (Q_ref^S/Q_test), silicone oil (test) only moves toward the right direction in the junction channel. Unstable fluidic behaviors, such as co-laminar flow or droplets, still occur in the right side channel at certain flow-rate ratios, because the viscosity of silicone oil (test) is greater than that of DIW (ref). However, these unstable fluidic behaviors in one of the side channels do not affect viscosity measurement accuracy, because the present method is fundamentally based on flow-switching in the junction channel, rather than in both side channels. When the flow-rate ratio between the reference fluid and test fluid (Q_ref/Q_test) was set to 4.57, the reference fluid (DIW) immediately moved toward the left direction in the junction channel. Using Eq. 11, the viscosity ratio of the test fluid (silicone oil) in relation to that of the reference fluid (DIW) is determined to be 4.57 (μ_test/μ_ref = 4.57). Similarly, the viscosity measurement procedure used for the silicone oil was applied to the mineral oil. The mineral oil exhibited reversal flow in the junction channel at a specific flow-rate ratio of 29.2 (Q_ref^S/Q_test = 29.2). For comparison, the conventional method was also applied to evaluate the viscosities of the two different oils. As summarized in Table TABLE I., the viscosity values measured by the proposed method are consistent with those obtained by the conventional method. Therefore, the proposed method based on fluidic flow-switching in the junction channel can be used to measure oil viscosities with sufficient accuracy, even under fluidic instability induced by the presence of oil-water phase flow in one of the side channels. In addition, based on experimental results using oil-water phase fluid (oil vs. DIW), oil can be applied to visualize an interface as reference fluid, when a test fluid is transparent and aqueous, and an interface between two liquids can be very difficult to image.

Blood viscosity measurement

As a final goal of this research, the proposed method was applied to blood passing in a narrow microfluidic channel. The viscosity of blood sample with varying (a) hematocrits at inlet, (b) chemically hardened RBCs, and (c) channel widths was determined using the proposed method. The flow rate of blood sample was fixed as 1 ml/h in the left side channel. Shear rate in the side channel is estimated to be above 1000 ($\dot{\gamma }$ > 1000 s⁻¹) by applying a shear rate formula in the rectangular channel.⁴⁷ At this higher shear rate regime, we believe that the blood sample behaves as a Newtonian fluid, and blood viscosity is independent of shear rates.

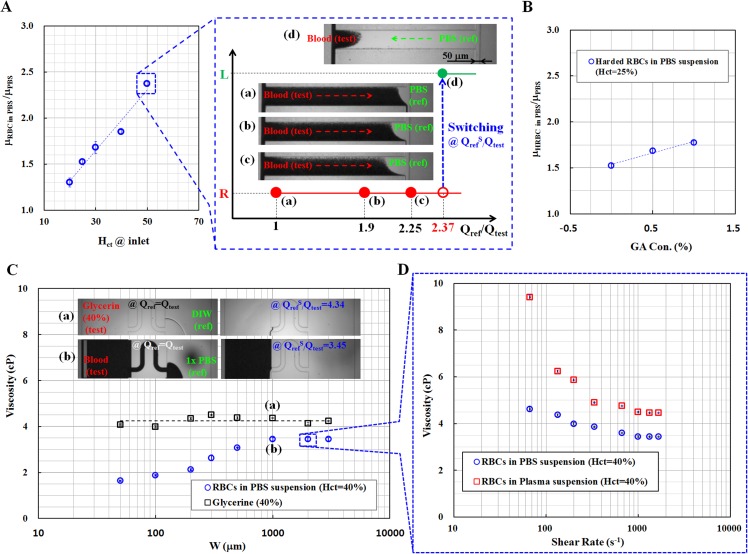
Fig. 5A shows the variations in blood viscosity ratio (μ_RBCsinPBS/μ_PBS) with respect to hematocrit level. The hematocrit of the blood sample was adjusted to ((a) H_ct = 20%, (b) H_ct = 25%, (c) H_ct = 30%, (d) H_ct = 40%, and H_ct = 50%) by adding either RBCs or 1 × PBS solution. In this experiment, 1 × PBS solution was used as the reference fluid to prevent rupture of RBC membrane due to different osmotic pressures when DIW was selected as the reference fluid. Both side channels had the same rectangular cross-section of 50 μm width and 50 μm depth. The microscopic images of the blood sample with 50% hematocrit are illustrated, and indicating the blood-flow direction in the junction channel for the following four flow-rate ratios ((a) Q_ref/Q_test = 1, (b) Q_ref/Q_test = 1.9, (c) Q_ref/Q_test = 2.25, (d) Q_ref^S/Q_test = 2.37). In this experiment, the flow rate of the blood sample was consistently maintained at 1 ml/h. The viscosity ratio of the blood sample in relation to that of 1 × PBS (ref) is determined to be 2.37 by measuring the switching flow-rate ratio, at which the blood reversely moves in the junction channel. Similarly, for other hematocrits of the blood sample, the specific flow-rate ratio, at which reverse flow occurs in the junction channel for each hematocrit condition was identified. Using the viscosity ratio formula ((Eq. 11), the viscosity of the blood sample (test) in relation to that of 1 × PBS (ref) for each hematocrit of the blood was determined as shown in Fig. 5A. The blood viscosity increases with respect to the hematocrit of the blood sample. Therefore, this proposed method can be effectively used to detect viscosity changes depending on hematocrit variations.

Figure 5.

Variation of blood viscosities determined by the proposed method, with respect to several factors such as hematocrit at inlet, chemically hardened RBCs by GA (glutaraldehyde), and widths of side channels. (A) The ratio of blood viscosity to that of the reference fluid (1 × PBS) with varying hematocrit of blood sample at inlet. The images captured by an optical microscopy were monitored to identify the fluidic flow-switching in the junction channel for various flow-rate ratios ((a) Q_ref/Q_test = 1, (b) Q_ref/Q_test = 1.9, (c) Q_ref/Q_test = 2.25, and (d) Q_ref^S/Q_test = 2.37) for blood sample of 50% hematocrit. (B) Variation of blood viscosity measured by the proposed method with respect to different concentrations of GA ranging from 0% to 1%. (C) Viscosity measurements of blood samples (H_ct = 40%) and the Glycerin (40%) with respect to channel widths (50 μm to 3000 μm) of the both side channels. Microscopic images at the right side represent the fluidic flow-switching in the junction channel for (a) Glycerin (Q_ref^S/Q_test = 4.34) and (b) blood (Q_ref^S/Q_test = 3.45). (D) Variation of blood viscosities identified by the proposed device (W = 2000 μm) using two different blood samples ((a) RBCs in 1 × PBS suspension (H_ct = 40%) and (b) RBCs in plasma suspension (H_ct = 40%)) with respect to shear rates.

The RBCs of patients with CVDs are known to have low deformability. This hemorheological deficiency severely hinders the microcirculation in narrow capillary vessels, and increases blood viscosity. To demonstrate the increase of blood viscosity due to hardened RBCs, the RBC membrane was chemically fixed to induce hardening by treating RBCs with 1 × PBS (1 ml) containing different concentrations of glutaraldehyde (GA) ((a) C_GA = 0.5%, and (b) C_GA = 1%) for 3 hours. The fixed RBCs were adjusted to have 25% hematocrit using a 1 × PBS solution. The 1 × PBS was also used as the reference fluid in this experiment. As shown in Fig. 5B, the blood viscosity is strongly affected by the chemical fixation of the RBC membrane. The blood viscosity tends to increase with the increasing GA concentration. In this experiment, we frequently observed a clogging phenomenon in the microfluidic channels, which would interrupt the unique features of the proposed device. Based on the experimental result, RBCs with less deformability strongly contributes to the increase of blood viscosity and occasionally hinder blood flows in the narrow channels.

We evaluated the reduction in viscosity due to the presence of a cell-free layer in the narrow channels. In this experiment, both side channels were designed to have the same widths ranging from 50 μm to 3000 μm. A blood sample was prepared to have 40% hematocrit (H_ct = 40%) by adjusting either the RBCs or using 1 × PBS solution. For comparison, the glycerin with 40% concentration was applied to evaluate the effect of channel size on viscosity measurement performance. The fluid viscosities of the blood sample and the Glycerin sample were measured by varying the widths of both side channels. For each microfluidic device with specified channel width, the flow rate of blood sample was appropriately selected to satisfy that blood sample behaves as Newtonian fluid, at higher shear rate ($\dot{\gamma }$ > 1000 s⁻¹). The insets in Fig. 5C show microscopic images illustrating the fluidic flow-switching in the junction channel for (a) Glycerin (Q_ref^S/Q_test = 4.34) and (b) blood (Q_ref^S/Q_test = 3.45), especially at the channel width of 1000 μm. The viscosities of the Glycerin and blood samples are determined to be 4.34 cP and 3.45 cP, respectively. As shown in Fig. 5C, these experimental results indicate that blood viscosity strongly depends on the channel width, and that blood viscosity tends to increase with increasing channel width. However, the blood viscosity becomes constant, when the width of the side channel is greater than 1000 μm. We compared these experimental results with those obtained by Fahraeus and Lindqvist.⁵⁰ For this comparison, the equivalent circular diameter (d) for the rectangular cross-section of 1000 μm width and 50 μm depth was approximately calculated as 252 μm by using a mathematical formula (d = 1.13 × (W × H)^0.5).⁴⁷ The equivalent diameter (d ≈ 252 μm) is consistent with the previous result obtained by Fahraeus and Lindqvist.⁵⁰ By contrast, the 40% Glycerin solution had constant viscosity and was independent of the channel width. This result implies that the viscosities of pure liquids are slightly affected by channel size. Therefore, we can assert that the blood viscosity decreases causes of cell-free layer, particularly when the width and depth of the side channels are smaller than 1000 μm width and 50 μm depth, respectively.

As illustrated in Fig. 5D, the microfluidic device with the channel width of both side channel (W = 2000 μm) was applied to measure two different blood samples ((a) RBCs in 1 × PBS suspension (H_ct = 40%) and (b) RBCs in plasma suspension (H_ct = 40%)), with respect to various shear rates. This result indicates that two blood samples behave as non-Newtonian fluids, as expected. At low shear rates, RBCs in plasma suspension has higher viscosities than those of RBCs in 1 × PBS suspension, owing to aggregation effect. In other words, blood viscosity is dominantly determined by the effect of aggregation, especially at lower shear rates. On the other hand, two blood samples represent Newtonian fluids, at the higher shear rates ($\dot{\gamma }$ > 1000 s⁻¹). In addition, RBCs in plasma suspension has higher viscosity than that of RBCs in 1 × PBS suspension, owing to different base solutions (1 × PBS, plasma).

From these experimental demonstrations, we can conclude that the present method proposed in this study is sufficiently capable of measuring the viscosities of complex fluids including human blood.

CONCLUSION

In this study, the fluidic flow-switching in the junction channel based on hydrodynamic balancing was used to measure viscosity of complex fluid, especially with label-free operation. Using this proposed method, the viscosities of various fluids with different phases (aqueous, oil, and blood) were accurately measured by adjusting the flow-rate ratio between the test and the reference fluids, thereby inducing a reverse flow of the test or the reference fluid in the junction channel. This method does not require tedious labelling using fluorescent particles or dyes. Using a discrete circuit model for the microfluidic device proposed in this study, an analytical viscosity formula was derived to determine the viscosity of a test fluid from experimental results. In the evaluation of the effects of various design factors that might affect the performance of the proposed method, the fluidic resistance ratio (R_JL/R_L) was found to have the strongest effect on the accurate viscosity measurement of the test fluid compared with the other factors, including the length of the junction channel (L_J), and the width ratio between the side channel and the junction channel (W/W_JL). The microfluidic device with smaller fluidic resistance ratios of R_JL/R_L < 1 can measure the viscosity of the test fluid with sufficient accuracy.

For single-phase liquids, including Glycerin and blood plasma, the proposed method was able to measure the viscosities of the test fluids accurately and easily. For oil-water phase fluid, the oil viscosity was also successfully determined, without any measurement constraints (flow rate) and technical problems, in contrast to the conventional method. The blood viscosity was also successfully measured under various hematocrits, RBC membrane deformability, and width of both side channels.

Based on these experimental demonstrations, the present method proposed in this study can be effectively used to measure the viscosities of various fluids accurately without additional operations, such as fluorescent labeling, and tedious calibrations. In the near future, the proposed method based on a microfluidic device will be applied to measure the hemorheological properties of an animal model with CVD_S under in vivo conditions.