Variability of tumor area measurements for response assessment in malignant pleural mesothelioma

Abstract

Purpose: The measurement of malignant pleural mesothelioma is critical to the assessment of tumor response to therapy. Current response assessment standards utilize summed linear measurements acquired on three computed tomography (CT) sections. The purpose of this study was to evaluate manual area measurements as an alternate response assessment metric, specifically through the study of measurement interobserver variability.

Methods: Two CT scans from each of 31 patients were collected. Using a computer interface, five observers contoured tumor on three selected CT sections from each baseline scan. Four observers also constructed matched follow-up scan tumor contours for the same 31 patients. Area measurements extracted from these contours were compared using a random effects analysis of variance model to assess relative interobserver variability. The sums of section area measurements were also analyzed, since these area sums are more clinically relevant for response assessment.

Results: When each observer's measurements were compared with those of the other four observers, strong correlation was observed. The 95% confidence interval for relative interobserver variability of baseline scan summed area measurements was [−71%, +240%], spanning 311%. For the follow-up scan summed area measurements, the 95% confidence interval for relative interobserver variability was [−41%, +70%], spanning 111%. At both baseline and follow-up, the variability among observers was a significant component of the total variability in both per-section and summed area measurements (p < 0.0001).

Conclusions: Despite the ability of tumor area measurements to capture tumor burden with greater fidelity than linear tumor thickness measurements, manual area measurements may not be a robust means of response assessment in mesothelioma patients.

INTRODUCTION

The current clinical method for tumor response assessment in malignant pleural mesothelioma (MPM) is the modified Response Evaluation Criteria in Solid Tumors (RECIST) guidelines, which calls for two linear measurements of tumor thickness from each of three computed tomography (CT) sections to be summed as the tumor burden measurement at a single time point.¹ Modified RECIST measurements, however, have a relative interobserver variability that can span a range of 30% under highly idealized image measurement conditions.^{2, 3} This interobserver variability is so large that from observer effects alone, a patient with truly stable disease (i.e., no actual change in tumor size between two time points) may be incorrectly classified as progressive disease or partial response (PD or PR, respectively).

While the goal of the modified RECIST measurement approach is to use linear measurements to capture changes in overall tumor burden and use these changes as a metric by which to gauge tumor response, the most complete measure of true tumor bulk is three-dimensional volume. Volume has been shown to be a significant predictor for overall and progression-free survival in patients with MPM,^{4, 5, 6} but the complete manual segmentation of MPM volumes on CT scans is prohibitively time consuming for clinical implementation as it would require the manual construction of tumor-encompassing contours on all sections in the scan. Frauenfelder et al.⁷ used a linear shape-based interpolation technique that required the creation of manual contours on “every fourth or fifth slice.” This study found that the interobserver agreement of semiautomated volumetric response classification was much greater than the interobserver agreement of manual modified RECIST response classification.

It is reasonable to expect that two-dimensional area measurements might serve as a compromise between linear measurements (with their high variability and limited ability to capture true tumor bulk) and volumetric measurements (with their reduced variability and nearly complete capture of tumor bulk, but with a substantial investment of time). The manual contouring of tumor on only three CT sections (to replicate the three sections required by modified RECIST) is certainly less time consuming than the manual contouring of tumor on all CT sections that is required to capture tumor volume, and the resulting extraction of tumor area captured by those contours should better represent tumor bulk than one-dimensional measurements obtained from those same three CT sections. Furthermore, the sum of area measurements from the three sections can be interpreted as a pseudovolume for use in response assessment, and these pseudovolumes may demonstrate the same improved interobserver agreement exhibited by full volume measurements.

The goal of this study was to evaluate the variability of CT-based tumor area measurements, which may provide a more complete metric for MPM tumor response assessment. Variability was quantified for two measurement tasks. First, variability in area measurements obtained from a single, baseline CT scan was examined; when observers construct contours to obtain tumor area on a baseline CT scan without reference to prior contours, the resulting contours are expected to exhibit a high degree of variability across observers due to the free-form nature of this task. Second, and perhaps more relevant clinically, variability in follow-up scan area measurements was examined. Follow-up scan contours (and the resulting measurements) are constructed with reference to the pre-existing baseline scan contours. It has been shown that the presence of initial contours strongly influences interobserver precision,⁸ and therefore interobserver variability will likely be reduced for follow-up measurements when compared with baseline measurements. Furthermore, changes in tumor measurements used for response assessment are often discretized by response classification criteria, and the interobserver agreement in response classification was quantified using relevant response criteria for area measurements.

MATERIALS AND METHODS

Patient cohort

The patient cohort in this study consisted of 31 patients (27 males, 4 females) with biopsy-proven MPM. The patients had a median age of 68 years at treatment initiation (range 49–81 years). All patients were part of a phase II clinical trial for a chemotherapy regimen consisting of cisplatin, pemetrexed, and bevacizumab.⁹ No scan was acquired specifically for this area measurement study.

Imaging

For each of the 31 patients, two scans were used in this study: the baseline scan acquired no more than four weeks prior to treatment initiation and the first follow-up scan acquired after two cycles of chemotherapy (median span between scans: 47 days). The diagnostic thoracic helical CT scans were performed on the Philips Brilliance 16-slice scanner (n = 39), Brilliance 40-slice scanner (n = 2), Brilliance 64-slice scanner (n = 20), or Brilliance iCT scanner (n = 1) at our institution. Each CT section was reconstructed as a 512 × 512-pixel image matrix, with pixel dimensions ranging from 0.54 to 0.90 mm. Axially reconstructed slice thickness was 3 mm for all scans. For 28 of the patients, iodinated contrast media was used for both scans, while for one patient each contrast was used on the first scan only, the second scan only, and neither scan.

Area measurement acquisition

On each of the 31 baseline CT scans, three sections with visible disease were selected by a single attending radiologist experienced in the interpretation of CT scans of mesothelioma patients. Sections were selected based on clinical considerations in a manner similar to the section-selection process required by the modified RECIST measurement technique. Preselection of CT sections was performed to eliminate section-selection differences among observers as a source of contour (and hence area measurement) variability. Using an inhouse software package,¹⁰ five observers (all attending thoracic radiologists who routinely evaluate pleural disease as part of clinical practice) independently contoured tumor on these 93 preselected baseline scan images. All observers had been trained in the use of the software and were given identical instructions for completing the study measurements. Observers were instructed to exclude regions of effusion and lung from their contours. The observers were able to browse the entire set of CT images for each patient, as well as adjust the window and level settings, but they were only able to contour tumor on the preselected sections. Contours were converted to area measurements using Green's theorem,¹¹ leading to 465 baseline scan area measurements (31 baseline CT scans, three sections per scan, five observers).

During the follow-up scan component of the study, four of the original five observers were independently shown the baseline scan with a fixed set of baseline scan contours for each patient. Each observer used the same set of baseline scan contours as reference for the construction of follow-up scan contours to eliminate differences in baseline contours as a source of follow-up contour (and hence follow-up area measurement) variability. For example, all four observers would see the baseline scan for patient 10 with baseline contours from observer 1 as reference while performing the follow-up contouring for patient 10. During follow-up measurement, each observer constructed follow-up scan contours to capture tumor area on the three sections from the follow-up scan that he/she believed to be anatomically matched to the three contoured sections in the baseline scan. This process replicated the clinical workflow typically used for response assessment using linear measurements at our institution, where the observer tasked with making follow-up measurements is able to visualize the previous scan and measurements but is wholly responsible for the placement of the new measurements. Again, follow-up scan contours were converted to enclosed area measurements.

For both the baseline and follow-up time points for each patient, area measurements were analyzed both on individual sections and as the sum of three section measurements per patient, which is more clinically relevant as a representation of tumor bulk. In total, there were 837 individual section area measurements (465 baseline and 372 follow-up scan measurements) and 279 summed area measurements (155 baseline and 124 follow-up scan measurements).

Data analysis

Baseline scan area measurement analysis

Estimating the variation in area measurements attributable to differences among observers was accomplished using a random effects analysis of variance (ANOVA) model.¹² Consider the linear model for the section-by-section area measurements,

$$y_{ijk}=\mu +{\alpha }_i+{\beta }_j+{\gamma }_{k\left(j\right)}+{\varepsilon }_{ijk},$$ (1)

where y_ijk represents the measurement for the ith observer (i = 1–5) in the jth patient ( j = 1–31) on the kth section (k = 1–3), μ is the overall mean, α_i represents the effects of the observers, β_j represents the effects of the different patients, γ_k(j) represents the effects of the different sections within each patient, and ɛ_ijk is the residual error. For summed area measurements (the sum of three sections per patient, representing a composite tumor area for a scan), the linear model is

$$z_{ij}=m+a_i+b_j+e_{ij},$$ (2)

where, analogous to Eq. 1, z_ij is the summed measurement, m is the overall mean, a_i is the observer effect, b_j is the patient effect, and e_ij is the residual error (note the absence of a section-effect term). The variance component attributable to each effect was estimated in the ANOVA model using the academic edition of Revolution R Enterprise (version 4.3).¹³

Once estimates for the variance components that involve the observer (${\widehat{\sigma }}_{\alpha }^2$ and ${\widehat{\sigma }}_{\varepsilon }^2$ for section-by-section variance estimates and ${\widehat{\sigma }}_a^2$ and ${\widehat{\sigma }}_e^2$ for summed area variance estimates) were obtained, the absolute interobserver variability was calculated. Absolute interobserver variability for section-by-section area measurements (i.e., variance in the difference of per-section area measurements between any two observers), ${\widehat{\sigma }}_y^2$, was computed according to Ref. 2

$${\widehat{\sigma }}_y^2=2\left({\widehat{\sigma }}_{\alpha }^2+{\widehat{\sigma }}_{\varepsilon }^2\right),$$ (3)

and a similar equation was derived for the absolute interobserver variability for summed area measurements, ${\widehat{\sigma }}_z^2$, with 95% confidence intervals (CI) of $\left[-1.96{\widehat{\sigma }}_y,+1.96{\widehat{\sigma }}_y\right]$ and $\left[-1.96{\widehat{\sigma }}_z,+1.96{\widehat{\sigma }}_z\right]$ for section-by-section and summed area measurements, respectively.

Relative interobserver variability involves the quantity

$$\frac{\left(y_{i^{\prime }jk}-y_{ijk}\right)}{y_{ijk}}=\frac{y_{i^{\prime }jk}}{y_{ijk}}-1,$$

the variability of which involves estimation of the variance of the ratio $y_{i^{\prime }jk}/y_{ijk}$ through the fitting of a random effects ANOVA model with log-transformed area measurements. Relative interobserver variability for section-by-section area measurements was computed according to

$${\widehat{\sigma }}_y^{\prime 2}=2\left({\widehat{\sigma }}_{\alpha }^{\prime 2}+{\widehat{\sigma }}_{\varepsilon }^{\prime 2}\right),$$ (4)

where the ${\widehat{\sigma }}_{*}^{\prime 2}$ were derived from fitting Eq. 1 with ln(y_ijk) instead of y_ijk. The 95% confidence interval on the relative interobserver variability for section-by-section area measurements is given by $\left[e^{-1.96{\widehat{\sigma }}_y^{\prime }}-1,e^{+1.96{\widehat{\sigma }}_y^{\prime }}-1\right]$. A similar derivation was used for summed area measurements.

The variance components obtained from the linear models were used to construct the intraclass correlation (ICC), which represents the proportion of total area measurement variation attributable to a specified source.^{14, 15} For example, the proportion of total variation attributable to patient effects in the summed area measurement model is

$${\mathrm{ICC}}_{\mathrm{pat}}^{\mathrm{sum}}=\frac{{\widehat{\sigma }}_b^2}{{\widehat{\sigma }}_a^2+{\widehat{\sigma }}_b^2+{\widehat{\sigma }}_e^2}.$$ (5)

Finally, agreement among observers was also quantified using the mean value of the Spearman rank correlation statistic (ρ) between each pair of observers.

Follow-up scan area measurement analysis

Follow-up scan area measurements were analyzed in a manner similar to that of the baseline scan measurements, with linear models and intraclass correlation calculated for both per-section and summed area measurements. Interobserver variability for follow-up scan measurements is more clinically relevant in the context of area measurement change between baseline and follow-up scans and the corresponding tumor response classification. The World Health Organization (WHO) guidelines for tumor measurements required the construction of two linear measurements (longest diameter and longest perpendicular diameter), the product of which represents the bidimensional tumor measurement (analogous to area).¹⁶ The WHO tumor response criteria then designated measurement changes between serial CT scans as PR for a measurement decrease of 50% or more, PD for a measurement increase of 25% or more, and SD for a measurement change between −50% and +25%. Although the WHO guidelines preceded RECIST and WHO-based measurements were not acquired in this study, the WHO criteria were used in this study to obtain tumor response classifications from the two-dimensional area measurements. Change in tumor area measurements and corresponding response classification were computed for each patient for each observer. Response classification agreement was evaluated using Fleiss’ Kappa statistic, which quantifies the extent to which observers agree with one another in terms of response classification rather than actual area measurements.¹⁷

RESULTS

Baseline scan measurements

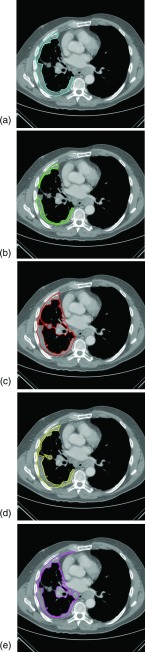
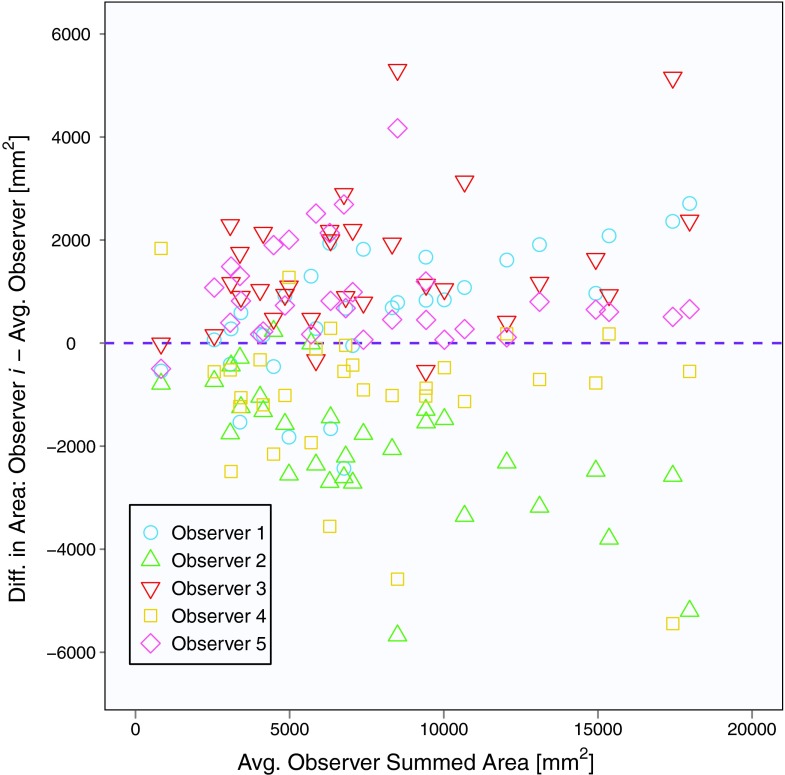
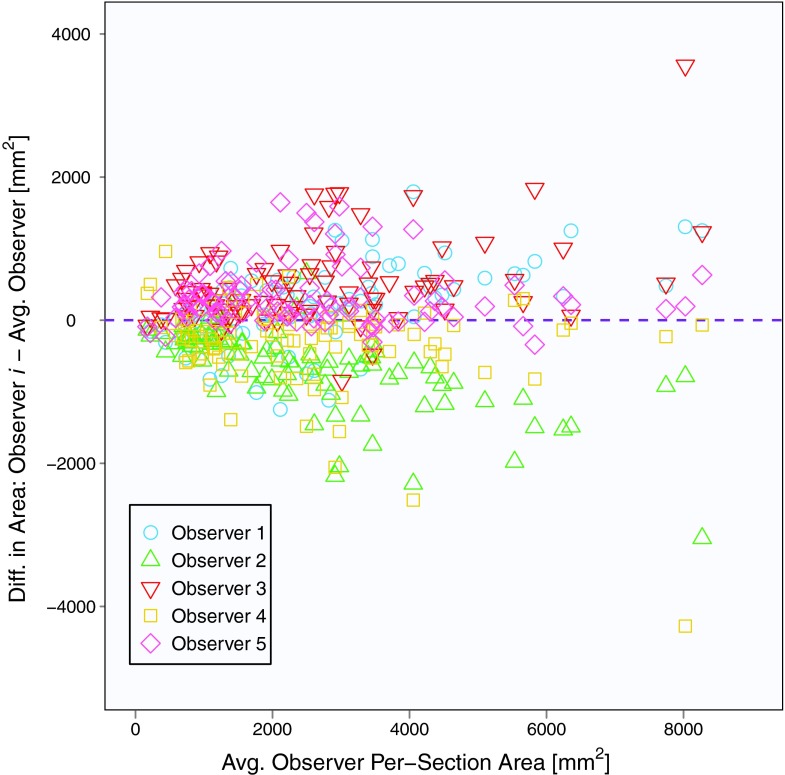
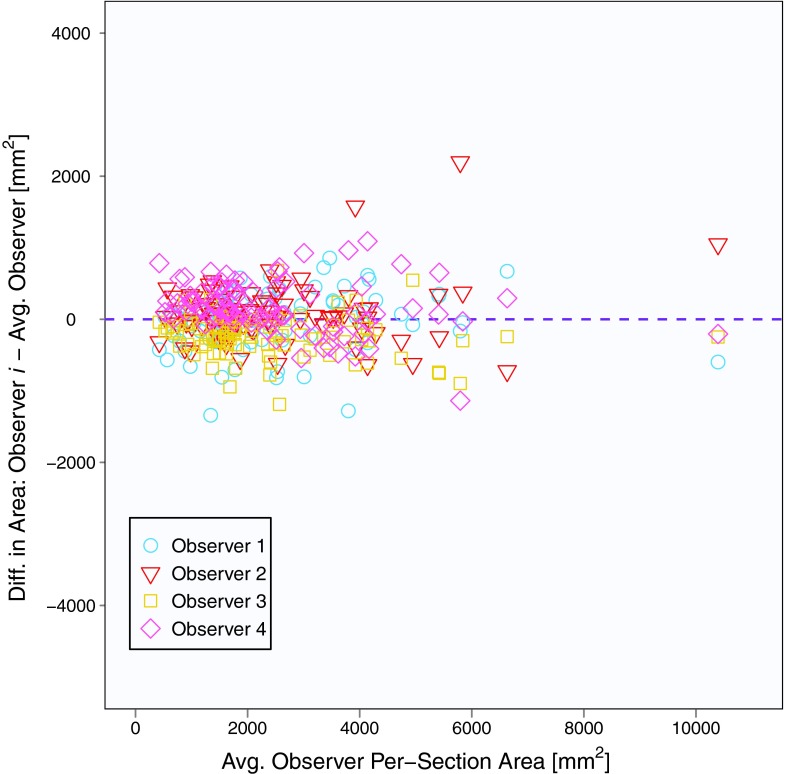
The mean baseline scan per-section area measurement across five observers and 31 patients (with three individual area measurements per patient) was 2562 mm², and the mean summed area measurement across five observers and 31 patients (with one summed area measurement per patient) was 7686 mm². Area contours of the five observers on the same baseline scan section are shown in Fig. 1. Similar to Bland-Altman analysis, Fig. 2 depicts the difference between an individual observer's baseline scan summed area measurement and the average of all five observers’ summed area measurements versus the average of all observers’ summed area measurements for each patient.^{18, 19} The mean difference between the individual observer's baseline scan summed area measurements and the mean of the other four observers’ summed area measurements was 678, −2510, 1885, −1246, and 1194 mm² for Observers 1, 2, 3, 4, and 5, respectively. Figure 3 shows a similar plot for baseline scan per-section area measurements. The mean difference between the individual observer's baseline scan per-section area measurements and the mean of the other four observers’ per-section area measurements was 226, −837, 628, −415, and 398 mm² for Observers 1, 2, 3, 4, and 5, respectively. The average bivariate rank correlation between observers (i.e., average value of ρ for each pairwise comparison) for baseline scan summed area measurements and per-section area measurements was ${\overline{\rho }}^{\mathrm{sum}}$ = 0.898 and ${\overline{\rho }}^{\mathrm{slice}}$ = 0.885 (both with p < 0.0001), respectively.

Figure 1.

Five observers’ contours of malignant pleural mesothelioma on a single section from a baseline CT scan. The corresponding areas of these five measurements are (a) 2756, (b) 1583, (c) 3877, (d) 2545, and (e) 3838 mm².

Figure 2.

Plot of baseline scan summed area measurements for 31 patients and five observers. The y-axis is the measurement difference between a given observer and the average of all observers, and the x-axis is the average of all observers.

Figure 3.

Plot of baseline scan per-section area measurements for 31 patients, three sections per patient, and five observers. The y-axis is the measurement difference between a given observer and the average of all observers, and the x-axis is the average of all observers.

The random effects model for absolute interobserver variability in baseline scan per-section area measurements yielded ${\widehat{\sigma }}_y$ = 1122 mm², with a 95% confidence interval of ±86% of the mean per-section area (Table 1). The model for absolute interobserver variability in baseline scan summed area measurements yielded ${\widehat{\sigma }}_z$ = 2871 mm², with a 95% confidence interval of ±73% of the mean summed area. The model for relative interobserver variability in baseline scan per-section area measurements and summed area measurements yielded ${\widehat{\sigma }}_y^{\prime }$ = 0.612 (95% confidence interval [−70%, +232%]) and ${\widehat{\sigma }}_z^{\prime }$ = 0.624 (95% confidence interval [−71%, +240%]), respectively.

Table 1.

95% CI for absolute and relative interobserver variabilities for per-section and summed area measurements of malignant pleural mesothelioma.

	Baseline scan			Follow-up scan
95% confidence interval	Lower bound	Upper bound	Range	Lower bound	Upper bound	Range
Absolute per-section (mm2)	−2200	2200	4400	−1268	1268	2536
Absolute summed (mm2)	−5627	5627	11 254	−3020	3020	6040
Absolute (% of mean), per-section	−86	86	172	−52	52	104
Absolute (% of mean), summed	−73	73	146	−41	41	82
Relative per-section (%)	−70	232	302	−51	103	154
Relative summed (%)	−71	240	311	−41	70	111

The values of the ICC statistics for baseline scan area measurements are summarized in Table 2. For per-section area measurements, interpatient variability accounted for 82.7% of the total variability, while interobserver variability accounted for 6.4% of the total. For summed area measurements, interpatient variability accounted for 82.6% of the total variability, while interobserver variability accounted for 8.7% of the total. For both the per-section and summed area measurements, interpatient variability comprised a significant majority of total variability, a finding consistent with the inherently wide range of tumor extent across patients. It should be noted that, despite the relatively small values, interobserver variability for both per-section and summed area measurements was significantly larger than zero.

Table 2.

Intraclass correlation statistics for the baseline scan area measurements, calculated from a random effects ANOVA model.

ICC statistic	Value	95% confidence interval
${\mathrm{ICC}}_{\mathrm{pat}}^{\mathrm{slice}}$	0.872	[0.710, 0.894]
${\mathrm{ICC}}_{\mathrm{obs}}^{\mathrm{slice}}$	0.064	[0.022, 0.365]
${\mathrm{ICC}}_{\mathrm{pat}}^{\mathrm{sum}}$	0.826	[0.635, 0.917]
${\mathrm{ICC}}_{\mathrm{obs}}^{\mathrm{sum}}$	0.087	[0.027, 0.452]

Follow-up measurements

The mean follow-up scan per-section area measurement across observers and patients was 2452 mm², and the mean summed area measurement was 7355 mm². Follow-up scan per-section area measurements were, on average, 9.8% lower than the corresponding baseline scan measurements. Similarly, follow-up scan summed area measurements were, on average, 10.9% lower than the corresponding baseline scan measurements.

Figure 4 depicts the follow-up scan contours of the four observers that correspond to the baseline scan section shown in Fig. 1 (specifically, observers used the contour in Fig. 1e as a reference during construction of the follow-up scan contour). Variability existed in the follow-up scan section-selection process, since observers chose the follow-up scan section they deemed the best anatomic match to the given contoured baseline scan section. Two different sections, on average, were contoured at follow-up for a given baseline scan contour across observers; for 12 of the 93 (12.9%) contoured baseline scan sections, all four observers selected a different section in the follow-up scan. The mean deviation in selected section among observers was 0.76 sections (approximately 2.3 mm).

Figure 4.

Four observers’ contours of malignant pleural mesothelioma on the follow-up CT scan of the patient in Fig. 1. All observers were shown the baseline scan contour in Fig. 1e as a reference for the construction of their follow-up scan contours. Note that not all observers selected the same follow-up scan section on which to construct the tumor contour. The corresponding areas of the four measurements are (a) 3813, (b) 3659, (c) 3853, and (d) 3139 mm².

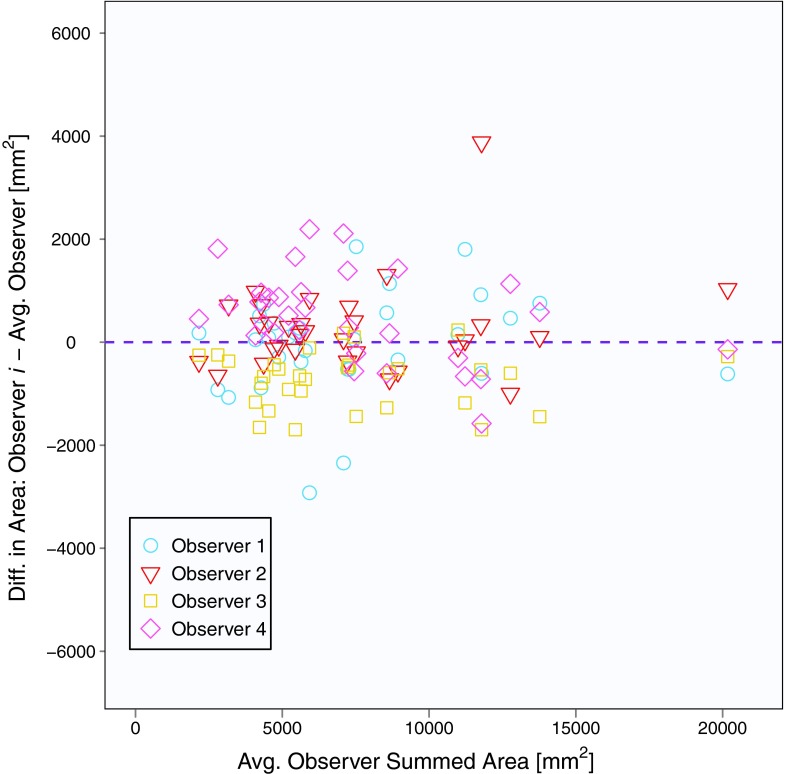
Figure 5 depicts the difference between an individual observer's follow-up scan summed area measurement and the average of all four observers’ summed area measurements versus the average of all observers’ summed area measurements for each patient. The mean difference between the individual observer's follow-up scan summed area measurements and the mean of the other three observers’ summed area measurements was −60, 352, −967, and 675 mm² for Observers 1, 2, 3, and 4, respectively. Figure 6 shows a similar plot for follow-up scan per-section area measurements. The mean difference between the individual observer's follow-up scan per-section area measurements and the mean of the other three observers’ per-section area measurements was −20, 117, −322, and 225 mm² for Observers 1, 2, 3, and 4, respectively.

Figure 5.

Plot of follow-up summed area measurements for 31 patients and four observers. The y-axis is the measurement difference between a given observer and the average of all observers, and the x-axis is the average of all observers. Note that the y-axis is identical to Fig. 2, highlighting the increased agreement among observers for follow-up scan measurements.

Figure 6.

Plot of follow-up scan per-section area measurements for 31 patients, three sections per patient, and four observers. The y-axis is the measurement difference between a given observer and the average of all observers, and the x-axis is the average of all observers. Note that the y-axis is identical to Fig. 3, highlighting the increased agreement among observers for follow-up scan measurements.

The random effects model for absolute interobserver variability in follow-up scan per-section area measurements yielded ${\widehat{\sigma }}_y$ = 647 mm², with a 95% confidence interval of ±52% of the mean per-section area (Table 1). The model for absolute interobserver variability in follow-up scan summed area measurements yielded ${\widehat{\sigma }}_z$ = 1541 mm², with a 95% confidence interval of ±41% of the mean summed area. The model for relative interobserver variability in follow-up scan per-section area measurements and summed area measurements yielded ${\widehat{\sigma }}_y^{\prime }$ = 0.360 (95% confidence interval [−51%, +103%]) and ${\widehat{\sigma }}_z^{\prime }$ = 0.270 (95% confidence interval [−41%, +70%]).

The values of the ICC statistics for follow-up scan area measurements are summarized in Table 3. For per-section measurements, interpatient variability accounted for 92.2% of the total variability, while interobserver variability accounted for 1.1% of the total. For summed area measurements, interpatient variability accounted for 92.6% of the total variability, while the interobserver variability accounted for 1.6% of the total. Interobserver variability comprised a significant majority of overall variability for both follow-up scan per-section and summed area measurements (p < 0.0001). The fraction of total variability in follow-up scan area measurements attributable to interobserver effects was less than that observed in baseline scans.

Table 3.

Intraclass correlation statistics for the follow-up scan area measurements, calculated from a random effects ANOVA model.

ICC statistic	Value	95% confidence interval
${\mathrm{ICC}}_{\mathrm{pat}}^{\mathrm{slice}}$	0.922	[0.887, 0.947]
${\mathrm{ICC}}_{\mathrm{obs}}^{\mathrm{slice}}$	0.011	[0.003, 0.142]
${\mathrm{ICC}}_{\mathrm{pat}}^{\mathrm{sum}}$	0.926	[0.864, 0.962]
${\mathrm{ICC}}_{\mathrm{obs}}^{\mathrm{sum}}$	0.016	[0.003, 0.201]

The relative change between the baseline scan summed area measurements and follow-up scan summed area measurements was calculated for all patients and observers, and the average bivariate rank correlation between observers for the change in summed area measurements from baseline to follow-up scans was ${\overline{\rho }}^{\Delta \mathrm{sum}}$ = 0.756 (p < 0.0001). Agreement among all four observers in classifying tumor response for each patient using the WHO classification criteria yielded κ = 0.544. Of the 31 patients, 29% (n = 9) had summed area measurements that resulted in inconsistent response classification among the four observers.

DISCUSSION

The purpose of this study was to assess manual area measurements of MPM as a metric for tumor response evaluation. Area measurements of baseline scans were used to investigate the measurement approach itself, and it was found that substantial variability was attributable to interobserver effects. The measurement approach was evaluated in terms of both individual section-by-section measurements and the sum of three sectional area measurements per patient. These summed measurements are more clinically relevant, just as summed linear measurements across three CT sections are currently used according to modified RECIST. The summed area measurements can be interpreted as “pseudovolumes,” that is, the volume of disease on a small subset of axial sections. If extended from three sections to all axial sections, the summed area measurements would be directly proportional to the full tumor volume. The number of axial sections across which the area measurements were summed was set at three simply to mimic the modified RECIST protocol for linear measurements.

The study then investigated corresponding follow-up scans to assess the variability of area measurements in a more practical context, since in clinical practice response assessment involves the acquisition of follow-up scan measurements in reference to previous baseline scan measurements. The variability of area measurements may be large when each observer is given a baseline scan as a “blank slate,” but in clinical practice only a single observer should obtain baseline scan measurements for a given patient. Measurements on the follow-up scan, then, are obtained with reference to this existing baseline scan measurement, which serves as a biased guide for follow-up scan measurements—implicitly constraining the thought process and actions of the observer and leading to a reduction in interobserver variability.

The results of this study support the notion that observers differed in their interpretation of identifiable MPM tumor, a finding previously reported.²⁰ If observers had simply been imprecise in their measurements (i.e., contours), a reduction in interobserver variability would be expected from the per-section area measurements to the summed area measurements as random fluctuations in contour construction would be averaged over the three sections. The results of the baseline scan study, however, indicate that interobserver variability is nearly equal between per-section and summed area measurements, leading to the conclusion that the variation results from different approaches to the contouring task or different perceptions of tumor boundaries among observers. Different contouring approaches could be explained by the fact that area measurements are not part of the standard clinical workflow, and therefore observers were not as familiar with the task as they are with the acquisition of linear measurements.

Relative interobserver variability estimates in follow-up scan area measurements, although lower than those of the baseline scan, still exhibited 95% confidence intervals that were considerably larger than the numeric values of the WHO tumor response classification criteria (−50%/+25%), which, presumably, would be imposed in any area-based tumor response paradigm. Lower interobserver variability in the follow-up scans was expected given a previous study that showed reference to existing contours biases observers;⁸ despite the reference to baseline scan contours, however, interobserver variability in follow-up scan area measurements remained a significant component of total variability. Relative interobserver variability of follow-up scan summed area measurements spanned a 95% confidence interval of [−41%, +70%], demonstrating that even these constrained follow-up measurements exhibited variability on the same level as the WHO criteria. This interobserver variability implies that differences among observers alone could result in measurement errors ranging from 41% below average to 70% above average; consequently, tumor response could be misclassified due to observer variability effects alone. This variability among observers likely was influenced by observers’ disparate interpretations of differences in disease presentation between baseline and follow-up scans, including differences in image acquisition parameters, differences in contrast administration, and differences in patient orientation in the CT scanner.

There are two sources of variability quantified in this study. The interobserver variability serves to reduce the robustness with which area measurements can be made and interpreted, and the interpatient variability is an underlying property of the disease itself. Differences among patients exist both in terms of initial disease burden at presentation and in terms of disease growth or decline after presentation. The larger interobserver variability becomes, the less we are able to reliably quantify meaningful differences in interpatient variability (both initial presentation and changes thereafter) and relate those differences to differences in patient response. This study demonstrates that manual area measurements (whether summed or per-section) have interobserver variability that would prevent meaningful response assessment.

Future studies with more patients and radiologists potentially would provide more complete estimates of interobserver variability; however, the collection of these data is time consuming. Even if follow-up scan variability were reduced further from the present results, manual area contours as a metric for response assessment would be impractical, since the time required to contour tumor area in this study was on the order of 20 min per scan. Although not nearly as widely available as basic contouring tools, semiautomated algorithms for complete disease volume segmentation have been reported to require less time^{5, 7} than that required to contour tumor area in the present study. Accordingly, future studies should seek to validate measurements of disease volume as a response assessment metric for patients with MPM.