Power output in vertical jumps: Does optimum loading depend on activity profiles?

Abstract

The previously proposed Maximum Dynamic Output hypothesis (MDO; i.e. the optimum load for maximizing the power output during jumping is one's own body) was tested on individuals of various activity profiles. Forty males (10 strength-trained athletes, 10 speed-trained athletes, 10 physically active non-athletes, and 10 sedentary individuals) performed different vertical jumps on a force plate while a pulley system was used to either reduce or increase the subject's body weight by 10–30%. As expected, an increase in external loading resulted in a significant increase (p < 0.001) in force output and a concomitant decrease of peak jumping velocity in all groups of participants. The main finding, however, was that all groups revealed the maximum peak and mean power output at approximately the subjects’ own body weight although their weight represented prominently different percentage of their maximum dynamic strength. While a significant (p < 0.05), albeit moderate, 'group × load' interaction in one jump was observed for the peak power output, the individual optimum load for maximizing the power output number did not differ among the groups. Although apparently further research on various types of movements is needed, the present results provide, so far, the strongest support of the MDO hypothesis.

Introduction

The production of maximum muscular power output has been considered as an important aspect of various athletic performances (Cormie et al. 2011; Cronin and Sleivert 2005). The performance of movement tasks, such as jumping, sprinting, throwing or kicking require maximization of the velocity of either the body segments or entire body, which is closely related with the ability of skeletal muscles to produce a high power output (Cormie et al. 2011). Therefore, the maximum power output of lower-body muscles has been frequently explored through the maximum vertical jumping (VJ) (Markovic and Jaric 2007; Driss et al. 2001; Vandewalle et al. 1987). The issue discussed is not only important from the theoretical aspect, such as dealing with fundamental properties and design of the muscular system (Jaric and Markovic 2009), but also from practical aspect. Namely, it has been frequently suggested that the maximum gains in both power output and movement performance could be achieved when training explosively with a single load that maximizes mechanical power output during ballistic exercises such as VJ (Harris et al. 2007; Cormie et al. 2007a; Cronin and Sleivert 2005).

The effect of external loading on the production of maximum power output in VJ has been frequently studied (Baker et al. 2001; Cormie et al. 2007a; Cormie et al. 2007d; Driss et al. 2001; Harris et al. 2007; McBride et al. 1999; Stone et al. 2003; Bevan et al. 2010). It has been generally presumed that, similar to the mechanical properties of an in vitro muscle (Hill 1938), there could be an optimum external loading that allows for maximization of muscle power output in natural human movements. The experimental findings have been generally inconsistent revealing the optimum load for maximizing the muscle power output in VJ being between 0% (i.e., subject’s body weight; BW) and 59% of one repetition maximum (1RM) squat (Nuzzo et al. 2010b; Markovic and Jaric 2007; Harris et al. 2007; Cormie et al. 2007a; Sleivert and Taingahue 2004; Stone et al. 2003; Baker et al. 2001). The relatively wide loading range observed could be a result of various methodological issues, such as the differences in the data collection and calculation techniques used (Hori et al. 2007), type and position of the external loads applied (Jaric and Markovic 2009; Markovic and Jaric 2007; Cronin and Sleivert 2005), selection of the dependent variables (e.g., peak or mean power; Cronin and Sleivert 2005), and, particularly, from the task specificity (Cronin and Sleivert 2005; Kawamori and Haff 2004). Consequently, the issue of optimum loading to maximize muscle power output in VJ still remains largely unresolved (see also, Cormie et al. 2007a; Dugan et al. 2004).

Despite conflicting results in literature, most authors that applied ‘zero’ (i.e. subject’s BW) and positive-only external loads during VJ observed a decrease in maximum power output with an increase in external loading, suggesting that the optimum loading that maximizes the muscle power output in VJ could be close to the subject’s BW (Cormie et al. 2007b; Constable and Carpenter 1995; Cormie et al. 2007c; Cormie et al. 2007d; Davies and Young 1984; Driss et al. 2001; Dugan et al. 2004; McBride et al. 1999; Stone et al. 2003; Bevan et al. 2010). In fact, the concept of optimum loading for maximizing the power output during VJ that occurs at one's own BW originates from classical works of Cavagna and co-workers (1972) and Margaria (1973). After observing additional experimental support from studies that applied both positive and negative loading during VJ (Markovic and Jaric 2007; Avela et al. 1994), Jaric and Markovic (2009) suggested that this hypothesis be identified or named as the maximum dynamic output (MDO) hypothesis. Although recently supported by two studies from independent laboratories (Argus et al. 2011; Nuzzo et al. 2010b), the MDO hypothesis still lacks firm experimental support with respect to a number of potentially important factors, such as the individual’s training history, the type of the movement task (e.g., different types of VJ and other movements performed predominantly with lower limbs), etc.

Regarding the potential role of activity profiles due to different training histories, it has been already known for several decades that the exercise at high velocity and low resistance can shift the force-velocity of the involved muscles and muscle groups (Kaneko et al. 1983). This phenomenon has been considered as a part of the general effect of velocity specificity on the subsequent muscular adaptation (Cormie et al. 2011) that implicitely suggests that the optimum loading should depend on the individual activity profiles (Driss et al. 2001; Stone et al. 2003). Several studies have revealed the differences in the optimum load among the various groups of athletes and non-trained individuals (Baker et al. 2001; Bevan et al. 2010; Cormie et al. 2007d; Driss et al. 2001; Harris et al. 2007; Sleivert and Taingahue 2004; Stone et al. 2003; Nuzzo et al. 2010b); however, none of the studies applied a ‘negative loading’ during VJ. Conversely, at least two studies found no or only minor effect of activity profiles on the external loading that allows for maximizing the muscle power in VJ (Nuzzo et al. 2010b; McBride et al. 1999). Note, however, that the cited studies either did not apply the negative loading (McBride et al. 1999), or applied an unloading counter-mass that inevitably increased the total inertia (Nuzzo et al. 2010b).

To address the above reviewed unresolved issues, we designed an experiment with the aim to investigate the loading associated changes in the maximum power output in VJ in the groups of strength-trained athletes, speed-trained athletes, and the age-matched physically active and sedentary individuals. Note that the same participants tested in our recent study (Pazin et al. 2011) revealed optimum loading for maximizing the power output in 6-s maximum cycling sprint test that was higher in athletes than in non-athletes. To obtain a more robust findings, we tested both the countermovement jump performed with arm swing (CMJa) and squat jump (SJ) since they are not only based on partly different movement patterns and performance (Asmussen and Bonde-Petersen 1974), but also on different neuro-mechanical mechanisms (Schenau et al. 1997; Harman et al. 1990). Since the effects of both the loading and unloading needed to be evaluated, we applied extended rubber bands that exerted approximately constant vertical forces upon the subject's body that mimicked change in their BW (but not inertia; Leontijevic et al. 2012) within the interval from −30% to +30%. In line with the MDO hypothesis, our first hypothesis was that the optimum external loading for maximizing the power output would be 1) close to the subject’s own BW, and 2) within the well-known optimum loading range for maximizing the power output of skeletal muscles (i.e., within 20% to 50% of maximum dynamic strength of leg extensor muscles). Based on findings reviewed above, as well as on the differences in the optimum load obtained from the same subjects in the 6-s maximum cycling sprint test (Pazin et al. 2011), our second hypothesis was that the optimum external loading would be different for individuals with different training and activity profiles. The findings were expected to reveal important results regarding understanding some basic aspects of both the design and adaptation of the muscular system, as well as to provide potentially important guidelines for refinement of various training and rehabilitation procedures.

Methods

Participants

Based on the sample size estimate conducted in our previous study (Pazin et al. 2011) based on the differences in muscle strength, power, and velocity among similar groups of participants, we recruited 40 healthy male participants. Based on their training history, they were allocated into the following four groups: Strength (highly strength trained bodybuilders; n = 10; age 24.7 ± 4.6 yrs), Speed (elite karate competitors; n = 10; 23.5 ± 3.9 yrs), Active (n = 10; 22.0 ± 1.4) yrs, and Sedentary group (n = 10; 24.8 ± 2.7 yrs).

The participants in both the Strength and Speed group were selected on the basis of their sport experience (minimum 3 yrs), current physical activity (minimum 3 training sessions a week), and athletic proficiency. The sample of bodybuilders consisted of medalists on either international or national championships. They should qualify to be ‘highly strength trained’ due to their weekly training protocol prior to the testing session. Specifically, it involved 3–4 sessions aimed to hypertrophy (i.e., 60–80% 1RM) and 2–3 sessions aimed towards strength (85–100% 1RM). Regarding the Speed group, five karate competitors were members of the national team that became the world champions in the same year when the testing was conducted, while the remaining five were national champions. Note that elite karate competitors demonstrate outstandingly higher speed of leg movements than the amateurs (Sbriccoli et al. 2010). The Active group involved sport and physical education students who were active only through their standard academic curriculum that included 6–8 activity classes per week that involved both low and high intensity exercises. However, none of these subjects have had experience with regular resistance training. The Sedentary group consisted of low to moderately active individuals with no current or prior experience with any kind of athletic training. Their level of physical activity was assessed by a standard questionnaire (Taylor-Piliae et al. 2006), where six of the participants reported light and four moderate levels of physical activity. None of the participants reported any medical problems or recent injuries that could compromise the tested performance. The participants were informed regarding the potential risks associated with the applied testing protocol and asked to sign an informed consent document prior to the testing protocol. All participants gave written informed consent to the experiments, which was in accordance to the Declaration of Helsinki, and approved by the Institutional Review Board of the University of Delaware.

The pulley device

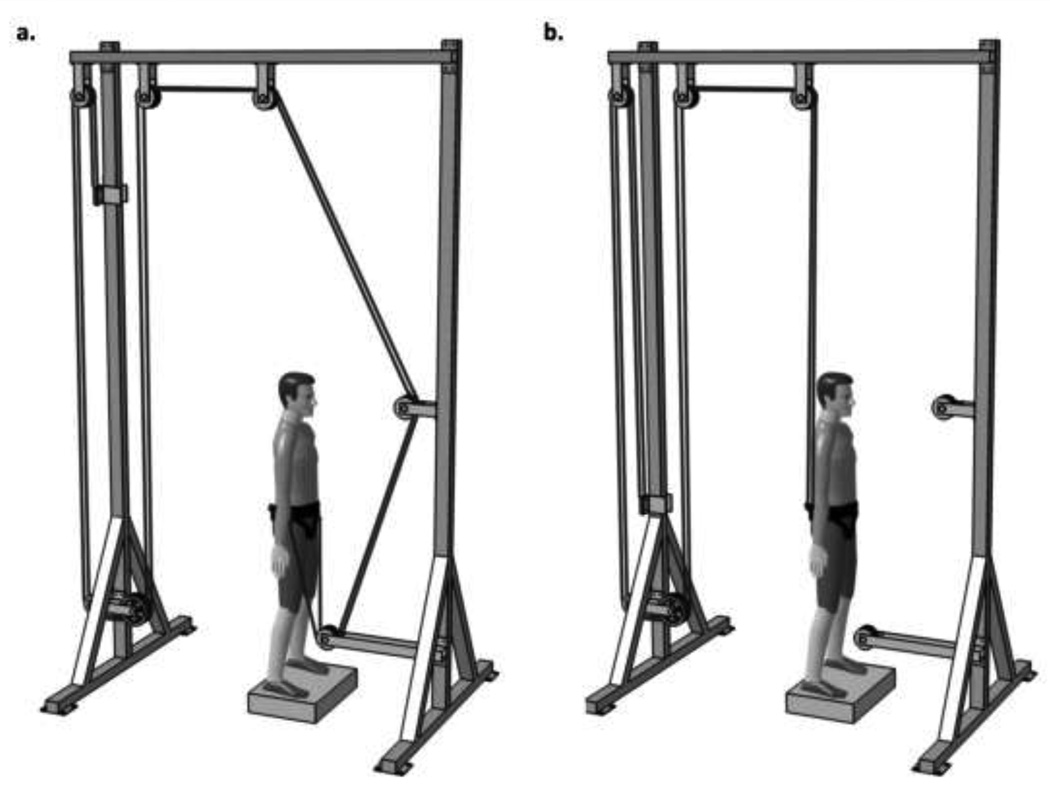
For the purpose of this study, we developed a pulley system to simulate either an increase (Figure 1a) or a decrease (Figure 1b) in BW. In particular, two long rubber bands (resting length 13.5 m, coefficient of elasticity 21 N/m) were stretched to provide the pulling force up to 30% of the subject’s BW. They were attached to both lateral sides of a belt fixed approximately at the subject's waist and stretched over a system of low friction and low inertia plastic wheels. The loading system allowed for performing VJ without any particular movement constrains when applied to pull subjects either vertically upward (negative load) or vertically downward (positive load). Note that the subjects moved their waist during the eccentric and concentric phase of jumps vertically approximately within a 0.32 m interval. Therefore, the relative change in their stretched length was approximately between 4% and 17% (when exerting the external force between 10% and 30% of BW in either direction), yielding similar change in the acting force. Therefore, one could assume that the applied pulling forces were relatively constant during the jumping trials and, therefore, mimicked the alterations of BW. A force platform placed beneath the subjects' feet allowed for an accurate adjustment of the loading force. Since the applied pulley device exerted either unloading or loading force that corresponded to 10%, 20% and 30% of the participants' BW, the loading conditions mimicked alteration of the total weight to 0.7, 0.8, 0.9, 1.0, 1.1, 1.2 and 1.3 of BW where, for example, 0.7BW and 1.3BW corresponded to the external unloading and loading by 30% of BW, respectively, while 1.0BW corresponded to no loading applied.

Fig 1.

Schematic representation of the applied pulley system used to simulate either an increase (a) or decrease (b) in body weight in vertical jumps

Experimental protocol

The experimental protocol was carried out through three sessions separated by 2 days of rest. The first testing session included anthropometric measurements and medical screening, followed by strength testing (i.e. one repetition maximum squat). The second session served for familiarization and consisted of 5–7 practice trials of both CMJa and SJ performed under each loading conditions. The third session consisted entirely of testing the effects of loading on kinematic, kinetic and power output in CMJa and SJ. The subjects were instructed to avoid any strenuous exercise both 48 hours prior and during the experiment.

Testing procedures

Anthropometric measures were taken according to the procedures recommended by the International Society for the Advancement of Kinanthropometry (Norton et al. 2000). Body height and body mass were measured to the nearest 0.5 cm and 0.1 kg, respectively. Body composition (lean body mass and percentage of body fat content) was assessed through the skinfold measurements. They were taken from biceps, triceps, thigh, calf, chest, and abdomen to the nearest 0.2 mm using a skinfold caliper (John Bull, British Indicators Ltd., Bedfordshire, UK) by the same experienced investigator. The skinfolds were measured in triplicate and the average value was taken for further analysis.

Following the anthropometric measurements, a standard procedure (McBride et al. 1999) was applied to assess the leg extensor strength through one repetition maximum of squats (1RM). Prior to the start of the warm-up procedure, a manual goniometer was used to visually demonstrate the attainment of a 90° knee flexion angle while squatting. The applied loading and the number of the associated warm-up trials were as follows: 30% (8 repetitions), 50% (4–6 repetitions), 70% (2–4 repetitions), and 90% (1 repetition) of an estimated 1RM either based on the subjects recommendation or on calculated 1.5–2 times the subject’s BW. The test required between 2 and 3 trials to assess 1RM. Each subject was asked to control lowering of the bar to the level that provided the 90° of knee angle. Following the reaching of the lowest position, they were instructed to immediately move the weight upward in a controlled but forceful fashion back to the starting position. Adequate rest was allowed between trials (3–5 min).

Within the third session, each subject performed one practice and two consecutive experimental CMJa and SJ trials under each of the seven loading conditions (0.7BW, 0.8BW, 0.9BW, 1.0BW, 1.1BW, 1.2BW and 1.3BW; see above for details). The sequence of loads and the type of jumps under each load was randomized for each subject. Regarding CMJa, the subjects were instructed to perform an unconstrained maximum vertical jump from standing upright position that includes the initial counter movement which included the arm swing. Regarding SJ, the subjects were instructed to perform maximum vertical jump from the static starting position where the knee joint angle was fixed at 90°, while keeping their hands on the hips. Visual inspection of the force signal was additionally used to detect possible additional counter movement prior to SJ. When detected, the trials were repeated.

In line with previous studies, one minute of rest was allowed between two consecutive jumping trials, and 2–3 min between the consecutive loading conditions and fatigue was never an issue (Markovic et al. 2011). All sessions were preceded by a standard warm-up procedure (5 min cycling and 10 min of callisthenic and dynamic stretching).

Data processing and analysis

The force plate (AMTI, Inc., Newton MA, USA; sampling frequency 1000 Hz) was mounted and calibrated according to the manufacturer’s specifications. Custom-designed software (LabVIEW, National Instruments, Version 8.2, Austin, TX) was used to record and process the vertical component of the ground reaction force (GRF). The data were low-pass filtered (a second-order recursive Butterworth filter at a cut-off frequency of 10 Hz) and the velocity and position of the center of mass were calculated by consecutive integrations of the acceleration signal assessed from GRF. Although we were primarily interest in the muscle power output, we also recorded several kinematic and kinetic variables related to the jumping pattern and jumping performance that could potentially reveal the mechanisms of the group-specific adaptation to the applied loading. In particular, we calculated the maximum lowering of the center of mass during the eccentric jump phase (Δh_ecc; for CMJa only), duration of the concentric jump phase (T_con), and peak GRF during the concentric jump phase (F_peak). Since the external force applied through the pulley device alters body acceleration during the flight phase, we assessed the jumping performance through the peak velocity of the body’s center of mass during the concentric phase (V_peak) instead by the jump height (Markovic and Jaric 2007). Finally, the power output was assessed through the peak power (P_peak) and mean power output (P_mean) assessed from the concentric jump phase and calculated as a product of the velocity and GRF. For each loading condition, the trial with higher P_peak was used for further analyses. The reliability of the calculated mechanical variables has been shown to be high across the range of applied loads (Markovic and Jaric 2007).

Statistical analyses

Descriptive statistics were calculated for all experimental data as mean and standard deviation (SD). The percent body fat was calculated using a previously recommended Matiegka’s method (Montagu 1960). Although the differences in body mass among the groups were somewhat below the significant level (see Results), they were relatively large (e.g., about 10% between the Strength and Sedentary group). Therefore, 1RM squat, F_peak, P_peak and P_mean were appropriately normalized for body size using the body mass raised to the power of 0.67 (i.e., in W/kg^0.67; Jaric 2002).

One-way analysis of variance (ANOVA) with a Tukey post hoc comparisons test was used for the between-group analyses of the subject characteristics (i.e., age, height, weight, percent of body fat, lean body mass, 1RM squat, 1RM/body mass^0.67). The normality of the distribution for all dependent variables was tested by means of the Kolmogorov-Smirnov test. Homogeneity of variance between samples was confirmed for all dependent variables (p > 0.05). Since all sets of data revealed normal distribution (p > 0.11), a two-way mixed model ANOVA was used to evaluate the main effects of ‘load’ (0.7BW, 0.8BW, 0.9BW, 1.0BW, 1.1BW, 1.2BW and 1.3BW) and 'group' (Strength, Speed, Active, and Sedentary group) on all dependent variables. A Greenhouse-Geisser adjustment was made to the degrees of freedom in case of violation of the sphericity condition. When the main effects were revealed, Tukey post-hoc tests were applied. In addition, the partial eta squared (_pη²) was calculated for the ANOVAs with the values of 0.01, 0.06 and above 0.15 considered to be small, medium and large, respectively (Cohen 1988). To additionally test the possible differences in optimum loads among the groups, we found individual optimum load for each participant. Thereafter, the differences among the averages of four tested groups were tested by the Kruskal-Wallis test. Finally, we also expressed the optimum load as a percentage of maximum dynamic strength (MDS) as assessed by the sum of 1RM squat and subject’s body mass minus shank mass (for details see, Cormie et al. 2007a). Also, one-way ANOVA with a Tukey post hoc comparisons test were used to analyze group differences in this dependent variable. Statistical significance was set at p = 0.05. All statistical tests were performed using SPSS 16.0 (SPSS Inc, Chicago, IL).

Results

Subject characteristics

The subject characteristics are summarized in Table 1. One-way ANOVA revealed significant group differences in percent body fat (F_{[3 ,36]} = 16.1, p < 0.001) and lean body mass (F_{[3, 36]} = 7.8, p < 0.001), while the group differences among other anthropometric variables were not statistically significant (all p > 0.05). Of particular importance could be the marked group differences in absolute (F_{[3 ,36]} = 45.2, p < 0.001) and body mass-normalized maximum squat strength (F_{[3 ,36]} = 31.7, p < 0.001).

Table 1.

Subjects anthropometric characteristics and squat strength (mean ± SD)

Variable	Strength group (n = 10)	Speed group (n = 10)	Active group (n = 10)	Sedentary group (n = 10)
Height (m)	1.76 ± 0.04	1.82 ± 0.06	1.82 ± 0.10	1.80 ± 0.08
Body mass (kg)	85.5 ± 7.4	82.5 ± 7.2	79.5 ± 7.2	77.9 ± 7.4
Lean body mass (kg)	81.5 ± 7.3	76.5 ± 4.1	73.1 ± 6.4 a,b	68.6 ± 6.4 a,b
Body fat (%)	4.7 ± 0.8	7.3 ± 1.6	8.5 ± 2.7 a,b	11.9 ± 3.7 a,b,c
1RM squat (kg)	206.0 ± 19.2	163.0 ± 19.2 a	131.8 ± 19.1 a,b	116.0 ± 17.3 a,b
1RM squat/body mass0.67	10.5 ± 1.0	8.5 ± 1.0 a	7.1 ± 1.2 a,b	6.3 ± 0.9 a,b

1RM - one repetition maximum.

^aSignificantly different from Strength group at level p < 0.05

^bSignificantly different from Speed group at level p < 0.05

^cSignificantly different from Active group at level p < 0.05

Power output, movement pattern and performance

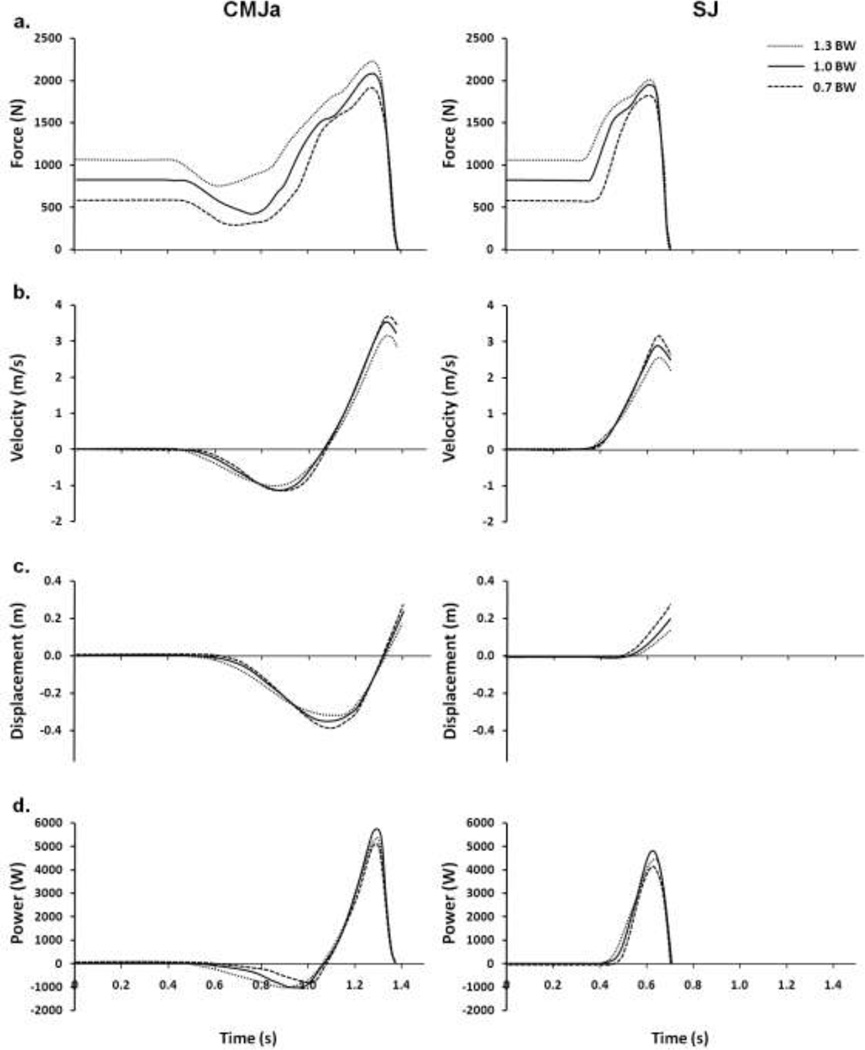
The typical time series of the mechanical variables observed in a representative subject under three loading conditions are shown in Figure 2. As expected, an increase in external load was associated with both an increase in GRF (Figure 2a) and a decrease in V_peak (Figure 2b). The subject also demonstrated a marked load-associated decrease in Δh_ecc during the eccentric jump phase of CMJa (Figure 2c). Finally, P_peak appeared to be higher under no load condition (i.e., 1.0BW) than under either minimum or maximum load in both CMJa and SJ (Figure 2d).

Fig 2.

Time series of the ground-reaction force (a), velocity of the center of mass (b), position of the lowering center of mass (c), and instantaneous power (d) obtained from a representative subject under three selected loading conditions (i.e., 0.7, 1.0, and 1.3BW) for both CMJa and SJ. Time series are aligned with respect to the instant of the takeoff

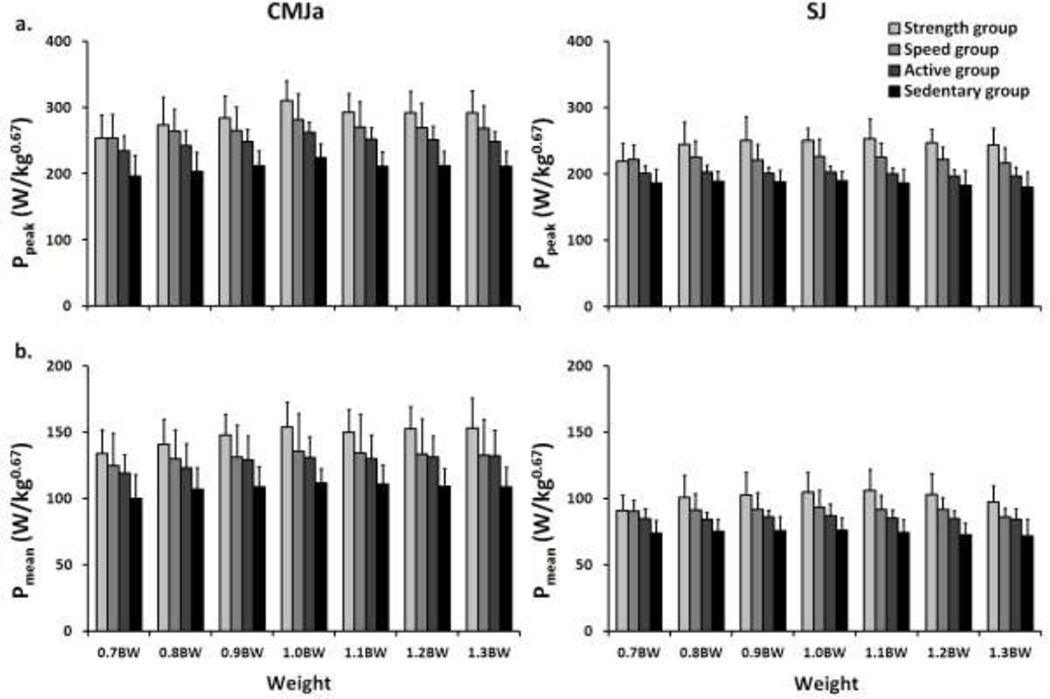
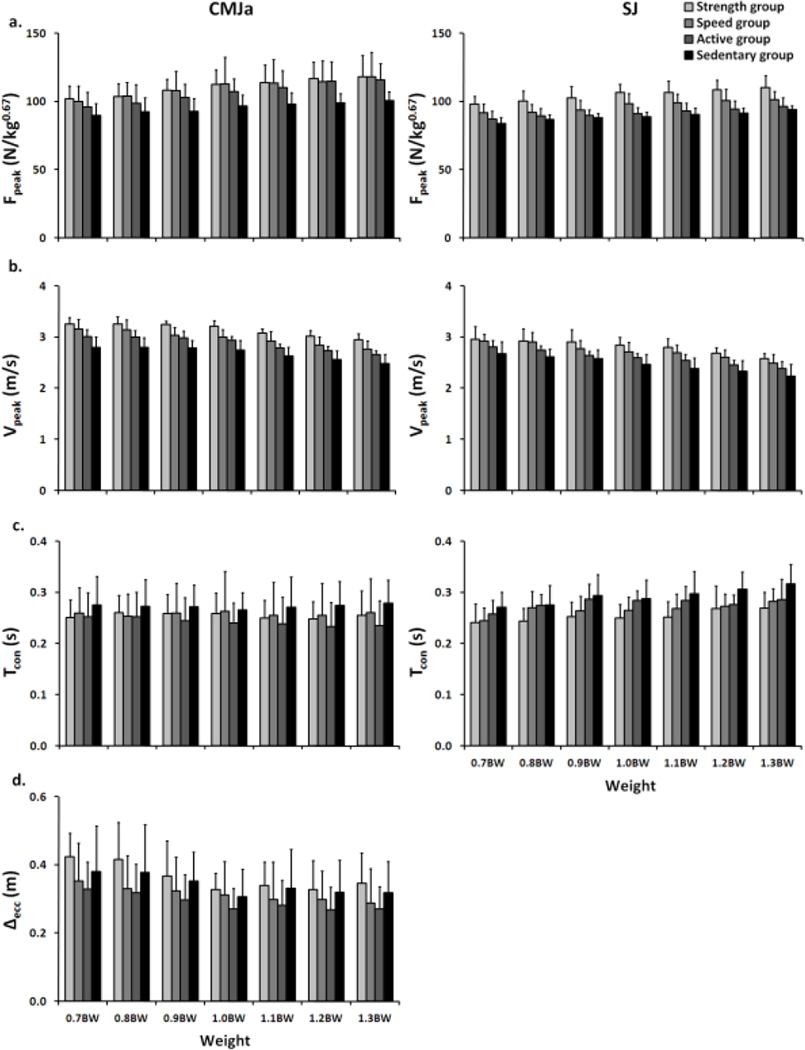
The following figures show the averaged across the subject values of the variables depicting the power output (Fig 3), as well as the corresponding kinematic and kinetic patterns (Fig 4) observed under the different loading conditions applied on four participant groups in both tested jumps. The main effects of ‘group’, ‘load’, and their interactions, as well as the corresponding post hoc tests of the main effects are presented separately for CMJa (Table 2) and SJ (Table 3).

Fig 3.

Performance and dynamic output of CMJa (left hand panels) and SJ (right hand panels) revealed as the peak power (P_peak; a) and mean power (P_mean; b) observed during the concentric phase under different loading conditions (data averaged across the groups with standard deviation error bars)

Fig 4.

Kinematic and kinetic patterns of CMJa (left hand panels) and SJ (right hand panels) revealed through the peak ground reaction force (F_peak; a), peak velocity (V_peak; b), duration of the concentric phase (T_con; c) and lowering of the center of mass during eccentric phase (Δh_ecc; d, for CMJa only) observed under different loading conditions (data averaged across the groups with standard deviation error bars)

Table 2.

Main effects of the 'group' and 'load', the post hoc tests, and the corresponding effect sizes for CMJa

Variable	ANOVAs	F	p	Effect size pη2	Effect size descriptor	Post hoc
	Group	13.94	0.000	0.53	Large	Sedentary < Active = Speed ≤ Strength
Ppeak	Load	38.89	0.000	0.51	Large	0.7 < 0.8 = 0.9 < 1.0 > 1.1 = 1.2 = 1.3
	Interaction	2.00	0.025	0.14	Medium
	Group	7.55	0.000	0.38	Large	Sedentary = Active ≤ Speed = Strength
Pmean	Load	23.14	0.000	0.39	Large	0.7 < 0.8 < 0.9 = 1.0 = 1.1 = 1.2 = 1.3
	Interaction	1.11	0.356	0.08	/
	Group	3.88	0.017	0.24	Large	Sedentary = Active ≤ Speed = Strength
Fpeak	Load	66.31	0.000	0.64	Large	0.7 = 0.8 < 0.9 < 1.0 = 1.1 < 1.2 = 1.3
	Interaction	1.36	0.201	0.10	/
	Group	24.25	0.000	0.66	Large	Sedentary < Active = Speed < Strength
Vpeak	Load	112.93	0.000	0.75	Large	0.7 = 0.8 ≥ 0.9 = 1.0 > 1.1 > 1.2 >1.3
	Interaction	0.86	0.859	0.07	/
	Group	0.77	0.518	0.06	/	Sedentary = Active = Speed = Strength
Tcon	Load	0.93	0.446	0.02	/	0.7 = 0.8 = 0.9 = 1.0 = 1.1 = 1.2 = 1.3
	Interaction	0.78	0.664	0.06	/
	Group	1.64	0.198	0.12	/	Sedentary = Active = Speed = Strength
Δhecc	Load	14.53	0.000	0.28	Large	0.7 = 0.8 ≥ 0.9 = 1.0 = 1.1 = 1.2 = 1.3
	Interaction	0.55	0.897	0.04	/

CMJa - counter movement jump with arm swing; P_peak – peak power; P_mean – mean power; F_peak – peak force; V_peak – peak velocity; T_con - duration of the concentric jump phase; Δh_ecc - maximum lowering of the center of mass during the eccentric jump phase.

< > - lower/higher; ≤ ≥ - equal with first and lower/higher than others; = equal. Statistically significant at the level p = 0.05.

Table 3.

Main effects of the 'group' and 'load', the post hoc tests, and the corresponding effect sizes for SJ

Variable	ANOVAs	F	P	Effect size pη2	Effect size descriptor	Post hoc
	Group	18.11	0.000	0.595	Large	Sedentary = Active ≤ Speed ≤ Strength
Ppeak	Load	5.83	0.000	0.136	Medium	0.7 = 0.8 = 0.9 ≤ 1.0 = 1.1 > 1.2 = 1.3
	Interaction	3.19	0.001	0.205	Large
	Group	15.59	0.000	0.558	Large	Sedentary < Active = Speed ≤ Strength
Pmean	Load	3.71	0.004	0.091	Medium	0.7 = 0.8 = 0.9 = 1.0 = 1.1 = 1.2 = 1.3
	Interaction	1.28	0.229	0.094	/
	Group	15.90	0.000	0.563	Large	Sedentary = Active ≤ Speed < Strength
Fpeak	Load	79.17	0.000	0.682	Large	0.7 = 0.8 ≤ 0.9 < 1.0 = 1.1 < 1.2 < 1.3
	Interaction	1.38	0.176	0.100	/
	Group	10.46	0.000	0.459	Large	Sedentary = Active ≤ Speed = Strength
Vpeak	Load	113.42	0.000	0.754	Large	0.7 = 0.8 ≥ 0.9 > 1.0 ≥ 1.1 > 1.2 >1.3
	Interaction	0.95	0.494	0.072	/
	Group	4.36	0.010	0.261	Large	Sedentary ≥ Active = Speed = Strength
Tcon	Load	12.99	0.000	0.260	Large	0.7 = 0.8 ≤ 0.9 = 1.0 = 1.1 = 1.2 ≤ 1.3
	Interaction	1.14	0.329	0.085	/

SJ - squat jump; P_peak – peak power; P_mean – mean power; F_peak – peak force; V_peak – peak velocity; T_con - duration of the concentric jump phase.

< > - lower/higher; ≤ ≥ - equal with first and lower/higher than others; = equal. Statistically significant at the level p = 0.05.

From the perspective of the tested hypotheses, of foremost importance are the data depicting the power output. The maxima of the peak power (P_peak) in individual groups of subjects were found at approximately 1.0 BW. Although most of the differences among the applied loads were below the significant level, the mean power (P_mean) was also higher at 1.0BW than either at 0.7BW or 1.3BW in both CMJa (133.1 W/kg^0.67 vs. 119.5 W/kg^0.67 and 131.6 W/kg^0.67, respectively) and SJ (90.5 W/kg^0.67 vs. 85.0 W/kg^0.67 and 85.1 W/kg^0.67, respectively). A significant albeit moderate 'group × load' interaction was observed only in P_peak. A visual inspection of the data suggests that the interaction could mainly originate from the relative advantage of the Strength over the Speed group under the heavier, but not lighter loads. However, the medians of the individual optimum loads revealing the maximum values of P_peak and P_mean in both jumps appeared to be close to 1.0BW in all 4 groups (Table 4). The Kruskal-Wallis test revealed no significant differences among the groups in both jumps.

Table 4.

Optimum load expressed as percentage of body weight (BW; medians of individual values for each group) that provides maximum power output.

Group	CMJa (Ppeak)	CMJa (Pmean)	SJ (Ppeak)	SJ (Pmean)
Sedentary	1.00	1.05	0.95	0.85
Active	1.00	1.00	1.00	1.00
Speed	1.00	1.05	1.00	1.05
Strength	1.00	1.10	1.05	1.00
Chi-Square X2	0.37	0.58	3.93	0.58
p - value	0.95	0.90	0.27	0.90

CMJa – countermovement jump with the arm swing; SJ- squat jump; P_peak – peak power; P_mean – mean power.

When viewed as the percentage of MDS, loads that maximized P_peak and P_mean during CMJa differed significantly among groups (F_{[3 ,36]} = 5.8–7.8, p < 0.003), with Strength group revealing the lowest, and Sedentary group revealing the highest optimum load (Table 5). Similar findings were also observed for SJ, although statistically significant group differences were observed for P_mean (F_{[3 ,36]} = 3.8, p = 0.02), but not for P_peak (F_{[3 ,36]} = 2.6, p = 0.07), respectively.

Table 5.

Load expressed as percentage of maximal dynamic strength (MDS; mean ± SD) that provides maximum power output.

Group	CMJa (Ppeak)	CMJa (Pmean)	SJ (Ppeak)	SJ (Pmean)
Sedentary	43.9 ± 7.1 a,b	45.6 ± 6.9 a,b	38.2 ± 6.4	40.8 ± 11.6 a
Active	40.3 ± 5.8 a	43.0 ± 8.8 a	38.9 ± 8.3	39.9 ± 9.0 a
Speed	35.8 ± 6.9	37.2 ± 6.3	33.6 ± 6.6	35.2 ± 6.4
Strength	31.7 ± 3.5	34.0 ± 4.9	32.0 ± 5.4	29.6 ± 4.7

CMJa – countermovement jump with the arm swing; SJ- squat jump; P_peak – peak power; P_mean – mean power.

^aSignificantly different from Strength group at level p < 0.05

^bSignificantly different from Speed group at level p < 0.05

Regarding the kinematic and kinetic variables (Figure 4), the data revealed expected 'group' and 'load' effects. For example, the Speed and particularly the Strength group individuals mainly showed higher peak forces (F_peak), peak velocities (V_peak ; suggesting even more prominent differences in jump height, see further text), and power outputs than the remaining two groups. Regarding the main effect of load, an increase in the applied load was associated with an increase in F_peak, and a decrease in both V_peak and the lowering of the center of mass (Δh_ecc). None of the tested variables revealed a group × load interaction.

Discussion

In the present study, we evaluated both the effects of external load and activity profiles on the maximum power output in two distinctive types of VJ. The data were mainly in line with our first (i.e., MDO) hypothesis suggesting that that the optimum external loading for maximizing power output would be close to the subject’s own BW (i.e., 1.0BW). However, despite marked differences in strength, power, and jumping performance among the tested groups, the data related to the hypothesized effect of the activity profiles remained inconclusive.

Prior to discussing the main findings, several important methodological aspects need to be stressed. While a loading associated decrease in the jumping performance as assessed by V_peak could be considered as a trivial finding, prominent across the groups differences in V_peak justify our selection of subjects of different activity profiles. However, of particular importance could be that the applied pulley system should have had several advantages over systems that were applied in previous studies (Argus et al. 2011; Nuzzo et al. 2010b; Markovic and Jaric 2007). First, study of Markovic and Jaric (2007) revealed that some subject could have had concerns regarding the insufficient height of the applied pulley system (i.e., for unloading conditions, the top of the pulley system was relatively close above head of the subject). Second, in a recent study Nuzzo and co-workers (2010b) unloaded body by a counter-mass hanging onto a cable-pulley system that reduced the weight, but inevitably also increased inertia, which likely confounded the observed outcomes (Leontijevic et al. 2012). Third, the application of the external load at the subject's shoulders, as performed by Argus et al. (2011), could affect the jumping mechanics (Kellis et al. 2005). Furthermore, the former study used short (i.e. ∼1.5–2m long) elastic bands for negative loading during VJ, while VJs with positive loading were performed on a Smith machine. As a result, (a) external force during unloaded VJ in unlikely to be relatively constant, and (b) Smith machine could have constrained the optimum jumping pattern during loaded VJ. Therefore, it is important to stress that the pulley system employed in the present study allowed for applying the external loading in the vicinity of the center of gravity, which enabled subjects to perform relatively unconstrained jumps. Note also that, in addition to the vertical jump performed from a fixed squat position (i.e., SJ), we also tested the 'natural' vertical jump that involved both the preceding counter-movement and the arm swing (i.e., CMJa). Taken together with the high reliability of the measured mechanical variables (Markovic and Jaric 2007) and appropriate familiarization applied regarding both the range of the loads and jumps tested, the above discussed issues collectively support our methodological approach to studying both the effect of load and activity profiles on the power output in VJ.

The first main finding of the study is the observed optimum loading close to the load originating from subject's own body (i.e., 1.0BW) that allows for maximization of the muscle power output in VJ. This finding is in line with the results of several studies that applied both positive and negative loading during either jump squat (Argus et al. 2011) or CMJ without arm swing (Nuzzo et al. 2010a; Markovic and Jaric 2007; Cavagna et al. 1972). Conversely, Vuk and co-workers (2012) observed the optimum loading somewhat below 1.0BW. However, their applied pulley system also added a light external mass during negative loading and, therefore, inertia, while even more important could be that the authors tested CMJ without arm swing. The later difference could also explain the loading-associated decrease in Δh_ecc that was much more prominent than the observed in the present study. Nevertheless, since this is the first study that, in addition to the individuals of different activity profiles, also evaluated two distinctive VJ, the observed loading effect on maximizing the muscle power output should be considered as the most robust support of the MDO hypothesis yet. Interestingly, while supporting the MDO hypothesis, our first main finding also supported a widely accepted view that the neuromuscular system generates maximum of power at loads ranging between 20% and 50% of its maximum force capacity. Indeed, average load that maximized peak and mean power output in both SJ and CMJa ranged between 30% do 46% of subjects’ maximal dynamic strength (i.e., MDS) was in line with the theoretical predictions and experimental results obtained in both single-joint movements (Kaneko et al. 1983) and complex ballistic tasks (Nuzzo et al. 2010b; Cormie et al. 2007a).

To interpret the results related to the second hypothesis, one first has to take into account the prominent differences among the tested groups in absolute and body mass-normalized squat strength, overall power output, and performance. We recently observed marked differences in the optimum load for maximizing the power output in the maximum cycling (i.e., the task that does not require overcoming the weight and inertia of one's own body) when testing the same groups of participants (Pazin et al. 2011). However, here we only observed a relatively weak group × load interaction in P_peak, but not P_mean, while no differences in the individual optimum loads appeared among the groups regarding P_peak or P_mean in both jumps. Therefore, most of the data do not support the second hypothesis, suggesting that the optimum load for maximizing the power output in both tested VJ could be close to one's own body independently of the individual training history and activity profiles. When viewed from the perspective of percentage of maximum dynamic squat strength, the load that maximizes the VJ power output differed significantly among groups. In fact, the optimum load for maximizing the VJ power output, as expressed as percentage of MDS, was inversely related to the maximum strength capacity of subjects among the tested groups (see Tables 1 and 5). This finding, also observed by Nuzzo et al. (2010b), is in contrast to experimental observations that training against heavy resistance shift the optimum load maximizing power peak towards heavy loads (Toji et al. 1997; Moss et al. 1997; Duchateau and Hainaut 1984).

The discussed finding that provide a robust support for MDO hypothesis could be interpreted in two different ways. Recent study of Samozino and co-workers (2012) strongly suggests a trade-off between the maximum velocity and maximum strength of lower limb neuromuscular system maximizing the power output when acting against body weight. Therefore, the athletic training associated improvements in physical abilities could result in an overall increase in both muscle strength, muscle power, and movement performance (as recorded in the present study) within a wide range of external loads, while the optimum load for maximizing the power output in VJ could still remain the subjects' own body. McBride et al. (1999) and Driss et al. (2001) also recorded minor differences in the load-power relationship in individuals with different activity profiles, although it should be noted that the negative loading was not applied. In another study, Nuzzo and co-workers (2010b) applied both positive and negative loading during VJ, and showed that significant differences in maximum leg strength between strength-power athletes and untrained individuals did not affect the load that maximized the VJ power output.

Alternatively, rather than as additional support to the MDO hypothesis, the lack of the marked effect of the activity profiles on the optimum load could be explained by three additional factors. First, note that we manipulated the external loading within an interval that corresponded to only about 40–55% of MDS of the tested participant. Therefore, it remains possible that the relatively narrow loading range did not provide sufficiently sensitive data that could discern among the optimum loads of the tested groups. Second, note that we explored the hypothesized effects on CMJa that allow for a wide range of adjustment of the kinematic and kinetic pattern to different movement conditions (Cavagna et al. 1972; Lees et al. 2004). The maximum lowering of the body (Δh_ecc) in CMJa could give us a clue since the visual inspection of the data in Figure 4 suggests that the Strength and Active group revealed the highest and lowest Δh_ecc, respectively, across the applied load range. However, those differences remained somewhat below the significant level probably due to an overall high variance of Δh_ecc. Third, the kinematic and kinetic pattern of the arm swing performed in CMJa could also play a role in the discussed adaptations (Lees et al. 2004). Conversely, one could argue that the discussed possibility of the adaptation of the CMJa movement pattern that preserves the optimum loading at approximately 1.0BW should be ruled out since similar results were also obtained from SJ. However, although the starting knee angle in SJ was fixed at 90°, the three available leg angles in a 2-D movement (such as in VJ) still allowed for different combinations of ankle and hip angles, not to mention possible adaptations in the upper body joints as well. Therefore, we believe that a comprehensive exploration of adaptation of VJ mechanical (and, perhaps, EMG) patterns to different loading conditions could explain not only the observed findings, but also reveal some fundamental neuromechanical mechanisms underlying the phenomena related to MDO hypothesis.

Regarding the possible practical implications of the present study, note that recent studies have suggested that the jump training performed with negative loading could be more effective in improving jumping performance than either the jump training with no loading or with positive loading (Markovic et al. 2011). However, there is also a convincing body of evidence that the training with spectrum of loads could be more efficient for improving jumping (Cormie et al. 2007a; Harris et al. 2000; Fatouros et al. 2000) and, possibly, other rapid movement performance (van den Tillaar 2004) than a training with any particular load. Therefore, the employed methodology could allow for applying both the negative and positive external loading that could improve the outcomes of future training procedures based on maximum vertical jumping and, possibly other maximum performance tasks.

Conclusions

The present study provided a robust set of results that support the MDO hypothesis. Specifically, despite marked differences in the maximum dynamic strength among the tested groups of subjects, two distinctive vertical jumps revealed the maximum power output when the subjects were loaded only with their own body. The underlying neuro-mechanical mechanisms certainly deserve further exploration, such as the adaptation of the associated kinematic and kinetic patterns to different loads (Cavagna et al. 1972; Lees et al. 2004), selective effects of weight and inertia (Leontijevic et al. 2012), or the long-term adaptation of the muscles' force-velocity properties (Samozino et al. 2012). Nevertheless, in addition to understanding some basic properties of the muscular system design, the present data could also motivate further development of standard athletic training and rehabilitation procedures aimed towards the improvement of both the power production and performance of various gross body movements.