Network link prediction by global silencing of indirect correlations

Abstract

Predicting physical and functional links between cellular components is a fundamental challenge of biology and network science. Yet, correlations, a ubiquitous input for biological link prediction, are affected by both direct and indirect effects, confounding our ability to identify true pairwise interactions. Here we exploit the fundamental properties of dynamical correlations in networks to develop a method to silence indirect effects. The method receives as input the observed correlations between node pairs and uses a matrix transformation to turn the correlation matrix into a highly discriminative silenced matrix, which enhances only the terms associated with direct causal links. Achieving perfect accuracy in model systems, we test the method against empirical data collected for the Escherichia coli regulatory interaction network, showing that it improves on the best preforming link prediction methods. Overall the silencing methodology helps translate the abundant correlation data into valuable local information, with applications ranging from link prediction to inferring the dynamical mechanisms governing biological networks.

The currently incomplete maps of molecular interactions between cellular components limit our understanding of the molecular mechanisms behind human disease^1-6. Ultimately, high-throughput mapping projects^7-10 are expected to provide the accurate maps of interactomes necessary to systematically unlock disease mechanisms. Yet, as a complete interaction map is at least a decade away, we need to develop tools that allow us to infer the structure of cellular networks from empirically obtained biological data^11,12. Many current tools designed to infer functional and physical interactions in the cell rely on the global response matrix,

$$G_{ij}=\frac{d{x}_i}{d{x}_j},$$ (1)

which captures the change in node i's activity in response to changes in node j's¹³. This matrix can be measured directly from gene knockout or overexpression experiments, or inferred indirectly using related measures such as Pearson or Spearman correlations¹⁴, mutual information^15,16 or Granger causality¹⁷. Traditional methods for predicting links^15,16,18,19 assume that the magnitude of G_ij correlates with the likelihood of a direct functional or physical link between nodes i and j. Yet G_ij cannot distinguish between direct and indirect relationships: a path i → k → j can result in a significant response measured between i and j, falsely suggesting the existence of a direct link between them (Fig. 1a-b).

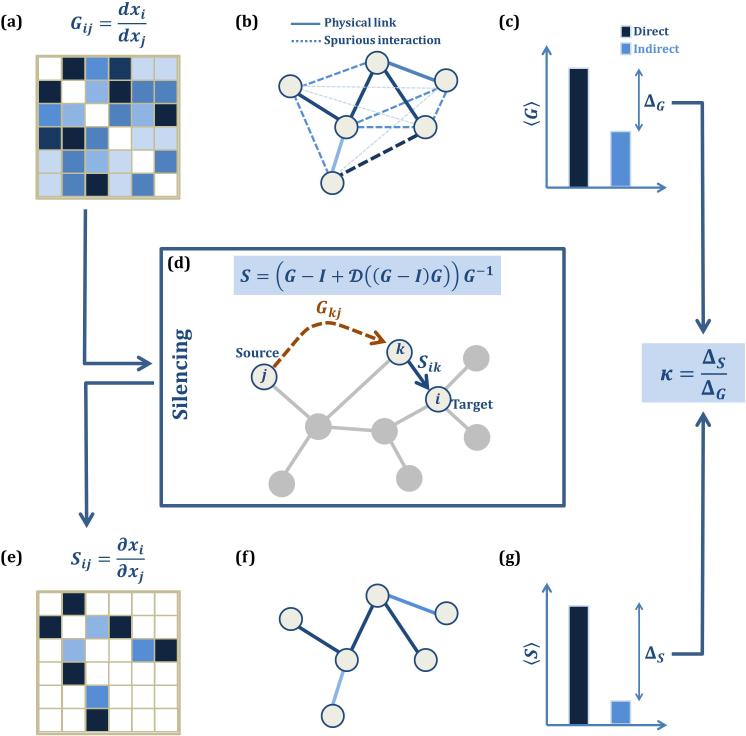
Figure 1. Silencing indirect links.

(a) The experimentally observed global response matrix, G_ij, accounts for direct as well as indirect correlations, with no clear separation between them. The source of G_ij could be gene coexpression data, statistical correlations or genetic perturbation experiments. (b) In the absence of a clear separation in G_ij assigned to direct and indirect correlations, our ability to infer direct physical links (solid lines) is limited. Simple thresholding, i.e. accepting all links for which G_ij exceeds a predefined threshold, is known to predict spurious links (strong dashed lines) and overlook true links (light solid lines). (c) While the average G_ij terms associated with direct links (dark blue) are higher than the average terms associated with indirect links (light blue), as captured by the discrimination ratio, Δ_G, the difference is not sufficient to identify direct and indirect links. (d) Silencing is achieved through Eq. (5), which exploits the flow of information in the network: the flow from the source (j) to the target (i) is carried through the indirect effect G_kj (orange) coupled with the direct impact S_ik of the target's nearest neighbor κ (blue). By silencing the indirect contributions, Eq. (5) provides the local response matrix, S_ij , whose non-zero elements correspond to direct links. (e) – (f) In S_ij the terms associated with indirect links are silenced, allowing us the detect only the direct links of the underlying network. (g) As indirect terms become much smaller in S_ij, we obtain a greater discrimination ratio, Δ_S. The degree of silencing, κ, captures the increase observed in the discrimination ratio by the transition from G_ij to S_ij (5).

Several methods correcting for such effects have been proposed: information theoretic approaches evaluate the association between nodes by measuring the entropy of their mutual activities, where a low entropy indicates a statistical dependence between the node activities^16,18,20; probabilistic models, such as the graphical Gaussian model, allow one to evaluate the correlation between i and j, while controlling for the state of node k, and thereby provide a more indicative measure of direct linkage^21-25; other models rely on assumptions pertaining to the network topology, such as the tendency of real networks to exhibit strong degree correlations²⁶. The ultimate solution, however, should enable us to fully unwind the direct from the indirect effects, providing a measure which distinctly indicates the existence of direct links. Consequently, here we focus on the local response matrix

$$S_{ij}=\frac{\partial x_i}{\partial x_j},$$ (2)

in which the contribution of indirect effects is eliminated. In contrast with (1), which allows for global changes in i and j's environment, here the “∂” indicates that S_ij is defined to capture only local effects, namely the response of i to changes in j when all surrounding nodes except i and j remain unchanged. Hence S_ij > 0 implies a direct link between i and j.

Here we derive a method for calculating the local response matrix (2) from experimentally accessible correlation measures, allowing us to mathematically discriminate direct from indirect links. We show that the resulting S_ij matrix, in which the contribution of indirect paths is silenced, is more discriminative than the empirically obtained G_ij matrix, enhancing our ability to extract direct links from experimentally collected correlation data.

Results

The silencing method

To extract S_ij from the experimentally accessible G_ij, we formally link (1) and (2) via

$$\{\begin{array}{cc}\frac{d{x}_i}{d{x}_i}=1\hfill & \hfill \\ \frac{d{x}_i}{d{x}_j}=\sum _{k=1}^N\frac{\partial x_i}{\partial x_k}\frac{d{x}_k}{d{x}_j}\hfill & i\ne j\hfill \end{array}\phantom{\}}.$$ (3)

Equation (3) is exact and the sum accounts for all network paths connecting i and j (Supplementary Note S.I.1 - 2). It is of limited use, however, as it requires us to solve N² coupled algebraic equations. In Supplementary Note S.I.1 we show that (3) can be reformulated as

$$S=(G-I+\mathcal{D}(S\cdot G))G^{-1},$$ (4)

where I is the identity matrix and $\mathcal{D}\left(M\right)$ sets the off-diagonal terms of M to zero. To obtain an approximate solution for S we use that fact that typically, perturbations decay rapidly as they propagate through the network, so that the response observed between two nodes is dominated by the shortest path between them. This allows us to approximate $\mathcal{D}(S\cdot G)$ with $\mathcal{D}\left((G-I)G\right)$ (Supplementary Note S.I.3), obtaining

$$S=(G-I+\mathcal{D}\left((G-I)G\right))G^{-1}.$$ (5)

Equation (5), our main result, provides S_ij from the experimentally accessible G_ij. It achieves this through a 'silencing effect’, in which direct response terms are preserved, while indirect responses are silenced. To understand this consider a specific term in G_ij, documenting the response of node i to j's perturbation. As indicated by Eq. (3), this response is a consequence of all direct and indirect paths leading from j to i. As we document below, the transformation (5) detects the indirect paths and silences them, maintaining only the contribution of the direct paths (Fig. 1d-f).

Silencing in model systems

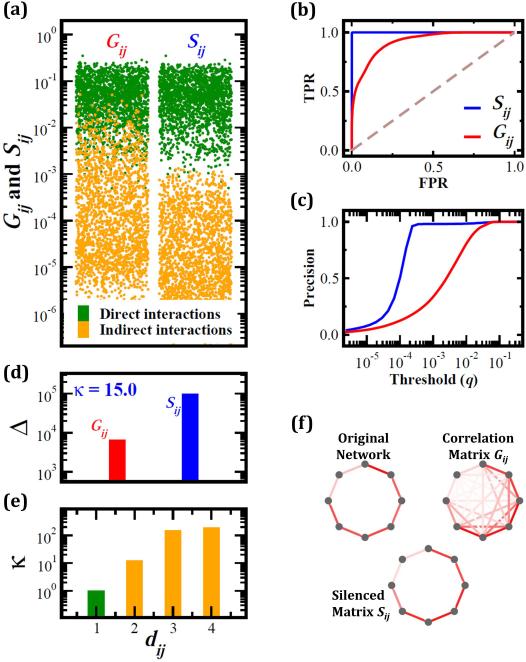
To demonstrate the predictive power of (5), we implemented Michaelis-Menten dynamics on a model network (Supplementary Note S.III), as commonly used to model generegulation^27,28. We obtained G_ij by perturbing the activity of each node and then calculated S_ij using (5). Figure 2a shows the G_ij and S_ij terms associated with interacting (green) and non-interacting (orange) node pairs. Although G_ij is higher for direct interactions, the overlap between the orange and the green symbols indicates a lack of a clear threshold q that separates direct and indirect interactions. In contrast, S_ij displays a clear separation between direct and indirect interactions, accurately predicting each direct link. Indeed, the ROC curve derived from G_ij (Fig. 2b, red) has an area of AUROC = 0.91, reflecting inherent limitations in separating direct from indirect interactions based on G_ij only. In contrast for S_ij we obtain AUROC = 0.997 (blue), where the true positive rate (TPR) reaches 100% with a false positive rate (FPR) of less than 10^–3. Also, although for G_ij precision increases gradually with the threshold q (Fig. 2c), for S_ij precision jumps to one for q > 10^–4. Hence, in our well controlled model system effectively any non-zero S_ij corresponds to a direct link.

Figure 2. Network inference in model systems.

We numerically simulated Michaelis-Menten dynamics on a scale-free network [40-42], extracting the correlations G_ij between all pairs of nodes (see Sec. S.III for details). (a) G_ij and S_ij associated with interacting (green) and non-interacting (orange) node pairs. S_ij silences the correlations associated with indirect interactions, resulting in a clear separation between direct and indirect interactions, a phenomenon absent from G_ij. (b) ROC curve obtained from G_ij (red, area 0.91) and S_ij (blue, area 0.997). The S_ij network reaches 100% accuracy with a negligible amount of false positives. (c) Precision obtained for threshold q for G_ij (red) and S_ij (blue). The gradual rise of the G_ij-based precision indicates that for a broad range of thresholds only a small fraction of the links will be identified. In contrast, the steep rise in precision for S_ij indicates its enhanced discriminative power between direct and indirect links: virtually any non-zero S_ij corresponds to a directly interacting pair. (d) The discrimination ratio, Δ, is much higher in S_ij (blue) compared to G_ij (red). This indicates that S_ij is a much better predictor of direct vs. indirect interactions. The silencing (5), which captures the increase in the discrimination ratio is κ = 15.0. (e) Silencing increases with the path length d_ij between i and j, so that the more indirect is the link the more dramatic is the silencing. (f) The source of S_ij's success is the silencing effect, here illustrated on correlations measured for a linear cascade. The reconstruction of the cascade from G_ij is confounded by numerous non-vanishing indirect correlations. In S_ij the indirect correlations are silenced, providing a perfect reconstruction.

The performance of (5) is due to the silencing effect: it leaves G_ij unchanged if i and j are linked, while it systematically lowers all G_ij not rooted in a direct interaction. To quantify this effect we measured the discrimination ratio Δ_G = 〈G_ij〉_Dir/〈G_ij〉_Indir (Δ_S = 〈S_ij〉_Dir/〈S_ij〉_Indir) which captures the ratio between G_ij (S_ij) terms associated with direct links and those associated with indirect links (Fig. 1c and g). We find that S_ij is much more discriminative than G_ij owing to its silencing of indirect responses. To quantify this effect we measure the silencing

$$\kappa =\frac{{\Delta }_S}{{\Delta }_G},$$ (6)

which captures the increased power of S_ij to discriminate between direct and indirect links compared to G_ij. In our model system we find that κ = 15, a silencing of more than an order of magnitude (Fig. 2d). Furthermore, the longer is the distance d_ij between two nodes, the larger is the silencing (Fig. 2e). As an illustration, consider a linear cascade in which changes in any node result in a finite response G_ij by all other nodes (Fig. 2f). Equation (5) silences all indirect responses, while leaving the response of direct links effectively unchanged, offering a discriminative measure that enables a perfect reconstruction of the original network.

Predicting molecular interactions in E. coli

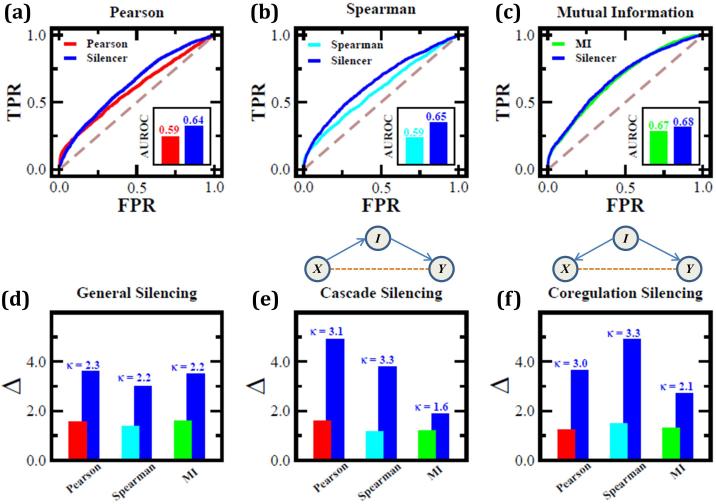
To test the predictive power of (5) on real data we used the E. coli datasets distributed by the DREAM5 network inference challenge¹⁹. The input data include a compendium of microarray experiments measuring the expression levels of 4,511 E. coli genes (141 of which are known transcription factors) under 805 different experimental conditions (Supplementary Note S.IV.1). We constructed three separate global response matrices G_ij between the 141 transcription factors and their 4,511 potential target genes, based on (i) Pearson correlations; (ii) Spearman rank correlations; and (iii) mutual information, which are three commonly used methods for link detection (Supplementary Note S.IV.3). From each of the three G_ij matrices we obtained S_ij via (5), and compared the performance of G_ij with the pertinent S_ij. To validate our predictions we relied on the gold standard used in the DREAM5 challenge, consisting of 2,066 established gene regulatory interactions. Measuring AUROC from G_ij and S_ij, we find an improvement of 56% for Pearson correlations (Fig. 3a), 67% for Spearman rank correlations (Fig. 3b) and a smaller improvement of 6% for mutual information (Fig. 3c), e.g. allowing us to improve upon the top performing inference methods¹⁹.

Figure 3. Inferring regulatory interactions in E. coli.

(a) Starting from gene expression data, we used Pearson correlations in expression patterns to construct G_ij for 4,511 E. coli genes, obtaining S_ij via (4). We compared our predictions to a gold standard of experimentally verified genetic regulatory links [19]. The area under the ROC curve (AUROC) is increased from 0.59 to 0.64 in the transition from G_ij to S_ij, representing a 56% improvement (above the baseline of 0.5 for a random guess). (b) An improvement of 67% is observed for Spearman rank correlations. (c) A less dramatic improvement of 6% is shown when G_ij is constructed using mutual information. (d) The discrimination ratio for all three methods compared with that obtained from the pertinent S_ij matrix. The transition to S_ij (4) increases the discrimination between direct and indirect interactions by a factor of two or more, so that indirect interactions have a significantly lower expression in S_ij. (e) - (f) This observation becomes even more dramatic when focusing on two specific motifs: cascades and co-regulators. In G_ij the indirect correlation between X and Y, which is induced by the intermediate node, I, may lead to the false prediction of the spurious X – Y link. Thanks to silencing, the discrimination between the direct and indirect links in these motifs is increased by a factor of three or more for Pearson and Spearman correlations, and by a factor of about two for mutual information.

We further tested the discrimination ratio, Δ, and the silencing, κ, for each of these methods, finding that indirect correlations are subject to an average of two-fold silencing in the transition from G_ij to S_ij (Fig. 3d). Silencing is especially crucial in the presence of the cascade and co-regulation motifs shown in Figures 3e-f, where most inference methods indicate a spurious link between X and Y owing to the indirect correlation mediated by node I. Indeed, the transformation (5) silences these indirect correlations by a factor of three or more for Pearson and Spearman correlations and by a smaller factor for mutual information, overcoming one of the most common hurdles of inference methods, which tend to over-represent triadic motifs¹⁹.

The effects of noise and uncertainty

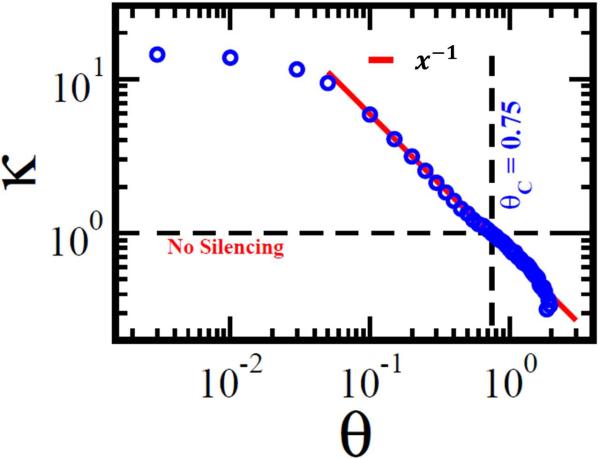
As all experimental data is subject to noise, the global response matrix, G_ij, is characterized by some degree of uncertainty. To test the performance of our methodology in the presence of noise, we repeated the numerical experiment of Figure 2, this time adding Gaussian noise to G_ij, which allows us to calculate silencing as a function of increasing the signal to noise ratio θ (Fig. 4). As expected, silencing is unaffected by small values of θ, so that κ features a plateau below θ ≲ 0.1. For large θ, silencing decays as κ ~ θ^–1, demonstrating that the performance of the method decreases slowly with increasing the signal to noise ratio. Indeed, as opposed to a rapid exponential decay, the observed slower power-law dependence indicates that the method is rather tolerant against noise. Silencing is lost only when the noise reaches the critical level θ_C ≈ 0.75, when the signal is almost completely overridden by noise, leading to κ = 1 (Supplementary Note S.V.1).

Figure 4. Silencing in a noisy environment.

To test the method's performance in the presence of a noisy input we added Gaussian noise to the numerically obtained G_ij, and measured the silencing, κ, vs. the signal to noise ratio θ. For low noise levels (θ ≲ 0.1) silencing is relatively unharmed. At higher noise level silencing decreases as κ ~ θ^–1, a slow decay that supports the robustness of the method. Silencing is lost at θ_C ≈ 0.75, when the signal is almost fully driven by the noise.

Hidden nodes offer another source of uncertainty. They represent the fact that in most cases we are unable to read the states of all nodes in the system²⁹. To illustrate the effect of the hidden nodes on the performance of the silencing method, we consider the case of a simple cascade i → k → j, where the intermediate node k is hidden. In this scenario, Eq. (5) will not be able to silence the indirect i → j link because in the observable system the G_ij term cannot be attributed to any indirect path. Hence, absent any other information about the system, it is mathematically impossible to infer the indirectness of G_ij, as the removal of k isolated i from j³⁰. This touches upon the fundamental mechanism of silencing: as illustrated in Figure 1 (and Supplementary Note S.I.2) the silencing transformation (5) exploits the flow of information through indirect paths. Consequently, if as a result of hidden nodes the network fragments into several components such that the node pair i and j become isolated from each other, then all indirect paths between them became hidden and the pertinent G_ij term will not be silenced (Fig. 5a–b). Hence silencing is expected to fail only when the network breaks into many isolated components so that most node pairs become isolated. Fortunately, a fundamental property of complex networks is that with average degree 〈k〉 >> 1, one needs to remove a large fraction of the nodes to fragment the underlying giant connected component^31-34. Therefore we can build on percolation theory, which allows us to analytically predict how the size of the largest connected component changes with the random removal of a certain fraction of nodes^35,36. The calculation shows that silencing is maintained as long as the fraction of hidden nodes is smaller than

$${\eta }_{\mathrm{C}}\approx 1-\frac{\Omega }{\langle k\rangle },$$ (7)

where $\Omega =\sqrt{2}\ln (\sqrt{2}+2)\approx 1.7$ (Supplementary Note S.V.2). This equation indicates that for large 〈k〉 the method will be reliable even if a large fraction of the nodes are hidden.

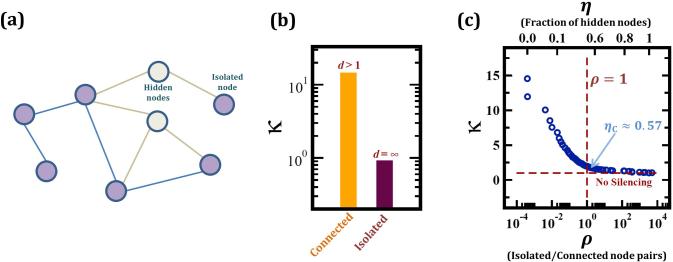
Figure 5. Performance with hidden nodes.

(a) A network with N = 8 nodes of which a fraction η = 1/4 are hidden. The observable sub-network has six nodes, five forming a connected component (with 10 connected node pairs) and one isolated (6 isolated pairs). The ratio between isolated and connected node pairs here is ρ = 6/10. Equation (5), applied to the observable network, successfully silences the indirect G_ij terms among the nodes of the connected component. However the correlations between the isolated node and the rest of the network, lacking an indirect path, are not silenced. (b) To test the silencing in the presence of hidden nodes we used the numerically obtained G_ij (Fig. 2) from which we eliminated a fraction η of the nodes, obtaining an observable network with 10⁴ isolated node pairs (ρ ≈ 10³). After applying Eq. (5) to the remaining nodes we find that the silencing of G_ij terms associated with connected node pairs is unaffected (orange bar), while for the isolated node pairs silencing drops to κ = 1, namely no silencing (purple bar). Hence for the isolated node pairs S_ij is not more predictive than G_ij. (c) Increasing the fraction of hidden nodes, η (top horizontal axis), we measured κ vs. ρ. As expected, silencing is observed as long as most node pairs are connected via finite paths (ρ < 1). However, when the number of hidden nodes is increased to the point that the isolated pairs dominate (ρ > 1), silencing is no longer observed (κ = 1). The critical fraction of hidden nodes, η_C, corresponds to ρ = 1, the point where silencing no longer plays a significant role. Here we find η_C ≈ 0.57 (blue arrow), in agreement with the prediction of Eq. (7).

To test this prediction, we revisited the numerically obtained G_ij analyzed in Figure 2 and measured the degree of silencing after randomly removing an increasing fraction of nodes. In each case we also measured the ratio between isolated and connected node pairs (ρ). We find that, as predicted, the degree of silencing is driven mainly by ρ, approaching κ ≈ 1 (no silencing) when ρ ≥ 1, namely when the isolated pairs begin to dominate the network (Fig. 5c). Here as 〈k〉 = 4, Eq. (7) predicts η_C ≈ 0.57, i.e. the method will fail only when almost 60% of the nodes are hidden. Note that for biological networks 〈k〉 is expected to be in the range of³⁷ 〈k〉 ≲ 10, predicting η_C ≲ 0.8. Namely, one needs to lose access to 80% of the nodes for silencing to lose its effectiveness.

Discussion

With computational complexity $\mathcal{O}\left(N^3\right)$, Eq. (5) is scalable and requires no assumptions about the network topology. By silencing indirect effects, it turns the raw correlation data into a predictive S_ij matrix, dominated by direct interactions. It is especially suited to treat perturbation data, such as genetic perturbation experiments, in which case G_ij describes the response of all genes (dx_i) as a consequence of the perturbation of the source gene (dx_j)³⁸. In practice, however, G_ij could be the result of a broader set of experimental realizations where other measures are used to evaluate the association between nodes, typically statistical measures such as Pearson or Spearman correlation coefficients. Still, our empirical results (Fig. 3) clearly show that the transformation (5) successfully applies to these empirically accessible measures as well. Hence silencing is largely insensitive to the specific process by which G_ij was constructed.

The method's broad applicability is rooted in the fact that it does not depend on the value of each specific term in G_ij, but rather on the global relationships between them. Indeed, the global structure of G_ij reflects the patterns of propagation of the perturbations along the network. Equation (5) helps uncover these paths from the raw data, disentangling the direct from the indirect effects. These patterns of information flow are inherent to the underlying network structure, and should not depend on the specific experimental realization of (1). For instance, a cascade i → j → k will be characterized by a decreasing correlation propagating along the arrows, a large correlation between i and j and a weaker one between i and k. Although the magnitude of these correlations might depend on the size or the form of i's perturbation as well as on the statistical measure we used to evaluate them, the decay pattern required to infer the structure of the cascade is an inherent property of the network flow and can be successfully detected by the silencing method (Supplementary Note S.I.4).

The silencing transformation is derived from fundamental mathematical principles of dynamical correlations in networks. Hence it is expected to apply under rather general conditions. However, as Equation (5) indicates it requires that the input matrix, G_ij, is invertible. This imposes some limitations when constructed from statistical correlation measures. For instance in the empirical results of Figure 3a we constructed G_ij from Pearson correlations, using the states of 4,511 nodes measured under 805 experimental conditions. In general, if the number of experimental conditions is smaller than the number of nodes the resulting Pearson correlation matrix may be singular. In this case additional processing will be required before (5) could be applied. Here, following the DREAM5 protocol, we only focused on the correlations between the 141 known transcription factors and the rest of the nodes, which lead to an invertible G_ij (Supplementary Note S.IV). Other means to ensure G_ij's invertibility are discussed in Supplementary Note S.IV.4.

Isolating indirect effects in correlation data, a fundamental challenge of network inference, is typically approached through local probabilistic tools^12,14-18. In contrast, the success of the silencing method is rooted in its exploitation the global network topology³⁹: it relies on the fundamental principles of network structure and dynamics to identify and silence the effects of indirect paths. The ability to extract S_ij from G_ij could also have implications for our understanding of network dynamics. Indeed, G_ij is a global network measure, as its magnitude is determined by the numerous indirect paths connecting i and j. Hence, for a given dynamics, the G_ij matrix will take a different form depending on the network topology, making it a poor predictor of the system's dynamics. By eliminating indirect effects, S_ij measures the effect gene i would have on gene j had they been isolated from the rest of the network. It thus helps us quantify the dynamical mechanism that governs individual pairwise interactions, avoiding the convolution of dynamical and topological effects present in experimental data. For instance, consider a set of perturbation experiments providing G_ij. The structure of G_ij reflects the microscopic mechanisms that govern the pairwise interactions, e.g. genetic regulation and biochemical processes. It is difficult, however to extract this information from G_ij since its terms are a convolution of many interactions, reflecting the many paths leading from i to j. The transition to S_ij , via (5), allows us to treat each isolated interaction on its own, providing a direct observation into the microscopic interaction mechanism. Direct application of this fact could be the derivation of a rate equation that governs the system's dynamics from G_ij, as well as predicting the universality class and the scaling laws governing the system's response to perturbations. Hence (5) helps translate the ever-growing amount of data on global correlations into valuable local information.