A crossed random effects modeling approach for estimating diagnostic accuracy from ordinal ratings without a gold standard

Abstract

In diagnostic studies without a gold standard, the assumption on the dependence structure of the multiple tests or raters plays an important role in model performance. In case of binary disease status, both conditional independence and crossed random effects structure have been proposed and their performance investigated. Less attention has been paid to the situation where the true disease status is ordinal, with the exception of Wang et al [1] who assumed conditionally independent multiple tests when studying traditional Chinese medicine and Wang and Zhou [2] who assumed a normal subject random effect but a fixed rater effect. In this paper, we propose crossed subject- and rater-specific random effects to account for the dependence structure and assess the robustness of the proposed model to misspecification in the random effects distributions. The models are applied to data from the Physician Reliability Study which focuses on assessing the diagnostic accuracy in a population of raters for the staging of endometriosis, a gynecological disorder in women. Using this new methodology, we estimate the probability of a correct classification and show that regional experts can more easily classify the intermediate stage than resident physicians.

1. Introduction

In public health and medical research, it is of importance to study the diagnostic accuracy of new tests or raters (e.g., [3, 4]). This is usually done by comparing the diagnostic results from the tests or raters with the true disease status (i.e., the gold standard). In many cases, however, a gold standard may not be measured due to cost constraints, concerns of the invasive nature of the diagnostic procedure, or a lack of biotechnology to obtain a definitive result. There has been extensive literature on estimating diagnostic accuracy without a gold standard, with the latent class approach (LCA) widely being used (e.g., [4, 5, 6]).

It is usually assumed in LCA that the multiple tests or raters are independent conditional on the true disease status. However, the conditional independence assumption may not be valid in practice and models with such an assumption may not fit the data well. Alternatively, Qu et al [7] developed a LCA by including normally distributed subject-specific random effects to model conditional dependence among binary tests. Albert and Dodd [8] demonstrated that, when the unknown disease status is binary, the model is weakly identified in the random effects distribution in the sense that different random effects distributions may fit the data equally well.

LCA can also be utilized when the true outcome of interest is ordinal rather than binary. Wang et al [1] extended the work of Zhou et al [6] on binary outcome to ordered multiple symptom categories and applied it to data from traditional Chinese medicine. In a further extension, Wang and Zhou [2] incorporated normal subject-specific random effects while assuming fixed effects for the raters. In this paper, we are interested in relaxing the conditional independence assumptionin Wang and Zhou [1] by proposing crossed subject- and rater-specific random effects to account for the dependence structure in the data. We are interested in assessing the robustness of the proposed models to misspecifications in the Gaussian random effects by considering a mixture of normals for both subject- and rater-specific random effects.

This article is motivated by the Physician Reliability Study (PRS) [9] that investigated the reliability of endometriosis between different physicians and settings. In the PRS, 12 physicians in obstetric and gynecology (OB/GYN) separately reviewed participant clinical information (digital intra-uterus image taken during laparoscopy, surgeon notes, MRI and histopathology reports) and assessed the endometriosis staging. Each physician conducted the review in a sequence of four settings, with each successive setting having an additional piece of clinical information to the reviewing physicians. In this article, we evaluate the diagnostic accuracy of 8 physicians (4 regional experts and 4 residents) who are practicing at the same medical center (Utah) when each of them reviewed the digital images (setting 1). Our interest here is evaluating the diagnostic accuracy in the population of these physicians; hence we treat physicians as a random rather than a fixed effect.

Endometriosis is a gynecological disorder in women that occurs when cells from the lining of the uterus grow in other area of the uterus. The cause of endometriosis is unknown and the accurate staging of the disease is subject to substantial errors. In this article, we focus on the 5 stagings of endometriosis: no endometriosis, stage I (minimal), stage II (mild), stage III (moderate) and stage IV (severe). In PRS, 79 subjects have complete staging results from the 8 physicians of interest and constitute the study sample. Among the 632(= 79 × 8) reviews, 155(25%) are no endometriosis while 250(40%), 136(21%), 63(10%) and 28(4%) are stages I to IV, respectively. Table 1 presents the averaged conditional sample proportions of endometriosis staging by one physician given the staging by another that are based on 10000 bootstrapped samples (drawn with replacement from the original data set) of the diagnostic results of two arbitrary physicians. As an indication of agreement, the kappa statistics is estimated to be 0.379.

Table 1.

Average conditional sample proportions of the endometriosis staging rated by one physician given the staging by another physician in the PRS data. Based on 10000 bootstrapped samples of the diagnostic results of arbitrary two physicians on all 79 subjects.

		Physician 2
		No endo	Stage I	Stage II	Stage III	Stage IV
Physician 1	No ENDO	0.686	0.180	0.076	0.080	0.061
	Stage I	0.225	0.570	0.400	0.144	0.062
	Stage II	0.049	0.202	0.371	0.237	0.102
	Stage III	0.028	0.039	0.126	0.371	0.326
	Stage IV	0.011	0.009	0.027	0.168	0.449

More specific substantive questions include (1) do the physicians have worse diagnostic accuracy at higher stages (moderate and severe) than at lower stages (no disease and minimal)? (2) are the extreme stages (no disease, minimal and severe) easier to diagnose than the middle stages (mild and moderate)? (3) how accurate are the physicians at correctly staging endometriosis? Off by only 1 stage? Off by 2 stages? (4) do the two groups of physicians (regional experts and residents) have different misclassification matrices in diagnosing endometriosis? From a statistical methodological perspective, we are interested in evaluating the robustness of our proposed crossed random effects model with respect to misspecification to the random effects distributions.

The remainder of this article is organized as follow. In Section 2, we propose a latent class model with crossed random effects for estimating the diagnostic accuracy of ordinal tests for ordinal true disease status. In Section 3, we present a Monte-Carlo EM algorithm for parameter estimation. In Section 4, we perform simulation studies to assess the convergence of the maximum likelihood estimators (MLE) obtained from a Monte-Carlo EM algorithm and assess the operating characteristics of the procedure. In Section 5, we apply the proposed model to data from the PRS in the staging of endometriosis. Conclusions and discussions are provided in Section 6.

2. Methods

Let Y_ij denote the ordinal diagnostic test result of the stages of endometriosis (Y_ij = 0, …, K) for the ith subject by the jth rater (i.e. physician), i = 1, …, I and j = 1, …, J. In the PRS, there are four stages of endometriosis and we have 79 subjects who had complete diagnoses from four regional experts and four residents; thus K = 4, I = 79 and J = 8. We denote D_i as the true disease status of the ith subject, where for each subject D_i = 0 denotes absence of endometriosis and D_i = 1, 2, 3 and 4 denote the four stages of endometriosis respectively. Investigators are interested in estimating the average accuracy across physician group rather than physician-specific accuracy. We parameterize the cumulative probability by the following model with two crossed random effects ({b_i}, {c_j}) and p covariates:

$$P(Y_{ij}\le k\mid d_i,b_i,c_j,X_i^j)\equiv \Phi ({\gamma }_{d_i,k}+{\sigma }_{d_i}{b}_i+{\tau }_{d_i}{c}_j+X_i^j{\beta }_{d_i}),$$ (1)

where ${\left\{b_i\right\}}_{i=1}^I$ are subject-specific random effects with scale parameters $\sigma \equiv {\left\{{\sigma }_{d_i}\right\}}_{d_i=0}^D,{\left\{c_j\right\}}_{j=1}^J$ are rater-specific random effects with scale parameters $\tau \equiv {\left\{{\tau }_{d_i}\right\}}_{d_i=0}^D,-\infty ={\gamma }_{d_i-1}\le {\gamma }_{d_i,0}\le \cdots \le {\gamma }_{d_i},K-1\le {\gamma }_{d_i},K=\infty$ are monotonically nondecreasing cut-points for disease status d_i, $X_i^j$ is the ith row of the I × p matrix X^j, which is the design matrix of the jth rater, and β_di is the d_i-th column of β_{p × D}, the matrix of coefficients for the covariates. Let

$$\gamma =\left[\begin{array}{cccc}\hfill -\infty \hfill & \hfill -\infty \hfill & \hfill -\infty \hfill & \hfill -\infty \hfill \\ \hfill {\gamma }_{0,0}\hfill & \hfill {\gamma }_{1,0}\hfill & \hfill \cdots \hfill & \hfill {\gamma }_{D,0}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\gamma }_{0,K-1}\hfill & \hfill {\gamma }_{1,K-1}\hfill & \hfill \cdots \hfill & \hfill {\gamma }_{D,K-1}\hfill \\ \hfill \infty \hfill & \hfill \infty \hfill & \hfill \infty \hfill & \hfill \infty \hfill \end{array}\right],$$

be a matrix of cut-off points with rows corresponding to the rating and columns corresponding to the true unknown category.

The model specifications above differ from that in Wang and Zhou [2] in that the rater-specific effect is assumed to be random in addition to the subject-specific effect. This is important since in PRS the physicians were chosen from a population of OBGYNs and it is of interest to obtain the average estimate across the population. The random effects ${\left\{b_i\right\}}_{i=1}^I$ and ${\left\{c_j\right\}}_{j=1}^J$ can each be assumed to follow a standard normal distribution. In addition, to allow for a more flexible random effects structure, we can also consider mixture of normals (MixNs). Define G_b and G_c to be random variables from a Bernoulli distribution with success probabilities λ_b and λ_c respectively, then

$$\begin{array}{cc}\hfill g_b(b\mid G_b)=& I(G_b=1)\varphi (b,{\mu }_{1b},{\nu }_b^2)+I(G_b=0)\varphi (b,{\mu }_{2b},{\nu }_b^2);\hfill \\ \hfill g_c(c\mid G_c)=& I(G_c=1)\varphi (c,{\mu }_{1c},{\nu }_c^2)+I(G_c=0)\varphi (c,{\mu }_{2c},{\nu }_c^2),\hfill \end{array}$$ (2)

where φ(•, μ, ν²) is the density of normal distribution with mean μ and variance ν². For model identification, we impose the restrictions on g_b(•):

$$\begin{array}{cc}\hfill E\left[b\right]& =E\left[E\right(b\mid G_b\left)\right]={\lambda }_b{\mu }_{1b}+(1-{\lambda }_b){\mu }_{2b}=0\text{with}{\mu }_{1b}<{\mu }_{2b};\hfill \\ \hfill var\left[b\right]& =E\left[var\right(b\mid G_b\left)\right]+var\left[E\right(b\mid G_b\left)\right]={\nu }_b^2+{\lambda }_b(1-{\lambda }_b)({\mu }_{1b}^2+{\mu }_{2b}^2)=1\hfill \end{array}$$

with similar restrictions for g_c(•). Let π_di = P (D_i = d_i) and note that π_d (d = 0, 1, …, D) is the prevalence of stage d of the disease. The probability that rater j rates subject i as k given the true disease stage and random effects b_i and c_j can be expressed as

$$P(Y_{ij}=k\mid D_i=d_i,b_i,c_j,X_i^j)=\Phi ({\gamma }_{d_i,k}+{\sigma }_{d_i}{b}_i+{\tau }_{d_i}{c}_j+X_i^j{\beta }_{d_i})-\Phi ({\gamma }_{d_i,k-1}+{\sigma }_{d_i}{b}_i+{\tau }_{d_i}{c}_j+X_i^j{\beta }_{d_i}).$$ (3)

As in the PRS, we assume D = K = 4, which means that the number of rating categories (i.e. stages) is the same as the number of true categories. Similar to Wang et al [1], extensions to the case when D ≠ K can be considered. Given random effects ${\left\{b_i\right\}}_{i=1}^I$ and ${\left\{c_j\right\}}_{j=1}^J$, the ratings are each conditionally independent and have a multinomial distribution. Thus, the conditional distribution of each measurement is

$$\prod _{k=0}^{K}P{(Y_{ij}=k\mid D_i=d_i,b_i,c_j,X_i^j)}^{I(Y_{ij}=k)}.$$

Let θ = (γ, σ, τ, π, β)’ be a vector of the unknown parameters. The likelihood is given by

$$L(\theta \mid y)=\int \cdots \int \sum _{d_1=0}^D\cdots \sum _{d_I=0}^D\left[\prod _{i=1}^I\prod _{j=1}^J\prod _{k=0}^{K}P{(Y_{ij}=k\mid D_i=d_i,b_i,c_j,X_i^j)}^{I(Y_{ij}=k)}\right]\times \prod _{i=1}^I{\pi }_{d_i}{g}_b\left(b_i\right)d{b}_i\prod _{j=1}^J{g}_c\left(c_j\right)d_{c_j}.$$ (4)

Once we obtain $\widehat{\theta }$ which is the MLE of θ from (4), for covariate X = x, we obtain the MLE of $P(\tilde{Y}\le k\mid \tilde{D}=d,b,c,X=x)$ by (1), where we use $\tilde{Y}$ and $\tilde{D}$ to denote the generic test and generic disease status respectively rather than any specific rater or subject.

We consider the misclassification matrix as a measure of diagnostic accuracy, where the (K + 1) × (D + 1) misclassification matrix has elements given by

$$P(\tilde{Y}=k\mid \tilde{D}=d,X=x)\equiv \int \int P(\tilde{Y}=k\mid \tilde{D}=d,b,c,X=x)\times g_b\left(b\right)g_c\left(c\right)dbdc$$ (5)

in the (k + 1)th row and (d + 1)th column of the matrix. The misclassification matrix is square (D = K) and it can be estimated by (5) once we obtain $\widehat{\theta }$. By the invariance property of MLE, we can estimate the probability of a correct classification as $\widehat{P}(\tilde{Y}=\tilde{D}\mid X=x)={\sum }_{d=0}^D\widehat{P}(\tilde{Y}=d\mid \tilde{D}=d,X=x){\widehat{\pi }}_d$, where $\widehat{P}(\tilde{Y}=d\mid \tilde{D}=d,X=x)$ is a function of $\widehat{\theta }$.

3. Maximum Likelihood Estimation: MCEM Algorithm

In this section, we introduce the method for obtaining the MLEs of the model parameters. Due to the high dimensional integration and summation, it can be challenging to use the classical EM algorithm to estimate (4). Instead, we follow Wei and Tanner [10] in using the Monte-Carlo EM (MCEM) algorithm. The MCEM incorporates a Monte Carlo implementation into the E-step of EM algorithm so that the required expectation can be approximated by the average of the Monte-Carlo samples from the target distribution. By using the Metropolis-Hasting algorithm to draw samples from target distributions, McCulloch [11] developed maximum likelihood algorithms for generalized linear mixed models. Robert and Casella [12] gave examples of R implementations using the MCEM algorithm. Here, we treat the true disease status ${\left\{D_i\right\}}_{i=1}^I$, subject-specific random effects ${\left\{b_i\right\}}_{i=1}^I$ and rater-specific ${\left\{c_j\right\}}_{j=1}^J$ as missing data. For notational brevity, let $Y^{\ast }=(Y_1^{\prime },\dots ,Y_I^{\prime })$ be the observed data, $Z^{\ast }={\{{\left\{D_i\right\}}_{i=1}^I,{\left\{b_i\right\}}_{i=1}^I,{\left\{c_j\right\}}_{j=1}^J\}}^{\prime }$ be the missing data and W* = (Y*, Z*)’ be the complete data. Accordingly, the complete-data likelihood is

$$\log f(w^{\ast }\mid \theta )=\sum _{i=1}^I\sum _{j=1}^J\sum _{k=0}^{K}I(Y_{ij}=k)\log P(Y_{ij}=k\mid D_i=d_i,b_i,c_j,X_i^j)+\sum _{i=1}^I\log \left[g_b\right(b_i\left)\right]+\sum _{j=1}^J\log \left[g_c\right(c_j\left)\right]+\sum _{i=1}^I\log {\pi }_{d_i}+\text{constant},$$ (6)

For our purpose, we can obtain the kernel of the target distribution by Bayes Rule:

$$\begin{array}{cc}\hfill f(z^{\ast }\mid y^{\ast },\theta )=& \frac{f(y^{\ast }\mid z^{\ast },\theta )f(z^{\ast }\mid \theta )}{f(y^{\ast }\mid \theta )}\propto f(y^{\ast }\mid z^{\ast },\theta )f(z^{\ast }\mid \theta )\hfill \\ \hfill & \propto \prod _{i=1}^I\prod _{j=1}^J\prod _{k=0}^K\left[P{(Y_{ij}=k\mid d_i,b_i,c_i,X_i^j)}^{I(Y_{ij}=k)}\right]\times \prod _{i=1}^I\left[g_b\right(b_i\mid \theta \left)\right]\times \prod _{j=1}^J\left[g_c\right(c_j\mid \theta \left)\right]\hfill \\ \hfill & \times {\pi }_1^{I_1}\times {\pi }_2^{I_2}\times \cdots \times {\pi }_D^{I_D}\times {\left(1-\sum _{d=1}^D{\pi }_d\right)}^{(1-{\Sigma }_{d-1}^D{I}_d)},\hfill \end{array}$$

where $I_d={\sum }_{i=1}^{I}I(D_i=d)$ for d = 0, 1, …, D. We implement the MCEM algorithm as follows:

1. Start by initial values θ⁽⁰⁾ = (γ⁽⁰⁾, σ⁽⁰⁾, τ⁽⁰⁾, π⁽⁰⁾, β⁽⁰⁾)’ and set r = 0.

2. Generate M groups of values z*⁽¹⁾, z*⁽²⁾, …, z*^(M) from the target distribution f(z*|y*, θ^(r)) and choose θ^(r+1) to maximize

   $$\frac{1}{M}\sum _{m=1}^M\log \left[f\right(w^{\ast \left(m\right)}\mid \theta \left)\right]f(z^{\ast \left(m\right)}\mid y^{\ast },{\theta }^{\left(r\right)}),$$

   which is the Monte-Carlo estimate of

   $$Q(\theta \mid {\theta }^{\left(r\right)})=E\left[\log f\right(W^{\ast }\mid \theta )\mid y^{\ast },{\theta }^{\left(r\right)}]=\int \log f(w^{\ast }\mid \theta )f(z^{\ast }\mid y^{\ast },{\theta }^{\left(r\right)})d{z}^{\ast },$$

   where θ^(r) is the parameter value from the rth iteration and set r = r + 1. The maximization is subject to the restrictions that elements in each column of matrix γ are nondecreasing from the top to the bottom, all the elements in σ, τ and π are nonnegative and that all the elements in π sum up to one. R function nloptr can be employed for such constrained maximization. We generate sample z*^(m) (m = 1, …, M) from the target distribution by Metropolis-Hasting algorithm:

   1. Let ${\tilde{f}}^{\left(r\right)}(d,b,c\mid w^{\ast },{\theta }^{\left(r\right)})\equiv {\prod }_{i=1}^I{\tilde{f}}_D^{\left(r\right)}\left(d_i\right){\tilde{f}}_b^{\left(r\right)}\left(b_i\right){\prod }_{j=1}^J{\tilde{f}}_c^{\left(r\right)}\left(c_j\right)$ denote the candidate distribution with ${\tilde{f}}_D^{\left(r\right)}\left(d_i\right)$ being the empirical distribution of d_i and ${\tilde{f}}_b^{\left(r\right)}\left(b_i\right)$ and ${\tilde{f}}_c^{\left(r\right)}\left(c_j\right)$ being t distribution centered at the means of b_i and c_j sampled from the rth iteration of the EM algorithm respectively. Choose z₀ from the support of the target distribution.
   2. For n = 1, 2, …: generate U_n ~ uniform(0, 1) and $v_n\sim {\tilde{f}}^{\left(r\right)}(d,b,c\mid y^{\ast },z_{n-1},{\theta }^{\left(r\right)})$. Set

      $$z_n=\{\begin{array}{cc}{v}_n\hfill & \text{if}{U}_n\le \omega \hfill \\ z_{n-1}\hfill & \text{if}{U}_n>\omega \hfill \end{array}\phantom{\}},\text{where}\omega =\min \left(\frac{f(v_n\mid y^{\ast },{\theta }^{\left(r\right)}){\tilde{f}}^{\left(r\right)}(z_{n-1}\mid y^{\ast },z_{n-1},{\theta }^{\left(r\right)})}{f(z_{n-1}\mid y^{\ast },{\theta }^{\left(r\right)}){\tilde{f}}^{\left(r\right)}(v_n\mid y^{\ast },z_{n-1},{\theta }^{\left(r\right)})},1\right).$$

      As n → ∞, z_n converges to z* ~ f(z*|y*, θ) in distribution. In order to generate random effects b_i’s and c_j’s from the candidate distribution, we choose 30 as the degrees of freedom of the t distributions mentioned in part (a) so that they do not have heavy tails.

   We repeat Step 2 a sufficient number of iterations until the estimates become stable.

In the simulation studies and the analysis of the PRS data presented in Sections 4 and 5, we run the algorithms 200 steps. We take M = 50 for iterations r = 1, …, 50, M = 200 for iterations r = 51, …, 80 and M = 1000 for iterations r = 81, …, 200. Final estimates are computed by averaging ${\widehat{\theta }}^{\left(r\right)}(r=191,\dots ,200)$ over the last ten iterations.

We wish to compare different random effects distributions for {b_i}, {c_j} in (2) using penalized likelihood method such as the Akaike information criterion (AIC). However, the likelihood is difficult to evaluate given the high dimension of the random effects. We use the simulated likelihood approach by Geyer and Thompson [13] to overcome this difficulty. Specifically, let $\widehat{\theta }={(\widehat{\gamma },\widehat{\sigma },\widehat{\tau },\widehat{\pi },\widehat{\beta })}^{\prime }$ be the MLE obtained from the MCEM algorithm and in (4) consider

$$L(\theta \mid y)=E\left[\prod _{i=1}^I\prod _{j=1}^J\prod _{k=0}^{K}P{(Y_{ij}=k\mid D_i=d_i,b_i,c_j,X_i^j)}^{I(Y_{ij}=k)}\right],$$

where the expectation is taken over all random effects {b_i}, {c_j} and {d_i}. The maximized likelihood $L(\widehat{\theta }\mid y)$ can be approximated by

$$\widehat{L}(\widehat{\theta }\mid y)=\frac{1}{T}\sum _{t=1}^T\left[\prod _{i=1}^I\prod _{j=1}^J\prod _{k=0}^K\widehat{P}{(Y_{ij}=k\mid D_i=d_i^{\left(t\right)},b_i^{\left(t\right)},c_j^{\left(t\right)},X_i^j)}^{I(y_{ij}=k)}\right]\times \prod _{i=1}^I{\widehat{\pi }}_{d_i^{\left(t\right)}}{g}_b\left(b_i^{\left(t\right)}\right)\prod _{j=1}^J{g}_c\left(c_j^{\left(t\right)}\right),$$

where $b_i^{\left(t\right)}$, $c_j^{\left(t\right)}$ and $d_i^{\left(t\right)}$ are the t-th simulated realizations from the density functions g_b for the i-th subject, g_c for the j-th rater and mass functions multinomial $\left(1,({\widehat{\pi }}_0,\dots ,{\widehat{\pi }}_D)\right)$ for the i-th subject respectively, T is the total number of such simulated realizations and

$$\begin{array}{cc}\hfill & \widehat{P}(Y_{ij}=k\mid D_i=d_i^{\left(t\right)},b_i^{\left(t\right)},c_j^{\left(t\right)},X_i^j)\hfill \\ \hfill & =\Phi ({\widehat{\gamma }}_{d_i^{\left(t\right)},k}+{\widehat{\sigma }}_{d_i^{\left(t\right)}}{b}_i^{\left(t\right)}+{\widehat{\tau }}_{d_i^{\left(t\right)}}{c}_j^{\left(t\right)}+X_i^j{\beta }_{d_i^{\left(t\right)}})-\Phi ({\widehat{\gamma }}_{d_i^{\left(t\right)},k-1}+{\widehat{\sigma }}_{d_i^{\left(t\right)}}{b}_i^{\left(t\right)}+{\widehat{\tau }}_{d_i}^{\left(t\right)}{c}_j^{\left(t\right)}+X_i^j{\beta }_{d_i}^{\left(t\right)})\hfill \end{array}$$

by (3). The Monte-Carlo estimate of the Akaike Information Criteria $\widehat{AIC}\equiv 2\times n_{par}-2\log \widehat{L}(\widehat{\theta }\mid y)$ can be used to compare different models for the random effects, where n_par is the number of parameters in the model. In the simulation studies and the analysis of the PRS data, we take T = 5000

Proving global identifiability for complex latent class models such as the one we are proposing is a difficult and challenging problem. In fact, at the very least, these models lack identifiability due to a label-switching problem. Practitioners need to be cautious when applying these methods to be sure that results are scientifically sensible. Various authors have worked on the issue of local identifiability (e.g., [14, 15]). This latter form of identifiability can be proved by showing that the Hessian matrix is non-singular. Unfortunately this is difficult for our model since the Hessian matrix can only be estimated by using Monte-Carlo method and its estimate can be unstable when the number of parameters is large.

4. Simulation Study

In this section, we perform simulation studies to assess the convergence and operating characteristics of the MCEM algorithm. For simplicity, we focus on the case of a homogeneous group of physicians (i.e., no covariates in the model). For notational brevity, we therefore write $P(\tilde{Y}=\tilde{D})$ in place of $P(\tilde{Y}=\tilde{D}\mid X=x)$. Data were simulated according to model (1) with random effects following distribution (2). All simulations were performed with I = 100 subjects and J = 10 raters. The true prevalences are 0.3, 0.25, 0.2, 0.15, 0.1 for no endometriosis, stage I to IV respectively, and the true misclassification matrix is as in Table 2. These values are chosen to be close to the parameter estimates in the PRS shown in Section 5. Based on the parameters in Table 2, the true probability of a correct classification is $P(\tilde{Y}=\tilde{D})=0.454$.

Table 2.

True misclassification matrix in the simulation studies.

		d = 0	d = 1	d = 2	d = 3	d = 4
P(Y = k|D = d)	k = 0	0.7	0.2	0.25	0.05	0.15
	k = 1	0.2	0.55	0.46	0.28	0.1
	k = 2	0.05	0.2	0.25	0.35	0.15
	k = 3	0.04	0.03	0.03	0.21	0.35
	k = 4	0.01	0.02	0.01	0.11	0.25

4.1. Convergence

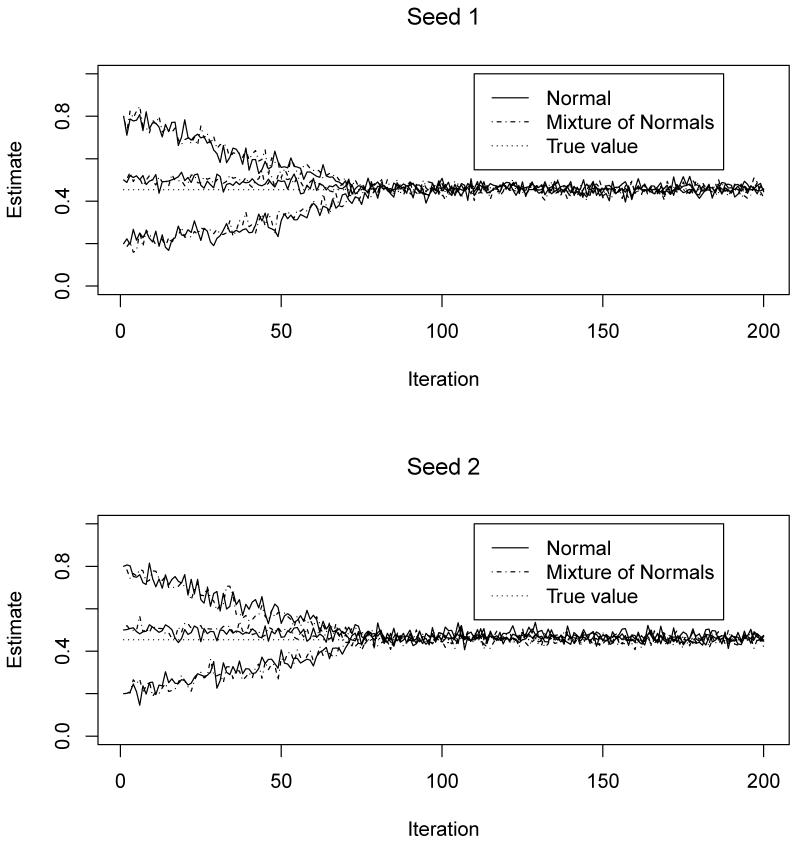
To assess the convergence of the MCEM algorithm and the Monte-Carlo variations, we simulated data sets based on random effects with normal and MixNs respectively. We obtained the MLEs of the parameters by assuming that the random effects follow the true corresponding distributions. The algorithm was performed based on two different seeds and three different starting values of the probability of a correct classification: 0.8, 0.2 and 0.5, for larger than, smaller than and close to the true value respectively. We show in Figure 1 that the convergence of the estimated probability of a correct classification $\widehat{P}(\tilde{Y}=\tilde{D})$ is insensitive to the choice of either the starting values or the seeds of the MCEM algorithm. This empirically suggests that the model is locally identifiable. The convergence of each element in θ is similar to that of $\widehat{P}(\tilde{Y}=\tilde{D})$ and is not presented here to save space. Specifically, the algorithm converges at around the 80^th iteration and appears stable thereafter with tolerable Monte-Carlo variations. This is probably because we increased the size of Monte-Carlo samples from the target distribution in the E-step from 200 to 1000 at the 80^th iteration. Similar results are observed regardless of whether the distributions of random effects are normal or MixNs. We performed similar simulations using different parameter values and observed the same results (data not shown). For the algorithm to reach the approximate convergence (within Monte-Carlo error), it took approximately 16 hours on an NIH linux cluster with a 2.8 GHz Intel X5660 processor.

Figure 1.

Convergence of the MCEM algorithm by seeds and starting values under true random effect distributions.

4.2. Operating characteristics

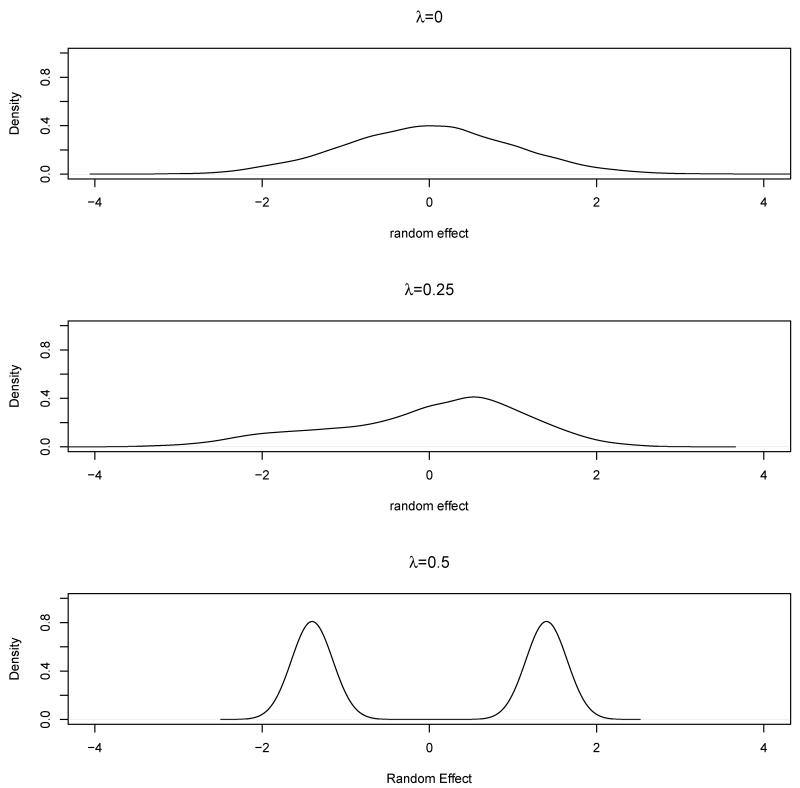
To assess the operating characteristics of the MCEM algorithm, we simulated different data sets based on different random effects distributions. More specifically, in (2), we choose λ = λ_b = λ_c = 0, 0.25 or 0.5 with the corresponding distributions shown in Figure 2. For each λ, we generated 200 data sets and obtained the MLEs of model parameters using each individual data set.

Figure 2.

The distribution of random effects under different λ values.

In Table 3, we summarize the estimated prevalence, with the standard error in parentheses. When λ = 0, the data are simulated according to normally distributed subject-specific and rater-specific random effects. When a normal distribution is assumed as the working model, the estimates are mostly unbiased. This is also true when MixNs are assumed since normal random effects are special cases of MixN random effects. In contrast, when λ ≠ 0, the data are simulated according to a model with the subject and rater-specific random effects following MixNs. When MixNs are assumed as the working model, the estimates are nearly unbiased. However, when normal distributions are assumed, most estimates are biased. Moreover, the biases are more profound when λ = 0.5 where the misspecification of the random effects distribution is more severe than when λ = 0.25 (see Figure 2). The estimated misclassification matrix in Table 4 shows a similar pattern. For example, when λ = 0, the estimates of P (Y = 4|D = 4) are nearly unbiased under both random effects distributions, 0.262 and 0.271 for normal and MixNs respectively compared to the true value of 0.25; when λ ≠ 0 and MixNs are assumed as the working model, the estimates are mostly unbiased: 0.237 and 0.231 for λ = 0.25 and 0.5 respectively. When normal distributions are assumed, the estimates are biased: 0.326 and 0.381 for λ = 0.25 and 0.5 respectively. Clearly the bias is larger (0.381) when λ = 0.5 than that (0.326) when λ = 0.25. When normal distributions are assumed for the random effects in the true model and either normal or MixNs in the working model, the estimated probabilities of a correct classification $\widehat{P}(\tilde{Y}=\tilde{D})$ (standard errors) are 0.466(0.087) and 0.472(0.127) respectively, and both are close to the true probability of a correct classification, 0.454. However, when λ = 0.25 or 0.5, namely the true distributions of the random effects are MixNs, fitting a working model with normal random effects distribution resulted in a biased probability of a correct classification: 0.548(0.095) and 0.602(0.105), respectively (compared with a true value of 0.454). In comparison, the corresponding estimates under a correctly specified working models are 0.466(0.139) and 0.464(0.146) respectively.

Table 3.

Average estimated prevalence π_d (standard deviation) in the simulation study based on different assumptions on the distributions of random effects. Based on 200 simulated data sets. The true prevalences are 0.3, 0.25, 0.2, 0.15 and 0.1 for no endometriosis, Stage I to IV, respectively.

λ	Working random effects	No ENDO	Stage I	Stage II	Stage III	Stage IV
0	Normal	0.314(0.10)	0.239(0.08)	0.223(0.12)	0.138(0.03)	0.086(0.03)
0	MixN	0.320(0.12)	0.231(0.14)	0.228(0.14)	0.129(0.07)	0.092(0.09)
0.25	Normal	0.360(0.08)	0.205(0.14)	0.271(0.08)	0.112(0.11)	0.052(0.05)
0.25	MixN	0.311(0.10)	0.236(0.16)	0.221(0.16)	0.141(0.14)	0.091(0.09)
0.5	Normal	0.401(0.08)	0.179(0.12)	0.272(0.08)	0.109(0.11)	0.039(0.04)
0.5	MixN	0.318(0.18)	0.231(0.23)	0.216(0.07)	0.139(0.13)	0.096(0.10)

Table 4.

Estimated misclassification matrices in simulation studies based on different distributions of random effects (subject, rater). In the body of the table, we list averageP̂(Y = k|D = d), the elements of misclassification matrix with their standard deviations based on 200 simulated data sets in parentheses. The true parameters are in Table 2, rows 2-6.

λ = 0	Normal	d = 0	d = 1	d = 2	d = 3	d = 4
	k = 0	0.718(0.11)	0.178(0.05)	0.236(0.10)	0.043(0.04)	0.143(0.12)
	k = 1	0.181(0.08)	0.532(0.09)	0.443(0.06)	0.298(0.09)	0.093(0.09)
	k = 2	0.068(0.07)	0.212(0.10)	0.276(0.05)	0.334(0.15)	0.167(0.09)
	k = 3	0.027(0.03)	0.036(0.04)	0.036(0.04)	0.209(0.12)	0.335(0.07)
	k = 4	0.006(0.01)	0.042(0.04)	0.009(0.01)	0.116(0.12)	0.262(0.17)
	MixN	d = 0	d = 1	d = 2	d = 3	d = 4
	k = 0	0.726(0.19)	0.172(0.12)	0.227(0.13)	0.038(0.04)	0.139(0.14)
	k = 1	0.175(0.16)	0.523(0.12)	0.435(0.14)	0.306(0.09)	0.088(0.09)
	k = 2	0.072(0.07)	0.226(0.13)	0.286(0.07)	0.329(0.17)	0.175(0.15)
	k = 3	0.020(0.02)	0.042(0.04)	0.042(0.04)	0.219(0.16)	0.327(0.08)
	k = 4	0.007(0.01)	0.037(0.04)	0.010(0.01)	0.108(0.11)	0.271(0.18)
λ = 0.25	Normal	d = 0	d = 1	d = 2	d = 3	d = 4
	k = 0	0.781(0.12)	0.151(0.08)	0.212(0.16)	0.032(0.03)	0.099(0.10)
	k = 1	0.132(0.08)	0.633(0.11)	0.428(0.09)	0.321(0.11)	0.072(0.07)
	k = 2	0.073(0.07)	0.150(0.14)	0.322(0.13)	0.305(0.11)	0.191(0.14)
	k = 3	0.011(0.01)	0.050(0.05)	0.036(0.04)	0.295(0.14)	0.312(0.08)
	k = 4	0.003(0.00)	0.016(0.02)	0.002(0.00)	0.047(0.05)	0.326(0.17)
	MixN	d = 0	d = 1	d = 2	d = 3	d = 4
	k = 0	0.721(0.13)	0.173(0.16)	0.231(0.17)	0.041(0.04)	0.167(0.17)
	k = 1	0.171(0.17)	0.539(0.13)	0.441(0.13)	0.296(0.13)	0.091(0.09)
	k = 2	0.063(0.06)	0.218(0.14)	0.272(0.17)	0.332(0.18)	0.174(0.14)
	k = 3	0.022(0.02)	0.040(0.04)	0.033(0.03)	0.230(0.18)	0.331(0.13)
	k = 4	0.023(0.02)	0.030(0.03)	0.023(0.02)	0.101(0.10)	0.237(0.21)
λ = 0.5	Normal	d = 0	d = 1	d = 2	d = 3	d = 4
	k = 0	0.802(0.10)	0.122(0.10)	0.156(0.16)	0.028(0.03)	0.046(0.05)
	k = 1	0.096(0.06)	0.681(0.13)	0.403(0.07)	0.322(0.11)	0.054(0.05)
	k = 2	0.079(0.08)	0.129(0.13)	0.394(0.11)	0.271(0.09)	0.213(0.14)
	k = 3	0.011(0.01)	0.053(0.05)	0.036(0.04)	0.336(0.14)	0.306(0.06)
	k = 4	0.012(0.01)	0.015(0.01)	0.011(0.01)	0.043(0.04)	0.381(0.15)
	MixN	d = 0	d = 1	d = 2	d = 3	d = 4
	k = 0	0.719(0.19)	0.175(0.11)	0.236(0.24)	0.032(0.03)	0.171(0.17)
	k = 1	0.168(0.17)	0.531(0.15)	0.438(0.13)	0.335(0.15)	0.103(0.10)
	k = 2	0.067(0.07)	0.183(0.16)	0.268(0.20)	0.278(0.18)	0.169(0.17)
	k = 3	0.024(0.02)	0.037(0.04)	0.039(0.04)	0.236(0.17)	0.326(0.08)
	k = 4	0.022(0.02)	0.074(0.07)	0.019(0.02)	0.119(0.12)	0.231(0.23)

Since it is important to specify the distribution of random effects correctly, we are interested in the empirical rates that the penalized likelihood criteria select the true model. By simulation, Zhang et al [16] showed that when the true disease status and outcomes from raters are both binary, penalized likelihood criteria empirically select the true model at the rate of 55%, which is slightly higher than 50%. Here, when the true disease status and outcomes are both ordinal, the empirical rate that penalized likelihood criteria select the true model is 74%, 73% and 76% for λ = 0, 0.25 and 0.5 respectively. Thus, compared to the method of dichotomizing ordinal data, the proposed method is empirically more likely to select the true model and estimate the parameters accurately. This is likely due to the increased information contained in the ordinal data.

5. Application

We now apply the proposed modeling framework to data from the Physician Reliability Study [9]. Eight physicians (4 residents and 4 regional experts) reviewed digital images on 79 subjects. Scientific substantive questions include: (1) how did these physicians stage endometriosis? Were they more likely on target or within one stage? (2) are the physicians better at diagnosing some particular stages as compared to others? (3) are the findings in questions (1) and (2) different for the 4 residents as compared with the 4 regional experts?

With respect to the 8 physicians, we first ignore their difference, treating them as a homogeneous group. Later we will account for their difference (residents vs regional experts) in the modeling framework.

Among all the four possible combinations of subject and rater-specific random effects the AIC is the smallest (3219.47) for the model with normal subject-specific random effects and MixN rater-specific random effects. Under the best model, the prevalences of the five stages are estimated at 0.321(0.11), 0.238(0.08), 0.211(0.03), 0.151(0.06) and 0.079(0.06) respectively, and the estimated misclassification matrix (with the bootstrap standard errors based on 1000 bootstrapped samples in parentheses) is presented in Table 5. The estimated probability of a correct classification is $\widehat{P}(Y=D)=0.515$. In Table 5, the diagonal elements represent the average diagnostic accuracy across the population of the physicians for each true endometriosis stage. For example, when the true stage of endometriosis is mild (d = 2), the average probability that the physicians would correctly stage the disease is 0.289. In each row, the elements adjacent to the diagonal elements are important since they represent the situation when the physicians categorize the diagnostic result only one stage off from the truth. In the PRS, the physicians are more likely to underestimate the severity by one stage than overestimate by one stage. Moreover, it appears that these physicians are better at diagnosing lower stages of endometriosis (no endometriosis and mild stage) than higher ones, with the correction classification of 75%, 63%, 29%, 26% and 29% for the five stages (from low to high), respectively.

Table 5.

Estimated misclassification matrix in the PRS based on normal subject-specific random effects and MixN rater-specific random effects when pooling the 8 physicians. In the body of the table, we list each element with the bootstrap standard errors based on 1000 bootstrapped samples in parentheses.

		d = 0	d = 1	d = 2	d = 3	d = 4
P̂(Y = k|D = d)	k = 0	0.754(0.11)	0.155(0.08)	0.256(0.12)	0.087(0.06)	0.114(0.11)
	k = 1	0.163(0.08)	0.628(0.07)	0.421(0.08)	0.237(0.09)	0.122(0.08)
	k = 2	0.045(0.04)	0.157(0.13)	0.289(0.09)	0.315(0.12)	0.133(0.09)
	k = 3	0.034(0.03)	0.046(0.05)	0.028(0.03)	0.262(0.08)	0.342(0.12)
	k = 4	0.004(0.00)	0.014(0.01)	0.006(0.01)	0.099(0.09)	0.289(0.10)

Since there are two physician groups (residents and regional experts) serving as raters, it is of interest to see whether the above conclusions hold when we account for the difference between the two groups of physicians with different levels of experience. In doing so, we utilize a modified version of model (1):

$$P(Y_{ij}\le k\mid d_i,b_i,c_j,X_i^j)\equiv \Phi ({\gamma }_{d_i,k}+{\sigma }_{d_i}{b}_i+{\tau }_{d_i}{c}_j+{\beta }_{d_i}I(j\text{is resident}\left)\right),$$

where I(•) is an indicator function.

Among all the four combinations of random effects distributions, the model assuming normal subject-specific random effects and normal rater-specific random effects had the smallest AIC (3211.36), with the probability of a correct classification for resident and regional expert being 0.463 and 0.489 respectively. The estimated prevalences and coefficients for the group indicator as well as the misclassification matrices for both groups (with the bootstrap standard errors based on 1000 bootstrapped samples in parentheses) are listed in Tables 6 and 7 respectively. By including the group indicator as covariate, we have smaller AIC than when the two groups are treated as homogeneous, suggesting that the resident and regional expert group might be different at staging endometriosis. More specifically, we can see from Table 7 that when the true disease stage is mild (d = 2), the probability that regional experts make the right judgement is 0.342, which is significantly higher than 0.151, the probability that residents make the right judgement. This difference in the physician type may also explain why a MixNs distribution is needed for the rater-specific random effects when the 8 physicians are treated homogeneously. It appears that failure to include an important binary rater-specific covariate will induce a bimodal structure in the random effects distribution.

Table 6.

Estimated prevalence and coefficients for the group indicator (1 = resident, 0 = regional expert) based on normal subject- and rater-specific random effects in the PRS. In the body of the table, we report bootstrap standard errors based on 1000 bootstrapped samples in parentheses. The coefficients that are more than two estimated standard errors from 0 are in bold.

	d = 0	d = 1	d = 2	d = 3	d = 4
${\widehat{\pi }}_d$	0.290(0.04)	0.275(0.04)	0.159(0.03)	0.183(0.03)	0.093(0.02)
${\widehat{\beta }}_d$	−0.035(0.02)	0.054(0.03)	− 0.146(0.04)	−0.022(0.05)	− 0.133(0.06)

Table 7.

Estimated misclassification matrices in PRS based on normal subject- and rater-specific random effects. In the body of the table, we report P̂(Y = k|D = d) with their bootstrap standard errors based on 1000 bootstrapped samples in parentheses for each value of the covariate (resident and regional expert group) respectively.

	d = 0	d = 1	d = 2	d = 3	d = 4
Residents
k = 0	0.693(0.05)	0.196(0.04)	0.213(0.07)	0.060(0.02)	0.118(0.07)
k = 1	0.203(0.04)	0.622(0.05)	0.611(0.07)	0.307(0.07)	0.090(0.06)
k = 2	0.052(0.03)	0.166(0.03)	0.151(0.05)	0.348(0.07)	0.185(0.06)
k = 3	0.051(0.04)	0.015(0.02)	0.013(0.01)	0.224(0.05)	0.327(0.07)
k = 4	0.001(0.00)	0.001(0.00)	0.013(0.01)	0.061(0.04)	0.280(0.09)
Regional Experts
k = 0	0.748(0.05)	0.171(0.04)	0.256(0.07)	0.062(0.02)	0.141(0.07)
k = 1	0.170(0.04)	0.562(0.04)	0.344(0.06)	0.244(0.06)	0.087(0.05)
k = 2	0.041(0.02)	0.189(0.04)	0.342(0.07)	0.298(0.06)	0.089(0.05)
k = 3	0.034(0.02)	0.049(0.02)	0.047(0.02)	0.218(0.05)	0.430(0.11)
k = 4	0.006(0.01)	0.028(0.02)	0.012(0.01)	0.177(0.06)	0.253(0.10)

6. Discussion

In this article, we have described a method for evaluating diagnostic accuracy without gold standard by latent class approach with crossed random effects for ordinal tests. This work generalizes Wang and Zhou [2] to allow for the rater effect to be treated as random rather than fixed and for the incorporation of flexible random effect distributions. We show that estimate of diagnostic accuracy may be sensitive to assumptions on the random effects distributions and that unlike for the binary case (see Zhang et al [16]), penalized likelihood comparisons can be used for assessing the adequacy of these distributions.

The proposed method was motivated by the Physician Reliability Study in staging endometriosis. To that end, we have found that it is important to incorporate covariates in the modeling framework to capture heterogeneity in raters. Substantively, we found that regional experts make better diagnoses than the residents when the true disease is mild, that physicians in PRS are more likely under-staging than over-staging, and that they are better at diagnosing lower stages of endometriosis than higher ones. These interesting findings can be useful in helping training physicians in the field.

In the analysis of the PRS, the covariate is binary, making it easy to present the misclassification matrix for both realizations of the covariate. For more complicated case of covariates, we recommend plotting the elements of the misclassification matrix as a function of changes in these covariates. In particular, since we can write the misclassification matrix in a close-form as presented in the Appendix, we can plot each element of it against a continuous covariate.

One feature in both our simulation study and the application is that the number of raters is small. With such small numbers of random effects, estimate of the corresponding variance component (τ_d) can be biased. We indeed observed this bias in a separate simulation study with J = 10 and near unbiasedness with J = 100. For example, with the true τ₄ = 0.1, we obtained ${\widehat{\tau }}_4=0.26$ when J = 10, reflecting substantial bias, and ${\widehat{\tau }}_4=0.11$ when J = 100, reflecting little bias. Estimates of the subject-specific variance component in both cases are unbiased. Interestingly, regardless of J = 10 or 100, the estimated misclassification matrices, the primary focus of our work, are unbiased.

APPENDIX: CLOSED FORM EXPRESSION OF EQUATION (5)

The closed form expression of the element in the misclassification matrix can be written as

$$\begin{array}{cc}\hfill & P(\tilde{Y}=k\mid \tilde{D}=d,X=x)\hfill \\ \hfill & ={\lambda }_b{\lambda }_c\left[\Phi \left(\frac{{\gamma }_{d,k}+x{\beta }_d+{\sigma }_d{\mu }_{1b}+{\tau }_d{\mu }_{1c}}{\sqrt{1+{\nu }_b^2{\sigma }_d^2+{\nu }_c^2{\tau }_d^2}}\right)-\Phi \left(\frac{{\gamma }_{d,k-1}+x{\beta }_d+{\sigma }_d{\mu }_{1b}+{\tau }_{d{\mu }_{1c}}}{\sqrt{1+{\nu }_b^2{\sigma }_d^2+{\nu }_c^2{\tau }_d^2}}\right)\right]\hfill \\ \hfill & +{\lambda }_b(1-{\lambda }_c)\left[\Phi \left(\frac{{\gamma }_{d,k}+x{\beta }_d+{\sigma }_d{\mu }_{1b}+{\tau }_d{\mu }_{2c}}{\sqrt{1+{\nu }_b^2{\sigma }_d^2+{\nu }_c^2{\tau }_d^2}}\right)-\Phi \left(\frac{{\gamma }_{d,k-1}+x{\beta }_d+{\sigma }_d{\mu }_{1b}+{\tau }_d{\mu }_{2c}}{\sqrt{1+{\nu }_b^2{\sigma }_d^2+{\nu }_c^2{\tau }_d^2}}\right)\right]\hfill \\ \hfill & +(1-{\lambda }_b){\lambda }_c\left[\Phi \left(\frac{{\gamma }_{d,k}+x{\beta }_d+{\sigma }_d{\mu }_{2b}+{\tau }_d{\mu }_{1c}}{\sqrt{1+{\nu }_b^2{\sigma }_d^2+{\nu }_c^2{\tau }_d^2}}\right)-\Phi \left(\frac{{\gamma }_{d,k-1}+x{\beta }_d+{\sigma }_d{\mu }_{2b}+{\tau }_d{\mu }_{1c}}{\sqrt{1+{\nu }_b^2{\sigma }_d^2+{\nu }_c^2{\tau }_d^2}}\right)\right]\hfill \\ \hfill & +(1-{\lambda }_b)(1-{\lambda }_c)\left[\Phi \left(\frac{{\gamma }_{d,k}+x{\beta }_d+{\sigma }_d{\mu }_{2b}+{\tau }_d{\mu }_{2c}}{\sqrt{1+{\nu }_b^2{\sigma }_d^2+{\nu }_c^2{\tau }_d^2}}\right)-\Phi \left(\frac{{\gamma }_{d,k-1}+x{\beta }_d+{\sigma }_d{\mu }_{2b}+{\tau }_d{\mu }_{2c}}{\sqrt{1+{\nu }_b^2{\sigma }_d^2+{\nu }_c^2{\tau }_d^2}}\right)\right].\hfill \end{array}$$ (7)

For the special case of normal random effects with λ_b = λ_c = 1, μ_1b = μ_1c = 0 and ν_b = ν_c = 1, we have the following closed form of the misclassification matrix for an arbitrary realization of covariate x.

$$P(\tilde{Y}=k\mid \tilde{D}=d,X=x)=\Phi \left(\frac{{\gamma }_{d_i,k}+x{\beta }_d}{\sqrt{1+{\sigma }_d^2+{\tau }_d^2}}\right)-\Phi \left(\frac{{\gamma }_{d_i,k-1}+x{\beta }_d}{\sqrt{1+{\sigma }_d^2+{\tau }_d^2}}\right).$$

Equation (7) can be derived by considering the following.

$$\begin{array}{cc}\hfill & P(\tilde{Y}\le k\mid \tilde{D}=d,X-x)\hfill \\ \hfill =& P(G_b=1,G_c=1)P(\tilde{Y}\le k\mid \tilde{D}=d,X=x,G_b=1,G_c=1)\hfill \\ \hfill & +P(G_b=1,G_c=0)P(\tilde{Y}\le k\mid \tilde{D}=d,X=x,G_b=1,G_c=0)\hfill \\ \hfill & +P(G_b=0,G_c=1)P(\tilde{Y}\le k\mid \tilde{D}=d,X=x,G_b=0,G_c=1)\hfill \\ \hfill & +P(G_b=0,G_c=0)P(\tilde{Y}\le k\mid \tilde{D}=d,X=x,G_b=0,G_c=0)\hfill \\ \hfill =& {\lambda }_b{\lambda }_{c}P(\tilde{Y}\le k\mid \tilde{D}=d,X=x,G_b=1,G_c=1)\hfill \\ \hfill & +{\lambda }_b(1-{\lambda }_c)P(\tilde{Y}\le k\mid \tilde{Y}\le k\mid \tilde{D}=d,X=x,G_b=1,G_c=0)\hfill \\ \hfill & +(1-{\lambda }_b){\lambda }_{c}P(\tilde{Y}\le k\mid \tilde{D}=d,X=x,G_b=0,G_c=1)\hfill \\ \hfill & +(1-{\lambda }_b)(1-{\lambda }_c)P(\tilde{Y}\le k\mid \tilde{D}=d,X=x,G_b=0,G_c=0).\hfill \end{array}$$

Note that since $b\mid G_b=1\sim \mathrm{N}({\mu }_{1b},{\nu }_b^2)$, we have $W_b\equiv \frac{b-{\mu }_{1b}}{{\nu }_b}\sim \mathrm{N}(0,1)$ given G_b = 1 and similarly $W_c\equiv \frac{c-{\mu }_{1c}}{{\nu }_c}\sim \mathrm{N}(0,1)$ given G_c = 1. It follows that

$$\begin{array}{cc}\hfill & P(\tilde{Y}\le k\mid \tilde{D}=d,X=x,G_b=1,G_c=1)\hfill \\ \hfill =& {\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }P(\tilde{Y}\le k\mid \tilde{D}=d,b,c,X=x)\times g_b(b\mid G_b=1)g_c(c\mid G_c=1)dbdc\hfill \\ \hfill =& {\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\Phi ({\gamma }_{d,k}+{\sigma }_{d}b+{\tau }_{d}c+x{\beta }_d)\varphi (b,{\mu }_{1b},{\nu }_b^2)\varphi (c,{\mu }_{1c},{\nu }_c^2)dbdc\hfill \\ \hfill & {\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\Phi \left({\gamma }_{d,k}+{\nu }_b{\sigma }_d\left(\frac{b-{\mu }_{1b}+{\mu }_{1b}}{{\nu }_b}\right)+{\nu }_c{\tau }_d\left(\frac{c-{\mu }_{1c}+{\mu }_{1c}}{{\nu }_c}\right)+x{\beta }_d\right)\hfill \\ \hfill & \times \frac{1}{\sqrt{2\pi }}\exp \left(-\frac{{(b-{\mu }_{1b})}^2}{2{\nu }_b^2}\right)\times \frac{1}{\sqrt{2\pi }}\exp \left(-\frac{{(c-{\mu }_{1c})}^2}{2{\nu }_c^2}\right)d\left(\frac{b-{\mu }_{1b}}{{\nu }_b}\right)d\left(\frac{c-{\mu }_{1c}}{{\nu }_c}\right)\hfill \\ \hfill & ={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\Phi ({\gamma }_{d,k}+x{\beta }_d+{\sigma }_d{\mu }_{1b}+{\tau }_d{\mu }_{1c}+{\nu }_b{\sigma }_d{W}_b+{\nu }_c{\tau }_d{W}_c)\times \varphi (W_b,0,1)\times \varphi (W_c,0,1)d{W}_{b}d{W}_c\hfill \\ \hfill =& \Phi \left(\frac{{\gamma }_{d,k}+x{\beta }_d+{\sigma }_d{\mu }_{1b}+{\tau }_d{\mu }_{1c}}{\sqrt{1+{\nu }_b^2{\sigma }_d^2+{\nu }_c^2{\tau }_d^2}}\right),\hfill \end{array}$$

where the last equation simply extends the argument by Qu, Tan and Kutner [7]. Similarly, we can obtain $P(\tilde{Y}\le k\mid \tilde{D}=d,X=x,G_b=1,G_c=0)$, $P(\tilde{Y}\le k\mid \tilde{D}=d,X=x,G_b=0,G_c=1)$ and $P(\tilde{Y}\le k\mid \tilde{D}=d,X=x,G_b=0,G_c=0)$. By using $P(\tilde{Y}=k\mid \tilde{D}=d,X=x)=P(\tilde{Y}\le k\mid \tilde{D}=d,X=x)-P(\tilde{Y}\le k-1\mid \tilde{D}=d,X=x)$, we obtain $P(\tilde{Y}=k\mid \tilde{D}=d,X=x)$.