ACCELERATING MR PARAMETER MAPPING USING SPARSITY-PROMOTING REGULARIZATION IN PARAMETRIC DIMENSION

Abstract

MR parameter mapping requires sampling along additional (parametric) dimension, which often limits its clinical appeal due to a several-fold increase in scan times compared to conventional anatomic imaging. Data undersampling combined with parallel imaging is an attractive way to reduce scan time in such applications. However, inherent SNR penalties of parallel MRI due to noise amplification often limit its utility even at moderate acceleration factors, requiring regularization by prior knowledge. In this work, we propose a novel regularization strategy, which utilizes smoothness of signal evolution in the parametric dimension within compressed sensing framework (p-CS) to provide accurate and precise estimation of parametric maps from undersampled data. The performance of the method was demonstrated with variable flip angle T₁ mapping and compared favorably to two representative reconstruction approaches, image space-based total variation regularization and an analytical model-based reconstruction. The proposed p-CS regularization was found to provide efficient suppression of noise amplification and preservation of parameter mapping accuracy without explicit utilization of analytical signal models. The developed method may facilitate acceleration of quantitative MRI techniques that are not suitable to model-based reconstruction because of complex signal models or when signal deviations from the expected analytical model exist.

INTRODUCTION

Quantitative mapping of fundamental MRI contrast parameters, longitudinal (T₁) and transverse (T₂) relaxation times, may offer potentially more sensitive and specific information about tissue properties than conventional radiological MRI (1). Further, advanced T₁/T₂ relaxometry based on multicomponent models may provide additional specificity to microstructural properties, such as myelination of white matter (2–4). Depending on the mapping approach, estimation of T₁/T₂ requires acquisition of multiple datasets with different operator-controlled pulse sequence parameters (or control parameters), e.g. flip angles, echo times (T_E), inversion times (T_I), which are subsequently fit to a model equation to yield quantitative maps of parameters (free parameters). The parametric mapping typically incurs a several-fold increase in scan time thereby limiting its overall applicability in many clinical situations (1).

The advent of parallel MRI opened an elegant way to mitigate the aforementioned problems of MRI relaxometry by accelerating acquisition of individual measurements (5,6). The inherent SNR penalties of parallel MRI related to noise amplification may be offset using prior information to regularize the reconstruction, for example, via classical Tikhonov formalism (7–9), including quadratic regularization to control noise by encouraging smooth signal transitions in image space (10–12). Efficient regularization may be also achieved utilizing sparsity models of the underlying signals (13–16) within compressed sensing (CS) framework (17). However, any regularization, except in trivial cases, may introduce errors caused by potential mismatches between prior information invoked by a regularization term and informational content of the actual object. This effect is most pronounced at higher accelerations where the reconstruction has to rely more heavily on prior knowledge to compensate for missing data. In quadratic Tikhonov regularization, the mismatch may introduce aliasing artifacts and/or lead to resolution loss (8,9). In sparsity promoting CS regularization, the artifacts caused by bias towards the assumed sparsity model may have different appearance. For example, in total variation (TV) regularization (piecewise constant model), images may suffer from blurring and patchy artifacts (14,18), while regularization by a two-dimensional wavelet transform may yield incorrect (albeit less visually perceptible) representation of tissue boundaries because of wavelets’ inefficiency for representation of line singularities (19).

A distinct feature of MR parameter mapping is the existence of the control parameter dimension, p, which may offer additional means for acceleration when the reconstruction problem is addressed jointly in x-p space (20). Indeed, casting the problem in an x-p framework allows exploiting inter-image dependencies in the parametric dimension as a source of a priori knowledge to allow estimation from limited data. Several methods (20–23) have been proposed to utilize analytical models or their linearization to constrain signal evolution in the parametric dimension. While powerful, these approaches depend on availability of a simple analytical representation of the signal. However, in some applications, signal models may be too complex to utilize (21), for example, in tissues with multiple exchanging compartments with different relaxation behavior such as in brain white/gray matter (WM/GM) (4,24).

In this work, we propose a novel method to regularize reconstruction of parametric image series (and improve parametric mapping) that avoids making any assumptions about spatial structure of the images and does not require explicit knowledge of analytical models. Instead, we limit our assumptions about signal in the parametric dimension to the fact that it is described by a smooth (differentiable) function (25,26). The smoothness enters the CS-type regularized minimization problem in x-p space in the form of a penalty term on the size of derivatives in the parametric dimension. The image series obtained as the solution of this minimization problem is then fit to a parametric model to yield parameter maps of interest. We demonstrate the performance of the proposed approach on single (27) and multi-component (4) relaxometry based on steady state acquisitions.

THEORY

Overview of Regularized Reconstruction and Rationale

In MRI, a digital image needs to be estimated from a discrete set of measurements. This problem can be written in the matrix form as

$$d=Ef+\epsilon$$ [1]

where d is the vector of measured data from all receiver channels, f is the column vector of length M corresponding to the unknown image, E is the encoding matrix that includes Fourier terms and coil sensitivities, and ε corresponds to the complex noise in the measurements, which we assume to be identically independently distributed (i.i.d.) Gaussian (28). In the general case, the elements in the signal vector d are indexed both by k-space sample number (total N_k samples) and coil receiver number (total N_c ≥ 1), and the size of the encoding matrix E is N_k N_c × M. If row rank of E (the number of linearly independent rows) is less than M, the number of unknowns, then the problem of estimating f is ill-posed and Eq. [1] has an infinite number of solutions. Otherwise, when rank(E) ≥ M, an SNR-optimized estimation of image can be accomplished in the least squares sense:

$$f=arg\underset{f}{min}{\left|\right|Ef-d\left|\right|}_2^2$$ [2]

where ||·||₂ is the l₂ norm. Still, the system of Eq. [1] may be poorly conditioned, for example, when using high undersampling factors in multicoil parallel MRI reconstruction. One existing approach to improve estimation of f is based on dimensionality reduction of the matrix E by assuming that f belongs to a low-dimensional subspace, i.e. f= Pc, where vector c has a small number of elements. Then, the product matrix EP is typically much better conditioned than E, so a more stable solution c can be obtained by embedding the transformation into the data consistency term and performing minimization of l₂ norm of the residual:

$$f=arg\underset{c}{min}{\left|\right|\mathit{EPc}-d\left|\right|}_2^2$$ [3]

This approach is at the foundation of several model-based methods (22,23). The low-dimensional subspace provides model linearization and is obtained through compression of a dictionary by principal component analysis (PCA) in parametric dimension (22) or its Fourier transform (23). The dictionary comprises a set of signals satisfying the given analytical model evaluated on a densely sampled grid of free parameters. We will refer to this family of methods as PC-basis, or PCB, techniques.

In this paper, we explore a different approach to improve estimation of f by minimizing a cost functional that includes additional regularization terms:

$$f=arg\underset{f}{min}\left({\left|\right|Ef-d\left|\right|}_2^2+\sum _{i=1}^K{\lambda }_i{\mathfrak{R}}_i(f)\right)$$ [4]

Design of the penalty functionals ℜ_i is governed by available knowledge or model assumptions about the images f (prior information) and, to lesser extent, by the feasibility of implementation/computational complexity. Parameters λ_i provide balance between the data fidelity (first term) and prior information assumptions (the remaining terms). Usually,

$${\mathfrak{R}}_i(f)={\left|{\mathrm{\Phi }}_{i}f\right|}_{X_i}$$ [5]

where Φ_i is some transform, e.g. identity transform, discrete derivative, or wavelet transform, usually applied in the spatial domain (13,14), and X_i is an appropriately chosen (semi-)norm. Typically, X_i is chosen to be l_p norm defined as

$${\left|\right|x\left|\right|}_p={\left(\sum _k{\left|x_k\right|}^p\right)}^{1/p},p\ge 1$$ [6]

with p= 2 (Tikhonov-type regularization aimed to optimize noise) or p= 1 (CS-type regularization promoting sparsity of the reconstructed images). The benefits of both norms may be combined in norms with tunable hybrid l₁/l₂ behavior (29), which penalize outliers by approximating l₁ norm for large values of x, while treating small values in l₂ fashion to optimize noise.

In the case of acquisition of an image series for parameter mapping, the joint reconstruction problem may be formulated in x-p space by combining all individual images f_k, k-space measurements d_k, and all corresponding encoding matrices E_k into aggregate vectors f̄, d̄ and a matrix Ē, respectively:

$$\overline{f}=arg\underset{f}{min}\left({\left|\right|\overline{E}\overline{f}-\overline{d}\left|\right|}_2^2+\sum _{i=1}^K{\lambda }_i{\mathfrak{R}}_i(\overline{f})\right)$$ [7]

Here, regularization terms can act on the image series as a whole or on individual images.

Models used for CS regularization often rely on spatial sparsity, which may be hard to attain since MR images have large variability in spatial structures, especially in the presence of pathological tissue. In this work, we refrain from making assumptions about spatial properties of the underlying images and propose to restrict the action of the transform operators Φ_i to parametric dimension. In particular, we formulate the regularized reconstruction of a parametric image series as:

$$\overline{f}=arg\underset{\overline{f}}{min}\left({\left|\right|\overline{E}\overline{f}-\overline{d}\left|\right|}_2^2+\lambda {\left|{\mathrm{\Phi }}^p\overline{f}\right|}_{l_1/l_2}\right),$$ [8]

where Φ^p is a transform acting in the parametric dimension. In the Results sections, we illustrate the utility of the proposed sparsity promoting (CS) regularization in the parametric dimension (p-CS) by applying it to single- and multi-component T₁/T₂ relaxometry based on variable flip angle (VFA) steady-state acquisitions (4,27,30). Below we explain our rationale for the choice of Φ^p based on the general properties of the parametric image series for these imaging techniques.

Application to Variable Flip Angle T₁ Mapping

VFA T₁ mapping exploits the dependency of spoiled gradient echo (SPGR) signal on the excitation flip angle using a single compartment model:

$$S(T_1,\alpha )=M_{0}sin\alpha \frac{1-e^{-T_R/T_1}}{1-e^{-T_R/T_1}cos\alpha }$$ [9]

where M₀ is proton density, α is flip angle, T_R is repetition time. Several images are acquired for multiple flip angles and a fixed T_R and the resulting system of equations arising from Eq. [9] is solved for the unknown values of M₀ and T₁. The dependence of the SPGR signal on α is described by a smooth (infinitely differentiable) function. Figure 1 (a) shows a representative signal curve along with its first and second derivatives, illustrating the conjecture that differential operators may act as sparsifying transforms on sets of smooth functions. We further examine sparsifying properties of such transforms by considering a simulated VFA scan of a realistic 3D digital brain phantom (Brainweb database, http://www.bic.mni.mcgill.ca/brainweb/) and the first and second derivatives of this image series in the flip angle dimension. We normalize the maximal values (l_∞-norm) of resulting image series to 1 and compare non-increasing rearrangements (31) obtained by sorting all absolute values in each series. Non-increasing rearrangements preserve l₁ norm of functions (31), thus providing an illustrative tool for the comparison of sparsifying properties of various operators. Areas under the corresponding curves in Fig. 1 (b) show that both first and second derivative operators in parametric dimension provide a sparsification of the image series, with the second order differentiation exhibiting a more consistent performance as a sparsifying operator.

Figure 1.

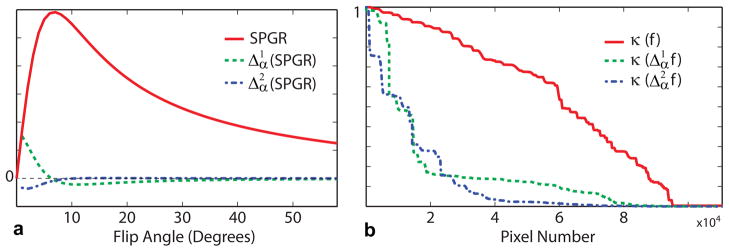
Illustration of signal evolution and the effect of differentiation operators in the flip angle dimension on SPGR signal (digital phantom data, T₁=1 s, T_R=8 ms). a: Dependence of SPGR signal and its first and second derivatives on the flip angle. Note that the second derivative is close to zero in the range of interest. b: Normalized non-increasing rearrangements of the VFA image series and its 1st and 2nd divided differences in flip angle dimension. The corresponding l₁ norms are 0.3624, 0.1239, and 0.1031.

We will further study the performance of these transforms by comparing series of images reconstructed by solving:

$$\overline{f}=arg\underset{f}{min}\left({\left|\right|\overline{E}\overline{f}-\overline{d}\left|\right|}_2^2+\lambda {\left|{\mathrm{\Delta }}_{\alpha }^n\overline{f}\right|}_{l_1/l_2}\right)$$ [10]

with n = 1 and 2. In what follows, we will refer to these variants of the problem as ${\mathrm{\Delta }}_{\alpha }^1$ and ${\mathrm{\Delta }}_{\alpha }^2$ p-CS regularization, respectively.

Application to Multi-Component Relaxometry in Steady State

Relaxation behavior of different tissue compartments as revealed by T₁ and T₂ spectra may elucidate important information about tissue microstructure. For example, in white matter imaging, signal with the short T₂ values (less than 50 ms) from the so-called myelin water component is associated with water trapped between myelin sheath layers (2). The ratio of the short T₂ signal to the total signal, or myelin water fraction (MWF), is a specific imaging marker of myelination and may play an important role in treatment and management of demyelinating diseases like multiple sclerosis (32).

One promising approach to quantify the water component within the myelin bilayers is to fit a two-compartment model (mcDESPOT) of T₁ and T₂ relaxation to VFA SPGR and VFA bSSFP (balanced steady-state free precession) measurements (4). The mcDESPOT modeling equations contain seven free and four control parameters and thus may be too complex to utilize for stable parameter mapping using approaches based on analytical models (21). We note that similar to the SPGR signal (Fig. 1), a smooth dependence on flip angle values exists for the bSSFP signal, making the previous assumptions and reconstruction design for SPGR acquisitions also valid for bSSFP (26). Therefore, we also investigated the use of Eq. [10] to reconstruct not only VFA SPGR but also VFA bSSFP datasets in mcDESPOT method for accelerated mcDESPOT MWF mapping.

METHODS

Implementation Details

We compare image reconstruction and parametric map estimation from the image series obtained by minimizing the expression in Eq. [10] with the first and second discrete derivatives (divided differences) in the parametric dimension as well as using iterative SENSE (28), spatial total variation (TV) sparsity constraint (14), and a basic version of PCB technique (Eq. [3]) based on dimensionality reduction through PCA of the discretized analytical signal model (22). We also consider regularization with ℓ₂ norm in Eq. [10] to study the effect of the norm on reconstruction results. For each reconstructed image series, T₁ (or longitudinal relaxation rate R₁=1/T₁) values were estimated using pixelwise non-linear least squares fit of Eq. [9];.

All reconstruction and data fitting algorithms were implemented in Matlab (MathWorks, Inc., Natick, MA, USA). Implementation details of p-CS algorithm are provided in the Appendix. For the solution of both the problem in Eq.[10] and TV minimization, we implemented iteratively reweighted least squares algorithm (33) (total 10 reweighting). The least squares inversion step was performed via a conjugate gradient algorithm for all methods. The iterations were continued until relative error, defined as a ratio of squared norms of k-space residual on the n-th step and first step, fell below a preset tolerance (ε) or maximal number of iterations (N) were reached (34). These parameters were set at ε = 1e-7 and N = 200 for noisy data and ε = 1e-16 (numerical precision) and N = 2000 in the noise-free case. Following (22), we obtained a PC basis by applying PCA to the matrix formed by sampling analytical signal model of Eq. [9] on a dense grid (total of 1000 samples) of T₁ values in the physiologically relevant range in human head at 1.5 T ([0.1 4.3] s) (35). The first three principle components were chosen to form the basis for PCB reconstruction (ℓ₂ compression error ~0.8%).

Simulation Studies

For the simulation studies, we used a realistic digital brain phantom from the Brainweb database (www.bic.mni.mcgill.ca/brainweb/) that describes image pixels as a mix of different tissues (36). An eight-channel VFA SPGR 2D Cartesian acquisition (Eq. [9]; image matrix 128×128, FA=[1, 2, 3, 4, 5, 6, 8, 10, 13, 16]°, T_R = 5 ms) of the digital brain was simulated using brain tissue parameters at 1.5 T (35). The coil sensitivities were obtained in a separate phantom scan (5) and combined with information about object support to facilitate convergence of iterative SENSE reconstruction (28). To assess sparsifying properties of the transforms in conditions closely approximating the theoretical requirements of compressed sensing (37), we started with a random sampling pattern with uniform distribution and with zero noise level in the data samples. This was done by randomly selecting columns of the encoding matrix used to obtain the reference data for each undersampling factor R from R=1 (fully sampled case) to R=12. The central 8×8 square in kx-ky plane was always fully sampled. We carried out a series of reconstructions for a range of λ to determine the optimal value, chosen as the one minimizing normalized root mean square error (nRMSE) of R₁ estimates in a specific brain region:

$$\mathit{nRMSE}=\frac{{\left|\right|R_1-{\stackrel{\sim }{R}}_1\left|\right|}_{2,\mathrm{\Omega }}}{{\left|\right|R_1\left|\right|}_{2,\mathrm{\Omega }}}$$ [11]

where R₁ and R̃₁ are computed from the fully sampled reference and accelerated data, respectively, and ||·||_2,Ω denotes the l₂ norm measured over the brain region Ω composed of white matter, gray matter and CSF regions as defined in the realistic digital brain phantom (36).

To study two independent sources contributing to a composite nRMSE measure, estimation bias (accuracy) and noise propagation (precision), separately, we carried out a series of Monte-Carlo experiments. One hundred realizations of i.i.d. Gaussian noise (K=100, mean SNR of 60 for fully sampled case) were added to k-space data and each data set was reconstructed with the proposed methods and subsequently fit to Eq. [9] to yield R₁ maps $R_1^{(k)}$, k=1, …, K₁. Additionally, the same number of reconstructions from fully sampled data with the same noise levels was performed. The reconstruction bias was assessed by taking a pixelwise mean across all reconstructed Monte-Carlo samples

$$\langle R_1\rangle =\frac{1}{K}\sum _{k=1}^K{R}_1^{(k)}$$ [12]

and calculating nRMSE for the obtained map. The propagation of noise to R₁ was estimated by calculating a noise amplification factor equivalent to g-factor in parallel MRI (5):

$$g_{R_1}=\frac{{\sigma }_R}{{\sigma }_F\sqrt{R}}$$ [13]

where ${\sigma }_R^2$ and ${\sigma }_F^2$ are noise variances for reduced (by a factor of R) and full data reconstructions calculated across Monte-Carlo samples as follows:

$${\sigma }^2=\frac{1}{K-1}\sum _{k=1}^K{\left(\langle R_1\rangle -R_1^{(k)}\right)}^2$$ [14]

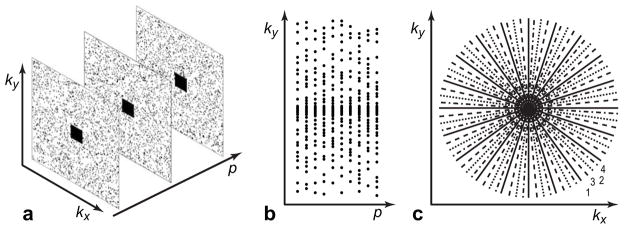
The Monte-Carlo experiments were additionally repeated for two practical sampling schemes: randomly selected phase encoding lines with variable density undersampling rate linearly changing from 1 in the center of k-space (6 fully sampled lines) to 6 at the edges of k-space (total R=4), referred to as VD sampling, and radial sampling pattern (R=10) interleaved with bit reverse scheduling (38). Images in Fig. 2 illustrate sampling patterns used in the Monte-Carlo experiments.

Figure 2.

Sampling patterns used in Monte-Carlo experiments: a: Uniform density random undersampling of k-space with fully sampled center (the first three frames). b: Variable density random undersampling of phase encoding lines (the fully sampled read-out direction is perpendicular to the drawing plane). c: Radial trajectory with bit-reversed scheduling of interleaves in parametric direction (the first four frames).

In-Vivo Data

Informed consent was obtained from all human volunteers prior to the exams (total number of 6). Fully sampled data were acquired on a clinical GE 3.0 T scanner (GE Healthcare, Waukesha, WI, USA) using an 8-channel head coil. The hybrid radial (in-plane)/Cartesian (through-plane) SPGR data (FOV=220×220 mm, slice thickness = 3 mm, 20 slices, FA=[1, 3, 5, 7, 9, 11, 13, 15, 17, 19]°, T_R = 6 ms) were retrospectively undersampled (R=6) in an interleaved manner with bit reverse scheduling (38). Flip angle maps were acquired in the same session with actual flip angle imaging (AFI) (39,40) and were used to correct for spatial variation in the excitation flip angles on T₁ estimation stage. The fully sampled T₁ maps were supplied to FAST tool from FSL software library (FSL; FMRIB, Oxford, UK) to produce a 3-class segmentation (WM/GM/CSF).

Datasets for mcDESPOT processing were collected with image matrix 96×96 and 2-mm³ isotropic resolution (SPGR: T_R = 3.7 ms, FA =[3, 4, 5, 6, 7, 9, 13, 18]°; bSSFP: T_R = 4.5 ms, FA=[10, 14, 18, 23, 29, 35, 45, 60]°). Balanced SSFP scans were repeated twice for ϕ = 0°/180° hase cycling to remove the effect of SSFP banding artifacts to avoid areas of signal zeroing and estimate B₀ field as described in (41). Next, all mcDESPOT datasets were retrospectively undersampled in the phase encoding direction and reconstructed using parallel imaging alone and ${\mathrm{\Delta }}_{\alpha }^2$ p-CS. Note that model-based PCB reconstruction was not applied in this case due to excessive complexity of the multi-parametric model. MWF maps were derived from the resulting image series and compared to the maps obtained from the fully sampled data.

RESULTS

Simulations

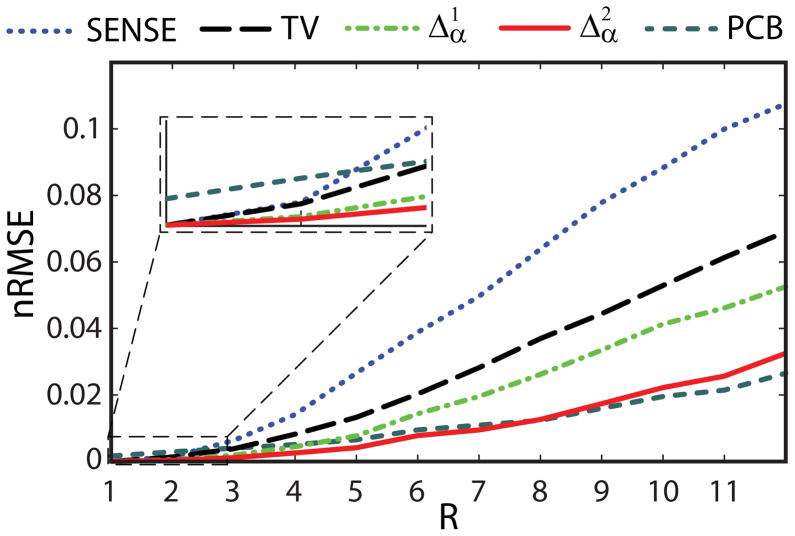
Plots in Fig. 3 illustrate the dependence of R₁ estimation error on the acceleration factor for noise-free, randomized data samples. All considered regularization approaches, as well as model-based PCB method, clearly outperform SENSE, indicating that use of prior knowledge can efficiently reduce the error of image reconstruction, especially at higher reduction factors. Methods relying on prior information in parametric dimension ( ${\mathrm{\Delta }}_{\alpha }^1/{\mathrm{\Delta }}_{\alpha }^2$ p-CS regularization and PCB) consistently outperform image space regularization with TV penalty. ${\mathrm{\Delta }}_{\alpha }^2$ p-CS regularization entails a significantly more accurate reconstruction than ${\mathrm{\Delta }}_{\alpha }^1$ p-CS regularization, as a result of improved sparsification in parametric dimension. The errors of model-based PCB reconstruction and ${\mathrm{\Delta }}_{\alpha }^2$ p-CS regularization remain close, with the latter outperforming the former for R<8 and the trend reversing for R>8. For model-based PCB approach, a non-zero error exists even for the fully sampled case (R=1), due to linearization of the nonlinear signal model, which may cause a mismatch between the assumed model and actual signal and propagate into final solution through data consistency term, the effect mentioned in (22). For higher accelerations, the relative effect of the mismatch becomes less significant compared to undersampling error, hence performance of PCB approaches that of ${\mathrm{\Delta }}_{\alpha }^2$ p-CS regularization or slightly exceeds it for very high acceleration factor R>8.

Figure 3.

Comparison of error in R₁ maps versus total acceleration factor R for images obtained with iterative SENSE, SENSE with spatial TV penalty, proposed p-CS regularized reconstructions using first and second divided differences in the flip angle dimension, and analytical model-based PC-basis reconstruction (PCB) (randomized trajectory).

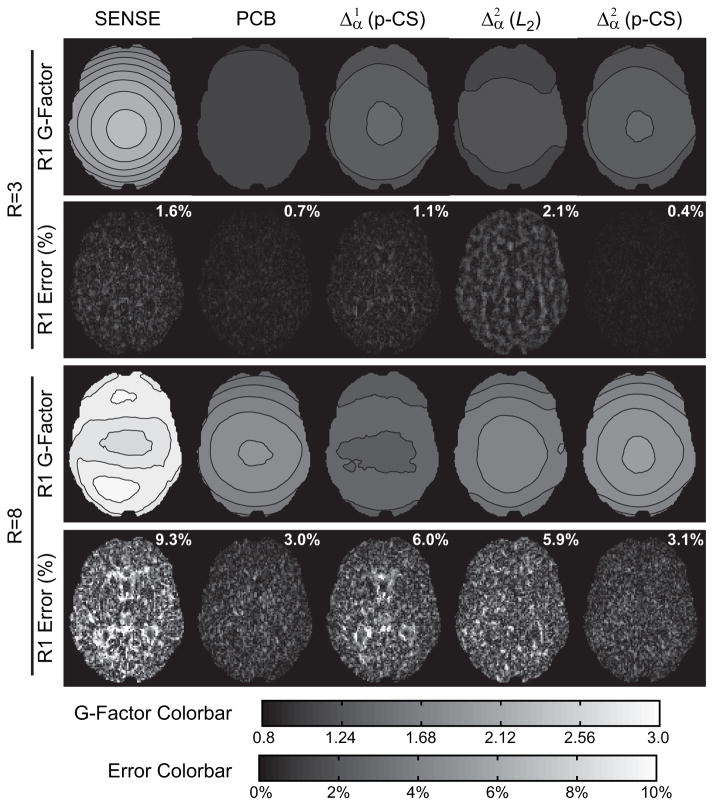
Figure 4 shows results of studying noise propagation and accuracy of R₁ mapping for the methods employing prior information in parametric dimension (two representative acceleration factors R=3 and 8, noisy data). The p-CS regularization with second derivative ( ${\mathrm{\Delta }}_{\alpha }^2$) significantly outperforms the first ( ${\mathrm{\Delta }}_{\alpha }^1$) in terms of accuracy, especially in high acceleration regime (R=8), which may be attributed to better sparsifying properties of the second derivative operator (Fig. 1). At the same time, noise amplification (g-factor) for ${\mathrm{\Delta }}_{\alpha }^2$ p-CS in this regime exhibits somewhat higher values while still staying within a tolerable range (g-factor less than 2), which may be explained by additional differentiation compared to ${\mathrm{\Delta }}_{\alpha }^1$ and is further addressed in the Discussion section. PCB reconstruction and second difference ( ${\mathrm{\Delta }}_{\alpha }^2$) p-CS regularization demonstrate comparable performance both in terms of accuracy and noise propagation, both significantly outperforming non-regularized SENSE reconstruction. At the same time, utilization of the second difference operator ( ${\mathrm{\Delta }}_{\alpha }^2$) with ℓ₂ norm, which heavily penalizes outliers, results in a significant loss of accuracy compared to ℓ₁-based p-CS regularization, which indicates that ${\mathrm{\Delta }}_{\alpha }^2$ does not provide a complete sparsification of signal evolution in the parametric dimension.

Figure 4.

Results of Monte-Carlo experiments for randomized Cartesian data (R=3,8). Rows 1 and 3: g-factor for R₁ maps. Rows 2 and 4: R₁ bias (accuracy) maps with the corresponding normalized mean squared errors.

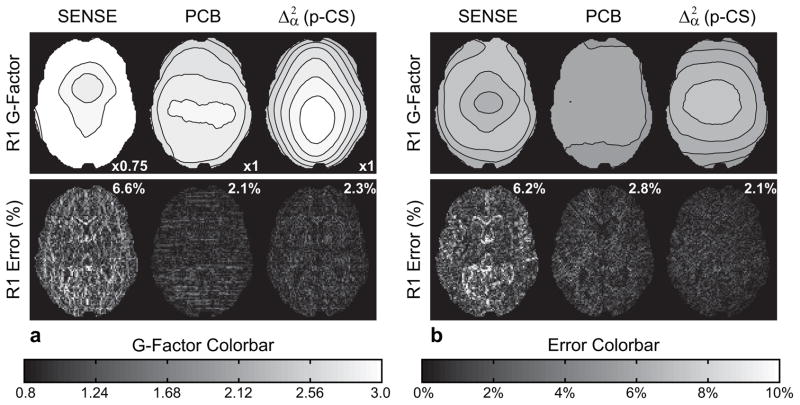
The performance of these two constrained reconstruction approaches, as well as iterative SENSE, was further compared for two practical k-space sampling trajectories (VD and radial sampling) (Fig. 5). The relative performance of the three algorithms remains the same with both p-CS and PCB exhibiting similarly low reconstruction bias and high quantitative accuracy as confirmed by T₁ values measured in ROIs in white and gray matter (Table 1). However, noise properties are significantly affected by the choice of sampling trajectory. Indeed, even for constrained ${\mathrm{\Delta }}_{\alpha }^2$ p-CS and PCB reconstructions values of g-factor at R=4 VD sampling exceed g-factor values for R=8 random sampling and R=10 radial sampling, while non-regularized SENSE reconstruction predictably is affected the most. This stark difference in noise properties is due to uncontrolled large gaps at k-space edges produced by random undersampling of phase encoding lines and somewhat coherent undersampling artifacts, both of which may be hard to resolve even by utilizing prior information. By contrast, the controlled undersampling of k-space by radials and dispersed undersampling artifacts provide a more benign acquisition. Even for a high R= 10, accuracy degradation occurs mostly along edges, which indicates problems with the reconstruction of higher spatial frequency content (the most undersampled portion of k-space in radial acquisitions).

Figure 5.

Results of Monte Carlo experiments: g-factor (top) and bias (bottom) of R₁ maps for VD (R=4) sampling (left) and radial (R=10) sampling (right) with the corresponding normalized mean squared errors of R₁ error maps.

Table 1.

ROI-based T₁ measurements in GM/WM in simulation studies for practical k-space sampling trajectories.

	Reference T1, ms	VD Cartesian (R=4)			Radial (R=10)
		SENSE	PCB	${\mathrm{\Delta }}_{\alpha }^2$ p-CS	SENSE	PCB	${\mathrm{\Delta }}_{\alpha }^2$ p-CS
WM	781.8	837.7	780.1	780.5	793.7	784.4	781.3
GM	1102.5	1138.7	1109.0	1109.6	1110.7	1099.3	1106.2

In-Vivo Experiments

Figure 6 shows the reconstruction results for in-vivo radial acquisition. Table 2 shows results of quantitative measurement of T1 values in ROIs defined in Fig. 6a. A representative SENSE image is degraded by streaking artifacts and correlated noise, which propagate in the T1 map causing a significant bias of resulting T1 values (Table 1), which is consistent with T1 bias observed in low-SNR conditions (42). These effects are reduced in TV-regularized SENSE, which, however, exhibits loss of spatial resolution through blurring. ${\mathrm{\Delta }}_{\alpha }^2$ p-CS regularization and model-based PCB reconstruction efficiently suppress noise in the source images and subsequently derived T₁ maps without compromising spatial resolution. For most ROIs consisting predominantly of a single tissue type (ROI#1-5), both methods exhibit high compliance with quantitative measurements derived from fully sampled data. However, model-based PCB gives a noticeably higher error than p-CS approach for ROI#6, which contains pixels with partial voluming.

Figure 6.

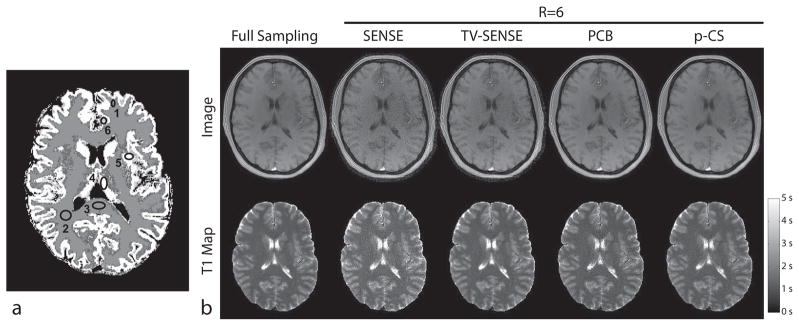
Results of in-vivo radial T1 mapping experiments. a) Brain segmentation with numbered ROIs. b) Representative images and corresponding T1 maps from different reconstruction methods.

Table 2.

Results of T₁ measurements in brain ROIs in Fig. 6a (in-vivo studies, radial trajectory).

ROI #	Reference T1, ms	$T_1^{\mathit{true}}-T_1^{\mathit{recom}}$, ms
		SENSE	TV-SENSE	PCB	${\mathrm{\Delta }}_{\alpha }^2$ p-CS
1	1106.8	− 190.7	−19.2	1.5	−1.6
2	1198.2	− 184.3	−19.5	−7.1	−1.1
3	1239.4	− 227.4	−15.2	6.9	6.6
4	1608.4	−245.7	−9.6	16.4	5.7
5	1707.3	−361.4	−68.4	−14.7	2.0
6	2021.3	−523.2	−60.5	−37.6	0.5

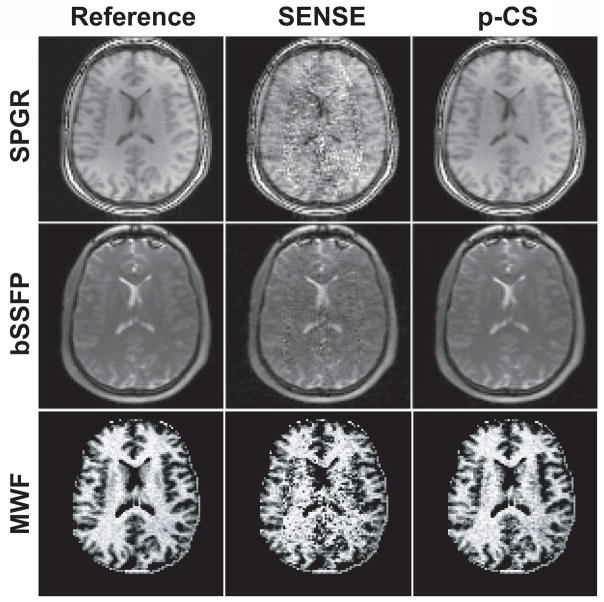
Similar distinctions between ${\mathrm{\Delta }}_{\alpha }^2$ p-CS regularized and unregularized reconstructions can also be observed for MWF mapping with mcDESPOT (Fig. 7). Again, SENSE images contain increased, spatially non-uniform noise due to high g-factor. The proposed ${\mathrm{\Delta }}_{\alpha }^2$ p-CS regularization significantly suppresses noise in the reconstructed images and in the resulting myelin water fraction (MWF) maps.

Figure 7.

Performance of p-CS for mcDESPOT (uniformly undersampled Cartesian data, R=3.95). Top and middle rows: representative source images for mcDESPOT obtained with SPGR (α= 9°) and one of bSSFP (α= 29°, phase cycling ϕ= 180°) acquisitions, respectively. Bottom row: myelin water fraction (MWF) maps obtained by mcDESPOT processing.

DISCUSSION

We described a novel method for accurate accelerated MR parameter mapping via improved reconstruction of the corresponding image series from incomplete data. The proposed method utilizes the parametric dimension to implement sparsity-promoting CS-type regularization (p-CS). Briefly described in (25,26), our algorithm relies on the assumption that signal varies smoothly in the parametric dimension, thereby admitting sparsification by differentiation in this dimension. The parametric image series is reconstructed by solving a joint regularized minimization problem in x-p space with a penalty term on the size of the derivatives in the parametric dimension as measured by a CS-like, sparsity promoting robust norm. Regularization by the second derivative ( ${\mathrm{\Delta }}_{\alpha }^2$) demonstrated an excellent combination of low reconstruction bias and efficient suppression of noise amplification for both low and high accelerations without typical deficiencies of image-space based regularization such as resolution loss (Fig. 7). The proposed method was successfully demonstrated with VFA T₁ mapping and mcDESPOT myelin water fraction (MWF) mapping.

The proposed p-CS regularization compared favorably (Figs. 3–6, Tables 1–2) with a basic implementation (without additional spatial regularization terms) of approach of (22), which relies on availability of analytical signal model in parametric dimension to design a new reconstruction basis through PCA. Although a comparable performance of a method based on a general transform (the proposed technique) and a method based on a more accurate problem-tailored prior knowledge (PCA-based technique) may seem paradoxical at first, it can be explained by the fundamental difference between the two approaches. Our method exploits sparsity in parametric dimension in the traditional CS sense, i.e. by employing sparsity promoting ℓ₁ norm during reconstruction, while the model-based approach relies on dimensionality reduction in the least squares problem (Eq. [3]) by learning a sparse representation from the analytical signal model through a PC basis prior to reconstruction. From the mathematical point of view, this solution is equivalent to finding the best ℓ₂ approximation to the hyperplane defined by the data consistency term from a finite-dimensional subspace of a fixed low dimension. Since in such problem formulation the solution is sought only among images whose signal evolution in parametric dimension can be represented exactly by a linear combination of PC basis elements, it is critical to choose a basis that can provide a most accurate representation of the signal for a range of free parameters. It appears that for the cases, when the analytical signal model is known, PC basis may provide a near-optimal choice of approximation subspace, though a residual approximation error exists even in a non-accelerated case (Fig. 3). Similar least squares approximation accuracy cannot be achieved by a general transform/approximation basis, such as the second derivative operator proposed in this work, as illustrated by the results in Fig. 4 of using ${\mathrm{\Delta }}_{\alpha }^2$ with ℓ₂ norm. However, when used in conjunction with a robust ℓ₁ norm, ${\mathrm{\Delta }}_{\alpha }^2$ p-CS regularization exhibits performance comparable to the PCB reconstruction. Hence, the use of ℓ₁ norm promoting sparsity in parametric dimension was essential for reconstruction success in our method, while it is not required in PCB approaches (22,23). We anticipate that a combination of model-based dimensionality-reduction techniques with ℓ₁ norm acting in parametric dimension may further improve performance of MRI relaxometric techniques, which is a subject of continuing research (43,44). Additional performance gains may be expected for both PCB and p-CS methods with inclusion of ℓ₁ norm-based spatial regularization terms, as was proposed in a full version of REPCOM technique (22) or using nonlinear image enhancement on the post-processing stage (45). As the proposed regularization relies on a general type of knowledge about signal evolution in the parametric dimension rather than on precise knowledge of the analytical signal model, we believe that the proposed ${\mathrm{\Delta }}_{\alpha }^2$ p-CS regularization may be especially useful in situations when it is infeasible to use the analytical model because of its high complexity (21), as in case of multi-parametric methods such as mcDESPOT, or in the presence of signal deviations from the expected analytical models, for example, due to partial voluming (Table 2).

In this paper, we additionally studied the effect of k-space sampling trajectories on the performance of the tested methods. We undertook an incremental approach, starting with randomized sampling with uniform distribution in undersampled areas (37) and then proceeding with more practical choices of acquisition trajectories, such as randomized phase encodes with variable density undersampling and radial sampling. All randomized sampling schemes demonstrated increased noise amplification (g-factor) often accompanied by loss of accuracy compared to a radial trajectory undersampled with much higher reduction factor (Fig. 5). As randomized sampling schemes often produce large k-space gaps, the need to resolve uncertainty about missing spatial frequencies led to tradeoffs between restoration of higher spatial frequencies and noise amplification, with the non-regularized reconstruction often incurring unacceptably large errors (Fig. 4, 5). Although regularized approaches mollified this effect to different degrees, irregularity of sampling hindered their performance as well. This phenomenon was most pronounced for VD sampling, where the detrimental effect of large regions of missing high spatial frequency information was coupled with semi-regular aliasing artifacts from the choice of sampling pattern. Although VD sampling was demonstrated in (46) to minimize sampling basis coherence for the case of signals, which are sparse in Haar basis (TV minimization), this sampling strategy appears to be suboptimal in terms of g-factor properties for the considered problem of p-CS based reconstruction. At the same time, for an interleaved radial acquisition, we observed a significantly more benign behavior of g-factors and improved reconstruction accuracy for all reconstruction approaches even at high acceleration factors. Thus, trajectories with controlled gap size may be a better practical match for constrained reconstruction approaches as was previously noted in (47). Thus, a trajectory with controlled maximal distance between neighboring samples (such as radials and regularly undersampled Cartesian (Fig. 7) or Poisson disk sampling in 3D (48), may be more valuable for practical implementation of sparsity promoting regularization with improved noise/accuracy performance. This observation is consistent with conclusions made previously by other authors studying the effect of sampling schemes on performance of CS-driven techniques (49). Finally, although a proper choice of sparsifying transform is important to ensure unbiased estimation, for a more optimized performance the design of CS-like, sparsity promoting reconstruction may need to include consideration of noise properties of both trajectory design and the sparsifying transform. For instance, while application of higher order derivatives in parametric dimension may provide a better sparsification of the image series, increased noise penalty incurred from additional differentiation may negate the sparsity advantage for ${\mathrm{\Delta }}_{\alpha }^n$ for n>2.

Similar to methods relying on knowledge of the analytical models, the proposed method requires a sufficient number of measurements in the parametric dimension to support regularization (from our experience, eight and more for ${\mathrm{\Delta }}_{\alpha }^2$ -regularization). The requisite number of measurements does not impose any additional scan time penalties as many MR parameter mapping techniques already satisfy this requirement. Indeed, while in theory VFA T₁ mapping needs only two “ideal” angles to estimate a particular T₁ value, typically more angles are required to obtain optimized estimates for a range of T₁ values observed in different tissues/pathologies. Several studies suggest using 6–10 different flip angles to estimate T₁ in the human brain (50,51). A typical mcDESPOT protocol acquires 8–10 flip angle points for both SPGR and bSSFP (potentially with and without phase cycling) datasets to fully describe the two-compartment model of T₁/T₂ relaxation. In addition, p-CS may be effective for quantitative MRI methods that acquire many more measurements along smoothly varying signal curves in the dimension of control variable such as spin-echo T₂ mapping, inversion-recovery T₁ mapping (preliminary results obtained but not shown), and quantitative magnetization transfer imaging (1).

CONCLUSIONS

In this work, we described and evaluated a method that utilizes smoothness of signal evolution in the parametric dimension as a base for a novel CS-type, sparsity promoting regularization strategy for parametric image series reconstruction from incomplete data. The method was successfully applied to VFA T₁ mapping and mcDESPOT myelin water fraction (MWF) mapping. The proposed p-CS regularization may be a valid alternative to image space-based regularization or to analytical model-based reconstruction, when traditional representation systems are inadequate for modeling of actual image content or when it is not feasible to use the underlying analytical image model. The developed method may facilitate the use of relaxometric techniques, including whole brain mcDESPOT MWF mapping, in clinical settings by making scan times more tolerable for patients who have difficulties remaining still for extended periods of time (children and elderly populations).

APPENDIX

Choice of Hybrid Norm

Although other choices are available for a definition of hybrid l₁/l₂ norm (18) used in Eq.[10], we followed (52) setting:

$${\left|\right|x\left|\right|}_{l_1/l_2}=\sum _k\left(\sqrt{1+{|x_k/\sigma |}^2}-1\right)$$ [15]

where the balance between l₁ and l₂-like behavior is determined by the parameter σ. As in (52), we defined σ to be 0.6 of the standard deviation of x after the first reweighting. Then, we gradually decreased its value in the subsequent reweightings similar to (53) with one tenth of the original value in the last reweighting in order to shift the norm behavior more towards l₁ mode.

Discretization of Derivatives

Our approach to discretization of the derivatives takes into account the fact that parametric dimension may be sampled in a non-uniform fashion, e.g. as proposed in (4) for multi-component relaxometry. For signal values (s₁, s₂, …, s_P) corresponding to flip angle values(α₁,α₂, …, α_P), we approximate the values of derivatives ∂S∂α and ∂²S∂α² by the corresponding divided differences:

$${\mathrm{\Delta }}_{\alpha }^1{s}_k=\frac{s_{k+1}-s_k}{{\alpha }_{k+1}-{\alpha }_k}$$ [16]

$${\mathrm{\Delta }}_{\alpha }^2{s}_k=\frac{{\mathrm{\Delta }}_{\alpha }{s}_{k+1}-{\mathrm{\Delta }}_{\alpha }{s}_k}{({\alpha }_{k+1}+{\alpha }_{k-1})/2}$$ [17]

For these definitions to be applicable to the first and last points in the sequence, we need to augment the vectors (s_k) and (α_k) in a consistent way. For example, for ${\mathrm{\Delta }}_{\alpha }^n$, since our model assumes sparsity of the second derivative, we pad these sequences linearly by setting

$$s_0=2s_1-s_2,s_{-1}=2s_0-s_1,s_{P+1}=2s_P-s_{P-1},s_{P+2}=2s_{P+1}-s_P$$ [18]

The same augmentation approach was used for the vector (α_k). This ensures that the second divided difference vanishes in the additionally introduced endpoints.