Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Aug 12;3:2384. doi: 10.1038/srep02384

Friction coefficient dependence on electrostatic tribocharging

Thiago A L Burgo 1, Cristiane A Silva 1, Lia B S Balestrin 1, Fernando Galembeck 1,2,a
PMCID: PMC3740278  PMID: 23934227

Abstract

Friction between dielectric surfaces produces patterns of fixed, stable electric charges that in turn contribute electrostatic components to surface interactions between the contacting solids. The literature presents a wealth of information on the electronic contributions to friction in metals and semiconductors but the effect of triboelectricity on friction coefficients of dielectrics is as yet poorly defined and understood. In this work, friction coefficients were measured on tribocharged polytetrafluoroethylene (PTFE), using three different techniques. As a result, friction coefficients at the macro- and nanoscales increase many-fold when PTFE surfaces are tribocharged, but this effect is eliminated by silanization of glass spheres rolling on PTFE. In conclusion, tribocharging may supersede all other contributions to macro- and nanoscale friction coefficients in PTFE and probably in other insulating polymers.

Triboelectricity is formed whenever two solids rub, slide or roll on each other1,2 and the resulting charges on both surfaces contribute electrostatic forces to their mutual interactions3. Attraction between oppositely charged surfaces should push the solids together thus requiring additional pull to slide one solid on the other, according to Amontons' law4,5. Surprisingly, the extent of the effect of triboelectricity on friction coefficients has not yet been demonstrated for friction between two dielectric solids at the macroscale, under well-defined conditions, even though many authors have raised this possibility in other cases. In a recent review6 on friction and energy dissipation mechanisms in adsorbed molecules and molecular thin films, Krim states that insulating materials undergo contact electrification and subsequent charge transfer to a passing AFM tip that result in large electrostatic frictional forces. According to Krim, studies of this effect are quite challenging, yet increasingly important.

In the nanoscale there is rich information on the electronic and phononic contributions to friction in metals and semiconductors. Park et al.7,8 studied the electronic contributions to friction in silicon pn junctions and Qi et al.9 examined GaAs, while Altfeder and Krim10 studied levitation and atomic-scale friction of Fe on YBCO by magnetic force microscopy. They discussed the results considering the underlying atomic-scale electronic and phononic mechanisms that give rise to friction and the later concluded “that contact electrification and static electricity may play a significant role in the non-superconducting phase”. These authors further suggest that static electricity effects should be included in comprehensive atomic-scale treatment of friction whenever insulating materials are involved. These examples show that nanotribology is currently a dynamic area that is bringing new information relevant to the comprehension of macroscopic friction phenomena11.

Budakian and Putterman12 did macroscopic measurements of metal-insulator (poly(methyl methacrylate) – gold ball) surfaces in relative motion and found a quantitative correlation between charge and friction, suggesting that triboelectrification and friction have a common origin.

The effect of triboelectricity on macroscopic friction coefficients in metals was also demonstrated using films coated with self-assembled monolayers13, electrodes14 and bearing steel15. The effect of AC and DC fields on friction angle of steel on PZT (lead zirconium titanate) was also observed by Seto16 who found equal effects of positive and negative bias.

However, the models and mechanisms described in the literature for friction and wear seldom mention the tribocharging effects that are necessarily observed whenever two solids are in mutual contact and these have not been considered in a recent and detailed experimental-theoretical analysis17. Classical work on the validity of Amontons' law assigns the effect of increasing normal forces on friction to the plastic and elastic deformation of surface protuberances and increasing contact area18,19. Another classical paper demonstrated mass transfer between PTFE surfaces sliding on other solids, which were considered to be the main factor for decreased friction coefficients20 but without considering the associated charge effects. Current work on friction acknowledges a number of surface composition (including adsorbed layers21), morphology, environment, geometry22 and other factors on friction coefficients. Great progress in this direction was obtained thanks to the introduction of scanning probe techniques that led to progress in relating surface molecular features to friction coefficients, in the nanoscale6,7,8,9,10,11,23,24. To achieve control of the charging state of the surface, this work is often done on samples immersed in aqueous solutions25 that is adequate from the fundamental point of view but is not relevant to dry insulator surfaces. Thus, results on dry insulating surfaces did not yet provide direct information on their electric state but these are likely to be more or less charged while friction measurements are being performed, even in nanocomposite26 and other systems specially designed for tribological applications. A careful recent work on this subject closes by stating some questions, and the following one clearly presents the problem: “What are the mechanisms of the charging phenomena, of charge trapping-detrapping and of charge movement? Is this related to stresses in the material under pressure or during rubbing27?”

We assign the current backward situation in dielectrics to the still widespread lack of understanding of the mechanisms and patterns of electrostatic charging of insulators, at the atomic-molecular level28, as opposed to metals and semiconductors. This can be understood considering the state of knowledge on contact and tribocharge formation at the molecular level and it was expressed by Ireland29 in this phrase: “The primary obstacle to inclusion of sliding triboelectrification into our model is the mysterious and complex nature of the process”. Many authors have reviewed this topic28,30 pointing to the open questions and opposing views concerning the nature of the charge-bearing species, including conflicting conclusions on the relative importance of electrons or ions.

The mutual effect of electrostatic forces between charged dielectrics on friction coefficients has been shown only indirectly as yet, in the literature. For instance, macroscopic crystals were formed by self-assembly of polymer spheres charged by contact electrification31 and surface charging by scratching with a scanning AFM tip was also observed32. In a different context, the force applied to textile thread was shown to depend on the nature and electrostatic charging ability of the sliding thread supports33. Nakayama34 scratched sintered alumina, soda lime glass, Si3N4 and PTFE with a diamond stylus, finding concurrent changes between potential and friction force.

Fortunately, steep progress has been achieved in the last few years30. Recent work from the present authors35 showed the formation of macroscopic charge patterns in solid surfaces, instead of the often assumed uniform charging due to one-way charge transfer, which is implicit in the widespread but disputed36 concept of triboelectric series2. It is now clear that rubbing two polymers or a polymer and glass causes the formation of domains with excess positive charge side by side with domains with excess negative charge in both contacting solid surfaces, even though the overall charge on each solid is non-zero. Moreover, it is now clear that in the tribocharged polytetrafluoroethylene (PTFE)-polyethylene (PE) pair the positive ions derive from mechanochemical transformation of PE chains while the negative ions derive from PTFE35. Both types of ions are selectively extracted by rinsing with common solvents and this is now the basis for a simple but effective technique for static charge removal from polymers and other insulators37.

Besides, it is now possible to prepare stable, charged macroscopic dielectric polymer surfaces35 e.g. by sliding glass over a PTFE film that produces a largely negative surface with lower local variations than other pairs of materials. Half-life for potential decay in these surfaces is in the range of a few days so that samples can be prepared for mapping static potential distribution on their surfaces and they can be selected for further use as well-defined and stable charged polymer surfaces. In this work, they were used to measure the friction coefficient dependence on the electrostatic surface potential of an insulator, for the first time.

Results

Four sets of results are described here, on rolling38,39 and sliding friction. In some experiments, PTFE was tribocharged prior to measuring the friction coefficients, while in others tribocharge formation was followed by observing particle immobilization on the PTFE substrate. In one of these, static friction coefficients were measured on the tribocharged particles.

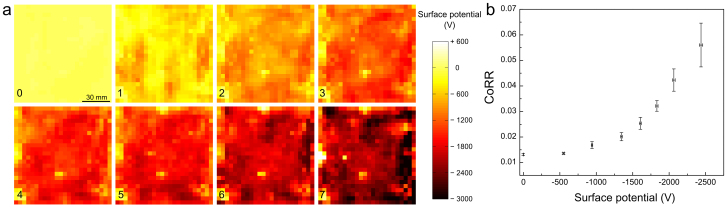
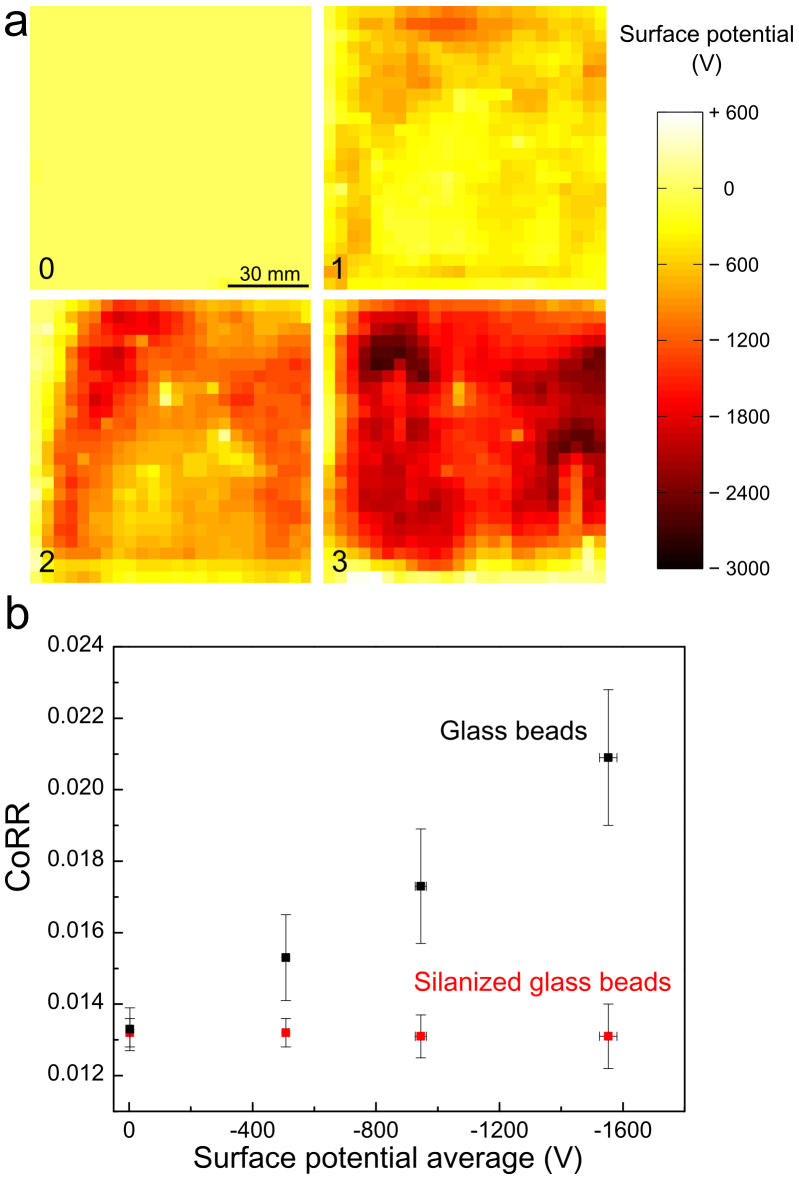
The first set of data shows that rolling friction of glass spheres increases with electrostatic potential on PTFE films. These were previously charged by repeatedly rubbing flat glass over PTFE and thus producing PTFE films with electrostatic potential in the +300 to −3.300 V range, as shown in Fig. 1a. Neutral glass spheres roll over charged PTFE but they quickly stop, after moving for only a fraction of the distance observed in uncharged PTFE, showing that film charging introduces a powerful mechanism for mechanical energy dissipation. The widely used standard for friction assessment, the coefficient of rolling resistance (CoRR) of glass spheres on charged films was measured and it is shown in Fig. 1b, as a function of the average potential on the film. CoRR increases many-fold in charged PTFE, in a potential range that is easily achieved by rubbing this polymer with glass and other common materials. On the other hand, as seen in Fig. 2, CoRR is unaltered when hydrophobic glass beads prepared by treating with CH3SiCl roll over tribocharged PTFE.

Figure 1. Determination of CoRR of glass beads rolling on tribocharged PTFE surfaces.

Figure 1

Open in a new tab

(a) The potential map for each plate used. (b) CoRR versus average surface potential of tribocharged PTFE plates. Vertical error bars are mean standard deviations from ten replicate measurements while the horizontal bars are standard deviations of average potential for all the pixels on each plate.

Figure 2. CoRR measurements of different glass beads.

Figure 2

Open in a new tab

Comparison between the effects of PTFE tribocharging on silanized and neat glass spheres. No tribocharging effect is observed on silanized spheres.

In a related experiment, uncharged glass spheres are placed on the surface of an uncharged, framed PTFE film and the whole setup is mounted on a reciprocating table. The beads move quickly and independently to start with but they later form clusters and stop. Fig. 3 shows three sum images obtained at different times, from the start to later in the experiment. Initially, the sum image shows little superposition of the spheres in successive pictures but at longer times superposition is easily observed, showing that many spheres are immobilized or slowed-down (see Supplementary Fig. S1). A photo of the spheres at the end of the experiment is also shown, together with two potential maps, one obtained by scanning the spheres over the film and another acquired after removing the beads by quickly turning the film upside down. It is clear from the last image that the areas where beads accumulate and park are negative but the beads are positive so that the bead-covered film areas are closer to neutral. The fallen beads were collected in a Faraday cup and their charge was measured, +5.56 ± 0.02 nC/g.

Figure 3. Triboelectrification of PTFE with rolling glass beads.

Figure 3

Open in a new tab

(a), (b) and (c) are the sum images of two subsequent frames (1 s apart) where the beads from the first frame are false-colored red, those from the second frame are green and the yellow areas are thus the result of particle superposition in two consecutive frames, revealing the slow-moving or immobilized particles. (d) Picture of glass beads after 300 minutes shaking over PTFE on a planetary table; (e) the respective electrostatic map, where the areas covered with beads are less negative than most bare areas. The electrostatic map shown in (f) was obtained by scanning the PTFE film but after removing the glass beads; potential on the bead-trapping areas is largely negative (<−3 kV) (See also Supplementary Video online).

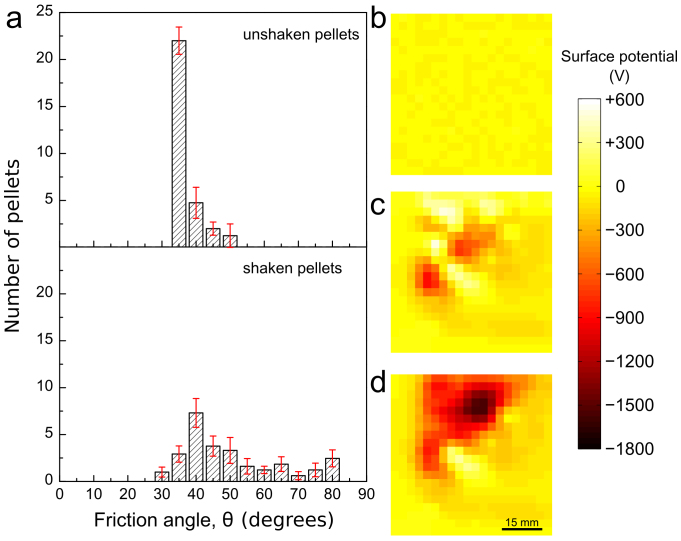
The effect of tribocharging on sliding friction was examined by sliding polyethylene (PE) pellets on PTFE film, until they were immobilized by triboelectrification. Friction angles and static friction coefficients μs = tan θ40 were then measured and they are shown in Fig. 4. The distribution of friction angles of uncharged PE pellets and PTFE peaks at 40° but it spreads towards much higher and also to lower angles (>90° down to 30°) after a short sliding time.

Figure 4. Tribocharging effect on friction angles of PE pellets on PTFE.

Figure 4

Open in a new tab

(a) Control measurement using unshaken pellets (top) and the distribution of values obtained by averaging the results of 13 shaking runs using 30 pellets each (bottom). Potential maps of: (b) PE pellets on clean PTFE prior to shaking, (c) pellets shaken for 300 seconds on PTFE and (d) PTFE after removal of PE pellets. Error bars are standard deviations of the average.

These macroscopic results led us to consider the effect of tribocharges on lateral force microscopy (LFM)41 measurements. This technique has been invaluable in providing friction data with high spatial resolution and it has attracted the attention of many distinguished authors, concerned with calibration procedures42,43,44,45,46,47 and adhesion48,49 effects on friction, derived from surface energies50 measured at the nanometric scale.

To verify the effect of tribocharges on LFM measurements, PTFE samples were tribocharged with glass and then LFM images were acquired and the results are displayed in Fig. 5, showing that lateral force is close to zero on uncharged PTFE but it largely increases when the polymer surface potential is previously tribocharged.

Figure 5. Lateral Force Microscopy (LFM) of neutral and tribocharged PTFE sheets.

Figure 5

Open in a new tab

Topography (left) and lateral force images (right) obtained by LFM on (a) cleaned and (b), (c) tribocharged (average potential indicated on each sample, was measured with a macroscopic Kelvin probe) PTFE samples. Loop of friction signal profiles traced in LFM images are shown in (d). See also Supplementary Fig. S4.

The roughness of the lateral force vs. distance in Fig. 5c is also much higher for the charged sample and the average fractal dimension D in Fig. 5 (see Supplementary Fig. S4 and S5) is 1.69 ± 0.04. This can be compared to data for electrostatic potential vs. distance in polymer surfaces51, D = 1.67 ± 0.05 (see Supplementary Fig. S6 and S7) while the fractal dimension of surface topography profiles is significantly lower, 1.53 ± 0.04. Fractal dimensions of lines scanned along potential distribution maps and lateral force maps are in the same range and this is easily understood considering that they have a common origin: local tribocharge excess determines both surface potential and tip-surface friction coefficient. Incidentally, the AFM topography images in Fig. 5 show that surface morphology is largely modified in the tribocharging process when broad stripes are formed, but the relevant line profile fractal coefficients are not altered. Thus, the connection between macroscale and nanoscale charge-dependent friction phenomena is established by the fractal nature of charge distribution patterns.

Finally, charge induction on the AFM tip was verified by measuring force-distance (Fd) curve52 that yield information on surface interactions, adhesion, elasto-plastic properties and even glass transition temperature53, which makes it a fundamental tool in surface science. Fd curves were obtained for neutral and previously tribocharged PTFE, yielding the results shown in Fig. 6. Tip interaction with neutral PTFE is negligible, until short distance is attained and van der Waals attraction effect is observed. Force dependence on penetration depth as well as tip-sample adhesion are observed, as usual. Following tip detachment from the surface, its interaction with PTFE is also negligible. On the other hand, when PTFE is tribocharged, tip attraction during tip approach (but not during retraction) is observed at distances in excess of 500 nm54,55. Moreover, tip-surface adhesion is largely increased. The hysteresis on Fd curves that is evidenced by the non-overlap of approach and retract curves, is typical for elasto-plastic materials like polymers and it is largely due to viscous forces that dissipate mechanical energy while the cantilever is retracted52,53. It is remarkable that Coulombian interactions are not observed between the leaving tip and the surface. This may be assigned to either net neutralization of the surface or to tip coating with PTFE fragments, making it hydrophobic as in the glass silanization experiment.

Figure 6. Force-distance (Fd) curves on tribocharged PTFE.

Figure 6

Open in a new tab

Fd curves for approach and retraction of a silicon nitride tip from neat, uncharged PTFE and tribocharged PTFE. Average potential measured over the polymer with a macroscopic Kelvin electrode is −192 V.

Discussion

The results presented in this paper provide direct and quantitative data showing that tribocharging makes a major contribution to friction coefficients of insulators, at least in the case of the common materials used in this work. This answers another open question in the literature (“What is the quantitative part of the electrostatic forces in surface forces compared to other contributions?”27), since friction coefficients in charged polymer surfaces are many times larger than in the absence of charge.

The present results show that the electrostatic effects observed at the microscopic scale17 are also decisive in macroscopic experiments: charged outer surface layers increase friction due to the contribution of Coulomb forces to normal force. The intervening mechanism receives contributions from both increased adhesion between surfaces and increased contact area between the contacting surfaces, depending on their respective viscoelastic properties20,56. This is within the framework set by Gao et al.17, when these authors concluded that “The trends obtained through molecular dynamics (MD) simulations agree with recent and past experiments and with Amontons' law, and they suggest that the local energy-dissipating mechanisms are not merely “mechanical”, as assumed in most models, but “thermodynamic” in nature....” Concerning the CoRR measurements on glass surfaces, we recall that charge induction in hydrophilic surfaces is now well established57 but there is not, at this point in time, sufficient data to allow the development of a quantitative model for friction dependence on surface potential due to tribocharges. Nevertheless, the effect of tribocharges on rolling friction is effectively suppressed by surface modification of glass beads, showing how simple surface modification procedures can effectively control friction.

However, the control experiments of CoRR measurement using the PP film coated with biased aluminum film and PP electrets (see Supplementary Table S1) prevent us from presenting a broadly applicable and detailed model for the effect of static charges on friction, which has to wait for further detailed examination of other systems.

Tribocharging PE pellets with PTFE leads to much higher friction angles but also to a few lower values and this is understood by recalling that friction between these two solids produces mostly negative but also some positive domains35 on PTFE that are seen in Fig. 4d, while PE pellets are largely positive. When positive areas on PE and PTFE face each other, repulsion contributes to lower the static friction coefficient (see Supplementary Fig S2).

An important issue is the presence of water58 thin islands or pores59 on PTFE surfaces, under 50% relative humidity. Water vapor has a complex effect on electrostatic charging of surfaces. On hydrophilic isolated solids it donates charge60 but in isolated hydrophobic surfaces it contributes to charge dissipation that is very slow. The half-life of corona-charged polyethylene under 60% RH is ca. 30 hours61 and tribocharged PTFE does not show significant charge decay up to 60 hours, at 60% RH35. Results on the effect of humidity on adhesion and friction coefficients for hydrophobic polymer surfaces are given by Jung and Bhushan62. Friction coefficients of a borosilicate glass ball probe on PMMA and PS coated with perfluorodecyltriethoxisilane self-assembled monolayers are lower than 0.1 and they change by less than 10% when the humidity increases from 5 to 80%. Thus, the large effects observed in the present work cannot be assigned to neither are they countered by adsorbed water.

Previously detected tribocharging15 in steel samples is transient, causing only short-lived spikes in the friction coefficients – quite different from the steady charging of PTFE. This produces an interesting difference between these systems: clean steel surfaces show higher friction coefficients than the oxidized ones, while clean polymer surfaces show lower friction coefficients than tribocharged ones.

Most important, knowing that polymer friction produces charges that in turn contribute to increased friction coefficients allows us to avoid experimental limitations imparted by electrical charge effects to macro and micromachines27 by using effective charge removal or by suppressing charge formation, using techniques described in recent work from this group35,37 or chemical surface modification, as in this work. For most polymers, charged species are easily removed by immersion in ethanol or propanol and charge formation is suppressed by mildly swelling their surfaces with these and other common liquids. It is interesting to observe that the effect of alcohol vapour63 on friction coefficients in diamond-coated and other well-defined surfaces has been demonstrated64,65 but the involved mechanisms are not yet clearly defined.

Since tribocharge patterns are fractal, their contribution to friction coefficients is also fractal. This conclusion can prove helpful in allowing us to interpret macroscopic friction phenomena as the result of microscopic interactions.

To conclude, tribocharges produced by friction have a large effect on the friction coefficients of dielectrics that may exceed all other factors for mechanical energy dissipation. Controlling surface electrostatics should thus open the way to new approaches for controlling friction in many important systems and equipment.

Methods

Sample preparation

Polytetrafluoroethylene (PTFE) sheets for technical use were washed with water and immersed in ethanol for 2 hours prior to tribocharging experiments. Precision soda lime glass beads (type P, 2.5 mm diameter, Sigmund Lindner) were cleaned with boiling ethanol in a Soxhlet apparatus for 2 hours. Silanization was done by dipping glass beads in NaOH/H2O/ethanol 1:2:2 (w/w) solution for 60 minutes, followed by rinsing with ethanol and dried at 65°C for 12 hours. After drying time, glass beads were immersed in an alcohol solution of 10% (w/w) of trimethylchlorosilane (Me3Si-Cl) for 8 hours, rinsed with ethanol, dried and reserved in a desiccator.

Tribocharging techniques

Two tribocharging techniques procedures were used: (a) Square sheets (10 × 10 cm2) of PTFE were supported on an aluminum holder and rubbed with soda lime glass sheet or felt wool66 (14 × 14 cm2) with pressure adjusted to 1.0 ± 0.15 kPa that was slid for 4 cm at the speed of 1 cm s−1; (b) PTFE (5 × 5 cm2) was mounted on top of a framed aluminium plate that laid on the horizontal table of a shaking table with 2 g of glass beads spread on top of the sample and the set-up was shaken for 4 hours, at 5 Hz reciprocating frequency and 10 mm amplitude.

Friction measurements

Coefficient of rolling resistance (CoRR) measurements followed the ASTM Standard (G194-08). Glass beads were placed at a height h = 1.25 mm on an aluminum smooth ramp with 10 degrees inclination angle and then allowed to roll down onto a flat tribocharged PTFE surface. The distance roamed by each sphere on the PTFE surface, d, was measured with a caliper (±0.05 mm, Mitutoyo), and CoRRs were calculated as the h/d ratio. These experiments were performed on a leveling table (micro-g 63–552, TMC).

Friction angle measurements and static friction coefficients were obtained using an inclined plane built in the departmental workshop. Samples were clean, uncharged PTFE sheets framed on a thick aluminum sheet, carrying 30 PE pellets randomly placed on its surface. This setup was placed on a reciprocating table and shaken for 5 minutes, when it was mounted on the swinging arm of the inclined plane, this was gradually raised in 5° steps and the number of pellets sliding at each angle was recorded. Thirty pellets only used in each run to avoid mutual interference while sliding but this number is insufficient to produce reasonable statistics. For this reason, these experiments were repeated at least thirteen five times and pooled. The shaking steps as well as the friction angle measurements were video-recorded to document that pellets slid and did not roll, during these experiments.

Lateral force microscopy (LFM) was done on PTFE 5 mm square pieces cut from 1.5 mm thick sheet, cleaned by immersion in ethanol followed by drying under air and imaged in contact mode. A scanning probe microscope (SPM-9600, Shimadzu) was used with gold/chromium backside-coated silicon nitride probes (OMCL-TR800PSA-1, Olympus). The LFM scanning system is enclosed within an environmental chamber control under controlled temperature (25 ± 1°C) and relative humidity (50 ± 1%). Force-distance curves between the tip and an incompressible sample (silicon wafer, Ted Pella) were used to determine the normal deflection sensitivity, defined as the slope of the f-d curve after the AFM tip makes contact with the surface47 whereas the spring constant was calculated via Sader method67,68. Topographic and lateral force images (512 × 512 pixels) were obtained at 0.25 Hz scan rate 90° relative to the direction of the long axis of the cantilever, while the normal load was kept at 12 nN. Calibration of lateral forces followed the widely used wedge calibration method42,43. For the wedge method a 2D200 XY-Standard sample produced by Nanosensors (Neuchatel, Switzerland) was imaged in contact mode at a scan angle of 90 degrees under different loads. The standard sample consists of a 2-dimendional lattice of inverted square pyramids with 200 nm pitch, sidewall angles of θ = 54.7° and etched into a silicon chip (for more details see Supplementary Fig. S3). Fractal dimension D of topography and lateral force was calculated using the box count method: as implemented in Fraclab version 2.0 (developed by INRIA, Saclay) toolbox of Matlab version 7.12.0.635, R2011a or using the public domain software ImageJ 1.44o69. Force distance curves between the tip and neutral or tribocharged PTFE were recorded using the same AFM setup described to LFM. Measurements were performed in randomly chosen locations while the normal load was kept at 12 nN.

Electrostatic potential and charge measurements

The scanning apparatus for non-contact electric potential measurements and the controlling software were built by Optron (Campinas). Samples are held on a 10-mm thick aluminium plate and scanned in the x–y plane with a disc-shaped 5 mm diameter Kelvin electrode kept at 2 mm above the surface and connected to a voltmeter (347, Trek). This measurement range is ±3.3 kV. Electrostatic potential scans started immediately after sample preparation. Time allowed for the electrode equilibration at each pixel is 1 s. After potential measurements, samples were placed within a Faraday cup for charge measurement using a 6514 electrometer (Keithley Instruments).

Author Contributions

T.A.L.B. contributed with experimental work, data treatment, the discussion of results and (less) paper writing. C.A.S. contributed with experiments on PE friction on PTFE, data treatment and discussion. L.B.S.B. contributed CoRR measurements on PP films charged by biasing a coating Al fim or by using Chudleigh's method. F.G. is the supervisor, participated in experimental design and some experiments, discussion, interpretation and writing.

Supplementary Material

Supplementary Information

SUPPLEMENTARY INFO

srep02384-s1.pdf (9.5MB, pdf)
Supplementary Information

PTFE tribocharged with glass beads

Download video file (3.1MB, mov)
Supplementary Information

PTFE tribocharged with PE pellets

Download video file (8.3MB, mov)

Acknowledgments

This work was supported by CNPq and Fapesp (Brazil) through Inomat, National Institute (INCT) for Complex Functional Materials. TALB and CAS hold fellowships from CNPq.

References

  1. Loeb L. B. The basic mechanisms of static electrification. Science 102, 573–576 (1945). [DOI] [PubMed] [Google Scholar]
  2. Diaz A. F. & Felix-Navarro R. M. A semi-quantitative tribo-electric series for polymeric materials: the influence of chemical structure and properties. J. Electrostat. 62, 277–290 (2004). [Google Scholar]
  3. Horn R. G. & Smith D. T. Contact electrification and adhesion between dissimilar materials. Science 256, 362–364 (1992). [DOI] [PubMed] [Google Scholar]
  4. Gerde E. & Marder M. Friction and fracture. Nature 413, 285–288 (2001). [DOI] [PubMed] [Google Scholar]
  5. He G., Muser M. H. & Robbins M. O. Adsorbed layers and the origin of static friction. Science 284, 1650–1652 (1999). [DOI] [PubMed] [Google Scholar]
  6. Krim J. Friction and energy dissipation mechanisms in adsorbed molecules and molecularly thin films. Adv. Phys. 61, 155–323 (2012). [Google Scholar]
  7. Park J. Y., Ogletree D. F., Thiel P. A. & Salmeron M. Electronic control of friction in silicon pn junctions. Science 313, 186–186 (2006). [DOI] [PubMed] [Google Scholar]
  8. Park J. Y., Qi Y., Ogletree D. F., Thiel P. A. & Salmeron M. Influence of carrier density on the friction properties of silicon pn junctions. Phys. Rev. B 76, 064108 (2007). [Google Scholar]
  9. Qi Y., Park J. Y., Hendriksen B. L. M., Ogletree D. F. & Salmeron M. Electronic contribution to friction on GaAs: An atomic force microscope study. Phys. Rev. B 77, 184105 (2008). [Google Scholar]
  10. Altfeder I. & Krim J. Temperature dependence of nanoscale friction for Fe on YBCO. J. Appl. Phys. 111, 094916 (2012). [Google Scholar]
  11. Gulseren O. et al. A. New trends in nanotribology. Tribol. Lett. 39, 227 (2010). [Google Scholar]
  12. Budakian R. & Putterman S. J. Correlation between charge transfer and stick-slip friction at a metal-insulator interface. Phys. Rev. Lett. 85, 1000–1003 (2000). [DOI] [PubMed] [Google Scholar]
  13. Akbulut M., Godfrey Alig A. R. & Israelachvili J. N. Triboelectrification between smooth metal surfaces coated with self-assembled monolayers. J. Phys. Chem. B 110, 22271–22278 (2006). [DOI] [PubMed] [Google Scholar]
  14. Zhu Y., Kelsall G. H. & Spikes H. A. Triboelectrochemistry on a nanometre scale. Tribol. Lett. 2, 287–312 (1996). [Google Scholar]
  15. Morris S., Wood R. J. K., Harvey T. J. & Powrie H. E. G. Electrostatic charge monitoring of unlubricated sliding wear of a bearing steel. Wear 255, 430–443 (2003). [Google Scholar]
  16. Seto T. Effects of an electric field on the static friction of a metal on a ferroelectric material. Appl. Phys. Lett. 67, 442–443 (1995). [Google Scholar]
  17. Gao J. et al. Frictional forces and Amontons' law: from the molecular to the macroscopic scale. J. Phys. Chem. B 108, 3410–3425 (2004). [Google Scholar]
  18. Archard J. F. Elastic deformation and the laws of friction, Proc. R. Soc. Lond. A 243, 190–205 (1957). [Google Scholar]
  19. Bowden F. P. & Tabor D. Friction and Lubrication. 2nd ed., Oxford (1954). [Google Scholar]
  20. Makinson K. R. & Tabor D. Friction and transfer of polytetrafluoroethylene. Nature 201, 464–476 (1964). [Google Scholar]
  21. Marino M. J. et al. Is ultra-low friction needed to prevent wear of diamond-like carbon (DLC)? An alcohol vapor lubrication study for stainless steel/DLC interface. Tribol. Lett. 42, 285–291 (2011). [Google Scholar]
  22. Burris D. L. & Sawyer W. G. Addressing practical challenges of low friction coefficient measurements. Tribol. Lett. 35, 17–23 (2009). [Google Scholar]
  23. Israelachvili J. N. & Tabor F. R. S. The measurement of van der Waals dispersion forces in the range 1.5 to 130 nm. Proc. R. Soc. Lond. A 331, 19–38 (1972). [Google Scholar]
  24. Israelachvili J. N., Tandon R. K. & White L. R. Measurement of forces between two mica surfaces in aqueous poly(ethylene oxide) solutions. Nature 277, 120–121 (1979). [Google Scholar]
  25. Raviv U. et al. Lubrication by charged polymers. Nature 425, 163–165 (2003). [DOI] [PubMed] [Google Scholar]
  26. Burris D. L., Boesl B., Bourne G. R. & Gregory Sawyer W. G. Polymeric nanocomposites for tribological applications. Macromol. Mater. Eng. 292, 387–402 (2007). [Google Scholar]
  27. Guerret-Piécourt C., Vallayer J. & Tréheux D. Limitation induced by electrical charges effects on micromechanisms. Wear 254, 950–958 (2003). [Google Scholar]
  28. Schein L. B. Recent progress and continuing puzzles in electrostatics. Science 316, 1572–1573 (2007). [DOI] [PubMed] [Google Scholar]
  29. Ireland P. M. Dynamic particle-surface tribocharging: The role of shape and contact mode. J. Electrostat. 70, 524–531 (2012). [Google Scholar]
  30. Williams M. W. What creates static electricity? Am. Sci. 100, 316–323 (2012). [Google Scholar]
  31. Grzybowski B. A., Winkleman A., Wiles J. A., Brumer Y. & Whitesides G. M. Electrostatic self-assembly of macroscopic crystals using contact electrification. Nature Mater. 2, 241–245 (2003). [DOI] [PubMed] [Google Scholar]
  32. Knorr N. Squeezing out hydrated protons: low-frictional-energy triboelectric insulator charging on a microscopic scale. AIP Advances 1, 022119 (2011). [Google Scholar]
  33. Truncyte D., Gutauskas M., Zebrauskas S. & Virbalis J. Triboelectricity in the pairs of polymeric materials. J. Appl. Polym. Sci. 110, 3532–3537 (2008). [Google Scholar]
  34. Nakayama K. Tribocharging and friction in insulators in ambient air. Wear 194, 185–189 (1996). [Google Scholar]
  35. Burgo T. A. L. et al. Triboelectricity: macroscopic charge patterns formed by self-arraying ions on polymer surfaces. Langmuir 28, 7407–7416 (2012). [DOI] [PubMed] [Google Scholar]
  36. Baytekin H. T., Baytekin B., Incorvati J. T. & Grzybowski B. A. Material transfer and polarity reversal in contact charging. Angew. Chem. Int. Ed. 51, 4843–4847 (2012). [DOI] [PubMed] [Google Scholar]
  37. Francisco K. R., Burgo T. A. L. & Galembeck F. Tribocharged polymer surfaces: solvent effect on pattern formation and modification. Chem. Lett. 41, 1256–1258 (2012). [Google Scholar]
  38. Eldredge K. R. & Tabor D. The Mechanism of Rolling Friction. I. The Plastic Range. Proc. R. Soc. Lond. A 229, 181–198 (1955). [Google Scholar]
  39. Tabor D. The Mechanism of Rolling Friction. II. The Elastic Range. Proc. R. Soc. Lond. A 229, 198–220 (1955). [Google Scholar]
  40. Feynman R. P., Leighton R. B. & Sands M. The Feynman lectures on physics. Vol. 1, 2nd ed., Addison Wesley (1971). [Google Scholar]
  41. Mate C. M., MacClelland G. M., Erlandsson R. & Chiang S. Atomic-scale friction of a tungsten tip on a graphite surface. Phys. Rev. Lett. 59, 1942–1945 (1987). [DOI] [PubMed] [Google Scholar]
  42. Ogletree D. F., Carpick R. W. & Salmeron M. Calibration of frictional forces in atomic force microscopy. Rev. Sci. Instrum. 67, 3298–3306 (1996). [Google Scholar]
  43. Varenberg M., Etsion I. & Halperin G. An improved wedge calibration method for lateral force in atomic force microscopy. Rev. Sci. Instrum. 74, 3362–3367 (2003). [Google Scholar]
  44. Tocha E., Schönherr H. & Vancso G. J. Quantitative nanotribology by AFM: a novel universal calibration platform. Langmuir 22, 2340–2350 (2006). [DOI] [PubMed] [Google Scholar]
  45. Cain R. G., Biggs S. & Page N. W. Force calibration in lateral force microscopy. J. Coll. Inter. Sci. 227, 55–65 (2000). [DOI] [PubMed] [Google Scholar]
  46. Cannara R. J., Eglin M. & Carpick R. W. Lateral force calibration in atomic force microscopy: A new lateral force calibration method and general guidelines for optimization. Rev. Sci. Instrum. 77, 053701 (2006). [Google Scholar]
  47. Asay D. B. & Kim S. H. Direct force balance method for atomic force microscopy lateral force calibration. Rev. Sci. Instrum. 77, 043903 (2006). [DOI] [PubMed] [Google Scholar]
  48. Marti A. Haehner G. & Spencer N. D. Sensitivity of frictional forces to pH on a nanometer scale: a lateral force microscopy study. Langmuir 11, 4632–4635 (1995). [Google Scholar]
  49. Carpick R. W., Agrait N., Ogletree D. F. & Salmeron M. Variation of the interfacial shear strength and adhesion of a nanometer-sized contact. Langmuir 12, 3334–3340 (1996). [Google Scholar]
  50. Mate C. M. Tribology on the small scale: a bottom up approach to friction, lubrication, and wear. Oxford University Press, (2008). [Google Scholar]
  51. Santos J. P., Corpart P., Wong K. & Galembeck F. Heterogeneity in styrene-butadiene latex films. Langmuir 20, 10576–10582 (2004). [DOI] [PubMed] [Google Scholar]
  52. Cappella B. & Dietler G. Force-distance curves by atomic force microscopy. Surf. Sci. Rep. 34, 1–104 (1999). [Google Scholar]
  53. Kaliappan S. K. & Cappella B. Temperature dependent elastic–plastic behaviour of polystyrene studied using AFM force–distance curves. Polymer 46, 11416–11423 (2005). [Google Scholar]
  54. Eve J. K., Patel N., Luk S. Y., Ebbens S. J. & Roberts, C. J. A study of single drug particle adhesion interactions using atomic force microscopy. Int. J. Pharm. 238, 17–27 (2002). [DOI] [PubMed] [Google Scholar]
  55. Bunker M. J., Davies M. C., James M. B. & Roberts C. J. Direct observation of single particle electrostatic charging by atomic force microscopy. Pharmaceut. Res. 24, 1165–1169 (2007). [DOI] [PubMed] [Google Scholar]
  56. Tabor D. Surface forces and surface interactions. J. Colloid Interface. Sci. 58, 1–13 (1977). [Google Scholar]
  57. Soares L. C., Bertazzo S., Burgo T. A. L., Baldim V. & Galembeck F. A new mechanism for the electrostatic charge build-up and dissipation in dielectrics. J. Braz. Chem. Soc. 19, 277–286 (2008). [Google Scholar]
  58. Awakuni Y. & Calderwood J. H. Water vapour adsorption and surface conductivity in solids. J. Phys. D: Appl. Phys. 5, 1038 (1972). [Google Scholar]
  59. Sumner A. L. et al. The nature of water on surfaces of laboratory systems and implications for heterogeneous chemistry in the troposphere. Phys. Chem. Chem. Phys. 6, 604–613 (2004). [Google Scholar]
  60. Gouveia R. F. & Galembeck F. Electrostatic charging of hydrophilic particles due to water adsorption. J. Am. Chem. Soc. 131, 11381–11386 (2009). [DOI] [PubMed] [Google Scholar]
  61. Burgo T. A. L., Rezende C. A., Bertazzo S., Galembeck A. & Galembeck F. Electric potential decay on polyethylene: role of atmospheric water on electric charge build–up and dissipation. J. Electrostat. 69, 401–409 (2011). [Google Scholar]
  62. Jung Y. C. & Bhushan B. Contact angle, adhesion and friction properties of micro- and nanopatterned polymers for superhydrophobicity. Nanotechnology 17, 4970–4980 (2006). [Google Scholar]
  63. Asay D. B., Dugger M. T., Ohlhausen J. A. & Kim S. H. Macro- to nanoscale wear prevention via molecular adsorption. Langmuir 24, 155–159 (2008). [DOI] [PubMed] [Google Scholar]
  64. Liu Y., Erdemir A. & Meletis E. I. A study of the wear mechanism of diamond-like carbon films. Surf. Coat. Tech. 82, 48–56 (1996). [Google Scholar]
  65. Marino M. J. et al. Understanding run-in behavior of diamond-like carbon friction and preventing diamond-like carbon wear in humid air. Langmuir 27, 12702–12708 (2011). [DOI] [PubMed] [Google Scholar]
  66. Hogue M. D., Mucciolo E. R. & Calle C. I. Triboelectric, corona, and induction charging of insulators as a function of pressure. J. Electrostat. 65, 274–279 (2007). [Google Scholar]
  67. Sader J. E. et al. Spring constant calibration of atomic force microscopy cantilevers of arbitrary shape. Rev. Sci. Instrum. 83, 103705 (2012). [DOI] [PubMed] [Google Scholar]
  68. Green C. P. et al. Normal and torsional spring constants of atomic force microscope cantilevers. Rev. Sci. Instrum. 75, 1988–1996 (2004). [Google Scholar]
  69. Fractal dimension measurement in ImageJ. http://www.nist.gov/lispix/doc/fractal/image-java-box-count.htm. (2013).

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

SUPPLEMENTARY INFO

srep02384-s1.pdf (9.5MB, pdf)
Supplementary Information

PTFE tribocharged with glass beads

Download video file (3.1MB, mov)
Supplementary Information

PTFE tribocharged with PE pellets

Download video file (8.3MB, mov)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES