Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Aug 12;3:2411. doi: 10.1038/srep02411

Tunable Dirac Fermion Dynamics in Topological Insulators

Chaoyu Chen 1, Zhuojin Xie 1, Ya Feng 1, Hemian Yi 1, Aiji Liang 1, Shaolong He 1, Daixiang Mou 1, Junfeng He 1, Yingying Peng 1, Xu Liu 1, Yan Liu 1, Lin Zhao 1, Guodong Liu 1, Xiaoli Dong 1, Jun Zhang 1, Li Yu 1, Xiaoyang Wang 2, Qinjun Peng 2, Zhimin Wang 2, Shenjin Zhang 2, Feng Yang 2, Chuangtian Chen 2, Zuyan Xu 2, X J Zhou 1,a
PMCID: PMC3740283  PMID: 23934507

Abstract

Three-dimensional topological insulators are characterized by insulating bulk state and metallic surface state involving relativistic Dirac fermions which are responsible for exotic quantum phenomena and potential applications in spintronics and quantum computations. It is essential to understand how the Dirac fermions interact with other electrons, phonons and disorders. Here we report super-high resolution angle-resolved photoemission studies on the Dirac fermion dynamics in the prototypical Bi2(Te,Se)3 topological insulators. We have directly revealed signatures of the electron-phonon coupling and found that the electron-disorder interaction dominates the scattering process. The Dirac fermion dynamics in Bi2(Te3−xSex) topological insulators can be tuned by varying the composition, x, or by controlling the charge carriers. Our findings provide crucial information in understanding and engineering the electron dynamics of the Dirac fermions for fundamental studies and potential applications.

Topological insulators represent a new state of matter that has an insulating bulk state but a conducting surface/edge state which hosts an unique spin texture and a linear dispersion relation compatible with massless Dirac fermions1,2,3. In addition to their potential applications in spintronics and quantum computing4,5, the topological insulators also provide a promising platform for realizing a number of novel and exotic quantum phenomena including quantum spin Hall effect6, fractional charge and quantized current7, dynamical axion field8, magnetic monopole9, Majorana fermions10,11 and quantum anomalous Hall effect12. Some of the phenomena have been observed experimentally in two-dimensional topological insulators, such as quantum spin Hall effect13 and quantum Hall effect14 in the HgTe quantum wells. However, in the case of three-dimensional topological insulators like Bi2(Te, Se)3 family15,16,17,18, in spite of intensive efforts from transport experiments19,20,21,22,23, attempts to observe electronic transport signatures of the surface Dirac fermions have been hampered by a couple of obstacles. First, contrary to usual expectation that the bulk is insulating in topological insulators, the presence of defects in Bi2(Te, Se)3 system makes the bulk conducting24 and the transport properties are then dominated by the bulk state instead of the desired surface state20. Second, in several cases where the surface transport signatures are identified, more than one frequency or one type of charge carriers contribute to the quantum oscillation21,22,23, indicating the complexity of sample surface exposed to atmosphere or protection layers25. Third, the transport mobility of charge carriers in the Bi2(Te, Se)3 topological insulators, μ′ ~ 104 cm2V−1s−1 (Refs. 19,23,26) is not sufficiently high compared to those from HgTe quantum wells(1.5 × 105 cm2V−1s−1)13,14 and graphene(2.3 × 105 cm2V−1s−1)27,28,29. Although strict electron backscattering is forbidden in topological insulators due to time reversal symmetry invariance, it is important to uncover other scattering channels that limit the transport mobility of the two-dimensional Dirac fermions26.

The charge transport properties are dictated by the electron dynamics in materials. In particular, the scattering of electrons by other entities such as other electrons, phonons and disorder, determines the lifetime of the quasiparticles, and thus the electron mobility and mean free path in the transport process30. Angle-resolved photoemission spectroscopy (ARPES) has become a powerful tool to directly probe such many-body effects31,32. Under the sudden approximation, ARPES measures a single particle spectral function

graphic file with name srep02411-m1.jpg

with k and ω representing electron momentum and energy, respectively. The real and imaginary parts of electron self-energy, ReΣ(k, ω) and ImΣ(k, ω), carry all the information about the band renormalization and quasiparticle lifetime in an interacting system31,32.

There have been a few investigations on the dynamics of Dirac fermions in Bi2(Te, Se)3 topological insulators using ARPES33,34 or helium atom surface scattering probes35. However, the results obtained so far are not consistent. While the electron-phonon coupling strength (λ) was reported to be 0.25 in Bi2Se3 from temperature-dependent photoemission measurements33, it was claimed that the electron-phonon coupling is exceptionally weak in Bi2Se3 in another measurement34. The inconsistency comes presumably from two issues related to the ARPES study on many-body effects in topological insulators. First, the coexistence of bulk bands and surface bands near the Fermi level, due to the bulk doping by defects, complicates the identification of weak band renormalization effects in the surface bands. Second, the small momentum space and energy window of the Dirac fermions and the weak many-body effects require high precision ARPES measurements. The momentum space occupied by the surface state, ~ ± 0.1 Å−1 for Bi2Se3 (Fig. 1a) and ~ ± 0.04 Å−1 for p-type Bi2Te3 (Fig. 2a), is rather small17,18,25. To overcome these problems, it is ideal to first suppress the interference of the bulk bands in the measurements. Since the as-grown Bi2Se3 is electron-doped (n-type) while Bi2Te3 can be hole-doped (p-type)25, balancing the proportion of selenium and tellurium in Bi2(Se,Te)3 system may neutralize the bulk carrier doping and reduce the effect of the bulk bands on the surface state. Furthermore, vacuum ultra-violet (VUV) laser-based ARPES36 can help suppress the bulk bands25, in addition to its super-high energy and momentum resolutions (Supplementary Fig. S2) that are desirable in studying many-body effects in topological insulators.

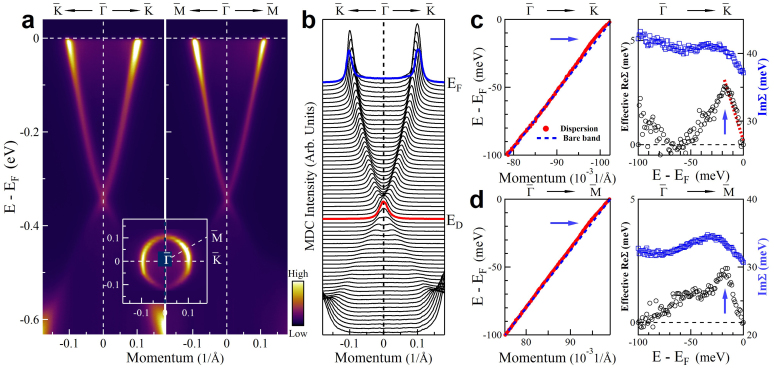
Figure 1. Observation of electron-phonon coupling in Bi2Se3.

Figure 1

Open in a new tab

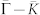(a) Surface state dispersions along Inline graphic(left panel) and Inline graphic(right panel) directions. The inset shows the Fermi surface of Bi2Se3. (b) Momentum distribution curves (MDCs) of the surface state dispersion along Inline graphic. Red line and blue line indicate the MDCs at the Dirac point (ED) and the Fermi level (EF), respectively. 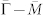(c) Dispersion and effective electron self-energy of surface state band along Inline graphic direction. The left panel shows the measured dispersion (red circles) obtained from MDC fitting. The blue dotted line represents an empirical bare band that is a straight line connecting two points in the measured dispersion, one at EF and the other at 100 meV binding energy. The right panel shows the effective real part of the electron self-energy, ReΣ(k, ω) (black circles), and imaginary part of the electron self-energy, ImΣ(k, ω) (blue squares). The red dashed line is a linear fit to the low-energy region of ReΣ(k, ω). Blue arrows indicate the characteristic energy scale of the electron-phonon coupling. (d)Dispersion and effective electron self-energy of surface state band along Inline graphic direction.

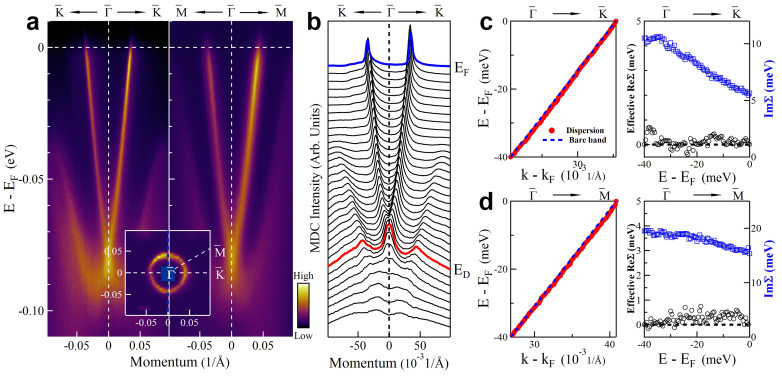
Figure 2. Extremely weak electron-phonon coupling in p-type Bi2Te3.

Figure 2

Open in a new tab

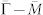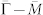(a) Surface state dispersions along Inline graphic(left panel) and Inline graphic(right panel) directions. The inset shows the Fermi surface of p-type Bi2Te3. (b) Momentum distribution curves (MDCs) of the surface state dispersion along Inline graphic. Red line and blue line indicate the MDCs at the Dirac point (ED) and the Fermi level (EF), respectively. (c) Dispersion and effective electron self-energy of surface state band along Inline graphic direction. The left panel shows the measured dispersion (red circles) obtained from MDC fitting. The blue dotted line represents an empirical bare band that is a straight line connecting two points in the measured dispersion, one at EF and the other at 40 meV binding energy. The right panel shows the effective real part of the electron self-energy, ReΣ(k, ω) (black circles), and imaginary part of the electron self-energy, ImΣ(k, ω) (blue squares). (d)Dispersion and effective electron self-energy of surface state band along Inline graphic direction.

Results

Signatures of electron-phonon coupling in Bi2Se3

The Bi2Se3 sample shows sharp surface state band (Fig. 1a) that facilitates the investigation of the Dirac fermion dynamics in the material. The momentum distribution curves (MDCs) at different binding energies (Fig. 1b) show well-defined sharp peaks that can be fitted by Lorentzian lineshape to obtain peak position and peak width (Full-Width-at-Half-Maximum, ΓMDC) (Supplementary Fig. S3). The obtained MDC peak position as a function of the binding energy gives the measured dispersion relation (left panels of Fig. 1c and 1d). We assume a bare band as a linear line that connects the two points on the measured dispersion, one at the Fermi level and the other at 100 meV binding energy. This is reasonable within such a small energy window and particularly for the Dirac fermions that shows a linear dispersion over a large energy range. The effective real part of the electron self-energy (ReΣ) is obtained by subtracting the measured dispersion with the bare band, as shown in right panels of Fig. 1c and Fig. 1d (black empty circles). The imaginary part of the electron self-energy (ImΣ) is obtained from the fitted MDC width: ImΣ = ΓMDC × v0/2 with v0 being the Fermi velocity of the bare band (right panels of Fig. 1c and Fig. 1d, blue empty squares)32.

The extraction of the electron self-energy provides full information for understanding the electron dynamics in a material where the electron scattering usually involves three main processes: electron-electron interaction, electron-phonon coupling, and electron-disorder interaction37,38. The electron-disorder interaction is characterized by the imaginary part of the electron self-energy at zero energy (Fermi level) since the contribution from the electron-electron interaction and electron-phonon coupling approaches zero at the zero energy at very low temperature. The electron-phonon interaction is characterized by the band renormalization (usually a kink in dispersion, corresponding to a peak in the real part of the electron self-energy) and a drop in the imaginary part of the electron self-energy. As exemplified in Fig. 1 for Bi2Se3, there are clear indications of electron-phonon coupling revealed, such as the kink in dispersions (left panels of Fig. 1c and Fig. 1d), peak in the real part of the electron self-energy and a drop in the imaginary part of the electron self-energy (right panels of Fig. 1c and Fig. 1d). The characteristic energy scale of the phonons involved (ω0) is determined by the peak position of the real part of the electron self-energy; in the case of Bi2Se3, it is ~ 18 meV as marked by arrows in Fig. 1c and 1d. The electron-phonon coupling strength, λ, can be determined by the slope of the line near the zero energy in the real part of the electron self-energy. As shown by red dashed line in the right panel of Fig. 1c, it is determined to be λ~0.17 for Bi2Se3. The electron-electron interaction manifests itself more clearly in the imaginary part of the electron self-energy. In a typical Fermi liquid case, its contribution is proportional to the (E-EF)2: Imee = β(E-EF)2. Since the electron-phonon contribution is constant above the characteristic phonon scale, the deviation from the constant above the phonon scale gives a measure of the electron-electron interaction involved. For Bi2Se3 and the Bi2(Se,Te)3 series, we find that the electron-electron contribution is weak (β~0.014 for Bi2Se3), particularly when compared with the dominant electron-disorder interaction and the electron-phonon coupling. Therefore, in the following, we will mainly focus on the electron-phonon coupling and electron-disorder interaction.

As shown in Fig. 1, our measurements clearly indicate that there is an obvious electron-phonon coupling (λ~0.17) in the electron dynamics of the Dirac fermions in Bi2Se3. It is nearly isotropic because similar behaviors are observed along the 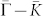Inline graphic(Fig. 1c) and 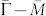Inline graphic(Fig. 1d) momentum cuts. The characteristic energy scale, ~ 18 meV, is consistent with the highest-frequency phonon mode (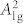Inline graphic) at ~ 20 meV in Bi2Se3 from both theoretical calculations39 and Raman measurements40 (Supplementary Fig. S7). This is in strong contrast to a recent report where exceptionally weak electron-phonon coupling was claimed and no dispersion kink was resolved in Bi2Se334. We believe that the clear manifestation of electron-phonon coupling in our measurements is most likely due to much improved instrumental resolution we have achieved.

Extremely weak electron-phonon coupling in p-type Bi2Te3

The electron-phonon coupling is extremely weak in the p-type Bi2Te3 sample, as seen in Fig. 2. This sample was prepared under similar condition as the above Bi2Se3 sample and it is p-type because the Fermi level intersects with the bulk valence band25. Even measured with such a super-high instrumental resolution (Supplementary Fig. S2), we do not resolve any clear signature of electron-phonon coupling. The measured dispersion is basically a straight line, corresponding to a real part of electron self-energy that is nearly zero (black empty circles in right panels of Fig. 2c and Fig. 2d). There is no clear drop in the imaginary part of the electron self-energy (blue empty squares in right panels of Fig. 2c and Fig. 2d). All these observations point to an extremely weak electron-phonon coupling in the p-type Bi2Te3 sample. In the mean time, the p-type Bi2Te3 also exhibits a rather weak electron-disorder scattering when compared with Bi2Se3. As seen from the right panel of Fig. 2c, the imaginary part of the electron self-energy at zero energy is only 5.6 meV along the Inline graphic direction. This is significantly lower than 37 meV along the same direction in Bi2Se3 topological insulator (right panel of Fig. 1c).

Tunability of Dirac fermion dynamics in the Bi2(Te3−xSex) series

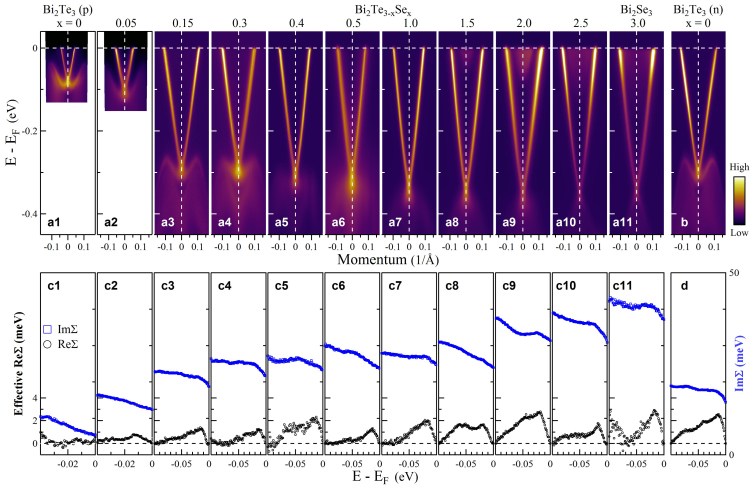
The dramatically different behaviors between Bi2Se3 (Fig. 1) and p-type Bi2Te3 (Fig. 2) motivated us to further investigate the composition dependence of the Dirac fermion dynamics in the Bi2(Te3−xSex) series. We observe a systematic evolution of band structure, electron-phonon coupling, and electron-disorder scattering, with the change of composition x in Bi2(Te3−xSex) (Fig. 3). Note that all these samples are prepared under similar conditions. First, the location of the Dirac point (ED) moves monotonically to higher binding energy with increasing x. For 0 ≤ x ≤ 0.05, the samples are p-type because the Fermi level intersects with the bulk valence band. For 0.15 ≤ x < 1.5, the Fermi level intersects with the surface state bands only. For 1.5 ≤ x ≤ 3, the samples become n-type because the Fermi level intersects with the bulk conduction band. Note that the Dirac point exhibits a big jump when x changes from 0.05 to 0.15. Second, there is an overall increase of electron-disorder interaction with increasing x in Bi2(Te3−xSex). This can be seen from the increase of the imaginary part of the electron self-energy and hence its value at zero energy with increasing x. This indicates that the Bi2(Te3−xSex) system gets more disordered with increasing x. Third, there is also an overall increase in the electron-phonon coupling strength with increasing x in Bi2(Te3−xSex). Although no indication of electron-phonon coupling is observed in p-type Bi2Te3, a slight substitution of Te by Se, with x = 0.05, already renders a clear observation of electron-phonon coupling in Bi2(Te2.95Se0.05), as seen in the appearance of a peak in the real part of the electron self-energy (black circles in Fig. 3c2). The electron-phonon coupling strength increases from nearly zero for p-type Bi2Te3 to λ~0.17 for Bi2Se3.

Figure 3. Evolution of surface state band structure and electron self-energy with the composition, x, in Bi2(Te3−xSex) system.

Figure 3

Open in a new tab

(a) The surface state band structure of Bi2Te3−xSex with various compositions, x, measured along the Inline graphic direction. (b) The surface state band structure of n-type Bi2Te3 along the Inline graphic direction. (c) Corresponding effective real part of the electron self-energy (black circles) and imaginary part of the electron self-energy (blue squares) for Bi2(Te3−xSex) with different compositions. (d) Corresponding effective real part of the electron self-energy (black circles) and imaginary part of the electron self-energy (blue squares) for n-type Bi2Te3.

It is interesting that for the same Bi2Te3 nominal composition, when prepared under different conditions, samples can become either p-type or n-type that exhibit dramatic difference in their Dirac fermion dynamics. As shown in Fig. 3b, the Dirac point of the n-type Bi2Te3 lies nearly 310 meV below the Fermi level which differs significantly from the 85 meV location in the p-type Bi2Te3 (Fig. 3a1). Particularly, the n-type Bi2Te3 exhibits a pronounced electron-phonon coupling, as seen from the obvious peak in the real part of the electron self-energy (black circles in Fig. 3d) and a drop in the imaginary part of the electron self-energy (blue squares in Fig. 3d). The resultant electron-phonon coupling constant is λ~0.19, which is even slightly larger than that in Bi2Se3 (λ~0.17). The electron-disorder scattering also increases in the n-type Bi2Te3 compared to the p-type one, as the value of the imaginary part of the electron self energy at zero energy becomes much larger (Fig. 3d). However, compared with Bi2Se3, the disorder scattering in n-type Bi2Te3 remains much weaker(Fig. 3c11). The first principle calculation, which expects a rather weak electron-phonon coupling in Bi2Te3 (λ~0.05)41, is hard to explain the strong electron-phonon coupling in n-type Bi2Te3 and particularly the disparity of electron-phonon coupling between the n-type and p-type Bi2Te3.

The different electron dynamics between Bi2Se3 and Bi2Te3, and between n-type Bi2Te3 and p-type Bi2Te3, is intriguing. We note that the native majority defect types are totally different in these samples, i.e., Se vacancies in Bi2Se3, Te-Bi antisites in the n-type Bi2Te3, and Te vacancies in the p-type Bi2Te3. The difference of the electron-disorder interaction can be due to such different types of disorders and their densities in the samples. In addition, as the main difference between the n-type and p-type Bi2Te3 lies mainly in the relative position between the Fermi level and the bulk bands, it is reasonable to deduce that the bulk bands may play a role in the electron dynamics of the Dirac fermions. This is consistent with the observation that, for n-type Bi2Te3 (x = 0), although its composition is rather different from Bi2(Te2.85Se0.15) (x = 0.15), their Dirac fermion dynamics is quite similar in both the electron-phonon coupling and electron-disorder interaction (Figs. 3 and 4). The distinction of the electron-phonon coupling between the n-type and p-type Bi2Te3 indicates that the control of the charge carrier doping can be an alternative way to tune the Dirac fermion dynamics in topological insulators.

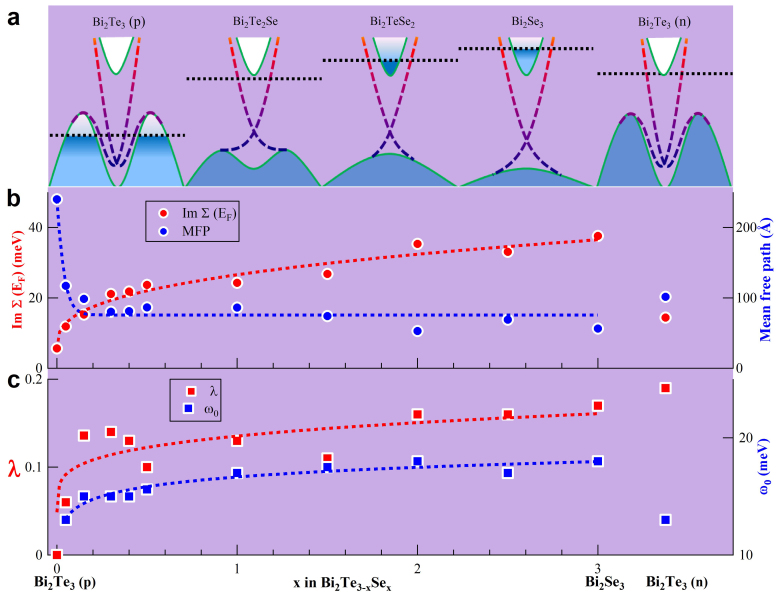
Figure 4. Variation of electron-phonon coupling and electron-disorder scattering with composition, x, in Bi2(Te3−xSex) topological insulators.

Figure 4

Open in a new tab

On the far right side, data on n-type Bi2Te3 are also included. (a) Schematic band structure at several typical compositions to show the relative position between the topological surface states (color dashed lines) and the bulk states (green solid lines). Black dashed lines indicate the Fermi level. (b) Variation of the electron-disorder scattering (red circles) with composition, x, in Bi2(Te3−xSex) topological insulators. It is obtained by taking the value of the imaginary part of the electron self-energy at zero energy (EF) as shown in Fig. 3c. Also shown is the electron mean free path (blue circles) calculated from the measured MDC width at the Fermi level. (c) Variation of the electron-phonon coupling strength λ (red squares) and characteristic energy scale ω0 with the composition, x, in Bi2(Te3−xSex) topological insulators and in n-type Bi2Te3. The dashed lines in (b) and (c) are guide to the eyes.

One may wonder whether the origin of the observed inelastic scattering in Bi2(Se,Te)3-based topological insulators is related to the materials themselves (defect, atomic arrangement and etc.) or the intrinsic topological properties associated with the time reversal symmetry (TRS) invariance. The TRS-protection may reduce the scattering strength because strict backscattering is not allowed, but it is difficult to quantitatively analyze this weakening effect. Note that the entire Bi2(Te,Se)3 series are topological insulators. Therefore, we believe the systematic evolution of their electron dynamics is mainly a manifestation of the usual many-body effects, other than a manifestation of the intrinsic TRS-related topological properties.

Fig. 4 gives a quantitative summary of the electron-phonon coupling and electron-disorder scattering in the Bi2(Te3−xSex) system. The relative position between the Dirac point and the bulk band is depicted in Fig. 4a for a couple of typical compositions and both p- and n-type Bi2Te3. With increasing x in Bi2(Te3−xSex), there is an abrupt jump in the electron-phonon coupling strength from x = 0 to x = 0.15, accompanied by a transition from p-type to n-type. Further increase of x leads to an overall slight increase of electron-phonon coupling (Fig. 4c). Meanwhile, the characteristic energy scale, ω0, also increases with x, which is consistent with the increase of the phonon frequency from Bi2Te3 to Bi2Se3 (Supplementary Fig. S7). This indicates that the (Te,Se) vibrations play a major role in dictating the electron-phonon coupling strength in the Bi2(Te3−xSex) system. This is also consistent with the observation that the characteristic energy scale is identical in n-type and p-type Bi2Te3 because their phonon frequencies are quite similar (Supplementary Fig. S7) although they have different electron-phonon coupling strength. It is clear that electron-disorder scattering is dominant in the scattering process. As seen from Fig. 4b, the imaginary part of the electron self-energy at zero energy ImΣ(EF), which gives a good measure of the electron scattering rate, shows an overall increase from the p-type Bi2Te3 for x = 0 to Bi2Se3 for x = 3 in the Bi2(Te3−xSex) system (red circles in Fig. 4b). The quasi-particle mean free path, ℓ′, which can be determined from the MDC width ΓMDC, ℓ′ = 1/ΓMDC, first decreases abruptly from the p-type Bi2Te3 (x = 0) to x = 0.15, followed by an overall slight decrease with x in Bi2(Te3−xTex) (blue circles in Fig. 3b). The electron mobility of the Dirac fermions (μ′) is directly related to the quasi-particle mean free path, μ′ = eℓ′/(ℏkF), with kF being the Fermi momentum. It is then estimated that the electron mobility in p-type Bi2Te3 is near 1000  cm2V−1s−1(Supplementary Fig. S4). By comparison, the electron mobility in Bi2Se 3 and n-type Bi2Te3 is ~ 70 and ~100 cm2V−1s−1, respectively, which are significantly lower than that of p-type Bi2Te3. We note that, although the electron mobility obtained from ARPES is not strictly the same as the electron mobility in the transport properties, they have good correspondence, especially for materials with circular Fermi surface and nearly isotropic electron scattering.

Discussion

The present study will provide important information for engineering the Dirac fermion dynamics in Bi2(Te3−xSex) topological insulators. It clearly indicates the presence of electron-phonon coupling and dominant role of the electron-disorder scattering in dictating the Dirac fermion dynamics in the system. The Dirac fermion dynamics can be tuned by varying either the composition or the charge carrier concentration. Specifically for the Bi2(Te3−xSex) system, our results clearly show that Bi2Te3 system is superior over Bi2Se3 in achieving higher electron mobility both due to its weak electron-phonon coupling and its weak electron-defect scattering. To further enhance the electron mobility in searching for novel quantum phenomena, it is necessary to choose a system with weak electron-phonon coupling and reduced disorder scattering.

Methods

High quality single crystals of Bi2(Te3−xSex) (0 ≤ x ≤ 3) were grown by the self-flux method. The mixed materials were heated to 1000°C, held for 12 hours and then slowly cooled down to 500°C over 100 hours before cooling to room temperature. Single crystals of nearly one centimeter in size were obtained by cleaving. The angle-resolved photoemission measurements were carried out on our vacuum ultra-violet (VUV) laser-based angle-resolved photoemission system, with an overall energy resolution of ~ 1 meV. The momentum resolution is ~ 0.004 Å−1 for 30° angular mode and ~ 0.002 Å−1 for 14° angular mode of the R4000 electron energy analyzer. The samples were all cleaved and measured in vacuum with a base pressure better than 5 × 10−11 Torr and a temperature T ~ 20 K. For more details about the experimental methods, see supplementary information.

Author Contributions

C.Y.C. and X.J.Z. conceived and designed the research; C.Y.C. performed measurements; Z.J.X., Y.F., H.M.Y., A.J.L., S.L.H., D.X.M., J.F.H., Y.Y.P., LX.L., Y.L., L.Z., G.D.L., X.L.D., J.Z., L.Y., X.Y.W., Q.J.P., Z.M.W., S.J.Z., F.Y., C.T.C., Z.Y.X. and X.J.Z. contributed new reagents/analytic tools; C.Y.C. and X.J.Z. analyzed data and wrote the paper.

Supplementary Material

Supplementary Information

Supplementary Information

srep02411-s1.pdf (7.7MB, pdf)

Acknowledgments

We thank Mr. Yuan Pang and Prof. Li Lu for providing us n-type Bi2Te3 single crystals, Prof. Liling Sun and Prof. Zhong-xian Zhao for their help in the characterization of the samples. We thank Mr. Quansheng Wu, Dr. Hongming Weng, Prof. Xi Dai and Prof. Zhong Fang for helpful discussions. This work is supported by the National Natural Science Foundation of China (91021006) and the Ministry of Science and Technology of China (973 program 2011CB921703 and 2013CB921700).

References

  1. Hasan M. Z. & Kane C. L. Colloquium:Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010). [Google Scholar]
  2. Moore J. E. The birth of topological insulators. Nature 464, 194–198 (2010). [DOI] [PubMed] [Google Scholar]
  3. Qi X. L. & Zhang S. C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011). [Google Scholar]
  4. Qi X. L. & Zhang S. C. The quantum spin Hall effect and topological insulators. Phys. Today 63, 33–38 (2010). [Google Scholar]
  5. Moore J. Topological insulators the next generation. Nat. Phys. 5, 378–380 (2009). [Google Scholar]
  6. Bernevig B. A., Hughes T. L. & Zhang S. C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006). [DOI] [PubMed] [Google Scholar]
  7. Qi X. L., Hughes T. L. & Zhang S. C. Fractional charge and quantized current in the quantum spin Hall state. Nat. Phys. 4, 273–276 (2008). [Google Scholar]
  8. Li R. D. et al. Dynamical axion field in topological magnetic insulators. Nat. Phys. 6, 284–288 (2010). [Google Scholar]
  9. Qi X. L. et al. Inducing a magnetic monopole with topological surface states. Science 323, 1184–1187 (2009). [DOI] [PubMed] [Google Scholar]
  10. Fu L. & Kane C. L. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008). [DOI] [PubMed] [Google Scholar]
  11. Fu L. & Berg E. Odd-parity topological superconductors: theory and application to CuxBi2Se3. Phys. Rev. Lett. 105, 097001 (2010). [DOI] [PubMed] [Google Scholar]
  12. Yu R. et al. Quantized anomalous Hall effect in magnetic topological insulators. Science 329, 61–64 (2010). [DOI] [PubMed] [Google Scholar]
  13. Konig M. et al. Quantum spin hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007). [DOI] [PubMed] [Google Scholar]
  14. Brune C. et al. Quantum Hall effect from the topological surface states of strained bulk HgTe. Phys. Rev. Lett. 106, 126803 (2011). [DOI] [PubMed] [Google Scholar]
  15. Fu L., Kane C. L. & Mele E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007). [DOI] [PubMed] [Google Scholar]
  16. Zhang H. J. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438–442 (2009). [Google Scholar]
  17. Xia Y. et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 5, 398–402 (2009). [Google Scholar]
  18. Chen Y. L. et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3. Science 325, 178–181 (2009). [DOI] [PubMed] [Google Scholar]
  19. Qu D. X. et al. Quantum oscillations and Hall anomaly of surface states in the topological insulator Bi2Te3. Science 329, 821–824 (2010). [DOI] [PubMed] [Google Scholar]
  20. Butch N. P. et al. Strong surface scattering in ultrahigh-mobility Bi2Se3 topological insulator crystals. Phys. Rev. B 81, 241301 (2010). [Google Scholar]
  21. Taskin A. A. et al. Observation of Dirac holes and electrons in a topological insulator. Phys. Rev. Lett. 107, 016801 (2011). [DOI] [PubMed] [Google Scholar]
  22. Analytis J. G. et al. Two-dimensional surface state in the quantum limit of a topological insulator. Nat. Phys. 6, 960–964 (2010). [Google Scholar]
  23. Ren Z. et al. Observations of two-dimensional quantum oscillations and ambipolar transport in the topological insulator Bi2Se3 achieved by Cd doping. Phys. Rev. B 84, 075316 (2011). [Google Scholar]
  24. Hor Y. S. et al. p-type Bi2Se3 for topological insulator and low-temperature thermoelectric applications. Phys. Rev. B 79, 195208 (2009). [Google Scholar]
  25. Chen C. Y. et al. Robustness of topological order and formation of quantum well states in topological insulators exposed to ambient environment. Proc. Natl. Acad. Sci. U.S.A. 109, 3694–3698 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kim D. et al. Intrinsic electron-phonon resistivity of Bi2Se3 in the topological regime. Phys. Rev. Lett. 109, 166801 (2012). [DOI] [PubMed] [Google Scholar]
  27. Novoselov K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005). [DOI] [PubMed] [Google Scholar]
  28. Zhang Y. B. et al. Experimental observation of the quantum Hall effect and Berry's phase in graphene. Nature 438, 201–204 (2005). [DOI] [PubMed] [Google Scholar]
  29. Bolotin K. I. et al. Ultrahigh electron mobility in suspended graphene. Solid State Commun. 146, 351–355 (2008). [Google Scholar]
  30. Grimvall G. The Electron-Phonon Interction in Metals. (North-Holland, 1981). [Google Scholar]
  31. Damascelli A., Hussain Z. & Shen Z. X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 75, 473–541 (2003). [Google Scholar]
  32. Zhou X. J., Cuk T., Devereaux T., Nagaosa N. & Shen Z. X. Handbook of High Temperature Superconductivity, edited by Schrieffer, J. R. (Springer, Berlin, 2006), Chap. 3. [Google Scholar]
  33. Hatch R. C. et al. Stability of the Bi2Se3 (111) topological state: Electron-phonon and electron-defect scattering. Phys. Rev. B 83, 241303 (2011). [Google Scholar]
  34. Pan Z. H. et al. Measurement of an exceptionally weak electron-phonon coupling on the surface of the topological insulator Bi2Se3 using angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 108, 187001 (2012). [DOI] [PubMed] [Google Scholar]
  35. Zhu X. T. et al. Interaction of phonons and Dirac fermions on the surface of Bi2Se3: a strong kohn anomaly. Phys. Rev. Lett. 107, 186102 (2011). [DOI] [PubMed] [Google Scholar]
  36. Liu G. D. et al. Development of a vacuum ultraviolet laser-based angle-resolved photoemission system with a superhigh energy resolution better than 1 meV. Rev. Sci. Instrum. 79, 023105 (2008). [DOI] [PubMed] [Google Scholar]
  37. Valla T., Fedorov A. V., Johnson P. D. & Hulbert S. L. Many-body effects in angle-resolved photoemission: quasiparticle energy and lifetime of a Mo(110) surface state. Phys. Rev. Lett. 83, 2085 (1999). [Google Scholar]
  38. LaShell S., Jensen E. & Balasubramanian T. Nonquasiparticle structure in the photoemission spectra from the Be(0001) surface and determination of the electron self energy. Phys. Rev. B 61, 2371 (2000). [Google Scholar]
  39. Cheng W. & Ren S. F. Phonons of single quintuple Bi2Te3 and Bi2Se3 films and bulk materials. Phys. Rev. B 83, 094301 (2011). [Google Scholar]
  40. Richter W. & Becker C. R. A Raman and far-infrared investigation of phonons in the rhombohedral V2–VI3 compounds Bi2Te3, Bi2Se3, Sb2Te3 and Bi2(Te1−xSex)3 (0 < x < 1), (Bi1−ySby)2Te3 (0 < y < 1). Phys. Stat. Sol. (b) 84, 619–628 (1977). [Google Scholar]
  41. Huang G. Q. Surface lattice vibration and electron-phonon interaction in topological insulator Bi2Te3 (111) films from first principles. EPL 100, 17001 (2012). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep02411-s1.pdf (7.7MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES