US Valuation of the SF-6D

INTRODUCTION

Health outcomes of alternative interventions, systems, and policies are expressed in terms of their impact on quality and quantity of life. Valuation studies enhance the interpretation of this evidence by translating health outcomes into a preference-based measure (i.e., value) for economic evaluations. A quality-adjusted life year (QALY; i.e., 1 year of life in optimal health) is one such value measure that combines survival and health-related quality of life (HRQoL).(1) An array of patient-reported outcomes (PROs) instruments have been developed and validated to systematically capture HRQoL; however, only one general health descriptive system, the EQ-5D, has a preference-based scoring algorithm based on a nationally representative sample of US respondents.(2, 3) In this article, we describe the first US valuation of another general health descriptive system, the SF-6D, a 6-item instrument based on the Medical Outcomes Study (MOS) 36-Item Short Form (SF-36). (4)

Unlike the EQ-5D, the SF-36 was originally developed in US at RAND and is in the public domain.(5) Its strong psychometric properties and free availability have allowed the SF-36 to become the most prominent instrument for general health measurement in the US. Brazier and colleagues increased the potential use of the SF-36 system by reclassifying 8 of its dimensions into a 6-item descriptive system (SF-6D), which is more similar to the EQ-5D instrument. The SF-6D instrument has fewer items and levels than the SF-36, which reduces response burden and facilitates valuation studies.

The original SF-6D valuation study applied an innovative standard gamble (SG) protocol with an analytical sample of 611 UK subjects.(6) Specifically, the certainty of 10 years in a SF-6D state was compared to gambles involving 10 years in the best and worst possible SF-6D states. Unlike the EQ-5D time trade-off (TTO) task (7), this SG task avoided difficulties with worse-than-death comparisons and unequal durations. As a final SG task, respondents also completed a conventional SG task for the worst possible SF-6D health state (i.e., pits), which traded risks of 10 years in optimal health, “pits,” and “immediate death,” , which allowed the mapping of SF-6D values to a QALY scale. Adaptive trade-off designs, such as TTO or SG, are scale-based and introduce starting point biases, ceiling and floor effects, and numeracy issues. In addition to these psychometric issues, the original SF-6D analysis changed 26.5% of the pits SG responses to arbitrarily bound the QALY estimates above-1 QALY, a practice inherited from EQ-5D valuation studies and corrected in subsequent work. (8-11)

This paper describes the first SF-6D valuation study in the United States. Furthermore, we applied a pivoted paired comparison design that is novel for health valuation. In a pivoted design, a base scenario (or pivot) is introduced and the respondents choose between 2 alternative changes in the based scenario (i.e., paired comparison). By varying only 2 contrasting attributes at a time, the pivot design reduces cognitive difficulty and response times, similar to partial profile designs.(12) The primary difference between the SG task and paired comparisons is that the SG task selects the next pair to show to a respondent based on his or her response to the previous pair, a form of adaptive paired comparison. By doing so, errors in past choice affect whether downstream comparisons are shown, leading to biased choice data. In paired comparison, the pair set is fixed and does not vary based on upstream responses.

In this study, 666 US respondents completed assigned sets of 24 pivoted pairs comparing SF-6D episodes (i.e., 10 years on state A or 10 years in state B) and 6 full profile (FP) pairs comparing SF-6D gambles (i.e., 10 years in state A with 20% chance of immediate death or 10 years in state B with 10% chance of immediate death). Like the UK study, the final 6 FP pairs locate the values of “immediate death” and optimal health relative to the values of the other SF-6D states, enabling QALY scaling. Unlike trade-off responses, the paired comparisons are not adaptive, reflect decisional utilities (not judgments) (13), are based on well-founded psychometric methods, (14-16) and render ordinal responses that facilitate econometric analysis (e.g., no independence of irrelevant alternatives assumption).(17)

Discrete choice experiments (DCEs) for valuation of health present researchers with some distinct challenges as compared to DCEs for the valuation of goods and services.(18) First, QALYs express value on an anchored scale, such that the value of a year in optimal health and dead are fixed at one and zero, respectively.(19) The part-worth utilities of goods and services are not scaled, thereby avoiding health econometric issues with the non-optimal gap.(17) Second, a person can “opt-out” of receiving goods or services, but cannot “opt-out” of health, necessitating forced-choice designs.(20) Third, attributes of health are naturally correlated (e.g., pain and social functioning), while attributes of goods and services can be randomly combined under a manufacturing process (e.g., wait time and out-of-pocket cost). For coherent responses, a health valuation study must exclude attribute combinations that are counterintuitive (e.g., extreme pain and no problems with social functioning).(21) Fourth, a description of a person's quality and quantity of life is typically more complex than descriptions of goods and services, which can be decomposed into interchangeable component parts. The complexity of health motivates the use of a pivoted design (i.e., pairs that differ on only a small number of attributes). Fifth, goods and services can be traded on a secondary market (i.e., strategic choice). Choosing between health scenarios is more similar to how voters choose their elected official than the demand for products and services, because these votes guide the allocation of public resources and offices. Differences such as these necessitate the adaptation of DCE techniques for health valuation.

In addition to conducting the first US SF-6D valuation study, the purposes of this article are to describe the pivoted design for health valuation, to introduce the stacked probit model for paired comparison responses, and to compare the US and UK SF-6D values on a QALY scale. Limitations of this study and future work are discussed after the results.

THEORY

The episodic random utility model (ERUM) specifies that the utility of a health episode depends on its HRQoL and its duration with an additive error term.(22) In this paper, ERUM was adapted to include risk of “immediate death,” 1-p, such that its additive error term is also assumed to be independent of risk of death, not just duration (U_gamble= p*U(h,t) +(1-p)*U_Dead + ε). Under this model, episode utility, U(h,t), is unrelated to the risk of death, attributes beyond health (e.g., income, privacy), the health of others, or events before the episode (i.e., tabla rasa [blank slate] bias).(23) The probability of a choice between 2 gambles, A and B, depends on the differences in episode utilities, risks of death, and the probability distribution of the difference in errors, Pr(A>B)=Pr(U_A-U_B>ε_B-ε_A). The non-proportionality assumption added to ERUM has no influence on the choice probability when A and B have a common duration and risk of death, but it is an essential assumption when the gambles differ in duration or risk, because it assumes that the error is independent of this difference. The only exception to this probability specification is when preference is certainty by construction, such as 2 gambles that are identical, except that one has greater quality or quantity of life, making the choice logically defined.(24)

Upon its introduction, ERUM was adapted to express value on a QALY scale, which requires that episode utility be proportional to duration and HRQoL, U(h,t)=V_h×t, such that V_opt=1 and V_dead=0. Specifically, SF-6D described HRQoL using 6 items resulting in response vectors that range from optimal health, 111111, to pits, 645655 (Table I). This range may be expressed using an additive multi-attribute utility (MAU) specification of 25 possible decrements, $V_h=1-\sum d_h$. For example, the value of pits, V_pits, is 1 minus the sum of all 25 SF-6D decrements. The assumption of a pure additive model (i.e., no interaction terms) implies that the value of any health state can be expressed by the sum of its decrements. This theoretical framework is the same for the recently published UK SF-6D and EQ-5D estimates. (3, 8)

Table I.

Multi-Attribute Utility Regression Models for SF-6D Health States

666 Respondents and 19,980 Responses (30 responses per respondent)	dh	95% CI		UK
Physical Functioning (PF)
PF1 Your health does NOT limit you in vigorous activities	-	-	-	-
PF2 Your health limits you a little in vigorous activities	0.0069	0.0000	0.0121	0.000
PF3 Your health limits you a little in moderate activities	0.0148	0.0103	0.0203	0.066
PF4 Your health limits you a lot in moderate activities	0.0572	0.0451	0.1122	0.015
PF5 Your health limits you a little in bathing and dressing	0.0021	0.0000	0.0086	0.000
PF6 Your health limits you a lot in bathing and dressing	0.0731	0.0570	0.1407	0.141
Role Limitations (RL)
RL1 You are NOT limited in the kind of work or other regular daily activities	-	-	-	-
RL2 You are limited in the kind of work or other regular daily activities as a result of your physical health	0.0525	0.0388	0.1010	0.000
RL3 You accomplish less than you would like as a result of your emotional problems	0.0447	0.0344	0.0850	0.067
RL4 You are limited in the kind of work or other regular daily activities as a result of your physical health and accomplish less than you would like as a result of your emotional problems	0.0306	0.0238	0.0573	0.013
Social Functioning (SF)
SF1 Your health limits your social activities none of the time	-	-	-	-
SF2 Your health limits your social activities a little of the time	0.0228	0.0172	0.0395	0.082
SF3 Your health limits your social activities some of the time	0.0171	0.0127	0.0266	0.005
SF4 Your health limits your social activities most of the time	0.0507	0.0393	0.0985	0.004
SF5 Your health limits your social activities all of the time	0.0595	0.0464	0.1147	0.052
Pain (PN)
PN1 You have NO pain	-	-	-	-
PN 2 You have pain but it does NOT interfere with your normal work	0.0240	0.0195	0.0368	0.000
PN3 You have pain that interferes with your normal work a little bit	0.0273	0.0215	0.0520	0.059
PN4 You have pain that interferes with your normal work moderately	0.0408	0.0320	0.0773	0.023
PN5 You have pain that interferes with your normal work quite a bit	0.0494	0.0389	0.0955	0.057
PN6 You have pain that interferes with your normal work extremely	0.0796	0.0618	0.1552	0.094
Mental Health (MH)
MH1 You feel tense or downhearted and blue none of the time	-	-	-	-
MH2 You feel tense or downhearted and blue a little of the time	0.0330	0.0255	0.0617	0.072
MH3 You feel tense or downhearted and blue some of the time	0.0309	0.0240	0.0563	0.007
MH4 You feel tense or downhearted and blue most of the time	0.0760	0.0592	0.1486	0.051
MH5 You feel tense or downhearted and blue all of the time	0.0743	0.0574	0.1434	0.044
Vitality (VT)
VT1 You have a lot of energy all of the time	-	-	-	-
VT2 You have a lot of energy most of the time	0.0000	0.0000	0.0033	0.000
VT3 You have a lot of energy some of the time	0.0291	0.0223	0.0481	0.000
VT4 You have a lot of energy a little of the time	0.0269	0.0210	0.0507	0.067
VT5 You have a lot of energy none of the time	0.0639	0.0500	0.1253	0.045
Stacked Probit Parameters
σ1 Scaling parameter of 1st Gaussian Density	0.0151	0.0110	0.0325
σ2 Scaling parameter of 2nd Gaussian Density	0.8637	0.6390	1.9890
θPP Probability of 1st Gaussian Density for PP pairs	0.4921	0.4374	0.5615
θFP Probability of 1st Gaussian Density for FP pairs	0.7506	0.7182	0.7932

* The 95% CI were computed using bootstrap percentile techniques. (Efron and Tibshirani, 1993)

**Taken from UK SF-6D study. (Craig, Under Review-a)

METHODS

Online Panel Survey

The SF-6D valuation study was conducted as part of a larger project examining US health preferences using US adult respondents.(25) All study procedures were approved by the University of South Florida Institutional Review Board. By using a separate panel company (invited subjects) and survey software company (hosted the survey website), we constructed an automated checks-and-balances system to independently measure response rates, secure respondent anonymity, and verify data authenticity, as well as reduce cost when compared with face-to-face or postal surveys or the use of a full-service consultancy (e.g., Knowledge Networks). For every invitation, the panel company provided each panelist's entry data (e.g., age, gender, race/ethnicity, state, and date of enrollment), as well as invitation dates and incentives. The survey software collected paradata (data about the process by which the survey data were collected), such as the IP address, browser type, screen resolution, and response time for each person who came to the invitation page. Using the IP addresses and time zone, we were able to automatically remove “ex-patriot” respondents who were completing the survey outside the US, respondents whose IP address did not match their state address listed with the panel company, as well as persons who did not have the software necessary to complete the survey.

Panel members who clicked on the email invitation survey link sent by the panel company were immediately directed to the initial consent page on the survey website. At this stage and in line with the Checklist for Reporting Results of Internet E-Surveys (CHERRIES), (26) each panel member was considered a unique site visitor. After consent and upon survey entry, respondents self-reported their age, gender, race, Hispanic ethnicity education, and income using items identical to the panel company's entry survey. Respondents were also asked their state and ZIP code, which the survey software compared to their IP address state. Discordant state respondents were removed as a second check of US residency. To participate, consenting respondents must: (1) be 18 years of age or older, (2) be a current US resident; and (3) use an Internet browser that is capable of processing JavaScript code for the collection of paradata. JavaScript coding has a coverage rate of more than 99%, making it the optimal choice when designing interactive survey features. (27)

SF-6D Valuation Study

After survey entry questions, respondents were asked to complete the SF-36 version 1. As an introduction to the SF-6D item descriptions and as an example of paired comparisons, respondents were shown an image of an apple and an orange and asked to choose which fruit they preferred (see Appendix 1). This example was followed directly by 2 pivoted sets of 12 paired comparisons. Under the pivoted design, each set began with a base scenario description (i.e., pivot) followed by a series of 12 pairs comparing alternative adjustments. These adjustments (e.g., more pain and less fatigue vs. less pain and more fatigue) allowed respondents to focus on particular attributes of health, where the remaining attributes were common to both scenarios could be referenced by clicking a button, which returned them to the base scenario description. The pivoted design was originally created to facilitate DCEs with a large number of attributes, such as health valuation studies. Like with partial profile designs, the pivoted design highlights only the differences between the alternatives, which reduces cognitive burden and estimation error relative to FP designs.(12) Without the introduction of the pivoted design, health valuation studies using paired comparisons are not feasible due to the complexity of the health episode descriptions.

The paired comparisons were presented in a page-by-page format, and respondents were asked to read the alternate scenarios carefully and imagine that he or she must live in the scenario for 10 years and then die.(28) To proceed, respondents clicked the circle under the preferred scenario, then clicked the next button.(29) The use of paging helped decrease survey break-off and non-substantive responses (30) as compared with scrolling. No scrolling was required to read the page, and respondents were allowed to change responses prior to proceeding, but were not allowed to return to previous pages. (31, 32) In addition to choice, response times and response changes were recorded via paradata software.(33, 34) The survey was designed to timeout after 30 minutes of screen inactivity. After the first set of 12 pivoted pairs, respondents read a second base scenario description and completed 12 additional pivoted pairs.

After completing both pivoted sets, as an example, respondents completed a simplified, introductory FP pair based on the 5-level general health question (Excellent, Very Good, Good, Fair, and Poor) (see Appendix 2). In this pair, they choose between greater risk of immediate death and improved health for 10 years followed by death (e.g., Excellent health for 10 years and 20% increased risk of immediate death or Good health for 10 years and 5% increased risk of immediate death). For each pair, a better health state with greater mortality was located on the left-hand side of the page; thereby forcing the respondent to choose between greater quality of life and reduced risk of death. Mortality ranged from 5% to 25% across all FP to deter death avoidance and was expressed using text and a pictograph.(35) The choices from the pivoted and FP paired comparisons were combined to estimate the 25 decrements of the SF-6D MAU model on a QALY scale.

To deter order effects, the pivoted sets were randomly ordered; the pair sequence within each set was randomized; and the left-right, top-bottom presentation for each pair was randomly rotated.(36) For the final 6 FP pairs, the pair sequence was also randomized, but the left-hand scenario always had greater quality of life and risk of “immediate death.” After the SF-6D valuation study, the respondents completed follow-up questions regarding difficulty in understanding, responding, reading the survey, handedness, eyesight quality, glasses/contact wearers, and an open comment box. (37, 38) Payment was based on the panel company point system as listed on the emailed invitation.

Power Calculation

We conducted a power calculation to guide the selection of pivoted and FP pairs and the number of responses per pair. The SF-6D descriptive system has 18,000 possible health states (6×4×5×6×5×5), rendering 161,991,000 possible pairs (9,000*17,999). The pivoted design simplified the pair selection to include only pairs that differed on 2 contradictory attributes (i.e., bipeds). Furthermore, we limited the bipedal pairs to those where each attribute differed on the same number of levels (i.e., steps). For example, pain level 1, vitality level 3 vs. pain level 2, vitality level 2 is a 1-step biped (i.e., 2 attributes changing 1 step in contrary directions). Ignoring the attributes common to both scenarios, the SF-6D descriptive system contains orthogonal arrays with 259 one-step, 146 two-step, and 69 three-step bipeds (see Appendix 2). Arrays with great level differences (e.g., 4-step) were excluded to limit complexity.(39) Before selecting pivoted pairs from the 3 arrays, the base scenario descriptions were identified using a US sample of SF-6D responses.

Two base scenario descriptions were identified using 3 criteria: 1) the rank of the descriptions was clear by construction to allow the descriptions to be incorporated in the 6 FP pairs; 2) each description was worse than optimal health and better than pits to allow symmetric variability; and 3) each description occurred with moderate prevalence (i.e., common SF-6D response). To aid in the third criteria, we examined the baseline SF-36 responses from the US Medicare Health Outcomes Survey (MHOS), 1998 to 2003 (N=259,243), which is a large survey of older adults enrolled in the Medicare Advantage program.(40) Among those adults who reported fair health (N=53,078), the third most frequent state (0.6%) was 544534. Among those adults who self-reported good health (N=111,668), the eighteenth most frequent state (0.7%) was 311212. These FAIR and GOOD base scenario descriptions satisfied the 3 criteria and were selected as the basis for the pivoted and FP pairs.

The arrays of 1-step, 2-step, and 3-step PP pairs were applied to the GOOD and FAIR base scenario descriptions, creating 1,148 pairs from 529 SF-6D states. Together these states represented 32% of the MHOS sample. While all 529 responses are possible, some were improbable and may have been difficult for respondents to imagine as hypothetical states. Pairs comparing infrequent responses were removed, halving the number of states (48%; 255/529) and reducing the MHOS coverage to 28%. Including the 971 dropped pairs may have increased statistical efficiency and MHOS coverage (4% gain), but may have also reduced respondent effort due to doubts about the study quality and quadrupled the study cost. As discussed previously, conjoint analysis software packages offer alternative efficiency criteria, which have yet to be adapted for health valuation, where realism is mandatory. (41, 42) Although the applied framework for pair selection began with complete orthogonal arrays, the final pair selection (See Appendix) is not an orthogonal array, because we erred toward realism and practicality over pursuing an arbitrarily selected measure of statistical efficiency.

Among the 177 pivoted pairs selected, the GOOD and FAIR base scenarios served as the basis for 67 pairs each and the remaining 43 pairs were randomly applied to both base scenarios. After the 2 sets of 12 pivoted pairs, respondents completed 6 FP pairs containing the 2 FP descriptions: [optimal,GOOD], [optimal,FAIR], [Optimal,Pits], [GOOD,FAIR], [GOOD,pits], and [FAIR,Pits], with different risks of immediate deaths. For either, the 177 pivoted pairs or the 60 FP pairs (see Appendix 2), a sample size of 95 choices per pair would identify a difference between 50% and 75%, with a significance level of 0.05 and a power of 0.95. However, the analytical sample had over 600 respondents (similar to the UK SF-6D study) to estimate 29 parameters (including 25 decrements and 4 ancillary parameters) and each decrement represented a comparison of 2 health states with a 1-step difference. With 30 pairs per respondent, this equates to 621 choices per decrement (600*30/29), which would identify a difference between 50% and 60%, with a significance level of 0.05 and a power of 0.94. (43)

Econometrics of QALY Estimation

The analysis of paired comparison responses required the adaptation of standard econometric methods to address excess kurtosis, scaling, and clustering.(14) Common cumulative densities for binary responses, such as Gaussian and logistic, may not accommodate the excess kurtosis in online DCEs due to satisficing (an economic term blending satisfy and suffice, where a person chooses a response that meets the survey requirements to proceed in the study, but this response may be sub-optimal, even random).(44) In other words, the estimation requires a functional form that can accommodate thick tails caused by heterogeneous effort and attention to detail between respondents and among responses. In this paper, we introduce the stacked probit, a mixture model of 2 Gaussian distributions that share the same mean but different variances.

$$Pr(A>B)={\theta }_p\Phi \left(\frac{V_A{t}_A-V_B{t}_B}{\sqrt{2}{\sigma }_1}\right)+(1-{\theta }_p)\Phi \left(\frac{V_A{t}_A-V_B{t}_B}{\sqrt{2}{\sigma }_2}\right)$$

Where $V_h=1-\sum d_h$ is the SF-6D MAU model, t is the episode duration, d_h are non-negative decrements on a QALY scale for health state, h, Φ(.) is the Gaussian cumulative density, θ_p is the pivoted mixing probability, and σ₁ and σ₂ are scaling parameters, such that 0 < σ₁ < σ₂. The single-density Gaussian distribution is nested within the stacked model (i.e., θ_p = 1), with the primary advantage of the stacked probit being that it allows for excess kurtosis. For example, the stacked probit can approximate the logistic distribution, where θ=0.565, σ₁= 0.921 and σ₂=1.625. At these parameters, the absolute difference between logistic and stacked probit cumulative distributions (i.e., area between S curves) is 0.006, much less than the 0.078 difference found between the logit and rescaled probit($\sqrt{2}\sigma =1.702$). (45)

The stacked probit also has a more nuanced psychometric justification. Under the single Gaussian specification of the ERUM (a.k.a., probit), the variance of the difference between two episode utilities is twice the variance of a single episode utility; therefore, the probit scaling parameter is the standard deviation in episode utility and describes the probability of identifying a 1 QALY difference, $\Phi \left(\frac{1}{\sqrt{2}\sigma }\right)$. The stacked probit is a mixture of two Gaussian distributions with a common mean and ranked scaling parameters, such that the first density describes a person with greater discriminatory capacity (i.e., connoisseurs). A non-unity mixing probability, θ < 1, implies that the responses are a mixture of connoisseur and less-refined preferences, each with normal errors.(16) For our purposes, the stacked probit also includes a second mixing parameter for the FP responses, θ_FP, to allow for differences in connoisseur prevalence between FP and pivoted pairs.

The more common logit model assumes the episode utilities come from an extreme value type-1 (EV-1) distribution. When independent, EV-1 differences are symmetrically distributed, but the utilities alone are asymmetrically distributed. Unlike the logit model, the probit imposes the same distributional shape on episode utilities and their differences and can accommodate the fact that the utility of optimal health and dead episodes have no variance on a QALY scale.(17) When A is a non-optimal health state in a FP pair, the responses can be modeled as:

$$Pr(A>B)={\theta }_{FP}\Phi \left(\frac{p_A{V}_A{t}_A-p_B{V}_B{t}_B}{\sqrt{p_A^2+p_B^2}{\sigma }_1}\right)+(1-{\theta }_{FP})\Phi \left(\frac{p_A{V}_A{t}_A-p_B{V}_B{t}_B}{\sqrt{p_A^2+p_B^2}{\sigma }_2}\right)$$

Where p_A and p_B are survival probabilities and V_Dead = 0. The value of a dead episode has no variance, thereby reducing the denominators in each density, $\sqrt{p_A^2+p_B^2\sigma }$, to be less than $\sqrt{2}\sigma$. When A is an optimal health episode, the specification further simplifies to:

$$Pr(A>B)={\theta }_{FP}\Phi \left(\frac{p_{Opt}{t}_{Opt}-p_B{V}_B{t}_B}{p_B{\sigma }_1}\right)+(1-{\theta }_{FP})\Phi \left(\frac{p_{Opt}{t}_{Opt}-p_B{V}_B{t}_B}{p_B{\sigma }_2}\right)$$

Where V_Opt = 1. The value of an optimal health episode also has no variance, thereby reducing the denominators to p_Bσ.

The 29 parameters of the stacked probit model (d₁...d₂₅, θ_p, θ_FP, σ₁, and σ₂) are estimated by maximum likelihood estimation with clustering, and their 95% confidence intervals are estimated by1000 iteration percentile bootstrap with cluster replacement.(46) The decrement estimates are compared to the UK decrement estimates. (3) The US and UK QALY predictions for SF-6D states are compared visually and formally (Lin's coefficient of agreement and mean absolute difference) using the SF-6D responses from the US MHOS (N=259,243). (47)

RESULTS

The panel company recruited 3,152 respondents through email invitation. Most consented to participate in the study (98%) (Figure 1); however, the survey software was unable to verify the US residency of a third of the respondents (33%). A few dozen of foreign IP addresses and time zones were identified, suggesting that some of the excluded respondents were taking the survey abroad (either ex-patriot Americans or foreign impostures). The majority of unidentified respondents may have been domestic and excluded due software compatibility issues. An additional 4.5% exited while completing the SF-36 instrument and 18% of the respondents who entered the SF-6D valuation study exited prior to completion. Some of these later drop-outs may be attributable to automatic exclusions after spending more than 20 minutes on a single screen. Table II compares the included and excluded respondents based on their demographic and socioeconomic characteristics at the time of panel entry and shows no statistically significant differences, except that persons who did complete the survey had higher income responses.

Figure 1.

Participation Flow Chart

Table II.

Panel Entry Characteristics of Excluded Respondents and Panel vs. Survey Entry Characteristics of Included Respondents

	Excluded (N=1,344)	Included (N=666)			2000 US Census %
Self-reported Characteristics	Entry	Entry	Survey
	N (%)	N (%)	N (%)	p-value*
Age				0.954
18 to 24	45 (3)	22 (3)	22 (3)		13.0
25 to 34	143 (11)	62 (9)	63 (9)		19.1
35 to 44	203 (15)	79 (12)	85 (13)		21.6
45 to 54	323 (24)	156 (23)	162 (24)		18.0
55 to 65	395 (29)	211 (32)	212 (32)		11.6
+65	235 (17)	136 (20)	122 (18)		16.7
Gender				0.860
Male	428 (32)	213 (32)	210 (32)		48.3
Female	916 (68)	453 (68)	456 (68)		51.7
Race				0.138
White	1137 (85)	569 (85)	568 (85)		77.4
Black	58 (4)	21 (3)	35 (5)		11.4
Other	136 (10)	71 (11)	63 (9)		11.2
Non-response	13 (1)	5 (1)
Ethnicity				0.739
Hispanic	47 (3)	17 (3)	17 (3)		11.0
Other	1155 (86)	578 (87)	649 (97)		89.0
Non-response	142 (11)	71 (11)
Income				0.002
<$30,000	366 (27)	183 (27)	213 (32)		35.1
$30,000 to $69,999	451 (34)	229 (34)	265 (40)		42.4
>$70,000	406 (30)	206 (31)	152 (23)		22.5
Non-response	121 (9)	48 (7)
Education				0.097
High School or less	283 (21)	139 (21)	151 (23)		48.2
Some College	511 (38)	262 (39)	279 (42)		27.4
College or more	396 (29)	194 (29)	158 (24)		24.4
Non-response	154 (11)	71 (11)
Census Division				1.000
New England	58 (4)	30 (5)	32 (5)		4.9
Middle Atlantic	185 (14)	103 (15)	99 (15)		14.1
East North Central	232 (17)	121 (18)	121 (18)		16.0
West North Central	97 (7)	45 (7)	46 (7)		6.8
South Atlantic	308 (23)	135 (20)	135 (20)		18.4
East South Central	76 (6)	28 (4)	30 (5)		6.0
West South Central	122 (9)	62 (9)	61 (9)		11.2
Mountain	101 (8)	54 (8)	55 (8)		6.5
Pacific	165 (12)	88 (13)	87 (13)		16.0

^*p-value represents Entry versus Survey

Table II also shows the included respondents’ panel entry characteristics and survey responses, as well as the 2000 US Census for comparison.(48) Comparing the self-reported characteristics at panel entry to those at survey entry, the differences are not statistically significant, except for income, where respondents appear to have lower incomes in 2010. Within the analytical sample, 79% provided identical demographic information on both their panel entry form and the survey entry page. Although the analytical sample is representative of the 9 US Census divisions, the respondents are older, more likely to be female, more likely to be white, and less likely to be of Hispanic ethnicity compared to the US census. In terms of socioeconomics, the income distributions are similar, but respondents are also more likely to have some higher education. These sampling biases are in addition to the unobservable bias due to non-probability sample and are discussed in the interpretation of the results.

In the analytical sample, sample sizes for the pivoted pairs ranged from 63 to 109 responses with a median of 91. For the FP pairs, the sample sizes ranged from 49 to 89 with a median of 67 responses. The maximum probabilities are 97% for the pivoted pairs and 94% for the FP pairs, suggesting that less than 6% satisficing (i.e., random responses). The median pair completion time is 30 seconds (IQR 23 to 44) for pivoted pairs and 35 seconds (IQR 26 to 49) for FP pairs. The proportion of changed responses is 2% for pivoted pairs and 1% for FP pairs. The median time to complete the first pivoted set was 7.55 minutes (IQR 5.98 to 10.10), the second pivoted set was 6.32 minutes (IQR 5.08 to 8.49), and the 6 FP pairs was 3.80 minutes (IQR 2.98 to 5.13).

Table I describes the decrement estimates from the stacked probit. The estimates are on a QALY scale, and 22 out of 25 are significantly non-zero at 0.05 significance level. The 3 remaining decrements (PF1 to PF2, PF4 to PF5, and VT1 to VT2) also had no value based on the UK SF-6D valuation study evidence. The value of pits is 1 minus the sum of the decrement (0.0129 QALY; 95% CI 0.201,-0.818) and is not significantly better than or worse than dead. Item importance (i.e., sum of item decrements) ranges from 0.12 (Vitality) to 0.22 (Pain). At a 0.05 significance level, pain and mental health are the most important items, and vitality and role limitations are the least important items. The stacked probit parameter estimates demonstrate excess kurtosis well beyond the more common probit and logit specifications. Furthermore, the difference between the FP and pivoted pair mixing probabilities suggests that respondents were better able to identify a difference on 1 QALY using the FP pairs than the pivoted pairs.

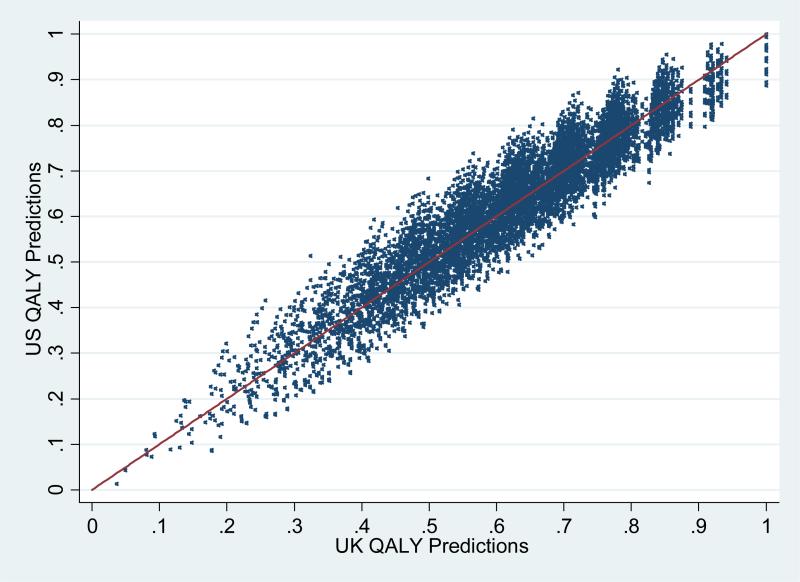
Instead of comparing the UK and US SF-6D QALY prediction for all 18,000 possible SF-6D responses, we examined the subset of 8,428 responses in the MHOS. Figure 2 shows the US QALY predictions on the Y axis and the UK QALY predictions on the X axis with a 45 degree line representing their equivalence. The scatter plot illustrates the commonality between the predictions even though the studies were conducted with different valuation tasks and sampling. Lin's coefficient of agreement is 0.941 and the mean absolute difference is 0.043.

Figure 2.

US and UK SF-6D QALY Predictions*

* Line represents a 45 degree angle demarcating the equivalence between US and UK QALY predictions

DISCUSSION

This study introduced a pivoted design for health valuation, the stack probit for QALY estimation, and the first US value set for the SF-6D descriptive system. Based on a sample of 666 US panelists, the survey results enhance comparative effectiveness research (CER) by translating SF-6D responses into US QALYs. The US QALY predictions were remarkably similar to the UK value set given differences in experimental design, format, and sampling.

The underlying theoretical framework for the study design and econometric analysis builds from ERUM and the concept of QALYs and inherits their limitations. In a recent editorial, Menzies and Salomon were critical of the ERUM in its application to trade-off responses, because the adaptive design of TTO task inherently changed duration as episode utility decreases, leading to a bias against eccentric worse-than-death responses.(49) The pair comparison approach is not adaptive; thereby, addressing this potential limitation. Furthermore, this approach does not require the TTO constant proportionality assumption for QALY estimation. All episodes in these pairs were 10 years in duration, therefore, the estimates may be interpreted on a more general scale, where 0 is equal the value of immediate death and 10 is the value of 10 years in optimal health followed by death. Nevertheless, the estimation relies on 60 pairs of health gambles for scaling, similar to the original UK SG valuation study, and requires constant proportionality in risk-based expected utility theory. Alternatively, a valuation study might ask respondents to choose directly between immediate death and a poor health episode; however, gambles with non-zero risk of immediate death seem to be a more appropriate framework than suicide.(19)

Unlike the commonly used face-to-face interview format, such as the UK SF-6D study or US EQ-5D studies, the US SF-6D valuation study is an online survey.(6) In face-to-face interviews, interviewers may aid respondents who undergo potentially complicated valuation tasks (e.g., SG) or may visually monitor participant effort put into the task. Interviewers may also introduce Hawthorne effects (respondents modify their behavior in response to being studied) and social desirability biases (tendency to respond more favorably).(50, 51) In the US study design, we allowed for excess kurtosis in the econometric specification to address potential saliency issues and designed the valuation task to reduce cognitive burden (i.e., paired comparisons).

The stacked probit revives Thurstonian Case V scaling as a mixture model that allows for excess kurtosis beyond the Bradley-Terry-Luce model. (16, 52, 53) The evidence of excess kurtosis is not surprising due to the potential for satisficers in online surveys; yet, this is the first study to measure excess kurtosis in health preferences. The stacked probit was the natural conclusion of a lesser known observation that stacking densities can create densities with greater kurtosis, but not lesser kurtosis. The Gaussian distribution has no excess kurtosis, making it a reasonable candidate for stacking. In this case, stacks of 2 Gaussian densities can closely replicate a logistic distribution; however, stacks of logistics cannot replicate a Gaussian density. If unaddressed, excess kurtosis may compress parameter estimates by pushing them between the narrow tails of a constraining distribution.

The use of a non-probability sample with observable demographic and socioeconomic differences compared to the 2000 US census affects the interpretation of the estimates. Application of sampling weights may reduce differences in the observable characteristics, but does not address non-probability sampling (i.e., unobservable biases). Also, weights are estimated and derived for an arbitrarily selected array of self-reported responses. Variability in the estimates or responses increase standard error in the valuation estimates, and may not improve generalizability. Instead, this paper provides unweighted results from a national sample of US panelists, which is the best available evidence for the translation of SF-6D responses to QALYs.

The feasibility of online health valuation studies using a pivoted design suggests potential expansion for additional health descriptive systems, such as the EQ-5D 5L and SF-12, as well as disease-specific instruments. Further methodological research is needed to examine order effect, the implications of pair selection, non-additive MAU models, framing effects of FP descriptions, satisficing controls, logical consistency, and variability in health preferences by respondent characteristics and time of survey completion.