New Insights into the Folding of a β-Sheet Miniprotein in a Reduced Space of Collective Hydrogen Bond Variables: Application to a Hydrodynamic Analysis of the Folding Flow

Abstract

A new analysis of the 20 μs equilibrium folding/unfolding molecular dynamics simulations of the three-stranded antiparallel β-sheet miniprotein (beta3s) in implicit solvent is presented. The conformation space is reduced in dimensionality by introduction of linear combinations of hydrogen bond distances as the collective variables making use of a specially adapted Principal Component Analysis (PCA); i.e., to make structured conformations more pronounced, only the formed bonds are included in determining the principal components. It is shown that a three-dimensional (3D) subspace gives a meaningful representation of the folding behavior. The first component, to which eight native hydrogen bonds make the major contribution (four in each beta hairpin), is found to play the role of the reaction coordinate for the overall folding process, while the second and third components distinguish the structured conformations. The representative points of the trajectory in the 3D space are grouped into conformational clusters that correspond to locally stable conformations of beta3s identified in earlier work. A simplified kinetic network based on the three components is constructed and it is complemented by a hydrodynamic analysis. The latter, making use of “passive tracers” in 3D space, indicates that the folding flow is much more complex than suggested by the kinetic network. A 2D representation of streamlines shows there are vortices which correspond to repeated local rearrangement, not only around minima of the free energy surface, but also in flat regions between minima. The vortices revealed by the hydrodynamic analysis are apparently not evident in folding pathways generated by transition-path sampling. Making use of the fact that the values of the collective hydrogen bond variables are linearly related to the Cartesian coordinate space, the RMSD between clusters is determined. Interestingly, the transition rates show an approximate exponential correlation with distance in the hydrogen bond subspace. Comparison with the many published studies shows good agreement with the present analysis for the parts that can be compared, supporting the robust character of our understanding of this “hydrogen atom” of protein folding.

1. INTRODUCTION

A complete description of how proteins fold into their native state is one of the primary objectives of structural biology. In principle, computer programs for molecular dynamics (MD) simulations, such as CHARMM¹, AMBER², and Desmond³, can provide details about the folding process in the form of time-dependent positions and velocities of the atoms constituting the protein chain as the protein progresses from the unfolded to the native state. Because of the time scale of folding for even small fast folding proteins (μs to ms), such folding simulations have only recently become possible using special computer hardware⁴. However, even when statistically significant numbers of such trajectories become more widely available, as they will, their utilization for understanding the essential features of the folding process requires special techniques for their interpretation. One approach is to determine the free energy surface (FES) of the folding reaction as a function of a small number (often two) collective variables that include the essential features; examples of coordinates that have been used are the radius of gyration, the fraction of native contacts and a set of hydrogen bonds^5–9. Another approach is to calculate the free energy disconnectivity graphs (FEDG)^10–14, which show the populations of various free energy basins at equilibrium and the barriers by which these basins are connected. A related approach constructs equilibrium kinetic networks (EKNs), in which the protein conformations along a long MD trajectory with many folding/unfolding events are divided into clusters on the basis of kinetic connectivity and/or root-mean-square-deviation (RMSD) of the conformations^15,16. The FEDG and EKN can be projected on a one-dimensional reaction coordinate to give a one-dimensional free energy profile (FEP) for the folding process¹⁷. Also, the conformation space can be reduced to a space of a few collective variables using Principal Component Analysis¹⁸ and various non-linear reduction methods^19–26, as in the previous studied of protein folding^23,27,28.

The antiparallel β-sheet miniprotein (beta3s, Fig. 1) is one of the few systems for which the protein folding reaction has been simulated in sufficient detail, albeit with an implicit solvent model, to make possible meaningful applications of the analysis methods mentioned above²⁹. An all-atom representation was employed and the CHARMM program¹ was used to calculate “equilibrium” folding and unfolding trajectories; the temperature for the simulations (330K) was chosen so that the denatured and native state were significantly populated at equilibrium. Ferrara and Caflisch²⁹, and later Marai et al.³⁰, have used the fractions of the native contacts formed in the N-terminal (residues 1–13) and C-terminal (residues 7–20) β-hairpins as the essential coordinates. Qi et al.³¹ performed an extensive analysis based on the genetic neural network (GNN) method of So and Karplus³² to find optimum collective variables to describe the folding reaction. They found that the hydrogen bond distances between residues 3 and 10 and 5 and 8 in the N-terminal hairpin and those between residues 11 and 18 and 13 and 16 in the C-terminal hairpin are most important; in fact, the sum of these distances is a good simple reaction coordinate for the overall description of the folding process. Carr and Wales have built the FEDGs and examined specific pathways of folding³³, while Rao and Caflisch³⁴ have constructed the EKN for the folding process. Most folding events followed two pathways: in one of them (most frequent), the C-terminal β-hairpin is formed first followed by the N-terminal β-hairpin, and in the other (less frequent), these hairpins are formed in reverse order. A more detailed kinetic analysis³⁵ showed that the conformations that have the N-terminal hairpin formed and the C-terminal unstructured and those with the C-terminal hairpin formed and the N-terminal unstructured, correspond to free energy basins which are separated from the native state basin by the transition state ensembles. Further studies of beta3s folding have mainly focused on the consideration of one-dimensional FEP by the projection of the EKN on a single progress coordinate^35–38). This coordinate was determined in various ways, using the direct p_fold method of Du et al.³⁹ and its modifications, such as the node-p_fold (Rao et al.⁴⁰) and p_fold(τ_commit) (Snow et al.⁴¹ and Rao et al.⁴⁰), p_foldf (Krivov and Karplus¹⁷), and the mean-first-passage-time (MFPT) (Park et al.⁴²). All these methods lead to similar results for beta3s folding^37,38. Also, recently Zheng et al.⁴³ used the LSDMap method²⁶ to reduce the conformation space of beta3s to a few collective variables that describe the protein behavior at different time scales. Comparisons with a number of these studies are made in the manuscript.

FIG. 1.

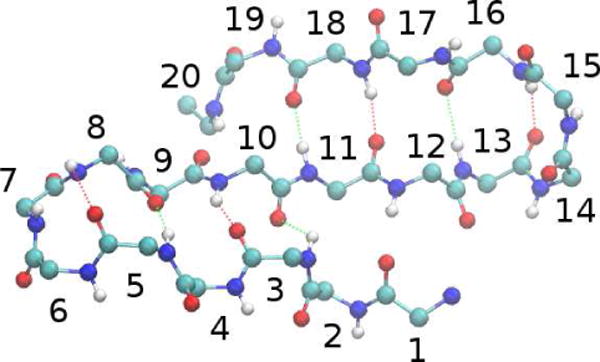
Native structure of beta3s. The lower part of the protein corresponds to the N-terminal hairpin, and the upper part to the C-terminal hairpin. The dashed lines indicate hydrogen bonds.

All of the analyzes of beta3s mentioned above have been based on a set of equilibrium folding/unfolding trajectories of up to 20 μs in length reported previously³⁵. We use the same (20 μs) trajectory data in the present study. The conformation space is characterized with the hydrogen bond distances and reduced to a three-dimensional (3D) space of collective variables with the PCA method. To make structured conformations more pronounced, only the formed bonds are taken into consideration. The representative points are grouped into clusters of conformations, and a spatial (3D) kinetic network is constructed, which shows not only how the clusters are connected but also how they are disposed in the 3D conformation space. The collective variables corresponding to the first three PCA components are projected onto the hydrogen bond space to determine the most representative bonds.

The analysis of folding kinetics is complemented by a “hydrodynamic” description of the folding process (Chekmarev et al.⁴⁴). It is based on a reduced space determined with a modified PCA method. In the hydrodynamic approach, the calculated folding trajectories are used to determine the fluxes of the representative points of a system in the reduced space from which the vector fields of folding flows and the “streamlines” of the flows are constructed. In contrast to the FESs, which determine the probability for the system to be found in a certain conformation state, such flows show the direction in which the system proceeds in local regions of the conformation space. This leads to more insight into the actual folding dynamics and provides an efficient separation of different folding pathways, which makes it ideally suited for studying beta3s. The tracer paths representing the “streamlines” of folding flows are calculated to examine the dynamics of beta3s folding. For an earlier application of the hydrodynamic approach to a SH3 domain, see Kalgin et al.^45,46). Beta3s is an ideal system for applying the hydrodynamic analysis not only because it has been extensively studied with different approaches as mentioned above. In addition, the earlier studies have indicated that the beta3s folding dynamics is complex, in part due to the fact that the denatured state consists notably of an “entropic” region, but also has a helical basin and several misfolded traps.

The paper is organized as follows. Section 2 describes the methods we used to perform molecular dynamics simulations (2.1), to characterize the conformation space and collective variables (2.2), to construct one-dimensional FEP (2.3), to cluster conformations (2.4), to analyze secondary structures (2.5) and to present the folding behavior in the form of “hydro-dynamic” flows and the paths of passive tracers (2.6 and 2.7). Section 3 presents the results of the study and their discussion, including clustering the representative points (3.1), spatial kinetic network (3.2), the hydrodynamic picture of the folding dynamics and its comparison with the FES (3.3), and the dependence of the rates of transitions between the clusters upon the distances between the clusters (3.4). Section 4 contains a concluding discussion.

2. METHODS

2.1. Simulation System and Molecular Dynamics Simulations

The designed three-stranded antiparallel 20-residue peptide (called beta3s) (Thr1-Trp2-Ile3-Gln4-Asn5-Gly6-Ser7-Thr8-Lys9-Trp10-Tyr11-Gln12-Asn13-Gly14-Ser15-Thr16-Lys17-Ile18-Tyr19-Thr20 with charged termini⁴⁷) was modelled with the CHARMM program¹. All heavy atoms and the hydrogen atoms bound to nitrogen or oxygen atoms were considered explicitly; PARAM19 force field⁴⁸ and a default cutoff of 7.5 Å for the nonbonding interactions were used. A meanfield approximation based on the solvent-accessible surface (SAS) was employed to describe the main effects of the aqueous solvent⁴⁹. It has been shown²⁹ that at T = 330K, irrespective of the initial conformation, this model yields reversible folding of the solvated beta3s to the conformation determined by NMR⁴⁷ (23 of the 26 nuclear Overhauser effect constraints are satisfied). The neglect of collisions with water molecules (frictional effects) in the simulations with the implicit solvent model, leads to rates that are about 100 times faster than the experimental values. However, importantly the relative rates of folding for different secondary structural elements are comparable to the values observed experimentally; i.e., helices fold in about 1 ns⁵⁰, β-hairpins in about 10 ns⁵⁰, and triple-stranded β-sheets in about 100 ns⁵¹ compared to experimental values of ~ 0.1⁵², ~ 1⁵², and ~ 10 μs⁴⁷, respectively.

The simulations were performed with the time step of 2 fs using the Berendsen thermostat (coupling constant of 5 ps) at T = 330K. The number of folded and unfolded conformations at this temperature has shown that for the present protein model it is slightly above the melting temperature⁵³. Ten MD trajectories with different initial distributions of atomic velocities generated in a previous study of the Caflisch group³⁵, each of 2 μs length, were grouped into a single “equilibrium” trajectory. During the total time of 20 μs, the protein experiences about one hundred folding/unfolding events³⁴. The atomic coordinates (“frames”) were saved every 20 ps, which resulted in 10⁶ snapshots.

2.2. Conformation Space and Collective Variables

As mentioned in the Introduction, various variables can be used to characterize the configuration of a protein. Based on the results of the analysis of possible variables by Qi et al.³¹, we employed the hydrogen bond distances. For comparison, the interatomic distances were tried but they were found to be less efficient in separating representative points of the protein into clusters (see Supporting Information). Using hydrogen bond distances, the configuration is determined by the distances between the oxygen atom in the (CO)_i group and the nitrogen atom in the (NH)_j group for \j − i\ > 2, where i and j are the numbers of the residues (see Fig. 1).

To simplify the description for further analysis, it is useful to introduce a small number of collective variables. The reduced variable space should be sufficient to represent the full configuration space, while being orthogonal. Although, in some cases, such variables can be selected on physical grounds, as, for example, groups of native contacts for the final stage of folding of the SH3 domain⁴⁶, an unbiased choice is preferable. Many methods are available for this purpose. They include the early quasiharmonic analysis⁵⁴, the PCA¹⁸ (in application to protein folding, e.g.,^27,28) as well as a variety of methods in which the projection of a nonlinear manifold onto a space of lower dimension is more or less effective in limiting the overlap of the variables. Examples include the Isomap (IM)¹⁹, Landmark Isomap (LIM)²⁰, Local Linear Embedding (LLE)²¹, Hessian Locally Linear Embedding (HLLE)²², Full Correlation Analysis (FCA)²³, Manifold Sculpting (MS)²⁴, Diffusion Map (DF)²⁵ and the Locally Scaled Diffusion Map (LSDMap)²⁶ methods. In the present study, we tried a number of these methods (PCA, LLE, FCA and MS) but found that each of them had certain failings (Supporting Information). Consequently, we use a modification of the standard PCA method, as described below, that was satisfactory for the beta3s peptide.

One disadvantage of the standard PCA method in its application to the present problem is that it poorly resolves well-organized conformations among a large number of unstructured conformations (Supporting Information, Figs. S1 and S2). This problem arises in beta3s at temperatures close to and higher than the melting temperature, particularly in the case of equilibrium folding when the protein spends a comparably long time in the denatured state. One way to solve this problem is to consider for the state vector a residue contact vector, whose component for each pair of residues is augmented if, and only if, the bond between these residues is formed. With this restriction, the relative weight of the unformed bonds, and thus the unstructured conformations, decreases. This approach has been successfully used to study folding of an amyloidogenic lattice protein (Palyanov et al.²⁷) and off-lattice models of protein G and src SH3 domain (Hori et al.²⁸). The algorithm used in the present paper is described in Supporting Information. Briefly, for each current vector of the hydrogen bond distances h = (h₁, h₂, …, h_D), where D is the number of possible hydrogen bonds (dimension of conformation space), a conjugate vector of states p = (p₁, p₂, …, p_d) is introduced, in which component p_i is equal to 1 if the corresponding hydrogen bond is formed and 0 otherwise. Then, applying the standard PCA algorithm¹⁸, the conformation space h is reduced to a K-space of collective variables g₁, g₂, ..., g_k, which are directed along the eigenvectors corresponding to the largest eigenvalues. As a result, the protein conformation with hydrogen bond distances h₁, h₂, …, h_D is determined by the values of the collective variables $g_j={\displaystyle {\sum }_{i=1}^D{w}_{ij}{h}_i}$, where w_ij indicates the contribution of the bond i into the variable j, i.e. the original h = (h₁, h₂, …, h_D) space is mapped onto the reduced g = (g₁, g₂, …, g_k) space of collective variables. Since the collective variables are linear combinations of the original variables, they are measured in the same units as the latter, i.e. in angstroms. In what follows we refer to this algorithm to as the Hydrogen Bond PCA (HB PCA) method.

The coefficients w_ij, determining the contributions of the hydrogen bonds to the collective variables, are essential for the interpretation of the present analysis. If w_ij is small, it indicates that j collective variable does not capture dynamics of formation of the i bond, which must appear in another collective variable. If w_ij is large, not only the value of w_ij but its sign is significant; it indicates whether bond i is forming or breaking as g_j varies; i.e. whether the length of the bond decreases or increases. It should be noted, however, that it is not known a priori which sign of w_ij corresponds to the formation (or the breaking) of the bond, because the PCA algorithm does not distinguish between the positive and negative directions of an eigenvector (they both are equally acceptable). Consequently, this choice has to be based on the general picture of the folding process.

In the present paper, we use a 3D space of collective variables, g = (g₁, g₂, …, g₃) for the analysis, although this space could easily be extended to higher dimension. The spectrum of the largest twenty five eigenvalues is shown in Fig. 2 (the eigenvalues are normalized so that their sum is equal to 1). The first three modes account for 30% of the data variation (calculated as a sum of the corresponding eigenvalues¹⁸). Although larger percentages might be desirable, the fact that a large number of small contributions are required to obtain significantly higher percentages (e.g. 25 modes yield ~ 70%) suggests that their inclusion would not change the analysis significantly. Also, we have done some analysis with only the first two components because of their simpler graphical representation; they account for ~ 25% of the data.

FIG. 2.

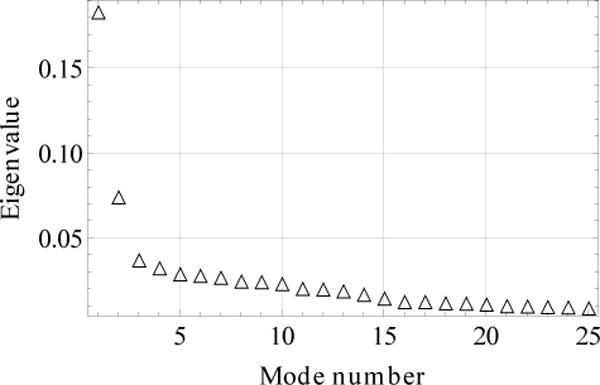
Spectrum of the largest eigenvalues.

2.3. One-dimensional Free Energy Profile

To calculate the one-dimensional free energy profile (FEP), we followed the pfoldf method of Krivov and Karplus¹⁷. The calculation is started by constructing the equilibrium kinetic network (EKN). For this, the chosen reaction coordinate in the g space was divided into bins, and the protein conformations occurring along the simulated folding trajectory were distributed among these bins. These bins were considered to be the nodes of the EKN. Having the EKN, the p_fold value of node i (p_i) was calculated as the solution of the equation pi = Σ _jp_ijp_j with the boundary conditions p_a = 1 and p_b = 0, where p_i is the probability for the system to be in node i, p_ji is the probability of transition from node j to i, A is the node corresponding to the native state, and B to a “denatured” state. To determine the FEP, node B was considered to represent every node not belonging to native basin. Each value p_c between 0 and 1 can then be used to cut the network into set A containing all nodes with p_fold> p_c and set B containing the nodes with p_fold < p_c. For each cut, a point with the abscissa Z_a/Z and the ordinate ΔG = – k_BT ln Z_ab/Z is obtained, where G is the free energy, k_B the Boltzmann constant, Z_a the partition functions of node A, Z the total partition function, and Z_ab the number of EKN transitions between the two sets. To obtain the FEP along the original reaction coordinate, the progress variable Z_a/Z is then transformed to this coordinate.

2.4. Clustering the Conformations

As a result of the reduction of the conformation space, the representative points are distributed in a 3D space of the collective variables, g = (g₁, g₂, g₃). To divide these points into clusters, we used the MCLUST method by Fraley and Raftery⁵⁵. In this method, the collection of points is approximated by a set of multidimensional (in our case 3D) Gaussian functions with generally different covariance matrices and different weights. Each function represents a cluster of the points. To determine the optimal number of clusters and distribute the points among them, a maximum-likelihood estimation is employed. To perform the calculations, we used the MCLUST codes available at the website⁵⁶.

2.5. Secondary Structure Analysis

As in the previous studies^34,35,38, protein conformations were discriminated according to the secondary structure strings (SSSs) encoded with the DSSP alphabet⁵⁷, i.e. the letters H, G, I, E, B, T, S, and “-” stand for α-helix, 3₁₀-helix, π-helix, extended, isolated β-bridge, hydrogen bonded turn, bend, and unstructured segments, respectively. With this coding, the native state (Fig. 1) is represented by the string “-EEEETTEEEEEETTEEEE-”³⁴. The program WORDOM⁵⁸ was used to perform the analysis.

2.6. “Hydrodynamic” Description of the Folding Process

The hydrodynamic description of protein folding⁴⁴ is based on the calculation of the transitions in the space of the collective variables g. These transitions are organized into the local transition probability fluxes j(g). In the case of three variables, g = (g₁, g₂, g₃), the g₁-component of the flow at a point g is determined as

$$j_{g1}(\text{g})=[{\displaystyle \sum _{{\text{g}}^{\prime },{\text{g}}^{″}(\text{g}\subset \text{g}\ast )}^{g_1″-g_1\prime >0}n({\text{g}}^{″},{\text{g}}^{\prime })-}{\displaystyle \sum _{{\text{g}}^{\prime },{\text{g}}^{″}(\text{g}\subset \text{g}\ast )}^{g_1″-g_1\prime <0}n({\text{g}}^{″},{\text{g}}^{\prime })]/t_f}$$ (1)

where t_f is the total time length of the simulated events, n(g″,g′) is the total number of transitions from state g′ to g″, and g ⊂ g^* is a symbolic designation of the condition that the transitions included in the sum have the straight line connecting points g′ to g″, which crosses the plane g₁ = const within the square of unit length (typically of 1 Å ) centered at the point g. The first term on the right-hand side of the equation corresponds to the transitions in the positive direction of g₁, and the second term to those in the negative direction (Fig. 3). The g₂- and g₃-components of j(g) are determined in a similar way, except that one selects the transitions crossing the planes g₂ = const and g₃ = const, respectively. With these fluxes, the flow is divergence free, i.e. for every cell in the 3D space the incoming flow is equal to the outgoing flow. We note that small values of the fluxes can be the result of a small number of transitions between two states or a larger number of transitions in one direction that are compensated by the transitions in the opposite direction. This occurs when detailed balance holds approximately as is expected in equilibrium folding trajectories.

FIG. 3.

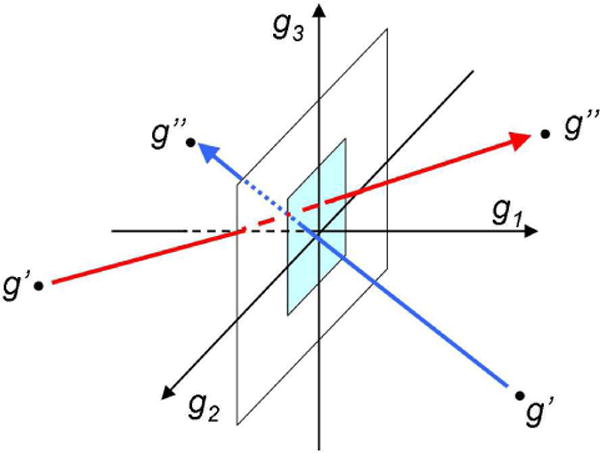
Scheme illustrating Eq. (1). The red and blue arrows are for the transitions in the positive and negative directions of g₁. The light blue square is the unit square.

2.7. Visualization of the Streamlines

Once the fluxes j(g) have been determined from the trajectories, it is possible to construct the “streamlines” of the folding flows, i.e. the lines which are tangent to the local directions of the j(g) vectors. In the case of two dimensions, they are easily obtained by calculation of so called stream function⁵⁹. Due to the continuity equation ∂j_g1/∂g₁ + ∂j_g2/∂g₂ = 0, the fluxes can be determined as j_g1= ∂Ψ/∂g₂ and j_g2= −∂Ψ/∂g₁, where Ψ(g₁, g₂) is the stream function. Then Ψ(g₁, g₂) can be calculated as

$$\mathrm{\Psi }(g_1,g_2)={\displaystyle {\int }_{g=0}^{g=g_2}{j}_{g1}(g_1,g)dg}$$ (2)

The stream function is constant at each streamline and changes from one streamline to another, so that the difference between the stream functions for two streamlines determines the fraction of the total flow in the “stream tube” between the streamlines. We have used this approach to study folding of two model proteins, a lattice α-helical hairpin⁴⁴ and an off-lattice fyn SH3 domain⁴⁵, and found that the folding flows do not follow the FES landscape.

Determining the stream function in a 3D space is not so simple. In this case, the continuity equation leads to a 3D vector potential⁵⁹, which does not offer a suitable means for flow visualization (when the 3D flow is reduced to a 2D flow, only a single component of the vector potential remains nonzero, which is perpendicular to the 2D plane and represents the stream function). Therefore, the streamlines of a 3D flow are usually visualized by seeding the flow with weightless point particles (“passive tracers”), which follow the streamlines of the flow due to the absence of any inertia⁶⁰. To calculate the paths of the passive tracers, the equation

$$\frac{d\mathbf{g}}{d\tau }=\mathbf{\text{j}}(\mathbf{\text{g}})$$ (3)

is numerically integrated starting from various points of the g space, where j(g) is the flux vector determined by Eq. (1), and τ is a parameter (“time”). Since j(g) are known only at the discrete points of the g space, corresponding to the snapshots, their values at intermediate points were calculated by a (linear) interpolation between the neighboring points according to the algorithm by Darmofal and Haimes⁶¹. To initiate tracer paths, we typically chose the points at which the flux vectors had the largest values (see below).

3. RESULTS AND DISCUSSION

3.1. Three Dimensional Distribution and Clustering of the Representative Points

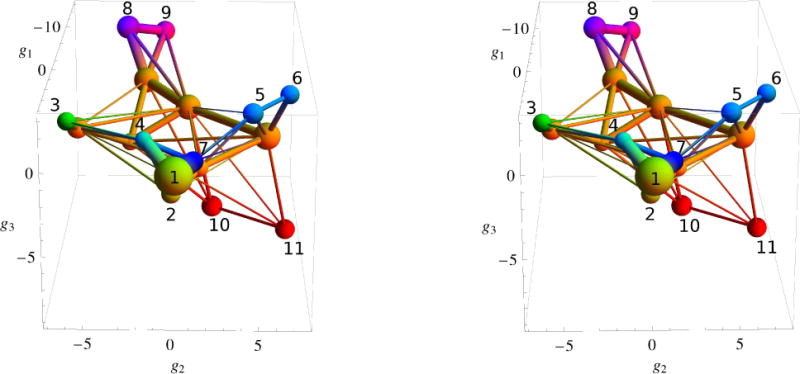
Figure 4 presents the distribution of the representative points in the 3D space of the collective variables g = (g₁, g₂, g₃) obtained with the HB PCA method (Sect. 2.2). Clusters associated with different protein conformations are colored in Fig. 4 in accord with the color pallete. Table I shows the clustering of the points with the MCLUST program^55,56; see Methods 2.4. The points are taken from the 20 μs equilibrium trajectory at T = 330K at 20 ps interval; thus, the total number of points is 10⁶. In Table I, the first column is the cluster number, and the 2nd column shows the relative number of points in the cluster (in percentage of the total number of 10⁶ points). Also, Table I contains information about the protein secondary structures characteristic of each cluster. The 3th column presents the number of conformations that have different SSSs; the 4th column shows the SSSs of two most populated secondary structures, and the 5th column the weight of these structures in the cluster. Finally, the last column indicates the type of the representative protein conformation with which the cluster is associated according to the SSSs. The representative conformations are labeled as in the previous studies of folding of beta3s miniprotein^34–36,38; i.e. “Native” stands for native-like structures, “Ns-or” for conformations in which the C-terminal hairpin is formed and the N-terminal hairpin is unstructured (“out of register”), “Cs-or” for conformations with the N-terminal hairpin formed and the C-terminal unstructured, “Ch-curl” for curl-like structures in which the C-terminal hairpin is formed and the N-terminal is arranged antiparallel to the C-terminal hairpin, and “Helical” for conformations which contain a helical region. To associate a cluster with a certain protein conformation (the last column of Table I), we took into account not only the SSSs for the most populated secondary structures but also the relative weights of these structures W_rel= W_str/N_str, where W_str is the weight of the given structure in the cluster (in percentage), and N_str is the number of unique SSSs in the cluster (Table I). Specifically, it was assumed that the given cluster represents a certain protein conformation if W_rel ≳ 0.01 for this conformation. For example, cluster 13 has as its most populated SSSs one that is very similar to those in clusters 1 and 2, which were associated with the native state. However, its relative weight is one order of magnitude less than the weight in cluster 2 (≈2 × 10⁻³ versus ≈2× 10⁻²), so it is considered separately.

FIG. 4.

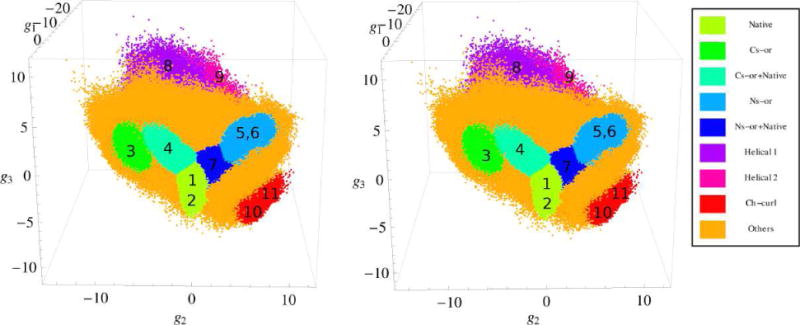
Stereo view of the distribution of the representative points of beta3s in the 3D space of collective variables g = (g₁, g₂, g₃). Clusters are numbered according to Table I. The units of the g₁, g₂ and g₃ variables are in Angstroems.

TABLE I.

Clusters of Protein Conformations

Clustera	Wclstb	Nstrc	Most populated structured	Wstre	Cluster typef
1	21.5	523	-EEEETTEEEEEETTEEEE- -EEEETTEEEEEETTEEE--	38.6 37.0	Native
2	3.9	939	-EEEETTEEEEEETTEEEE- -EEEETTEEEEEETTEE---	16.2 14.1
3	2.6	2337	-EEEETTEEEEEEEEEEE-- -EEEETTEEEEEEEEEEEE-	12.3 9.8	Cs-or
4	3.1	1173	-EEEETTEEEEE-SS-EEE- -EEEETTEEEEE-SS-EE--	7.2 5.6	Cs-or+Native
5	3.0	773	-EEE-SSS-EEEETTEEEE- -EEEESSSEEEEETTEEEE-	46.1 5.5	Ns-or
6	2.5	631	-EEE-SSS-EEEETTEEEE- -EEEESSSEEEEETTEEEE-	22.3 19.8
7	5.0	1005	-EEEETTEEEEEETTEEE-- -EE--SSS-EEEETTEEEE-	8.4 6.6	Ns-or+Native
8	7.6	48567	--HHHHHHHHHHHT------ ---HHHHHHHHHHT------	0.4 0.2	Helical 1
9	5.1	33302	--SS--HHHHTTT------- --SS--HHHHHHHSS-----	0.3 0.3	Helical 2
10	3.3	2347	-B-SSSSS--EEETTEE-B- -B--SSS---EEETTEE-B-	5.6 4.5	Ch-curl 1
11	4.4	5758	-B-SSSSS-EEEETTTEEE- -B-SSSS--EEEETTTEEE-	3.3 3.2	Ch-curl 2
12	4.6	13206	-EEEETTEEEE--SS----- -EEEETTEEEE-SSS-----	1.5 1.3	Others
13	3.2	3799	-EEEETTEEEEEETTEEEE- ----BTTEEEEEETTEEEE-	7.1 3.0
14	8.4	15590	-----SS--EEEETTEEEE- ----SSS--EEEETTEEEE-	1.5 1.3
15	8.7	47727	-EE-SSS-EE---SS---B- -EEE-SSS-EEEEEEEEE--	0.7 0.4
16	3.4	17009	-EEEETTEEE---SS----- -B---SSS-----SSS--B-	0.6 0.5
17	9.7	63733	-EEETTTEEEETTTEEEE-- ----SSS-----SSS-----	0.3 0.2

^aCluster number.

^bCluster weight equal to the number of the representative points in the cluster relative to the total number of the points (in %).

^cThe number of conformations that have different secondary structure strings.

^dThe secondary structure strings of the most populated conformations.

^eWeight of the given conformation in the cluster (in %).

^fCorresponds to Fig. 4.

We note that the variables g₁, g₂ and g₃ in Fig. 4, as well as in similar figures below, are measured in angstrom units. The distance between two points in the g space is found to be approximately linearly proportional to the all-atom RMSD between the protein conformations corresponding to these points, and the coefficient of the proportionality is approximately the same for all direction in the g space (Supporting Information, Fig. S7). Figure 5 presents the average RMSD as a function of $g={[{(g_1^2-g_1^1)}^2+{(g_2^2-g_2^1)}^2+{(g_3^2-g_3^1)}^2]}^{1/2}$, where the upper indices 1 and 2 denote two different points in g space. To calculate this dependence, 10³ conformations were chosen at random. It is seen that at the distances larger than the hydrogen bond distances (g > 3.6 Å ), beyond which the protein conformations do not overlap in the h space, the linear proportionality holds well. According to the slope of the best fit line, one unit in the g space corresponds to approximately 0.14 Å in the RMSD space. It follows that the spatial distribution of the points in the g = (g₁, g₂, g₃) space that represent essentially different conformations, in particular, the distribution of the clusters, can be also viewed as a distribution in the all-atom RMSD space, which complements the usual schematic networks used in the past (see below).

FIG. 5.

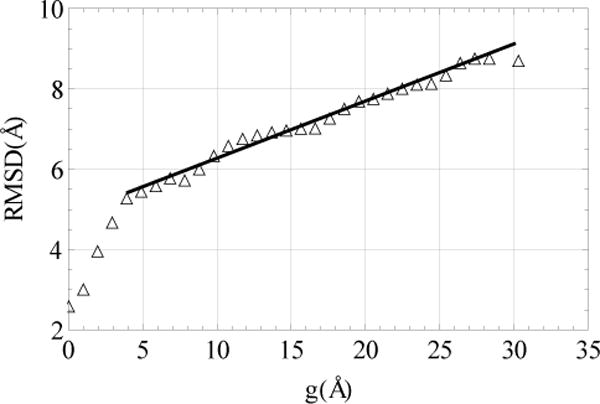
The all-atom RMSD as a function of the distance in the g space. The solid line show the best fit to the data with the slope ≈ 0.14.

According to Table I, the first eleven clusters represent the Native, Cs-or, Ns-or, Ch-curl and Helical conformations, and the other six less structured conformations. The list of the structured conformations is the same as in the previous studies^{29,30,34–36,38,43}, but the clustering results are somewhat different, e.g., instead of single clusters for the native-like and Ns-or conformations^35,38, two clusters for each of these conformations are observed. The present clustering is generally consistent with the results of Zheng et al.⁴³, where the FESs were constructed as functions of two collective variables (for details, see Supporting Information). One variable represented the first eigenfunction (the slowest collective motion) and the other the second to forth eigenfunctions for different FESs (faster motions). Similar to this work, we observe two clusters for the native-like conformations (clusters 1 and 2), a single cluster for the Cs-or conformations (cluster 3), two clusters for the Ns-or conformations (5 and 6), and two clusters for the Ch-curl conformations (10 and 11). A difference is that instead of a single cluster for helical conformations⁴³, two clusters (8 and 9) are observed, which is in agreement with Krivov et al.³⁸. In addition to these clusters, two other clusters are observed. They are positioned between the Native cluster and the Cs-or and Ns-or clusters (clusters 4 and 7, respectively, in Fig. 4) and contain mixtures of the native-like and the corresponding Cs-or and Ns-or conformations (Table I).

Table II compares the weights of the clusters for different conformations with those previously calculated^35,36,38. For this comparison, the intermediate Cs-or+Native and Ns-or+Native state clusters were associated with the native state; i.e. the weight of the Native cluster was calculated as a sum of the weights of clusters 1, 2, 4 and 7. It is seen that the results are in good agreement. Concerning the weight of the Native state, it has to be noted that secondary structure grouping resulted previously in a native basin³⁸ with about 35% of the snapshots (the first basin on the cFEP in Fig. 2) while clustering according to all-atom RMSD with a 2.5 Å threshold in that work yielded a native basin with about 28% of the snapshots (cFEP in Fig. S4).

TABLE II.

Weights of Clusters (in %) from Previous and Present Works

Cluster type	KGAa	pfoldfb	REMDc	CTMDd	Present worke
Native	36.4	35.0	37.8	37.1	33.5
Cs-or	3.6	2.6	5.3	5.3	2.6
Ns-or	7.4	6.2	7.3	6.3	5.4
Helical	11.6	11.2	–	–	12.8
Ch-curl	6.0	4.9	3.9	1.8	7.8

^aKinetic grouping analysis (KGA)^35,38.

^bp_fold analysis based on an equilibrium kinetic network (pfoldf), Ref.³⁸.

^cReplica exchange molecular dynamics (REMD)³⁶.

^dConstant temperature molecular dynamics (CTMD)³⁶.

^eCs-or+Native and Ns-or+Native clusters are added to the Native cluster.

We recall that the clusters listed in Table I, and so also in Table II, are associated with the protein conformations that have the largest weights according to their SSSs, similar to what was done previously^35,36,38. Since these weights are not dominant (Table I), it cannot be ruled out that the clusters contain considerable portions of less structured conformations or conformations of different types. Some examples of unstructured conformations are shown in Supporting Information.

It is of interest to determine which hydrogen bonds make the major contributions to the collective variables g₁, g₂ and g₃. Figure 6 shows the first eight bonds that have the largest projections of the variable onto the hydrogen bond distance space; in each case, the total contribution is about fifty percent (for the contribution of the other bonds, see Supporting Information, Figs. S8 and S9). The bonds involved in g₁ (the upper panel) are exactly the bonds Qi et al. have found most appropriate to describe folding of beta3s³¹, and Zheng et al. have indicated as the bonds that make the major contribution to the first “diffusion” coordinate⁴³. Moreover, the contributions of different bonds are approximately equal, as was assumed³¹ and confirmed⁴³ previously. A nonzero projection of g₁ onto a bond indicates that g₁ changes as the length of the bond changes. Since these eight bonds are characteristic of the native state (Fig. 1) and they contribute in the same direction of g₁, the coordinate g₁ determines the deviation from the native state and can serve as a reaction coordinate for an overall description of the folding process. Moreover, the sum of the distances can also serve as a reaction coordinate, as has been previously indicated by Qi et al.³¹.

FIG. 6.

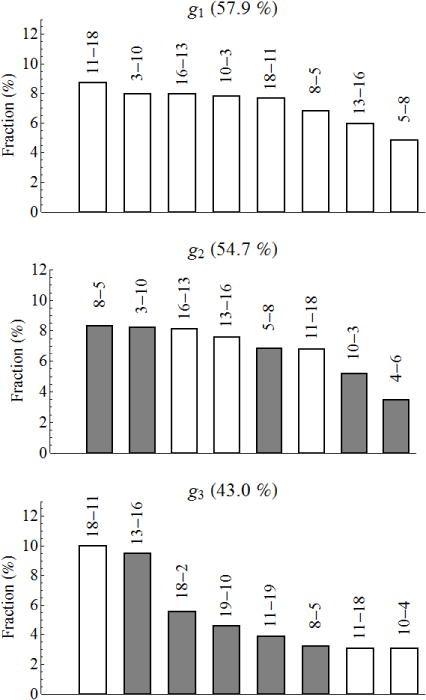
Fractions of the hydrogen bonds which make a major contribution to the collective variables g₁, g₂ and g₃. The figures at the top of each bar denote the bond; the first figure is the number of the residue with the oxygen atom and the second figure is that with the nitrogen atom. The empty and solid bars are for the bond contributions to the negative and positive directions of the collective variable, respectively. The numbers in percentage at the top of each panel are the total contribution of the given bonds to the collective variable.

The same above mentioned eight bonds are observed for the second variable g₂ (the middle panel of Fig. 6), except that bond 4–6 appears instead of bond 18–11. The former, however, has a weight just 0.2% larger than that of the latter, so that the 18–11 bond can be included equally well. The principal difference between g₁ and g₂ is that the bonds all contribute in the same direction in the former, while the bonds contribute in different directions in the latter. Specifically, the pairs of bonds 11–18 and 18–11 (which replaces 4–6 bond) and 13–16 and 16–13 contribute in the negative direction, and the pairs of bonds 3–10 and 10–3 and 5–8 and 8–5 in the positive direction. According to Fig. 4, the negative direction of g₂ corresponds to conformations in which the C-terminal hairpin is unstructured (Cs-or), which is consistent with the negative contribution of bonds 11–18, 18–11, 13–16 and 16–13 (Fig. 1). Similar consistency is observed for the positive direction of g₂, in which the N-terminal hairpin unstructured conformations (Ns-or) reside (Fig. 4); here bonds 3–10, 10–3, 5–8 and 8–5 make the corresponding positive contribution. Hence, the second collective variable g₂ discriminates between the conformations in which one hairpin is formed and the other is unstructured. The third variable g₃ (the bottom panel) has several bonds characteristic of the deviation from the native state (8–5, 11–18, 18–11, and 13–16), the bonds that appear when one strand shifts with respect to the other (10–4, 11–19, and 19–10), and one bond characteristic of the Ch-curl conformations (18–2). In contrast to the other two variables, g₃ does not have clear fingerprints of the Ch-curl and Helical conformations. This variable accumulates information about other conformations (structured and unstructured) that is not captured by the variables g₁ and g₂. The characteristic (occurring with a pronounced probability) bonds in the Ch-curl and Helical structures are as follows: In the Ch-curl 1 cluster (see Table I), the bonds with the probabilities not less than 0.5 (the number in the parentheses) are 13–16 (0.79), 2–18 (0.78), 20–2 (0.73), 19–11 (0.68), 18–11 (0.64), 16–13 (0.62), 10–19 (0.55), and 11–19 (0.52), and in the Ch-curl 2 cluster they are 10–19 (0.77), 2–18 (0.72), 19–10 (0.70), and 20–2 (0.62). The number of different structures in the Helical clusters are larger than in the Ch-curl clusters, therefore the probability of the most frequently occurring bonds are smaller then in the latter: in the Helical 1 cluster the bonds with the probabilities not less than 0.2 are 10–6 (0.31), 11–7 (0.28), 13–9 (0.28), 12–8 (0.25), and 14–10 (0.22), and in the Helical 2 cluster they are 11–7 (0.37), 12–8 (0.32), 13–9 (0.30), 10–6 (0.29), 14–10 (0.22), and 10–7 (0.20). These sets of the bonds are in very good agreement with those previously found by Zheng et al.⁴³ for the Ch-curl and Helical structures.

3.2. Free Energy Profiles and Spatial Kinetic Network

To obtain further insight into the significance of the reduced coordinate space, Figure 7 compares three free energy profile (FEPs), based on the equilibrium simulation. To calculate two of them, the pfoldf method suggested by Krivov and Karplus¹⁷ was used. One profile (the blue curve) uses the sum of distances for the above eight bonds as the reaction coordinate (i.e., that used by Qi et al.³¹), and the other (the red curve) the collective variable g₁; the reaction coordinate was divided into bins of width 0.01 Å and 0.005 Å respectively. Since the reaction coordinates are not identical, we matched their left and right boundaries to compare the FEPs. It is seen that the profiles are in good agreement, confirming that the sum of the bond distances³¹ and the first principal coordinate determined with the HB PCA method (Sect. 2.2) can both serve as reaction coordinates for the overall description of the folding process. It should be noted that in both cases the helical conformations do not form a basin on the FEP (Fig. 7), similar to what Qi et al.³¹ observed, while the RMSD clustering reveals such a basin³⁸. However, if the clustering is performed in the whole g = (g₁, g₂, g₃) space, i.e. taking the elementary cubes in the g space as the nodes to construct the EKN, the basin for helical conformations appears (Supporting Information, Fig. S10). It was also interesting to calculate the FEP by direct summation of the representative points of Fig. 4 over the variables g₂ and g₃ for the current value of g₁ (the green curve), i.e. not using the EKN. It is seen that even in this case the basins for the characteristic conformations are placed correctly, although the overall profile is biased toward the native state; i.e., the free energy difference between the native state and the other structures is larger than that shown by the blue and red curves.

FIG. 7.

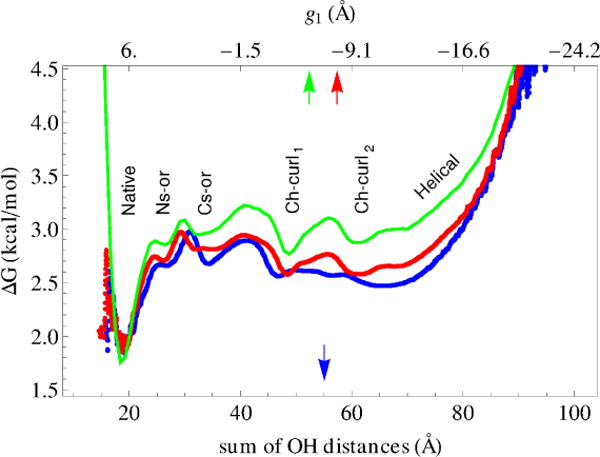
One-dimensional free energy profile. Blue and red curves show the profiles calculated with the pfold method by Krivov and Karplus¹⁷: the blue curve is for the reaction coordinate calculated as the sum of distances for eight hydrogen bonds of the upper panel of Fig. 6 (similar to Qi et al.³¹), and the red curve is for g₁ as the reaction coordinate. Green curve is the profile obtained by the summation of the representative points over g₂ and g₃ collective variables.

As has been shown in the previous works^{29,30,37,38,43}, the Native, Cs-or, Ns-or, Ch-curl and Helical clusters correspond to the enthalpically stabilized basins on the FES, and all other, i.e., the unstructured conformations (see Table 1), form an “entropic” basin through which the former basins are kinetically connected. The distribution of clusters inside the entropic basin in Fig. 4 generally agrees with this picture of the kinetics. More detailed information is obtained by calculating the number of transitions between the clusters. For this, at each subsequent 20 ps step, we determined the cluster in which the representative point had the maximum probability of being according to their Gaussian distributions (Sect. 2.4). If the system was found in a cluster which was different from the cluster it had resided in, this event was counted as the transition, and if in the same cluster, it increased the residence time in the cluster. Figure 8 presents a spatial kinetic network, which is based on the distribution of the representative points in the 3D space of collective variables of Fig. 4, the clustering of the conformations of Table I, and the calculated transitions between the clusters. Balls and tubes represent, respectively, the clusters and the transitions between them. Ball volumes are proportional to the numbers of intra-cluster transitions (i.e. the residence times in the clusters), and the tube cross-sections to the numbers of inter-cluster transitions. The latter are calculated as one-half of the total number of the forward and backward transitions between the two clusters; they were found to be very similar, indicating that detailed balance is essentially fulfilled (see Table S7 in Supporting Information).

FIG. 8.

Stereo view of the spatial kinetic network. Clusters are numbered as in Table I and colored according to the pallete of Fig. 4. The units of the g₁, g₂ and g₃ variables are in Angstroems.

Figure 8 shows that the clusters that have similar conformations (similar SSSs) are well connected, i.e. clusters 1 and 2 for the native conformations, clusters 5 and 6 for the Ns-or conformations, clusters 8 and 9 for the helical conformations, and clusters 10 and 11 for the Ch-curl conformations. Also, it is seen that the “intermediate” clusters (4 and 7) are much better connected to the Native cluster than to the corresponding Cs-or and Ns-or clusters, which supports the association of these clusters with the native conformations. Another feature of Fig. 8 is that the Native and intermediate clusters are considerably better connected to the clusters corresponding to unstructured conformations than to the nearest Cs-or and Ns-or clusters. This indicates that the folding pathways connect the native state with the entropic basin mostly directly rather than through the Cs-or and Ns-or states, in agreement with Krivov et al.³⁸. We note that in contrast to commonly constructed 2D kinetics networks, e.g., to Fig. 7 in the work of Krivov et al.³⁸, the clusters of conformations are not arbitrarily arranged in space but they are positioned according to their coordinates in the g space. Moreover, because of approximate proportionality between the distances in the g and the all-atom RMSD spaces (Fig. 5), the relative distribution of the clusters in Fig. 8 can be viewed approximately as the corresponding distribution in the RMSD space.

The results obtained here are consistent with those of Zheng et al.⁴³, who employed the LSDMap technique by Rohrdanz et al.²⁶ and found that the first principal coordinate plays the role of the reaction coordinate for the folding process and the others, which correspond to smaller eigenvalues, discriminate between the clusters of representative conformations of the protein (basins on the FES). The difference is that in contrast to the variables we use, the variables used by Zheng et al.⁴³ correspond to different time scales, so that the spatial distributions are “time biased” (see Supporting Information).

3.3. Hydro dynamic Analysis

Figure 9 presents 3D passive tracers calculated with Eq. (3) in Section 2.7. They were initiated at 900 representative points of Fig. 4 with the largest fluxes j(g) and continued for some finite “time” τ. According to Eq. (3), the lengths of the tracer paths are proportional to the values of j(g). Therefore, the tracer paths have different lengths; some of them, which were initiated at the points with relatively small values of j(g) and/or cross the regions with small values of j(g), are short, and the others, corresponding to large values of j(g), are long. As can be seen from the definition of j(g) (Sect. 2.6), they present the average fluxes of transitions, so that a small value of the flux can be due either to a small number of transitions or to good detailed balance between neighboring states. Figure 9 makes evident the fact that the dynamics of the folding process is more complex than the kinetic network (Fig. 8) seems to imply; i.e., the streamlines of folding flow are not organized into bundles connecting the clusters of characteristic conformations, as is suggested by the simple kinetic network, but they span all intermediate regions between the clusters.

FIG. 9.

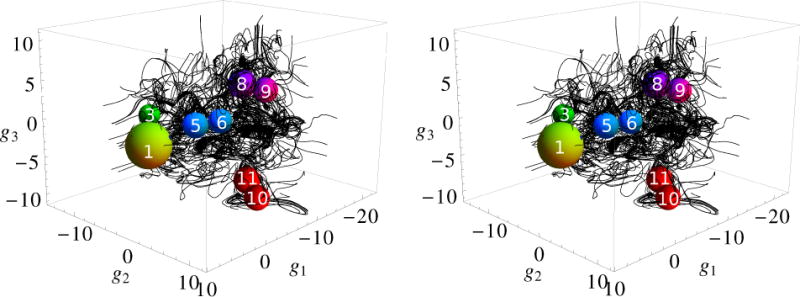
Stereo view of passive tracer paths. The balls represent the Native, Cs-or, Ns-or, Ch-curl and Helical clusters shown in Fig. 8. The radii of the balls are increased for illustrative purpose.

A clearer picture of the folding dynamics is obtained in the 2D representation, where the flow of the system from the unfolded to the folded state can be mapped directly on the FES constructed from the simulation^44,45. The FES depends on the two variables g₁ and g₂ and is given by F(g₁, g₂) = – k_BTln[P(g₁, g₂)], where [P(g₁, g₂)] is the probability of the system to be at the point (g₁, g₂). The latter was obtained by summing the points of Fig. 4 over the g₃ variable. To determine the streamlines, we calculated the stream function using Eq. (2). The 2D folding fluxes j_g1(g₁, g₂) and j_g2(g₁, g₂) necessary for these calculations were obtained by summing these components of the 3D fluxes j(g) over g₃, similar to the way P(g₁, g₂) was calculated. Panel a of Fig. 10 shows the results. The FES is relatively flat, but it has several well pronounced local minima (colored in blue-green), which correspond to the clusters of conformations that are indicated in Table I and Figs. 4, 8 and 9. The folding flow field is quite complex. A number of small regions restricted by closed streamlines are present. As has been shown previously^44,45, such regions correspond to vortices of folding flows, which arise from repeated local rearrangements of the protein, e.g., due to its partial folding and unfolding. Some vortices are formed at the local minima, which is consistent with the FES landscape and signals that the protein spends some time in these minima. However, many of them are formed in flat regions of the FES between the minima, indicating that the folding flows do not generally follow the FES landscape, in agreement with the previous results for an α-helical hairpin⁴⁴ and the fyn SH3 domain⁴⁵.

FIG. 10.

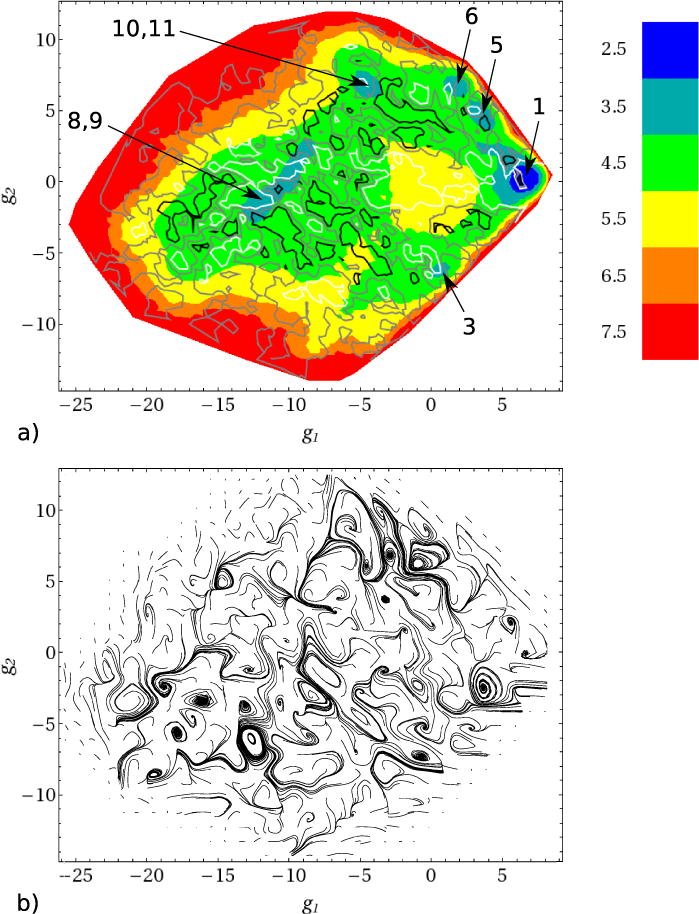
Two dimensional (g₁, g₂) presentation: (a) free energy surface (in kcal/mol). The blue local minima on the surface correspond to the clusters indicated in Table I and Figs. 4, 8 and 9. The white, gray and black lines correspond to the stream function values Ψ = −0.01, Ψ = 0 and Ψ = 0.01, respectively. Closed white and black streamlines correspond to the vortex regions, in which the rotation of folding flows is, respectively, clockwise and anti-clockwise. (b) The paths of passive tracers.

Panel b of Fig. 10 also shows the 2D tracer paths initiated at the same points as in Fig. 9. They were calculated using Eq. (3) with the above mentioned 2D fluxes j_g1(g₁, g₂) and j_g2(g₁, g₂). A comparison of the paths of the passive tracers in Fig. 10b with the streamlines (Fig. 10a) shows that the vortex regions restricted by closed streamlines represent basins of attraction of tracer paths, in which the tracer paths follow scroll-like trajectories to the end. However, as has previously been shown for the fyn SH3 domain⁴⁶, the closed streamlines do not mean that the system is completely trapped in such regions; these regions are open in the direction that extends the 2D space to a 3D space. The tracer paths initiated beside these regions reveal 3D eddies that contain attractors at which the tracer paths behave as saddle trajectories, i.e. they approach the attractor, execute several cycles, and then leave it⁴⁶. One example is shown in Fig. 11, which presents 3D tracer paths in a region spanning the Cs-or basin and its vicinity; in panels a and b of Fig. 10 this region corresponds to the white closed streamline at the Cs-or basin (labelled as 3) and the clockwise scroll-like tracer path, respectively.

FIG. 11.

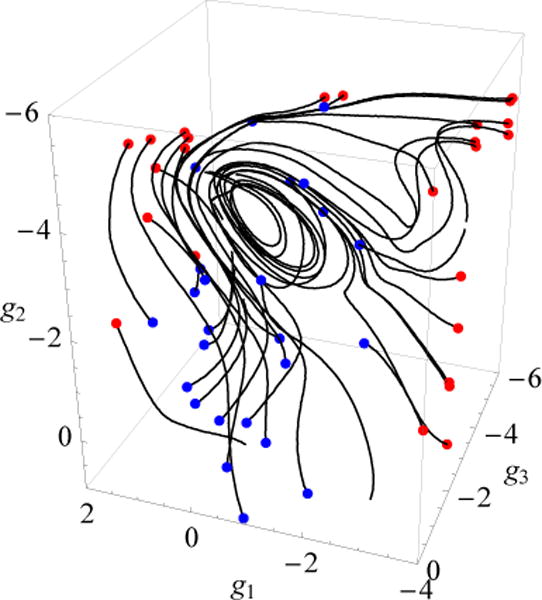
The 3D tracer paths for a region at the Cs-or basin (see text for details). The blue and red dots denote the initial and terminal points of the tracers in this region.

3.4. Relation of transitions rates to cluster distances

It is of interest to see if the rates of transitions between the clusters of representative conformations indicated in Table I and Figs. 4, 8 and 9 correlate with the distances between the clusters. We use as the distance measure that in g space; i.e., the distance between the clusters was determined as the distance between their centers in the g space (d_g). The rate of transitions from cluster i to cluster j was calculated as r_ji= N_ji/t_tot/N_i, where N_ji is the number of the transitions from cluster i to j (which was taken as one-half of the total number of the forward and backward transitions between these clusters since detailed balance is satisfied), t_tot is the total simulation time equal to 20 μs, and N_i is the number of conformations in cluster i among the 10⁶ conformations stored (see Table I). Figure 12 shows the results. We see that there is a clear distance dependence. It is essentially exponential, although considerable scatter is present. This dependence is in accord with the fact that the distance in g space is correlated with the change in hydrogen bonding required to go from one cluster to another (Sect. 3.1). However, there is no direct correlation between the rate of transitions from cluster i to j and the change of the number of hydrogen bonds in cluster i with respect to cluster j (results not shown). This is probably due to the fact that the collective variables g₁, g₂ and g₃ obtained with the HB PCA algorithm (Sect. 3.1) involve hydrogen bonds which have different importance to the folding process. In Supporting Information we also show the corresponding results for the atomic coordinate space, determined as the RMSD between the atomic conformations which had the values of the collective variables g₁, g₂ and g₃ nearest to the centers of the clusters in g space (Fig. S11). The correlation is much poorer here, which is somewhat surprising in view of Fig. 5, according to which the RMSD distance is approximately linear proportional to the distance in the g space. The correlation is, however, reestablished on a coarse-grain scale, when the rates of transitions and the corresponding RMSD distances are averaged over the bins in the g space (as large as of 5 Å in size), see Supporting Information (Fig. S12). These results suggest that the clustering of the conformations on the basis of hydrogen bonds plays a key role for the correlation between the rates of transitions and the distances, and the distance in the g space is most appropriate to represent this correlation.

FIG. 12.

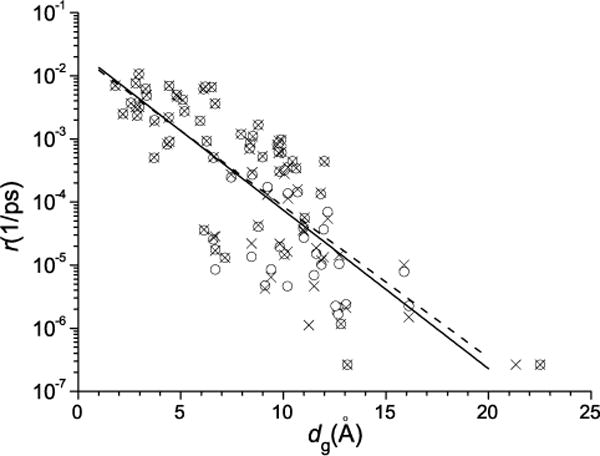
Rates of transitions between the clusters of conformations vs the distances between the centers of the clusters in the g space. Crosses and circles are for the transitions from smaller and larger populated clusters, respectively. The dashed line corresponds to the best fit for the crosses [r ∼ exp(−0.55d_g)], and the solid line to that for the circles [r ∼ exp(−0.58d_g)].

4. CONCLUDING DISCUSSION

We have analyzed the kinetics and dynamics of folding of a three-stranded antiparallel β-sheet miniprotein (beta3s) at T = 330K, which is slightly above the melting temperature. Simulations were performed using the CHARMM program¹ with the implicit solvent approach. Using the Berendsen thermostat to simulate constant temperature conditions, a long 20μs MD trajectory has been studied. To characterize protein conformations, we employed the hydrogen bond distances between (CO)_i and (NH)_j backbone groups, where i and j are the numbers of the residues, and \j — i\ > 2. The hydrogen bonds involving the C- and N-terminal residues were discarded to avoid noise due to fluctuations of the termini. To facilitate the analysis, this multidimensional bond space was reduced to a 3D space of the most representative collective variables. The standard PCA method and some recent nonlinear methods, such as the Local Linear Embedding (LLE)²¹, Full Correlation Analysis (FCA)²³, and the Manifold Sculpting (MS)²⁴ methods have been found not as satisfactory for obtaining a manifold of the representative points that could be successfully grouped into clusters. Motivated by the suggestion that this is due to the fact that the structured conformations have too low a weight in comparison with the unstructured ones (which is typical for the equilibrium folding above the melting temperature), we used a bond PCA method^27,28, i.e. just the formed hydrogen bonds were taken to contribute to the state vector; we refer to this approach as the Hydrogen Bond PCA (HB PCA) method. Three principal components corresponding to the largest eigenvalues were used as the collective variables to represent the conformation space of the protein g = (g₁, g₂, g₃).

The resulting spatial distribution of the representative points in the 3D space was then clustered using the MCLUST method of Fraley and Raftery⁵⁵. With this method the representative points are divided into 17 clusters. Structural analysis of the protein conformations in the clusters, based on the secondary-structure strings (SSSs)⁵⁷, similar to those used in previous studies^34,35,38, showed that eleven clusters can be associated with well structured protein conformations and the other six with mostly unstructured conformations. Based on the similarity of the SSSs, the clusters for the structured conformations were grouped into five “consolidated” clusters, which represent locally stable characteristic conformations that were described previously^34,35,38, and two intermediate clusters. The former represent the native-like conformations, the Cs-or conformations in which the N-terminal hairpin is formed and the C-terminal unstructured, the Ns-or conformations with the C-terminal hairpin formed and the N-terminal unstructured, the Ch-curl conformations presenting curl-like structures with the C-terminal hairpin formed, and the helical conformations that contain a helical region. The latter two intermediate clusters contain mixtures of the Ns-or or Cs-or conformations with the native-like conformations and are positioned between the Native cluster and the Ns-or or Cs-or clusters, respectively. With these intermediate clusters joined to the Native cluster, the residence probabilities of the system in the Native, Ns-or and Cs-or, Ch-curl and Helical clusters are in good agreement with the results of the previous studies^36,38. The clusters which present unstructured conformations form a pool of conformations (an “entropic” basin³⁸) that connects the clusters for the structured conformations. We note that recent beta3s simulations with a free-energy guided sampling protocol indicate that the first basin on the cFEP of beta3s has a statistical weight of only 20% using residues 3–18 for RMSD clustering with 2.5 Å threshold (Figure 5 of Zhou and Caflisch⁶²) which is congruent with the 21% weight of cluster 1 alone. The origin of these differences and their relation to convergence of the simulations is under investigation.

By counting the numbers of transitions between the clusters, the 3D distribution of the representative points can be presented in the form of a spatial kinetic network. In contrast to the previously constructed equilibrium kinetic networks^34–36,38, it shows not only how the clusters of conformations are connected but also how they are disposed in a 3D (g or RMSD) conformation space. Two interesting observations emerge from the additional 3D-spatial information. First, the helical and Ch-curl clusters are both kinetically and geometrically the most distant from the Native cluster. Second, the spatial kinetic network reveals that the Native and intermediate clusters are considerably better connected to the clusters of unstructured conformations than to the nearest Cs-or and Ns-or clusters. This indicates that the folding pathways tend to connect the native-like states directly with the entropic basin rather than through the Cs-or and Ns-or states. A possible explanation of the large kinetic distance of the Ns-or (Cs-or) state from the Native cluster is that the N-terminal strand (C-terminal strand) is out of register by one residue in Ns-or (Cs-or). Thus, all side chains of the out of register, misfolded strand point in the wrong orientation with respect to the rest of the three-stranded β-sheet which requires almost complete unfolding of the N-terminal (C-terminal) hairpin for reaching the Native cluster despite the relatively small backbone deviation between Ns-or (Cs-or) and the Native structure.

Projecting the collective variables g₁, g₂ and g₃ onto the hydrogen bond space has allowed further insight into the folding process. The largest eight projections of g₁ and g₂, with the total contribution to each variable of about fifty percent, correspond to the bonds that Qi et al.³¹ have found most appropriate for describing the folding of beta3s, and Zheng et al.⁴³ have indicated to be the bonds that make the major contribution to the reaction coordinate. Because these bonds determine the native contacts in the N- and C-terminal hairpins, the larger the projections of g₁ and g₂ onto the bonds, the more distant the conformation from the native state. For g₁, which is the first principal component, the projections have the same signs, so that it measures the distance from the native state. Consequently, the first principal component can serve as a good reaction coordinate for the overall description of the folding process, similar to the sum of the distances of the bonds³¹. Constructing the free energy profiles¹⁷ along g₁ and the sum of the bond distances has shown that these profiles are very similar. In contrast to g₁, the projections of the second component, g₂, onto the bond space have different signs. This variable discriminates between Ns-or and Cs- or conformations, which are positioned along g₂ approximately symmetrically with respect to the native state. The third component, g₃, “accumulates’ information about all other conformations (structured and unstructured) that is not captured by the variables g₁ and g₂.

The analysis of the folding kinetics has been amplified by use of the “hydrodynamic” description^44–46, which demonstrates that the folding dynamics are much more complex than the kinetic network suggests. Most indicative is a comparison of the folding streamlines with the FES in the g₁, g₂ space. A number of small regions restricted by closed streamlines occur. They correspond to vortices of folding flows. As has been previously shown, such vortices are the result of repeated partial folding and unfolding of the protein^44,45. Some vortices are located at the FES minima corresponding to clusters of conformations, which indicates that the protein spends some time in these minima in accord with the conventional view of the FES landscape. However, many vortices occur in relatively flat regions of the FES outside the minima, which indicates that the folding flows do not generally follow the FES landscape. This is in agreement with what we previously observed for an α-helical hairpin⁴⁴ and fyn SH3 domain⁴⁵.

An approach recently proposed by Zheng et al.⁶³ in their study of folding of a Trp-Cage mini-protein, is of interest to compare with the “hydrodynamic” description of the folding process⁴⁴. Based on a set of protein conformations obtained with replica exchange molecular dynamics and some estimates for the reaction rates between the clusters of conformations in a reduced configuration space, they generated folding pathways using transition-path theory^64,65. Depending on their distance in the configuration space, the folding pathways were grouped into folding “tubes”, somewhat similar to stream tubes (Sect. 2.7). However, in contrast to the latter, the folding tubes were found to follow the FES. The essential difference between the hydrodynamic^44,45 and Zheng et al.⁶³ approaches is that in the former, the local fluxes of transitions are not necessarily directed to the folded state of the protein, while in the latter the pathways are based exclusively on the folding fluxes that advance p_fold (the committor probability) values (see also Noé et al.⁶⁵). Because of this, for example, the pathways thus calculated ignore possible vortex regions on the FES, in which the protein repeatedly partially folds and unfolds.

One essential feature of the collective variables g₁, g₂ and g₃ determined with the HB PCA algorithm is that the transition rates approximately correlate with the distances between the clusters of characteristic conformations: the larger the distance, the smaller the rate. Moreover, the rates decrease with distances exponentially, suggesting that it is the FES barriers that increase with distance. This provides a new relation between the 3D spatial distribution of the clusters and their folding kinetics.

In summary, by introducing combinations of hydrogen bonds to define a three-dimensional space, the “g” space, to describe the folding kinetics and dynamics of miniprotein beta3s, we have been able to characterize some previously unknown aspects of the folding of this well-studied system. Specifically, we have been able (i) to find an inverse correlation between the rate of transitions between pairs of clusters and their distance in the g space, (ii) to determine the cluster distribution and kinetic network in the g space, and (iii) to show an approximately linear relation between RMSD and the distance in the g space. Equally important, the hydrodynamic analysis has demonstrated that the folding is much more complex than it appears in the usual kinetic network description and that flow vortices occur that do not follow the low free energy regions.

5. ASSOCIATED CONTENT

5.1. Supporting Information Available

The Supporting Information includes the technique of determining the collective vari­ables, the results of clustering of the representative points using the PCA, LLE, FCA and MS methods, the comparison of the weights of the clusters obtained with these methods, examples of unstructured conformations of beta3s, the dependence of the all-atom RMSD on the distance in the g space, the projection of the g₁, g₂ and g₃ variables onto the hydrogen bond distance space, the FEP with clustering in g space, the numbers of transitions between the clusters, a comparative discussion of the Zheng et al.⁴³ approach, the dependences of the rates of transitions between the clusters of conformations on the distances in the atomic coordinate space, and the corresponding coarse-grained dependences for the atomic coordinate and g spaces. This information is available free of charge via the Internet at http://pubs.acs.org/.