Abstract
Tuberculosis is a worldwide health problem with 2 billion people infected with Mycobacterium tuberculosis (Mtb, the bacteria causing TB). The hallmark of infection is the emergence of organized structures of immune cells forming primarily in the lung in response to infection. Granulomas physically contain and immunologically restrain bacteria that cannot be cleared. We have developed several models that spatially characterize the dynamics of the host–mycobacterial interaction, and identified mechanisms that control granuloma formation and development. In particular, we published several agent-based models (ABMs) of granuloma formation in TB that include many subtypes of T cell populations, macrophages as well as key cytokine and chemokine effector molecules. These ABM studies emphasize the important role of T-cell related mechanisms in infection progression, such as magnitude and timing of T cell recruitment, and macrophage activation. In these models, the priming and recruitment of T cells from the lung draining lymph node (LN) was captured phenomenologically. In addition to these ABM studies, we have also developed several multi-organ models using ODEs to examine trafficking of cells between, for example, the lung and LN. While we can predict temporal dynamic behaviors, those models are not coupled to the spatial aspects of granuloma. To this end, we have developed a multi-organ model that is hybrid: an ABM for the lung compartment and a non-linear system of ODE representing the lymph node compartment. This hybrid multi-organ approach to study TB granuloma formation in the lung and immune priming in the LN allows us to dissect protective mechanisms that cannot be achieved using the single compartment or multi-compartment ODE system. The main finding of this work is that trafficking of important cells known as antigen presenting cells from the lung to the lymph node is a key control mechanism for protective immunity: the entire spectrum of infection outcomes can be regulated by key immune cell migration rates. Our hybrid multiorgan implementation suggests that effector CD4+ T cells can rescue the system from a persistent infection and lead to clearance once a granuloma is fully formed. This could be effective as an immunotherapy strategy for latently infected individuals.
Keywords: Agent-based model, Mtb, Multi-organ models, Cell trafficking
1. Introduction
1.1. Epidemiology of TB
Tuberculosis (TB) is a deadly infectious disease caused by Mycobacterium tuberculosis (Mtb) in humans (Kumar and Robbins, 2007): inhalation of a single droplet containing just a few bacteria (as few as 2–5) can lead to infection (Behr et al., 1999; Nicas et al., 2005). This is remarkable, especially when considering that most infectious diseases require an initial dose of more than 1000 bacteria, and some as high as 109 bacteria (Zak and Sande, 1999). If the immune response does not clear initial infection (clearance scenario), Mtb is able to persist in a (clinically) asymptomatic latent state in the majority of infected hosts (called latent TB infection or LTBI). There is, however, a small chance that an infected individual will initially progress to active TB (Kumar and Robbins, 2007; Selwyn et al., 1989) (characterized as uncontrolled bacterial growth and/or disseminating infection), which, if untreated, can result in death rates of more than 50% of infected hosts (Onyebujoh et al., 2006). Approximately 2 million deaths due to TB occurred in 2008, including 500,000 people with HIV-1/AIDS (2009). Moreover, each person with active TB can infect on average 10–15 people every year (2009). Clinical epidemiological data have revealed that the risk of progression to active disease (3–10%) of infected individuals, defined as a PPD (purified protein derivative) skin test conversion, is much higher for the first few years waning over time (Vynnycky and Fine, 2000). Of particular importance is that factors resulting in these different infection outcomes in humans are not well-characterized. Of great concern is that TB persists as a latent infection in one-third of the world population (~2 billion people), providing a reservoir of potential disease and contagion: individuals with latent infection have a 10% lifetime chance of reactivation, a number that increases in the presence of HIV-1/AIDS.
Treatment of both latent and active TB is difficult and requires long courses of multiple antibiotics. Antibiotic resistance is a growing problem, leading to untreatable cases such as (extensively) multi-drug-resistant tuberculosis (XDR-TB), which occurs when resistance to second-line drugs develops on top of multi-drug-resistant tuberculosis (MDR-TB).
1.2. Host immunity to TB
TB manifests in different forms, but the most common in adults is pulmonary TB. This work focuses on TB infection in the lung, while in other work we consider TB meningitis (in preparation). Upon introduction into lung alveoli environment, Mtb is taken up by antigen presenting cells (APCs) such as macrophages (Mϕs) and dendritic cells (DCs). TB bacteria have evolved strategies to evade many of the typical protective host immune mechanisms, especially in macrophages (such as neutralizing reactive nitrogen intermediates or preventing phagosome/lysosome fusion) (Rohde et al., 2007). DCs are less permissive for Mtb replication and change their phenotype upon internalization of the pathogen (Giacomini et al., 2001): they start expressing co-stimulatory and adhesion molecules, and migrate through the lymphatics to lung draining lymph nodes. Dissemination of bacteria to the draining lymph node occurs following aerosol infection and the lymph node itself is the first site of expression of effector function for T cells (Chackerian et al., 2002). In some cases, further spread occurs through the bloodstream to other tissues and organs where secondary TB lesions can develop (kidneys, brain, and bone (Herrmann and Lagrange, 2005; Kumar and Robbins, 2007)).
Priming (and activation) of specific immune cell types (lymphocytes like CD4+ and CD8+ T cells) in the lymph node is key to the generation of protective adaptive immunity and host resistance to Mtb infection (Mogues et al., 2001; Orme, 1987). Priming is performed by APCs in the T cell zone of a lymph node. The slow or delayed induction of expression of effector functions of these primed T cells seen in Mtb infection has been shown to be detrimental to the ultimate success of the response (Chackerian et al., 2002). This could be due to mechanisms occurring between Mtb and the host; factors such as inhibiting either cell migratory activity, modulating antigen presenting cell (APC) function (Chang et al., 2005) and danger signals (Matzinger, 2002), or by its extremely slow proliferation rate compared with other bacteria (Mtb divides every 16–24 h) (Cox, 2004).
Although most exposed individuals do not become infected, exposure to Mtb results in the development of a strong Th1 host response (Flynn and Chan, 2001). This is characterized by a host cellular immune response in the lung, recognizing mycobacterial antigens that leads to the production of type I cytokines and activating infected macrophages that kill or at least contain the bacterial infection (Cooper et al., 1993; Flynn and Chan, 2001; Flynn et al., 1993).
Tuberculosis is classified as one of the granulomatous inflammatory conditions. In fact, the hallmark of Mtb infection is the emergence of self-organizing structures of immune cells forming primarily in the lung in response to bacterial invasion. The purpose of the granuloma is to physically contain and immunologically restrain bacteria that cannot be cleared. Infection triggers inflammation in the pulmonary alveoli environment where cytokine and chemokine signals (Flynn and Chan, 2001) are released activating cells and recruiting more immune cells to aid in granuloma formation. Macrophages, T and B cells and fibroblasts are among the cells that cluster together, with T cells surrounding a core of infected macrophages. T cells secrete cytokines such as interferon gamma (IFN-γ), which activates macrophages to kill their intracellular bacterial load (Kaufmann, 2002). Cytotoxic T cells can also directly kill infected cells, by secreting perforin and granulysin (Houben et al., 2006). Importantly, bacteria are not always eliminated within the granuloma, but can become dormant, a metabolic state often associated with latent TB infection (Kumar and Robbins, 2007). Another feature of the granuloma in humans is the development of areas of cell death, called caseum or necrosis, in the center of granulomas (Grosset, 2003). Due to anoxic conditions killing of trapped bacteria and bacteria replication are both inhibited in these regions. There are various types of human TB granulomas, including caseous (cheese-like) necrotic, non-necrotizing, fibrotic, calcified, and suppurative (neutrophilic necrosis). The factors that lead to different types of granulomas are not known, but each type may have different immune and microbial microenvironments (Barry et al., 2009). The most common granuloma is the caseous granuloma, where necrotic cell debris in the center is surrounded by a rim of large macrophages and a thin zone of T cells.
1.3. Mathematical and computer models to aid understanding of TB
To spatially characterize mechanisms that control the complex dynamics and emerging behavior in the lung during TB granuloma formation and development and to describe the interplay between bacteria and host, we published the first agent-based model (ABM) of granuloma formation in TB in 2004 (Segovia-Juarez et al., 2004). Based on our parallel studies with equation based models of TB dynamics (Fallahi-Sichani et al., 2010; Marino and Kirschner, 2004; Marino et al., 2011, 2004, 2007b; Sud et al., 2006), we recently developed next generation granuloma agent-based models (Fallahi-Sichani et al., 2011; Ray et al., 2009) that include additional T cell populations (e.g., effector CD8+ T cells and regulatory T cells), as well as key cytokine and chemokine effector molecules (e.g., tumor necrosis factor-TNF and three different chemokines, see (Lin et al., 2010)). In the last study (Fallahi-Sichani et al., 2011), the ABM has been updated to capture the immune response to Mtb over three biological scales: molecular, cellular and tissue. This multi-scale computational modeling platform revealed a critical role for TNF receptor dynamics in TB granuloma formation. These ABM studies (Fallahi-Sichani et al., 2011; Ray et al., 2009; Segovia-Juarez et al., 2004) emphasize the important role of T-cell related mechanisms in infection progression, such as magnitude and timing of T cell recruitment, T cell movement and macrophage activation. However, the current ABM formulation lacks any mechanism to capture T cell priming, differentiation and recruitment of immune cells to the lung as these events occur in the lung draining lymph node. Thus, studying these processes in more mechanistic detail is warranted to obtain a deeper understanding of their role in infection dynamics.
In other work (Linderman et al., 2010; Marino and Kirschner, 2004; Marino et al., 2004), we have developed a 2-compartmental ODE model capturing the dynamics of immune cells in the lung and a single draining LN. This multi-organ model was able to identify trafficking as an important factor for the outcome of infection in the lung: delays in either DC migration to the draining lymph node or T cell trafficking to the site of infection can alter the outcome of Mtb infection, defining progression to primary disease or latent infection and reactivated tuberculosis. That model, however, considered the lung a well-stirred tank, with no spatial aspects. Thus, although we know trafficking of cells between lung and LN is important during TB, we cannot identify mechanisms that will lend more insight into these dynamics that can then aid in predicting strategies for treatments and vaccines for TB.
The work in this paper combines our modeling efforts of TB in both the lung and lymph node. Herein we have developed for the first time to our knowledge, a multi-organ model that is hybrid: an ABM for the lung compartment and a non-linear system of ODE representing the lymph node compartment. The computational aspects of linking the two compartments will be described, along with the details of how to perform sensitivity and uncertainty analysis of a hybrid multi-organ model.
The main finding of this work is that APC trafficking to the lymph node is a key control mechanism for protective immunity: the entire spectrum of infection outcomes can be achieved by regulating APC migration only. More APCs enhance a protective T cell response in the lung, where both CD4+ and CD8+ effector functions can successfully stop bacterial invasion and clear infection before a granuloma is fully established. Our spatial multi-organ implementation suggests that only effector CD4+ T cells can rescue the system once a granuloma is fully formed: the peculiar granuloma structure walls off CTL killing (extracellular bacteria are in the center of the granuloma and they are very difficult to reach by CTL cells) and only macrophage activation (dependent on effector CD4+ T cells) can be effective as an immunotherapy strategy for latently infected individuals. This hybrid multi-organ approach to study TB granuloma formation in the lung and immune priming in the LN allows us to dissect protective mechanisms that cannot be achieved using the single compartment or multi-compartment ODE only system.
2. Methods
2.1. Multi-organ model implementation
We review some general specifications of the computational modeling platform used herein. The readers can find all the details in the published manuscripts for the individual model systems (Fallahi-Sichani et al., 2011; Ray et al., 2009), as well as in the diagrams shown in Supplementary Material. We develop our hybrid model in a computational framework. First, we describe the ABM of the lung granuloma, and then the ODE system for the LN. Then we describe how we link them together. Finally, we refine our methodology for performing uncertainty and sensitivity analysis and apply it here.
2.2. ABM of granuloma formation-lung compartment
The ABM of the lung granuloma is defined by four concepts: environment, agents within the environment, rules for agent-agent and agent-environment interactions, and timescales of these interactions. The virtual granuloma environment captures a 2 mm × 2 mm section of lung tissue (i.e., parenchyma, where the granuloma typically forms) as a 100 × 100 two-dimensional (2D) grid with micro-compartments scaled approximately to the size of a macrophage (20 mm in diameter (Krombach et al., 1997)). Use of the 2D grid speeds computation considerably and other work has shown that the 2D model approximated well the 3D model results (Forrest et al., 2006). In addition, the 2D model serves the purpose here well in creating the hybrid system. A quick summary of the rules follows.
Cells are represented as discrete agents on the grid: they move and respond to their environment based on rules reflecting known biological activities. Effector molecules such as chemokines (e.g., CCL2, CCL5, and CXCL9) and the cytokine TNF are modeled by partial differential equations. Since Mtb is a non-motile bacterium, we assume that bacteria do not diffuse and we capture their proliferation according to a logistic growth function within a single micro-compartment with a discretized ordinary differential equation.
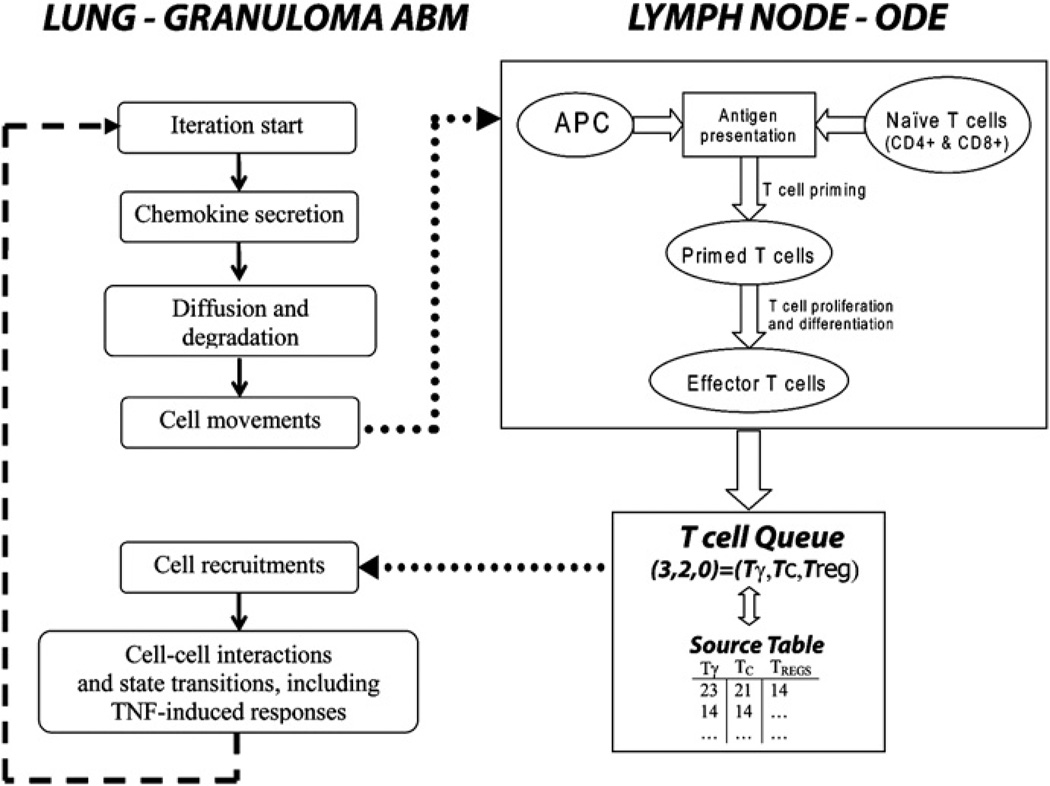
We defined each subtype of T cell based on their immunological functions: interferon-γ (IFN-γ)-producing T cells (Tγ), cytotoxic T cells or CTL (TC) and regulatory T cells (Treg). As the lungs are highly vascularized, 50 vascular sources are randomly placed on the grid and serve as entries for resting macrophages and effector T cells, representing 0.5% of the grid (personal communication by JoAnne Flynn). The initial number of macrophages represents ~1% coverage of the grid (Condos et al., 1998; Law et al., 1996; Schwander et al., 1998). Resting macrophages populate the grid in the absence of infection, then post-infection, they can become infected, chronically infected and activated, depending on intracellular and extracellular bacterial load, and cell–cell interaction with IFN-γ (via Tγ) and/or TNF. Each cell type can die of age or apoptosis (TNF-dependent, Tγ-cells dependent) or killing. Infected macrophages can be killed by CTLs and chronically infected macrophages can burst. Each mechanism can affect the bacterial count. A flowchart of the algorithm of the simulation is also shown in Fig. 1.
Fig. 1.
Schematic of the hybrid model (granuloma ABM linked to a Lymph Node ODE). The left-hand side of the figure shows some basic steps of the ABM algorithm in the lung compartment. After cell movement is completed on the grid, the LN-ODE module (right-hand side of the figure) retrieves information from the grid (i.e., the sum of infected and chronically infected macrophages) to initialize the APC equation in the LN-ODE system. Antigen presentation, T cell priming, proliferation and differentiation are computed for a time span of 10 min. Effector T cell fluxes (continuous) from the LN to the lung are generated and passed to a recruitment function that updates a T cell Queue (discrete) and a Source Table at each iteration (see text for details). The T cell Queue lists randomly all the effector T cells ready to be input onto the grid. The Source Table lists all the vascular sources that are enabled on the grid (per T cell phenotype). At any iteration, we empty the T cell Queue if enough sources are available. Otherwise, the remaining effector T cells will be placed onto the grid in the next iteration. Effector cells in the queue have a lifespan of 3 days.
2.3. ODE priming model: lymph node compartment
We use the lymph-node compartment portion of our two-compartmental ODE model (Marino et al., 2010b) to capture mechanisms of APC and T cell trafficking, as well T cell priming and differentiation. For the purpose of this study, we simplify the LN-ODE model, and do not directly account for bacterial and cytokine dynamics. The LN-ODE system captures the dynamics of antigen-bearing APCs, such as DCs which bring bacterial antigen to the LN to present to T cells, as well as several subpopulations of T cells (naı¨ve, precursor and effector CD4+ and CD8+ T cells). A system of 13 equations total shown below is numerically solved by an Euler discretization scheme for a 10 min time span (fixed time step of 6 s).
During any infection, but in particular TB, it is the arrival of antigen presenting cells-APCs (DCs, macrophages, etc.) at the draining tissue LN that kick starts the development of adaptive immunity. To capture this in the model, we define the sum of infected (MI) and chronically infected macrophages (MCI) in the granuloma lung compartment at time t as a proxy for the number of APCs migrating from the site of infection to the lymph node at any iteration (10 min loop). After an APC successfully finds and phagocytoses mycobacteria, it migrates out of the lung compartment through lymphatics (ultimately reaching the closest draining lymph node). Because an APC encounters several possible delays during this migration, we have defined a parameter that scales this representation (scalingAPC): it is set to 1 for the containment scenario (no scaling) but we also can vary it to simulate vaccination and immunotherapy strategies (see Section 3.7). The equation for APC dynamics is a simple linear decay kinetics (with half-life given by the parameter µAPC):
| (1) |
with initial condition at time t (i.e., APC(t)) seeded by scalingAPC[-MI(t)+MCI(t)] from the lung compartment. Naïve CD4+ T cells are described in Eq. (2) with a constant source term (sN4), recruitment by an APC-dependent recruitment term (k13 term), natural death, and differentiation to precursor Th1 that depends on APCs (k14 term). Eq. (3) models precursor Th1 cell dynamics. It accounts for the differentiation of naïve CD4+ T cells, proliferation of Th1 cells (logistic growth with rate constant k15), differentiation, and migration into the blood (ξ1 term). Eq. (4) describes Th1 cell dynamics, incorporating differentiation via APCs (k20a term) and migration to the blood (ξ1a term). Eq. (5) models naïve CD8+ T cell dynamics, and is similar to the naïve CD4+ cell Eq. (2). There is a source term (sN8), and mechanisms for recruitment by APCs (k16 term), natural death, and differentiation to T80 cells (k17 term). The k17 term captures the role of licensed DCs in priming CD8+ T cells. Licensing is achieved by initial successful CD4+ T cell priming: that is why CD8+ T cell priming is only possible if either precursor or fully effector Th1 cells are present. Eq. (6) describes primed CD8+ T cell dynamics, with mechanisms for CD8+ T cell proliferation (k18 term), differentiation and migration into the blood (ξ2 term), similarly to Eq. (3). Eqs. (7) and Eqs. (8) describe IFN-γ-producing T8 cell and CTL dynamics in the lymph node. Both equations capture differentiation induced by ACPs (k24a term) and migration to the blood (ξ2a and ξ2b terms). Parameter m allows for an overlap between IFN-γ-producing CD8+ T cell and CTLs. Eqs. (9)–Eqs. (13) represent the fluxes of precursor and effector CD4+ and CD8+ T cells arriving at the site of infection. These fluxes are used to initialize the new T cell recruitment function within the lung compartment. The scaling factor γ accounts for the possibility of multiple LN locations for T cell priming surrounding the lung and eventually multiple sources for effector T cell influx on the grid. We set it to 2 for the baseline scenario. Parameter and initial condition values for the LN model are shown in Table 1.
Table 1.
List of initial conditions and parameter names, descriptions, values, and the ranges used to initialize the LN compartment ODE model, as well as for uncertainty and sensitivity analysis. Rates are per day.
| Name | Description | Baseline (containment) | LHS ranges |
|---|---|---|---|
| µAPC | Death rate for antigen presenting cell (APC) | 3E–1 | [2E–1,4E–1] |
| µN4 | Death rate for Naïve CD4 + | 2.5 | [1E–4,1E1] |
| N4 (0) | Initial (uninfected) Naïve CD4 + T cell population | 3E5 | |
| sN4 [=µN4N4 (0)] | Constant source of N4 (LN) | 7.5E5 | |
| k13 | Naïve CD4+ T cells maximum APC-dependent recruitment rate (LN) | 1E1 | [1E–3,1E4] |
| hs13 | MDC half-sat Naïve CD4 + T cells recruitment rate (LN) | 1E3 | [1,1E4] |
| k14 | Rate (likelihood) of Naïve CD4 + T cell priming when encountering an APC (LN) | 1E–2 | [1E–6,1] |
| k15 | Precursor Th1 proliferation rate (LN) | 5 | [1E–3,1E4] |
| ρ2 | Precursor Th1 carrying capacity (LN) | 1E7 | [1E5,1E8] |
| k20a | Maximum Th1 differentiation rate, dependent of IL-12 and APC (LN) | 1E–1 | [1E–6,1E1] |
| hs20a | MDC half-sat on IL-12 and APC dependent Th1 differentiation (LN) | 1E3 | [1,1E4] |
| ξ1 | Precursor Th1 cells migration rate out of the LN into the blood | 1E1 | [1E–2,1E3] |
| ξ1a | Th1 cells migration rate out of the LN into the blood | 1E–1 | [1E–2,1E3] |
| µN8 | Death rate for Naïve CD8 + | 2.5 | [1E–4,1E1] |
| N8 (0) | Initial (uninfected) Naïve CD8 + T cell population | 2.4E5 | |
| sN8 [=µN8*N8 (0)] | Constant source of N8 (LN) | 6E5 | |
| k16 | Naïve CD8 + T cells maximum MDC-dependent recruitment rate (LN) | 1E1 | [1E–3,1E4] |
| hs16 | MDC half-sat Naïve CD8 + T cells recruitment rate (LN) | 1E3 | [1,1E3] |
| k17 | Maximum rate (likelihood) of Naïve CD8 + T cell priming when encountering an APC (LN) | 1E–2 | [1E–6,1] |
| hs17 | Th1 half-sat rate for Naïve CD8+ T cell priming when encountering an APC (LN) | 1E1 | [1,1E2] |
| k18 | Precursor T8/CTL proliferation rate (LN) | 5 | [1E–3,1E4] |
| ρ3 | Precursor T8/CTL carrying capacity (LN) | 1E7 | [1E5,1E8] |
| k24a | Maximum T8/CTL differentiation rate, dependent of IL-12 and APC (LN) | 5E–1 | [1E–6,1E1] |
| hs24a | MDC half-sat on IL-12 and APC dependent T8/CTL differentiation (LN) | 1E3 | [1,1E3] |
| ξ2 | Precursor T8/CTL cells migration rate out of the LN into the blood | 1E1 | [1E–2,1E3] |
| ξ2a | T8 cells migration rate out of the LN into the blood | 1E–1 | [1E–2,1E3] |
| ξ2b | CTL cells migration rate out of the LN into the blood | 1E–1 | [1E–2,1E3] |
| wT80 | Weight factor between precursor Th1 and Th1 in Naïve CD8 differentiation | 0.5 | [1E–2,1] |
| γ | Scaling factor between LN and Lung compartments (proxy for multiple LN sources) | 2 | [1E–1,1E1] |
| ScalingAPC | Scaling factor between Lung and LN compartments (proxy for delays in DC trafficking) | 1 | [1E–2,2] |
| m | Fraction of overlap between T8 (IFN producing CD8+ T’s) and CTL phenotypes | 0.75 | [1E–1,1] |
| GR-ABM module | |||
| τNFkb | TNF thresholds for Nfkb activation of Macs | 0.05 | [1E –2, 1E –1] |
Without infection, naïve CD4+ and CD8+ T cells remain at their initial values. Containment and disseminating infection scenarios are described in Section 3:
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
2.4. Linking the two models
Effector T cell generation and recruitment are the main novelties of this new multi-organ ABM implementation. In the previous versions of the ABM, T cells were recruited to the lung granuloma through vascular sources at the site of infection (lung) as already fully differentiated effector T cells in some local chemokine-gradient dependent fashion. The 50 vascular sources were sequentially scanned every 10 min and for each source a T cell type was randomly selected from a uniform probability density function, with 54%, 36%, and 10% probabilities of choosing a Tγ, TC, or Treg, respectively. These effector T cells were always available. After the T cell type was chosen, threshold conditions for recruitment were checked. These thresholds are calculated by weighted linear combination of TNF and chemokine concentrations at the source (see Ray et al. (2009), and Supplementary Text in Fallahi-Sichani et al. (2011)). This is based on TNF-dependent and independent recruitment of T cells via effector molecules (Ray et al., 2009). If satisfied, a T cell was input onto the grid and the next source was scanned. T cell recruitment was enabled only after day 20 post-infection. This reflected the ‘delay’ in mounting adaptive immunity.
Our new implementation uses the LN compartment to generate fluxes of effector T cells to be input onto the lung ABM grid (see Fig. 1). These fluxes are a function of the magnitude and timing of the infection in the lung compartment. The result is a hybrid multi-compartment mathematical/computational model, where a discrete/stochastic module is represented by the granuloma/lung ABM and the continuous/deterministic module is captured by a lymph node ODE model. Information is exchanged between the two compartments at every time step.
2.5. APC trafficking: from the lung to the LN
A full iteration of the ABM is represented by a 10 min time span. For the purpose of describing the linking of the two compartments, we label the initial and final times ti and ti + 10 (i=0,1,2,…,N), respectively. By construction, ti+10=ti+1. The algorithm computes chemokines and TNF secretion, diffusion and degradation first, cell movement and then cell recruitment (macrophage first, then T cells). Cell recruitment function relies on the numerical solution of the LN-ODE, seeded by inputs from the lung compartment (see Fig. 1). Initial conditions at the beginning of the simulation (time t0, onset of infection) for the LN compartment are all zeros except for naïve T cells (see Table 1 for naïve CD4+ andCD8+ T cell initial conditions). The LN-ODE is then solved for a 10 min time span (t0+10) and all the solutions at time t0+10 are saved. Then, the fluxes generated by Eqs. (10), (12), and (13) are passed to a recruitment function which inputs effector T cells on the ABM grid (see the next section, T cell recruitment: from the LN to the lung).
The algorithm continues by calculating cell–cell interactions and state transitions, and then starts the new iteration t1. The sum of infected and chronically infected macrophages (multiplied by scalingAPC) is updated starting at time t1 (after the first 10 min of simulation) and it will be used as initial condition for Eq. (1) for all the subsequent iterations.
To preserve the continuity of the ODE system, the initial conditions for the LN compartment at time ti (i > 0) are retrieved from the solutions of the LN-ODE saved in the previous time step ti−1 + 10. We define ΔAPC the difference between the sum of infected and chronically infected macrophages between contiguous iterations (ti+1 and ti): if ΔAPC > 0, then the initial condition for Eq. (1) is updated by adding ΔAPC to the previous solution (e.g., APC(ti+1)=APC(ti+10)+ΔAPC). It is left unchanged otherwise (as for the rest of the variables of the ODE system). Since the increments in infected macrophages are discrete (by integers), the changes in the lung compartment are reflected in the LN-ODE as pulses of APCs over 10 min intervals. Fig. S1 in the Supplementary Material shows a numerical solution of the APC Eq. (1) based on the time course of [MI(t)+MCI(t)] in the grid from a containment scenario. The time course of APC is usually lower than the combined infected macrophage trajectories: APC dynamics mirror [MI(t)+MCI(t)] time courses with a natural delay induced by the differential Eq. (1) form and by the parameter scalingAPC.
2.6. T cell recruitment: from the LN to the lung
The sum of the fluxes of Eqs. (10) and (12) is used to generate Interferon γ-producing cells (Tγ), while the flux of Eq. (13) describes cytotoxic T cells (TC) dynamics. Regulatory T cells (Treg) are calculated as 10% of Tγ cells.
Given APC inputs, the LN-ODE generates continuous fluxes of effector T cells that need to be converted into integers before entering the lung compartment (T cell agents are discrete). We define a ΔTcell for each T cell subset and check if ΔTcell > 1 between contiguous iterations (ti+1 and ti): if the condition is fulfilled we add the correspondent T cell subtype (more than one if the integers crossed are more than one) to a queue (T cell queue). During macrophage recruitment, we generate a table (Source table) of enabled vascular sources. To enable a vascular source for T cell recruitment, threshold conditions are checked for each source, and if satisfied, the corresponding source is added to a list (one list per T cell subtype), sorted by the highest gradient.
Then, a random T cell is chosen from the T cell queue and if the Source table is not empty for the selected T cell phenotype, the source on top of the list is selected (highest gradient/threshold recruitment condition) and the T cell is placed onto the grid and the T cell queue updated. If the T cell cannot be input onto the grid (microcompartment is occupied or no source enabled for that specific phenotype), a separate queue of stand-by cells is generated (T cell Queue off). This queue (if not empty) has a priority in the next round of recruitment. T cell recruitment ends when the Source Table is empty or when both queues are empty. T cells in the T cell Queue off have a lifespan of 3 days: death cells are deleted and the queue updated.
2.7. Model implementation
This section gives a brief top-level overview of the developed software; for a more detailed description see (El-Kebir, 2010). For efficiency reasons, we preferred to do the memory management manually as our computations involved the creation and deletion of many objects representing various agents. That is why we used C++ rather than a managed language such as Java (Oracle, 2010) or any of the .NET languages (Microsoft, 2010). In order for our software to be cross-platform among Linux, Windows and MacOS X, we made use of the Qt framework (Nokia, 2010). Qt is a framework for developing cross-platform applications with a graphical user interface (GUI). The various visualization techniques including color mapping, isolines, height plots and agent visualization have been implemented using OpenGL (Khronos, 2010). Through the GUI, the user is able to zoom in on a specific part of the grid, inspect the contents of a particular microcompartment and also view simulation-wide attributes and statistics in real-time. All of this proceeds without any observable delays while the simulation is running. The software also allows the user to save and load model states and alter parameters, enabling the user to perform depletion experiments regarding a particular cytokine or chemokine.
Initially we implemented the two-compartmental model as two separate modules: the lung ABM in pure C++, and the lymph node ODE model as a Matlab function which takes as input a vector of initial conditions and returns the same vector with updated values. Using the Matlab compiler (Mathworks, 2010), we generated an executable that we called every time step of the ABM. It turned out, however, that with this approach there was a significant computational time slowdown mainly due to the penalty incurred by initializing the Matlab Compiler Runtime (MCR) every time the executable is called. In addition, it often occurred that the MCR would crash and output an error dialog box effectively blocking progress of the entire application. For these reasons, we chose to re-implement the lymph node compartment internally. We did this by employing a forward Euler integration strategy for solving the ODEs, and verified that our solving method gave the same results as the method used by Matlab. Using the Valgrind profiler (Developers, 2010), we could see that the bottleneck in the computation was, similarly to the lung ABM model, the diffusion of cytokines and chemokines rather than in the LN ODE compartment.
2.8. Parameter estimation and model validation
Mechanisms of the host–pathogen system are captured by rates and rate constants of the mathematical model representation, and these must be estimated from many different experimental sources or by mathematical means in order to perform simulations. Values for most model parameters of the models are estimated from published experimental data obtained from the murine model, and where possible from the non-human primate model. Mtb experiments are favored over other mycobacterial species. There is an intrinsic biological and experimental variability in rates measured from in vivo or in vitro studies. Further, some interactions in the Mtb-host system are not currently measurable, particularly at the level of the lung granuloma. This complicates accurate estimation of model parameters (baseline values are unknown) as well as model validation.
We conduct model validation in three steps. First we perform negative control simulations and establish steady state dynamics with no infection: cells levels are set to known baseline homeo-static values in both compartments. Then, as a second step, the TB models must replicate qualitatively typical TB infection outcomes, such as latency and dissemination. Total bacterial load is usually used as the best informative marker of TB disease in the ODE models, where bacterial levels can distinguish between different scenarios: latent infection (steady state, low stable bacterial levels), dissemination (unchecked bacterial growth) and clearance (no Mtb present at the site of infection). In the ABM framework, we coupled bacterial load with spatial information on disease progression, such as granuloma size.
As a last validation step, the model should qualitatively recapitulate experimental data available in the literature from gene knockouts and neutralization studies. These can be simulated with a mathematical/computational model as virtual deletion and depletion experiments, respectively. Virtual deletions remove an element from the system at day zero while virtual depletions mimic experimental conditions where an element can be depleted or neutralized via antibody treatment at any time during the infection. Virtual deletion and depletion experiments can be performed for all of the relevant cells and cytokines in the model where the experimental results are known.
Since our goal is to inform the human condition for TB granuloma formation and T cell priming, we rely on non-human primates (NHPs) data, which are similar to humans in almost all aspects (Chackerian et al., 2002; Herrmann and Lagrange, 2005). However, comprehensive and accurate in vivo data collection in NHPs still remains very difficult and expensive due to technical limitations and to the slow-progression of TB in this animal model. This makes quantitative model validation particularly hard, especially for cell counts by different phenotype during infection.
2.9. Model calibration
Given a certain set of parameter values (see Table 1), clearance, containment, and disseminating infection can be replicated by the model. These baseline parameter sets are chosen after extensive exploration of the parameter space through uncertainty analysis (see Section 2.10). We have simulated a significant number of different types of granuloma that could identify a spectrum within each outcome (via different parameters and stochasticity). Model robustness is always tested for each infection scenario (replicating many times the simulation with a fixed parameter set and different seeds for the stochastic components): this ensures that any particular outcome of infection is the result of some biological mechanism in place rather than a random effect. We focused on varying the LN-ODE module, allowing very few changes in the parameter values obtained in our previous studies for the ABM lung compartment. Model calibration for containment has been performed in a semi-quantitative fashion: LN-ODE model parameters have been varied and we chose the sets that returned a typical containment scenario in the lung compartment, with stable and low total bacterial load, mostly intracellular and stable granuloma size. Clearance and dissemination outcomes are chosen similarly, checking for either bacterial clearance or uncontrolled growth. The results of the sensitivity analysis also guided our search for mechanisms (parameters) to target in order to achieve these outcomes.
2.10. Uncertainty and sensitivity analysis: determining key factors that control infection outcomes
We quantify the importance of each host mechanism involved directly and indirectly in the infection dynamics using statistical techniques known as uncertainty and sensitivity analyses. We recently published a review on uncertainty and sensitivity (US) analyses techniques, with the focus on systems biology applications (Marino et al., 2008). There we showed how multidimensional parameter spaces can be globally sampled in a computationally efficient manner by Latin hypercube sampling (LHS) algorithms. Correlations between model output and parameter values can then be determined using partial rank correlation coefficients (PRCC). Time dependent correlations can also be identified. When combined, these uncertainty and sensitivity analysis tools (Blower and Dowlatabadi, 1994; Greenland, 2001; Helton and Davis, 2002; Sanchez and Blower, 1997) guide our understanding as to how and what extent variability in parameter values affects infection outcomes. We have used this approach in our previous equation-based studies (i.e., ordinary, partial and delay differential equation systems), as well as agent-based model settings (Gammack et al., 2004; Ganguli et al., 2005; Marino et al., 2007a; Ray et al., 2009; Segovia-Juarez et al., 2004).
Given the multicompartment nature of our system, detailed uncertainty and sensitivity (US) analyses was applied to our model to explore dynamics within the same compartment (intra-compartmental/intra-scale) or between different compartments or scales (inter-compartmental/inter-scale). Examples of multiscale/compartment sensitivity analyses can also be found in our recent work (Chang et al., 2005, 2008; Kirschner et al., 2007). Here, we vary 28 parameters total: all the parameters in the LN compartment (27) and 1 in the lung compartment (see Table 1 for the parameters varied and the ranges used). Our previous ABM studies highlight a key role for TNF in TB infection dynamics, in particular TNF thresholds for Nfkb activation of Macs (τNFkb). Experimental data also suggest how TNF plays an important role in proper granuloma formation and control. This new implementation should confirm that finding and we chose to include at least 1 parameter (e.g., the most important, τNFkb), in the uncertainty and sensitivity analysis. In addition, our focus in this work is on results occurring in the lung compartment and how variations in the LN-compartment affect granuloma formation and function in the lung. We looked at 5 time points during infection progression: 7, 21, 50, 100, and 200 days.
2.11. Scaling initial conditions of the multi-organ model
In 2-D, the environment of our model represents one complete slice of a lung parenchyma of a NHP, the tissue where granulomas form. Each microcompartment of the ABM grid is 20 µm3 and the total volume represented by the ABM is 2 mm × 2 mm × 20 µm= 0.08 mm3. There is large variation in granuloma sizes, weights and volumes. Assuming from data on humans and NHPs that a granuloma is approximately shaped like a sphere, we can project a volume of 4.2 mm3 for a lesion of 2 mm in diameter: the 3D grid would be 100 times larger in volume (a cube of 2 mm × 2 mm × 2 mm). Thus we would need to scale up the values we derive to compare with data. Data on cell trafficking from the site of infection (lung) to the LN, as well as fluxes of effector T cells reaching the granuloma in the lung, migrating from the LN, are not available. Since we are seeding the LN ODE with real-time output from the 2D ABM, the LN-ODE captures the dynamics of 1/100 of a whole NHP LN. We then set the initial conditions for naïve CD4+ and CD8+ T cells in the LN-ODE module to approximately 1/100 of the known data for uninfected LN in human and NHP (Biancotto et al., 2007; Haase, 1999; Hogue et al., 2008). Based on our murine data (see (Riggs et al., 2008)), we use a 6 to 5 CD4/CD8 ratio (although some other data suggest higher ratios of 2:1, see (Latif et al., 2001)): initial conditions for naïve CD4+ T’s are set to 3e5 and for naïve CD8+ T cells are set to 20% less (i.e., 2.4e5). The model can accommodate any ratio.
3. Results
3.1. Outcomes of the hybrid, multi-organ model: containment and disseminated infection
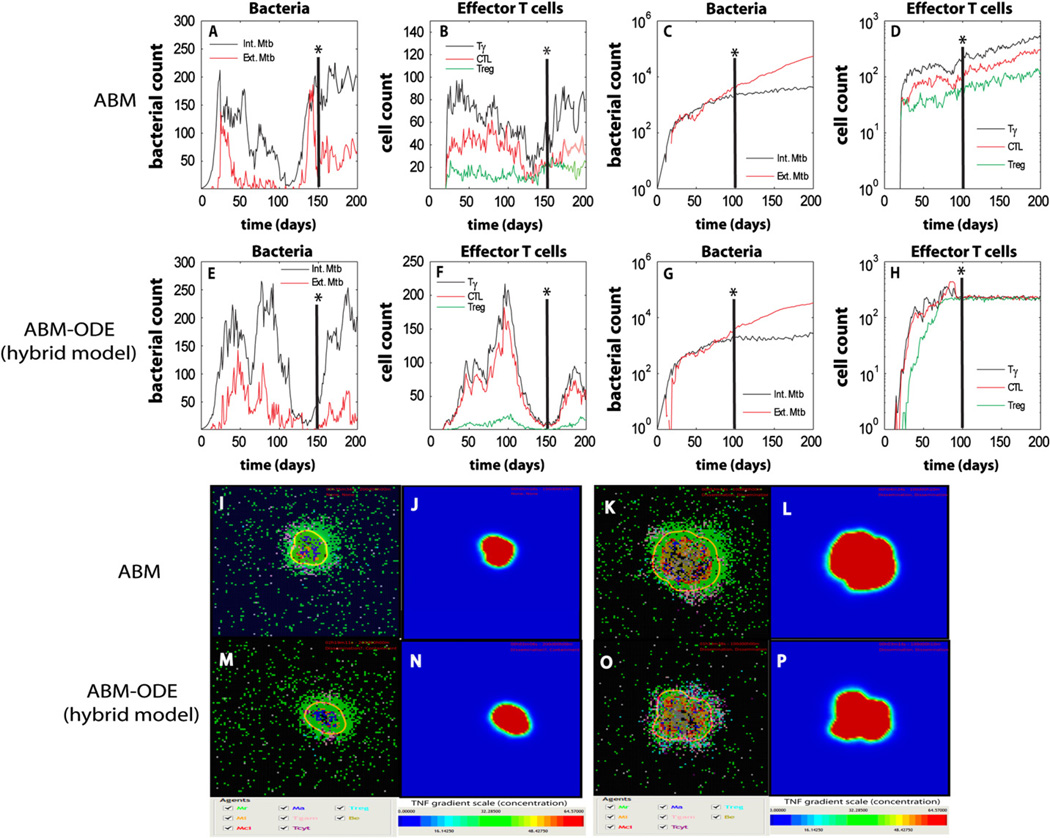
We simulated the hybrid model for 200 days post-infection, with an initial inoculum of 1 infected macrophage (with 1 intracellular bacterium) in the lung model and 1 extracellular bacterium into a neighboring compartment (the model gives similar results for other initial conditions). Our focus is on results occurring in the lung compartment and how variations in the LN-compartment affect granuloma formation and function in the lung. Fig. 2 shows typical containment and dissemination snapshots of the granulomas at day 200 for 2 different parameter sets (see Table 1). We compare our hybrid model (ABM–ODE) time courses of bacteria and T cells to the previous version without the LN-ODE compartment. Fig. 2 also shows the corresponding TNF gradient for each snapshot during infection. In addition, TNF and IFNγ virtual deletion experiments confirm known experimental data: both result in dissemination and uncontrolled growth scenarios (although IFNγ deletion has a faster progression, data not shown).
Fig. 2.
Time courses and snapshots of infection progression during containment and dissemination outcomes as predicted by our ABM. We compare outputs of the original version of the ABM (without the LN-ODE compartment, Panels A–D and I–L) to the current implementation (ABM–ODE—hybrid multi-compartmental model, Panels E–H and M–P). A vertical axis (see the *) on the top panels shows the corresponding time of the snapshot in the lower panels. For each snapshot, the corresponding TNF gradient is also shown (TNF gradient could be use as a proxy for granuloma size). Panels A,B, E, F, I, J, M, and N represent containment. Panels C, D, G, H, K, L, O, and P represent dissemination.
3.2. Scaling cell number predictions in the granuloma to NHP data
Latent and active TB are clearly different both in physiology and pathology. However, there is a large variability in the data due to an observed wide spectrum governing infection progression (Capuano et al., 2003; Lin et al., 2009). Moreover, reliable CFU and cell count (e.g., macrophages and T cells) data from NHP and human granulomas are difficult to collect (Lin et al., 2009). Here we use the model as a predictive tool for CFU and cell numbers in human/NHP TB granulomas during containment and active infection. Since bacterial load and cell numbers depend on the size of a granuloma, we need to scale our results from 2D to 3D. To do this, we measure the diameter of the granuloma emerging at the end of our model simulation and use it as our radius for the 3D axis. Table 2 shows the volume of the 2D disk as a function of lesion diameter (e.g., area of the circle multiplied by the 20 µm thickness of a single micro-compartment) and the volume of a sphere with the same diameter. The fourth column illustrates the percentage of volume in the sphere occupied by the 2D disk and the Projection factor column shows the scaling needed to get a reasonable approximation of the cell and bacterial counts at the end of the 200 days simulation in a 3D granuloma with a specific diameter. We assume that 2D densities are preserved in the sphere. Therefore, if in a containment scenario at 200 days post-infection we have 150 Tγ cells in a granuloma of 1 mm in diameter, a rough estimate of the number of Tγ cells will be 5000 (i.e., 150×33.33). No NHP or human data are available on cell counts for effector T cells and macrophage subpopulations (activated and infected) per single granuloma. Some estimates are available per gram of tissue, while others show T cell data broadly classified by CD4+ and CD8+ phenotype, without differentiating subtypes or specificity (Lin et al., 2009). Using the parameter values outlined in Table 1, the lesions we obtain for a containment scenario are very small, between 0.3 and 0.6 mm diameter. Lesions for active infection and uncontrolled growth are usually larger, between 0.7 and 1 mm in diameter. For reasonable bacterial and cell number predictions we then apply the scaling factors shown in Table 2, depending on the emergent lesion diameter at day 200. Table 3 shows some prediction ranges for bacterial and cell numbers in typical infection scenarios. Bacterial load predictions are in line with data measured by our collaborators on CFU counts per gram of granuloma tissue (see Table 7 in Marino et al., 2004). According to some recently published data from Flynn’s group for CD4+ and CD8+ T cell counts in the LN (see Table 5 in Lin et al., 2009), our LN-ODE predictions are within the same order of magnitude (given a scaling factor of 1e2, that accounts for the initial 1/100 scaling of the LN-ODE volume). The values we predict for CD4+ and CD8+ T cells are very similar and they are not significantly different between infection outcomes (i.e., ~1.65–2.5e7 for both phenotypes in both scenarios). Our data are taken at 200 days post-infection, while the data from (Lin et al., 2009) are averaged over the time of necropsy, which is different for each monkey (varies between 150 and 400 days).
Table 2.
Projection factors to scale the 2D granuloma predictions (cell and bacterial numbers) to a 3D spherical granuloma of equivalent diameter. List of diameter sizes and corresponding 2D and 3D volumes (assuming a microcompartment volume of 0.08 mm3). The percentage volume occupied by the 2D volume in the 3D sphere is obtained dividing the 3D by the 2D volume. The projection factor column lists the scaling needed to project cell and bacterial numbers into a 3D spherical granuloma. A complete table with granuloma sizes from 0.1 to 2 mm in diameter is available in the Supplementary Material (Table S1).
| Diameter granuloma (mm) | Volume 2D (mm3) | Volume 3D (mm3) | Percentage of volume occupied by the 2D disk | Projection factor |
|---|---|---|---|---|
| Containment | ||||
| 0.3 | 0.001413717 | 0.014137 | 10 | 10 |
| 0.4 | 0.002513274 | 0.03351 | 7.5 | 13.33333 |
| 0.5 | 0.003926991 | 0.06545 | 6 | 16.66667 |
| 0.6 | 0.005654867 | 0.113097 | 5 | 20 |
| Dissemination | ||||
| 0.7 | 0.007696902 | 0.179594 | 4.285714 | 23.33333 |
| 0.8 | 0.010053096 | 0.268083 | 3.75 | 26.66667 |
| 0.9 | 0.01272345 | 0.381704 | 3.333333 | 30 |
| 1 | 0.015707963 | 0.523599 | 3 | 33.33333 |
Table 3.
Bacterial and cell number predictions for a NHP or human TB granuloma in typical infection scenarios. The predictions are based on granuloma diameter at day 200 post-infection. The scaling factors are shown in Table 2.
| T cells |
||||
|---|---|---|---|---|
| Tγ | TC | Treg | ||
| Containment | 800–1700 | 600–1300 | 100–220 | |
| Dissemination/active TB | 5.4–7.7e3 | 5–7.1e3 | 4.8–7e3 | |
|
Macrophages |
||||
| Resting | Infected | Chronically infected | Activated | |
| Containment | 1.5–3.1e4 | 120–240 | 90–180 | 700–1400 |
| Dissemination/active TB | 2.3–3.3e4 | 2–2.8e3 | 1.3–1.9e3 | 5.3–7.7e3 |
|
Bacteria |
||||
| Intracellular | Extracellular | Total | ||
| Containment | 1800–3700 | 300–600 | 2000–4500 | |
| Dissemination/active TB | 3–4.2e5 | 1.5–2.2e5 | 1.8–2.7e5 | |
3.3. Investigating immune mechanisms driving infection outcomes, before and after a granuloma is established
In keeping with our goal of ascertaining how a more mechanistic LN compartment affects the dynamics within the lung granuloma, we performed uncertainty and sensitivity analysis as described in Methods and in Marino et al. (2008). Results guided our search for mechanisms occurring in the LN compartment that can drive the lung system to clearance or active infection starting from initial infection or from a containment scenario. This helps us explore what factors control both the formation and the maintenance of a granuloma. The outputs that we correlate to parameter variations are total bacterial load, macrophage numbers (infected, chronically infected, and activated), effector T cells on the ABM grid (Tγ, CTL, and Tregs) and granuloma size as in Ray et al. (2009). Bacterial load and infected macrophages, as well as Tγ and Tregs, share the same set of significant PRCCs. Table S2 in the Supplementary Material shows our detailed LHS-PRCC results. Below we discuss the most significant findings.
3.4. Early impact of T cell priming and proliferation on disease progression
Proliferation rate of precursor effector CD4+ T cells (k15), and the maximum Th1 differentiation rate dependent on APCs (k20a) both have a strongly negative correlation on bacterial load during early infection (<3 weeks post-infection, see Table S2). Increased precursor effector CD4+ T cell proliferation and differentiation rates (k15 and k20a) result in lower bacterial loads at the onset of infection. Not surprisingly, increasing APC efficiency in priming naïve CD4+ T’s (k14), as well precursor effector T cell proliferation (k15) and differentiation (k20a) in the LN has a positive impact on the levels of fully effector T cells in the lung. This finding is important, implying that they are having the biggest impact early at the onset of infection and not after the granuloma has been established.
3.5. Lymph node shut-down: better chance for clearance?
There are inconclusive data for T cell proliferation at the site of infection. We input onto the granuloma grid only fully activated effector T cells: precursor T cells migrating out of the LN are not accounted for and no differentiation mechanism is captured in the granuloma. This explains why rates of precursor T cells migration from the LN to the blood (on the way to the lung, ξ1 and ξ2), are consistently significantly correlated to most of the outcome variables we tracked (see Table S2). We can relate these rates to a concept known as ‘lymph node shut-down’, a transient, proportional accumulation of all T cell subsets in a lymph node draining a site of inflammation (Cahill et al., 1976; Hall and Morris, 1965; MartIn-Fontecha et al., 2003): higher T cell LN emigration rates (larger ξ1 and ξ2 rates) translate into decreased lymph node shut-down, and vice versa. LN shut-down likely facilitates an efficient T cell priming and successful effector T cell differentiation. Recent findings showed a direct role for migrating APCs in T cell accumulation in the LN (MartIn-Fontecha et al., 2003): it is not clear if this accumulation is a common feature of any viral or bacterial infection. The positive correlation of ξ1 and ξ2 to bacterial load can be explained by a faster migration out of the LN translating into less chances for full T cell differentiation in that compartment, therefore less effector T cells are available for the lung, less Tγ cells and less CTL killing in the granuloma (confirmed by the negative correlation of ξ1 and ξ2 to T cell counts). We tested the impact of increased ξ1 and ξ2: protective immunity is not impaired and a sufficient level of macrophage activation is observed (i.e., containment is achieved). On the other hand, decreasing values for ξ1 and ξ2 has a major impact on infection progression and may contribute to bacterial clearance. This is only successful early during infection before the granuloma is established: infection (see Table S2, Early column) cannot be cleared by decreasing ξ1 and ξ2 once the granuloma has been established. Another trafficking parameter, the scaling factor γ, is consistently negatively correlated to bacterial burden and granuloma size. γ is a proxy for multiple LN sources of precursor and effector T cells: increasing γcan partially account for additional T cell differentiation mechanisms once precursor T cells migrate out of the LN (see Supplementary Text S1 for more details on sensitivity analysis results for the scaling factor γ).
3.6. TNF-dependent macrophage activation: a necessary protective mechanism
The TNF threshold for NFkb activation of macrophages (τNFkb) has a consistently strong positive correlation to granuloma size, late during infection (>100 days). If we increase this threshold, higher TNF concentrations are required for macrophage activation, therefore less activated macrophages are generated and less bacterial killing is observed. More cytokines and TNF are then secreted due to increased bacterial load and more effector T cells (Tγ, CTL, and Tregs) are recruited to the lung. The next section will address if single parameter changes in the LN compartment can protect the host and have a significant impact on granuloma formation and maintenance.
3.7. Vaccination and cell-based immunotherapy strategies
Stimulating the immune response leading to immunological memory, via use of an infectious agent, is known as immunization. Vaccinations involve the administration of one or more immunogens (molecules or antigenic material that stimulate the immune response): if they are live bacteria, they are less virulent than the pathogen itself and only serve the purpose to produce immunity to a disease and prevent (or ameliorate) the effects of infection by future exposure to pathogens.
Immunotherapy is related to immunization and vaccination in the sense that refers to the treatment of disease by inducing, enhancing (activation immunotherapy), or suppressing (suppression immunotherapy) an immune response. The active agents of immunotherapy are called immunomodulators: they are usually cytokines, but recent effort has been devoted to cell-based immunotherapy, where APCs and T cells are stimulated ex-vivo and transferred into a patient to generate the appropriate immune response. Based on our uncertainty and sensitivity analysis results (Table 1), we predict key mechanisms in driving granuloma formation and infection outcomes. We then study the impact of manipulating some of these mechanisms on infection progression, suggesting potential vaccination and immunotherapy strategies.
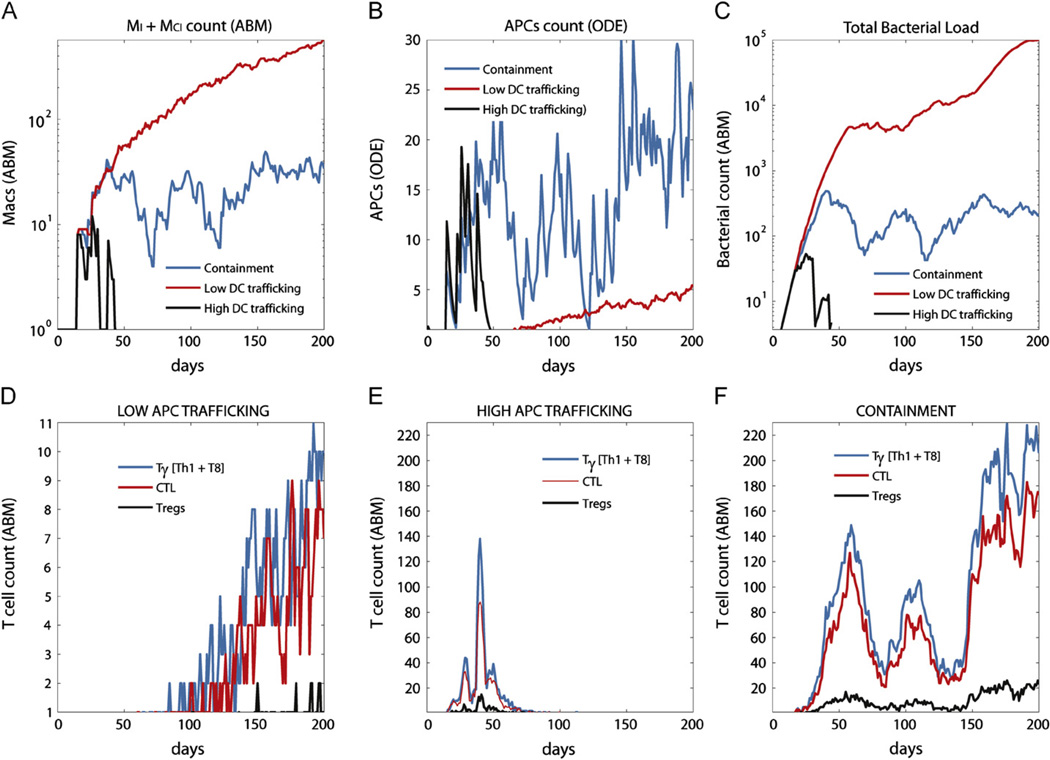
For example, since scalingAPC is one of the parameter consistently negatively correlated to bacterial load, infected macrophages and granuloma size, we choose to target APC trafficking to the LN as a possible vaccination strategy. We vary the parameter scalingAPC in the range [0.01,2] (baseline for containment it is set to 1) and the impact on infection outcome is significant. For low values of scalingAPC the system progresses to active infection and dissemination, while clearance can be obtained with values close to 2. Fig. 3 compares time courses of MI+MCI, APC, effector T cells and bacterial load in low and high APC trafficking scenarios (containment is also shown for comparison). For high DC trafficking (scalingAPC =1.75) a higher number (comparing to containment) of APCs reaches the LN at the onset of infection: although the difference is not dramatic, a few more APCs in the LN early during infection have a significant impact on the infection progression (first month, Fig. 3B). A spike in effector T cells by day 40 (Fig. 3E) results in a fast declining number of infected and chronically infected macrophages (Fig. 3A) and in bacterial clearance (Fig. 3C). This highlights the key role of APCs in regulating a protective immune response to Mtb. The number of effector T cells is 20 times lower in the low trafficking scenario comparing to containment (Fig. 3F), and they reach the granuloma site when it is already too late to control infection (Fig. 3D).
Fig. 3.
Enhancing APCs trafficking as a vaccination strategy. Shown are time courses of infected macrophages (Panel A), APCs (Panel B), bacterial counts (Panel C) and effector T cells (Panels D–F) for a vaccination strategy that manipulates APC trafficking. We show low and high APC trafficking scenarios, compared to containment. The x-axis represents days post-infection and the y-axis the number of cells or number of bacteria.
Similar clearance scenarios can be obtained by increasing APC efficiency in priming naïve CD4+ T’s (k14) or naïve CD8+ T’s (k17). We use values of 1e-1 and 1 for k14 and k17. Coupling the effect (e.g., both k14 and k17 are set to high values, such as 1) has a similar result (clearance). Interestingly, lowering the efficiency of T cell priming does not compromise a protective immune response: a stable granuloma always forms (but with a slightly higher bacterial load) and containment is always achieved by day 200 (data not shown). This result suggests how different levels of bacterial load are possible within the spectrum of latency, as shown in Lin et al. (2009).
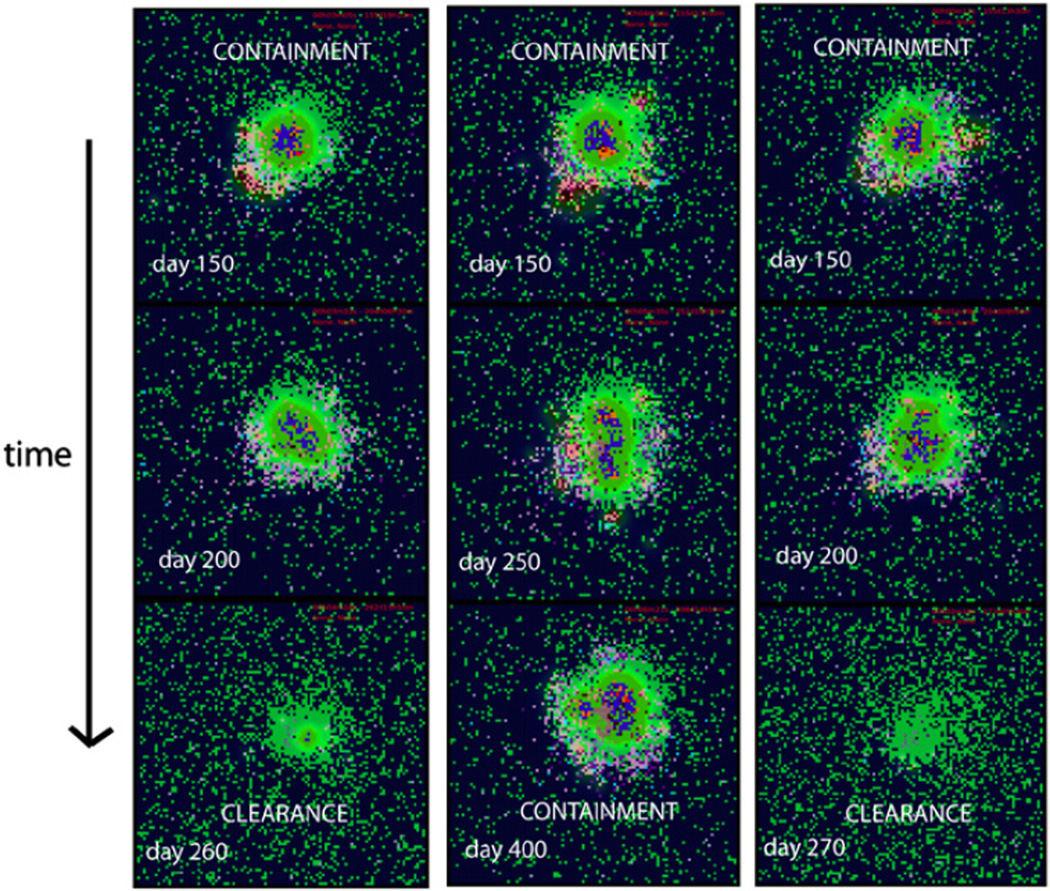
We then tested how to disturb a stable granuloma to manipulate a containment scenario to try to shift the system to clear infection. Increasing APC trafficking can rescue the system and clear infection: bacteria are gradually cleared and subsequently the granuloma slowly dissolves (Fig. 4, enhanced APC trafficking column).
Fig. 4.
Immunotherapy strategies. Snapshots of granuloma state at different days after the initiation of different immunotherapy strategies. The initial conditions are for a typical containment scenario at day 150 post-infection. The first column represent enhanced CD4 priming strategy, the second column enhanced CD4 and CD8 priming and the last column enhanced APC trafficking. It takes approximately 10–15 days to resolve the inflammation after bacteria is cleared.
A similar outcome can be achieved by enhancing only CD4+ T cell priming (Fig. 4, enhanced CD4 priming column).In contrast, increasing CD8+ T cell priming does not affect granuloma stability and can impair the beneficial effect of enhancing CD4+ T cell priming: when combined, both effects do not achieve clearance (Fig. 4, enhanced CD4/CD8 priming column). This likely follows since once a macrophage is activated (CD4+ T cell dependent), its intracellular bacterial load is completely cleared. CTL killing releases some bacteria in the extracellular domain: in a very densely packed environment such as an already formed granuloma, bacteria released into the extracellular domain are most likely internalized by other resting macrophages rather than killed. This process will prevent immediate bacterial killing and sustain the infection and the granuloma.
4. Discussion
CD4+ and CD8+ T cell priming in a LN is a key step to mounting a protective immune response to most bacterial infection, and Mtb is no exception. For TB, how events occurring in LNs can impact granuloma formation and maintenance is still an open question. Only a multi-organ model that takes into account trafficking events can be used to capture the complexity of TB and be useful for testing therapeutic and preventive strategies to combat this disease. This study takes a multi-organ approach to study TB granuloma formation, building onto an existing agent-based model of the lung some of the main mechanisms of T cell priming occurring in the lung-draining LN. The cellular dynamics of the lymph node model are described with a sufficient level of detail by a temporal-only representation (i.e., ODE system), while the lung compartment requires spatial details to capture the emergence of a unique spatial structure, a granuloma. We recapitulate typical infection outcomes and predict both cell and bacterial numbers in containment and dissemination scenarios, based on the granuloma diameter (presently not measurable experimentally).
Here we show that enhanced APC trafficking can drive the system to clearance, both before or after a granuloma has been established, suggesting a potential mechanism for successful vaccination and immunotherapy strategies. We also show how impaired APC migration can result in dissemination and uncontrolled growth of the bacteria. Unfortunately, the molecular and cellular mechanisms governing pulmonary DC trafficking to the lymph node are poorly understood. Most data are derived from studying the migration of skin DCs, and it remains to be determined whether these findings are applicable to DCs in other tissues (Randolph et al., 2005). Assays that directly analyze DCs transiting through lymphatic vessels are not available yet (Randolph et al., 2005) and whether the regulation of this trafficking controls the nature of adaptive immune responses in the lung and in the granulomatous tissue is still an open question (Cook and Bottomly, 2007).
Overall, we find that the role of effector T cells remains essential for a successful initial immune response to Mtb invasion: even if few effector T cells are present at the site, the IFNγ and TNF produced guarantee the necessary macrophage activation and containment is achieved ad well as a stable granuloma. Manipulating the efficiency of T-cell–APC contacts in vivo rather than the number of APC migrating to the LN can also be a viable strategy to clear an infection, before a granuloma is fully developed. This can be accomplished by increasing the duration of the interaction (Celli et al., 2005, 2007), the cognate frequency of naïve T cells (Linderman et al., 2010; Zheng et al., 2008) or having DC into the system that are highly immunogenic (Steinman, 2001).
Another finding of our spatial multi-organ model is how enhancing only effector CD4+ T cell differentiation can represent a viable immunotherapy strategy for latently infected individuals, where an infection can be cleared once a granuloma is fully formed. CTL activity is a key to controlling the onset of infection and possibly for clearance, but not when a granuloma has already been established.
The computational modeling platform described herein can be improved. First and obviously, more mechanisms and cells can be included. For example anti-inflammatory cytokines (such as IL-10) will be modeled explicitly (work in progress), as well as including alternatively activated (AAM) and classically activated (CAM) macrophages that we have explored previously (Marino et al., 2010b) Two key improvements will be in modeling explicitly dendritic cells and model bacterial dynamics in more detail. We do not model bacteria metabolic states and we plan to address replicating/slow replicating/dormant Mtb states in future work. This will also give us the opportunity to capture mechanisms of tissue liquefaction (extracellular bacilli do not grow unless there is liquefaction, see Grosset (2003)) and test the dynamic hypothesis, suggested in recent work (Cardona, 2009). In mice, the necrotic center of a granuloma comprises a ring of foamy macrophages (Russell et al., 2009): we have not modeled the kinetics of foamy macrophages from the granuloma to the alveolar space, some of them carrying non-replicating bacilli, as observed by different groups (Caceres et al., 2009; Cardona et al., 2003; Ordway et al., 2006; Skold and Behar, 2008).
It is important to emphasize the modularity and tunable resolution (Marino et al., 2010a) of this computational platform. By tunable resolution we mean that we have the ability to fine-grain or coarse-grain model components at will. We can achieve containment “turning off” the LN-ODE component by using a completely stochastic recruitment function, as shown in Fig. 2. “Turning on” the LN-ODE component with its more mechanistic features allows us to gain insights into the trade-off between number and quality of APCs migrating from the lung to the priming compartment. We have previously predicted the nonlinear properties of these trade-offs within a virtual lymph node environment (Linderman et al., 2010). Here, these key mechanisms are explicitly modeled in a computational representation of granuloma formation and they can be manipulated to ultimately control infection outcome.
A likely improvement will be to refine the granuloma environment in 3D. The limiting factor of a 3D implementation revolves around how efficiently we model chemokine and cytokine diffusion in a 3D environment. A single run of 200 days on a current generation workstation takes approximately 1 h to complete, with approximately 90–95% of the CPU time spent on calculating diffusion. In 3D this results in an increase of the total CPU time by a factor of 300–500 which poses issues of computational cost and time, especially if a comprehensive uncertainty and sensitivity analysis is going to be performed (which means hundreds of simulations).
We recently published a review (Marino et al., 2010a) emphasizing the importance of multi-scale, multi-organ modeling platforms to capture the complexity of host–pathogen interactions in TB as well as in any bacterial/viral infections. The work herein shows the potentials of this approach, with a multi-organ (compartment) agent-based model implementation. By incorporating events occurring in both the lung and the draining LN, we gain insights into immune mechanisms operating in different compartments that regulate granuloma formation and maintenance. Ultimately, our suggestions for viable vaccination and immunotherapy strategies can be tested experimentally to aid in the prevention of spread of infection and for treatment of latent TB.
Supplementary Material
Acknowledgments
This work was supported by National Institute of Health (NIH) Grants R33HL092844, R33HL092853, and N01 AI50018 awarded to DK. We thank reviewers for helpful comments.
Footnotes
Appendix A. Supporting information
Supplementary data associated with this article can be found in the online version at doi:10.1016/j.jtbi.2011.03.022.
References
- Barry CE, III, Boshoff HI, Dartois V, Dick T, Ehrt S, Flynn J, Schnappinger D, Wilkinson RJ, Young D. The spectrum of latent tuberculosis: rethinking the biology and intervention strategies. Nat. Rev. Microbiol. 2009;7:845–855. doi: 10.1038/nrmicro2236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behr MA, Warren SA, Salamon H, Hopewell PC, Ponce de Leon A, Daley CL, Small PM. Transmission of Mycobacterium tuberculosis from patients smear-negative for acid-fast bacilli. Lancet. 1999;353:444–449. doi: 10.1016/s0140-6736(98)03406-0. [DOI] [PubMed] [Google Scholar]
- Biancotto A, Grivel JC, Iglehart SJ, Vanpouille C, Lisco A, Sieg SF, Debernardo R, Garate K, Rodriguez B, Margolis LB, Lederman MM. Abnormal activation and cytokine spectra in lymph nodes of people chronically infected with HIV-1. Blood. 2007;109:4272–4279. doi: 10.1182/blood-2006-11-055764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blower SM, Dowlatabadi H. Sensitivity and uncertainty analysis of complex-models of disease transmission—an HIV model, as an example. Int. Stat. Rev. 1994;62:229–243. [Google Scholar]
- Caceres N, Tapia G, Ojanguren I, Altare F, Gil O, Pinto S, Vilaplana C, Cardona PJ. Evolution of foamy macrophages in the pulmonary granulomas of experimental tuberculosis models. Tuberculosis (Edinburgh) 2009;89:175–182. doi: 10.1016/j.tube.2008.11.001. [DOI] [PubMed] [Google Scholar]
- Cahill RN, Frost H, Trnka Z. The effects of antigen on the migration of recirculating lymphocytes through single lymph nodes. J. Exp. Med. 1976;143:870–888. doi: 10.1084/jem.143.4.870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Capuano SV, III, Croix DA, Pawar S, Zinovik A, Myers A, Lin PL, Bissel S, Fuhrman C, Klein E, Flynn JL. Experimental Mycobacterium tuberculosis infection of cynomolgus macaques closely resembles the various manifestations of human M. tuberculosis infection. Infect. Immun. 2003;71:5831–5844. doi: 10.1128/IAI.71.10.5831-5844.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cardona PJ. A dynamic reinfection hypothesis of latent tuberculosis infection. Infection. 2009;37:80–86. doi: 10.1007/s15010-008-8087-y. [DOI] [PubMed] [Google Scholar]
- Cardona PJ, Gordillo S, Diaz J, Tapia G, Amat I, Pallares A, Vilaplana C, Ariza A, Ausina V. Widespread bronchogenic dissemination makes DBA/2 mice more susceptible than C57BL/6 mice to experimental aerosol infection with Mycobacterium tuberculosis . Infect. Immun. 2003;71:5845–5854. doi: 10.1128/IAI.71.10.5845-5854.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Celli S, Garcia Z, Bousso P. CD4 T cells integrate signals delivered during successive DC encounters in vivo. J. Exp. Med. 2005;202:1271–1278. doi: 10.1084/jem.20051018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Celli S, Lemaitre F, Bousso P. Real-time manipulation of T cell–dendritic cell interactions in vivo reveals the importance of prolonged contacts for CD4+ T cell activation. Immunity. 2007;27:625–634. doi: 10.1016/j.immuni.2007.08.018. [DOI] [PubMed] [Google Scholar]
- Chackerian AA, Alt JM, Perera TV, Dascher CC, Behar SM. Dissemination of Mycobacterium tuberculosis is influenced by host factors and precedes the initiation of T-cell immunity. Infect. Immun. 2002;70:4501–4509. doi: 10.1128/IAI.70.8.4501-4509.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang ST, Linderman JJ, Kirschner DE. Multiple mechanisms allow Mycobacterium tuberculosis to continuously inhibit MHC class II-mediated antigen presentation by macrophages. Proc. Natl. Acad. Sci. USA. 2005;102:4530–4535. doi: 10.1073/pnas.0500362102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang ST, Linderman JJ, Kirschner DE. Effect of multiple genetic polymorphisms on antigen presentation and susceptibility to Mycobacterium tuberculosis infection. Infect. Immun. 2008;76:3221–3232. doi: 10.1128/IAI.01677-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Condos R, Rom WN, Liu YM, Schluger NW. Local immune responses correlate with presentation and outcome in tuberculosis. Am. J. Respir. Crit. Care Med. 1998;157:729–735. doi: 10.1164/ajrccm.157.3.9705044. [DOI] [PubMed] [Google Scholar]
- Cook DN, Bottomly K. Innate immune control of pulmonary dendritic cell trafficking. Proc. Am. Thorac. Soc. 2007;4:234–239. doi: 10.1513/pats.200701-026AW. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper AM, Dalton DK, Stewart TA, Griffin JP, Russell DG, Orme IM. Disseminated tuberculosis in interferon gamma gene-disrupted mice. J. Exp. Med. 1993;178:2243–2247. doi: 10.1084/jem.178.6.2243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox RA. Quantitative relationships for specific growth rates and macro-molecular compositions of Mycobacterium tuberculosis, Streptomyces coelicolor A3(2) and Escherichia coli B/r: an integrative theoretical approach. Microbiology. 2004;150:1413–1426. doi: 10.1099/mic.0.26560-0. [DOI] [PubMed] [Google Scholar]
- Developers V. Valgrind. 2010 Available from: < http://valgrind.org/>.
- El-Kebir M. Modeling Tuberculosis in Lung and Central Nervous System. Master’s Thesis, Vrije Universiteit Amsterdam, Faculty of Sciences; 2010. [Google Scholar]
- Fallahi-Sichani M, Schaller MA, Kirschner DE, Kunkel SL, Linderman JJ. Identification of key processes that control tumor necrosis factor availability in a tuberculosis granuloma. PLoS Comput. Biol. 2010;6:e1000778. doi: 10.1371/journal.pcbi.1000778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fallahi-Sichani M, El-Kebir M, Marino S, Kirschner DE, Linderman JJ. Multiscale computational modeling reveals a critical role for TNF-alpha receptor 1 dynamics in tuberculosis granuloma formation. J. Immunol. 2011;86:3472–3483. doi: 10.4049/jimmunol.1003299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flynn JL, Chan J. Immunology of tuberculosis. Annu. Rev. Immunol. 2001;19:93–129. doi: 10.1146/annurev.immunol.19.1.93. [DOI] [PubMed] [Google Scholar]
- Flynn JL, Chan J, Triebold KJ, Dalton DK, Stewart TA, Bloom BR. An essential role for interferon gamma in resistance to Mycobacterium tuberculosis infection. J. Exp. Med. 1993;178:2249–2254. doi: 10.1084/jem.178.6.2249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forrest S, Orton T, Pedder D, Meyer SE, Herbst B, Sances A, Jr, Kumaresan S. Investigation of injury potential through matched pair drop testing. Biomed. Sci. Instrum. 2006;42:488–494. [PubMed] [Google Scholar]
- Gammack D, Doering CR, Kirschner DE. Macrophage response to Mycobacterium tuberculosis infection. J. Math. Biol. 2004;48:218–242. doi: 10.1007/s00285-003-0232-8. [DOI] [PubMed] [Google Scholar]
- Ganguli S, Gammack D, Kirschner DE. A metapopulation model of granuloma formation in the lung during infection with Mycobacterium tuberculosis . Math. Biosci. Eng. 2005;2:535–560. doi: 10.3934/mbe.2005.2.535. [DOI] [PubMed] [Google Scholar]
- Giacomini E, Iona E, Ferroni L, Miettinen M, Fattorini L, Orefici G, Julkunen I, Coccia EM. Infection of human macrophages and dendritic cells with Mycobacterium tuberculosis induces a differential cytokine gene expression that modulates T cell response. J. Immunol. 2001;166:7033–7041. doi: 10.4049/jimmunol.166.12.7033. [DOI] [PubMed] [Google Scholar]
- Greenland S. Sensitivity analysis, Monte Carlo risk analysis, and Bayesian uncertainty assessment. Risk Anal. 2001;21:579–583. doi: 10.1111/0272-4332.214136. [DOI] [PubMed] [Google Scholar]
- Grosset J. Mycobacterium tuberculosis in the extracellular compartment: an underestimated adversary. Antimicrob. Agents Chemother. 2003;47:833–836. doi: 10.1128/AAC.47.3.833-836.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haase AT. Population biology of HIV-1 infection: viral and CD4+ T cell demographics and dynamics in lymphatic tissues. Annu. Rev. Immunol. 1999;17:625–656. doi: 10.1146/annurev.immunol.17.1.625. [DOI] [PubMed] [Google Scholar]
- Hall JG, Morris B. The immediate effect of antigens on the cell output of a lymph node. Br. J. Exp. Pathol. 1965;46:450–454. [PMC free article] [PubMed] [Google Scholar]
- Helton JC, Davis FJ. Illustration of sampling-based methods for uncertainty and sensitivity analysis. Risk Anal. 2002;22:591–622. doi: 10.1111/0272-4332.00041. [DOI] [PubMed] [Google Scholar]
- Herrmann JL, Lagrange PH. Dendritic cells and Mycobacterium tuberculosis: which is the Trojan horse? Pathol. Biol. (Paris) 2005;53:35–40. doi: 10.1016/j.patbio.2004.01.004. [DOI] [PubMed] [Google Scholar]
- Hogue IB, Bajaria SH, Fallert BA, Qin S, Reinhart TA, Kirschner DE. The dual role of dendritic cells in the immune response to human immunodeficiency virus type 1 infection. J. Gen. Virol. 2008;89:2228–2239. doi: 10.1099/vir.0.83600-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houben EN, Nguyen L, Pieters J. Interaction of pathogenic mycobacteria with the host immune system. Curr. Opin. Microbiol. 2006;9:76–85. doi: 10.1016/j.mib.2005.12.014. [DOI] [PubMed] [Google Scholar]
- Kaufmann SH. Protection against tuberculosis: cytokines, T cells, and macrophages. Ann. Rheum. Dis. 2002;61(Suppl. 2):i54–ii58. doi: 10.1136/ard.61.suppl_2.ii54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khronos G. OpenGL. 2010 Retrieved from: < www.opengl.org>.
- Kirschner DE, Chang ST, Riggs TW, Perry N, Linderman JJ. Toward a multiscale model of antigen presentation in immunity. Immunol. Rev. 2007;216:93–118. doi: 10.1111/j.1600-065X.2007.00490.x. [DOI] [PubMed] [Google Scholar]
- Krombach F, Munzing S, Allmeling AM, Gerlach JT, Behr J, Dorger M. Cell size of alveolar macrophages: an interspecies comparison. Environ. Health Perspect. 1997;105(Suppl. 5):1261–1263. doi: 10.1289/ehp.97105s51261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar V, Robbins SL. Robbins Basic Pathology. Philadelphia, PA: Saunders/Elsevier; 2007. [Google Scholar]
- Latif R, Kerlero de Rosbo N, Amarant T, Rappuoli R, Sappler G, Ben-Nun A. Reversal of the CD4(+)/CD8(+) T-cell ratio in lymph node cells upon in vitro mitogenic stimulation by highly purified, water-soluble S3–S4 dimer of pertussis toxin. Infect. Immun. 2001;69:3073–3081. doi: 10.1128/IAI.69.5.3073-3081.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Law K, Weiden M, Harkin T, Tchou-Wong K, Chi C, Rom WN. Increased release of interleukin-1 beta, interleukin-6, and tumor necrosis factor-alpha by bronchoalveolar cells lavaged from involved sites in pulmonary tuberculosis. Am. J. Respir. Crit. Care Med. 1996;153:799–804. doi: 10.1164/ajrccm.153.2.8564135. [DOI] [PubMed] [Google Scholar]
- Lin PL, Rodgers M, Smith L, Bigbee M, Myers A, Bigbee C, Chiosea I, Capuano SV, Fuhrman C, Klein E, Flynn JL. Quantitative comparison of active and latent tuberculosis in the cynomolgus macaque model. Infect. Immun. 2009;77:4631–4642. doi: 10.1128/IAI.00592-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin PL, Myers A, Smith L, Bigbee C, Bigbee M, Fuhrman C, Grieser H, Chiosea I, Voitenek NN, Capuano SV, Klein E, Flynn JL. Tumor necrosis factor neutralization results in disseminated disease in acute and latent Mycobacterium tuberculosis infection with normal granuloma structure in a cynomolgus macaque model. Arthritis Rheum. 2010;62:340–350. doi: 10.1002/art.27271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linderman JJ, Riggs T, Pande M, Miller M, Marino S, Kirschner DE. Characterizing the dynamics of CD4+ T cell priming within a lymph node. J. Immunol. 2010;184:2873–2885. doi: 10.4049/jimmunol.0903117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marino S, Kirschner DE. The human immune response to Mycobacterium tuberculosis in lung and lymph node. J. Theor. Biol. 2004;227:463–486. doi: 10.1016/j.jtbi.2003.11.023. [DOI] [PubMed] [Google Scholar]
- Marino S, Beretta E, Kirschner DE. The role of delays in innate and adaptive immunity to intracellular bacterial infection. Math. Biosci. Eng. 2007;4:261–288. doi: 10.3934/mbe.2007.4.261. [DOI] [PubMed] [Google Scholar]
- Marino S, Linderman JJ, Kirschner DE. A Multifaceted Approach to Modeling the Immune Response in Tuberculosis. Wiley Interdisciplinary Reviews: Systems Biology and Medicine. 2010 doi: 10.1002/wsbm.131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marino S, Hogue IB, Ray CJ, Kirschner DE. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008;254:178–196. doi: 10.1016/j.jtbi.2008.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marino S, Myers A, Flynn JL, Kirschner DE. TNF and IL-10 are major factors in modulation of the phagocytic cell environment in lung and lymph node in tuberculosis: a next-generation two-compartmental model. J. Theor. Biol. 2010;265:586–598. doi: 10.1016/j.jtbi.2010.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marino S, Pawar S, Fuller CL, Reinhart TA, Flynn JL, Kirschner DE. Dendritic cell trafficking and antigen presentation in the human immune response to Mycobacterium tuberculosis . J. Immunol. 2004;173:494–506. doi: 10.4049/jimmunol.173.1.494. [DOI] [PubMed] [Google Scholar]
- Marino S, Sud D, Plessner H, Lin PL, Chan J, Flynn JL, Kirschner DE. Differences in reactivation of tuberculosis induced from anti-TNF treatments are based on bioavailability in granulomatous tissue. PLoS Comput. Biol. 2007;3:1909–1924. doi: 10.1371/journal.pcbi.0030194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MartIn-Fontecha A, Sebastiani S, Hopken UE, Uguccioni M, Lipp M, Lanza-vecchia A, Sallusto F. Regulation of dendritic cell migration to the draining lymph node: impact on T lymphocyte traffic and priming. J. Exp. Med. 2003;198:615–621. doi: 10.1084/jem.20030448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathworks. MATLAB Compiler. 2010 Available from: < http://www.mathworks.com/products/compiler/>.
- Matzinger P. The danger model: a renewed sense of self. Science. 2002;296:301–305. doi: 10.1126/science.1071059. [DOI] [PubMed] [Google Scholar]
- Microsoft. NET. 2010 Available from: < http://msdn.microsoft.com/netframework>.
- Mogues T, Goodrich ME, Ryan L, LaCourse R, North RJ. The relative importance of T cell subsets in immunity and immunopathology of airborne Mycobacterium tuberculosis infection in mice. J. Exp. Med. 2001;193:271–280. doi: 10.1084/jem.193.3.271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicas M, Nazaroff WW, Hubbard A. Toward understanding the risk of secondary airborne infection: emission of respirable pathogens. J. Occup. Environ. Hyg. 2005;2:143–154. doi: 10.1080/15459620590918466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nokia. Qt. 2010 Available from: < http://qt.nokia.com/>.
- Onyebujoh P, Rodriguez W, Mwaba P. Priorities in tuberculosis research. Lancet. 2006;367:940–942. doi: 10.1016/S0140-6736(06)68385-2. [DOI] [PubMed] [Google Scholar]
- Oracle. Java. 2010 Available from: < www.java.com>.
- Ordway D, Harton M, Henao-Tamayo M, Montoya R, Orme IM, Gonzalez-Juarrero M. Enhanced macrophage activity in granulomatous lesions of immune mice challenged with Mycobacterium tuberculosis . J. Immunol. 2006;176:4931–4939. doi: 10.4049/jimmunol.176.8.4931. [DOI] [PubMed] [Google Scholar]
- Orme IM. The kinetics of emergence and loss of mediator T lymphocytes acquired in response to infection with Mycobacterium tuberculosis . J. Immunol. 1987;138:293–298. [PubMed] [Google Scholar]
- Randolph GJ, Angeli V, Swartz MA. Dendritic-cell trafficking to lymph nodes through lymphatic vessels. Nat. Rev. Immunol. 2005;5:617–628. doi: 10.1038/nri1670. [DOI] [PubMed] [Google Scholar]
- Ray JC, Flynn JL, Kirschner DE. Synergy between individual TNF-dependent functions determines granuloma performance for controlling Mycobacterium tuberculosis infection. J. Immunol. 2009;182:3706–3717. doi: 10.4049/jimmunol.0802297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riggs T, Walts A, Perry N, Bickle L, Lynch JN, Myers A, Flynn J, Linderman JJ, Miller MJ, Kirschner DE. A comparison of random vs. chemotaxis-driven contacts of T cells with dendritic cells during repertoire scanning. J. Theor. Biol. 2008;250:732–751. doi: 10.1016/j.jtbi.2007.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohde KH, Abramovitch RB, Russell DG. Mycobacterium tuberculosis invasion of macrophages: linking bacterial gene expression to environmental cues. Cell Host Microb. 2007;2:352–364. doi: 10.1016/j.chom.2007.09.006. [DOI] [PubMed] [Google Scholar]
- Russell DG, Cardona PJ, Kim MJ, Allain S, Altare F. Foamy macrophages and the progression of the human tuberculosis granuloma. Nat. Immunol. 2009;10:943–948. doi: 10.1038/ni.1781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez MA, Blower SM. Uncertainty and sensitivity analysis of the basic reproductive rate. Tuberculosis as an example. Am. J. Epidemiol. 1997;145:1127–1137. doi: 10.1093/oxfordjournals.aje.a009076. SSSS. [DOI] [PubMed] [Google Scholar]
- Schwander SK, Torres M, Sada E, Carranza C, Ramos E, Tary-Lehmann M, Wallis RS, Sierra J, Rich EA. Enhanced responses to Mycobacterium tuberculosis antigens by human alveolar lymphocytes during active pulmonary tuberculosis. J. Infect. Dis. 1998;178:1434–1445. doi: 10.1086/314454. [DOI] [PubMed] [Google Scholar]
- Segovia-Juarez JL, Ganguli S, Kirschner D. Identifying control mechanisms of granuloma formation during M. tuberculosis infection using an agent-based model. J. Theor. Biol. 2004;231:357–376. doi: 10.1016/j.jtbi.2004.06.031. [DOI] [PubMed] [Google Scholar]
- Selwyn PA, Hartel D, Lewis VA, Schoenbaum EE, Vermund SH, Klein RS, Walker AT, Friedland GH. A prospective study of the risk of tuberculosis among intravenous drug users with human immunodeficiency virus infection. N. Engl. J. Med. 1989;320:545–550. doi: 10.1056/NEJM198903023200901. [DOI] [PubMed] [Google Scholar]
- Skold M, Behar SM. Tuberculosis triggers a tissue-dependent program of differentiation and acquisition of effector functions by circulating monocytes. J. Immunol. 2008;181:6349–6360. doi: 10.4049/jimmunol.181.9.6349. [DOI] [PubMed] [Google Scholar]
- Steinman RM. Dendritic cells and the control of immunity: enhancing the efficiency of antigen presentation. Mt. Sinai. J. Med. 2001;68:160–166. [PubMed] [Google Scholar]
- Sud D, Bigbee C, Flynn JL, Kirschner DE. Contribution of CD8+ T cells to control of Mycobacterium tuberculosis infection. J. Immunol. 2006;176:4296–4314. doi: 10.4049/jimmunol.176.7.4296. [DOI] [PubMed] [Google Scholar]
- Vynnycky E, Fine PE. Lifetime risks, incubation period, and serial interval of tuberculosis. Am. J. Epidemiol. 2000;152:247–263. doi: 10.1093/aje/152.3.247. [DOI] [PubMed] [Google Scholar]
- Zak O, Sande MA. Handbook of Animal Models of Infection: Experimental Models in Antimicrobial Chemotherapy. San Diego: Academic Press; 1999. [Google Scholar]
- Zheng H, Jin B, Henrickson SE, Perelson AS, von Andrian UH, Chakraborty AK. How antigen quantity and quality determine T-cell decisions in lymphoid tissue. Mol. Cell Biol. 2008;28:4040–4051. doi: 10.1128/MCB.00136-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.