Performing Taxometric Analysis to Distinguish Categorical and Dimensional Variables

Abstract

A fundamental question facing clinical scientists is whether the constructs they are studying are categorical or dimensional in nature. The taxometric method was developed expressly to answer this question and is being used by a growing number of investigators to inform theory, research, and practice in psychopathology. The current paper provides a practical introduction to the method, updating earlier tutorials based on the findings of recent methodological studies. We offer revised guidelines for data requirements, indicator selection, parameter estimation, and procedure selection and implementation. We illustrate our recommended approach to taxometric analysis using idealized data sets as well as data sets representative of those found in clinical research. We close with advice to help newcomers get started on their own taxometric analyses.

Introduction

Beginning in the 1960s, Paul Meehl pioneered the development of a technique to determine whether a latent variable—the construct underlying observed measures, or indicators—was categorical or dimensional. Several data-analytic procedures could be used to examine the relationships among indicators, providing nonredundant clues to the structure of the latent variable. In a series of technical reports, Meehl and his colleagues presented these procedures to help test a central claim of his etiological theory of schizophrenia. Meehl’s (1990) theory posits a genetic liability for the disorder only among schizotypes, a discrete group hypothesized to comprise approximately 10% of the general population. Meehl sought a method to test for a categorical boundary between these schizotypes and individuals with no such susceptibility to schizophrenia. Dissatisfied with the ability of available methods to distinguish between categorical and dimensional latent variables, he created his own taxometric method as a practical solution to a pressing problem in psychopathological research (Meehl, 1995).

In the nearly half a century since the first of these technical reports was circulated (Meehl, 1965), the taxometric method has seen extensive growth, refinement, evaluation, and application. Haslam (in press) provides the most recent review of applied taxometric investigations, including 111 published studies of dozens of psychological constructs. Perhaps owing to its origins in psychopathology, personality, and clinical assessment, taxometric studies continue to be performed most often in these areas. The enduring popularity of Meehl’s method, its continued methodological development, and the accelerating pace of its application attest to researchers’ embrace of the utility of taxometric analysis. Many other data-analytic approaches can be used to test the structure of latent variables (e.g., cluster analysis, mixture modeling or factor mixture modeling, latent class or latent profile analysis). Elsewhere, we have discussed some of the relative strengths and weaknesses of these approaches (e.g., Ruscio, Haslam, &, 2006; Ruscio & Ruscio, 2004c). In this paper, we focus on the taxometric method because of its particular strengths for addressing a central question in the study of psychopathology: whether clinical constructs are most accurately represented as categories or dimensions.

We begin with a brief overview of why one might want to test the structure of a latent variable, then show how to do this using taxometric analysis. Two earlier tutorial-style papers covered similar ground (Ruscio & Ruscio, 2004c, 2004a), and we update those reviews based on the findings of several methodological studies published since that time. Ruscio (2007) emphasized the need for empirical guidelines to facilitate appropriate and effective implementation of taxometric procedures. We discuss the options a researcher should consider when conducting a taxometric investigation and describe the empirical evidence available for guiding decisions. After reviewing and illustrating the current state of the art in the taxometric method, we conclude with some suggestions for how readers can get started on their own taxometric analyses.

Reasons to Distinguish Categorical and Dimensional Variables

Many researchers have preferences—sometimes very strong ones—for conceptualizing or assessing particular variables in categorical or dimensional ways. Making this distinction correctly, however, is important for the advancement of theory, research, and practice. For example, as Meehl’s (1990) theory of schizophrenia illustrates, knowing whether a construct is best fit by a categorical or dimensional model can help guide the development of causal theories or evaluate the fit of competing causal theories (Haslam, 1997; Meehl, 1992). This is because dimensional variation may arise from the sum of many small influences (e.g., additive genetic and environmental factors), whereas categorical variation requires a mechanism such as a dichotomous causal factor (e.g., a single gene or formative event necessary and sufficient to produce a disorder), interactive effects (e.g., a genetic predisposition and a high stress level are jointly sufficient to produce a disorder), or threshold effects (e.g., individuals can cope with stress to a point, but beyond this level stress triggers a disorder).

Categorical and dimensional variables should also be classified in different ways (Meehl, 1995). Many psychologists, coming from a psychometric tradition, propose that the next edition of the Diagnostic and Statistical Manual of Mental Disorders (DSM) should move toward dimensional classification, at least for the personality disorders (e.g., Widiger & Trull, 2007). In contrast, many psychiatrists, coming from a medical tradition, conceptualize mental disorders as entities that are either present or absent. As some psychopathological constructs appear to be categorical, whereas others appear to be dimensional, a one-size-fits-all classification scheme may not be appropriate (Haslam, in press; A. M. Ruscio, 2008).

Categorical and dimensional variables should be assessed in different ways (Meehl, 1992; Ruscio & Ruscio, 2002). Should an assessment tool be designed to classify individuals into groups or to locate their relative positions along dimensions? These are very different goals requiring very different approaches. For example, a relatively small number of items with discriminating power focused near a categorical boundary can maximize the accuracy with which individuals are assigned to groups. On the other hand, a larger number of items that provide discrimination across the full range of trait levels can maximize the precision with which individuals are located along dimensions.

Knowing whether a variable is categorical or dimensional has further implications for research design and statistical analysis. For example, the practice of using analogue samples (e.g., college students with subclinical symptom levels) is premised on dimensional structure and may be inappropriate for categorical variables. Conversely, the practice of dichotomizing continuous score distributions is justified when (a) the structure of a variable is categorical and (b) the selected threshold validly classifies cases into groups. If either condition is not satisfied, the use of dichotomous scores risks discarding important information and reducing the statistical power of analyses (DeCoster, Iselin, & Gallucci, 2009; MacCallum, Zhang, Preacher, & Rucker, 2002). These and other implications of categorical versus dimensional structure (for a more detailed treatment, see Ruscio, Haslam, and Ruscio, 2006) underscore the importance of studying, rather than presuming, which structure best fits the data.

Characteristics of the Taxometric Method

Readers who have made it this far have hopefully been persuaded that it is worthwhile to test the latent structure of a construct of interest. We consequently turn our attention to key features of the taxometric method that make it a good choice for performing this test. None of these features are unique to taxometric analysis, but together they provide an appealing methodological approach.

One key feature of the taxometric method is that it can be used to compare the relative fit of competing structural models. Rather than presuming there are categories or dimensions and attempting to determine how many exist, the taxometric method can help to determine whether a categorical or a dimensional model better fits the data. Conceptually, this is analogous to testing for the presence or absence of a single categorical boundary (Ruscio & Ruscio, 2004c). As Waller and Meehl (1998) emphasized, whether or not such a boundary exists, there can be variation along one or more dimensions. Thus, the two competing structural models tested in the approach to taxometric analysis that we prefer are (a) the common factor model, which allows purely dimensional variation along one or more dimensions; and (b) a two-category model, which also allows for the possibility of dimensional variation within each group. The latter model specifies that individuals belong to one of two groups, each of which may—or may not—exhibit some degree of residual variation according to the common factor model. Successive iterations of taxometric analysis can be used to test for additional categorical boundaries (e.g., between more than two categories or between subgroups within a category). The taxometric method is not designed to test the number of latent dimensions underlying a construct, either in the full sample or within any category; exploratory or confirmatory factor analysis would be a more appropriate tool.

The “competing-models” inferential framework is not the only one that can be adopted when using the taxometric method, but it is the one that we prefer. An alternative “taxon-detection” framework is preferred by some researchers (e.g., Beauchaine, 2003). In this approach, dimensional structure is treated as a null hypothesis to be rejected if there is sufficiently strong evidence for the existence of discrete groups. Like traditional null-hypothesis significance testing, this framework does not allow researchers to “accept the null” (i.e., to conclude that latent structure is dimensional). Unfortunately, there is a long-standing ambiguity in the taxometric literature about which inferential framework is intended. There are reasonable arguments on both sides of this issue (for further discussion, see Ruscio, 2007 and Ruscio & Kaczetow, 2009). We believe that many, if not most, users of the taxometric method are seeking to differentiate competing categorical and dimensional models rather than searching solely for evidence of categorical structure. Most important, developments in taxometric methodology—specifically, the parallel analysis of categorical and dimensional comparison data—have placed the competing-models approach on a firm foundation. Without these developments, which we describe next, we believe that criticisms of the competing-models framework would carry considerably more weight.

A second key feature of the taxometric method is that it allows parallel analyses of categorical and dimensional comparison data. This approach has been developed within the past decade, during which the methods for generating comparison data have evolved and their use has become standard practice in taxometric research (Ruscio et al., 2010). The utility of parallel analyses of comparison data stems from the fact that taxometric procedures do not provide significance tests or fit indices. Instead, as we discuss in detail later, investigators examine results and reach a judgment based on their resemblance to prototypic results expected under categorical or dimensional structure. Unfortunately, empirical data seldom produce results that match these prototypes, in part because the characteristics of actual data diverge from the ideal conditions used to generate the illustrative data. For example, prototypes have typically been generated using normally distributed data. Micceri (1989) showed that normal distributions are uncommon, and Ruscio, Ruscio, and Keane (2004) showed that skewed distributions can exert a substantial influence on taxometric results.

This is where parallel analyses of comparison data enter the picture. Ruscio, Ruscio, and Meron (2007) introduced a technique for generating comparison data that reproduce important characteristics of an empirical data set (e.g., sample size, number of indicators, marginal distributions, correlation matrix) using either a categorical or a dimensional structural model. Ruscio and Kaczetow (2008) placed the data-generation technique on a more solid statistical foundation and improved its run-time efficiency. The technique begins by generating a population of comparison data using the categorical model, then generating a second population of data using the dimensional model. A series of random samples, each the same size as the empirical data set, is drawn from the two populations. All samples are then submitted to the same taxometric analyses as the empirical data set. This provides a very useful interpretive aid. Rather than comparing results for the empirical data to prototypical results for idealized categorical or dimensional data, one can compare results to those for artificial comparison data that hold constant important aspects of the empirical data but differ in their underlying structures. Do the empirical results more closely resemble those for the categorical or the dimensional comparison data? This question can be answered by visually comparing the results or by using an objective index of the relative fit of results for categorical versus dimensional comparison data. This Comparison Curve Fit Index (CCFI) has been shown in many studies to successfully differentiate the two structural models (e.g., Ruscio, 2007; Ruscio & Kaczetow, 2009; Ruscio & Marcus, 2007; Ruscio et al., 2007; Ruscio & Walters, 2009; Ruscio, Walters, Marcus, & Kaczetow, 2010; Walters, McGrath, & Knight, 2010; Walters & Ruscio, 2009). The first step in calculating the CCFI is to compute Fit_Cat as the root-mean-square distance between data points on curves for the empirical data and categorical comparison data. The more these two curves resemble one another, the smaller the value of Fit_Cat. Next, repeat to compute Fit_Dim as the root-mean-square distance between data points on curves for the empirical data and dimensional comparison data. Finally, calculate CCFI = Fit_Dim / (Fit_Dim + Fit_Cat).

As a relative, rather than absolute, fit index, the CCFI facilitates the use of the competing-models inferential framework. CCFI values can range from 0 (strongest support for dimensional structure, when Fit_Dim = 0) to 1 (strongest support for categorical structure, when Fit_Cat = 0). Moreover, CCFI values close to .50 are ambiguous, indicative of comparably good (or poor) fit with both models (i.e., Fit_Dim = Fit_Cat). This alerts the researcher that the analysis is not able to powerfully distinguish categorical from dimensional structure, and hence that strong conclusions should not be drawn.Ruscio et al. (2010) recommended treating CCFI values between .45 and .55 as ambiguous or, if one wanted to be even more confident in the accuracy of results—at the risk of failing to reach a structural conclusion—treating CCFI values between .40 and .60 as ambiguous. We consider the calculation of the CCFI and the designation of some results as interpretationally ambiguous an important asset of the parallel analysis approach. Meehl (2004) emphasized the value of knowing whether taxometric results provide strong support for categorical structure, provide strong support for dimensional structure, or are ambiguous, and the CCFI achieves this in an objective manner.

A third key feature of the taxometric method is that it affords many opportunities to check the consistency of results. From the earliest stages of development, Meehl emphasized the desirability of performing consistency tests as a bedrock principle of his taxometric method. He and his colleagues created multiple taxometric procedures that can be used to obtain nonredundant evidence, with converging results providing increasing confidence in a structural solution. Further checks of consistency can be obtained by performing the same analyses with multiple measures or in multiple samples. Just as the CCFI value for a single taxometric analysis can provide support for categorical structure, dimensional structure, or neither, an examination of results across many analyses can reveal consistent support for categorical structure, dimensional structure, or neither.

Data Requirements

Like any data-analytic tool, taxometric analysis requires that the data meet certain requirements in order to provide informative results. Each taxometric procedure examines the relations among the observed variables that serve as indicators of the target construct. There are a number of factors that should be considered to determine whether a particular data set is appropriate for taxometric analysis. Meehl (1995) provided rules of thumb for several of these factors, and systematic study has found that most of Meehl’s guidelines were quite prescient. Below, we summarize what is presently known about data requirements for taxometrics, relying heavily on a simulation study by Ruscio et al. (2010) in which 100,000 data sets (50,000 categorical and 50,000 dimensional) spanning a wide range of data conditions were analyzed using multiple taxometric procedures. Other large-scale simulation studies are also cited when their findings help to address specific issues.

Our impression from running a number of these simulations is that the failure to meet one or more of the criteria presented below may be offset by especially favorable characteristics on other criteria in the same data set. Especially if it appears that data are on the borderline with regard to some criteria but acceptable on others, there may be relatively little risk in performing taxometric analyses so long as parallel analysis of comparison data is used to identify ambiguous results and prevent unwarranted conclusions. With this in mind, we discuss six characteristics to consider when evaluating data for possible taxometric analysis, along with recommended criteria (see Table 1). After we review these criteria and their empirical support, we describe data sets based on these criteria that will be used in illustrative taxometric analyses later in the paper. These include idealized data sets that will be used to illustrate prototypical taxometric results as well as data sets that are more representative of empirical data in psychopathology research.

Table 1.

Data Requirements for Taxometric Analysis

Data Characteristics	Recommended Criteria	Values for Illustrative Data Sets
		IC	ID	RC	RD
Sample size (N)	N≥300	2,000	2,000	600	600
Size of putative	nt≥50,	1,000, .50	---	60, .10	---
taxon (nt, P)	P≥.05	(998, .50)	(1,105, .55)	(83, .14)	(192, .32)
Number of indicators (k)	k≥2a	6	6	4	4
	k≥5b
Number of ordered categories (C)	C≥4	20	20	5	5
Indicator validity (d)	d≥1.25	2.00	---	1.85	---
		(2.01)	(1.62)	(2.06)	(1.54)
Within-group	rwg≤.30	−.01	---	.22	---
correlation (rwg)		(−.01)	(.21)	(.07)	(.07)

Notes. Values in parentheses are estimates. IC = idealized categorical data set; ID = idealized dimensional data set; RC = representative categorical data set; RD = representative dimensional data set.

^aThis criterion applies if N and C are large.

^bThis criterion applies if N or C is not particularly large.

Sample Size

Sample size requirements for taxometric analysis are fairly large, with Meehl’s (1995) rule of thumb being N ≥ 300. For the 57 published taxometric studies reviewed byRuscio et al. (2006), the median sample size was 809 and only 4 studies (7%) performed analyses with N < 300.Ruscio et al. (2010) found that categorical structure was no more difficult to identify when N was as low as 100 but that the accuracy with which dimensional structure was identified deteriorated when N fell below 300. Because one cannot know latent structure in advance of doing the analyses, it seems prudent to strive for an N of at least 300.

Size of the Putative Taxon

By convention, the taxometric literature refers to a discrete latent class (e.g., schizotypes in Meehl’s theory of schizophrenia) as a taxon whose members can be distinguished from a mutually exclusive complement class (e.g., non-schizotypes). In a taxometric analysis, the size of the putative taxon must be sufficiently large for that taxon to be detected, if it exists. Meehl’s rule of thumb for the estimated taxon base rate (the proportion P of taxon members in the sample) is P ≥ .10. In theRuscio et al. (2010) study, although the rate of ambiguous results crept up slightly for categorical data with .05 < P < .10, erroneous results remained rare. Thus, there appears to be relatively little risk of extending Meehl’s rule of thumb downward a bit. Moreover, Ruscio and Ruscio (2004c) demonstrated that the absolute number of taxon members can be at least as important as the taxon base rate. For example, with a total sample size of N = 600, a taxon of size n_t = 60 would meet the criterion of P ≥ .10. All else being equal, these same 60 taxon members might still be sufficient to identify categorical structure even if total N was increased to 1,200, which would correspond to P = .05 and appear unsatisfactory. With the caveat that further research is required to flesh out guidelines for absolute taxon size, we tentatively suggest that researchers strive to satisfy two criteria: n_t ≥ 50 and P > .05.

Unlike total sample size, one cannot know with certainty how large a taxon may be. Indeed, to justify a taxometric analysis, one must have at least some doubt about whether there exists a taxon at all. This means that one is estimating quantities (n_t, P) to address a hypothetical question: If the data are categorical, is the size of the taxon sufficiently large for taxometric analysis? Although the question is hypothetical, showing that estimates conform to the guidelines above offers preliminary reassurance (later supplemented through parallel analysis of comparison data) that the data are capable of detecting a taxon and consequently may be appropriate for taxometric analysis. There are many ways to estimate n_t and p, and the best choice will depend on the research context. For example, if one is testing the structure of a mental disorder, one could estimate the size of the taxon by tallying the number (and proportion) of cases that meet the diagnostic criteria for the disorder. Alternatively, if there is a validated or conventional cutting score on a measure available in the data set, one can see how many cases score above this level. It is incumbent on the researcher to present a best-guess estimate, or perhaps a range of plausible estimates, of the size of the putative taxon. Contrary to occasional misconceptions, doing so does not mean that one believes a categorical model will fit the data better than a dimensional model. The point is to ensure that taxometric analysis is capable of providing an informative test between these two competing models.

Number of Indicators

By convention, the variables that are submitted to taxometric analysis are referred to as indicators. There is no rule of thumb for the number of indicators that is acceptable, but some tentative guidelines can be suggested. At least k = 2 indicators must be present to perform any taxometric analyses, and some procedures require k ≥ 3. Three simulation studies have evaluated the influence of k on the accuracy of taxometric results obtained using multiple taxometric procedures.Ruscio et al. (2010) found that there was little risk of incorrect results even with just k = 3, the smallest value included in the study, although the proportion of ambiguous results decreased further with larger values of k. Walters and Ruscio (2009) found that performance deteriorated for k < 5 when data varied along ordered categorical response scales (i.e., Likert-type scales with a fixed number of response options), especially with fewer than 4 ordered categories (i.e., response options). This is noteworthy given that Likert-type scales are commonly used in assessments of clinical constructs. Finally, Ruscio and Walters (in press) found that reasonably accurate taxometric results could be obtained with k = 2 provided that both sample size and the number of ordered categories were large (e.g., N ≥ 600 and C ≥ 10). The number of ordered categories was much more important than sample size, and accuracy increased steadily with the number of ordered categories.

So where does this leave us? We suggest that for large samples of data—roughly, with an N of at least 500 or 600—that vary along continuous scales (or scales with so many distinct values that they approximate continuity well), k ≥ 2 should suffice. Below, we discuss recommendations when data vary along ordered categories rather than approximating continuity, in which case more indicators are likely to be required for informative results. Our advice in these areas is based on the findings of simulation studies, but because the interactions between the relevant factors revealed graduated trends rather than step functions, we offer criteria hesitantly and caution against their rigid application.

Number of Ordered Categories

Here, too, no rule of thumb has been suggested, but a few investigations have studied the number of response categories along which the indicators vary. Walters and Ruscio (2009) found that accuracy was poor with C < 4 ordered categories (i.e., with dichotomous or trichotomous response scales). They recommended that, when analyzing ordered categorical data, one strive for a combination of C ≥ 4 and k ≥ 5. It is difficult to disentangle criteria for C and k, but we suggest that C ≥ 4 should be adequate under most circumstances. When C < 4, it may be possible to increase the number of ordered categories by summing or otherwise combining raw items into composite indicators, as we describe later. Sample size also interacted with C and k in determining the accuracy of taxometric results. The influence of sample size was not particularly strong, so one should only consider raising or lowering the criterion for k if working with an especially small or large sample.

Indicator Validity

Like the size of the putative taxon, indicator validity involves a hypothetical question: If the data are categorical, do the indicators differentiate members of the taxon and complement with sufficient validity for taxometric analysis? Even if data are categorical, if the groups overlap too much in their scores on the indicators, it would be impossible for taxometric procedures (or any other data-analytic tool) to distinguish this categorical structure from a purely dimensional structure. Meehl’s (1995) rule of thumb is that indicators must differentiate members of putative groups with a validity of d ≥ 1.25; this is usually indexed using Cohen’s d, the standardized mean difference between groups.Ruscio et al. (2010) found that accuracy does in fact decline sharply with d < 1.25, so we echo Meehl’s advice.

Estimating indicator validity requires assigning cases to putative groups so that d can be calculated. Once again, it is the researcher’s responsibility to justify the method used to classify cases for estimating indicator validity. Cases might be grouped on the basis of a diagnostic algorithm, a cutting score on a valid assessment instrument, or some other method. If no reasonable grouping variable is available, cases can be assigned to groups using the estimated taxon base rate P. This base-rate classification procedure involves calculating a total score across all indicators (after standardizing them, if necessary), then assigning the highest-scoring proportion P of cases to the putative taxon and all other cases to the complement (Ruscio, 2009). Throughout this article, we assume that taxon members score higher on each indicator, which may require reverse-scoring some or all indicators prior to analysis. Having classified cases in whatever manner seems most appropriate, Cohen’s d can then be calculated for each indicator.

Within-Group Correlations

Meehl’s (1995) rule of thumb for within-group correlations between indicators is r_wg ≤ .30. Ruscio et al.’s (2010) findings were consistent with this advice, so we reiterate it here. As with taxon size and indicator validity, considering this data characteristic involves a hypothetical question: If the data are categorical, are the indicators sufficiently independent of one another within groups for taxometric analysis? Note that this does not mean that indicators should be correlated at low levels in the full sample. If the indicators do in fact represent multiple facets of a target construct, they should be positively correlated in the full sample. The problem with large within-group correlations is that they interfere with the ability of taxometric procedures to produce different patterns of results for categorical and dimensional data.

Estimating within-group correlations can—and should—be done using the same classification of cases with which indicator validity was estimated. Provided that this neither accentuates nor masks outliers in a correlation matrix, usually the mean r_wg is reported for each group or, if these are similar in magnitude, a single mean is reported for all correlations within both groups. An unresolved question involves what to do if within-group correlations are widely dispersed, with an acceptable mean r_wg but some values above the conventional threshold. As discussed shortly, one might consider removing or combining indicators that yield unacceptably large within-group correlations.

Data Management and Reporting Parameter Estimates

Before taxometric analysis can begin, researchers must select or construct a set of indicators from what may be a much larger number of variables available in the data set. A few general principles can help to guide this process. First, strive for representation of theoretically important facets of the target construct. Although the clarity of taxometric results has been shown to increase with number of indicators, the objective is not to include as many indicators as possible. Such a “kitchen sink” strategy might backfire if the number of variables surpasses the number of conceptually distinct facets of the target construct, increasing the likelihood of problematically large within-group correlations. A better approach is to include only as many indicators as there are conceptually distinct facets of the construct under study.

This leads to our second principle: Combine or remove redundant variables to arrive at a set of reasonably distinct indicators. Variables that correlate very highly with one another within putative groups make good candidates for aggregation into composites that can then serve as indicators. In addition to reducing within-group correlations, forming composite indicators can increase the number of ordered categories per indicator (which is especially useful when the original variables range across few values) as well as increase the reliability and validity of the resulting indicators. For these reasons, composite variables can be more effective indicators than individual variables under many circumstances.

Third, take an iterative approach to the process of selecting or constructing indicators. Construct a set of candidate indicators based on theoretical considerations, then evaluate them empirically. Do the values (or estimates) of k, C, d, and r_wg appear acceptable for taxometric analysis? Can the indicators be improved by reconfiguring the raw variables in some way? Typical data sets in psychopathology research contain many features that make it challenging to obtain clear, interpretable taxometric results. Putative taxa are often small, their members’ scores often overlap substantially with members of the complement, response scales often span few ordered categories, and even variables that appear to be conceptually distinct are often correlated with one another within groups. It may take considerable effort in a trial-and-error process to craft a set of indicators that meet the data requirements of taxometric analysis.

Before leaving this section, we want to briefly discuss the purpose and practice of estimating parameters a priori and post hoc. A priori estimates, those obtained before performing the taxometric analyses that will ultimately be reported and interpreted, can be useful to demonstrate that a data set is appropriate for taxometric analysis. For this purpose, we recommend that researchers report a single set of parameter estimates (i.e., taxon size, indicator validity, within-group correlations) for that indicator set based on the single, best classification of cases available for the data. In taxometric reports, it is not uncommon for multiple sets of parameter estimates to be presented, typically one set for each taxometric procedure that was performed. We recommend instead that cases be assigned to groups in the most defensible manner possible, and that a priori parameter estimates be presented based on this classification alone. An important exception is in cases where more than one defensible classification is available, provided the multiple classification methods are chosen deliberately and justified clearly. For example, there may be multiple cutting scores that could reasonably be applied to a given assessment instrument (e.g., one for “clinically significant” and another for “severe” symptom levels), or different thresholds may be advocated by different authors for the same purpose. We have no qualms with estimating parameters a priori more than once if there is a good reason to do so. Rather, we discourage the reflexive reporting of parameter estimates appearing in the output of multiple taxometric procedures, which are each based on different, atheoretical classifications of cases that are probably less justifiable than one a thoughtful investigator can construct.

In contrast to the use of a priori parameter estimates to establish that a data set is appropriate for taxometric analysis, estimating parameters once the final series of analyses has been performed (post hoc) might be done in as many ways as possible to serve as a check on the consistency of results (Meehl, 1995). We discuss the practice of consistency testing toward the end of the next section. For now, we emphasize only that when one is estimating parameters a priori for the purpose of reporting the estimates as evidence that the data are suitable for taxometrics, we recommend using the most defensible classification of cases to generate a single set of estimates.

Taxometric Procedures

Many taxometric procedures have been proposed, but three procedures form the core of most contemporary taxometric studies: MAMBAC, MAXCOV (or the closely-related MAXEIG or MAXSLOPE), and L-Mode. We review the mechanics of each procedure, the decisions that must be made to implement it, and guidelines for making reasoned, thoughtful choices. We illustrate the procedures with analyses of four data sets whose characteristics are summarized in Table 1. Two of these data sets have characteristics that should make it very easy for taxometric analysis to yield informative results (e.g., large sample size, many indicators that span many ordered categories, and for the categorical data a large taxon); we refer to one as our idealized categorical (IC) data set, the other as our idealized dimensional (ID) data set. The other two data sets have characteristics designed to pose the kinds of challenges typical of psychopathology data (e.g., more modest sample size, fewer indicators that span fewer ordered categories, skewed indicators, and for the categorical data a small taxon).

As these are simulated data sets for which no conceptually meaningful a priori classification of cases was available, preliminary MAMBAC, MAXEIG, and L-Mode analyses were performed without comparison data to estimate the taxon base rate (see Table 2); the mean of these estimates was used to classify cases into groups in order to estimate latent parameters (i.e., size of the putative taxon, indicator validity, within-group correlations) and to generate a population of categorical comparison data. A single population of N = 100,000 was generated with categorical structure, then a second population of the same size was generated with dimensional structure. Each taxometric analysis was followed by parallel analysis of 100 random samples of data drawn from each simulated population of comparison data.

Table 2.

Taxon Base Rate Estimates for Taxometric Analyses

	Data Set
	Idealized Categorical	Idealized Dimensional	Representative Categorical	Representative Dimensional
MAMBAC	.497 (.065)	.514 (.030)	.206 (.068)	.302 (.107)
MAXEIG	.503 (.004)	.643 (.043)	.102 (.006)	.296 (.044)
L-Mode	.494a	.500a	.105b	.361b
Across Procedures	.498 (.005)	.552 (.079)	.138 (.059)	.320 (.036)

Notes: For MAMBAC and MAXEIG, values are M (SD) across curves. The bottom row presents the M (SD) of the three procedures’ estimates. MAMBAC = Mean Above Minus Below A Cut; MAXEIG = MAXimum EIGenvalue; L-Mode = Latent Mode.

^aBecause estimates based on the locations of the left and right modes were very similar, the mean of these two estimates was used.

^bBecause the location of the right mode was ambiguous (there was no local maximum), the estimate based on the location of the left mode was used.

Results for the four empirical data sets and corresponding comparison data are presented graphically in Figures 1 through 4. Each figure contains a panel of MAMBAC, MAXEIG, and L-Mode curves. Within each two-curve panel, the results for the empirical data (dark curve) are superimposed over the results for categorical (left graph) and dimensional (right graph) comparison data (plotted as bands of values bounded by ±1 SD from the M at each data point). All CCFI values appear in Table 3.

Table 3.

Comparison Curve Fit Index (CCFI) Values for Taxometric Analyses

	Data Set
	Idealized Categorical	Idealized Dimensional	Representative Categorical	Representative Dimensional
MAMBAC	.947	.079	.733	.459
MAXEIG	.958	.076	.757	.353
L-Mode	.964	.103	.771	.377
Mean	.956	.086	.754	.396

Notes: MAMBAC = Mean Above Minus Below A Cut; MAXEIG = MAXimum EIGenvalue; L-Mode = Latent Mode.

MAMBAC

The MAMBAC procedure (Mean Above Minus Below A Cut; Meehl & Yonce, 1994) requires only two indicators: one (the “input” indicator) is used to sort cases along a score distribution, and the other (the “output” indicator) is used to calculate mean differences for cases falling above and below a moving cutting score on this score distribution. This mean difference is plotted along the y axis of a MAMBAC graph, with case numbers plotted as the x axis. The first cutting score is located near the lowest-scoring case on the input indicator. Cutting scores are then advanced some number of cases until the final cutting score is reached; this will be located near the highest-scoring case. This yields a MAMBAC curve that shows how the mean difference for cases above and below the cut varies with the location of the cutting score. For prototypical categorical data, the MAMBAC curve is expected to be convex, with a maximum value near the cutting score that best distinguishes taxon and complement members. The location of the peak suggests the relative sizes of the taxon and complement; the further toward the right, the smaller the taxon (see Meehl & Yonce, 1994, for the algorithm used to estimate the taxon base rate from a MAMBAC curve). For prototypical dimensional data, the MAMBAC curve is expected to be concave, often described as “dish-shaped” in the taxometric literature.

Illustration

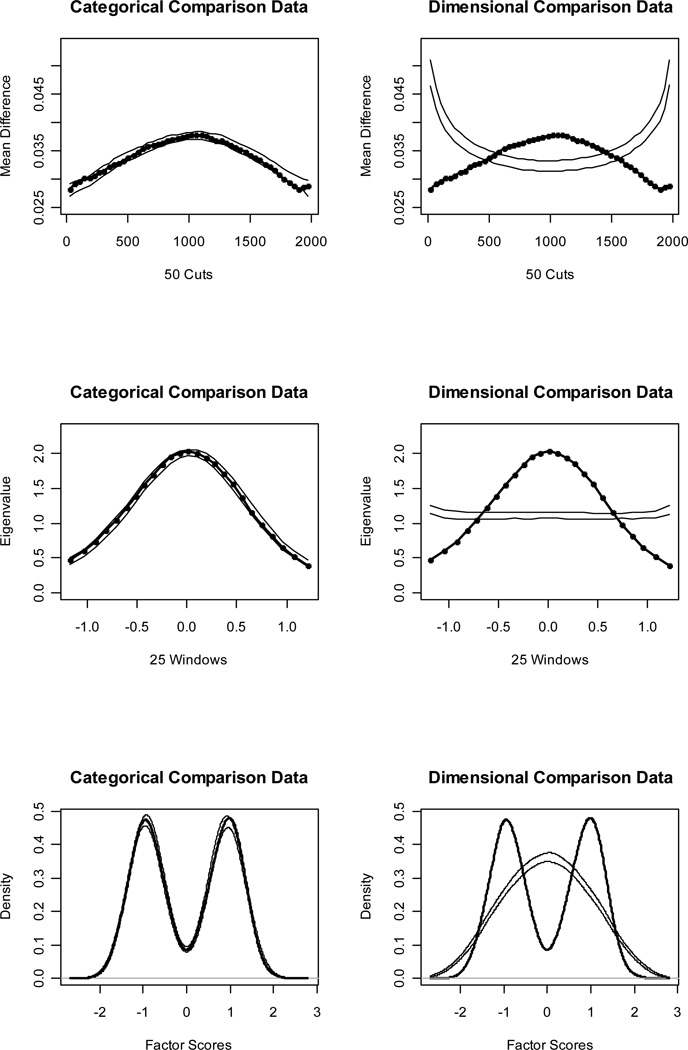
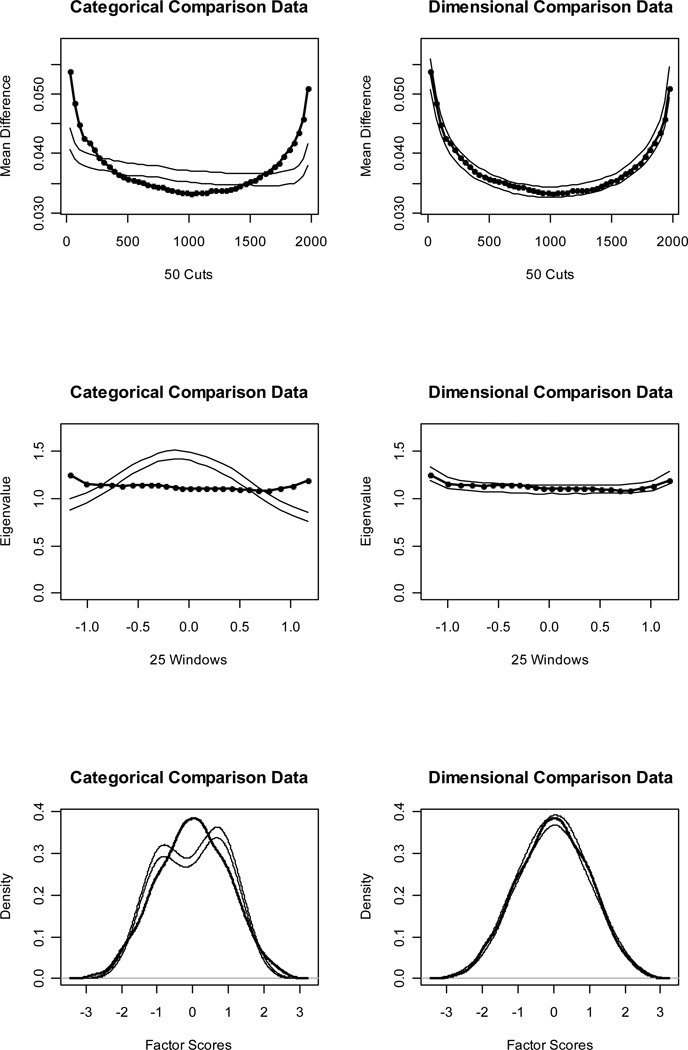
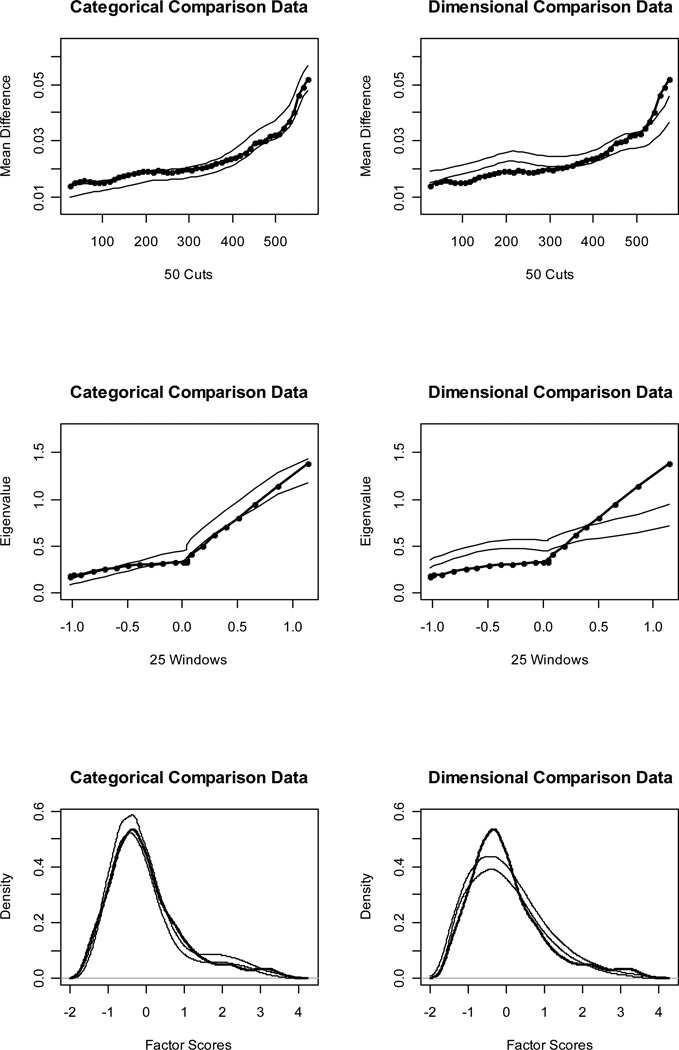
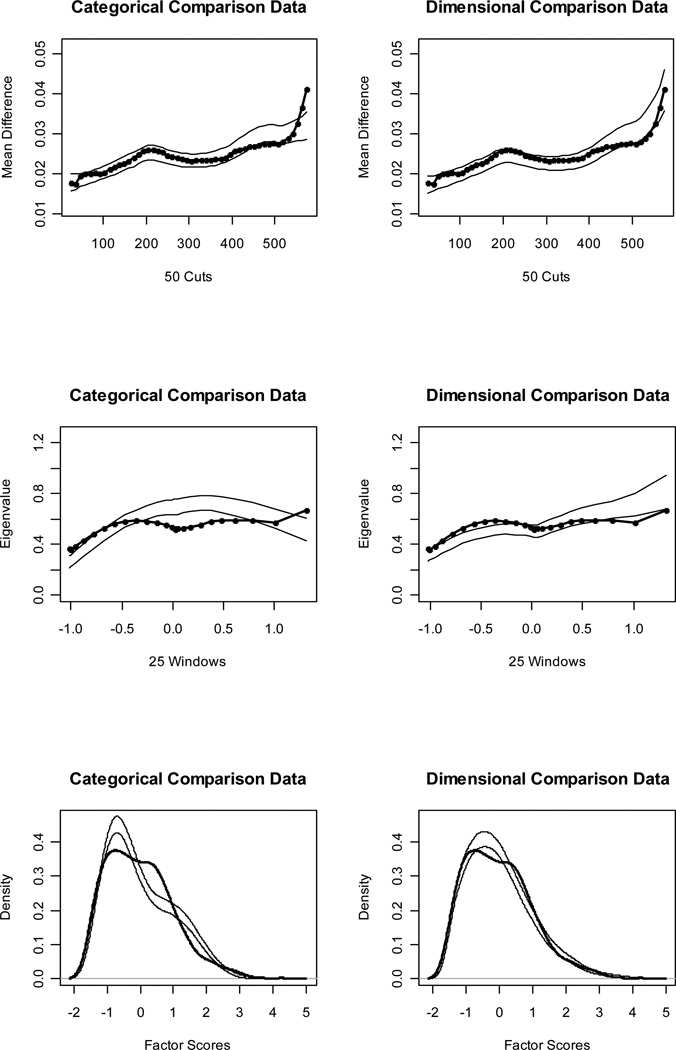
Figures 1 and 2 (top panels) show MAMBAC curves for our idealized categorical and dimensional data sets, respectively. Without even referring to the CCFI values, it is obvious that the IC curve perfectly matches the prototypical expectation for categorical data and the ID curve perfectly matches the prototypical expectation for dimensional data. The CCFI value of .947 provides extremely strong support for the superior fit of a categorical model for the IC data set, whereas the CCFI of .047 provides comparably strong support for the superior fit of a dimensional model for the ID data set. Figures 3 and 4 (top panels) show the MAMBAC curves for our representative data sets. Each curve rises toward a cusp at the right end, an interpretationally ambiguous shape. Notably, neither curve looks much like the prototypical MAMBAC results. It consequently is hard to tell whether these curves should be considered concave (indicative of dimensional structure) or whether the right-end cusp should be considered a peak in the curve (indicative of a very small taxon). The reason that the RC and RD data sets exhibit this pattern is that the indicators are positively skewed; all skewness values are approximately 1.00. Ruscio et al. (2004) demonstrated that positively skewed indicators tend to yield rising, ambiguously shaped MAMBAC curves of the sort shown here. Parallel analyses of comparison data help to resolve this ambiguity. For RC, it is clear that the empirical results resemble those for the categorical comparison data more closely than those for the dimensional comparison data; the CCFI value of .733 provides objective support for this interpretation. For RD, the results are less clear, but there is a closer visual match to the dimensional comparison data; the CCFI value of .459 favors a dimensional interpretation, but is close to the ambiguous value of .50 and should be interpreted with caution. In practice, we recommend drawing final conclusions based on the results from all procedures rather than relying solely on individual CCFI values. As we’ll see, the full array of CCFI values does provide consistent support for the dimensional structure of RD.

Figure 1.

Results for MAMBAC (top), MAXEIG (middle), and L-Mode (bottom) analyses of the idealized categorical (IC) data set. Dark lines show the results for the IC data set, and lighter lines show the results for parallel analyses of comparison data; the lines contain a band that spans ±1 SD from the M at each data point on the curve.

Figure 2.

Results for MAMBAC (top), MAXEIG (middle), and L-Mode (bottom) analyses of the idealized dimensional (ID) data set. Dark lines show the results for the ID data set, and lighter lines show the results for parallel analyses of comparison data; the lines contain a band that spans ±1 SD from the M at each data point on the curve.

Figure 3.

Results for MAMBAC (top), MAXEIG (middle), and L-Mode bottom) analyses of the representative categorical (RC) data set. Dark lines show the results for the RC data set, and lighter lines show the results for parallel analyses of comparison data; the lines contain a band that spans ±1 SD from the M at each data point on the curve.

Figure 4.

Results for MAMBAC (top), MAXEIG (middle), and L-Mode (bottom) analyses of the representative dimensional (RD) data set. Dark lines show the results for the RD data set, and lighter lines show the results for parallel analyses of comparison data; the lines contain a band that spans ±1 SD from the M at each data point on the curve.

Implementation

When performing MAMBAC, there are many decisions to be made about how to implement the procedure. Our analyses illustrate the choices we can recommend based on existing methodological research. First, we performed analyses using all pairwise configurations of indicators, with each indicator, in turn, serving as the input indicator while each other indicator served as output indicator. This yields k(k — 1) MAMBAC curves, which we averaged for presentation and calculation of the CCFI. Walters and Ruscio (2009) compared this pairwise strategy to the use of summed input indicators, wherein each indicator serves once as the output indicator and the sum of the remaining k — 1 indicators serves as the input indicator, yielding k MAMBAC curves. Results showed essentially equivalent accuracy across these two strategies. The pairwise strategy has the advantage of providing more opportunities to determine whether particular indicators, or combinations of indicators, yield especially clear or ambiguous results; this might be helpful for refining a set of indicators to provide a more informative analysis. When performing the analyses that will ultimately be reported and interpreted, there seems to be no empirical reason to prefer either technique.

A second decision concerns how to locate cuts along the input indicator. Walters and Ruscio (in press) compared five ways to do this, varying the number or proportion of cases beyond the two most extreme cuts while holding the total number of cuts along the input indicator constant at 50 (this is the norm, though it has not been empirically tested against smaller or larger values). Results showed that it made fairly little difference how cuts were located, with slightly greater accuracy when leaving a small, fixed number of cases beyond the extreme cuts; this finding was not qualified by an interaction with the size of the taxon in categorical data sets. We located the first and last cuts 25 cases from each end, and we used a total of 50 cuts.

Third, if there are tied scores on the indicators, we strongly recommend performing internal replications to counteract the effect of locating cuts arbitrarily between cases with tied scores. By internal replications, we refer to a procedure by which scores on the input indicator are randomly re-sorted to shuffle the order of cases with tied scores, and the analysis is re-run. After the full series of internal replications, the mean differences at each cut are averaged across the replications to produce the final results. Using a sufficient number of internal replications cancels out the obfuscating effects of locating cuts between cases with tied scores, where it is completely arbitrary which cases fall on either side of the cut. Indicators in the RC and RD data sets vary across only 5 ordered categories, and indicators in the IC and ID data sets vary across 20 ordered categories; both scenarios result in a large numbers of tied scores. Using 50 cuts may seem absurd when only 5 or 20 distinct values occur on the input indicator, as most of the cuts will be located between cases with tied scores. It turns out that this not only poses no problem, but actually yields smoother, more interpretable curves than a smaller number of cuts—provided that one uses internal replications. Naturally, there are diminishing returns with the use of larger numbers of internal replications, and the benefits need to be balanced against the increase in computing time required to complete the analysis. Ruscio and Walters (in press) examined the performance of MAMBAC with 1, 5, 10, or 25 internal replications and found that there was relatively little gain beyond 10 replications. There is no harm in using more, provided time allows this luxury. In our analyses, we used 25 internal replications.

Fourth and finally, one should determine whether or not it is appropriate to present an averaged MAMBAC curve rather than the full panel of curves. Our analyses of IC and ID yielded 30 curves each, and our analyses of RC and RD yielded 12 curves each. We examined the full panels of curves and judged them sufficiently consistent in shape that a single, averaged curve could represent the full panel well. Likewise, we calculated the CCFI using only averaged curves. Research has not yet examined the potential utility of calculating CCFI values for each curve in a full panel, but we do recommend inspecting the full panel to determine whether some indicators provide less interpretable results. This can be helpful to refine a set of indicators for a more powerful analysis. Please note that we are not advocating the selection of indicators based on whether one favors the results they provide. Rather, we are suggesting that if some indicators consistently yield ambiguous results, it may be reasonable to reconsider their use, perhaps combining them with other indicators or removing them from analysis.

MAXCOV

The MAXCOV procedure (MAXimum COVariance; Meehl & Yonce, 1996) requires three indicators, one serving as the input indicator along which cases are sorted, the other two serving as output indicators whose covariance is calculated within ordered subsamples of cases. Each covariance is plotted along the y axis of a MAXCOV graph above the mean score for that subsample on the input indicator, located on the x axis. This yields a MAXCOV curve that shows how the association (covariance) between two indicators varies across subsamples of cases scoring at low, intermediate, and high levels on the input indicator. For prototypical categorical data, the curve is expected to be peaked, with a maximum value occurring within the subsample that contains the most equal mixture of taxon and complement members. In lower-scoring subsamples that contain mostly complement members, the covariances should be lower because of the small within-group correlations among indicators. The same is true in higher-scoring subsamples. It is only when subsamples contain a mixture of groups that covariances should increase, as the combination of complement members with low scores on both output indicators and taxon members with high scores on both output indicators creates a positive association between these indicators. As with MAMBAC, the location of a peak suggests the relative sizes of the taxon and complement; the further toward the right, the smaller the taxon (see Meehl & Yonce, 1996, for the algorithm used to estimate the taxon base rate from a MAXCOV curve). For prototypical dimensional data, the MAXCOV curve is expected to be flat, exhibiting a fairly constant positive covariance due to shared loadings on one or more latent dimensions. When there are more than three indicators, analyzing them in triplets yields k(k — 1)(k — 2)/2 MAXCOV curves.

MAXEIG

Waller and Meehl (1998) introduced the MAXEIG procedure (MAXimum EIGenvalue) as a multivariate generalization of MAXCOV. Rather than calculating the covariance between two output indicators as in MAXCOV, one calculates the first (largest) eigenvalue of the covariance matrix (the usual variance-covariance matrix, with variances replaced on the diagonal by 0s to leave only covariances) for two or more output indicators. This allows all available indicators to be included in each analysis. Using each indicator once as input indicator (with the remaining k — 1 indicators serving as output indicators for that analysis) yields k MAXEIG curves. The interpretation of MAXEIG curves is the same as for MAXCOV, as is the algorithm for estimating the taxon base rate (see Ruscio et al., 2006, for details on how the MAXCOV technique was adapted for MAXEIG).

MAXSLOPE

Grove and Meehl (1993) introduced the MAXSLOPE procedure (MAXimum SLOPE) as a simplified version of MAXCOV that requires only two indicators. A scatterplot is constructed between the two variables, and from this a nonlinear regression is calculated using a technique such as Cleveland’s (1979) LOWESS (LOcally WEighted Scatterplot Smoother) procedure. For prototypical categorical data, the LOWESS curve is expected to follow an S-shaped trajectory, with fairly flat slopes among low-scoring cases (mostly complement members, among whom the indicators do not exhibit strong correlations) and high-scoring cases (mostly taxon members, among whom the indicators also do not exhibit strong correlations), but steeper slopes among intermediate-scoring cases including a mixture of group members. For prototypical dimensional data, the LOWESS curve is expected to be straight, with a fairly consistent positive slope.

Rather than displaying the scatterplot itself, Ruscio and Walters (in press) suggested changing the y axis from indicator scores to the slope of the LOWESS curve. Changing a MAXSLOPE graph from a scatterplot to a plot of slopes by indicator scores offers three significant benefits. First, the graph takes on an appearance similar to those for MAXCOV or MAXEIG, which renders the results easier to interpret for those more familiar with these procedures. Second, results for the full panel of k(k — 1) MAXSLOPE analyses can be averaged for presentation in a single graph. Third, results for parallel analyses of comparison data can be presented in the usual manner and a CCFI value can be calculated.

Selecting a Procedure

Because the MAXCOV, MAXEIG, and MAXSLOPE procedures are so closely related, it would not be advisable to perform more than one of these to contribute results for consistency testing. Any apparent consistency could too easily be spurious, owing more to the conceptual and mathematical similarities of the procedures than to anything else. While engaged in the iterative process of refining an indicator set for analysis, it might be helpful to use MAXSLOPE to examine the influence of particular indicators within paired combinations, or MAXCOV to examine the results within triplets. However, we recommend choosing just one of these procedures for the final series of analyses that will be reported and interpreted. MAXSLOPE is the only choice when just two indicators are available. MAXCOV and MAXEIG give virtually identical results with k = 3 indicators; the only difference in this instance is that the eigenvalues are the absolute value of the covariances and so cannot be negative.Ruscio et al. (2010) found that MAXCOV and MAXEIG produced nearly identical results even with k > 3 indicators; across the 100,000 data sets in that study, CCFI values for MAXCOV and MAXEIG were correlated at r > .999 and their difference scores were close to 0 (M = .000, SD = .006). Some researchers seem to prefer MAXCOV and others MAXEIG, but we are aware of no empirically supported reason to prefer either.

Illustration

Figures 1 and 2 (middle panels) show MAXEIG curves for our idealized data sets. Once again, the IC curve perfectly matches the prototypical expectation for categorical data and the ID curve perfectly matches the prototypical expectation for dimensional data. The CCFI values of .958 and .076 provide extremely strong support for the better fit of categorical and dimensional models, respectively, for these data sets. Figures 3 and 4 (middle panels) show the MAXEIG curves for our representative data sets. As was the case for MAMBAC, each of these rises toward a cusp at the right end, albeit in a somewhat choppy manner due to the small number of ordered categories. By the standards of prototypical MAXEIG curve shapes, these would be considered suggestive of a very small taxon. Again, however, the RC and RD data sets exhibit this pattern because the indicators are positively skewed (Ruscio et al., 2004), and parallel analyses of comparison data resolve the ambiguity. For RC, the empirical results more closely resemble those for the categorical than the dimensional comparison data; the CCFI value of .757 provides objective support for this interpretation. For RD, the results are clearer than they were for MAMBAC. There is a closer match to the dimensional comparison data and the CCFI value of .353 supports this.

Implementation

Performing MAXSLOPE is straightforward. Provided that one is comfortable with the scatterplot smoothing technique that a MAXSLOPE program uses (e.g., the LOWESS method), there is nothing to decide except whether or not to average curves. The issues involved are the same as for MAMBAC in that regard.

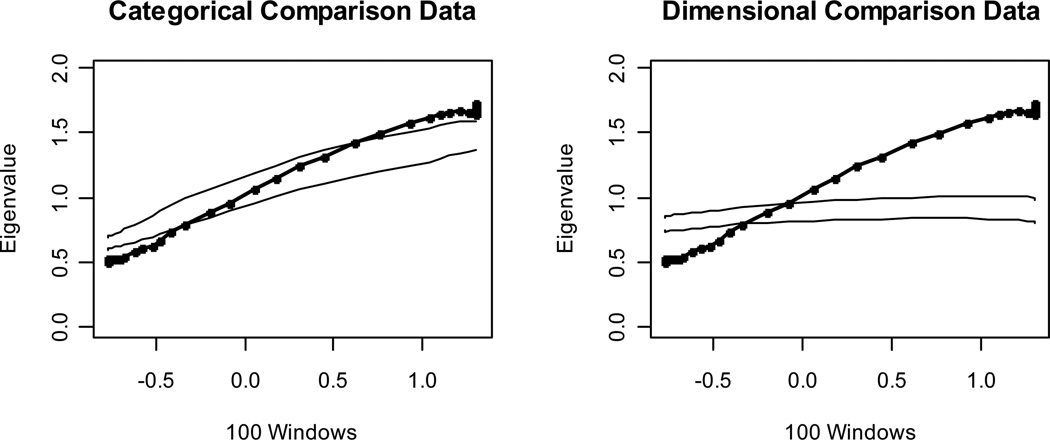
When performing MAXCOV or MAXEIG, though, there are important decisions to be made about how to implement the procedure. Again, our analyses illustrate choices that we can recommend based on ethodological research. First, we formed ordered subsamples along the input indicator using overlapping windows rather than nonoverlapping intervals. Prior to Waller and Meehl’s (1998) introduction of windows, the use of intervals was standard practice. For example, the 2,000 cases in our idealized data sets could have been divided into 10 deciles. This would have yielded 10 data points on our MAXEIG curves, each subject to sampling error based on n = 200 cases. Instead, we used 25 windows that overlapped 90% with one another. This yielded 25 data points, each subject to sampling error based on n = 588 cases (see Waller & Meehl, 1998, for how to calculate n per window). For any given subsample size n, one could use a much larger number of windows than intervals, which helps to flesh out the shape of a MAXCOV or MAXEIG curve. Walters and Ruscio (in press) compared 12 different ways to form ordered subsamples for MAXCOV or MAXEIG analyses. They varied three factors: windows vs. intervals, fixed number of subsamples vs. fixed subsample n, and the number/size of subsamples. Results supported the use of 25 windows. This was superior to using intervals, using a fixed subsample n, or using larger numbers of windows; these findings were not qualified by any interactions with the size of the taxon in categorical data sets.

Second, under certain circumstances one might wish to increase the number of windows to perform what is called the inchworm consistency test (Waller & Meehl, 1998). This was originally introduced as a way to determine whether a cusp at the upper end of a curve represents a small taxon or is merely the result of sampling error. With few windows, there may be so many cases in each that even in the uppermost windows complement members still outnumber taxon members. Hence, the MAXCOV or MAXEIG curve merely rises toward a cusp and does not fall again to fully define a peak. Increasing the number of windows decreases the number of cases in each, which would eventually allow taxon members to outnumber complement members in the uppermost windows. Once this happens, a peak (rather than a cusp) should emerge. Of course, reducing the subsample size increases sampling error, and this may obscure rather than clarify the curve shape.Ruscio et al. (2004) recommended the inchworm consistency test as a way to determine whether a cusp at the upper end of a MAXCOV or MAXEIG curve represents a small taxon or is merely the result of positively skewed indicators of a dimensional construct. Subsequent work has found that categorical structure can be differentiated from dimensional structure even with small taxa through the parallel analyses of comparison data (Ruscio & Marcus, 2007; Ruscio et al., 2010). Another reason to increase the number of subsamples, however, is to improve the accuracy of taxon base rate estimates. A well-defined peak may lead to more accurate estimates than a cusped curve, which is more ambiguous with regard to the location of a region in which groups are mixed in equal numbers.

Third, as with MAMBAC, we highly recommend using internal replications (at least 10) when there are tied scores on the indicators. Boundaries that are used to form windows might leave cases with tied scores in different subsamples, and internal replications will reduce the obfuscating effects of arbitrary ordering of such cases.

Fourth, there is a long-standing practice of creating summed input indicators when each varies along a small number of ordered categories. For example, two dichotomous indicators can serve as output indicators, and the remaining k — 1 indicators can be summed to serve as the input indicator for that analysis (Gangestad & Snyder, 1985). Walters and Ruscio (2009) tested the utility of this approach and found that it cannot be recommended. Even with indicators that span few ordered categories, allowing each to serve as an input indicator yielded superior results to summing them for analysis. We are not suggesting that one can necessarily obtain informative results for data spanning few ordered categories; rather, Walters and Ruscio’s findings suggest that under these circumstances, using summed input indicators will not help matters. This might seem surprising, but there is a parallel with MAMBAC analyses. With MAMBAC, good results can be obtained even when the number of cuts greatly exceeds the number of unique scores on the input indicator. With MAXCOV or MAXEIG, good results can be obtained even when the number of subsamples greatly exceeds the number of unique scores on the input indicator. The key in both instances is to recognize the value of forming subsamples (above and below a cut for MAMBAC, windows for MAXCOV or MAXEIG) at a series of successive case numbers. This can and does result in many cases with tied scores falling in different subsamples, but the use of internal replications handles this nicely.

For the reader who has trouble accepting this assertion, we present an extreme illustration with the hope that a picture will be worth a thousand words. Figure 5 shows the results of a MAXEIG analysis with 100 windows for a categorical data set with 8 dichotomous indicators and a taxon base rate of P = .10 in a sample of N = 600 (hence n_t = 60). Summed input indicators were not used; instead, the input indicator for each of the 8 MAXEIG curves varied across only two values, and the use of 25 internal replications helped to smooth the shape of the curves. We have seen reviewers flatly insist that the number of subsamples in a taxometric analysis cannot exceed the number of distinct values on the input indicator, else the results would be uninterpretable. This example disproves that strong claim. The CCFI value of .756 strongly supports the better fit of a categorical than a dimensional model. We hasten to add, however, that we are not recommending the analysis of dichotomous indicators. As noted earlier, Walters and Ruscio (2009) found that results were much less accurate with fewer than four ordered categories. Our point is that one need not worry about having more subsamples than input indicator scores, nor should one feel obliged—or even tempted—to form summed input indicators in a MAXCOV or MAXEIG analysis.

Figure 5.

Results for a MAXEIG analysis of a categorical data set with eight dichotomous indicators and a taxon base rate of P = .10. Dark lines show the results for the empirical data, and lighter lines show the results for parallel analyses of comparison data; the lines contain a band that spans ±1 SD from the M at each data point on the curve.

L-Mode

The L-Mode procedure (Latent Mode; Waller & Meehl, 1998) requires at least three indicators. The indicators are submitted to a factor analysis. Factor scores are estimated for the first factor using Bartlett’s (1937) weighted least squares method, and the density of their distribution is plotted. For prototypical categorical data, the distribution is expected to be bimodal and the location of each mode can be used to generate an estimate of the taxon base rate (see Waller & Meehl, 1998, for details). For prototypical dimensional data, the distribution is expected to be unimodal.

Illustration

Figures 1 and 2 (bottom panels) show such factor score density plots for our idealized data sets. The L-Mode graph for the IC data perfectly matches the prototypical expectation for categorical structure and the graph for the ID data perfectly matches the prototypical expectation for dimensional structure. The CCFI values of .964 and .103 provide extremely strong support for the better fit of categorical and dimensional models, respectively, for these data sets. Figures 3 and 4 (bottom panels) show the factor score density plots for our representative data sets. At first glance, each of these appears to be unimodal. For the RC distribution, there is some lumpiness in the right tail that one might interpret as evidence of a small taxon. However, by that standard one might be forced to judge the distribution for the RD data as bimodal, too, as the shoulders of this distribution appear to be separated by a slight dip. In our experience, L-Mode graphs based on non-idealized research data are often somewhat ambiguous.

Steinley and McDonald (2007) counted the modes in factor score density plots, with modes operationalized as local maxima, and found that this technique performed reasonably well in identifying dimensional data (i.e., counts yielded one mode) but poorly in identifying categorical data (i.e., counts yielded either too few or too many modes). Ruscio and Walters (2009) found that counting modes was not very accurate even for dimensional data when indicators were skewed, because the long right tail of a distribution was prone to exhibiting local maxima. They found that parallel analyses of comparison data were considerably more helpful than counting modes for distinguishing dimensional and categorical structure, especially using skewed indicators. In the present case, parallel analyses of comparison resolved the ambiguity well. For RC, the empirical results resemble those for the categorical comparison data more closely than those for the dimensional comparison data, and the opposite is true for RD. The CCFI values of .771 for RC and .377 for RD support these interpretations.

Implementation

L-Mode is a very straightforward procedure to perform. Unless one is considering the removal of an indicator during the iterative process of refining the indicator set, there appears to be little reason to perform L-Mode with a subset of the indicators rather than the full set. In any event, once a set of indicators is considered finalized for analysis, L-Mode should probably be performed only once using all available indicators. The advantage of performing multiple L-Mode analyses using systematically chosen subsets of the indicators would be to check the consistency of results. Because other effective means of checking consistency are available, as we describe below, we are not optimistic that multiple L-Mode graphs are worth the likely loss in power associated with submitting only a subset of indicators to each analysis.

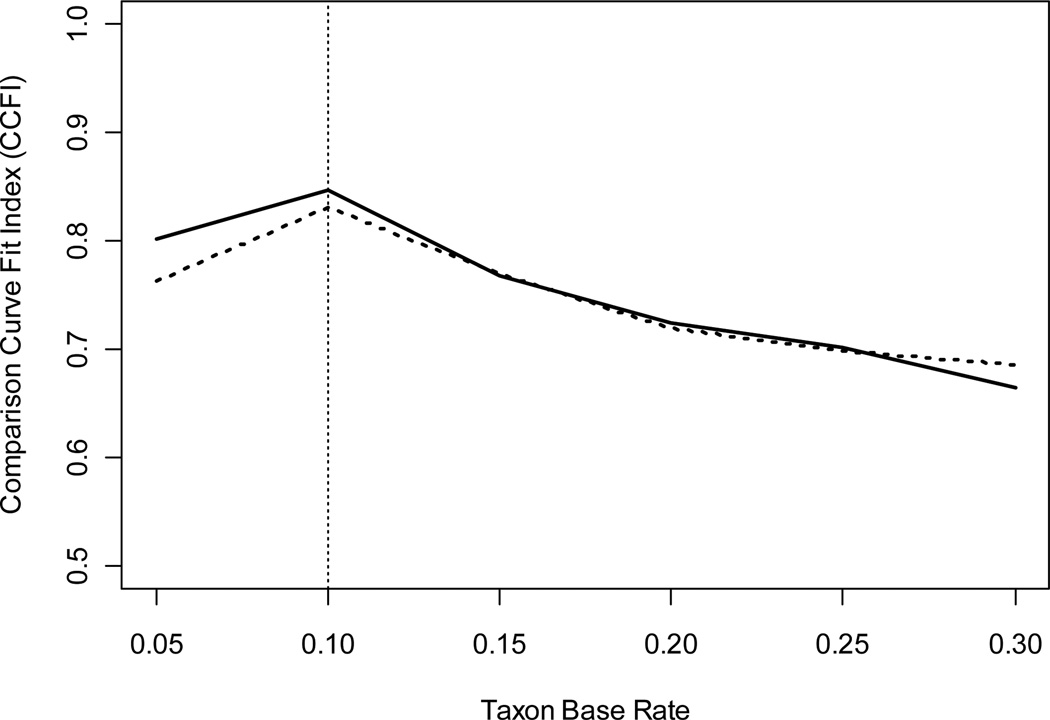
Ruscio and Walters (2009) also introduced a new technique for estimating the taxon base rate from L-Mode results. Waller and Meehl’s (1998) technique requires the location of two modes, and this is often a subjective process because two and only two local maxima may not emerge in a factor score density plot. Rather, there might be a single local maximum with one or more distinct “humps” in the downward sloping regions on either or both sides, or there might be more than two local maxima. Ruscio and Walters developed an approach that alleviates the need to locate modes. Instead, one generates multiple populations of categorical comparison data, each with a different taxon base rate, and uses each to calculate a CCFI value. The base rate used to generate the population of categorical comparison data that yielded the largest CCFI value serves as the taxon base rate estimate. Not only is this method applicable with no subjective judgment required to locate modes, it yielded greater accuracy than the original technique (Ruscio & Walters, 2009). To illustrate this approach, we performed six L-Mode analyses of RC using taxon base rate estimates of .05, .10, .15, .20, .25, and .30 to generate the populations of categorical comparison data for each (the same population of dimensional comparison data was generated for each analysis). Ruscio and Walters introduced this approach in a paper about L-Mode and tested it using that procedure, and Ruscio (2009) illustrated something very similar using MAXEIG. We suggest—though it merits rigorous testing—that this approach might work well if mean CCFI values are calculated across multiple taxometric procedures, rather than using L-Mode alone. Figure 6 plots the series of CCFI values obtained using L-Mode alone (dotted line) and the series of mean CCFI values obtained using MAMBAC, MAXEIG, and L-Mode (solid line). For each series, the maximum CCFI value emerged with a base rate of .10, which coincides with the actual taxon base rate in the RC data set.

Figure 6.

CCFI values for taxometric analyses performed using different taxon base rates. The dotted line shows results for L-Mode, the solid line shows the averaged results for MAMBAC, MAXEIG, and L-Mode. The vertical line highlights the actual taxon base rate (P = .10) for these data.

Consistency Testing

A hallmark of taxometric investigations is the examination of consistency of results across multiple data analyses.Ruscio et al. (2006) reviewed a wide range of consistency tests that have been proposed, noted that few of these had been subjected to rigorous empirical trials, and suggested that fewer still had fared well in such trials. As of that time, despite universal agreement in the taxometric literature on the importance of consistency testing, nobody had operationalized this practice. What tests should be performed? What counts as sufficiently consistent evidence to draw a conclusion? These questions had seldom been raised explicitly, let alone addressed empirically.

Until very recently, perhaps the most popular consistency test had been to compare the taxon base rate estimates derived from multiple taxometric procedures. Many procedures provide multiple estimates of the taxon base rate, typically one per curve produced by the procedure. It has long been argued that, if a taxon exists, its size should be estimated consistently within and across procedures, whereas for dimensional data, taxon base rate estimates should be dispersed more widely because there is no constant entity whose size is being estimated (Meehl, 1995). This reasoning seemed highly plausible, and we ourselves repeated the assertion in many places.

Based on rigorous study (e.g., Ruscio, 2007; Ruscio et al., 2006), however, we can no longer recommend the examination of taxon base rates as a taxometric consistency test. Under some data conditions categorical data yield a smaller SD of base rate estimates than dimensional data. However, under many other data conditions this is not true. In general, there does not appear to be a useful threshold that one can apply within or across procedures such that values below this threshold accurately identify categorical data and values above this threshold accurately identify dimensional data. Even the results for our four data sets, shown in Table 2, demonstrate the danger of drawing conclusions from the consistency (or inconsistency) of taxon base rate estimates. Values in parentheses are SDs of base rate estimates. All of these are small irrespective of latent structure, and for some comparisons they are smaller for dimensional than categorical data (e.g., SD across procedures was lower for RD than RC). More to the point, large-scale simulation studies have failed to support the utility of base rate consistency testing, and we find the evidence sufficiently compelling to recommend against its use. This recommendation runs counter to common practice, as most taxometric reports (86% of the 57 published studies reviewed by Ruscio et al., 2006) have included estimates of the taxon base rate, and nearly as many (72%) included some kind of base rate consistency test. Although some editors or reviewers may continue to expect this test, we advocate making a data-based argument against the practice.

So what do we recommend with regard to consistency testing? To our knowledge, the first rigorous evaluation of an operationalized method for consistency testing was presented byRuscio et al. (2010). They recommended performing multiple taxometric procedures, averaging the CCFI values, and using dual thresholds at .45 and .55 to draw conclusions. In other words, a mean CCFI less than .45 constitutes support for dimensional structure, a mean CCFI greater than .55 constitutes support for categorical structure, and a mean CCFI between .45 and .55 constitutes an ambiguous result from which no conclusions should be drawn. For those who wish to exercise greater caution against mistaken conclusions, Ruscio et al. recommended spreading the dual thresholds to .40 and .60 or using a non-compensatory technique (e.g., each procedure’s CCFI value must be outside the ambiguous range and in the same direction—all CCFIs < .45 [or .40] or all CCFIs > .55 [or .60]). Rates of accurate, ambiguous, and inaccurate results also varied depending on which taxometric procedure(s) were performed (see Ruscio et al. for details). Selecting a criterion for consistency involves a trade-off between accuracy and the likelihood of obtaining ambiguous results; if one is more willing to tolerate the risk of ambiguous results, the accuracy rate for results that are not ambiguous increases. It is too soon to tell whether this approach to consistency testing or these interpretive standards will prove to be most useful, but at present no alternatives have been operationalized and tested. We encourage researchers to operationalize and test alternative approaches to consistency testing; the 100,000 samples in which Ruscio et al. tested their approach can be recreated to compare the effectiveness of others. For now, we tentatively endorse the guidelines outlined by Ruscio et al. as the only empirically-supported way to demonstrate consistency of results.

Table 3 shows the mean CCFI values across the MAMBAC, MAXEIG, and L-Mode analyses for each of our four data sets. In each case, this mean value is not only outside the narrow dual thresholds of .45 to .55, but also outside the broad dual thresholds of .40 to .60. This suggests that, on the basis of these analyses, one could have considerable confidence that a categorical model is a better fit for IC (mean CCFI = .956) and RC (mean CCFI = .754), whereas a dimensional model is a better fit for ID (mean CCFI = .086) and RD (mean CCFI = .396).Ruscio et al. (2010) showed that CCFI values in these ranges leave remarkably little room for incremental improvements in accuracy; consequently, the present findings suggest little or no reason to seek additional checks of the consistency of results. While we wholeheartedly support the enterprise of consistency testing, we believe that its application is best limited to data-analytic techniques whose incremental validity—specifically, the contribution of valid information over and above what other results provide—has been demonstrated empirically.

Concluding Remarks on Getting Started

We hope that this review of data requirements and implementation decisions provides something fresh and valuable for those already familiar with Meehl’s taxometric method. For those new to the method, though, we would like to close with some advice on how to get started running your own taxometric analyses. Programs that can be used to perform all of the taxometric procedures described and illustrated in this paper, as well as some additional programs that can be helpful for related functions, are available for free at http://www.tcnj.edu/~ruscio/taxometrics.html. A comprehensive user’s manual is available at the same location; this describes the nuts and bolts of running the programs and illustrates them with sample commands and output. Interested readers will find detailed discussions of the many options available for implementing each program, including those discussed in this paper as well as more minor issues not considered here. The user’s manual also contains a brief introduction to the R computing environment in which the taxometric programs run; the R software is available for free at http://www.R-project.org.

The user’s manual contains numerous sample commands that one can run to become familiar with R and the taxometric programs. A good next step would be to modify the commands to get a feel for the options that are available for each procedure and the effect they can have on the results. One of the included programs allows users to create their own categorical or dimensional data sets, with easy control over many important data characteristics (e.g., sample size, number of indicators, indicator skew, number of ordered categories, and, for categorical data, the taxon base rate, indicator validity, and within-group correlations). Creating and analyzing artificial data sets is a useful way to experience firsthand how various data conditions and procedural implementations affect taxometric results, and serves as a bridge from reading the results of other people’s analyses to performing one’s own. The subsequent step of carrying out an independent taxometric investigation will be feasible for those who are willing to navigate through what may be an unfamiliar computing environment and who exhibit a healthy curiosity regarding an unfamiliar statistical methodology. Anyone who has grappled with the theoretical, methodological, and statistical challenges involved in doing good psychopathology research should be capable of becoming adept at taxometric analysis.