Experimental and computational analysis of the transition state for ribonuclease A-catalyzed RNA 2′-O-transphosphorylation

Abstract

Enzymes function by stabilizing reaction transition states; therefore, comparison of the transition states of enzymatic and nonenzymatic model reactions can provide insight into biological catalysis. Catalysis of RNA 2′-O-transphosphorylation by ribonuclease A is proposed to involve electrostatic stabilization and acid/base catalysis, although the structure of the rate-limiting transition state is uncertain. Here, we describe coordinated kinetic isotope effect (KIE) analyses, molecular dynamics simulations, and quantum mechanical calculations to model the transition state and mechanism of RNase A. Comparison of the ¹⁸O KIEs on the 2′O nucleophile, 5′O leaving group, and nonbridging phosphoryl oxygens for RNase A to values observed for hydronium- or hydroxide-catalyzed reactions indicate a late anionic transition state. Molecular dynamics simulations using an anionic phosphorane transition state mimic suggest that H-bonding by protonated His12 and Lys41 stabilizes the transition state by neutralizing the negative charge on the nonbridging phosphoryl oxygens. Quantum mechanical calculations consistent with the experimental KIEs indicate that expulsion of the 5′O remains an integral feature of the rate-limiting step both on and off the enzyme. Electrostatic interactions with positively charged amino acid site chains (His12/Lys41), together with proton transfer from His119, render departure of the 5′O less advanced compared with the solution reaction and stabilize charge buildup in the transition state. The ability to obtain a chemically detailed description of 2′-O-transphosphorylation transition states provides an opportunity to advance our understanding of biological catalysis significantly by determining how the catalytic modes and active site environments of phosphoryl transferases influence transition state structure.

Enzymes achieve powerful rate enhancements by providing multiple catalytic modes to stabilize reaction transition states, including electrostatic interactions and proton transfer (1). For RNA 2′-O-transphosphorylation reactions, interactions with acid, base, or metal ion catalysts in solution can influence transition state structure (2). Understanding biological catalysis therefore requires knowledge of chemical mechanisms, transition state structure, and transition state interactions for both enzymatic and nonenzymatic RNA cleavage reactions. Comparisons of enzymatic and nonenzymatic catalysis can provide information on which catalytic modes are used by enzymes and whether unique features of the active site environment may alter the transition state charge distribution (3).

RNA undergoes two competing transesterification reactions in solution: isomerization to a 2′,5′-phosphodiester and 2′-O-transphosphorylation to yield a cyclic 2′,3′-phosphodiester with concomitant release of the 5′O-nucleoside (4, 5). Reactions catalyzed by acid and by buffers yield both isomerization and cleavage products and proceed via a pentacoordinated phosphorane intermediate formed by an attack of the 2′OH at the adjacent phosphorus. The phosphorane intermediate may be neutral (I_neutral) (Fig. S1A) or monoanionic (I_monoanion) (Fig. S1B). It is not known whether 2′OH deprotonation occurs in a preequilibrium step or if its proton is transferred to water or one of the nonbridging phosphoryl oxygens (NPOs) during nucleophilic attack. Hydroxide catalysis proceeds by equilibrium deprotonation of the 2′OH, followed by nucleophilic attack (Fig. S1C), and only cleavage products are formed (5, 6). Linear free energy relationships (LFERs), stereochemical outcomes, kinetic isotope effects (KIEs), and computational simulations are consistent with either an overall concerted mechanism or transient formation of a dianionic phosphorane intermediate (>pH 9) (4, 5). This complex mechanistic landscape raises the question of which pathway(s) are favored by the active sites of ribonucleases.

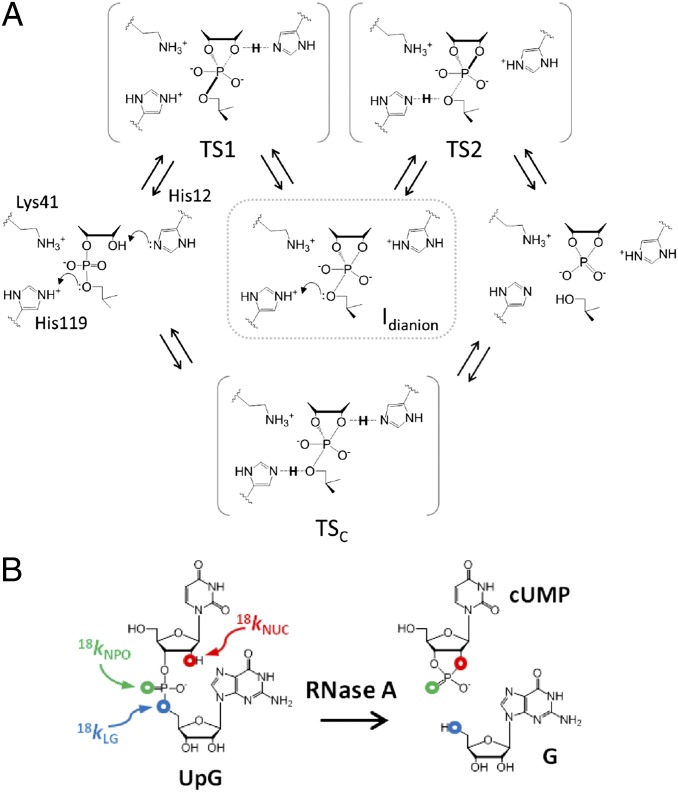
RNase A catalyzes RNA 2′-O-transphosphorylation, and investigation of its structure and function have provided foundational insights into the function of enzyme active site residues in acid/base catalytic modes (7). Although the mechanism is usually depicted as concerted, computational studies suggest the potential for a stepwise mechanism via an anionic phosphorane intermediate (8) (Fig. 1A, top pathway). Molecular dynamics (MD) simulations indicate that the RNase A active site provides electrostatic stabilization of the dianionic phosphorane while positioning His119 to act as a general acid (9). His12 and Lys41 are proposed to interact with the 2′OH and/or one of the NPOs, possibly stabilizing the transition state for nucleophilic attack (TS1) or anionic intermediates via H-bonding or proton transfer to form I_neutral or I_monoanion. However, lack of a strong thio effect renders the latter mode unlikely (10). Several lines of evidence implicate His119 as a general acid to facilitate departure of the 5′O in a stepwise or concerted mechanism [via a product-like transition state (TS2) or a concerted transition state (TS_c)]. Mutation of His119 has a large deleterious effect on catalysis of RNA cleavage but only a small effect on the reaction of a uridine-3′-p-nitrophenol phosphate model substrate, consistent with a role in leaving group stabilization (7). However, the more highly reactive p-nitrophenol leaving group may result in a change in mechanism compared with the less reactive ribose 5′O, making it difficult to interpret these results without an understanding of the mechanism and rate-limiting transition state. Substitution of His12 and His119 with 4-fluorohistidine (pK_a = 3.5) changes the apparent macroscopic pK_a values determined from analysis of the pH dependence of k_cat/K_m with their proposed roles in acid/base catalysis (11). However, effects of 4-fluorohistidine substitution on catalysis are only ca. 10-fold, suggesting a relatively small Brønsted effect, or that a nonchemical step is partially rate-limiting. Thus, even for this well-studied enzyme, significant ambiguity remains regarding the interactions with the transition state that provide catalysis.

Fig. 1.

(A) Proposed active site interactions and potential transition states for RNase A. A concerted mechanism with simultaneous nucleophilic attack, leaving group departure, and concomitant proton transfer involving both His12 and His119 is shown in the lowest pathway. The most likely stepwise mechanism involves nucleophilic attack (via TS1) and leaving group departure (via TS2) separated by a dianionic intermediate that may be only short-lived. (B) RNA dinucleotide substrate (UpG) reacts via 2′-O-transesterification to yield 2′,3′-cyclic uridine monophosphate (cUMP) and guanosine (G) products. Sites of isotopic substitution used to measure the KIEs for the ¹⁸k_NUC, ¹⁸k_NPO, and 5′O ¹⁸k_LG are indicated in red, green, and blue, respectively.

A powerful method to gain insight into mechanism and transition state structure is to determine the KIEs on substrate atoms and to use the results as benchmarks for evaluating computational simulations (12, 13). The effects of stable heavy atom isotope substitution on reaction rate constants arise mainly due to differences in vibrational zero point energies, and their magnitudes provide information on the differences in bonding between the ground state and transition state (14, 15). Leaving group and NPO KIEs for RNase A cleavage of uridine-m-nitrobenzyl phosphate were previously reported by Cleland and colleagues (16). However, this study lacked information on nucleophile bonding and involved a model substrate that lacks binding interactions present in authentic RNA substrates.

Here, KIE measurements on enzyme and solution RNA reactions are coordinated with MD simulations and quantum mechanical (QM) calculations to achieve a detailed model of the transition state for enzymatic RNA cleavage. Together, the results reveal a transition state with advanced 2′O-P bond formation and 5′O-P bond cleavage similar to the late anionic transition state for solution reactions catalyzed by a specific base. MD simulations are consistent with protonated His12 and Lys41 stabilizing an anionic, phosphorane-like transition state by H-bonding to the phosphoryl oxygens, whereas protonated His119 is poised to transfer a proton to the 5′O leaving group. Importantly, the KIEs for the RNase A reaction reveal a significant difference in 5′O bonding compared with solution reactions. Supported by QM calculations, we ascribe this difference to less advanced P-O bond cleavage and proton transfer (general acid catalysis) from His119.

Results and Discussion

Measurement of ¹⁸O KIEs on RNA 2′-O-Transphosphorylation Reactions.

KIEs are typically measured by competitive methods (12) in which mixtures of substrates containing either ¹⁶O or ¹⁸O at one of the reactive phosphoryl oxygens are analyzed (Fig. 1B). The larger rate constant for either the ¹⁸O- or ¹⁶O-containing RNA results in progressive depletion of that isotopologue in the unreacted substrate population. Quantitative analysis of the ¹⁸O/¹⁶O ratio as a function of reaction progress allows calculation of the KIE, which is expressed as the ratio of the rate constants for the light and heavy isotopologues (¹⁸k = k₁₆/k₁₈) (12). KIEs reflect both the extent to which the labeled atom participates in the reaction coordinate and differences in vibrations of the labeled atom in the ground state compared with the transition state (14). Bond breakage, or a “looser” bonding environment in the transition state relative to the ground state results in faster reactivity for the light isotopologue, and thus an ¹⁸k that is greater than unity (referred to as a normal KIE). Conversely, bond formation or a “stiffer” bonding environment favors the heavier isotopologue, and the observed KIE is less than unity (referred to as an inverse KIE). The fractionation of ¹⁸O will also depend on proton transfer in both preequilibrium and chemical steps (12), and may offset the contributions of O-P bonding. Additionally, both bonding and bending vibrational modes can influence the observed KIE on the nonbridging oxygens, and these effects may also be offsetting (13). Deciphering the relative contributions of proton transfer, O-P bonding, and other vibrational modes can be difficult; however, the magnitude of observed KIEs provides insight into mechanism and transition state bonding unobtainable by any other means.

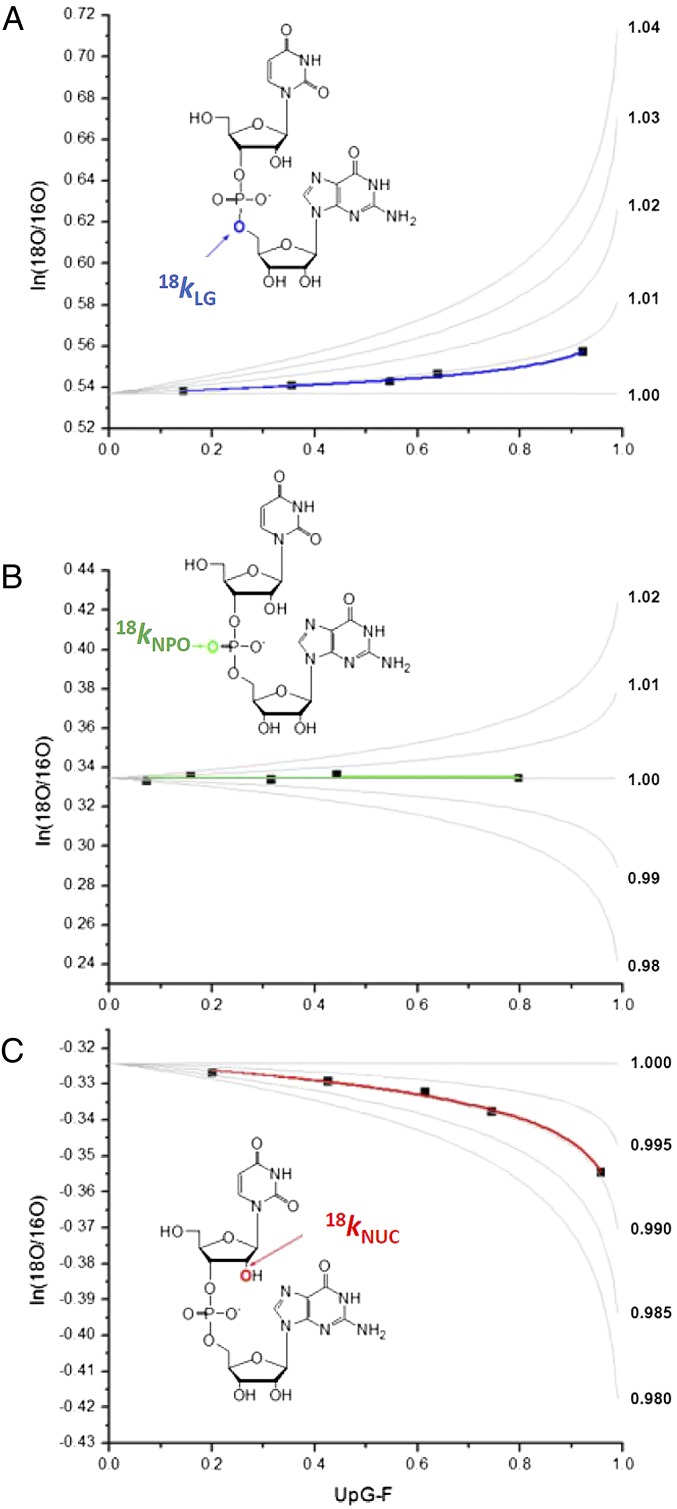
Substrate RNA dinucleotides enriched with ¹⁸O at the 2′O, 5′O, and NPO positions were synthesized (Fig. 1B) and reacted with acid and base and with RNase A. The fraction of reaction was measured by integration of RP-HPLC chromatograms in which the ¹⁸O/¹⁶O ratio was determined by MS (6) (SI Text and Fig. S2A). Two product ions contain the isotopically enriched positions: a species at m/z 476/478 resulting from loss of the uridine base and a 211/213 fragment composed of ribose phosphate (Fig. S2B). The KIE is observed as a change in the relative ratios of the product ions containing only ¹⁶O at all oxygens (M) and those containing ¹⁸O at one of the reacting phosphoryl oxygens (M + 2) (Fig. S2C). Fig. 2 shows the determination of KIEs for RNase A-catalyzed 2′-O-transphosphorylation of uridylyl-3′-guanosine [5′-UpG-3′ (UpG)] relative to simulations of ¹⁸O/¹⁶O ratio vs. F (the fraction of substrate UpG reacted to form a product) for a range of potential ¹⁸O KIEs.

Fig. 2.

Determination of KIEs for RNase A-catalyzed RNA 2′-O-transphosphorylation by analysis of the change in the ¹⁸O/¹⁶O ratio (ln¹⁸O/¹⁶O) as a function of reaction progress (F). The ¹⁸O/¹⁶O ratio determined by MS is plotted relative to reaction progress, and the data are fit as described in Methods. Example fits of data used to calculate the ¹⁸k_LG (A), ¹⁸k_NPO (B), and ¹⁸k_NUC (C) are shown. Experimental data points are shown as filled squares. Simulations for curves representing a range of potential KIEs are shown as gray lines.

Transition States of Solution Reactions Catalyzed by Acid and Base.

The nucleophile (¹⁸k_NUC), leaving group (¹⁸k_LG), and NPO (¹⁸k_NPO) KIE results presented in Table 1 for acid- and base-catalyzed 2′-O-transphosphorylation reactions of UpG, together with previous biophysical and biochemical studies, provide a framework for understanding the RNase A transition state. For solution 2′-O-transphosphorylation, previous experimental and computational data are consistent with the observed ¹⁸k_NUC being a combination of normal contributions from deprotonation and an inverse effect from advanced 2′O-P bond formation (6, 17). Together, these contributions result in the inverse values observed for the stepwise acid-catalyzed reaction (pH 0) and a similar inverse ¹⁸k_NUC for the late anionic transition state for base catalysis (pH 12) [0.990(4) and 0.996(2), respectively, with standard deviations in parentheses] (6, 18–20). These data are consistent with analyses of nucleophile bonding by LFERs of RNA reactions catalyzed by a specific base, which show that the 2′ oxyanion formed in a preequilibrium deprotonation step undergoes substantial loss of negative charge in the transition state (21).

Table 1.

Comparison of ¹⁸k_LG, ¹⁸k_NUC, and ¹⁸k_NPO KIE values for 2′-O-transphosphorylation catalyzed by acid, base, and RNase A

Catalyst	18kLG	18kNUC	18kNPO
RNase A, pH 7	1.014(3)	0.994(2)	1.001(1)
RNase A (QM)	1.026	0.998	1.006
Acid, pH 0	1.005(4)	0.990(4)	0.991(1)
Base, pH 12 (7, 8)	1.037(2)	0.996(2)	0.999(1)
Base, pH 14 (8)	1.034(4)	0.984(3)	—
Base, pH 14 (QM)	1.046	0.973	1.002

SDs for measured KIEs are shown in parentheses (Methods).

The observed ¹⁸k_NPO is an average of the KIEs on the two NPOs because only one of the two positions is enriched nonspecifically (20). Nonetheless, a late TS2 for the base-catalyzed reaction is further indicated by a near-unity ¹⁸k_NPO, which indicates a similar bonding environment in the transition state and in the ground state monoanion. In contrast, formation of a protonated phosphorane during acid catalysis is consistent with the observed inverse ¹⁸k_NPO [0.991(1)] as previously reported for acid catalysis of uridine-3′m-nitrobenzyl phosphate transphosphorylation (22).

The ¹⁸k_LG for acid catalysis is small [1.005(4)], consistent with models that propose rate-limiting phosphorane breakdown with concomitant transfer of a proton from a phosphoryl oxygen to the 5′O (22) (Fig. S1A). Base-catalyzed RNA 2′-O-transphosphorylation is sensitive to the pK_a of the leaving group, with a β_LG of −1.28 indicating that the alkoxide character of the 5′O is advanced (23), which is consistent with the observed large normal ¹⁸k_LG value [1.037(2)]. This value is near the expected maximum (ca. 1.04) for breakage of an O-P bond (13). Recent QM simulations of the base-catalyzed reaction identify a representative late transition state for breakdown of a transient dianionic phosphorane (TS2_B in Fig. S1C) that reproduces the observed inverse ¹⁸k_NUC, large normal ¹⁸k_LG, and near-unity ¹⁸k_NPO (6, 20). For a rate-limiting TS1, a normal ¹⁸k_NUC and a small normal ¹⁸k_LG are predicted (20). For a concerted mechanism a less inverse ¹⁸k_NUC, as well as a normal or inverse ¹⁸k_NPO, is observed depending on the associative or dissociative character of TS_c (2, 17, 24).

RNase A Kinetics and Substrate Binding Commitments.

KIEs measured by competitive methods are effects on k_cat/K_m; therefore, substrate binding steps may interfere with the KIE measurements for RNase A. If substrate dissociation is slow relative to chemistry, resulting in a “commitment” of the bound substrate to undergo chemical transformation, the commitment generates an attenuation of the observed KIEs relative to their intrinsic values (12). Several lines of evidence support the assertion that observed KIEs on the RNase A reaction approximate intrinsic effects on the chemical step (SI Text). Foremost, the KIEs for RNase A in Table 1 are nonzero, indicating that the chemical step is at least partially rate-limiting (6, 22). The leaving group KIE for RNase A is similar to the value measured by Cleland and colleagues (16) for the slow model substrate uridine-3′-m-nitrobenzyl phosphate. UpG is also a slow substrate with ca. 40-fold lower k_cat/K_m compared with an optimal uridylyl-3′-adenosine [5′-UpA-3′ (UpA)] dinucleotide substrate (Fig. S3). The k_cat/K_m for UpG is similar in magnitude to that for uridine 3′-p-nitrophenol phosphate substrate, which has been argued to react with a rate-limiting step subsequent to binding based on lack of sensitivity to solvent viscosity (25). The rate of UpG cleavage by RNase A under k_cat/K_m conditions is also insensitive to viscosity (Fig. S4). The pH dependence of k_cat/K_m for the reaction of the UpG (Fig. S5) is bell-shaped, as expected, and shows apparent macroscopic pK_a values (5.2 ± 0.2 and 6.3 ± 0.1) that are similar to the microscopic pK_a values of His12 and His119 determined by NMR (5.7 and 6.3) (26), which is also consistent with minimal binding commitments under conditions where KIEs were measured.

KIE Analysis of RNase A-Catalyzed RNA 2′-O-Transesterification.

The inverse ¹⁸k_NUC [0.994(2)] for RNase A suggests that 2′O-P bond formation is advanced in the rate-limiting transition state. A similar inverse ¹⁸k_NUC is observed for the stepwise mechanism for acid catalysis in which the phosphorane is sufficiently stable to undergo pseudorotation (Table 1). The base-catalyzed solution reaction also has an inverse ¹⁸k_NUC [0.996(2)], which becomes more inverse [0.984(3)] above the pK_a of the 2′OH consistent with loss of the contribution from 2′O deprotonation (6). QM simulations of the base-catalyzed reaction that are consistent with the KIE data indicate a late anionic transition state (TS2 in Fig. S1) and suggest the formation of a transient dianionic phosphorane (20, 27). Interpretation of advanced 2′O-P bonding in the RNase A transition state assumes that the measured ¹⁸k_NUC includes a large inverse contribution 2′O-P bonding that is partially offset by a normal equilibrium isotope effect (EIE) from alcohol deprotonation (28). The relative magnitudes of these contributions are difficult to assess, and combinations of less advanced 2′O-P bonding and partial proton transfer in the transition state (general base catalysis) cannot be entirely excluded.

The small ¹⁸k_NPO for the RNase A reaction indicates that the NPOs experience a similar bonding environment in both the ground state and transition state, which is also consistent with a late product-like transition state. An ¹⁸k_NPO near unity is inconsistent with protonation of an NPO. In this case, an inverse ¹⁸k_NPO would be predicted similar to that observed for acid catalysis [0.991(1)]. Together with the lack of a thio effect on RNase A (10), these results provide strong evidence against protonation. Rather, the small normal ¹⁸k_NPO we observe suggests that the NPO atoms gain anionic character in the transition state.

The normal ¹⁸k_LG for RNase A indicates breaking of the 5′O-P bond in the rate-limiting transition state similar to catalysis by a specific base in solution (6). However, the ¹⁸k_LG for the enzyme reaction is significantly less than the value observed for the solution reaction [1.014(3) vs. 1.037(2)], indicating a stiffer bonding environment for the 5′O in the enzyme active site. Alternatively, the smaller ¹⁸k_LG for RNase A could result from a small binding commitment, although available experimental evidence suggests this is unlikely (SI Text). In this case, the intrinsic ¹⁸k_NUC would be more inverse than the solution reaction, which seems unlikely because the measured value of ca. 0.994 is already characteristic of advanced 2′O-P bonding. The predicted large normal ¹⁸k_LG would indicate advanced 5′O-P bond cleavage with a minimal effect of enzyme interactions in mitigating the unfavorable accumulation of negative charge. If the effects accurately reflect intrinsic KIEs on the chemical step, the difference in ¹⁸k_LG could reflect less 5′O-P bond cleavage in the RNase A transition state. It is likely that proton transfer to the 5′O would result in a stiffer bonding environment, given the large inverse EIE in the direction of deprotonation of ca. 0.976 (28) and the proximity of His119.

MD Simulations and QM Calculations to Model the Mechanism and Transition State.

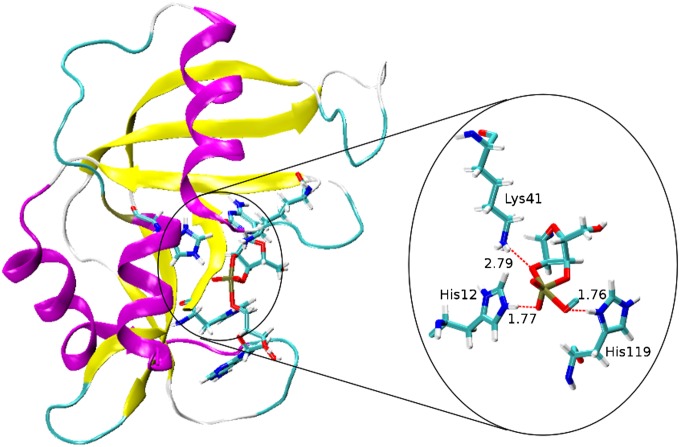
To gain further insight into the mechanistic implications of the KIE measurements, we performed MD simulations and QM calculations that build on previous work for RNase A (9) and nonenzymatic models (20, 27). Based on the KIE results supporting an anionic transition state with advanced 2′O-P bonding, we first performed MD simulations of RNase A with a dianionic phosphorane transition state mimic as described previously (9). Because transfer of the 2′ proton is considered to be complete in this model, His12 and His119 are protonated to characterize the electrostatic stabilization of the anionic transition state. The results summarized in Fig. 3 are derived from a 50-ns MD simulation and suggest that a protonated His12, formed in the general base step of a stepwise mechanism, can further provide electrostatic stabilization of an anionic phosphorane intermediate/transition state. Throughout the simulation, the imidazolium side chain of His119 forms a strong hydrogen bond with the 5′O (Fig. 3). Our findings suggest that RNase A can support a mechanism involving a transient anionic phosphorane intermediate or phosphorane-like transition state like the one implicated by theoretical and experimental studies of specific base catalysis (20, 27). Moreover, the MD results provide a basis for construction of a fully QM active site model from which transition state structures can be determined and KIEs can be estimated.

Fig. 3.

Structure of RNase A transition state mimic derived from a 50-ns MD simulation using the assisted model building with energy refinement (AMBER) FF10 force field in TIP4PEw water (1-ns average). The dianionic transition state is stabilized by interactions between His12, Lys41, and His119 and the transition state. In this model, His119 is poised for general acid catalysis, whereas His12, in its protonated form (after accepting a proton from the nucleophile), provides electrostatic stabilization to the transition state.

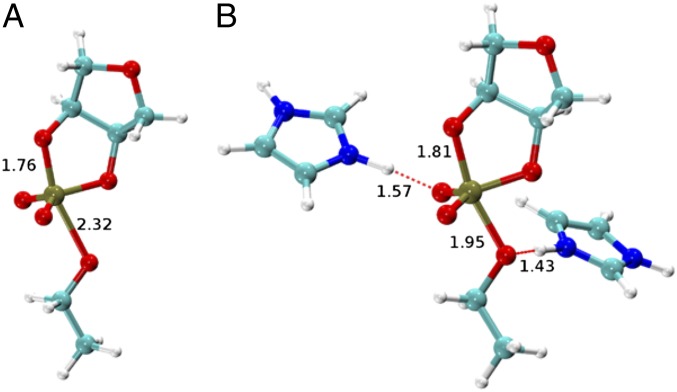
KIEs were calculated for both enzymatic and nonenzymatic reaction models using density-functional theory and a continuum model to treat solvation effects (Methods). The nonenzymatic model corresponds to alkaline conditions and assumes that the deprotonation of the 2′OH occurs in a prior step that is not rate-controlling. In the enzymatic model, the 2′OH is assumed to be protontated in the ground state; however, whether deprotonation occurs in a preequilibrium step or concomitant with nucleophilic attack is not known. The enzymatic reaction model was based on the MD simulation structures and consisted of the hypothesized dianionic phosphorane stabilized by hydrogen bonds donated from two histidine side chains (protonated imidazoles). Results for the nonenzymatic reaction model were similar to our previous results using an ethylene glycol phosphate methyl ester (20, 27) in which nucleophile bonding is advanced (1.8 Å compared with 1.7 Å for an O-P bond). Here, we included a more realistic ribose-like sugar ring and ethoxide leaving group, and obtained KIE results in better agreement with experimental data (Fig. 4 and Table 1). Comparison of the calculated KIEs for the nonenzymatic QM model with the measured values for the solution reaction catalyzed by a specific base (calculated/measured) reveal an inverse ¹⁸k_NUC (0.973/0.984), large normal ¹⁸k_LG (1.046/1.034), and near-unity ¹⁸k_NPO (1.002/0.999).

Fig. 4.

Transition state structures for the nonenzymatic dianionic transition state model for the specific base reaction (A) and for the enzymatic transition state model based on hydrogen bonding in the active site of the RNase A (B).

Alternative mechanistic models involving protonation of an NPO or the 5′O alone and 5′O protonation in the presence of H-bonding to an NPO were evaluated (Table S1 and Fig. S6). The calculated and measured KIE values are in good agreement for the enzymatic reaction model involving proton transfer from His119 to the 5′O, together with H-bonding between the active site and the NPO atoms [¹⁸k_NUC (0.998/0.994), ¹⁸k_LG (1.026/1.014), and ¹⁸k_NPO (1.006/1.001) (calculated/measured)] (Table 1). Importantly, the calculated ¹⁸k_LG for the base-catalyzed reaction simulation (1.048) is notably larger than the calculated ¹⁸k_LG for the enzymatic model (1.026), consistent with the observed experimental trend (1.034 vs. 1.017). In the simulations, the P-5′O bond length is considerably shorter for the RNase A transition state than that for the base-catalyzed reaction (1.95 Å vs. 2.3 Å) (Fig. 4) and it retains a higher degree of covalent bond character. Moreover, proton transfer from the general acid (His119) further creates a stiffer bonding environment for stabilizing the leaving group.

The results reported here are comparable to those of previous studies directed at determining the influence of active site environments on transition state structure. Herschlag and colleagues (29, 30) reported a large negative β_LG, as well as a large leaving group KIE for both alkaline phosphatase (AP) and nonenzymatic monoester hydrolysis. These results are consistent with a dissociative transition state both on and off the enzyme. However, a more inverse nonbridging oxygen KIE is observed for AP and is consistent with active site metal coordination in the transition state (29). In solution, acid-catalyzed hydrolysis of nucleoside glycosidic bonds occurs via dissociative transition states with considerable oxycarbonium ion character in the ribose ring (31, 32). Human and malarial purine nucleoside phosphorylases proceed through similarly dissociative transition states (33); however, more associative transition states are observed for NAD⁺ hydrolysis by both diphtheria toxin and human thymidine phosphorylase (34, 35). Nonenzymatic peptide bond formation occurs with equilibrium deprotonation and nucleophilic attack of a neutral amine and loss of a second proton from nitrogen on breakdown of a zwitterionic intermediate (36). Recent KIE and computational results by Hiller et al. (37) suggest that in the ribosome active site, the second deprotonation occurs concomitant with C-N bond formation. These examples illustrate that interactions with enzyme active site residues can subtly alter the transition state in a manner reflecting, in part, the nature of catalytic modes that are used.

In the present study, coordinated theory and experiment provide a chemically detailed comparison of transition state structures for RNA 2′-O-transphosphorylation in solution and in the active site of RNase A. The results reveal that both reactions can proceed via late anionic transition states with complete loss of the 2′O proton and advanced 2′O-P bonding. Nonetheless, the active site environment provides a combination of interactions (general acid and electrostatic catalysis), and thereby influences transition state structure. Electrostatic interactions with positively charged amino acid site chains (His12/Lys41), together with proton transfer from His119, render departure of the 5′O less advanced compared with the solution reaction and stabilize charge buildup in the transition state. Expulsion of the 5′O remains an integral feature of the rate-limiting step both on and off the enzyme, reflecting principles that are fundamental to RNA 2′-O-transphosphorylation reactions. In addition to mechanistic insights, the transition state structure reported here could aid inhibitor design through the construction of stable molecules that mimic its charge distribution. The ability to obtain a chemically detailed description of 2′-O-transphosphorylation transition states paves the way for a new frontier in understanding biological catalysis: defining how active site environments of phosphoryl transferases and substrate reactivity influence transition state structure.

Methods

Determination of ¹⁸O KIEs on RNA 2′-O-Transphosphorylation Reactions.

The reaction kinetics and KIEs on the ¹⁸k_NUC, ¹⁸k_LG, and ¹⁸k_NPO for UpG to form 2′,3′-cyclic uridine monophosphate and guanosine were analyzed essentially as described by Harris et al. (6) (SI Text and Fig. S2B). Briefly, KIEs were determined by analyzing the change in the ¹⁶O/¹⁸O ratio of an RNA substrate of defined sequence that has been site-specifically enriched with ¹⁸O at the 2′O, 5′O (6, 20, 38), or NPO position as a function of reaction progress. The KIE values determined in Fig. 2 and reported in Table 1 were calculated from plots of ln(¹⁸O/¹⁶O) vs. F by fitting to ln(¹⁸O/¹⁶O) = (1/¹⁸k − 1)ln(1 − F) + ln(R₀), where ¹⁸k is the isotope effect, F is the fraction of substrate consumed as determined from integration of HPLC chromatograms, and R₀ is the initial ¹⁸O/¹⁶O ratio in the unreacted substrate. Fitting errors and comparison of fits of the data to the equation, above, to simulations at different isotope effects at the same R₀ in Fig. 2 show the precision to be in the range of 0.2–0.5%.

MD Simulation and QM Calculation Methods.

Isothermal-isobaric (300 K, 1 atm) MD simulations of RNase A bound to a dinucleotide cytidylyl-3′-adenosine [5′-CpA-3′ (CpA)] having the 3′,5′-phosphodiester linkage replaced by a pentacovalent phosphorane 2′-O-transphosphorylation transition-state mimic (Fig. 3) were performed for 50 ns, starting from the X-ray crystal structure complexed with cytidilyl-3′-5′-adenosine (Protein Data Bank ID code 1RPG) (39). His12, His119, and Lys41 were in their protonated (+1) states. The assisted model building with energy refinement (AMBER) FF10 force field (40) was used to describe the RNase A protein, along with a set of specific force-field parameters to mimic the late transition state of the dinucleotide (41) and the TIP4PEw model for water (42). The software not (just) another molecular dynamics program (NAMD) was used for all MD simulations (43). For the QM calculations on the nonenzymatic and enzymatic models (Fig. 4), the structures of reactants and the transition states in solution were obtained through full geometry optimization using density-functional theory with solvation effects included through the polarizable continuum model (44) and with specialized atomic radii and smooth analytical gradients for treating the solvent effects (45–48). The hybrid B3LYP exchange-correlation functional was used together with the 6–31++G(d,p) basis set. Vibrational frequency analyses were performed to confirm the nature of all stationary points (minima and transition states). KIEs were then calculated from the Bigeleisen equation (14) at 37 °C based on the density functional theory (DFT) potential energy surface. The software package Gaussian 09 was used for all QM calculations (49).