Capturing the mutational landscape of the beta-lactamase TEM-1

Abstract

Adaptation proceeds through the selection of mutations. The distribution of mutant fitness effect and the forces shaping this distribution are therefore keys to predict the evolutionary fate of organisms and their constituents such as enzymes. Here, by producing and sequencing a comprehensive collection of 10,000 mutants, we explore the mutational landscape of one enzyme involved in the spread of antibiotic resistance, the beta-lactamase TEM-1. We measured mutation impact on the enzyme activity through the estimation of amoxicillin minimum inhibitory concentration on a subset of 990 mutants carrying a unique missense mutation, representing 64% of possible amino acid changes in that protein reachable by point mutation. We established that mutation type, solvent accessibility of residues, and the predicted effect of mutations on protein stability primarily determined alone or in combination changes in minimum inhibitory concentration of mutants. Moreover, we were able to capture the drastic modification of the mutational landscape induced by a single stabilizing point mutation (M182T) by a simple model of protein stability. This work thereby provides an integrated framework to study mutation effects and a tool to understand/define better the epistatic interactions.

The distribution of fitness effects (DFE) of mutations is central in evolutionary biology. It captures the intensity of the selective constraints acting on an organism and therefore how the interplay between mutation, genetic drift, and selection will shape the evolutionary fate of populations (1). For instance, the DFE determines the size of the population required to see fitness increase or decrease (2). To compute the DFE, direct methods have been proposed based on estimates of mutant fitness in the laboratory. These methods have some drawbacks: being labor intensive, they have been built at most on a hundred mutants, the resolution of small fitness effects (less than 1%) is hindered by experimental limitations, and finally, the relevance of laboratory environment is questionable. However, direct methods have so far provided some of the best DFEs using viruses/bacteriophages (3, 4) or more recently two bacterial ribosomal proteins (5). All datasets presented a mode of small effect mutations biased toward deleterious mutations, but viruses harbored an additional mode of lethal mutations.

For population genetics purposes, the shape of the DFE is in itself fully informative, yet from a genetics point of view, the large-scale analysis of mutants required to compute a DFE may also be used to uncover the mechanistic determinants of mutation effects on fitness (6, 7). The goal is then not only to predict the adaptive behavior of a given population of organism, but to understand the molecular forces shaping this distribution. This knowledge is required, at the population level, to extrapolate the observations made on model systems in the laboratory to more general cases. More importantly, it may pave the way to some accurate prediction of the effect of individual mutations on gene activity, a task of increasing importance in the identification of the genetic determinants of complex diseases based on rare variants (8, 9).

How can the effect of an amino acid change on a protein be inferred? Homologous protein sequence analysis established that the frequency of amino acids changes depends on their biochemical properties (10), suggesting variable effects on the encoded protein and subsequently on the organism’s fitness. A recent study using deep sequencing of combinatorial library on beta-lactamase TEM-1 showed for instance that substitutions involving tryptophan were the most costly (11). The classical matrices of amino acid transitions used to align protein sequences are meant to capture these effects. Consequently, the analysis of diversity at each site in a sequence alignment has been used to infer how costly a mutation may be (12, 13). More recently, a biophysical model proposed to integrate further the effects of amino acid changes by considering their effect on protein stability (14–17). This model assumes that most mutations affect proteins through their effects on protein stability, which determines the fraction of properly folded protein in the cell. Several empirical evidences support this model. First, the residues in proteins that are exposed to the solvent contribute less to protein stability and evolve faster (18). Second, using either general properties or in silico predictions of mutation effects on stability (14, 16), this model could explain the rate of loss of function of beta-lactamase TEM-1 with the accumulation of mutations. However, these evidences are indirect, based either on sequence analysis or on experimental analysis of mean effects. As such, they only give a qualitative support to the role of protein stability, and a more detailed analysis is needed.

To improve our knowledge on the DFE and its molecular determinants, we undertook a quasi-exhaustive approach and produced a large library of random mutants in the enzyme beta-lactamase TEM-1. There are several reasons for using TEM-1 as a model protein. First, about a fourth of all proteins in a bacterial species such as Escherichia coli are enzymes (19). Second, we know precisely TEM-1’s substrate, beta-lactams, and therefore its activity can be estimated at large scale on individual mutants with minimum inhibitory concentration (MIC) to beta-lactam amoxicillin. Third, TEM-1 being naturally present on plasmids is much easier to manipulate in its natural background than chromosomal genes. Fourth, it is a model enzyme in biochemistry with well-defined 3D structure (20) and thermodynamical characteristics (21), and the impact of some stabilizing mutations in that enzyme has already been described (11, 14, 22–24). Finally, it is a gene of medical importance that provides high-level resistance to first-generation beta-lactams, and evolved an extended spectrum to third-generation beta-lactams with a handful of point mutations (25, 26). Using TEM-1 as a model enzyme, we were able to uncover some universal determinants of mutation effects, to quantify how powerful they were to explain the impact of mutations and to define a simple model that could capture both mutation effect and their epistatic interactions.

Results

Distribution of Single Mutant’s MICs.

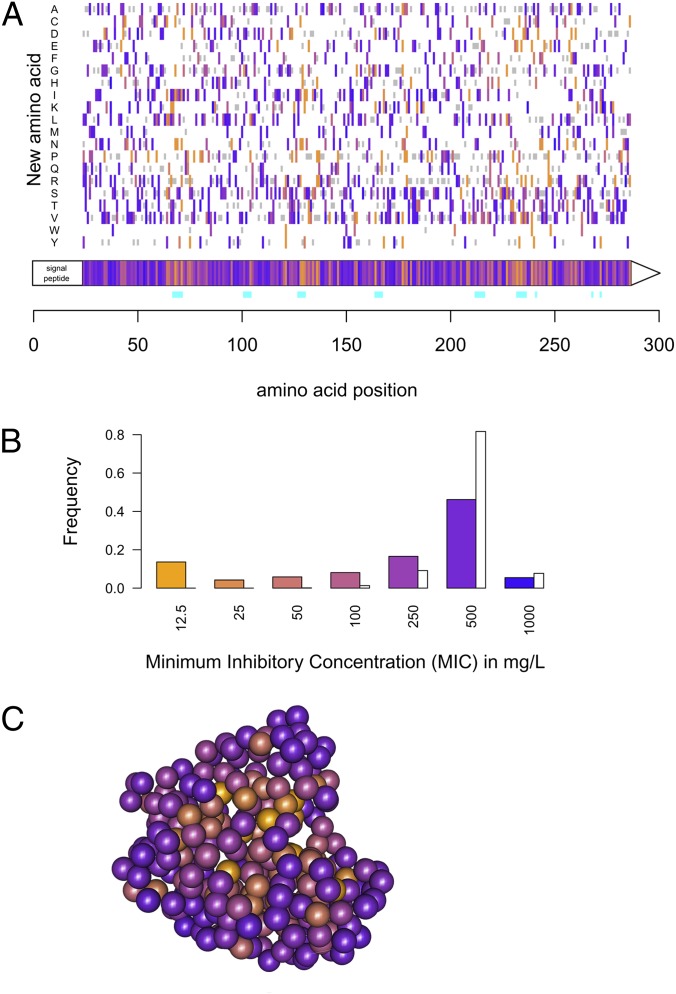
To investigate mutation effects on TEM-1, we produced 10,000 mutants using random mutagenesis with an average of 1.93 mutation per clone (Methods), resulting in 1,700 clones with no mutations or wild types, and 2,383 single mutants. On all mutants, an MIC to amoxicillin was performed on plates to control the emergence of de novo mutation in the assay (SI Appendix). MIC is a composite parameter that reflects the efficiency of enzyme production, folding, and activity on its substrate, and the cost of enzyme production on growth. MIC allows the detection of a large range of effects but is not discriminant for small effect mutations. As we are only interested in the enzyme activity, we discarded mutations in the signal peptide of the enzyme (residues 1–23), nonsense, and frame-shift mutations, 98.5% of the latter exhibiting minimal MIC. Wild-type clones and synonymous mutants shared a similar distribution, highly different from the one of nonsynonymous mutations. This suggests that synonymous mutation effects on this enzyme were marginal compared with nonsynonymous ones. We therefore extended the nonsynonymous dataset with the incorporation of mutants having a single nonsynonymous mutation coupled to some synonymous mutations and recovered a similar distribution (SI Appendix, Fig. S2). The dataset finally resulted in 990 mutants with a single amino acid change, representing 64% of the amino acid changes reachable by a single point mutation (Fig. 1A) and therefore presumably the most complete mutant database on a single gene. Similarly to viral DFE, the distribution of nonsynonymous MIC was clearly bimodal (Fig. 1B), composed of 13% of inactivating mutations (MIC < 12.5 mg/L) and a distribution with a peak at the ancestral MIC of 500 mg/L. No beneficial mutations were recovered, suggesting that the enzyme activity is quite optimized, although our method could not quantify small effects. We could fit different distributions to the logarithm of MIC (SI Appendix, Table S2 and Fig. S4). A shifted gamma distribution gave the best fit of all classical distributions.

Fig. 1.

Distribution of mutation effects on the MIC to amoxicillin in mg/L. (A) For each amino acid along the protein, excluding the signal peptide, the average effect of mutations on MIC is presented in the gene box with a color code, and the effect of each individual amino acid change is presented above. The color code corresponds to the color used in B. Gray bars represent amino acid changes reachable through a single mutation that were not recovered in our mutant library. Amino acids considered in the extended active site are associated with a blue bar beneath the gene box. (B) Distribution of mutation effects on the MIC is presented in color bars (n = 990); white bars illustrate the distribution of MIC of the wild-type clones (n = 1,594), in other words the noise in MIC measurement. (C) Representation of the average effect of mutations on MIC for each residue on the 3D structure of the protein.

Correlations Between Substitution Matrices and Mutant’s MICs.

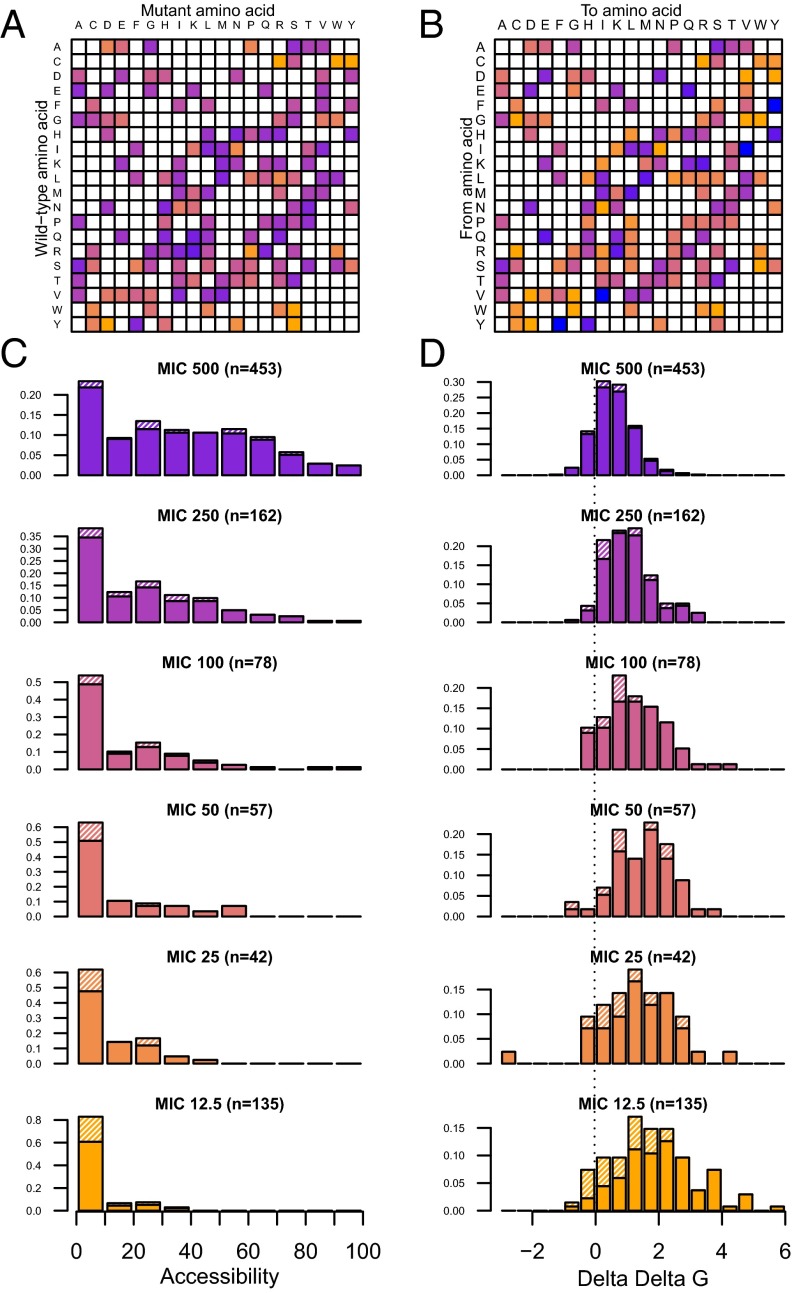
With this dataset, we went further than the description of the shape of mutation effects distribution, and studied the molecular determinants underlying it. We first investigated how an amino acid change was likely to affect the enzyme using amino acid biochemical properties and mutation matrices. The predictive power of more than 90 amino acid mutation matrices stored in AAindex (27) was tested with two approaches. First, we computed C1 as the correlation between the effect of the 990 mutants on the log(MIC) and the scores of the underlying amino acid change in the different matrices. Second, using all mutants, we inferred a matrix of average effect for each amino acid change on log(MIC) and computed its correlation, C2, with matrices from AAindex (SI Appendix). Correlations up to 0.40 were found with C1 (0.63 with C2), explaining 16% of the variance in MIC by the nature of amino acid change (Table 1). Interestingly, with both approaches, the best matrices were the BLOSUM matrices (C1 = 0.40 and C2 = 0.64 for BLOSUM62, SI Appendix, Fig. 2 A and B). BLOSUM62 (28) is the default matrix used in BLAST (29). It was derived from amino acid sequence alignment with less than 62% similarity. Hence the distribution of mutation effects observed in a specific enzyme in the laboratory is not only globally compatible with the information stored in pools of protein sequences that have diverged for millions of years, but also points to what is known as the best-performing matrix in protein alignment. At the biochemical level, the Grantham matrix (10) combining polarity composition and volume of amino acids had a performance quite similar to BLOSUM matrices (C1 = 0.36, C2 = –0.64). This comforted the idea that the damaging effect of mutations was linked to their impact on the local physical and chemical characteristics.

Table 1.

Fraction of variance of the mutants’ MIC explained by the different factors alone or in combination

Determinant	Variance explained
	Whole enzyme, with interaction	Active site excluded, with interaction
BLOSUM62	0.16	0.18
Accessibility	0.22	0.20
∆∆G Popmusic	0.19	0.27
∆∆G foldX	0.15	0.19
BLOSUM62 + Accessibility	0.38 (0.43)	0.39 (0.44)
BLOSUM62 + ∆∆G Popmusic	0.28 (0.28)	0.36 (0.36)
BLOSUM62 + ∆∆G foldX	0.24 (0.24)	0.28 (0.28)
Accessibility + ∆∆G Popmusic	0.27 (0.27)	0.31 (0.32)
Accessibility + ∆∆G foldX	0.30 (0.32)	0.31 (0.34)
BLOSUM62 + Accessibility + ∆∆G Popmusic	0.40 (0.44)	0.43 (0.48)
BLOSUM62 + Accessibility + ∆∆G foldX	0.42 (0.46)	0.43 (0.48)

Either the whole enzyme is considered or the active site is excluded. The adjusted R square is given for the combination of factors without or with (in parenthesis) interactions among factors.

Contribution of Protein Stability and Accessibility to MIC Changes.

Protein stability is one of the most widely cited biophysical mechanisms controlling mutation effects (15). The fraction of properly folded protein, Pf, and therefore the overall protein activity can be directly linked to protein stability, or free energy ∆G, through a simple function, using Boltzmann constant k and temperature T, modified from Wylie and Shakhnovich (16). If MIC is proportional to Pf with a scaling factor M, we have:

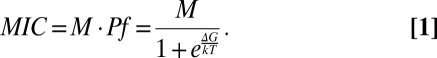Through this equation, we clearly see that an increase in ∆G leads to a lower fraction of folded proteins and therefore a decrease of MIC.

To quantify the contribution of stability to the mutant loss of MIC, we used two approaches.

First, as mutations affecting buried residues in the protein 3D structure tend to be more destabilizing, we tested how accessibility to the solvent could explain our distribution of MIC (Methods, Table 1, Fig. 2C). Accessibility could explain up to 22% of the variance in log(MIC). Mutants without damaging effect (MIC = 500 mg/L) were found at sites significantly more exposed to the solvent than expected from the whole protein accessibility distribution [Kolmogorov–Smirnov test (ks test) P < 3e-9]. Conversely, damaging mutants with MIC less than or equal to 100 affected an excess of buried sites (ks test, MIC 100, P < 0.005; MIC 50, P < 0.002; MIC 25, P < 0.001; MIC 12.5, P < 1e-16). No residue with an accessibility higher than 50% could lead to an inactivating mutation (Fisher test P < 2e-16).

Fig. 2.

Determinants of mutations effects on MIC. (A) Average effect of amino acid changes on MIC is presented as a matrix. The color code is identical to the one in Fig. 1. (B) Matrix BLOSUM62, representing amino acid penalty used in protein alignments using a color gradient of the same range as in A. In both matrices, only amino acid changes observed in the mutant library are colored. (C) Impact of accessibility to the solvent on mutant’s MIC. The distribution of accessibility of amino acids (buried = 0, fully accessible = 100) is plotted for different categories of mutants sharing the same MIC. Large effect mutations are enriched for buried sites. (D) Impact of predicted effect of mutations on protein stability (∆∆G estimated by PopMusic software) on mutant’s MIC. The distribution of ∆∆G of mutants (∆∆G > 0 is destabilizing, ∆∆G < 0, stabilizing) is plotted for different categories of mutants sharing the same MIC. Large effect mutations are enriched for destabilizing mutations. In C and D, hatched fractions represent amino acids included in the active site. The color code is similar to that of Fig. 1.

Second, we computed the predicted effect of mutants on the free energy of the enzyme with FoldX (30) and PopMusic (31) softwares (Fig. 2D). As the active site may lead to some damaging effects independent of the stability effect of mutations, we performed analysis including and excluding it (SI Appendix). For both softwares, the correlation between mutants predicted changes in stability, and log(MIC) was improved when the active site was omitted (Table 1). Using PopMusic predictions, up to 27% of variance in log(MIC) of mutants out of the active site could be explained. However, stability impact on MIC should be inferred through Eq. 1. However, as we do not know the ∆G of TEM-1 (∆G_TEM-1) in vivo, we looked for the ∆G_TEM-1 that would maximize the correlation between observed and predicted MIC through Eq. 1. Similar correlations could be recovered with a ∆G_TEM-1 around –1.73 kcal/mol (SI Appendix, Fig. S6).

Growth Rate of Mutants and V₀.

Although MIC is a discrete and quite rough measure of TEM-1 activity, we wanted to test our mutants either on a more direct fitness-linked phenotype or on a more enzymatic phenotype. We therefore sampled the mutants having a single nonsynonymous mutation (n = 757) and performed growth curves in triplicates at a low (6 mg/L) and a high concentration (100 mg/L) of amoxicillin. On 474 of these we measured the initial velocity on cell extracts, V₀, which represents a composite estimate of the functional enzyme concentration and its activity. First, a correlation of 80% (69%) was found between the maximum growth rates at low (high) concentration and the MIC scores. This suggests that MIC can be associated with fitness, particularly when a low concentration of antibiotic is used. Indeed, in such conditions, the correlation holds, if we exclude the clones with a null growth rate (r = 0.5) and even if we exclude clones with MIC of less than 100 (r = 0.15, P = 0.0004). Hence, even if clones have an MIC 10-fold higher than the antibiotic concentration, their MIC is still correlated to growth rate. Second, for both concentrations, all of the factors found to explain MIC were recovered (SI Appendix, Tables S3 and S4). However, the variance explained was consistently lower than for MIC. Concerning the V₀ on cell extracts, although the measure in 96-well plates was noisy, it correlated with MIC (r = 0.5) and with all three parameters identified (BLOSUM62 r = 0.3, Accessibility r = 0.33, and ∆∆G estimates r = –0.3), comforting the robustness of our results.

Impact of a Stabilizing Mutation on the Distribution of MIC.

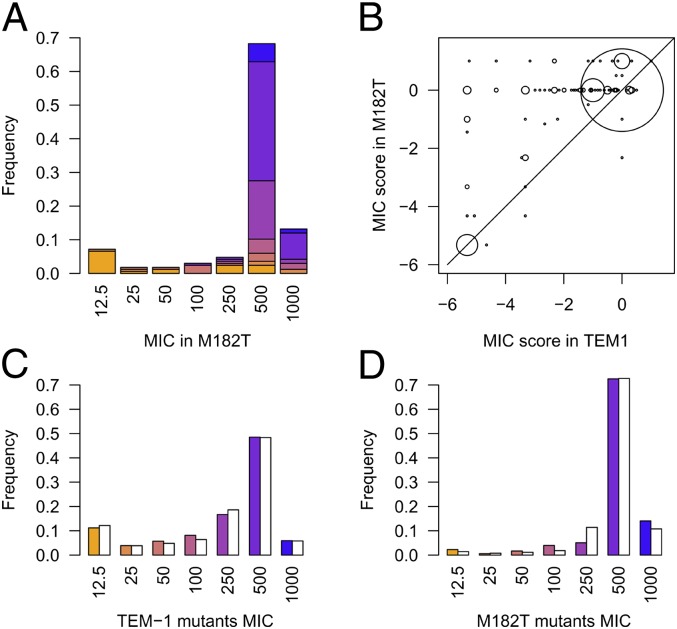
The stability model predicts a strong impact of stabilizing mutations on the distribution of mutations effects (14). We therefore produced another library of mutants, in the TEM-1 mutant having the M182T stabilizing mutation. This mutation has been shown to be selected for in the wild due to its stabilizing effect on a modified active site (21). The distribution of mutants in that background was drastically different from the previous one (ks test P < 2e-16), with more than 80% of mutants showing no change in MIC (Fig. 3A). Not only did the presence of M182T mutation decrease overall the effect of mutations on MIC (Fig. 3B), but some mutations classified as inactivating in its absence appeared as neutral in its presence. However, those mutations did not show any clear spatial localization toward M182T (SI Appendix, Fig. S9), comforting a global effect of M182T on the protein.

Fig. 3.

Epistatic interactions due to the stabilizing mutation M182T. (A) Distribution of mutation effects on MIC in M182T, for mutants also found in the TEM-1 library (n = 167). The color of the bars represents the MIC in the TEM-1 background of the mutants. A much larger fraction of mutants with no effect on MIC is found in M182T and is composed of mutants found to have some deleterious effects in TEM-1 background. (B) Plot of the MIC score in the two different backgrounds. The size of dots represents the number of mutants in that spot. The large fraction of points in the upper diagonal illustrates the compensating effect of mutation M182T. (C and D) Observed (colored bars) and predicted (white bars) distributions of mutant MICs in TEM-1 (C) and M182T backgrounds (D), using a three-parameter biophysical model of stability and excluding the active site.

Thermodynamic and Functional Properties of a Subset of Mutants.

To validate experimentally the contribution of enzyme stability/folding on the effect of mutations on MIC and their epistatic interactions, we explored the biochemical impact of two deleterious mutations, A36D and L250Q, both remote (>19 Å) from the active site. A36 and L250 are buried residues located in an alpha-helix and in a beta-sheet, respectively; they have a low MIC that was dramatically increased in the presence of M182T mutation. We studied, therefore, thermodynamic and enzymatic properties of TEM-1, M182T, A36D, A36D/M182T, L250Q, and L250Q/M182T mutants. Proteins were purified, and their activity and thermal stability were investigated. We first assayed the catalytic activity at different temperatures (27 °C to 67 °C). Then thermal denaturation was assessed through tryptophan fluorescence measurements (Table 2).

Table 2.

Susceptibility, thermodynamic, and enzymatic properties of TEM-1 and its variants

Genotype	MIC, mg/L	Vi/[Eo] at 37 °C, s−1	T1/2, °C	Tm, °C
Wild type	500	142 ± 2	47	49.5
M182T	500	145 ± 15	59	57
A36D	12.5	0.14 ± 0.01	n.m.*	57
A36D/M182T	250	108 ±− 6	46	43
L250Q	12.5	0.15 ± 0.01	n.m.†	57
L250Q/M182T	250	28 ± 2	40.5	41

n.m., not measured.

^*The activity of this mutant displays a complex temperature dependence with a residual activity at 67 °C of vi/[E₀] = 0.09 s⁻¹.

^†The activity of this mutant displays a bell-shaped temperature dependence with a maximum around 62 °C (vi/[E₀] = 0.29 s⁻¹).

TEM-1 and M182T presented similar catalytic activities at 37 °C (Table 2). We confirmed the stabilizing effect of M182T (22), characterized by an increased melting temperature and a better thermal stability of its enzymatic activity (Table 2). For all mutants, the enzymatic activities at 37 °C were consistent with the measured MICs (Table 2). In particular, the activities of A36D and L250Q were decreased by three orders of magnitude. As expected, the presence of the M182T mutation suppressed partially the effects on enzymatic activity of the deleterious mutations.

The high melting temperature of both deleterious mutants suggested that their low activity resulted from their folding in an alternative stable conformation competing with the active conformation. Presumably, mutation M182T, by enhancing the stability of the active conformation, shifts the competition toward that state and therefore strongly restores the activity in the double mutants.

A Simple Model of Protein Stability Accounts for Changes in the Distribution of MIC.

Drastic changes in mutation distribution due to a single mutation suggest that rather than using classical distributions to fit the data, some mechanistic-based approach is needed. We first used Eq. 1 to analyze the prediction of PopMusic on the combined TEM-1 and M182T mutant datasets, excluding the ones in the active site. Setting ∆G_TEM-1 = −1.73 kcal/mol as estimated before, we found that using the in vitro estimated stabilizing effect of M182T mutation (∆∆G_M182T = −2.7 kcal/mol) (21), the variance explained by PopMusic predictions, through Eq. 1, increased from 20% to 29% (95% confidence interval (CI) 0.24–0.33). Second, we tried to fit the distribution of MIC, using Eq. 1, assuming that the impact of mutations on ∆G can be represented as a shifted normal distribution (16). Because in vitro stability (16) can differ from in vivo stability, we fitted the stability parameters. Using the scaling parameter M, an average ∆∆G of mutants, µ, and a SD of mutants effects on ∆G, σ, we obtained the best fit to the distribution of MIC of TEM-1 mutants (SI Appendix, Table S2), outcompeting the gamma distribution. More interestingly, the distribution of mutants MIC in both TEM-1 and M182T backgrounds (without the active site) could be recovered (SI Appendix, Fig. 3 C and D) using the previously mentioned ∆G of TEM-1 and M182T [M = 377 mg/L (95% CI 372–382), µ = 0.76 kcal/mol (0.47–1.01), σ = 2.62 kcal/mol (2.36–2.90)].

Discussion

DFE Is Dynamical.

Using a model enzyme involved in antibiotic resistance, we analyzed the effects of a thousand independent single mutants on an enzyme. Even if we did not use a fitness estimate but MIC as a proxy, our results are similar with previous estimates of DFE for whole organisms and whole genes, with the exception of ribosomal proteins. As in viruses and enzymes, a fraction of inactivating mutations is found, such that a bimodal distribution is recovered with a skewed mode of neutral and deleterious mutations and one of lethal. This bimodal shape seems, therefore, to be the rule, and the absence of inactivating mutations as observed in ribosomal protein the exception. However, our work suggests that despite this qualitative shape conservation, the distribution of mutation effect is highly variable even within the same gene. Here a simple stabilizing mutation with no detectable effect on the activity of the enzyme results in a drastic shift of the distribution toward less damaging effects of mutations. Hence a static description of the DFE, using for instance a gamma distribution, is not enough and a model-based description that could account for these changes is required.

A Simple Model of Stability.

During the last decade, protein stability has been proposed as a major determinant of mutation effects. Here, using MIC of individual single mutants, rather than the fraction of resistant clones in a bulk of mutants with an average number of mutations, we could quantify this contribution and clearly demonstrate that a simple stability model could explain up to 29% of the variance of MIC in two genetic backgrounds. Previous models have been proposed to model the impact of mutations on protein stability. Some simplified models used stability as a quantitative trait but lacked some mechanistic realism (15, 32). Bloom et al. used a threshold function to fit their loss of function data, however such a function could not explain the gradual decrease in MIC observed in our data (14). Wylie and Shakhnovich (16) proposed a quantitative approach that inspired the equation used here. Their model requires, however, a fraction of inactivating mutations and a stability threshold of ∆G = 0, above which fitness was assumed to be null to mimic a potential effect of protein aggregation. However, as a consequence, the model does not allow stability to decrease the quantity of enzymes and therefore MIC by more than a twofold factor. More than a 16-fold decrease in MIC was, however, observed and confirmed with our biochemical experiments. Indeed our in vitro enzyme stability analysis suggested that it is not only the difference of free energy to the unfolded state that determines the fraction of active protein: the stability of nonactive conformations may also matter and could be affected by mutations. We therefore allowed positive ∆G in the model and obtained a better fit to the data.

Limits of the Model.

Despite the success of the stability approach to explain the MIC of mutants, some discrepancies between the model and the data remain. Although stability changes should both integrate the accessibility of residues and the type of amino acid change, we found that multiple regressions including the BLOSUM62 scores and the accessibility explained much better the data than stability change predictions (Table 1). Overall the best linear model to explain the data included all three factors and could explain up to 46% of the variance (Table 1). Using a random subsample of the data, linear predictive models based on these factors were derived and used to predict the MIC of the remaining mutants with a correlation of 0.67 between predicted and observed data (SI Appendix). The limited power of ∆∆G prediction softwares (33) may explain why BLOSUM62 and accessibility data improve the models. Alternatively, these discrepancies may also point to additional functional requirements beyond stability of the native state as computed. The impact of mutations on the in vivo folding dynamics or the existence of alternative stable conformations as our biochemical data suggest are, for instance, not accounted for by the softwares. These elements may explain why our estimate of ∆G_TEM-1 (–1.73 kcal/mol) and the variance in mutation effect on ∆G are much higher than in vitro estimates (–8 kcal/mol) (16).

Difference Between in Vitro and in Vivo Estimates of Protein Stability.

The discrepancy we observe between the in vitro stability of TEM-1 and that our analysis of mutants suggests is surprising. However, selection of stabilizing mutation after selection for modification of the active site is a common observation in protein evolution (34). Furthermore, overproduction of chaperone increased the evolvability of enzymes, as it could compensate the destabilizing effect of some beneficial mutations in the active site (35). Particularly in the case of TEM-1, the stabilizing mutation M182T has been shown to be beneficial in the hydrolysis spectrum extension of the enzyme, only when some destabilizing mutations in the active site were present (25, 26). However, the in vitro stability of these enzymes with modified active site is lower than –4 kcal/mol, suggesting that the effect of M182T should be marginal, and “challenging the notion that evolution is a balance between structure and function” (36). Our estimation of a much lower in vitro stability appears to be more compatible with the apparent selective pressures for stabilizing mutations, and may therefore suggest some limitations of the in vitro estimation of stability, at least in the case of TEM-1.

Predicting Mutation Effects in Disease.

Predicting the effect of single amino acid changes is an important challenge in human health. Progresses on complex diseases suggest that assigning a phenotypic status to rare variants is essential to uncover the genetic basis of diseases. Most mutation effect prediction softwares, such as SIFT (13) and Polyphen2 (12), use evolutionary information to infer the status of mutations: mutations in conserved site in amino acid alignment are more likely to be damaging. These approaches may suffer from two limitations: first a small fitness cost of 0.1% for instance may be efficiently counterselected by natural selection and therefore invariant in protein alignments and yet not enough to cause a disease. Second, sites are treated independently and epistatic effects are therefore not accounted for, whereas our analysis shows that they may have drastic effects. Recent developments of prediction softwares have now included some protein structural information. For instance, Polyphen 2 (12) uses accessibility of the residue as a criterion and improved its performance. However, so far no software, that we are aware of, uses the predicted impact of mutation on protein stability. As there is still some room for improvement for these methods, our work suggests that despite their imperfections, in silico estimates of mutation impact on stability offer an interesting improvement perspective.

Conclusion

With our extensive dataset, we identified some major determinants of mutation effects on an enzyme. Mutation type, residue accessibility, and mutation effect on stability are universal determinants that support the use of a reductionist approach on a single enzyme to give insights on all enzymes. Quantitative analysis of the impact of mutations on the fraction of those properly folded offers a successful framework from which a strong model of epistasis emerges (15), the impact of mutations being highly dependent on the enzyme global stability. Hence, although it may be possible to assess that mutations affecting an exposed residue are unlikely to be inactivating, the inactivating effect of buried residues may be highly dependent on the overall stability of the enzyme. This has some interesting evolutionary consequences: first, most deleterious mutations may be compensated by many different stabilizing mutations (37), and second, these compensations or fluctuations in the stability of the enzyme may allow the building up of strong dependencies among mutations. This may, for instance, explain the discrepancies observed between the low (high) conservation of a residue in protein alignments and the strong (low) impact of mutations affecting that residue (11). More generally, the epistatic interactions through stability effects may allow the fixation of destabilizing mutations that may contribute to the building of Dobzhansky–Müller incompatibilities or compensated pathogenic deviations among independent lineages (38, 39).

Methods

A detailed description of methods is available in SI Appendix, SI Methods.

Library Construction.

TEM-1 mutants were constructed using GeneMorph II Random Mutagenesis Kit (Stratagene) to obtain an average of one mutation per gene. The mutagenized amplicons were cloned into a modified pUC19 plasmid containing the pMB1 origin of replication from pBR322, NcoI and NotI flanking the start and stop codons of TEM-1’s ORF, and gentamicin resistance gene (aacC4) at the XbaI site. The ligation products were transformed into ElectroMax DH10B-T1 Phage Resistant E. coli Competent Cells (Invitrogen, Fisher Scientific) and plated on Luria–Bertani agar supplemented with gentamicin (20 mg/L). A total of 10,368 randomly picked TEM-1 mutants were stored into 384-well microplates and sequenced by Sanger method.

MIC Measurements.

The MIC was measured by a standard agar dilution method on Mueller Hinton (MH) agar plates containing a growing concentration of amoxicillin (0, 12.5, 25, 50, 100, 250, 500, 1,000, 2,000, and 4,000 mg/L). After 18 h of incubation at 37 °C, the MIC was defined as the first concentration of amoxicillin inhibiting the growth of bacteria.

MIC Score.

For each mutant, MIC was computed as the median of three independent MIC measurements. MIC score is computed as log2(MIC/500). It attributes a score of 0 to the wild type and a negative score to mutants with decreased MIC relative to that of the wild type. For amino acid changes that were found several times in the library as single amino acid changes, the average MIC score was retained.

Accessibility of Amino Acids and Prediction of Mutant’s Effect on Free Energy.

The 1BTL previously published entry from the Protein Data Bank was used to extract 3D structure information on TEM-1. Predictions of ∆∆G derived from foldX were kindly provided by Nobuhiko Tokuriki (Vancouver, British Columbia, Canada) (34). PopMusic predictions of ∆∆G and accessibility were computed online at http://babylone.ulb.ac.be/popmusic (31).

Amino Acid Matrices.

Amino acid substitution matrices were downloaded from www.genome.jp/aaindex/ (27).

Protein Purification.

Genes for TEM-1 and its variants were cloned into pET36b and transformed in E. coli BL21(DE3). The enzymes were overexpressed after induction by IPTG (1 mM), and purified on anion-exchange column (Q Sepharose FF, GE Healthcare) followed by gel filtration (Superdex 75 column, GE Healthcare).

Thermal Denaturation of Proteins.

TEM-1 and its variants were subjected to thermal denaturation (25–80 °C with 1.5 °C/min ramping rates). Intrinsic fluorescence (λ_ex = 295 nm; λ_em = 340 nm) was followed using a FP-8300 Jasco fluorescence spectrophotometer.

Enzyme Assays on Purified Enzymes.

Initial velocity was measured spectrophotometrically at 486 nm using the chromogenic substrate nitrocefin (32 µM) in the range of 27 °C to 67 °C with a 5 °C interval.

Enzyme Assays on Cell Extracts.

TEM-1 and its variants were grown overnight in 96-deep-well plates, and cells were lysed using Cell Culture Lysis Reagent (Promega). Lysates were diluted in potassium phosphate buffer pH 7.25 containing nitrocefin (50 µg/mL) inside microtiter plates. Initial velocity was measured spectrophotometrically at 486 nm using a Tecan infinite 96-well plate reader.

Maximum Growth Rate Determination.

Growth curves were performed at 37 °C in 96-well microtiter plates containing 200 µL MH broth supplemented with 6 or 100 mg/L of amoxicillin, using a Tecan infinite 96-well plate reader. The Maximum Growth Rate was determined as the maximum value of the derivative of the logOD₆₀₀, using R software.