Role of methyl-induced polarization in ion binding

Abstract

The chemical property of methyl groups that renders them indispensable to biomolecules is their hydrophobicity. Quantum mechanical studies undertaken here to understand the effect of point substitutions on potassium (K-) channels illustrate quantitatively how methyl-induced polarization also contributes to biomolecular function. K- channels regulate transmembrane salt concentration gradients by transporting K⁺ ions selectively. One of the K⁺ binding sites in the channel’s selectivity filter, the S4 site, also binds Ba²⁺ ions, which blocks K⁺ transport. This inhibitory property of Ba²⁺ ions has been vital in understanding K-channel mechanism. In most K-channels, the S4 site is composed of four threonine amino acids. The K channels that carry serine instead of threonine are significantly less susceptible to Ba²⁺ block and have reduced stabilities. We find that these differences can be explained by the lower polarizability of serine compared with threonine, because serine carries one less branched methyl group than threonine. A T→S substitution in the S4 site reduces its polarizability, which, in turn, reduces ion binding by several kilocalories per mole. Although the loss in binding affinity is high for Ba²⁺, the loss in K⁺ binding affinity is also significant thermodynamically, which reduces channel stability. These results highlight, in general, how biomolecular function can rely on the polarization induced by methyl groups, especially those that are proximal to charged moieties, including ions, titratable amino acids, sulfates, phosphates, and nucleotides.

Methyl groups play a central role in biomolecular function. As constituents of biomolecules, these groups define the biomolecule’s solvated configurations. Also, their posttranslational addition to peptides is regulated tightly to enable numerous physiological processes, including gene transcription and signal transduction (1). Furthermore, methylation of nucleotides is a crucial epigenetic modification that regulates many cellular processes, such as embryonic development, transcription, chromatin structure, genomic imprinting, and chromosome stability (2). The chemical property of methyl groups that renders them indispensable to these processes is their hydrophobicity, that is, their inability to hydrogen-bond with water molecules or, more generally, with polar groups.

Methyl groups are, however, also polarizable. For example, methanol differs from water chemically in that it includes a methyl group and has an average static dipole polarizability more than twice that of water (3.3 vs. 1.5 ų) (3). In addition, the average static dipole polarizabilities of alcohols increase with addition of methylene bridges (-CH₂-). Methanol, ethanol, and propanol have increasingly larger polarizabilities of 3.3, 4.5, and 6.7 ų, respectively (3). Although such trends indicate that methyl or methylene polarizability could be an important contributor to the electrostatic and polarization forces that drive biomolecular function, there exists only suggestive and qualitative evidence as to their actual role. Studies examining the effect of methylation on DNA stability (4) proposed that the enhanced stability of methylated DNA may be explained by considering that methylation of nucleotides increases their polarizability. In a different experimental study concerning the relative stabilities of DNA and RNA helices (5), it was proposed that the largest contribution to stabilization by methyl groups was due to increased base-stacking ability rather than favorable hydrophobic methyl–methyl contacts. We present investigations on K channels that illustrate quantitatively how methyl-induced polarization contributes to the functional properties of biomolecules.

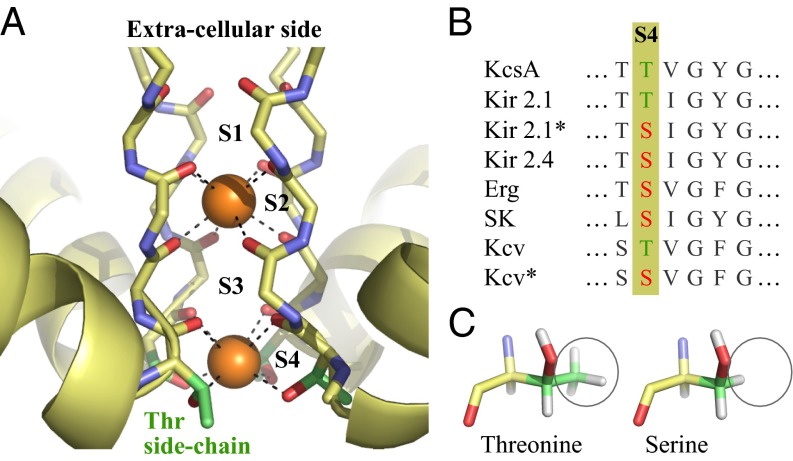
The primary function of K channels is to regulate transmembrane salt concentration gradients (6). K channels accomplish this task by transporting K⁺ ions selectively through their pores in response to specific external stimuli. Fig. 1A is a representative structure of the selectivity filter of their pores (7), which shows four preferred binding sites for K⁺ ions, S1–S4. Three of these binding sites, S1–S3, can be considered chemically identical because they provide eight backbone carbonyl oxygens for ion coordination. The fourth site, S4, is typically composed of four threonine residues that provide four backbone carbonyl oxygens and four side-chain hydroxyl oxygens for ion coordination. This S4 site is also the preferred binding site for Ba²⁺ ions that block K⁺ permeation (8–11). This inhibitory property of Ba²⁺ has proven vital toward understanding the mechanisms underlying K-channel function (8–10, 12–15, 17, 18).

Fig. 1.

(A) Selectivity filter of a representative K channel, KcsA (7). The orange spheres denote K⁺ ions bound to two of their four preferred binding sites, S2 and S4 (Protein Data Bank ID code 1K4C). Threonine (Thr) side chains that make up the S4 site are highlighted in green. (B) Sequence alignment of the selectivity filter region of K channels that have serine residues in their S4 sites. The K channels whose names are appended with an asterisk are engineered via site-directed mutagenesis and were functionally characterized recently by Chatelain et al. (16). (C) Representative configurations of threonine and serine amino acids.

Genetic selection and site-directed mutagenesis experiments on a viral K channel, Kcv, and the inward rectifier K channel, Kir 2.1, show that a threonine-to-serine (T→S) substitution in the S4 sites reduces channel susceptibility to Ba²⁺ block by over two orders in magnitude (16). In addition, this substitution reduces channel stability, including the channel’s mean open probabilities. Furthermore, the sequence alignment of K channels (19) shows that some K-channel subfamilies carry a serine residue instead of a threonine residue in their S4 sites (Fig. 1B). Among these serine-carrying channels, Kir 2.4 has also been found to exhibit similar characteristic differences with respect to the typical threonine-containing channels (20, 21).

The single chemical difference between a serine and threonine side chain is that serine has one less branched methyl group than threonine (Fig. 1C). Consequently, serine can be expected to be less polarizable than threonine. However, is the difference in electronic polarizability sufficient to explain the T→S-induced changes in K-channel properties, especially given that the ion in the S4 site resides at a distance greater than 5 Å from the branched methyl group (7)? Serine and threonine also have different hydrophobicities (22), so do T→S substitutions alter the manner in which their side-chain hydroxyl groups align with the permeation pathway and interact with ions?

The primary challenge associated with investigating these issues is to model accurately the broad range of molecular forces involved in ion complexation, in particular, polarization and dispersion, which contribute nontrivially to ion–ligand and ligand–ligand energetics (23–25). A consistent first-principles approach is therefore essential. Toward that end, we use density functional theory (DFT) with the semilocal Perdew–Burke–Ernzerhof (PBE) (26) and hybrid PBE0 (27, 28) exchange-correlation functionals. Because van der Waals (vdW) dispersion can be expected to be a major contributor to ion–methyl energetics in the 5-Å distance range (29), we describe it explicitly using the recently developed DFT+vdW method (30). In this method, the 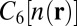coefficients of the interatomic interaction term 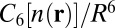are obtained from the self-consistent electron density 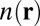. This method yields an accuracy of about 0.3 kcal/mol in comparison to “gold standard” quantum chemical calculations for a wide range of intermolecular interactions in molecular dimers (31). We find that for our systems, the 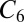coefficients of the ions depend strongly on their local coordination environments and can vary by an order in magnitude, making their explicit electron density-dependent evaluation critical to the accuracy of energetic and structural properties. These calculations show that the reduction in methyl-induced polarization of the S4 site associated with T→S substitutions is sufficient to explain the aforementioned experimental observations.

Results and Discussion

To understand how T→S substitutions in the S4 site affect K-channel function, we examine first the general consequences of methyl polarizability on the thermodynamics of ion binding. We estimate changes in enthalpies 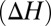and free energies 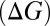for the substitution reactions

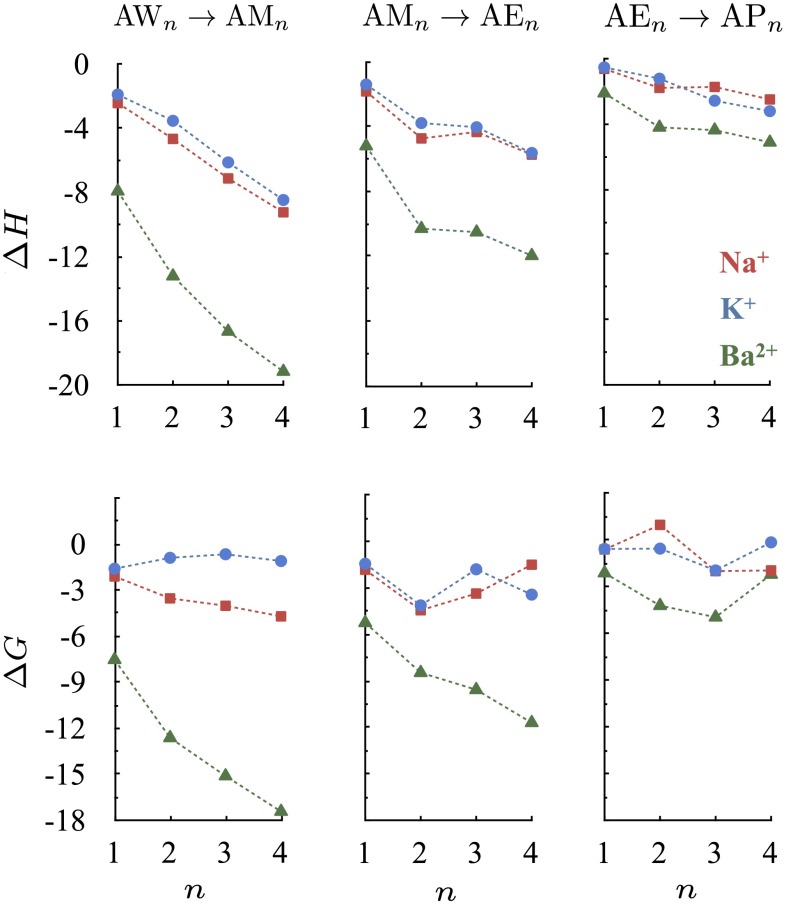
in the gas phase. We consider first the set of reactions in which A represents one of the ions Na⁺, K⁺, or Ba²⁺ and X represents one of the molecules water (W), methanol (M), ethanol (E), or propanol (P). Although these four small molecules all provide hydroxyl oxygens for ion coordination, they differ from each other in the number of methyl groups or methylene bridges they carry. Consequently, they have different static dipole polarizabilities of 1.5, 3.3, 5.4, and 6.7 ų, respectively (3). Note, however, that these four small molecules all have comparable gas phase dipole moments of 1.85, 1.70, 1.69, and 1.68 Debye, respectively (32). The PBE0 functional we use yields similar values for gas phase dipole moments, that is, 1.91, 1.68, 1.72, and 1.77 Debye, respectively. The results of the substitution reaction energy calculations are plotted in Fig. 2. The 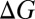values obtained for the set of reactions involving water molecules and methanols, for which experimental data are available (33–35), are in quantitative agreement with experimental values (Table S1). The explicit inclusion of dispersion improves the performance of PBE0 significantly.

Fig. 2.

Changes in ion complexation enthalpies 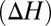and free energies 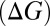due to an increase in the number of methyl groups or methylene bridges in the ion-coordinating ligands. 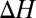and 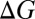are estimated at 298 K for the substitution reactions given by Eq. 1, which are denoted as 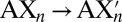. All energies are in units of kcal/mol.

We find that the stability of an ion complex, measured in terms of both enthalpy and free energy, increases with the numbers of methyl groups and methylene bridges in the coordinating ligand. This enhanced stability cannot be explained by considering the subtle differences in the gas phase dipole moments of the coordinating ligands (23), demonstrating that the enhanced stability is due to the larger ligand polarizabilities arising from the higher numbers of methyl groups or methylene bridges. The magnitude of the increase in stability, however, depends intricately on the interplay between several factors. Although the complex is stabilized less with each incremental change in hydrocarbon chain length, the increase in stability is still, for the molecules examined, large enough to be relevant physiologically. The 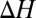and 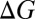associated with the substitution reactions also depend nonlinearly on ion coordination number. This nonlinearity emerges as a consequence of repulsion between the coordinating ligands (23, 36, 37). Finally, 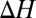and 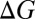also depend on the charge/size ratio of the ion, and once again, we find a nonlinear relationship between the charge/size ratio of the ion and the magnitude of the thermodynamic change. Doubling the charge/size ratio of the ion does not necessarily imply that the stability of the complex also increases by a factor of two, as may be the case when induced effects are small. For example, although the 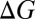associated with a K⁺W → K⁺M substitution is −1.9 kcal/mol, the 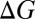associated with the Ba²⁺W → Ba²⁺M substitution is −7.9 kcal/mol, which is a fourfold change instead of a twofold change. This additional nonlinear effect also underscores the importance of explicit polarization effects in ion complexation (23). In a separate set of calculations, we find that although polarizable force fields can describe such trends, there can be notable quantitative differences with respect to PBE0+vdW (Fig. S1).

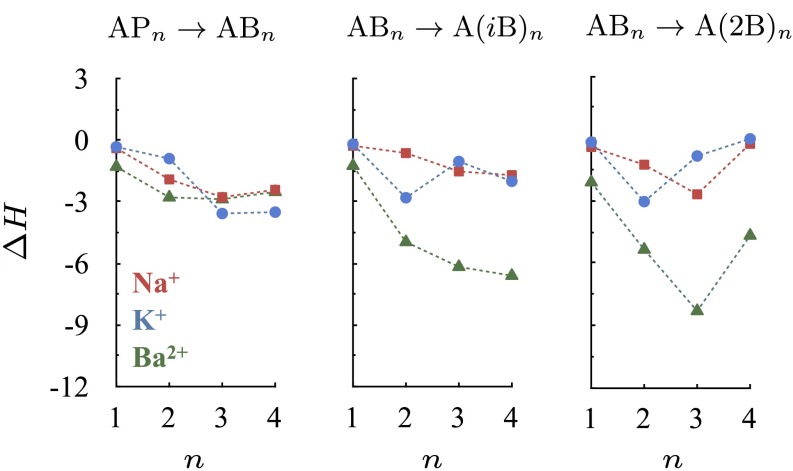
In the calculations above, the small molecules have similar gas phase dipole moments but markedly different polarizabilities. A ligand with a higher polarizability produces, in general, a more stable ion complex. Can ligands with similar gas phase dipole moments as well as static dipole polarizabilities produce complexes with markedly different stabilities? Butanol has three different isomers, l-butanol (B), isobutanol (iB) and 2-butanol (2B). Although these isomers have comparable gas phase dipole moments (∼1.7 Debye) and polarizabilities (∼8.9 ų) (3), the differences in their chemical structures will result in different distributions of methyl groups and/or methylene bridges around the ion. Consequently, despite their similar polarizabilities, they will respond to the spatially varying field differently. It may also be expected that ion complexes composed of isobutanol or 2-butanol, each of which carries one additional methyl group compared with l-butanol in its branched hydrocarbon chains, will have a denser packing of methyl groups near the central ion, and therefore higher stabilities compared with l-butanol.

To quantify this, we carry out substitution reactions (Eq. 1) involving these three butanol isomers. The results are plotted in Fig. 3. Indeed, we find that the isobutanol and 2-butanol complexes are, in general, more stable than the corresponding l-butanol complexes. Similar to the study above, 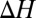depends nonlinearly on ion coordination number, a nonlinearity that emerges from ligand–ligand repulsion (23, 36, 37), which increases with ligand number. Therefore, packing increasingly higher numbers of methyl groups around the ion does not necessarily imply that the stability of the ion complex will increase. For example, although 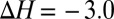kcal/mol for the substitution reaction 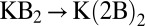, 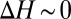for the substitution reaction 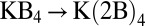. In addition, despite the fact that one of the two terminal methyl groups of 2-butanol is closer to the ion than that of isobutanol, complexes composed of 2-butanols are not necessarily more stable than the corresponding complexes of isobutanols. Thus, in addition to the static dipole polarizabilities of the methyl groups, their distribution around the ion matters.

Fig. 3.

Effect of butanol isomer on ion complexation enthalpies 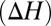. The enthalpies are estimated at 298 K for the substitution reactions given by Eq. 1, which are denoted as 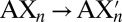. All energies are in units of kcal/mol.

We note that the distances of the ions from the closest methyl groups of 2-butanol (∼5 Å) are comparable to the distances of ions from the branched methyl group of threonine in the S4 site of KcsA (7, 11). In addition, the packing of the branched methyl group of threonine in the S4 site of KcsA is intermediate between the packing of branched methyl groups in fourfold complexes composed of 2-butanols and isobutanols (Fig. S2). This suggests that the reduction in methyl-induced polarization from T→S substitutions can reduce ion stabilities in the S4 sites of K channels. However, in the S4 sites of K channels, the ions coordinate with eight ligands and not just four hydroxyl ligands as studied above. Consequently, the repulsion between the coordinating ligands can be larger in the S4 site, which could reduce or wash out the contribution of the threonine methyl groups to the binding of ions at the S4 site. Furthermore, a T→S substitution may also alter the manner in which the coordinating groups of the S4 site interact with ions.

To resolve these issues and understand how the threonine methyl groups contribute to K-channel function, we consider an isolated S4 site composed of threonine residues. In this representative model, we substitute, in unit increments, the threonines with serines; that is,

and estimate the changes in free energy in the gas phase (Table 1). We find that the repulsion between the eight coordinating groups is not large enough to counteract the stabilization provided by the presence of methyl groups. The affinity of the S4 site for all three ions (Na⁺, K⁺, and Ba²⁺) diminishes, although nonlinearly, with each threonine substitution. Furthermore, these substitutions result in only minor configurational changes that do not alter the overall topology (geometry) of the S4 site (Fig. S3 and Table S2), which implies that the effect of T→S substitutions on configurational entropy will be minimal (38) and may be neglected. Although we find that the configurational change is generally higher in the case of Ba²⁺ complexes compared with Na⁺ and K⁺ complexes, we also note that optimizations of Ba²⁺ complexes following T→S substitutions, but under heavy atom position restraints, result in a higher drop in S4 site affinity. For example, a 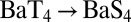substitution followed by a constrained optimization yields a single point energy difference, 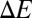= 8.8 kcal/mol, as opposed to the 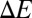= 5.2 kcal/mol obtained from an unconstrained optimization. This indicates that if the structure of the S4 site remained unchanged after a T→S mutation, the affinity of the S4 site for Ba²⁺ would drop even further than that reported in Table 1. Together, this suggests that the loss in affinity of the S4 site noted in Table 1 is not a result of altered ion binding topologies but is primarily due to a reduction in the methyl-induced polarization of the S4 site.

Table 1.

Free energy change 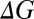(in kcal/mol) at 298 K associated with the substitution reaction given by Eq. 2

n	Na+	K+	Ba2+
1	1.5	1.4	2.3
2	2.2 (2.5)*	2.4 (1.7)*	3.4 (3.8)*
3	3.3	2.5	5.0
4	4.6	3.4	6.9

^*Two simultaneous T→S substitutions can be introduced in two different ways. In one case, the substitutions are made on adjacent threonine residues, and in the other case, the substitutions are made on nonadjacent threonine residues. The numbers in brackets correspond to T→S substitutions made on adjacent threonine residues.

When all four threonines are replaced by serines, the estimated drop in the affinity of the S4 site is the highest for Ba²⁺ (Table 1). The free energy difference of 6.9 kcal/mol is equivalent to a 10⁶-fold drop in binding affinity, where more than half of the affinity drop is due to a loss in dispersion energy (Table S3). The net drop in Ba²⁺ binding affinity accounts for the change in IC₅₀ values of Ba²⁺ seen in T→S substitution experiments (16). In addition, it accounts for the difference between the Kir 2.4 and Kir 2.1 experimental IC₅₀ values of Ba²⁺ (20, 21), because Kir 2.4 carries a serine and Kir 2.1 carries a threonine in the S4 site.

The computed drop in stability is, however, greater than that inferred from experiments (by over 3 kcal/mol). This discrepancy does not result from the pairwise approximation (31) used in the estimation of the dispersion energy. Although many body dispersion terms can contribute significantly to ligand binding (39), we find their contribution to be only 0.3 kcal/mol to the 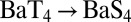substitution reaction (Table S3). We also do not expect this discrepancy to be due to the missing structural restraints from the protein matrix on the isolated S4 site, because the T→S substitutions are accompanied by only minor configurational changes (Table S2).

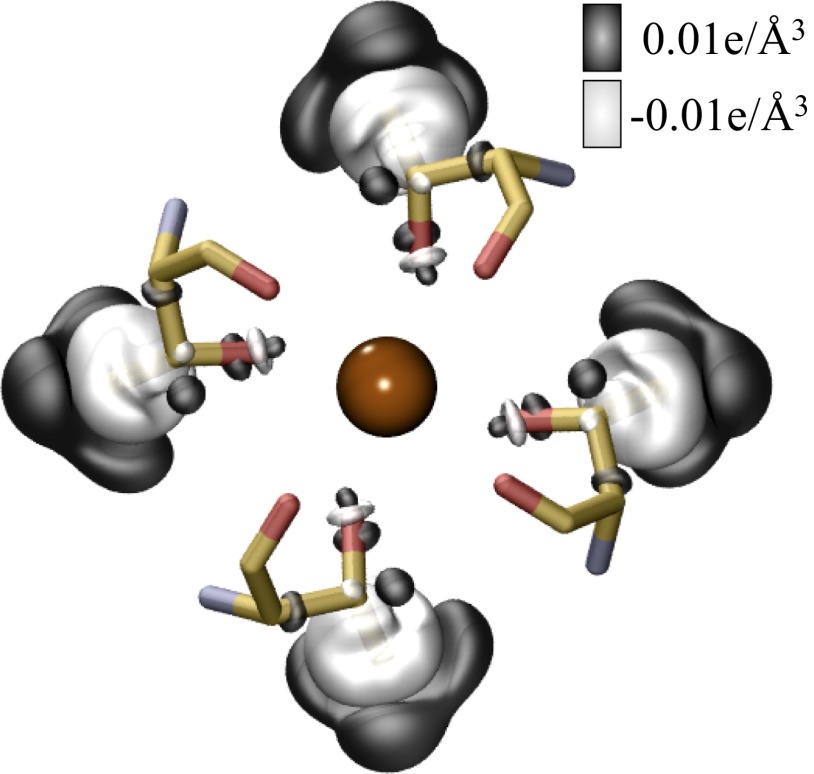
The overestimated drop in Ba²⁺ binding affinity is most likely because our calculations lack a polarization coupling between the S4 site and its external environment. Fig. 4 shows that the polarization in the electron density of the threonine methyl groups is along the electrical field of the Ba²⁺ ion, which maximizes the contribution of methyl polarization to Ba²⁺ binding. The presence of other polar chemical moieties proximal to the S4 site, including water molecules, can reduce the contribution of polarization, and thereby the overall effect of T→S substitutions on Ba²⁺ binding. Thermodynamically, this reduction will appear as an increase in the free energy penalty associated with threonine extraction from its local environment, which has been shown to influence ion binding (40, 41). Another possible explanation could be that the computed values may not be comparable directly with experimental estimates. It is plausible that a T→S substitution indeed causes the Ba²⁺ binding affinity of the S4 site to drop close to the computed value, and that in such an event, Ba²⁺ binds to an alternative site in the filter that is more favorable than the serine-containing S4 site. The experimental estimates of Ba²⁺ IC₅₀ values in the presence of threonines and serines could therefore correspond to two different binding sites of Ba²⁺ in the filter, instead of two different chemistries of an S4 binding site. Regardless, we find that the presence of methyl groups contributes significantly to the binding of Ba²⁺ ions to K channels.

Fig. 4.

Effect of T→S substitution on the electron density, ρ, of an isolated S4 site bound to Ba²⁺. This effect was estimated as 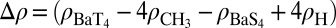using the PBE0+vdW functional. In the expression above, 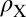are the electron densities of the isolated groups, X. The BaS₄ complex was constructed from the optimized geometry of the BaT₄ complex by first replacing its side-chain CH₃ groups with H atoms and then relaxing the H atom coordinates. Two separate isosurfaces of electron density (electrons/ų) are shown, one in black (0.01 e/ų) and the other in white (−0.01 e/ų).

From Table 1, we also see that when all four threonines are replaced by serines, the stability of the S4 site complexed with K⁺ ions drops by 3.4 kcal/mol. It is known that K⁺ binding to the selectivity filter contributes to the organization of the filter’s conductive state, as well as to the channel’s ability to assemble into tetramers (7, 42–44). A drop in K⁺ binding affinity at the S4 site could therefore destabilize the filter’s conductive state and/or impede the channel’s ability to form tetramers. Indeed, electrophoresis studies show that T→S substitutions in Kcv reduce the channel’s ability to assemble into tetramers (16). In addition, electrophysiological studies show that T→S substitutions in Kir 2.1 alter the channel’s mean open probabilities (16). The binding of K⁺ ions to the S4 site also plays a vital role in the concerted movement of ions along the permeation pathway (10, 45–52). A T→S substitution could therefore potentially also alter the kinetics of K⁺ transport through the channel, although no such effects were observed in experiments on Kcv and Kir 2.1 channels (16). Nevertheless, it is clear from Table 1 and Figs. 2 and 3 that the polarization induced by methyl groups can contribute significantly to how K⁺ ions interact with the channel, and therefore with the ions’ transport properties.

The data in Table 1 also indicate that T→S substitutions will lower the affinity of the S4 site for Na⁺ ions. This reduction is, in general, greater than that estimated in the case of K⁺ ions, which suggests that T→S substitutions will also increase the K/Na selectivity of the S4 site. This, however, does not imply that the overall selectivity of the channel will also increase. Thermodynamic calculations on KcsA indicate that the contribution of the S4 site to the channel’s K/Na selectivity is small (53). Furthermore, the channel’s overall selectivity also depends on the number of eightfold ion binding sites in the selectivity filter (54) and how these sites interact with their proximal environment, including with each other (40, 55, 56). Although it is not straightforward to ascertain how these effects will interplay to alter the selective properties of T→S mutant channels, electrophysiological studies show that T→S substitutions in Kcv channels do not alter K/Na selectivity (16).

Together, we find that the polarization induced by methyl groups stabilizes ion complexation significantly, and can therefore also be expected to influence the interactions of other biological charged species. The magnitude of the effect depends nonlinearly on ion charge and the proximity of the methyl group from the ion, as well as on the number of methyl groups present in the ion complex. T→S substitutions in the S4 sites of K channels result in removal of methyl groups from a distance greater than 5 Å from the ion. Although the architecture of the binding site is affected minimally, the stability of the S4 site for Ba²⁺ drops by several kilocalories per mole with the T→S substitution. This destabilization accounts for the changes in IC₅₀ values of Ba²⁺ seen in experiments. Additionally, the affinity of the S4 site drops for K⁺ ions, which correlates with changes in gating properties as well as a reduction in the overall stability of the channel. These results show how polarization induced by methyl groups is important to both K-channel function and stability.

Summary

Naturally occurring or engineered T→S substitutions at the S4 ion binding sites of K channels reduce the number of methyl groups near the ion. Despite this seemingly benign change in the number of hydrophobic groups, electrophysiological experiments show that T→S substitutions modify K-channel properties. Results from our first-principles quantum mechanical calculations account for these modifications. We find that the methyl-induced polarization is large enough that its reduction in S4 sites due to T→S substitutions reduces ion affinities dramatically, with minimal change in topology. This loss in ion affinity is consistent with experimental observations, such as changes in open channel probabilities, and IC₅₀ values of Ba²⁺. These results illustrate quantitatively how protein function can also rely on the polarization induced by methyl groups. Given the abundance of charged moieties in biological systems, such as ions, titratable amino acids, sulfates, phosphates, and nucleotides, it appears unlikely that we have uncovered an unwonted instance of where the polarizability of methyl groups matters. The recent advances in computational methods now permit a proper quantitative assessment of the role of methyl groups in biomolecular function.

Materials and Methods

Free energy changes 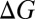associated with the substitution reactions (Eqs. 1 and 2) are obtained after relaxing each molecular complex separately using the DFT+vdW method (30) implemented in the all-electron, localized basis FHI-aims program package (57, 58). The vdW-corrected PBE (26) functional (PBE+vdW) is used for relaxations. Within the DFT+vdW method, PBE performs well against the S22 dataset (59), exhibiting a mean absolute error of only 0.3 kcal/mol (31). Relativistic corrections are used only for complexes containing barium ions, and using the atomic zeroth order regular approximation (ZORA) method (57, 60). We use the “tight” settings for integration grids and basis sets, as described by Blum et al. (57), which yield converged energy differences and negligible basis set superposition error. The starting geometries of the ion–water complexes are taken from the work of Varma and Rempe (41), and the starting geometries of the ion–alcohol complexes are constructed using the ion–water complexes as templates. The coordinates for the S4 site of the K-channel selectivity filter are taken from the X-ray structure of KcsA (7).

Following relaxation, the complex geometries are subjected to a single point calculation using the hybrid PBE0 (27, 28) +vdW functional. Due to the partial inclusion of exact exchange in PBE0, this functional improves the description of electron delocalization (61). This is important to the estimation of vdW contributions, 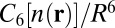, because they depend explicitly on the self-consistent electron densities, 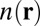. The translational, rotational, and vibrational contributions are estimated separately for each molecular complex, with the PBE+vdW functional, at a temperature of 298 K and a pressure of 1 atm. These contributions are then added to the PBE0+vdW single point energies to obtain the free energies G of individual complexes. The free energy changes 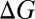associated with the substitution reactions are then obtained by subtracting the free energies of reactant complexes from the product complexes; that is, 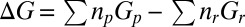, where 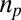and 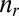are the stoichiometries of the products and reactants.