Abstract
We present a new approach to localization of sensors from noisy measurements of a subset of their Euclidean distances. Our algorithm starts by finding, embedding, and aligning uniquely realizable subsets of neighboring sensors called patches. In the noise-free case, each patch agrees with its global positioning up to an unknown rigid motion of translation, rotation, and possibly reflection. The reflections and rotations are estimated using the recently developed eigenvector synchronization algorithm, while the translations are estimated by solving an overdetermined linear system. The algorithm is scalable as the number of nodes increases and can be implemented in a distributed fashion. Extensive numerical experiments show that it compares favorably to other existing algorithms in terms of robustness to noise, sparse connectivity, and running time. While our approach is applicable to higher dimensions, in the current article, we focus on the two-dimensional case.
Keywords: Sensor networks, distance geometry, eigenvectors, synchronization, rigidity theory, spectral graph theory
1. INTRODUCTION
Consider a graph G = (V, E) consisting of a set of |V| = n nodes and |E| = m edges, together with a distance measurement associated with each edge. The graph realization problem is to assign to each vertex coordinates in so that the Euclidean distance between any two neighboring nodes matches the distance associated to that edge. In other words, for any edge (i, j) ∈ E, we are given the distance dij = dji between nodes i and j, and the goal is to find a d-dimensional embedding such that ||pi − pj|| = dij, for all (i, j) ∈ E. The graph realization problem comes up naturally in a variety of settings, such as wireless sensor networks [Biswas et al. 2006a; Tubaishat and Madria 2003], structural biology [Hendrickson 1995] and multidimensional scaling (MDS) [Cox and Cox 2001]. In such real-world applications, the given distances dij between nodes are not accurate, dij = ||pi − pj|| + εij where εij represents the added noise, and the goal is to find an embedding that realizes all known distances dij as best as possible.
When all n(n − 1)/2 pairwise distances are known, a d-dimensional embedding of the complete graph can be computed using classical MDS. However, when many of the distance constraints are missing, the problem becomes significantly more challenging, because the rank-d constraint on the solution is not convex. Applying a rigid transformation (composition of rotation, translation, and possibly reflection) to a graph realization results in another graph realization, because rigid transformations preserve distances. Whenever an embedding exists, it is unique (up to rigid transformations) only if there are enough distance constraints, in which case the graph is said to be globally rigid or uniquely realizable (e.g., [Hendrickson 1992]). The graph realization problem is known to be difficult; Saxe has shown that it is strongly NP-complete in one dimension and strongly NP-hard for higher dimensions [Saxe 1979; Yemini 1979]. Despite its difficulty, the graph realization problem has received a great deal of attention in the networking and distributed computation communities, and numerous heuristic algorithms exist that approximate its solution. In the context of sensor networks [Ji and Zha 2004; Aspnes et al. 2004, 2006; Anderson et al. 2009], there are many algorithms that solve the graph realization problem, and they include methods such as global optimization [Borg and Groenen 2005], semidefinite programming (SDP) [Biswas and Ye 2004; Biswas et al. 2006a, 2006b; So 2007; So and Ye 2005; Zhu et al. 2010], and local-to-global approaches [Moore et al. 2004; Shang and Ruml 2004; Koren et al. 2005; Singer 2008; Zhang et al. 2010].
In this article, we focus on the problem of sensor network localization (SNL) in the plane (), although the approach is applicable to higher dimensions (d > 2) as well. Sensor networks are a collection of autonomous miniature devices distributed over a geographical area that cooperate to monitor various physical or environmental conditions. Each sensor is capable of limited computing power and wireless communication capabilities. While the initial development was motivated mainly by military applications, the current range of applications of sensor networks includes video surveillance, medical devices, monitoring of weather conditions, and traffic control [Tubaishat and Madria 2003]. Since each sensor typically communicates with a small number of dynamic neighboring nodes, information flows through the network by means of adhoc routing algorithms. Traditional routing algorithms were based only on the connectivity of the measurement graph, but location-aware sensors lead to more efficient geographic routing. Such algorithms for geographically informed routing assume that nodes are located at precise coordinate locations or that the sensors are equipped with a GPS or similar localization systems. However, for certain applications, GPS devices may be too expensive, have high power consumptions, or may not be available, as in indoors applications. Sensors that are aware of their location are often referred to as anchors, and anchor-based algorithms make use of their existence when computing the coordinates of the remaining sensors. Since the presence of anchors is not a realistic assumption in some applications, it is important to have efficient anchor-free algorithms that are also robust to noise that can also incorporate the location of anchors if provided.
A popular model for the SNL problem is that of a disc graph model in which two sensors communicate with each other if and only if they are within sensing radius ρ of each other, that is, (i, j) ∈ E ⇔ dij ≤ ρ. The SNL problem is NP-hard also under the disc graph model [Aspnes et al. 2006]. Measuring inter-sensor distances is usually achieved by either the received signal strength indicator (RSSI), where the strength of the signal decays with the increase of the distance, or the time of arrival (ToA) technique that uses the difference in the arrival times of the radio signal. Figure 1 shows an example of a measurement graph for a dataset of n = 1,090 cities in the United States with sensing radius ρ = 0.032, for which each node knows, on average, the distance to its deg = 19 closest neighbors.
Fig. 1.
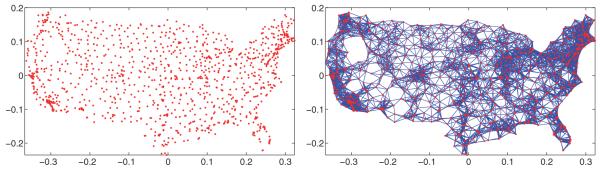
Original U.S. map with n = 1,090 cities (left) and the measurement graph with sensing radius ρ = 0.032 (right).
Solutions to the SNL problem are often measured by three criteria: (1) sensitivity to noise in the distance measurements and sparse connectivity; (2) scalability to large networks; and (3) the property of being fully distributable. The third criterion means that local computations at each sensor should be based only on information available at that sensor and its neighbors. Most of the SNL algorithms, while allowing for distributable implementations, are sensitive to noise and do not scale well as the size of the network increases.
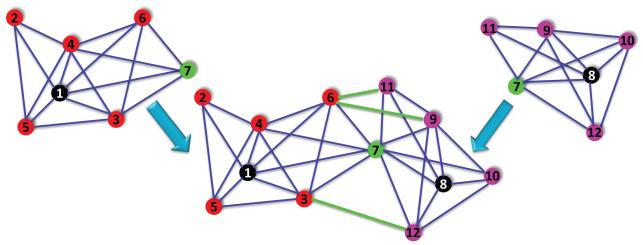
The algorithm we propose in this article belongs to the group of algorithms that integrate local distance information into a global structure determination. Our approach starts with identifying, for every sensor, globally rigid subgraphs of its 1-hop neighborhood that we call patches. Each patch is then separately localized in a coordinate system of its own using either the stress minimization approach of Gotsman and Koren [2004] or by SDP. In the noise-free case, the computed coordinates of the sensors in each patch must agree with their global positioning up to some unknown rigid motion, that is, up to translation, rotation, and possibly reflection. To every patch there corresponds an element of the Euclidean group Euc(2) of rigid transformations in the plane, and the goal is to estimate the group elements that will properly align all the patches in a globally consistent way. By finding the optimal alignment of all pairs of patches whose intersection is large enough, we obtain measurements for the ratios of the unknown group elements. Finding group elements from noisy measurements of their ratios is also known as the synchronization problem [Karp et al. 2003; Giridhar and Kumar 2006]. For example, the synchronization of clocks in a distributed network from noisy measurements of their time offsets is a particular example of synchronization over . Singer [2010] introduced an eigenvector method for solving the synchronization problem over the group SO(2) of planar rotations. This algorithm will serve as the basic building block for our SNL algorithm. Namely, we reduce the SNL problem to three consecutive synchronization problems that overall solve the synchronization problem over Euc(2). Intuitively, we use the eigenvector method for the compact part of the group (reflections and rotations) and use the least-squares method for the non-compact part (translations). In the first step, we solve a synchronization problem over for the possible reflections of the patches using the eigenvector method. In the second step, we solve a synchronization problem over SO(2) for the rotations also using the eigenvector method. And, in the third step, we solve a synchronization problem over for the translations by solving an overdetermined linear system of equations using the method of least squares. This solution yields the estimated coordinates of all the sensors up to a global rigid transformation. Figure 2 shows a schematic overview of our algorithm, which we call As-Synchronized-As-Possible (ASAP).
Fig. 2.
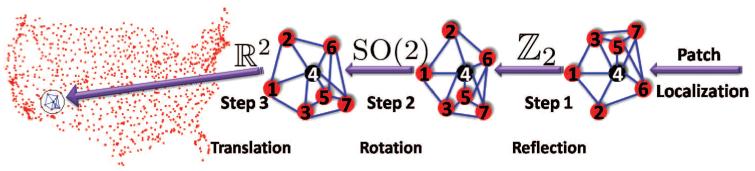
The ASAP recovery process for a patch in the U.S. cities graph. The rightmost subgraph is the embedding of the patch in its own local frame using a localization algorithm, such as stress minimization or SDP. To every patch, like the one shown here, there corresponds elements of Euc(2) that we try to estimate. Using the pair alignments, in Step 1 we estimate the reflection from an eigenvector synchronization computation over , in Step 2 we estimate the rotation angle by the same eigenvector synchronization method applied to SO(2), while in Step 3 we find the estimated coordinates by solving an overdetermined system of linear equations.
From the computational point of view, all steps of the algorithm can be implemented in a distributed fashion and scaled linearly in the size of the network, except for the eigenvector computation, which is nearly linear.1 We give a complexity analysis of the ASAP algorithm in Section 7 and demonstrate its scalability by localizing a network with 100,000 nodes. We conducted numerous numerical experiments that demonstrate the robustness of our algorithm to noise and to sparse connectivity of the measurement graph.
This article is organized as follows: Section 2 contains a survey of existing methods for solving the SNL problem. Section 3 gives an overview of the ASAP algorithm we propose. In Section 4, we motivate the robustness to noise using spectral graph theory. In Section 5, we explain the procedure for breaking up the initial large network into many smaller globally rigid subgraphs. In Section 6, we describe several methods for aligning pairs of overlapping patches that have enough nodes in common. Section 7 is a complexity analysis of each step of ASAP, and shows that the algorithm scales almost linearly in the size of the network. In Section 8, we detail the results of numerical simulations in which we tested the performance of our algorithm in comparison to existing state-of-the-art algorithms. Finally, Section 9 is a summary and a discussion of possible extensions of the algorithm and its usefulness in other applications.
2. RELATED WORK
An approximate solution to the SNL problem is a two-dimensional embedding that realizes all measured distances dij , (i, j) ∈ E as best as possible. A popular approach to solving the SNL problem is based on SDP and has attracted considerable attention in recent years [Biswas and Ye 2004; Biswas et al. 2005; Biswas et al. 2006a, 2006b; Zhu et al. 2010]. One possible way of solving the SNL problem is to find the embedding p1, … , pn that minimizes the following error function.
| (1) |
While this objective function is not convex over the constraint set, it can be relaxed into an SDP [Biswas et al. 2006a]. Although SDP generally can be solved (up to a given accuracy) in polynomial time, it was pointed out in Biswas et al. [2006b] that the objective function of Equation (1) leads to a rather expensive SDP, because it involves fourth-order polynomials of the coordinates. Additionally, this approach is rather sensitive to noise, because large errors are amplified by the objective function in Equation (1), compared to the objective functions in Equation (2) and (3) that are discussed next.
Instead of using the objective function in Equation (1), Biswas et al. [2006b] consider the SDP relaxation of the following penalty function.
| (2) |
In fact, they also allow for possible nonequal weighting of the summands in Equation (2) and for possible anchor points. The SDP relaxation of Equation (2) is faster to solve than the relaxation of Equation (1), and it is usually more robust to noise. Constraining the solution to be in is non-convex, and its relaxation by the SDP often leads to solutions that belong to a higher dimensional Euclidean space that are projected to the plane. This projection often results in large errors for the estimation of the coordinates. A regularization term for the objective function of the SDP was suggested in Biswas et al. [2006b] to assist it in finding solutions of lower dimensionality and preventing nodes from crowding together towards the center of the configuration. To improve the overall localization result, the SDP solution is used as a starting point for a gradient-descent method. The gradient-descent method generally fails to compute the global optimal solution of the non-convex problem unless a good initialization is provided.
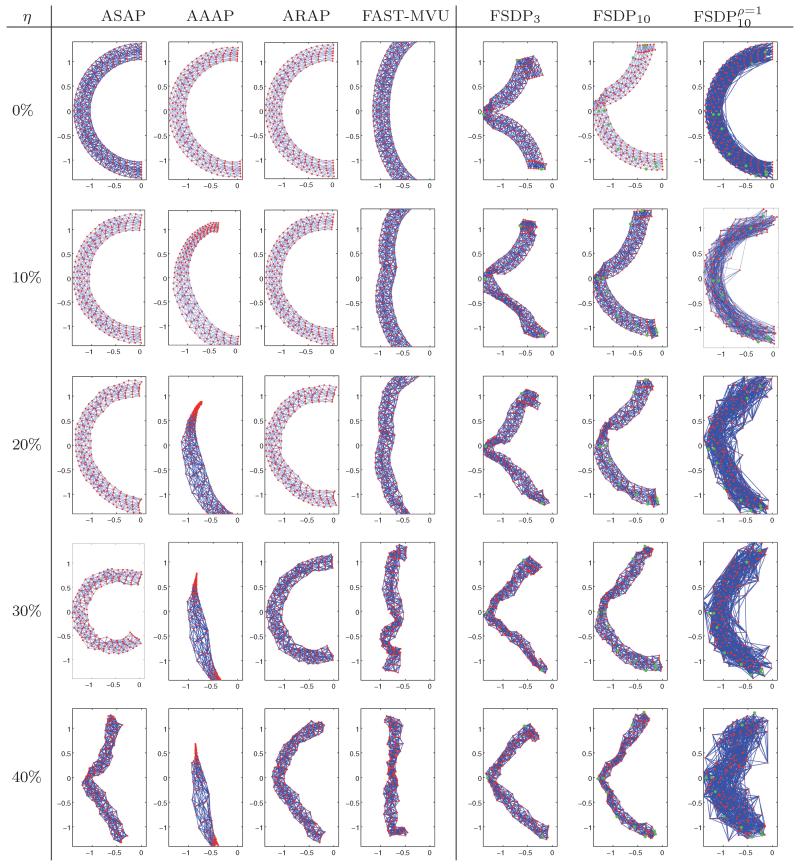
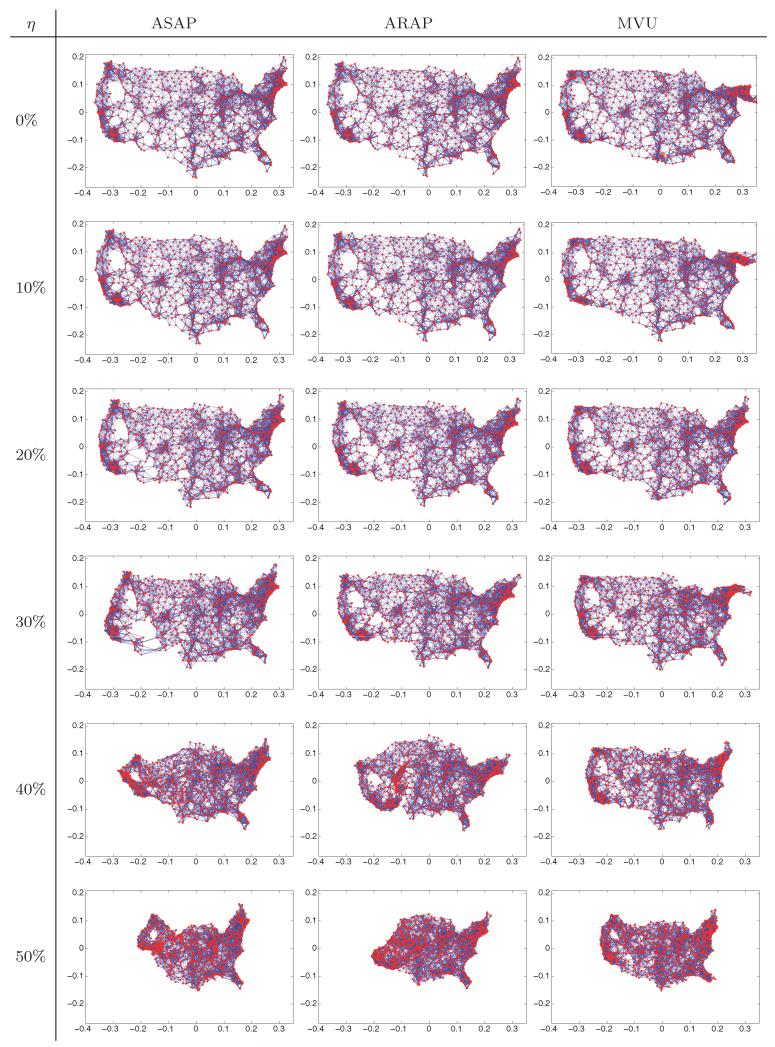
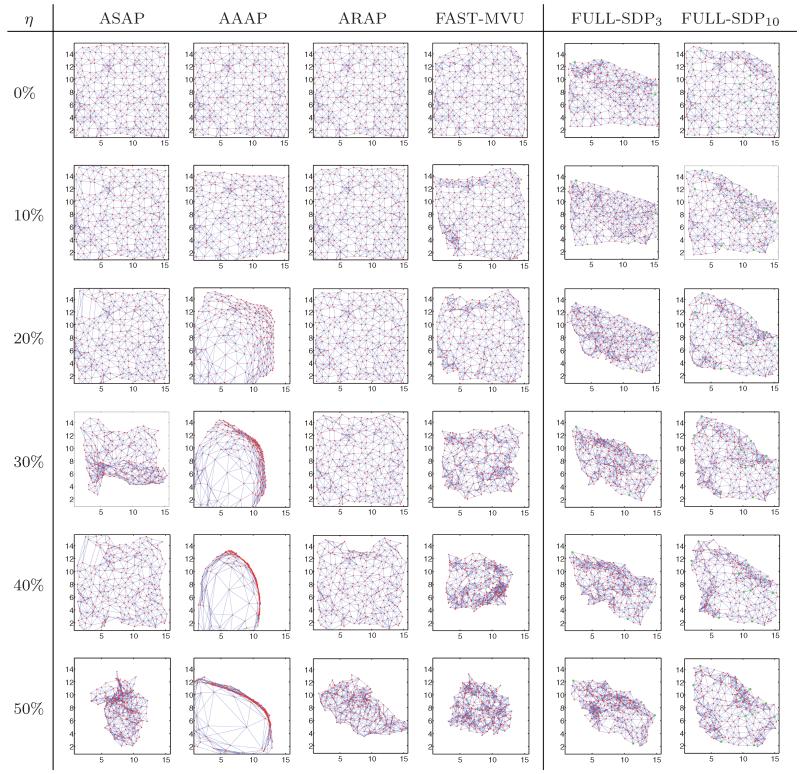
In our simulations, we find that in the absence of anchor points, the SDP approach works well when the sensing radius is large enough and for relatively low levels of noise. However, as the size of the network grows, solving one large SDP problem can become too expensive. The numerical simulations in Figures 21 and 22 (at the end of the article) show that the SDP approach is sensitive to high levels of noise, to sparse connectivity of the graph, and to the number and the locations of the anchors.
Fig. 21.
Reconstructions of the sparse C graph with n = 200 nodes, ρ = 0.17, and η = 0%, 10%, 20%, 30%, 40%.
Fig. 22.
Reconstructions of the dense C graph with n = 200 nodes, ρ = 0.28, and η = 35%,40%, 50%, 60%, 70%.
Another approach to solving the SNL problem is by minimizing the following stress function
| (3) |
over all possible configurations . One of the more recent iterative algorithms that was observed to perform well in practice compared to other traditional optimization methods is a variant of the gradient-descent approach called the stress majorization algorithm, also known as SMACOF [Borg and Groenen 2005], originally introduced by De Leeuw [1977]. The main drawback of this approach is that the stress function in Equation (3) is not convex, and the search for the global minimum is prone to getting stuck at local minima. This often makes the initial guess for gradient-descent-based algorithms important for obtaining satisfactory results. What usually happens at a local but not global minimum is a phenomenon known as foldovers, where large pieces of the graph realization fold on top of others. Long-range distance measurements help to prevent foldovers in the recovered solution, but such measurements are rarely available in applications and are completely absent in the disc graph model.
Moore et al. [2004] proposed an incremental algorithm which first tries to localize small subsets of the network. Each such local subset consists of four sensors forming a rigid graph, that is, the complete graph K4 on four vertices where all six pairwise distances are known (a quad). The procedure for embedding such quads is called trilateration, and the method is incremental in the sense that once a quad has been localized, another one is found which has a common triangle with the first one, and the alignment is performed by applying the best possible rigid transformation between the two. Using breadth-first-search, all the existing quads of the graph are localized with the intermediate embedding being improved at each step by running stress minimization. One drawback of this method, besides being incremental, is that it localizes only sensors contained in trilateralizable components of the network, but not all globally rigid graphs are trilateralizable.
Shang and Ruml [2004] describe a similar algorithm that first localizes small subsets of nodes and then stitches them together sequentially. The initial embedding of a patch is obtained by first computing all pairwise shortest paths in the weighted connectivity graph of the patch in order to estimate all missing distances, followed by MDS to obtain an initial estimate, which is then improved by running the stress minimization algorithm. The patches are glued together incrementally in a greedy fashion by finding the best affine transformation between a new patch and the current global layout. Finally, the complete network obtained in this manner is improved using stress minimization. The main drawback of such incremental algorithms is their sensitivity to noise due to accumulation of the errors.
In an attempt to depart from the noise-sensitive incremental methods, Koren et al. [2005] proposed PATCHWORK, an algorithm that avoids stitching patches together in a greedy manner. Their method embeds small local patches that are later glued together using a distributed global optimization process. Patches are mapped to a global coordinate system using affine transformations, and the patch overlaps yield a linear least-squares problem, enforcing that the transformations agree well on the common vertices.
Maximum variance unfolding (MVU) is a nonlinear dimensionality reduction algorithm proposed by Weinberger et al. [2007]. It produces a low-dimensional representation of the data by maximizing the variance of its embedding while preserving the original local distance constraints. MVU builds on the SDP approach and addresses the issue of the possibly high dimensional solution to the SDP problem. While rank constraints are non-convex and cannot be directly imposed, it has been observed that low dimensional solutions emerge naturally, maximizing the variance of the embedding (also known as the maximum trace heuristic). Their main observation is that the x and y coordinate vectors of the sensors are often well approximated by just the first few (e.g., 10) low-oscillatory eigenvectors of the graph Laplacian. This observation allows for replacing the original and possibly large-scale SDP with a much smaller SDP, which leads to a significant reduction in running time.
The Locally Rigid Embedding (LRE) algorithm [Singer 2008] is reminiscent of the Locally Linear Embedding (LLE) [Roweis and Saul 2000] technique used in machine learning for dimensionality reduction. LRE tries to preserve, in a global coordinate system, the local affine relationships present within patches. Each sensor contributes with a linear equation relating its location to those of its neighboring nodes, thus altogether setting up a global linear system. LRE builds up a specially designed sparse matrix whose eigenvectors give an embedding of all sensors from which a global affine transformation must be removed. The LRE algorithm is able to recover the global coordinates from local noisy measurements under the assumption that every node, together with its neighbors, forms a rigid subgraph that can be embedded uniquely, up to a rigid transformation.
Zhang et al. [2010] recently proposed an algorithm along the lines of PATCHWORK and LRE, called As-Rigid-As-Possible (ARAP). Their algorithm starts off by localizing small patches in a similar manner, but instead of finding a global embedding via affine mappings, they use rigid mappings. Again, the patch overlaps impose constraints on the mappings; however, the usage of rigid mappings has the advantage of better preserving the local relationships between patches. This comes at the price of resulting in a nonlinear optimization problem which is solved efficiently using a two-phase alternating least-squares method. The algorithm requires an initial guess for the nonlinear optimization which is obtained by As-Affine-As-Possible (AAAP), an improved version of the LRE and PATCHWORK algorithms. The reported experimental results, confirmed also by our own experiments, show that ARAP is more robust to sparse connectivity and noise in the measurement graph compared to all other algorithms surveyed in the preceding.
3. THE ASAP ALGORITHM
The gist of our algorithm is to break up the large graph into many smaller overlapping subgraphs that we call patches and “stitch” them together consistently in a global coordinate system with the purpose of localizing the entire measurement graph. To avoid foldovers in the final solution, each such patch needs to be globally rigid, and the entire measurement graphs needs to be globally rigid as well.2
The patches are determined in the following way. For every node i we denote by V(i) = {j:(i, j) ∈ E} ∪ {i} the set of its neighbors together with the node itself, and by G(i) = (V(i), E(i)) its subgraph of one-hop neighbors. If G(i) is globally rigid, then we embed it in . If G(i) is not globally rigid, we break it into maximally globally rigid subgraphs that we call patches and embed each patch in . The embedding of every patch in is given in its own local frame. The exact way we break up the one-hop neighborhood subgraphs into smaller maximally globally rigid subgraphs is detailed in Section 5. We denote by N the number of patches obtained in the preceding decomposition of the measurement graph and note that it may be different from n, the number of nodes in G, since the neighborhood graph of a node may contribute several patches or none.
For the embedding of local patches we usually use the Stress majorization algorithm as described in [Gotsman and Koren 2004]. Once each patch is embedded in its own coordinate system, one must find the reflections, rotations and translations that will stitch all patches together in a consistent manner, a process to which we refer as synchronization.
To every patch Pi there corresponds an element ei ∈ Euc(2), where Euc(2) is the Euclidean group of rigid motions in the plane. The rigid motion ei moves patch Pi to its correct position with respect to the global coordinate system. Our goal is to estimate the rigid motions e1, …, eN (up to a global rigid motion) that will properly align all the patches in a globally consistent way. To achieve this goal, we first estimate the alignment between any pair of patches Pi and Pj that have enough nodes in common (alignment methods are discussed in Section 6). The alignment of patches Pi and Pj provides a (perhaps noisy) measurement for the ratio in Euc(2). We solve the resulting synchronization problem in a globally consistent manner such that information from local alignments propagates to pairs of non-overlapping patches. This is done by replacing the synchronization problem over Euc(2) with three different consecutive synchronization problems. In the first synchronization problem, we find the reflections of all the patches using the eigenvector synchronization algorithm over the group . Once the reflections are estimated, we use the eigenvector synchronization method over SO(2) to estimate the rotations of all patches. Once both reflections and rotations are estimated, we estimate the translations by solving an overdetermined linear system. In other words, we integrate all the available local information into a global coordinate system over several steps by using the eigenvector synchronization algorithm and least squares over the isometries of the Euclidean plane. The main advantage of the eigenvector method is that it can recover the reflections and rotations even if some of the alignments are incorrect. The algorithm is summarized in Table I.
Table I.
Overview of the ASAP Algorithm
| INPUT | G = (V, E), |V| = n, |E| = m, dij for (i, j) ∈ E |
|---|---|
| Pre-processing Step |
|
| Step 1 Estimating Reflections |
|
| Step 2 Estimating Rotations |
|
| Step 3 Estimating Translations |
|
| OUTPUT | Estimated coordinates |
3.1. Step 1: Synchronization over to Estimate Reflections
As mentioned earlier, for every patch Pi that was already embedded in its local frame, we need to estimate whether or not it needs to be reflected with respect to the global coordinate system. We denote the reflection of patch Pi by zi ∈ {−1, 1}. These are defined up to a global reflection (global sign). The alignment of every pair of patches Pi and Pj whose intersection is sufficiently large provides a measurement zij for the ratio . However, some ratio measurements can be corrupted because of errors in the embedding of the patches due to noise in the measured distances. We denote by GP = (VP, EP) the patch graph whose vertices VP are the patches P1, …, PN, and two patches Pi and Pj are adjacent, that is, (Pi, Pj) ∈ EP, if and only if they have enough3 vertices in common to be aligned such that the ratio can be estimated.
The first step of the ASAP algorithm is to estimate the appropriate reflections of all patches. To that end, we use the eigenvector synchronization method, as it was shown to perform well even in the presence of a large number of errors. The eigenvector method starts off by building the following N × N sparse symmetric matrix Z = (zij).
| (4) |
We explain in more detail in Section 6 the procedures by which we align pairs of patches, if such an alignment is at all possible.
Prior to computing the top eigenvector of the matrix Z, as done in Singer [2010], we choose to normalize it as follows. Let D be an N × N diagonal matrix4 whose entries are given by . In other words,
| (5) |
where deg(i) is the node degree of patch Pi in GP, that is, the number of other patches that can be aligned with it. We define the matrix as
| (6) |
and note that although not necessarily symmetric, it is similar to the symmetric matrix D−1/2ZD−1/2 through
Therefore, the matrix has N real eigenvalues and N orthonormal eigenvectors , satisfying . In the eigenvector method, we compute the top eigenvector of , which satisfies
| (7) |
and use it to obtain estimators for the reflections of the patches in the following way:
| (8) |
The top eigenvector recovers the reflection of all patches up to a global sign, since if is the top eigenvector of , then so is . After estimating the reflection of all patches, we replace the embedding of patch Pi by its mirrored image whenever .
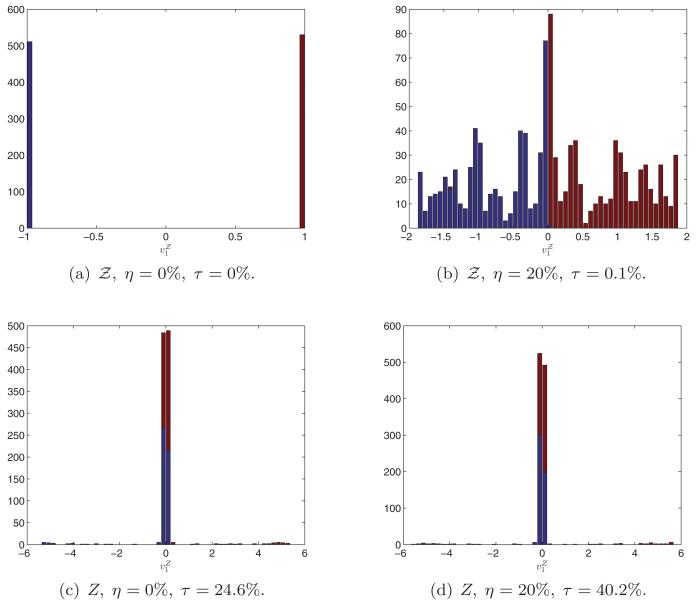
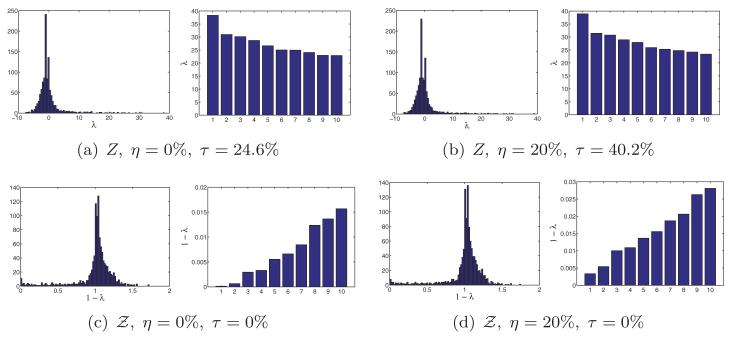
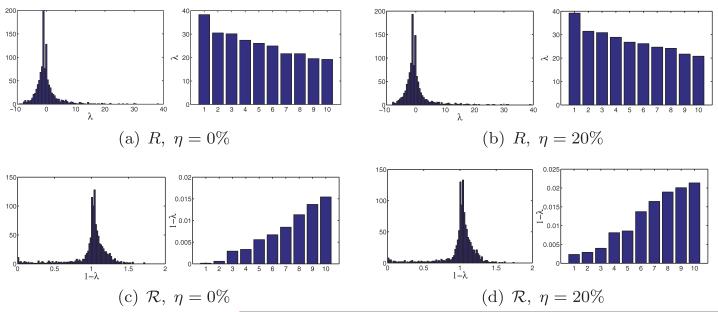
Both the success of the eigenvector method in estimating the correct reflections and the importance of the normalization in Equation (6) are demonstrated in Figures 4 and 5 that correspond to the U.S. cities graph with sensing radius ρ = 0.032 and average degree deg = 19. The percentages of patches for which the top eigenvector of failed to estimate the reflection correctly are only τ = 0% and τ = 0.1%, corresponding to distance measurement errors of η = 0% and η = 20%, respectively (η is defined in Equation (43)). That is, even when the measured distances are off by as much as 20% from their correct values, only 0.1% of the patches were assigned the wrong reflection. Without the normalization, however, extracting the signs of the top eigenvector of Z leads to significantly larger error rates (τ = 24.6% and τ = 40.2%). In Section 4, we provide the theoretical explanation for this behavior, but the numerical evidence in Figures 4 and 5 already provides some intuition. For example, Figure 4 shows that most entries of are close to zero (even in the noise-free case), and therefore sign confusion is probable, while only a few entries have large magnitude. On the other hand, for the normalized matrix , its top eigenvector in the noise-free case has only two possible values (1 and −1), and even in the noisy case in which entries have different magnitudes, their signs rarely get confused. Another difference between the two cases can be realized from Figure 5 that shows the eigenvalue histograms and bar plots for the matrices Z and . While the eigenvalues of Z are both negative and positive, all eigenvalues of seem to be nonnegative, as the latter matrix is related to the Laplacian of the patch graph, a fact that will be later explored in Section 4.
Fig. 4.
Histogram of the entries of the top eigenvectors and (scaled such that ) for various noise levels for the U.S. cities graph with sensing radius ρ = 0.032. Patches Pi for which z1 = −1 are colored blue, while patches for which zi = 1 are marked in red. Note that the top eigenvector is a good classifier between red and blue, while results in many misclassifications.
Fig. 5.
Histogram of all eigenvalues and bar plot of the top ten eigenvalues of Z and for the U.S. cities graph with ρ = 0.032 (deg = 19) and various noise levels η. The resulting error rate τ is the percentage of patches whose reflection was incorrectly estimated. To ease the visualization of the eigenvalues of , we choose to plot , because the top eigenvalues of tend to pile up near 1, so it is difficult to differentiate between them by looking at the bar plot of .
3.2. Step 2: Synchronization over SO(2) to Estimate Rotations
After estimating the reflections, we turn in Step 2 to estimate the rotations of all patches that will properly align them with respect to the global coordinate system, up to translations and a global rotation. To each patch, we associate an element ri ∈ SO(2), i = 1, …, N that we represent as a point on the unit circle in the complex plane ri = eiθi, = cos θi + ι sinθi. We repeat the alignment process from Step 1 to estimate the angle θij between two overlapping patches, that is, the angle by which one needs to rotate patch Pi to align it with patch Pj. When the aligned patches contain corrupted distance measurements, θij is a noisy measurement of their offset θi − θj mod 2π. Following a similar approach to Step 1, we build the N × N sparse symmetric matrix R = (rij) whose elements are either 0 or points on the unit circle in the complex plane.
| (9) |
Since θij = −θji mod 2π, it follows that R is a Hermitian matrix, that is, , where for any complex number w = a + ιb, we denote by its complex conjugate. Note that the patch graph GP may which is similar to the Hermitian matrix may change (have extra edges) from Step 1 to Step 2, because the registration method needs at least three nodes in the intersection of patches Pi and Pj in order to compute the relative reflection but only two such points to compute the rotation angle. However, for simplicity, we assume that the patch graph GP is the same for both Steps 1 and 2.
As in Step 1, we choose to normalize R using the diagonal matrix D, whose diagonal elements are also given by . We define the matrix
| (10) |
which is similar to the Hermitian matrix D−1/2RD−1/2 through
Therefore, has N real eigenvalues with corresponding N orthogonal (complex valued) eigenvectors , satisfying . We define the estimated rotation angles and their corresponding elements in SO(2), using the top eigenvector as
| (11) |
The estimation of the rotation angles is up to an additive phase, since is also an eigenvector of for any .
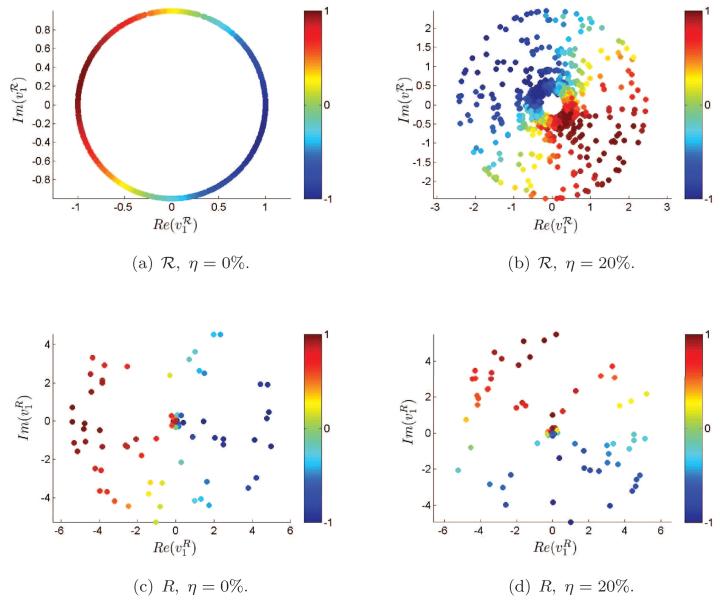
Note that the only difference between Step 2 and the angular synchronization algorithm in Singer [2010] is the normalization of the matrix prior to the computation of the top eigenvector. The usefulness of the normalization and the success of Equation (11) in estimating the rotation angles are demonstrated in Figures 6, 7, and 8.
Fig. 6.
Scatter plots in the complex plane of the entries of the top eigenvectors and for the U.S. cities graph with ρ = 0.032 (deg = 19) and various noise levels η. The color of the points correspond to cosθi = Re(ri).
Fig. 7.
Histogram of all eigenvalues and bar plot of the top ten eigenvalues of R and for the U.S. cities graph with ρ = 0.032 and various noise levels η. Note, as we did with , that we also plot for the histogram and bar plots of .
Fig. 8.
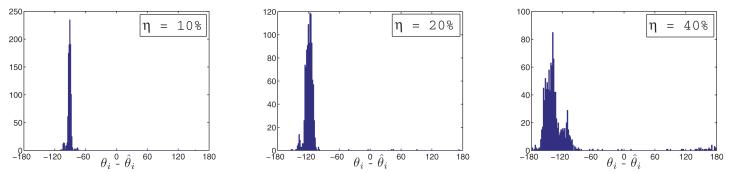
Histogram of the angle estimation error (in degrees) for the U.S. cities graph with ρ = 0.032 and various noise levels η. Note that angles are estimated up to an arbitrary phase and we have not mean shifted the histograms.
3.3. Step 3: Synchronization over to Estimate Translations
The final step of the ASAP algorithm is computing the global translations of all patches and recovering the true coordinates. For each patch Pk, we denote by Gk = (Vk, Ek)5 the graph associated to patch Pk, where Vk is the set of nodes in Pk, and Ek is the set of edges induced by Vk in the measurement graph G = (V, E). We denote by the known local frame coordinates of node i ∈ Vk in the embedding of patch Pk (see Figure 9).
Fig. 9.
An embedding of a patch Pk in its local coordinate system (frame) after it was appropriately reflected and rotated. In the noise-free case, the coordinates agree with the global positioning pi = (xi, yi)T up to some translation t(k) (unique to all i in Vk).
At this stage of the algorithm, each patch Pk has been properly reflected and rotated so that the local frame coordinates are consistent with the global coordinates, up to a translation . In the noise-free case, we should therefore have
| (12) |
We can estimate the global coordinates p1, …, pn as the least-squares solution to the overdetermined system of linear equations from Equation (14), while ignoring the by-product translations t(1), …, t(N). In practice, we write a linear system for the displacement vectors pi − pj for which the translations have been eliminated. Indeed, from Equation (12), it follows that each edge (i, j) ∈ Ek contributes a linear equation of the form6
| (13) |
In terms of the x and y global coordinates of nodes i and j, Equation (13) is equivalent to
| (14) |
| (15) |
We solve these two linear systems separately—once for x1, …, xn and once for y1, …, yn. Let T be the least-squares matrix associated with the overdetermined linear system in Equation (14), x be the n × 1 vector representing the x-coordinates of all nodes, and bx be the vector with entries given by the right-hand side of Equation (14). Using this notation, the system of equations given by Equation (14) can be written as and similarly, Equation (15) can be written as
| (16) |
and similarly, Equation (15) can be written as
| (17) |
Note that the matrix T is sparse with only two nonzero entries per row and that the all-ones vector 1 = (1, 1, …, 1)T is in the null space of T, that is, T1 = 0, so we can find the coordinates only up to a global translation.
To avoid building a very large least-squares matrix, we combine the information provided by the same edges across different patches in only one equation, as opposed to having one equation per patch. This is achieved by adding up all equations of the form of Equation (14) corresponding to the same edge (i, j) from different patches into a single equation, that is,
| (18) |
and similarly for the y-coordinates using Equation (15). We denote the resulting m × n matrix by and its m × 1 right-hand-side vector by . Note that has only two nonzero entries per row.7 The least-squares solution to
| (19) |
is our estimate for the coordinates p1, …, pn, up to a global rigid transformation. Figure 10 shows the original and estimated embedding (after rigid alignment) and the histogram of errors in the coordinates, where the error associated with node i is given by .
Fig. 10.
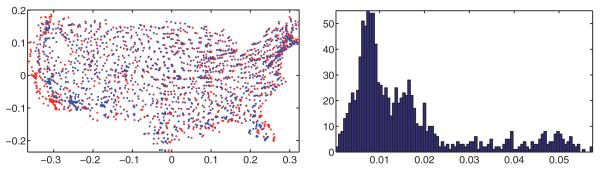
Left: estimated embedding (blue) after alignment with the true positions (red) for the U.S. cities graph with ρ = 0.032 and noise level η = 20%. Right: histogram of the errors .
The ASAP algorithm can easily integrate the information provided by anchors, if those exist. First, in the preprocessing step, if two or more anchors are contained in a patch, then this information can be used in localizing that patch. In Step 1, the relative reflection is solely determined for pairs of patches that have three or more anchor points in their intersection. Similarly, in Step 2, the relative rotation is determined for pairs of patches that have two or more anchors points in their intersection. In Step 3, we incorporate such information in the least-squares method. Suppose we have obtained a reconstruction without using the anchor information. Since the anchors take their coordinates from the original embedding (which is a rigid transformation of our reconstruction), we first need to properly align the anchors with respect to our reconstruction. Then, for every node i that is an anchor, we simply substitute the unknowns in Equation (18) with their true known value and solve for the remaining unknowns (and similarly for the y-coordinates). Figure 11 shows reconstructions of the U.S. cities map with noise η = 0.2 and different number of anchors.
Fig. 11.
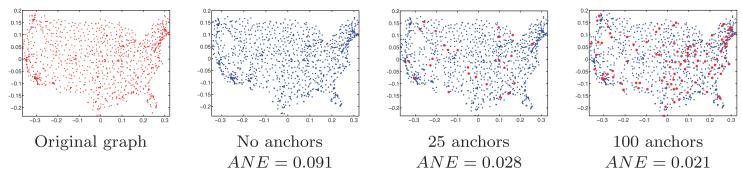
Reconstruction of the U.S. cities graph with ρ = 0.032 and noise level η 20% for different number of anchors points. The average normalized error (ANE) is defined in Equation (44).
Another way of including the anchor information in Step 3 is to substitute the anchor points pi in Equation (13) with Opi + t, where pi is known while O is an unknown 2 × 2 matrix, accounting for the possible rotation and reflection of the anchors with respect to the reconstruction (although in our solution, we cannot restrict O to be an orthogonal matrix), and t is an unknown 2 × 1 vector for the possible translation. Upon this substitution, Equation (13) becomes a linear system of equations for the coordinates of the non-anchor points, that is, for the entries of the matrix O and for the vector t. Note that this linear system can still be solved for the x-coordinates and the y-coordinates separately.
4. PRELIMINARY ANALYSIS OF THE EIGENVECTOR METHOD
As detailed in the previous sections, in Steps 1 and 2, we use the top eigenvectors of the normalized and matrices to recover the global orientations and global rotation angles of all patches. In this section, we analyze the algorithm from a spectral graph theory point of view that allows us to explain the success of the algorithm even in the presence of corrupted measurements.
We first analyze Steps 1 and 2 when the distance measurements are exact and the matrices Z and R contain no errors on the relative reflections and rotations of all overlapping pairs of patches. Denoting by Υ the N × N diagonal matrix with ±1 on its diagonal representing the correct reflections zi, that is, Υii = zi, we can write the matrix Z = (zij) as
| (20) |
where is the adjacency matrix of the patch graph GP given by
| (21) |
because in the noise-free case, for (i, j) ∈ EP. Similarly, we represent the matrix R = (rij) = (eιθij) as
| (22) |
where Θ is an N × N diagonal matrix with Θii = eιθi , because in the noise-free case, eιθij = eι(θi−θj) for (i, j) ∈ EP. The normalized matrices and can now be written as
| (23) |
and
| (24) |
Hence, , and D−1 AP all have the same eigenvalues. Since the normalized discrete graph Laplacian is defined as
| (25) |
it follows that in the noise-free case, the eigenvalues of and are the same as the eigenvalues of . These eigenvalues are all nonnegative, since is similar to the positive semidefinite matrix I − D−1/2APD−1/2, whose nonnegativity follows from the identity
In other words,
| (26) |
where the eigenvalues of are ordered in increasing order, that is, , and the corresponding eigenvectors satisfy . Furthermore, the sets of eigenvectors are related by
If the patch graph GP is connected, then the eigenvalue is simple, and its corresponding eigenvector is the all-ones vector 1 = (1, 1, … , 1)T. Therefore,
| (27) |
and, in particular,
| (28) |
This implies that in the noise-free case, the ASAP algorithm perfectly recovers the reflections and rotations, as shown in Figures 4(a) and 6(a).
Notice that the top eigenvectors and of the non-normalized matrices Z and R are related to the top eigenvector of the adjacency matrix AP via
| (29) |
Connectivity of the patch graph together with the Perron-Frobenius theorem imply that all entries of are positive, that is, , which in principle suffices to ensure that our rounding procedures of Equations (8) and (11) give the correct reflections and rotations. However, unlike the constant entries of the all-ones vector, the entries of can vary in their magnitude. In fact, when the patch graph is not regular (i.e., when the vertex degrees are not constant), it often happens that has only a few large entries and all other entries are significantly smaller, rendering numerical difficulties in the computation of , as indicated in Figures 4 and 6. Moreover, in the noisy case, such small entries are likely to change their sign (or phase), making the top eigenvector of Z (or R) sensitive to noise.
In order to understand why the entries of can vary so much, we first examine the matrix D−1AP and view it as a Markov transition probability matrix of a discrete random walk on the patch graph, whose top all-ones eigenvector expresses the fact that the steady state density is uniform. Denoting the maximum vertex degree of the patch graph by Deg = maxi deg(i), the matrix corresponds to a random walk with absorption, that is, it is possible to artificially add an extra terminal state to which the random walker jumps from node i with probability . Due to this absorption, the steady state distribution is trivially concentrated at the terminal state, but the approach to this steady state is governed by . We therefore expect vertices located away from absorption sites to have larger values in . For example, consider the path graph on N vertices with edges given by (i, i+1) for i = 1, … , N−1. For the path graph, deg(i) = 2 for i = 2, …, N − 1, while deg(1) = deg(N) = 1. The discrete random walk matrix is a discretization of the continuous diffusion process on the interval [0, 1] with absorption at the endpoints (homogenous Dirichlet boundary conditions), from which it can be deduced that in the limit N → ∞, the top eigenvector is approximately given by for i = 1, …, N. This agrees with our intuition that values near the center are larger than near the boundaries but also demonstrates the possible numerical instabilities, as the ratio between these values can be as large as O(N). Figure 12 demonstrates the variability of the node degrees of patches in the patch graph for the U.S. cities graph, rendering the importance of the normalization.
Fig. 12.

Histogram of the node degrees of patches in the patch graph GP for the U.S. cities graph with ρ = 0.032 and η = 20%.
At this point, we understand why the top eigenvectors of the normalized matrices and give superior results compared to the top eigenvectors of the non-normalized matrices Z and R. Since the (non-normalized) Laplacian L of the patch graph
also has the all-ones vector as an eigenvector (with smallest eigenvalue), another possible good way of estimating the reflections and rotations is by using the smallest eigenvectors of
and
We have seen that, in practice, the non-normalized Laplacian method (L) also performs well, giving results that are comparable to those of the normalized Laplacian method () used throughout this article.
We now turn to briefly discuss the analysis of the noisy distances scenario, dealing first with Step 1 for the reflections. For noisy data, the measurement zij of the reflection between patches Pi and Pj may be incorrect. That is, while the value of zij should really be , the alignment of the patches may give the false value . The effect of false measurements changes the matrices Z and from that of Equations (20) and (23)
| (30) |
and
| (31) |
where Δ = (δij) is the N × N symmetric error matrix
| (32) |
While the all-ones vector 1 is the top eigenvector of D−1 AP, it is no longer the top eigenvector of the perturbed matrix D−1 AP + D−1. If the perturbation D−1Δ is small (e.g., in terms of its spectral norm), then we can expect the top eigenvector to be sufficiently close to 1. In particular, many of the eigenvector entries are expected to remain positive, meaning that the reflections corresponding to these entries will be estimated correctly. A similar perturbation approach can also be applied to Step 2 for the rotations. The precise matrix perturbation analysis that quantifies the sign stability of the top eigenvector is beyond the scope of this article, however, and will be considered in a separate publication.
From the implementation perspective, it is important to note that the eigenvector method can be implemented in a distributed manner. The top eigenvector of the matrix can be efficiently computed by the power iteration method that starts from a randomly chosen vector b0 and iterates . Each iteration requires just a matrix-vector multiplication that takes only O(M) operations, where M = |EP| is the number of edges in the patch graph GP. The power iteration method has the advantage that it can be implemented in a distributed way with every sensor making local computations and communications with nearby sensors. The number of iterations required decreases as the spectral gap increases.
The iterations of the power method for computing the top eigenvector can also be viewed as integration of consistency relations along cycles in the patch graph GP. To see this, consider, for example, a length k cycle P1, P2, …, Pk, where (Pi, Pi+1) ∈ EP for i = 1, 2, …, k−1 and (Pk, P1) ∈ EP. In the noise-free case, the reflection measurements are given by , hence they must satisfy the consistency relation
| (33) |
Similarly, the noise-free rotation measurements rij = eι(θi−θj) also satisfy a similar consistency relation
| (34) |
In the iterations of the power method, the matrix (and similarly ) gets multiplied by itself, and the effect of this is twofold. First, the eigenvector method integrates the information in the consistency relations along cycles in the patch graph GP, and second, it propagates information to far-away patches that cannot be aligned directly. This gives yet another insight to understanding why the eigenvector method is robust to noise.
5. FINDING AND LOCALIZING GLOBALLY RIGID PATCHES
In this section, we turn to the problem of finding and localizing patches, which is a crucial preprocessing step of our algorithm. Most localization algorithms that use a local to global approach, such as PATCHWORK, LRE, and ARAP, simply define patches by associating with every node i its entire one-hop neighborhood G(i). It is possible, however, that the subgraph G(i) of one-hop neighbors of vertex i is not globally rigid. In such a case, G(i) has more than one possible realization in the plane. Therefore, whenever G(i) is not globally rigid, we find its maximally globally rigid components, which we call patches. The number of resulting patches can be 0, 1, or greater than 1. We note that Hendrickson [1995] also suggested a method for breaking up networks into maximally globally rigid components. However, as we show next, breaking up the one-hop neighborhood subgraph G(i) is easier than breaking up a general graph, by utilizing recent results of Connelly and Whiteley [2009] regarding the global rigidity property of cone graphs.
Star graph. We call a star graph a graph which contains at least one vertex that is connected to all remaining nodes. Note that in our definition, unlike perhaps more conventional definitions of star graphs, we allow edges between non-central nodes to exist. Note that for each node i, the local graph G(i) composed of the central node i and all its neighbors takes the form of a star graph.
k-connectivity. A graph is k-vertex-connected if and only if it remains connected even after the removal of any k − 1 vertices. Alternatively, a graph is k-vertex-connected if and only if every pair of vertices is connected by at least k disjoint paths. In a planar network, a necessary condition for global rigidity is 3-vertex-connectivity [Hendrickson 1992], meaning that the graph should remain connected after the removal of any two vertices. Note that 3-vertex-connectivity implies that the minimum degree of the graph is three, since any vertex of lower degree can be disconnected from the graph by removing its neighbors. An alternative characterization is in terms of cuts, also known as splitting pairs. A graph that is not 3-vertex-connected has a vertex cut of size two, that is, a pair of vertices whose removal disconnects the graph into two separated components. A graph with a cut of size two is not globally rigid, since one of the two components can be flipped across the line determined by the splitting pair. A similar definition holds for k-edge-connectivity, in which a graph is said to be k-edge-connected if there is no set of k − 1 edges whose removal disconnects the graph, and the smallest such k denotes the edge-connectivity of the graph. Note that if a graph is k-vertex-connected, then it is also q-edge-connected for q ≤ k.
Proposition 5.1. A star graph is generically globally rigid in if and only if it is 3-vertex-connected.
Proof. The process of coning a graph G adds a new vertex v and adds edges from v to all original vertices in G, creating the cone graph G * v. A recent result of Connelly and Whiteley [2009] states that a graph is generically globally rigid in if and only if the cone graph is generically globally rigid in .
Let H be a 3-vertex-connected star graph, v be its center node, and H* the graph obtained by removing node v, H* = H\v. Since H is 3-vertex-connected, then H* must be 2-vertex-connected, since otherwise, if u is a cut-vertex in H*, then {v, u} is a vertex-cut of size 2 in H, which is a contradiction. Since the vertex connectivity of a graph cannot exceed its edge-connectivity, it follows that H* is at least 2-edge-connected, which is a necessary and sufficient condition for generic global rigidity on the line. Using the coning theorem, the generic globally rigidity of H* in implies that H is generically globally rigid in . On the other hand, as mentioned before, if H is generically globally rigid, then it must be 3-vertex-connected.
Using Proposition 5.1, we propose the following simple algorithm for breaking up a star graph into maximally globally rigid components. We first remove all vertices of degree one, since no globally rigid subgraph can contain such a vertex. Note that a vertex of degree two can be only be contained in a triangle, provided its two neighbors are connected. Next, we search for the (maximal) 3-connected components in the graph, taking advantage of its structure as a star graph. In other words, we are looking for a decomposition of the graph into a union of 3-vertex-connected subgraphs of maximal size. For the case of star graphs, the following approach leads to a simple and efficient algorithm. We look for a cut set (of size one or two) containing the center node that separates the graph into two or more components and recurse on each one of them. In order to check for the 3-connectivity of a given one-hop neighborhood star graph G(i), it suffices to remove the center node i and check if the remaining graph G(i)\{i} is 2-connected, which can be done in O(m’) time, where m’ is the number of edges in G(i)\{i}.
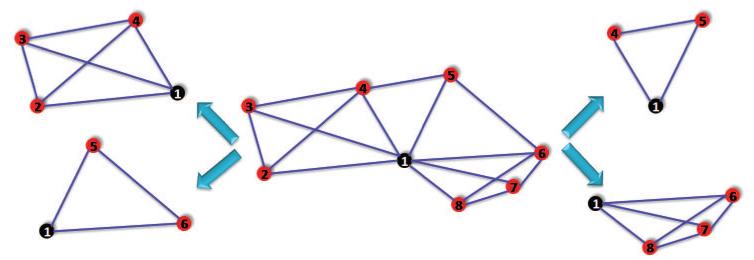
Figure 13 shows an example of a one-hop neighborhood graph where the center node is connected to all its neighbors in the measurement graph. The neighborhood graph has four 3-connected components that share edges vertices, each component being a star graph and hence globally rigid by the preceding result. Note that a globally rigid patch is allowed to be as small as a triangle.
Fig. 13.
The neighborhood graph of center node 1 is split into four maximally 3-connected-components (patches): {1, 2, 3, 4}, {1, 4, 5}, {1, 5, 6}, {1, 6, 7, 8}.
After finding the patches, it still remains to localize each of them separately in the plane. Localizing a small globally rigid subgraph is significantly easier in terms of speed and accuracy than localizing the whole measurement graph. First, the size of a patch is significantly smaller than the size of the whole network. For example, the typical patch size for the U.S. cities graph with n = 1,090 and sensing radius ρ = 0.032 is between 10 to 30 nodes, as shown in Figure 14 (left panel). Also, when embedding locally, we are no longer constrained to a distributed computation that can impose additional challenges due to inter-sensor communication. Since each node in the patch is connected to a central node, all the information can be passed on to this node, which will perform the computation in a centralized manner. Finally, under the assumptions of the disc graph model, it is likely that one-hop neighbors of the central node will also be interconnected, rendering a relatively high density of edges for the patches, as indicated by Figure 14 (right panel). This means that locally, the partial distance matrix of a typical patch usually has only a small number of missing entries, which makes the embedding of the patch more robust to noise and more efficient to compute. We have also observed in our experimental simulations that SDP localization algorithms tend to run considerably faster when the partial distance matrix is denser.
Fig. 14.
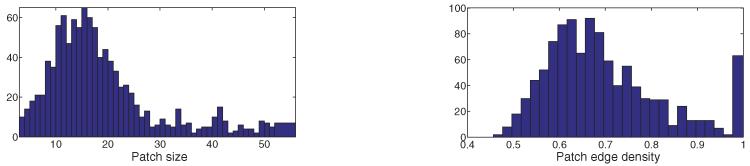
Histogram of patch sizes (left) and edge density (right). U.S. cities map, n = 1,090 and noise η = 20% (deg = 20).
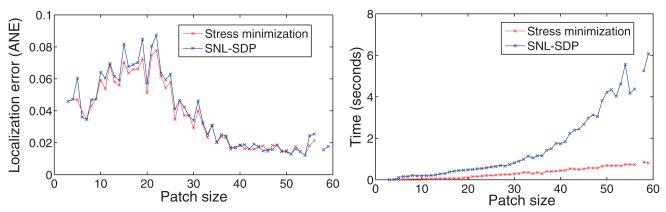
After experimenting with the different localization methods, our method of choice for embedding the patches was the three-stage procedure described in Gotsman and Koren [2004], due to its relatively low running time and its robustness to noise for small patches. When used for small patches (e.g., of size 20–30) rather than the entire network, the stress minimization is more reliable and less sensitive to local minima. Compared to an anchor-free SDP localization algorithm like SNL-SDP8, it produces similar results in terms of the localization error but with lower running times (see Figure 15). To the best of our knowledge, the SDP-based approaches (in particular those of [Biswas and Ye 2004; Biswas et al. 2006a, 2006b; So 2007; So and Ye 2005; Zhu et al. 2010]) have not been analyzed in the context of the disc graph model, and the SDP localization theory is built only on the known distances, without any additional lower and upper bounds that can be inferred from the disc graph assumption. However, experimental results reported by the same authors (via personal communication) reveal that when adding such additional constraints into the SDP formulation, the localizations become more accurate at the cost of increased running time.
Fig. 15.
Comparison of the three-stage algorithm labeled Stress minimization and SNL-SDP for the U.S. cities graph with ρ = 0.032 and noise level η = 20%.
The three-stage algorithm of Gotsman and Koren [2004] first estimates the missing distances for (i, j) ∉ Ek by making use of the disc graph assumption (for the lower bound) and the triangle inequality (for the upper bound). Second, the coordinates are computed by running the classical MDS on the complete set of pairwise distances. Third, the embedding is improved by running the stress minimization algorithm based only on the initial distances but not on the estimated missing distances:
Stage 1. Estimating missing distances. For each missing distance with (i, j) ∉ Ek, we denote its lower bound estimate (respectively, upper bound) by dij (respectively, ). Using the triangle inequality on all pairs of existing edges (i, k), (j, k) ∈ Ek, an upper bound on is given by
| (35) |
Using the disc graph model assumption, a lower bound dij is given by
| (36) |
The missing distances are estimated as , for (i, j) ∉ Ek.
Stage 2. Classical MDS. After estimating all missing distances, the classical MDS algorithm [Cox and Cox 2001] is used on the complete set of pairwise distances to compute local coordinates of all nodes of the patch.
Stage 3. Stress minimization. The embedding obtained from classical MDS is refined using the stress majorization algorithm (mentioned in Section 2). The stress function in Equation (3) is minimized by running the iterative majorization technique described in Gotsman and Koren [2004]. At each iteration, the coordinates of each node are updated according to the following rule.
| (37) |
where degi(Gk) denotes the degree of node i in patch Pk, and
| (38) |
We remark that we use classical MDS for patches that have no missing edges. Note that some patches can be much larger than others, rendering their embedding less accurate. We therefore restrict the size of the patches to some maximal prescribed size.
6. METHODS FOR ALIGNING PATCHES IN STEPS 1 AND 2
In this section, we describe several methods for aligning patches and for computing their relative reflections and rotations. Successful alignment of patches is important, since in order for the eigenvector method to succeed, the Z and R matrices from Steps 1 and 2 of ASAP need to have enough correct, or approximately correct, entries. Given two patches Pi and Pj, each embedded in its own coordinate system, we are first interested in estimating their relative reflection zij, where zij = −1 if Pi needs to be replaced by its mirrored image before being aligned with Pj, and zij = 1 if the two patches can be aligned via an angular rotation and translation without a reflection. Second, we are interested in estimating the offset angle θij = θi − θj mod 2π that aligns the two patches. Obviously, two patches that are far apart and have no common nodes cannot be aligned, and there must be enough overlapping nodes to make the alignment possible. Figure 14 shows a typical example of the sizes of the patches we consider as well as their intersection sizes. As expected, in the case of the disc graph model, the overlap is often small. It is therefore crucial to have robust alignment methods even when the overlap size is small.
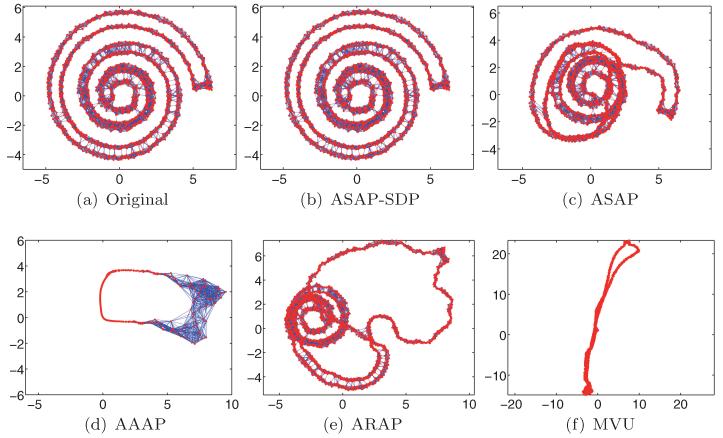
A closed-form solution to the registration problem in any dimension was given by [Horn et al. 1988], where the best rigid transformation between two sets of points is obtained by various matrix manipulations and eigenvalue/eigenvector decomposition. In our approach described in the following paragraph, we choose to convert this non-linear regression problem to a linear complex least-squares problem by using complex numbers to denote 2-by-2 rotation matrices.
Least-squares registration. Given two patches Pk and Pl that have at least three nodes in common, the registration process finds the optimal 2D rigid motion of Pl that aligns the common points (as shown in Figure 3). We denote by Vk,l = {v1, …, vs} the nodes in the intersection of patches Pk and Pl, that is, . We let be the coordinates of the set of nodes Vk,l in the embedding of patch Pk, and similarly be the coordinates of nodes Vk,l in the embedding of patch Pl. For a point , we denote by its mirrored image across the x-axis. For the purpose of the minimization problems we are about to describe, it is convenient to view the local frame of each patch as the complex plane instead of the Euclidean space . We write the coordinates of a node , as and represent its mirrored image by .
Fig. 3.
Optimal alignment of two patches that overlap in four nodes. The alignment provides a measurement for the ratio of the two group elements in Euc(2). In this example, we see that a reflection was required to properly align the patches.
Given two sets of planar labeled points and (viewed as elements of ), the registration problem is to find a rotation rθ = eιθ and a translation vector t = x + ιy that finds the optimal alignment of the two sets of points in the least-squares sense. In other words, we are interested in finding rθ and t that minimize the following objective function.
| (39) |
Since we do not know a priori the relative reflection zij of the pair of patches Pk and Pl, we use the registration method twice. We first register Pk and Pl by minimizing Equation (39) and then register Pk and , the mirrored image of patch Pl, by minimizing a similar objective function.
| (40) |
If the residual in the minimization of Equation (39) is smaller than the residual in the minimization of Equation (40), then the two patches are properly oriented; otherwise, one of the two patches needs to be replaced by its mirrored image. In other words, we define zij as
| (41) |
We rewrite Equation (39) (and similarly for Equation (40)) as ||Ax − b||2, where
Therefore, we solve the minimization problem of Equation (39) by the method of least squares and find rθ and t. By solving the registration problem using complex least squares, we are guaranteed to recover the optimal solution (best 2D rigid transformation) up to scaling [Schaefer et al. 2006]. For noisy distance measurements, rθ does not necessarily lie on the unit circle, in which case we extract its phase θ (but ignore its amplitude). For noisy data, the registration method becomes significantly more robust if the pair of patches have a large overlap (e.g., at least six or seven nodes). Also, note that for computing the relative reflection, the two patches must overlap in at least s ≥ 3 nodes, while for estimating the rotation (after finding the proper rotation), it suffices to have s ≥ 2.
Combinatorial score. The second alignment method we consider makes use of the underlying assumptions of the disc graph model. Specifically, we exploit the information in the non-edges that correspond to distances larger than the sensing radius ρ. The resulting method can be used to estimate both the relative reflection and rotation for a pair of patches that overlap in just two nodes (or more).
Consider two overlapping patches Pk and Pl that intersect at only two nodes {a, b} ∈ Vk ∩ Vl. We would like to decide whether the two patches have the same orientation with respect to the original complete network, or rather Pl needs to be replaced by its mirrored image.
As illustrated in Figure 16, there are two possible ways to align the two patches using the common edge ab in terms of their relative orientation. One with Pk and Pl, as they appear on the left-hand side of the figure, and one where the Pl patch is reflected across edge ab, shown on the right-hand side of the figure. Only one of the two scenarios is feasible, and to decide which one, we make use of the disc graph model assumption that two nodes are connected if and only if their distance does not exceed ρ. For each of the two scenarios, we count the number of violations of the disc graph assumption. There are two types of violations: distances that are predicted by the patch alignment to be smaller than ρ but are missing from the original measurement graph, and distances that are predicted by the patch alignment to be greater than ρ but also appear in the original measurement graph. One of the two scenarios will correspond to a foldover in the graph, causing nodes that were far apart in the original graph to become within sensing radius of each other (causing false edges), and nodes that were close in the original graph to become far apart (thus leading to missing edges). Of the two scenarios, we choose the one with the smaller number of violations.
Fig. 16.
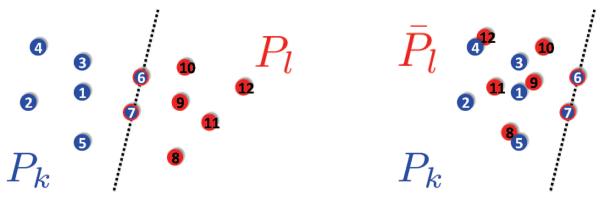
Using the combinatorial method to decide on the relative reflection of two patches: aligning Pk and Pl (left), and Pk and (right).
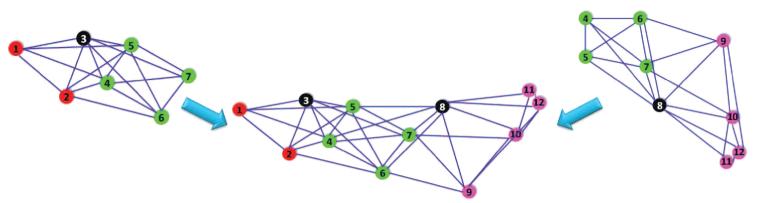
Link edges. The last alignment method we consider is useful whenever two patches have a small overlap but there exist many cross edges in the measurement graph that connect the two patches. Suppose the two patches Pk and Pl overlap in at least one vertex and call a link edge an edge (u, v) ∈ E that connects a vertex u in patch Pk (but not in Pl) with a vertex v in patch Pl (but not in Pk). We denote the number of link edges by q. Figure 17 shows two patches overlapping in only one vertex that have q = 3 such link edges.
Fig. 17.
Alignment of two patches Pi and Pj overlapping in just one node using link edges (green).
First, in order to factor out the translation, we align the center of mass of the intersection points. The next step is to find the rotation that optimally aligns the two patches. Of course, if there are enough common nodes (at least three), one can use the registration method to obtain the rotation angle. However, when the overlap size is small (up to four or five nodes), the results of the registration method are not very accurate in the presence of large noise. We want to be able to align patches robustly, even when they have only one or two common nodes, because there are many pairs with small overlap size, as the right panel of Figure 14 indicates. Each link edge adds a constraint between the two patches, and we would like to compute the optimal rotation angle that satisfies the link edge constraints as best as possible. If we denote the coordinates of node ui in patch Pk by , the penalty function we minimize is
| (42) |
where r = eιθ. Setting the derivative F’ (θ) = 0, we arrive at a cubic for rθ, and we pick the root that gives the minimum value for F(θ). To decide on the relative reflection for a pair of patches, we run this minimization twice—once for patches Pk and Pl, and a second time for patches Pk and . Whichever setup gives a smaller global minimum indicates the correct relative reflection of the two patches.
These three registration methods considered are useful in different scenarios. In practice, we only use the least-squares registration method which turns out to be the most robust to noise whenever the overlap between patches is large enough (e.g., six overlapping nodes or more). However, in some cases that we report in the proceeding section, we also use the combinatorial method that is useful when the overlap is small (e.g., two nodes or more). Although the link edges method is useful when the node overlap is just one, we did not use it in practice, as in our experiments, all patch graphs were already connected without using it. The link edges method is important for maintaining connectivity of the patch graph when the input measurement graph is very sparse. Figure 18 shows a histogram of the intersection sizes between pairs of patches in the U.S. cities graph.
Fig. 18.
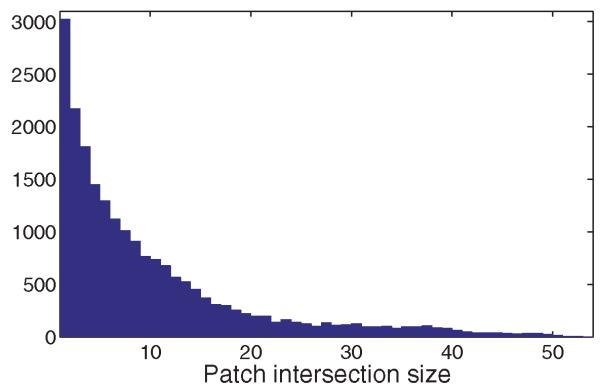
Histogram of the intersection size of patches in the U.S. cities graph ρ = 0.032 and η = 20%.
7. COMPLEXITY ANALYSIS
In this section, we give a complexity analysis of each step of the ASAP algorithm, showing that the time complexity scales almost linearly in the size of the network (number of nodes n and edges m) and augment this theoretical analysis with the running times of numerical simulations for the localization of networks of increasing sizes (n = 103, 104, 105), as detailed in Table XI. Tables II and III summarize the notation used throughout this section, respectively the complexity of each step of the ASAP algorithm.
Table XI.
Running Times (in Seconds) of the ASAP Algorithm on the SQUARE Graph with n = {103, 104, 105} Nodes inside the Unit Square, η = 0% and deg ≈ 12, 13
| Stage \# of nodes n | 1,000 | 10,000 | 100,000 |
|---|---|---|---|
|
| |||
| Break G into patches | 41 | 901 | 52,180 |
| Embedding patches | 414 | 4,325 | 37,140 |
| Patch intersections | 2 | 132 | 58,134 |
| Build | 8.7 | 90 | 2,237 |
| Compute | 0.8 | 13 | 926 |
| Build | 4.6 | 49 | 3,414 |
| Compute | 0.2 | 7 | 522 |
| Step 3 | 6 | 88 | 4,772 |
|
| |||
| Total Time (sec) | 477 | 5,605 | 159,325 |
Table II.
Summary of Notation Used to Describe the Graph of Sensors G = (V, E) and the Patch Graph Gp = (Vp, Ep)
| n | # of nodes in G, | V | = n | |
| m | # of edges in G, |E| = m | |
| k | upper bound on the size of a patch (user input) | |
| N | # of patches (nodes in the patch graph Gp), |VP| = N | N ≤ n(k − 1) |
| M | # of pairs of overlapping patches (edges in Gp), |Ep| = M | M ≤ Nk2/2 |
| dp | maximum degree in Gp | dp ≤ k2 |
| m’ | maximum # of edges in a patch | m’ ≤ k2/2 |
Table III.
Summary of the Complexity of Each Step of the ASAP Algorithm.
| Stage | Complexity | # of calls |
|---|---|---|
|
| ||
| Break 1-hop neighborhood into patches | O(k + m’) | n |
| Patch embedding by SMACOF | O(k3 + k3/2t) | N |
| Patch embedding by FULL-SDP | O(k2m’2.5 + m’3.5) | N |
| Patch intersection | O(k) | M |
| Patch alignment | O(k) | M |
| Top eigenvector computation | O(Mζ) | 2 |
| Linear least squares | 2 | |
|
| ||
| Total | ||
t denotes the number of iterations of the SMACOF algorithm, ζ the number of iterations of the power method, and κ the condition number of the matrix TT T (where T is the least squares matrix from Step 3).
Preprocessing step: Finding and localizing globally rigid patches. Breaking up the graph into maximally globally rigid components was presented in detail in Section 5 and represents the first computationally expensive task in ASAP. In light of Proposition 5.1, to check for the 3-connectivity of a given one-hop neighborhood star graph G(i)\{i}, it suffices to remove the center node i and check if the remaining graph G(i) i is 2-connected, otherwise extract its 2-connected components. Partitioning a graph into 2-connected components can be done in time linear in the number of nodes and number of edges of the graph. The (worst-case) complexity of this step is therefore O(k + m’). For convenience, we did not use an O(m’) implementation, but rather the O(m’2) näive algorithm that looks for cuts in the graph by examining all possible pairs of nodes. Despite the expected linear scaling of this step of the algorithm, the running times reported in Table XI do not seem to scale linearly, but we are able to explain this discrepancy as follows. In our experiments, the average patch size remains approximatively the same (e.g., ≈ 13) for n = {103, 104, 105}, and the maximum patch sizes are k = {24, 28, 31}. Since the number of patches M is bounded by nk, we attribute the slow running times to MATLAB’s added overhead when working with arrays of structures. A similar behavior can be observed in the Patch intersections preprocessing step, where we compute and store the intersection of pairs of overlapping patches. As shown in the following paragraphs, each patch overlaps with a constant number of other patches, and thus the number of patch intersections to compute and store scales linearly in the number of patches. We expect that an efficient implementation in C of these steps of the algorithm will scale linearly.
The next question we address is whether the resulting number of patches N is linear in the number of nodes n. We answer this question in the affirmative and show in the following analysis that N ≤ n(k − 1), where k is the user-chosen upper bound on the size of a patch. Denote by P1, P2, …, Pr, the maximally globally rigid components in the one-hop neighborhood graph G(i) of a given node i, with |Pl| ≥ 3 and |Pl| ≤ k ∀l = 1, … , r, since we restrict the size of the one-hop neighborhood to be at most k. Note that the union of two globally rigid graphs Pi and Pj that intersect in at least d + 1 = 3 nodes is itself a globally rigid graph. This observation, together with the maximality condition on the patch sizes, implyies that any two patches intersect in at most two vertices |Pi ∩ Pj| ≤ 2, as otherwise their union is a globally rigid component in G(i), and neither Pi nor Pj would be maximal. In addition, whenever a pair of patches overlap in two vertices, it must be the case that one of the two vertices is the center node i. If one were to draw an imaginary line through all edges originating at i (there are k − 1 such edges) and think of the resulting sectors (slices) as building blocks for the patches, then it becomes clear that a patch is comprised of adjacent sectors and has a left-end and a right-end edge. This also means that a patch overlaps with at most two other patches, and the intersection is given by the left-end and right-edges. Since there are k − 1 edges originating at i, it means that there are at most k − 1 patches contributed by the one-hop neighborhood of any node.
The running time for localizing the patches depends on the embedding method of choice, SMACOF or FULSDP. In terms of complexity, Asano et al. [2009] show that the SMACOF algorithm runs in O(k3 + k3/2t) time and O(k) space, where t is the number of iterations required to minimize the stress energy function introduced earlier in Equation (3). In our experiments, we limit the maximum size of a patch to a constant k ≈ 30 – 50 by including in the one-hop neighborhood of node i only the k − 1 nearest neighbors of i (if i has more than k − 1 neighbors). However, if we choose to use the SDP approach for embedding the patches, this task ismore expensive, since the computation complexity of SeDuMi (the SDP solver used here) is O(k2m’2.5 + m’3.5), since there are k number of decision variables (nodes of a patch) and m’ linear matrix (in) equality constraints (edges of a patch) [Peaucelle et al. 2002]. In either scenario, the embedding of a single patch remains polynomial in k, and the complexity of the preprocessing step adds up to O(N poly(k)), since there are N patches for which we check biconnectivity and compute their embedding.
Steps 1 and 2: Computing reflections and rotations. The computationally expensive tasks in Steps 1 and 2 are the registration of pairs of overlapping patches and the computation of the top eigenvectors of sparse N-by-N matrices. The registration method introduced at the beginning of Section 6 amounts to solving a complex linear leastsquares problem of the form Ax = b, where A is a matrix of size s × 3, and s is the number of points in the intersection of the two patches. The least-squares solution is given by x = (AT A)−1AT b, which can be computed in O(s) time. Since s ≤ k, the overall complexity of aligning two patches using least squares is O(k). Concerning the eigenvector computation, we note that every iteration of the power method is linear in the number of edges M of the patch graph GP, but the number of iterations is greater than O(1), as it depends on the spectral gap. Note that a pair of patches Pi and Pj overlap if and only if j is either a one-hop or two-hop neighbor of i. Since we limit the number of one-hop neighbors of a node to k, it follows that the number of two-hop neighbors is at most k2. In other words, k2 is an upper bound for the maximum degree in the patch graph GP, and we conclude that the number of edges M does not exceed Nk2/2, where N grows linearly in n. Note that in this analysis, we assumed each node contributes with one patch, but the result M = O(N) still remains valid if G(i) generates multiple patches (a constant depending on k).
Step 3: Least squares. To estimate the x- and y-axis translations and compute the final coordinates of the reconstruction, we solve the linear least-squares problems in Equation (19). One possible approach for solving such linear least-squares problems of the form T x = b is to use conjugate gradient iterations applied to the normal equations TT T x = TT b (which can be done without explicitly doing the expensive computation of the matrix TT T). The rate of convergence of the gradient iterations is determined by the condition number κ of the matrix TT T and the number of iterations required for convergence is [Trefethen and Bau 1997]. For matrices that are sparse or have exploitable structure, each conjugate gradient iteration has complexity as low as O(m). Recall that in our case, T is a sparse matrix with only two nonzero entries per row. Overall, the complexity of the linear least squares in Step 3 in our case is .
Adding up the complexity of all the steps of the algorithm, we get a running time of , which is almost linear in the size of the network.
8. EXPERIMENTAL RESULTS
We have implemented our ASAP algorithm and compared its performance with other methods across a variety of measurement graphs, varying parameters such as the number of nodes, average degree (sensing radius), and level of noise.
In our experiments, the noise is multiplicative and uniform, meaning that to each true distance measurement lij = ||pi − pj||, we add random independent noise εij in the range [−ηlij, ηlij], that is,
| (43) |
The percentage noise added is 100η, (e.g., η = 0.1 corresponds to 10% noise).
The sizes of the graphs we experimented with range from 200 to 105 nodes taking different shapes, with average degrees as low as 6.8 and noise levels up to 70%. Across all our simulations, we consider the disc graph model, meaning that all pairs of sensors within range ρ are connected. We denote the true coordinates of all sensors by the 2 × n matrix P = (p1 … pn) and the estimated coordinates by the matrix . To measure the localization error of our algorithm, we first factor out the optimal rigid transformation between the true embedding P and our reconstruction (using the registration method) and then compute the following average normalized error (ANE).
| (44) |
where is the center of mass of the true coordinates, and the Frobenius norm of an n1 × n2 matrix H is . The normalization factor in the denominator of Equation (44) ensures that the ANE is not only rigid invariant, but it is also scale free, that is, it is invariant to scaling all the distances by a constant factor.
Figure 20 shows reconstructions of the U.S. cities map at different levels of noise η = 0%, 10%, 20%, 30%, 40%, 50%. The number of nodes is n = 1,090 and the sensing radius ρ = 0.032 leads to an average degree between 19 and 23, depending on the noise level η. A high average degree improves significantly the accuracy of the reconstruction, even at high levels of noise. Table IV shows various measurements of the errors in Steps 1 and 2, and indicates that the eigenvector method is able to correct many of the input errors: The errors and are smaller than the input errors and . Table V compares the final reconstruction errors of ASAP, ARAP, and MVU, from which we conclude that ASAP and ARAP usually give very similar reconstruction errors. While FAST-MVU performs reasonably well for the U.S. cities graph, its performance deteriorates significantly for the other graphs considered in the following, despite the fact that unlike with the other tested algorithms, we allowed FAST-MVU to do the gradient-descent final step for minimizing the stress function. We remark that ARAP performs several alternating least-squares iterations (about 40) that refine the reconstruction until convergence, while ASAP is non-iterative and its resulting structure can be further improved with any refinement method. The ANEs reported in Table V for the U.S. cities graph and for all other graphs are averaged over ten runs with independent realizations of noise for the distances. Table VI shows the running time of the various steps of the ASAP algorithm corresponding to our not-particularly optimized MATLAB implementation on a PC machine equipped with an Intel® Core™ 2 Duo CPU E8500 @ 3.16GHz 4 GB RAM. Notice that all steps are amenable to a distributed implementation, thus a parallelized implementation would significantly reduce the running times. Building takes more time than building , since in Step 1, the registration method is performed twice for every pair of overlapping patches, while in Step 2, it is performed only once. We also remark that for η = 50%, we used the combinatorial method for aligning patches that overlap in 2, 3, 4, or 5 nodes, which resulted in a little improvement for the ANE from 0.57 to 0.54.
Fig. 20.
Reconstructions of the US cities graph with n = 1090 nodes, sensing radius ρ = 0.32 and η = 0%, 10%, 20%, 30%, 40%, 50%.
Table IV.
Error Rates for ASAP in Steps 1 and 2 For the U.S. Map with n = 1,090 Cities, ρ = 0.032, and Number of Patches N ≈ 1200 Depending on the Noise Level
| Step 1 (Reflections) | Step 2 (Rotations) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
|||||||||
| η | deg | M | τ | ||||||
|
> | |||||||||
| 0% | 19 | 10228 | 0% | 0.1% | 0% | 0.2 | 0.2 | 0.3% | 0.1% |
| 10% | 19 | 10589 | 0% | 0.2% | 0% | 1.7 | 1.2 | 0.8% | 0.3% |
| 20% | 20 | 11299 | 0.1% | 0.7% | 0.1% | 4 | 2.6 | 7.2% | 2.5% |
| 30% | 20 | 11730 | 2.4% | 2% | 0.4% | 7.7 | 4.2 | 21.1% | 8.9% |
| 35% | 21 | 12165 | 7.1% | 3% | 1.3% | 17.4 | 7.7 | 36.8% | 18.8% |
| 40% | 22 | 12479 | 7.1% | 5.5% | 2.9% | 18.3 | 8.3 | 44.2% | 23.1% |
| 45% | 23 | 14305 | 8.8% | 10.4% | 6.9% | 22.6 | 11.1 | 53.8% | 32.0% |
| 50% | 23 | 15295 | 10.5% | 16.1% | 10.8% | 26.8 | 12.2 | 61.7% | 39.1% |
M is the number of pairs of patches aligned (number of edges in the patch graph). τ denotes the percentage of patches incorrectly oriented, that is, the percentage of disagreements between and zi. is the percentage of errors in the matrix , that is, the percentage of disagreements between zij and restricted to (i, j) ∈ EP. is the percentage of disagreements between and also restricted to (i, j) ∈ EP. and denote the average angle error (in degrees) and the number of outlier angles (errors above 10°) in θij – (θi − θj) mod 2π for (i, j) ∈ EP. and denote the average angle error (in degrees) and the number of outlier angles (errors above 10°) in ) mod 2π for (i, j) ∈ EP.
Table V.
Reconstruction Errors (Measured in ANE) for the U.S. cities Graph with n = 1,090 Cities and Sensing Radius ρ = 0.032
| η | deg | ASAP | ARAP | MVU |
|---|---|---|---|---|
|
| ||||
| 0% | 19 | 0.01 | 0.02 | 0.10 |
| 10% | 19 | 0.05 | 0.04 | 0.09 |
| 20% | 20 | 0.09 | 0.08 | 0.09 |
| 30% | 20 | 0.18 | 0.16 | 0.15 |
| 40% | 22 | 0.32 | 0.40 | 0.25 |
| 45% | 22 | 0.41 | 0.53 | 0.32 |
| 50% | 23 | 0.54 | 0.62 | 0.38 |
Table VI.
Running Times of the ASAP Algorithm
| Stage | Time (sec) |
|---|---|
|
| |
| Break G into patches | 41 |
| Embedding patches | 52 |
| Build | 4.5 |
| Compute | 0.3 |
| Build | 1.7 |
| Compute | 0.3 |
| Step 3 (Least squares) | 3.9 |
|
| |
| Total | 103.6 |
U.S. map with n = 1,090 cities, η = 20%, deg = 20, N = 1,151 patches, average patch size = 15.6.
The C-shape graphs in Figure 21 have n = 200 nodes, sensing radius ρ = 0.17 leading to an average degree between 9 and 10, and were tested at noise levels η = 0%, 10%, 20%, 30%, 40%. The similar C-shape graphs in Figure 22 have the same number of nodes, but ρ = 0.28, the average degrees are between 20 and 28, and the noise levels are η = 35%, 40%, 50%, 60%, 70%. The simulation results in the two scenarios clearly illustrate a significant improvement in robustness to noise for the case of denser graphs. In addition to ARAP and FAST-MVU, we compare our results against the FULL-SDP algorithm [Biswas and Ye 2004] in three different scenarios. In the first two, we run FULL-SDP on the same measurement graph used by the other algorithms but provide FULL-SDP with additional three and ten anchors placed at random that are not provided to the other algorithms. We choose the anchors at random from the set of all sensors. In the third scenario, we use a measurement graph of (approximately) the same average degree deg as the one used by the other algorithms but allow FULL-SDP to use a much larger sensing radius ρ = 1. Each node has a large number of neighbors within reach, but we select on average deg nodes uniformly at random from the set of all nodes within the sensing radius. These experiments show that the FULL-SDP algorithm is somewhat sensitive to the sensing radius and the number of anchors used. As shown at the top of Figure 21, the recovery given by the FULL-SDP algorithm with ten random anchors and no noise (η = 0%) is rather poor compared to ASAP, ARAP, and FAST-MVU, that are not using any anchor points whatsoever. However, the usage of long-range distances significantly improves the solution of the FULL-SDP algorithm, as shown by the top-right plot in Figure 21. Tables VII and VIII provide the reconstruction errors for the C graphs. While ASAP and ARAP give comparable results, the errors of MVU are significantly larger.
Table VII.
Reconstruction errors (measured in ANE) for the C Graph with n = 200 Nodes, Sensing Radius ρ = 0.17, and Average Degree deg = 9
| η | ASAP | AAAP | ARAP | MVU | fullsdp3 | FULLSDP10 | FULLSDP*10 |
|---|---|---|---|---|---|---|---|
|
| |||||||
| 0% | 0 | 0.03 | 0.01 | 0.19 | 0.30 | 0.18 | 0 |
| 10% | 0.02 | 0.15 | 0.03 | 0.20 | 0.29 | 0.17 | 0.10 |
| 20% | 0.04 | 0.30 | 0.05 | 0.26 | 0.25 | 0.17 | 0.15 |
| 30% | 0.07 | 0.37 | 0.08 | 0.29 | 0.25 | 0.17 | 0.23 |
| 40% | 0.14 | 0.42 | 0.11 | 0.32 | 0.23 | 0.17 | 0.30 |
| 50% | 0.23 | 0.46 | 0.20 | 0.34 | 0.23 | 0.18 | 0.37 |
FULLSDPk denotes the FULLSDP algorithm with k anchors. FULLSDP*10 denotes the sameFULLSDP algorithm, but for a sensing radius ρ = 1 and a degree limit on each nodes that preserves the average degree deg.
Table VIII.
Reconstruction Errors (Measured in ANE) for the C graph with n = 200 Nodes and Sensing Radius ρ = 0.28
| η | deg | ASAP | ARAP | MVU | FULLSDP3 | FULLSDP10 | FULLSDP*10 |
|---|---|---|---|---|---|---|---|
|
| |||||||
| 0% | 20 | 0 | 0.01 | 0.45 | 0 | 0 | 0 |
| 35% | 22 | 0.15 | 0.18 | 0.61 | 0.25 | 0.24 | 0.28 |
| 40% | 22 | 0.19 | 0.23 | 0.57 | 0.28 | 0.24 | 0.33 |
| 45% | 23 | 0.23 | 0.28 | 0.72 | 0.28 | 0.24 | 0.37 |
| 50% | 24 | 0.32 | 0.32 | 0.72 | 0.30 | 0.25 | 0.47 |
| 55% | 25 | 0.40 | 0.38 | 0.82 | 0.34 | 0.28 | 0.49 |
| 60% | 26 | 0.47 | 0.47 | 0.76 | 0.37 | 0.29 | 0.54 |
| 65% | 27 | 0.58 | 0.56 | 0.90 | 0.42 | 0.32 | 0.58 |
| 70% | 28 | 0.67 | 0.62 | 0.81 | 0.47 | 0.35 | 0.58 |
For the PACM graphs in Figure 23, the sensor network takes the shape of the letters P, A, C, M that form a connected graph on n = 425 vertices. The sensing radius is ρ = 0.9 and the average degree deg ≈ 12. This graph was particularly useful in testing the sensitivity of the algorithm to the topology of the network. In Table IX, we show the reconstruction errors for various levels of noise η = 0%, 10%, 20%, 30%, 40%.
Fig. 23.
Reconstructions of the PACM graph with n = 425 nodes, ρ = 0.9, and noise levels η = 0%, 10%, 20%, 30%, 40%.
Table IX.
Reconstruction Errors (Measured in ANE) for the PACM Graph with n = 425 Vertices, Sensing Radius ρ = 0.9, and Average Degree deg = 12
| η | ASAP | AAAP | ARAP | MVU |
|---|---|---|---|---|
|
| ||||
| 0% | 0 | 0 | 0 | 0.20 |
| 10% | 0.06 | 0.11 | 0.02 | 0.22 |
| 20% | 0.20 | 0.24 | 0.03 | 0.22 |
| 30% | 0.23 | 0.30 | 0.06 | 0.23 |
| 40% | 0.32 | 0.34 | 0.13 | 0.24 |
Another graph that we tested is the GRID graph shown in Figure 24. It has n = 272 nodes, sensing radius ρ = 0.7, and average degree deg ≈ 10. Table X shows the reconstruction errors for various levels of noise η = 0%, 10%, 20%, 30%, 40%, 50%. To test the robustness to noise in the case of a very sparse graph, we experimented with the SQUARE graph with n = 250 nodes and average degree deg 6.8. The ASAP and ARAP algorithm can handle well up to 40% noise, with the latter being slightly more accurate. Figure 25 and Table XIII show the reconstruction errors for the SQUARE graph at noise levels η = 0%, 10%, 20%, 30%, 40%, 50%.
Fig. 24.
Reconstructions of the GRID graph with n = 272 nodes, ρ = 0.7, and noise levels η = 0%, 10%, 20%, 30%, 40%, 50%.
Table X.
Reconstruction Errors (Measured in ANE) for the GRID Graph with n = 272 Nodes, Sensing Radius ρ = 0.7, and Average Degree deg = 10
| η | ASAP | AAAP | ARAP | MVU | FULL-SDP3 |
|---|---|---|---|---|---|
|
| |||||
| 0% | 0 | 0.01 | 0 | 0.02 | 0 |
| 10% | 0.01 | 0.04 | 0.01 | 0.06 | 0.17 |
| 20% | 0.02 | 0.12 | 0.01 | 0.12 | 0.23 |
| 30% | 0.04 | 0.19 | 0.02 | 0.18 | 0.24 |
| 40% | 0.06 | 0.25 | 0.04 | 0.26 | 0.26 |
| 50% | 0.11 | 0.29 | 0.06 | 0.30 | 0.26 |
Fig. 25.
Reconstructions of the SQUARE graph with n 250 nodes, radius ρ = 1.51 and average degree deg = 6.8, for different levels of noise η = 0%, 10%, 20%, 30%, 40%, 50%.
Table XIII.
Reconstruction Errors (Measured in ANE) for the SQUARE Graph with n = 250 Nodes, Sensing Radius ρ = 1.51, and Average Degree deg = 6.8
| η | ASAP | AAAP | ARAP | MVU | FULLSDP3 | FULLSDP10 |
|---|---|---|---|---|---|---|
|
| ||||||
| 0% | 0.0000 | 0.0036 | 0.0060 | 0.0273 | 0.2329 | 0.0652 |
| 10% | 0.0155 | 0.0443 | 0.0092 | 0.0619 | 0.2917 | 0.1689 |
| 20% | 0.0524 | 0.1256 | 0.0165 | 0.1004 | 0.2858 | 0.1760 |
| 30% | 0.0835 | 0.2023 | 0.0277 | 0.1646 | 0.2767 | 0.1793 |
| 40% | 0.1543 | 0.2551 | 0.1114 | 0.2114 | 0.2588 | 0.1722 |
| 50% | 0.3150 | 0.2899 | 0.3132 | 0.2540 | 0.2558 | 0.1714 |
The second to last graph that we tested is the SPIRAL graph shown in Figure 19(a). This graph is made of n = 2,259 nodes that are spread near a spiral curve that starts at the origin, and once it gets to its outermost loop, it traces back towards the origin. The perturbation of the sensors from the curve ensures that the one-hop neighborhoods are not too close to being collinear. The sensing radius for this graph is ρ = 0.47. Despite the fact that the measured distances are noise free, the localizations obtained by ASAP, AAAP, ARAP, and MVU (Figures 19(c), 19(e), and 19(f)) deviate from the true positioning. The failure of ASAP to find the original embedding in this noise-free case is due to a failure of the SMACOF procedure to localize a small number of patches. Although there is no noise in the distance measurements, the stress minimization algorithm sometimes converges to a local minimum, resulting in patches that are incorrectly localized. Since the topology of this graph is that of a closed curve, such bad patches lead to incorrect twists and turns in our computed embedding. Although ASAP and ARAP are using the same algorithm to localize the patches, it is clear that the incorrectly localized patches are less harmful to ASAP as they are to ARAP. This is also indicated in the averaged normalized errors: ANE(ASAP) = 0.47, ANE(ARAP) = 1.30, ANE(MVU) = 3.43. Figure 19(b) shows the accurate embedding obtained by ASAP when SNL-SDP was used to localize the patches, denoted ASAP-SDP, for which ANE(ASAP-SDP) = 0.002. Although SNL-SDP requires more time to embed the patches (850 seconds compared to 250 seconds for SMACOF), this time was well spent in getting an improved reconstruction.
Fig. 19.
Reconstructions of the SPIRAL graph with n = 2,259 nodes, ρ = 0.47, and η = 0%. ASAP-SDP is a version of ASAP where we used SDP for the localization of the patches, instead of SMACOF.
Another difference between ASAP and ARAP for this SPIRAL graph is in the running time. While ASAP runs here for about 500 seconds (and 1,100 seconds with SNL-SDP), ARAP takes over 10,000 seconds, with the majority of its running time being spent on localizing the patches. We believe that this difference in running time is caused by ARAP’s attempt to localize the entire one-hop neighborhood of every node, rather than breaking up the one-hop neighborhoods into globally rigid patches, like ASAP does. The example of the SPIRAL graph shows that the embedding of some graphs can be challenging even in the noise-free case, but ASAP is doing relatively well even for this difficult graph.
Finally, in order to illustrate the scaling behavior of ASAP and compare its running time to that of the other algorithms, we experimented with random graphs with n = {103, 104, 105} nodes distributed uniformly at random in the unit square. For this experiment, we used a machine with 192 GB memory and 2.66GHz core. Since the sizes of the graphs are increasing in scale, we choose the radius ρ such that the average degree remains about the same deg = {12.8, 12.5, 12.8}. Table XI details the running times of the various steps of the ASAP algorithm for three graphs, and Table XII compares the running times of ASAP, AAAP, ARAP, FAST-MVU, and FULLSDP20 for a random graph on n = 103 nodes. FAST-MVU is by far the fastest method with only 2.7 seconds, but also the one least robust to noise. ASAP comes second with 477 seconds, 95% of which are spent in the preprocessing steps. ARAP9 took 1,201 seconds, and when run on n = 104 nodes, it did not produce an outcome within 48 hours. We could also move this earlier in this section. The FULL-SDP method takes over 5,000 seconds when run on a graph with n = 103 nodes and is unlikely to compare well to ASAP if we increase n to 104. We expect that an optimized implementation in C would further reduce the running time of ASAP, in particular, the steps of breaking G into patches and computing the patch intersections. For n = 105, these two steps account for almost 70% of the current running time, and an implementation where they would scale linearly means reducing the overall running time by more than 60% to only about 60,000 seconds.
Table XII.
Comparison of the Running Times (in Seconds) of Different Algorithms for the SQUARE Graph with n = {103,104} Nodes and η = 0%
| Algorithm | n = 1,000 | n = 10,000 |
|---|---|---|
|
| ||
| ASAP | 477 | 5605 |
| AAAP | 1170 | > 48 hours |
| ARAP | 1201 | > 48 hours |
| FAST-MVU | 2.7 | 10.8 |
| fullsdp20 | 5250 | - |
9. SUMMARY AND DISCUSSION
In this article, we introduced As-Synchronized-As-Possible (ASAP), a non-incremental, non-iterative, anchor-free algorithm for localizing sensor networks. As our numerical experiments show, ASAP is extremely robust to high levels of noise in the measured distances and to sparse connectivity of the measurement graph. Our algorithm starts with local coordinate computations based only on one-hop neighborhood information, but unlike existing incremental methods, it synchronizes all such local information in a noise-robust global optimization process using an efficient eigenvector computation.
Across all graphs that we have tested, ASAP and ARAP almost always give the best results in terms of the averaged normalized error. In particular, whenever another algorithm like MVU or SDP does well, ASAP and ARAP are also successful. Also, to the naked eye, the localization results of ASAP and ARAP best resemble the true positioning. The SPIRAL graph demonstrates that there are cases for which ASAP and ARAP can give significantly different results, in this case, to the favor of the former. When comparing ASAP and AAAP, both of which are fully ab-initio reconstructions, it is clear that ASAP gives much better results. Although ASAP and ARAP usually give similar results, there is a fundamental difference between the two algorithms. While ARAP requires an initial guess provided by AAAP to start its iterative refinement process, ASAP is a fully ab-initio reconstruction method that scales almost linearly in the size of the network, as demonstrated by our example of localizing a network with 100,000 nodes. In practice, ASAP can (and perhaps should) be followed by a refinement procedure, such as stress minimization or even ARAP.
The unit disc graph assumption, which comes up naturally in many problems of practical interest, is essential to the performance of the ASAP algorithm, as it favors the existence of many globally rigid patches of relatively large size. When the disc graph assumption does not hold, the one-hop neighborhood of a node may be extremely sparse, and thus, breaking up such a sparse star graph leads to many small maximally globally rigid components (i.e., most of them may contain only a few nodes), with only a few of them having a large enough pairwise intersection. Since small patches lead to small patch intersections, it would therefore be difficult for ASAP to align patches correctly and compute a robust final solution. Except for the combinatorial score method in Section 6, the ASAP algorithm does not (explicitly) make use of the sensing radius of the disc graph model assumption.
Although this article is concerned with the localization of planar networks, we remark that ASAP can be generalized to solve the localization problem in , a problem which is motivated by three-dimensional structure determination of macromolecules using NMR spectroscopy [Hendrickson 1995]. The three-dimensional localization problem can be formulated as a synchronization problem over Euc(3), and can be similarly solved in three steps: an eigenvector synchronization for the reflections over , an eigenvector synchronization for the rotations over SO(3), and a least-squares solution for the translations in . In the second step of the algorithm, the optimal rotations between pairs of patches will be represented by 3×3 rotation matrices, and the elements of SO(3) will be obtained from the top three eigenvectors instead of just the top one. We defer the complete description and analysis of ASAP for solving the three-dimensional case to a separate publication.
Combining both distance and angular measurements to increase accuracy and robustness to noise is another possible generalization. The inclusion of angular measurements in localization algorithms has not been studied as thoroughly as distance measurements, but recent papers, such as Bruck et al. [2009], provide insight for this potential improvement. In the context of the ASAP algorithm, angular measurements should lead to better localization and alignment of the patches.
There are a few possible ways in which the ASAP algorithm can be improved. First, it is possible to weigh the entries of the Z and R matrices from Steps 1 and 2. One possible weighing scheme would be to assign weights that are proportional to some confidence measure in the alignment of the patches. For example, a high residual obtained when aligning two patches hints that the relative reflection or rotation may be incorrect. Also, aligning two patches with a large overlap is significantly more robust than aligning two patches that overlap in just a few vertices. Another possible scheme is to design weights that will minimize the mixing time of the random walk on the patch graph, or equivalently, maximizing the second eigenvalue (the spectral gap) of the graph Laplacian. This approach is motivated by our unreported matrix perturbation analysis initiated in Section 4 and by the intuition that faster mixing of the random walk should assist the eigenvector method to integrate and propagate consistency relations over cycles in the patch graph. In Sun et al. [2006], it is shown that this fastest mixing design problem is convex and can be solved using SDP, which interestingly enough draws similarities with the MVU approach to localization. The synchronization problems in Steps 1 and 2 can be solved using SDP instead of the eigenvector method (see Singer [2010]), but our experience show that the improvement is usually marginal.
Targeting bad patches and bad distance measurements (outliers detection) is another approach that may increase the robustness of the algorithm to noise. After Step 1 of the algorithm, we have the estimated reflections , and it is possible now to target bad patches Pi for which differs from zij for a large number of neighboring patches Pj. Even before Step 1, one may wish to discard patches whose area inside their convex hull is too small, as such patches are likely to result in incorrect reflections. Also, in the spirit of the weighted-matrices scenario previously mentioned, one may start by aligning patches and localizing nodes only in regions of the graph that have a higher density of edges. Targeting and removing bad patches that have low confidence may disconnect the patch graph in Steps 1 and 2. One should then run the ASAP algorithm on each connected component of the patch graph, thus localizing all the nodes within them. Some of the missing distances can now be inferred and can be added to the problem by an iterative application of the ASAP algorithm. Although this method seems incremental in nature, at each step, the eigenvector computation will enforce global consistencies.
We believe that the eigenvector synchronization method has the potential of being useful in many applications other than the localization problem of sensor networks. In particular, in Singer and Shkolnisky [2011] and Singer et al. [2011] we demonstrated its usefulness in cryo-electron microscopy [Frank 2006] and showed its mathematical connection to the parallel transport and the connection-Laplacian operators from differential geometry. We are currently extending this approach to the 3D structure from motion problem in computer vision and to the analysis of high-dimensional data point clouds [Singer and Wu 2012, 2011], specifically to the generalization of Laplacian eigenmaps and diffusion maps [Belkin and Niyogi 2003; Coifman and Lafon 2006] that are popular methods for dimensionality reduction and spectral clustering.
ACKNOWLEDGMENTS
The authors would like to thank L. Zhang, L. Liu, C. Gotsman, and S. Gortler for providing them with their ARAP code, and Y. Ye and Z. Zhu for sharing their FULL-SDP code.
The work was supported by award number DMS-0914892 from NSF by award number FA9550-09-1-0551 from AFOSR, and by award number R01GM090200 from the National Institute of General Medical Sciences. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of General Medical Sciences or the National Institutes of Health.
Footnotes
Every iteration of the power method is linear in the number of edges of the graph, but the number of iterations is greater than O(1), as it depends on the spectral gap.
We remark that in the disc graph model, the non-edges also provide distance information, since (i,j)∉ E implies dij > ρ. This information sometimes allows for uniquely localizing networks that are not globally rigid to begin with. This information, however, is not used in the standard formulation of the ASAP algorithm except for extremely sparse networks, as discussed later in Section 6.
For example, three common vertices, although the precise definition of “enough” will be given later.
The diagonal matrix D should not be confused with the partial distance matrix.
Not to be confused with G(i) = (V (i), E(i)) defined in the beginning of this section.
In fact, we can write such equations for every i, j ∈ Vk but choose to do so only for edges of the original measurement graph.
Note that some edges in E may not be contained in any patch Pk, in which case the corresponding row in has only zero entries.
We used the SNL-SDP code of Toh et al. [2008].
Note that for testing ARAP, we used the MATLAB implementation kindly provided by its authors on November 2009.
Categories and Subject Descriptors: C.2.4 [Computer-Communication Networks]: Distributed Systems—Distributed applications; F.2.2 [Analysis of Algorithms and Problem Complexity]: Nonnumerical Algorithms and Problems—Routing and layout
General Terms: Algorithms, Theory
Contributor Information
MIHAI CUCURINGU, Program in Applied and Computational Mathematics (PACM), Princeton University, Fine Hall, Washington Road, Princeton VJ 08544-1000; mcucurin@math.princeton.edu.
YARON LIPMAN, Department of Computer Science and PACM, Princeton University, Fine Hall, Washington Road, Princeton VJ 08544-1000; ylipman@math.princeton.edu.
AMIT SINGER, Department of Mathematics and PACM, Princeton University, Fine Hall, Washington Road, Princeton VJ 08544-1000; amits@math.princeton.edu.
References
- Anderson BDO, Belhumeur PN, Eren T, Goldenberg DK, Morse AS, Whiteley W. Graphical properties of easily localizable networks. Wirel. Netw. 2009;15(2):177–191. [Google Scholar]
- Asano T, Bose P, Carmi P, Maheshwari A, Shu C, Smid M, Andwuhrer S. A linear-space algorithm for distance preserving graph embedding. Comput. Geom. 2009;42(4):289–304. [Google Scholar]
- Aspnes J, Eren T, Goldenberg DK, Morse AS, Whiteley W, Yang YR, Anderson BDO, Belhumeur PN. A theory of network localization. IEEE Trans. Mob. Comput. 2006;5(12):1663–1678. [Google Scholar]
- Aspnes J, Goldenberg DK, Yang YR. Proceedings of the 1st International Workshop on Algorithmic Aspects of Wireless Sensor Networks (ALGOSENSORS), Lecture Notes in Computer Science. Vol. 8121. Springer-Verlag; Berlin: 2004. On the computational complexity of sensor network localization; pp. 32–44. [Google Scholar]
- Belkin M, Niyogi P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 2003;15(6):1373–1396. [Google Scholar]
- Biswas P, Aghajan H, Ye Y. Semidefinite programming algorithms for sensor network localization using angle of arrival information. proceeding of the 39th Annual Asilomar Conference on Signals, Systems, and Computers. 2005:220–224. [Google Scholar]
- Biswas P, Lian TC, Wang TC, Ye Y. Semidefinite programming based algorithms for sensor network localization. ACM Trans. Sen. Netw. 2006a;2(2):188–220. [Google Scholar]
- Biswas P, Liang T, Toh K, Ye Y, Wang T. Semidefinite programming approaches for sensor network localization with noisy distance measurements. IEEE Trans. Autom. Sci. Eng. 2006b;3(4):360–371. [Google Scholar]
- Biswas P, Ye Y. Semidefinite programming for ad hoc wireless sensor network localization. Proceedings of the 3rd International Symposium on Information Processing in Sensor Networks. 2004:46–54. [Google Scholar]
- Borg I, Groenen PJF. Springer; New York, NY: 2005. Modern multidimensional scaling: Theory and applications. [Google Scholar]
- Bruck J, Gao J, Jiang A. Localization and routing in sensor networks by local angle information. ACM Trans. Sen. Netw. 2009;5:1. [Google Scholar]
- Coifman RR, Lafon S. Diffusion maps. Appl. Comput. Harmon. Anal. 2006;21(1):5–30. [Google Scholar]
- Connelly R, Whiteley WJ. Global rigidity: The effect of coning. Discrete Comput. Geom. 2009;43(4):717–735. [Google Scholar]
- Cox TF, Cox MAA. Monographs on Statistics and Applied Probability 88. Chapman & Hall/CRC; Boca Raton, FL: 2001. Multidimensional Scaling. [Google Scholar]
- De Leeuw J. Applications of convex analysis to multidimensional scaling. In: Barra JR, Brodeau F, Romierand G, Cutsem BV, editors. Recent Developments in Statistics. North Holland Publishing Company; Amsterdam: 1977. pp. 133–146. [Google Scholar]
- Frank J. Three-Dimensional Electron Microscopy of Macromolecular Assemblies: Visualization of Biological Molecules in Their Native State. 2nd Ed. Oxford University Press; 2006. [Google Scholar]
- Giridhar A, Kumar PR. Distributed clock synchronization over wireless networks: Algorithms and analysis. Proceedings of the 45th IEEE Conference on Decision and Control. 2006:4915–4920. [Google Scholar]
- Gotsman C, Koren Y. Distributed graph layout for sensor networks. Proceedings of the Internatitional Symposium on Graph Drawing. 2004:273–284. [Google Scholar]
- Hendrickson B. Conditions for unique graph realizations. SIAM J. Comput. 1992;21:65–84. [Google Scholar]
- Hendrickson B. The molecule problem: Exploiting structure in global optimization. SIAM J. Optim. 1995;5:835–857. [Google Scholar]
- Horn B, Hilden H, Negahdaripour S. Closed-form solution of absolute orientation using orthonormal matrices. J. Opt. Soc. Am. 1988;A 5(7):1127–1135. [Google Scholar]
- Ji X, Zha H. Proceedings of the Annual Joint Conference of the IEEE Computer and Communications Societies(INFOCOM. 2004. Sensor positioning in wireless ad-hoc sensor networks using multidimensional scaling; pp. 2652–2661. [Google Scholar]
- Karp R, Elson J, Estrin D, Shenker S. Tech. Rep. Center for Embedded Networked Sensing; University of California, Los Angeles: 2003. Optimal and global time synchronization in sensornets. [Google Scholar]
- Koren Y, Gotsman C, Ben-Chen M. PATCHWORK: Efficient localization for sensor networks by distributed global optimization. Tech. Rep. 2005 [Google Scholar]
- Moore D, Leonard J, Rus D, Teller S. Robust distributed network localization with noisy range measurements. Proceedings of the 2nd ACM Conference on Embedded Networked Sensor Systems. 2004:50–61. [Google Scholar]
- Peaucelle D, Henrion D, Labit Y, Taitz K. 2002. User’s guide for sedumi interface 1.04. www.laas.fr/~peaucell/software/sdmguide.ps.gz. [Google Scholar]
- Roweis ST, Saul LK. Nonlinear dimensionality reduction by locally linear embedding. Science. 2000;290:2323–2326. doi: 10.1126/science.290.5500.2323. [DOI] [PubMed] [Google Scholar]
- Saxe JB. Proceedings of the 17th Allerton Conference on Communication, Control, Computing. 1979. Embeddability of weighted graphs in k-space is strongly NP-hard; pp. 480–489. [Google Scholar]
- Schaefer S, Mcphail T, Warren J. Image deformation usingmoving least squares. Proceedings of the SIGGRAPH papers. 2006:533–540. [Google Scholar]
- Shang Y, Ruml W. Proceedings of the Annual Joint Conference of the IEEE Computer and Communications Societies. Vol. 23. Hong Kong, China: 2004. Improved MDS-based localization; pp. 2640–2651. [Google Scholar]
- Singer A. A remark on global positioning from local distances. PNAS. 2008;105(28):9507–9511. doi: 10.1073/pnas.0709842104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singer A. Angular synchronization by eigenvectors and semidefinite programming. Appl. Comput. Harmon. Anal. 2010;30(1):20–36. doi: 10.1016/j.acha.2010.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singer A, Shkolnisky Y. Three-dimensional structure determination from common lines in Cryo-EM by eigenvectors and semidefinite programming. SIAM J. Imag. Sci. 2011;4(2):543–572. doi: 10.1137/090767777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singer A, Wu HT. Orientability and Diffusion Maps. Applied and Computational Harmonic Analysis. 2011;31(1):44–58. doi: 10.1016/j.acha.2010.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singer A, Wu HT. Vector Diffusion Maps and the Connection Laplacian. Communications on Pure and Applied Mathematics. 2012;65(8):1067–1144. doi: 10.1002/cpa.21395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singer A, Zhao Z, Shkolnisky Y, Hadani R. Viewing angle classification of cryo-electron microscopy images using eigenvectors. SIAM Journal on Imaging Sciences. 2011;4(2):723–759. doi: 10.1137/090778390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- So AMC. A semidefinite programming approach to the graph realization problem: Theory, applications and extensions. Ph.D. dissertation. stanford University; Palo Alto, CA: 2007. [Google Scholar]
- So AMC, Ye Y. Proceedings of the 17th Annual ACM-SIAM Symposium on Discrete Algorithm (SODA) 2005. Theory of semidefinite programming for sensor network localization; pp. 405–414. [Google Scholar]
- Sun J, Boyd S, Xiao L, Diaconis P. The fastest mixing markov process on a graph and a connection to a maximum variance unfolding problem. SIAM Rev. 2006;48(4):681–699. [Google Scholar]
- Toh K, Biswas P, Ye Y. SNLSDP version 0 - a MATLAB software for sensor network localization. 2008 http://www.math.nus.edu.sg/~mattohkc/SNLSDP.html. [Google Scholar]
- Trefethen LN, Bau D. Numerical Linear Algebra. SIAM: Society for Industrial and Applied Mathematics. 1997 [Google Scholar]
- Tubaishat M, Madria S. Sensor networks: An overview. IEEE Potentials. 2003;22:20–23. [Google Scholar]
- Weinberger KQ, Sha F, Zhu Q, Saul LK. Graph laplacian regularization for largescale semidefinite programming. In: Schoolkopf B, Platt J, Hofmann T, editors. Advances in Neural Information Processing Systems (NIPS) MIT Press; Cambridge, MA: 2007. [Google Scholar]
- Yemini Y. Some theoretical aspects of location-location problems. Proceedings of the IEEE Symposium on Foundation of Computer Science. 1979:1–8. [Google Scholar]
- Zhang L, Liu L, Gotsman C, Gortler SJ. An As-Rigid-As-Possible approach to sensor network localization. ACM Trans. Sen. Netw. 2010;6:4. [Google Scholar]
- Zhu Z, So AMC, Ye Y. Universal rigidity: Towards accurate and efficient localization of wireless networks. Proceedings of the Annual Joint Conference of the IEEE Computer and Communications Societies. 2010 [Google Scholar]