Images of paraffin monolayer crystals with perfect contrast: minimization of beam-induced specimen motion

Abstract

Quantitative analysis of electron microscope images of organic and biological two-dimensional crystals has previously shown that the absolute contrast reached only a fraction of that expected theoretically from the electron diffraction amplitudes. The accepted explanation for this is that irradiation of the specimen causes beam-induced charging or movement, which in turn causes blurring of the image due to image or specimen movement. In this paper, we used three different approaches to try to overcome this image-blurring problem for monolayer crystals of paraffin. Our first approach was to use an extreme form of spotscan imaging, in which a single image was assembled on film by the successive illumination of up to 50,000 spots each of diameter around 7nm. The second approach was to use the Medipix II detector with its zero-noise readout to assemble a time-sliced series of images of the same area in which each frame from a movie with up to 400 frames had an exposure of only 500 electrons. In the third approach, we simply used a much thicker carbon support film to increase the physical strength and conductivity of the support. Surprisingly, the first two methods involving dose fractionation respectively in space or time produced only partial improvements in contrast whereas the third approach produced many virtually perfect images, in which the absolute contrast predicted from the electron diffraction amplitudes was observed in the images. We conclude that it is possible to obtain consistently almost perfect images of beam-sensitive specimens if they are attached to an appropriately strong and conductive support, but great care is needed in practice and the problem of how best to image ice-embedded biological structures in the absence of a strong, conductive support film requires more work.

1. Introduction

In structural biology, the signal-to-noise ratio of images of unstained biological molecules is fundamentally limited by the maximum dose that can be used to record the images before radiation damage destroys the structure. For such biological specimens and indeed for any organic material, a clear improvement is obtained by cooling the specimen to temperatures between that of liquid nitrogen and liquid helium. This allows an increased electron dose to be used because some of the molecular fragments that are created by beam damage remain frozen in place with an overall structure that resembles the undamaged original. Thus, electron cryo-microscopy offers a 5 to 10-fold increase in limiting dose compared with room temperature imaging [1,2] and has the advantage that molecules can be trapped by rapid freezing in amorphous ice [3], but this simply moves the fundamental barrier of electron dose to the higher limit.

As a result of this dose limitation, it is critically important to make use of the signal from every electron that interacts with the specimen. This makes it imperative to develop efficient detectors with high detective quantum efficiency (DQE), and such developments are imminent [4,5,6]. However, it is also imperative that the image contrast, which directly affects the signal-to-noise ratio, should not be degraded by imaging artifacts that cannot be corrected computationally. Note that the electron optical consequences on the image defined through the contrast transfer function (CTF) by defocus, astigmatism, spherical aberration and beam tilt can be treated exactly during image processing and do not reduce the envelope of image contrast. Illumination that is spatially or temporally incoherent does reduce the contrast envelope at high resolution, but fortunately modern field emission gun (FEG) electron sources are bright enough and have a sufficiently small energy spread that the effect on images at resolutions that are important in structural biology is minimal. Finally, with the promise of C_c corrected imaging systems [7] and Zernike quarter-wave plates [8,9,10], the theoretical contrast attainable at both high and low resolution ought to approach perfection. The principal remaining barrier to the realization of the full potential of electron microscopy in structural biology is to understand the origin of the image blurring that reduces contrast [11] and to develop procedures that eliminate or minimize it.

During electron microscopy of organic or biological specimens, the interaction of the electron beam with the specimen involves both elastic and inelastic scattering events. The wavefront of the elastically scattered electrons is responsible for the high-resolution phase-contrast image that provides the desired information on the structure of the specimen. However, the cross-section for inelastic events with organic and biological specimens, mainly from plasmon scattering, is 3 or 4 times higher than that for elastic events [12]. The inelastic events bring several consequences for electron microscopy of organic or biological specimens. These include the emission of secondary electrons and the breakage of covalent bonds, whose energy of stabilisation is much less than that deposited by the inelastic events. In addition, the secondary-electron emission causes a build-up of positive charge on the specimen during the exposure.

Covalent bond breakage causes atoms in the specimen to move apart by an amount at least as great as the difference between the covalent bond length (~1.5Å) and the van der Waals contact distance (~3.5Å) [13]. Bond breakage also creates fragments whose preferred physical state can be solid, liquid or gas depending on the specimen temperature and the size of the fragment. At room temperature, there is therefore considerable mass loss during the electron exposure even if minimal dose techniques are used. Bond rupture can lead to either expansion or shrinkage of the specimen, depending on whether the radiolytic fragments remain bound or evaporate, either of which would generate stress that might drive local as well as remote (long-range) movements in the specimen.

The mechanical movements caused by bond breakage, and other possible movements of either the specimen or the image caused by electrostatic forces, result in undesirable contrast loss or even visible blurring of the images in the worst case [3,11,14], whereas images of radiation stable materials such as vermiculite show the expected image contrast [11]. There have been several attempts to minimise this image blurring. The use of an objective aperture can partly neutralise the accumulating charge on the specimen with low-energy secondary electrons emitted from the objective aperture: this is widely believed to reduce blurring [15]. Spotscan imaging consists of a procedure in which the complete image is made up of successive exposures of small spots of illumination in a raster that scans over the specimen to build up a final image. Since only a small region is exposed at each moment and this is surrounded by areas that are exposed earlier or later, the effect of specimen movement on image blurring is minimised [16,17]. More recently, dose fractionation was attempted using a procedure named stroboscopic imaging [18], in which it was hoped that the image blurring in each frame would be less than that in the full exposure, and that better images could be recovered by the later computational removal of much of the cumulative image shift. Although the image degradation and contrast loss is reduced by these and other useful tricks, such as the use of pre-irradiated carbon support films [15], doped silicon-carbide support film [19] or symmetrical carbon sandwich techniques [20,21], the signal level in images generally remains well below what it is in the scattered electron wave. At present therefore, the high-frequency Fourier components of images (or any resulting three-dimensional structure) always need to be restored by sharpening to compensate for the blurring from specimen movement in the original images [22]. The crystallographic B-factors required range from about 200 to 1000 Ų [22,23]. There is therefore still some way to go before images can be obtained routinely that provide the contrast expected from basic physics [12].

In this paper, we push the limits of imaging conditions further than ever before, even beyond what might be usable in practice, to investigate the nature of the image blurring that is due to specimen movement. We have extended the range of both spatially limited (spot-scan) and time-fractionated (stroboscopic) illumination conditions, and in addition we have increased the thickness of the support film so as to increase its strength. We report here that neither further fractionation of the electron exposure, nor further reduction in the size of the illumination spot result in reliable improvement in data quality. A significant improvement is realized, however, by using carbon support films that are at least 35 nm in thickness. Although there is still some remaining variation in image quality, the contrast in the very best images now approaches that expected from theory.

2. Material and Methods

Specimens of monolayer paraffin crystals, shown schematically in Fig. 1, were grown on carbon films, floated off mica. Briefly, carbon films were evaporated onto freshly cleaved mica, floated one or a few days later onto a clean water surface and picked up on 400 mesh copper grids. After letting the films “age” for a week to 10 days in order for them to become more hydrophobic, a 2μl drop of a 1/3^rd-saturated solution of C₄₄H₉₀, tetratetracontane, from Sigma, in hexane was applied to the carbon surface and allowed to dry. Different thicknesses of carbon film were investigated, made by varying the evaporation time rather than by performing repeated cycles of evaporation. In the Results section we differentiate between ‘thin’ carbon, having a thickness of about 13 nm and ‘thick’ carbon, having a thickness of about 35 nm. While the thick carbon films floated easily from the mica, it is not always the case that they adhere well to the grids when the hexane solution is applied to the carbon. The thickness of the carbon films was determined by measuring the decrease in the intensity of the transmitted electron beam, using either a highly defocused image of an area illuminated with a beam of small diameter or a slightly defocused diffraction pattern with a very long camera length. This removes essentially all the elastically and inelastically scattered electrons from the beam whose intensity is then easy to measure. With a mean free path for inelastic and elastic scattering of ~85 nm, a carbon film of 35 nm thickness shows 66% transmission of a 120keV electron beam. For the supporting metal grid, other materials than copper, such as molybdenum and ceramic, were also tried but no significant differences in image quality with room temperature specimens were found.

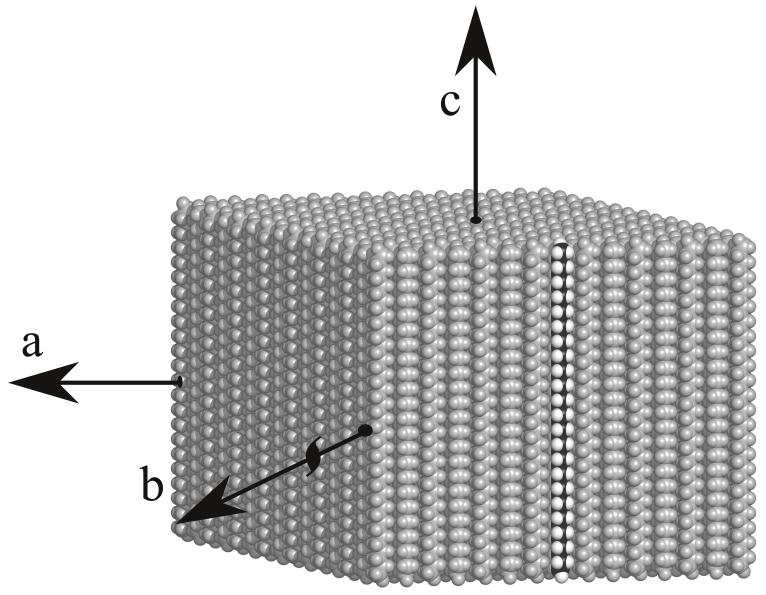
Fig. 1.

Computer generated model of the packing of paraffin molecules in the monolayer crystals used in this work. Each monolayer is essentially one half of a layer of unit cells from an orthorhombic 3D crystal [29] and the figure shows just the monolayer. One paraffin chain is shown in black and white, representing carbon and hydrogen, with all other molecules grey. The orthorhombic 3D crystal unit cell has twice the vertical height of the monolayer shown here. The diamond-shaped morphology of all the crystals has facets parallel to the (1,1) and (1,−1) directions, with the unit cell a and b axes along the diagonals.

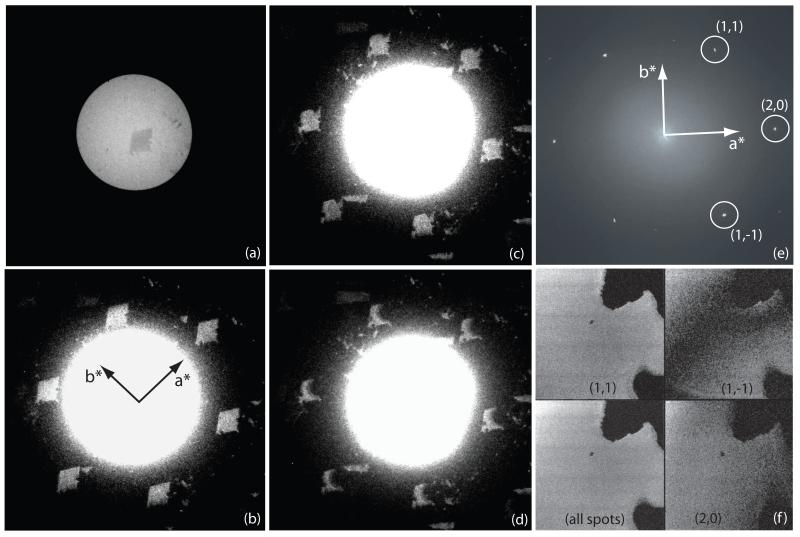
We used an FEI Tecnai F30 electron microscope for most of the experiments. Suitable crystals were located while viewing a defocused electron diffraction pattern in Search Mode on the microscope Low Dose System, using either a TVIPS F114 CCD camera or the Medipix II detector. The electron beam was adjusted so that a small circular region, defined by the C2 aperture, illuminated the paraffin crystal, and the six diffraction spots at ~4 Å resolution were positioned just outside the bright-field image. In this imaging mode, in addition to the defocused direct beam used to observe the crystal in bright-field, the diffraction spots are also defocused and take on the shape of the crystal, each showing a dark-field image of the crystal. Thus, the outline of the crystals and their electron diffraction patterns could be observed in the same image, albeit using different display thresholds. The camera length required for this arrangement was in the range 600-1000 mm, depending on the detector size and location. The flat crystals were usually within a few degrees of being perpendicular to the incident beam, as judged by the symmetry of the six ~4 Å diffraction spots. Often, a crystal would be visibly tilted by 1° to 5° due to an undulation in the carbon support, in which case a small amount of stage tilt could often be introduced to produce perfect alignment. Crystals that could not be aligned within ~0.5° when using just a single-axis tilt stage were not used for imaging. Thus, we could be sure that every crystal being imaged was in the proper diffracting position, and therefore that the high resolution images should show a properly aligned crystal. An example is shown in Fig. 2.

Fig. 2.

Explanatory figure showing a well-formed crystal, illustrating the principles used in the paper. Crystal A17044/thinC_122p/30.4.2009 is a small diamond-shaped crystal in which images were recorded at room temperature on a Tecnai F30 operated at 300keV using a 20μm C2 aperture.

1. bright-field defocused electron diffraction pattern showing paraffin crystal darker than surround due to the diffraction of the primary beam into the diffraction orders. The black square shows the central area used for the high magnification image.
2. dark-field defocused electron diffraction pattern, showing the six strong spots at 3.7 - 4.1 Å. Each of these dark-field diffraction spots contains about 1.2% of the direct beam intensity at 300keV, causing the crystal in (a) to appear darker than the incident beam, by 6-8% when the crystal is well aligned.
3. combination of (a) and (b) with contrast modified to show bright-field and dark-field in the same panel. Note that panels (a), (b) and (c) show the same image with different thresholds and gamma values.
4. spots in the computed diffraction pattern of the high magnification (39,000×) image
5. power in transforms of selected diffraction spots in the calculated Fourier transforms (diffraction patterns) of images, showing pseudo-dark-field images. Note that the region of the crystal being imaged at high resolution in this case is smaller than the crystal so the whole area is crystalline. These pseudo-dark-field images effectively show which regions of each crystal contribute to the Fourier component that is allowed through the mask, as explained in the last paragraph of section 3.

   1. power from all spots
   2. (2,0)
   3. (1,1)
   4. (1,−1)

Images were recorded on film at a magnification of 39,000×, using 300keV or 120keV electrons, with the specimen normally at room temperature. Images on the Medipix II or Medipix II-Quad detectors were recorded at 120keV, using a nominal magnification of 230,000×, but since the detector was 1.35× further away than the film, this was equivalent to ~305,000×. For computer analysis, film was digitized on a KZA film scanner [24] using 6 μm pixels equivalent to 1.5 Å, which allowed only the low resolution ~4 Å paraffin lattice spots (indices (1,1) (1,−1) (2,0)) to be observed in the computed diffraction pattern. To demonstrate the full resolution of the best images, the same films were also digitized with 2 μm pixels equivalent to 0.5 Å. Although this produced much larger files, it allowed diffraction spots out to 1.5 Å resolution to be seen from the best images. Note that the SCAI film scanner, manufactured originally by Zeiss and in wide use by the EM community, has a similar MTF to the KZA film scanner used here [24], but has a pixel size limited to 7μm. The Medipix detector has 55 μm pixels, so this was equivalent to 1.8 Å pixels, again allowing only the lower resolution paraffin lattice spots to be observed.

The images on film were also examined by optical diffraction [25], which allowed a quick evaluation of the resolution and contrast.

The electron optical arrangement used depended on the experiment. Since the purpose of all the experiments was to study the modulation of image contrast due to specimen movement, we chose conditions that offered ease of use rather than perfectly parallel electron-optical imaging [26]. A much smaller C2 aperture would have been required to produce parallel illumination. For normal images and for spotscan images using Tecnai microprobe mode, we used a 50 μm C2 aperture, which produces a measured beam divergence of +/−0.4 mrad under low-dose illumination conditions. The images were recorded with floodbeam illumination using a 1.0 sec exposure on SO-163 film and a beam diameter of about 3.0 μm. For microprobe spotscan images, the beam was focused to 0.1 - 0.25 μm, with the exposure being 12 - 30 msec per spot in a 10×10 raster. For the nanospotscan images, the microscope was used in nanoprobe mode with a 10 μm C2 aperture, the spots focused to ~7 nm at the specimen and the exposure per spot in the range 1.5 - 5.0 msec. In this condition, the beam divergence across the spots was +/−1.6 mrad. While this amount of beam divergence would cause shifts in the positions and therefore the phases of the Fourier components of the image, it has a negligible effect on image contrast provided this is evaluated in small enough regions of the image. In the nanospot images, the amount of defocus was kept within the range +/− 140 nm to ensure that the diffracted beams could recombine with the undiffracted beams to form an image.

Finally, the most difficult conditions to set up were those required for the Medipix time-sliced imaging series, where we wanted to have as few as 500 electrons in each frame of a movie with up to 400 frames. For the exposures, we used a 10 μm C2 aperture, with the FEG extraction voltage reduced to between 1500 V and 2000 V (normal extraction voltage is 3900 V), the gun lens increased to 8, spotsize (C1 lens) at its maximum (11), and the beam focused to diameter of 50 nm in microprobe mode. With these settings, the electron flux was reduced to be as low as 0.003 electrons/pixel in each frame, corresponding to 0.001 el/Ų, and the illumination could only be observed via the Medipix real-time image monitor. Thus, in each frame there would be a single count in one pixel and several hundred nearby pixels with zero counts. The Medipix II-Quad detector had a total active area of 516 × 516 pixels, four times that of Medipix II, so there were between 500 and 5000 electrons in each frame. The Search and Focus conditions differed from that used for the high resolution exposure in having a spotsize of 1 instead of 11, and sometimes the extraction voltage was also increased from 1500 to 2900 V, which increased the beam intensity several-thousand-fold. This allowed all the Search and Focus steps, as well as high resolution imaging, to be carried out using the Medipix detector. During the actual exposure series, the specimen accumulated a dose of around 1 el/Ų during several hundred frames, which resulted in some diminution of the intensity of the paraffin diffraction spots, but not complete fading. In practice, the illumination intensity was varied and the corresponding number of frames in the movie sequences ranged from 10 to 460 frames. The Medipix detector threshold was set to trigger when an event with an energy above 60keV (half the incident 120keV electron energy) was detected in a pixel. This ensured that no electron was counted twice, but did result in missing a few counts. The DQE(0) is ~0.75 and the DQE(Nyquist) is ~ 0.08 (i.e. 20% of theoretical best), with MTF(Nyquist) at ~0.38 under these conditions [27]. The readout time per frame was about 1 second but since pixels are accessed sequentially, there is essentially no dead time so readout speed was not a problem.

Most of the images were recorded on a Tecnai F30 with the specimen at room temperature. Electron diffraction experiments showed that the three spots at around 4 Å resolution (indices (1,1), (1-1) and (2,0) of the rectangular lattice) and their Friedel mates faded to half their initial intensity after exposure to 1.0 el/Ų at room temperature, and this fading time was used to determine the required beam intensity and the allowable number of frames to record during each exposure sequence. A few paraffin images were also recorded on thick carbon supports using a Tecnai Polara G2 microscope with the specimen at liquid nitrogen temperature using film with floodbeam illumination and a dose of 1-2 el/Ų, to see the highest resolution obtainable with our optimized conditions. Recording images at liquid nitrogen temperature worked well on thick carbon but much less well on thin carbon supports because the carbon film wrinkled due to the greater thermal contraction of the copper grid in comparison with the carbon film [28]. This wrinkling could be most easily seen in low magnification views of whole grid squares tilted at 60° (see later in Fig. 8).

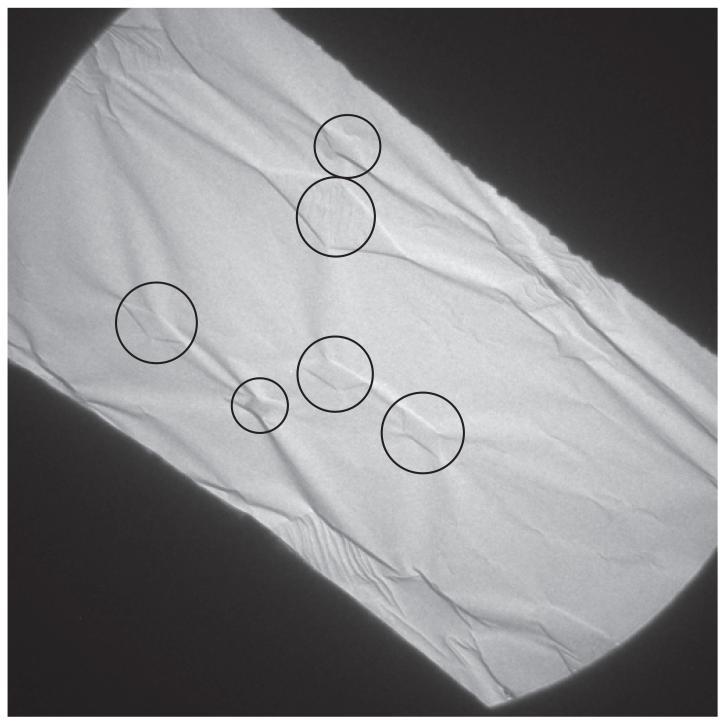
Fig. 8.

Low magnification image of a single grid square of a 60° tilted specimen of paraffin crystals on thin carbon, after cooling to liquid nitrogen temperature in FEI Polara. About 15 diamond-shaped paraffin crystals, with 6 of the most prominent circled, can be recognized from the footprint they show where the carbon film is wrinkled around each crystal. Our interpretation is that the paraffin crystals shrink by 1-2% in size when cooled from room temperature to liquid nitrogen temperature, whereas the copper grid shrinks only by ~0.3% and the carbon film by a negligible amount. As a result the carbon film becomes loose and the paraffin crystal can pull it into pronounced wrinkles, which then allows it to move easily as a result of stresses induced by radiation damage to the paraffin.

3. Theory of determination of image contrast

The molecular packing of paraffin molecules in the monolayer crystals and its relationship to crystal morphology is shown in Fig. 1. The paraffin crystals often formed nice diamond-shaped monolayers as seen in Fig. 2, although occasionally rectangular twinned morphologies could be seen. Each crystal has its straight-chain paraffin molecules arranged in a rectangular p12₁ 2D crystal with two molecules per unit cell of dimension a = 7.4 Å, b = 5.0 Å. Fig. 2 shows the relationship between crystal morphology, the cell axes and the diffraction spots. These monolayer crystals are essentially half a unit cell in the c-axis direction of the 3D orthorhombic Pca2₁ crystal form studied earlier by Teare [29], which contains 4 molecules/unit cell. We used C₄₄H₉₀ n-alkane, rather than C₃₆H₇₄ reported by Teare, with a proportionately longer c-axis cell dimension (116 Å rather than 95 Å) but the structure and packing is identical apart from a halving of the (longer) c-axis dimension to 58 Å. The a and b-axis cell dimensions are virtually identical to those in the 3D crystals, and the rocking curve showing how the diffraction intensities depend on crystal tilt are also consistent with the monolayer. Platinum-carbon shadowing showed a thickness of 50±10 Å, consistent with the expected thickness of half of the 3D crystal unit cell. Thus in the electron microscope, the untilted view shows very high contrast from the superposition of all the atoms along the full length of the hydrocarbon chains in a pseudo-hexagonal packing. Assuming the monolayer packing is identical to that in the 3D orthorhombic crystals apart from being only half a unit cell, there would be a screw axis along b, though the projection symmetry appears as pgg since the paraffin chains themselves have internal symmetry.

The approach [11] of Henderson & Glaeser (1985) was used to measure image contrast. Briefly, the ratio of the intensity I_g of an electron diffraction spot is measured as a fraction of the incident beam intensity I₀, giving the ratio I_g/I₀. The value of I_g in the defocused electron diffraction pattern is measured from a region in the centre of each diffraction spot and I₀ is measured from a corresponding region in the centre of the direct beam, where the bright field image of the crystal is visible. The electron diffraction intensities of the (1,1), (1,−1) and (2,0) spots from C₄₄H₉₀ crystals are almost identical as seen in Figs. 2(b), 5(a) and 6(b), and the value of their I_g/I₀ was measured as 0.018 at 120keV and 0.012 at 300keV. In the high-resolution image, the corresponding Fourier components are created by the interference of the wavefronts of the diffraction spots and the direct beam. The relative positions of the interference patterns (sinusoidal fringes) produced by a given diffracted beam and by its Friedel mate depend on defocus. The extent to which the two interference patterns either reinforce or cancel one another is described by the defocus phase-contrast transfer function (CTF). Thus the maximum value for F_g/F₀, at a peak in the CTF is 2*(sqrt(I_g/I₀)), which, based on the measured values above, is 0.27 at 120keV or 0.22 at 300keV for C₄₄H₉₀ crystals. The factor of two arises because each electron diffraction spot and its Friedel mate both contribute to an individual Fourier component in the image. Note that in both the electron diffraction patterns and the images, only the crystalline regions are used in the F_g and F₀ measurements, so the illumination beam diameter can be larger than the crystal. In the image A17044 shown in Fig. 2, which is one of the best low-dose floodbeam images of a crystal supported on thin carbon, the values of F_g/F₀ for each of the three spots derived from the whole area were 0.006, 0.007 and 0.014, corresponding to 2.7, 3.2 and 6.4 % of that expected from the electron diffraction intensities (0.22 at 300keV). Slightly larger values are obtained if the best area is selected from the micrograph, as shown in columns 5 and 6 in Table 1, for example up to 0.021 or 9.7% for the (2,0) reflection in A17044. After taking into account the modulation transfer function (MTF) of the film and film scanner, these range from 10 to 44 % of theoretical. This is typical of the very best paraffin images recorded in past work [11], but we should emphasize that images as good as this are very rare. Floodbeam images from specimens on thin carbon usually have only one or two spots at ~4Å resolution, and regions of the micrograph often show only one strong spot from one area and a different spot from a neighbouring area, indicating that the specimen has moved in different directions in different regions. While it is possible to select very small areas from such an image and find slightly higher values, such as the 44% for the (2,0) reflection in A17044, the goal of the work described here was to find a method that reliably improved the overall quality of the image. After correction for the MTF, there is a further need to take into account the presence of inelastically scattered electrons in the image, which do not contribute to the high resolution lattice image but do increase the value of I₀. From our measurements of the decreased intensity of the direct beam used to estimate carbon thickness, together with an estimated ratio of inelastic to elastic scatter of 3.5, this produces an additional factor of 1.12 for thin carbon at 120kV or 1.18 for thick carbon at 300kV. This correction has been applied to give the last column of Table 1. For the final six images in Table 1, fully corrected values for the maximum contrast compared with that expected from electron diffraction lie in the range 58-112%. No corrections for CTF were made but enough images were recorded to be sure that many would have CTF maxima at the spacing of the first order paraffin spots. It was also assumed that the envelope functions for the FEG microscopes used in this work were essentially 100% out to ~4 Å resolution.

Fig. 5.

Medipix images

1. defocused electron diffraction pattern of a crystal viewed on the Medipix II-Quad detector. Some of the pixel defects in the detector including a large damaged area just above the centre can be seen. The 6 diffraction spots at 4Å as well as all the higher resolution spots are clearly visible, showing the sharp outline of the crystal and all areas diffracting well. The central square area has been rendered at a lower level to show the much stronger direct beam and the bright field image of the crystal.
2. single frame from a 160-frame sequence, with a magnified insert at the top right, showing the individual pixels that have received a single count and the majority of pixels with no counts. Each frame in the series (para_22may_image07) had an exposure of 5000 electrons, corresponding to ~0.006 el/Ų.
3. transforms added together to show the diffraction spots. The calculation in this case was carried out by summing the 32 power spectra of a 5-frame running average. This was one of the few images that showed spots in all three directions. Others showed two or only one diffraction spot despite the visualization of all three pairs of spots during the initial crystal selection step. The background is much higher when intensities from individual frames are summed, rather than amplitudes being summed as in a single image where the dose has not been fractionated, so the signal-to-noise ratio of the spots is lower. Note that the summing of intensities in this way does not affect the measurement of I_g/I₀ and avoids the need to determine the image shifts due to stage drift between frames that builds up over the extended several minute duration of the exposure.

Fig. 6.

One of the best images (A03141) of a paraffin crystal on thick carbon that showed attainment of virtually perfect theoretical contrast at ~4Å resolution, with diffraction detectable out to 1.5Å, as is shown in Fig. 7. The image was recorded on a Polara G2 at 300keV with the specimen at liquid nitrogen temperature using floodbeam illumination with a 50 μm C2 aperture.

1. bright-field region in centre of defocused electron diffraction pattern showing the diamond-shaped paraffin crystal A03141. The conditions for recording the images shown in panels (a) to (d) are described in Materials and Methods, paragraph 2.
2. the same image as in (a) but with much lower threshold to show the dark-field defocused electron diffraction pattern region outside the illuminating beam. Recorded before the high resolution image exposure, it shows the 6 diffraction spots at 3.7 - 4.1 Å resolution with approximately equal intensity.
3. subsequent dark-field defocused image recorded immediately following the high resolution image exposure. It shows that, at liquid nitrogen temperature after an exposure of 2 el/Å2 at 300keV, well over half of the diffracted intensity remained in the ~4 Å diffracted spots.
4. final dark-field defocused image recorded after further irradiation with over 20 el/Ų, showing clearly the damage to the irradiated region.
5. computed diffraction pattern of high magnification image with indexing.
6. pseudo-dark-field images showing the regions of the image that contribute to each of the three spots at 3.7 - 4.1 Å resolution. The dark and light shadows are regions of CTF minima and maxima, dependent on defocus, crystal tilt (estimated to be less than ±15 nm across the field of view) and beam tilt.

Table 1. image contrast.

Image	Description	Overall image area  1.5 μm square		Selected image area  0.15 μm square		% theoretical - range of values for either overall or selected area
		Ig/I0	Fg/F0	Ig/I0	Fg/F0	Compared to electron diffraction	Corrected for detector  MTF	Corrected for inelastic  scattering
A17044 300kV	thinC floodbeam	0.4-2.0×10−4	0.006-0.014	0.4-4.6×10−4	0.006-0.021	2.7-9.7 %	10-44 %	11-47 %
011643 300kV	thinC microspotscan	4.3-7.5×10−4	0.021-0.027	3.9-15.7×10−4 *	0.020-0.039 *	9.1-17.7 %	41-63 %	43-67 %
A16973 120kV	thickC nanospotscan	1.7-3.5×10−4	0.013-0.019	4.9-8.4×10−4	0.022-0.029	4.8-10.7 %	27-47 %	37-64 %
A16984 120kV	thickC nanospotscan	(0.3-2.4×10−4)	(0.005-0.015)	0.4-3.3×10−4	0.007-0.018	2.6-6.6 %	14-29 %	19-40 %
para_22may_image07	thinC Medipix 120kV	1.7-5.1×10−4**	0.013-0.023**	-	-	4.8-8.5 %	10-18 %	18-20 %
A02026 300kV	thickC floodbeam	(0.8-2.8×10−4)	(0.009-0.017)	3.2-12.3×10−4	0.018-0.035	8.2-15.9 %	30-59 %	35-70 %
A02027 300kV	thickC floodbeam	(2.4-5.8×10−4)	(0.015-0.024)	4.5-16.6×10−4	0.021-0.041	6.8-18.8 %	31-79 %	36-93%
A02030 300kV	thickC floodbeam	-	-	3.7-8.6×10−4	0.019-0.029	8.6-13.2 %	39-49 %	46-58%
A03133 300kV	thickC floodbeam	2.5-5.7×10−4	0.016-0.024	7.9-15.7×10−4	0.028-0.040	7.3-18.2 %	33-67 %	39-79 %
A03134 300kV	thickC floodbeam	1.3-7.0×10−4	0.012-0.026	1.3-12.1×10−4	0.011-0.035	5.0-15.9 %	23-59 %	27-70 %
A03141 300kV	thickC floodbeam	0.9-6.8×10−4	0.010-0.026	5.9-31.8×10−4	0.024-0.056	4.4-25.6 %	16-95 %	19-112 %

Notes to Table 1:

^*The selected area in this case was only 0.11 μm square, which was the size of each spot in the spotscan raster.

^**The area in this case was only 0.1 μm square, which was the full size of the Medipix II-Quad detector.

The smallest and largest values given in columns 3 to 9 correspond to the weakest and strongest of the three reflections at ~4 Å resolution.

To calculate the % theoretical, the raw F_g/F₀ image values must first be divided by the values expected from electron diffraction, which are 0.22 for 300keV images, or 0.27 for 120keV images, as shown in column 7. All three reflections at ~4Å have very similar electron diffraction intensities.

The MTF envelope correction used to calculate column 8 has been taken from Fig.5 in reference [5] for film (1/0.18 and 1/0.23 for (2,0) and (1,1) respectively) and Medipix (1/0.40 and 1/0.47) at 120keV and from Fig.6 for film at 300keV (1/0.22 and 1/0.27 for (2,0) and (1,1) respectively). The MTF correction is larger for the (2,0) reflection because it is at higher resolution, 3.7Å compared with 4.1Å for the (1,1) and (1,−1) reflections. A further correction for the contrast reduction due to inelastic scattering is shown in column 9. The correction factors are 1.06 for thin carbon at 300keV, 1.12 for thin carbon at 120keV, 1.18 for thick carbon at 300keV and 1.37 for thick carbon at 120keV.

The numbers in brackets for some of the images in columns 3 and 4 are lower than they should be because the crystal was smaller than the overall image area. The area of A02030 included several twinned and untwinned crystals, so no numbers are given for the overall image area for than image.

In addition to calculating F_g/F₀ for the whole image, we were also able to observe the spatial distribution within each image of the power contributing to each diffraction spot, by calculation of pseudo-dark-field images as follows. The lattice of diffraction spots in the computed FFT is indexed, individual spots of interest are allowed to pass through a selective mask, the masked FFT is then backtransformed and the resulting power distribution, the mean value of the density squared, plotted to show which regions of the image contribute to which diffraction spots. The mask radius was selected to ensure that all the diffracted intensity from each selected Fourier component of the crystal was allowed through, otherwise regions of the crystal where there is a physical distortion of the lattice would be erroneously cut off.

4. Results

We show in Figs. 3, 4, 5 and 6 one example of each type of image of the C₄₄H₉₀ paraffin monolayer crystals.

Fig. 3.

Microspotscan image with a coarse raster of about 100 spots, recorded on Tecnai F30 at 300keV.

1. spotscan image 011643rmg, using 110 nm diameter spots, with an exposure of 12msec/spot using a 20 μm C2 aperture.
2. computed diffraction pattern of image and indexing of the main crystal. There are also arc-shaped diffraction spots from a smaller fragment of a different less well-ordered crystal, which partially overlaps with the main crystal and extends into the bottom right corner of the field of view.
3. pseudo-dark-field image showing power from all three diffraction spots shown in the image and from the individual spots, as in Fig. 2(e). The power in each illuminated spot, recorded sequentially in time, varies between and within the spots across the crystal. The crystal covers the whole area except for a small region in the bottom right corner. The slight Moire pattern visible in the (1,1) panel comes from interference with underlying fragment of the other crystal whose blurry diffraction pattern can be seen in (b).

Fig. 4.

Nanospotscan, using a raster of 200×200 very small illumination spots (each of diameter 7nm) to cover an area of about 1.5 μm square. The 120keV beam was defined by a 10 μm C2 aperture, and had a target underfocus of 130 nm.

1. image A16973 showing the raster of spots about 300 μm apart (7-8 nm at 39,000× magnification), recorded with an average exposure of 0.5 el/Ų. The inset shows a smaller area at higher defocus in which the raster is more apparent.
2. computed diffraction pattern of image. The three paraffin diffraction spots at 3.7-4.1 Å resolution are labeled. The pattern from the hexagonal nanospotscan lattice can also be seen near the origin.
3. pseudo-dark-field images from all spots, and from the individual (2,0), (1,1) and (1,−1) Fourier components, showing the regions of the image from which the power for each spot comes. The top edge is one edge of the scan raster seen also in (a). The bottom edge is a facet of the crystal. The dark spot is the damaged area in the centre of the scanned area, which was used to adjust the focus before recording the image. The dark and light shadows are regions of CTF minima and maxima, dependent on defocus, crystal tilt (estimated to be less than ±15 nm across the field of view) and beam tilt.

Fig. 3 shows one of our best spotscan images (011643). Good images using spotscan are obtained more frequently than when using floodbeam illumination, as noted previously [16], but they still display significant variability. It is clear that different regions of image 011643 show different contrast for different spots. There are regions where the (1,1) Fourier component is strong and the (2,0) component is weak. Regions with good contrast for the higher resolution spots (not shown) are much smaller in extent. We interpret this to indicate that the crystal is moving during image formation, often in different directions and by different amounts in different areas of a single micrograph, thereby causing varying degrees of contrast loss across the image. Since this is a spotscan image, the image of each spot is recorded at a different time from any other spot. Thus the crystal is moving during every successive spot in the spotscan sequence. Evaluation of F_g/F₀ in very small regions of this image shows values up to 0.039, but over the image as a whole, the contrast is relatively low, with F_g/F₀ around 0.021-0.027, or ~44% of theoretical after correcting for the MTF of the detector, in this case film plus densitometer (image 011643 in Table 1). This confirms earlier observations that spotscan imaging helps to increase image contrast.

Fig. 4 shows a nanospotscan image. Here the original image is made up of ~50,000 sequential mini-images each exposed for 1-5 msec, making a total exposure time of 1-4 min. The image A16973 was one of the best images recorded, with 47 % of theoretical contrast, after correcting for the MTF. However, good contrast over the whole nanospotscan area was obtained only when the specimen was prepared on thick carbon support-films, as it was for A16973. The nanospotscan images, because of the need for much shorter exposures, also had illumination that had to be more intense and thus less spatially coherent. Coupled with the small size of the spots (~7nm) and the effect of defocus in reducing the overlap of the diffracted and undiffracted beams, the contrast was still less than perfect.

Fig. 5 shows an example of a Medipix II time series of high resolution frames from a well-aligned paraffin crystal on a thin carbon film. Each frame in a given movie contained from a few hundred to a few thousand electrons (Fig. 5(b)). The Fourier components can still be seen even in the summed power spectra of the individual very low-dose frames. The signal-to-noise ratio is increased if a few adjacent image frames are summed before Fourier transformation and then the power spectra of these adjacent image averages is summed, as is expected because intensity is the square of amplitude. However, because the electron microscope stage drifts by about 5 nm over the several minutes required to record the whole movie at approximately 1 second per frame, the images from the paraffin crystal in these sequences cannot be simply summed over more than a few frames. In practice, the highest signal-to-noise ratio was obtained when 5-10 frames were added before Fourier transformation and power spectra summation (Fig. 5(c)). Evaluation of F_g/F₀ (Table 1) shows that the image contrast in the best images of crystals on thin carbon still falls short of the theoretical maximum. We conclude that the crystals can still move, causing image blurring and contrast loss, even with exposures as low as 500 electrons over an area of about 60 × 60 nm² (~0.001 el/Ų).

Finally, we show one of the best images recorded from a crystal on thick carbon support (Fig. 6) using floodbeam illumination. This image was recorded at liquid nitrogen temperature on a Polara but many more images with equally good contrast were recorded using thick carbon at room temperature on an F30, though at lower dose, so we can be sure that the improved contrast is due to the carbon film and not the temperature. Compared with the varying contrast seen across the images of crystals on thin carbon shown in Fig. 2(e) and Fig. 3(c), it is clear that the whole area of the image of the crystal seen in Fig. 6(f) is rather homogeneous, apart from the CTF zeros due to defocus and beamtilt. Images with similar consistency were obtained on thick carbon with spotscan and floodbeam illumination, so the use of thick carbon prevents the movement that spotscan is designed to reduce. In this case, the values of F_g/F₀ ranged from 0.010 to 0.056, representing 16 to 95 % of theoretical after taking into account the MTF of the film and our film scanner at this resolution. The pseudo-dark-field panel in Fig. 6 shows that not all the spots have been recorded at a CTF maximum and if we also consider that inelastic scattering has reduced the apparent contrast by a factor of 1.18 as shown in the last column of Table 1, we conclude that this image shows more-or-less perfect image contrast at a resolution of ~4Ǻ, and that the thick carbon has successfully prevented image blurring and contrast loss at this resolution. We have now reached the theoretically expected image contrast, and find the whole area of every crystal behaves much more reproducibly. A contrast of 70% of theoretical would correspond to a B-factor of about 20Ų. Note that the B-factors we discuss in this paper are purely associated with deficiencies that occur during recording of images and differ from the B-factor measured, for example, by the resolution dependence of electron diffraction intensities due to thermal or statistical disorder in the crystal structure, although the units [Ų] and the mathematical description [A=A₀exp(−B/4d²)] are identical. The overall B-factor for 3D maps obtained by single particle electron cryomicroscopy also includes additional contributions due to errors in orientation determination.

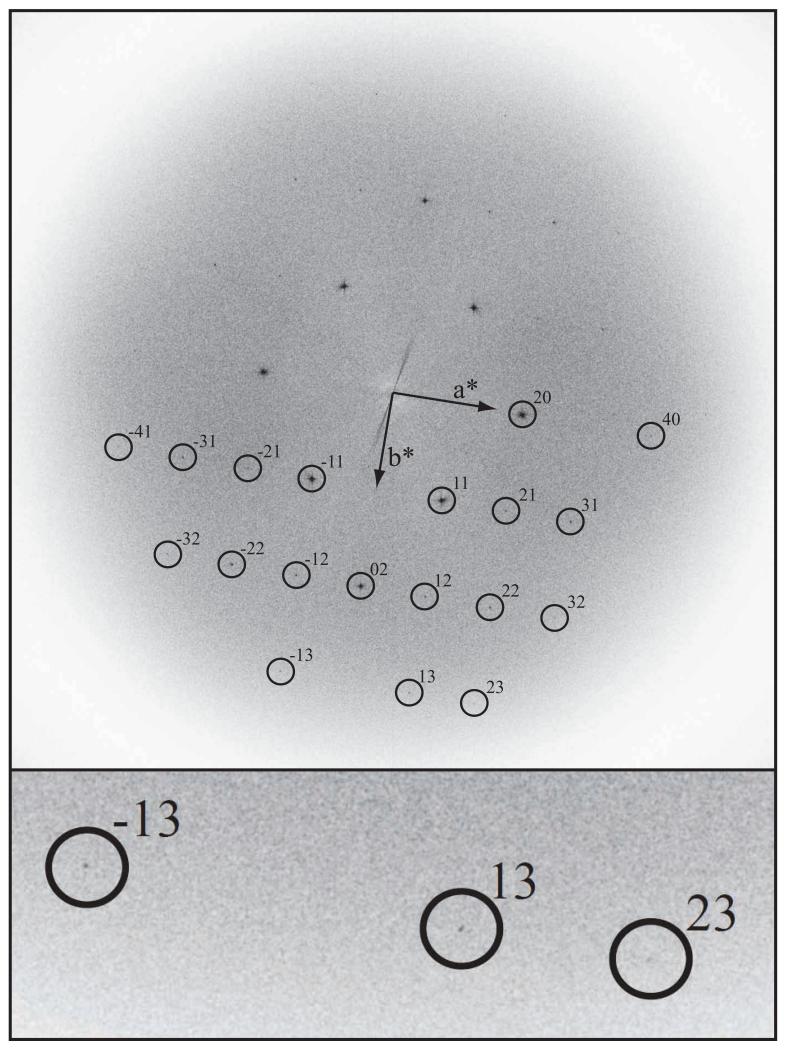
Table 2 and Fig. 7 show how the higher resolution Fourier components can be detected in the best region of this image. Note that although the ~4Å resolution spots in this image now look almost perfect, there is still some contrast loss at higher resolution presumably due to smaller residual specimen movement. Another observation that strengthens our conclusion that thick carbon support films are more effective than the other approaches is that most of the images recorded from specimens on thick carbon show many spots at higher resolution than those at ~4Å on which we have concentrated in this paper. None of the floodbeam images from thin carbon specimens ever produced images with such high resolution as those in Fig. 6 or Fig. 7, and while spotscan helped to increase the proportion of good images, the thick carbon support was necessary to make really good images routine. As can be deduced from the nearly sequential numbering of the last 6 images presented in Table 1, recorded in two sessions on the microscope, at least half of the images on thick carbon were excellent.

Table 2. diffraction orders visible in best images.

Spot (index)	Resolution (Å)	Comments	Teare (1959) X-ray structure amplitude
1,1	4.12	very strong	174
2,0	3.71	very strong	315
2,1	2.97	weak	77
0,2	2.48	strong	189
1,2	2.35	medium	89
3,1	2.21	medium	152
2,2	2.06	medium	131
4,0	1.85	very weak	33
3,2	1.75	very weak	70
4,1	1.73	very weak	71
1,3	1.61	weak (see inset in Figure 7)	50
2,3	1.51	very weak, highest resolution (inset to Figure 7)	63
5,1	1.42	- (not observed)	61
3,3	1.37	- (not observed)	45

Footnote to Table 2: The CTF is not known for any of the reflections in these low dose images, in which Thon rings from the supporting carbon film are not observed. The amplitudes of the higher order reflections will also be reduced by the envelope function of the microscope, which was not characterized in these experiments, and by the MTF of the film and film scanner.

Fig. 7.

Fourier transform of a 39,000× magnification image recorded at 300keV on FEI Polara showing amplitudes, from an 6000 × 6000 area digitized in 2μm steps, of a paraffin crystal (A02030) on thick carbon, with the specimen at liquid nitrogen temperature. This is the background-subtracted and slightly sharpened FFT of the raw, digitized image - i.e. no unbending was applied in order to sharpen the spots and thus improve the detectable resolution. Diffraction spots are visible out to 1.5 Å resolution, which is best appreciated in the inset that shows the three highest resolution spots. See also Table 2.

As a further illustration of the importance of a thick, strong supporting carbon film, we show in Fig. 8 an image of a number of paraffin crystals on a thin carbon film tilted to 60° after cooling to liquid nitrogen temperature. It is clear that the shrinkage in the dimensions of the copper supporting grid when cooled, combined with a lesser shrinkage of the carbon film, has caused the carbon film to become wrinkled. In addition, the paraffin crystals show clear evidence of the forces that attach them to the carbon film and the tilted image shows how the carbon film is pulled as the paraffin crystal shrinks, by 1-2%, on cooling. The paraffin crystals on thick carbon after cooling do not show such obvious bending, consistent with the greater strength of the thick film.

5. Discussion and conclusion

We have confirmed that image blurring due to specimen movement during low dose imaging remains a serious problem. The conclusion from the Medipix time-resolved image sequences is that stresses build up as a result of radiation damage even at doses hundreds of times lower than traditionally used for low dose imaging. Great care is still needed with every other aspect of the imaging procedure, including preparation of the specimen support and the beam-sensitive specimen itself, and the alignment of the microscope (minimizing beam convergence, and adjusting the pivot point and beam tilt using coma-free alignment, [26]). The use of thick carbon support films produced the most reliable reduction in image blurring. A priori, we do not know whether this improvement is due to the increased mechanical strength of the thicker carbon, although we believe this is most likely, or to the higher conductivity but this uncertainty highlights the value of continued work to develop stronger and more conductive films that have as little irregular structure as possible, such as graphene or metallic [31] films. It is possible that specimen temperature has some effect on beam-induced movement but this is not easy to demonstrate since so many other aspects of the microscopy and the physics of imaging and radiation damage depend on temperature. We can say that the use of a thick carbon support film has a major beneficial effect on image contrast and beam-induced specimen motion for both room temperature and cold specimens.

Our understanding of the steps needed to obtain high quality images of paraffin should now be extended to electron cryomicroscopy imaging in structural biology. While this may be straightforward for specimen preparation of 2D protein crystals, since thicker carbon films particularly at 300keV can easily be used (even 45 nm of carbon has only 25% elastic and inelastic scatter), it is still not clear how best to minimize specimen movement for ice-embedded specimens, since in this case the use of a thicker carbon film would increase the background noise in the image. For 2D crystals, the use of thick carbon films will reduce contrast somewhat because there will be an accompanying increase in inelastic electron scattering, which will directly reduce image contrast, plus additional noise from the elastic image of the supporting carbon film though for 2D crystals this is usually much less than the dominating shot noise from the low dose exposure. At high resolution, an energy loss of even the minimum 20eV observed from plasmons, means that the inelastically scattered electrons have a defocus that differs from that of the elastically scattered electrons by at least 200 nm, but which is different for different values of the energy loss. The inelastically scattered electrons thus contribute only noise to the image. As a result, in traditional electron crystallography, there will always be a compromise between the need for a thicker support film, to minimize specimen movement and image blurring, and the need for a thinner support film, to minimize the amount of elastic and inelastic scattering. However, the recent development of C_c correctors means that it is possible to obtain excellent high resolution images from inelastically scattered electrons [7], so the use of thick carbon supports for electron crystallography may become the norm once C_c correctors, cold stages and FEG illumination become available on the same microscope.

The unavoidable consequence of radiation damage is bond breakage. Indeed, one of the most important, initial steps in radiation damage is the breakage of the carbon-hydrogen bonds in organic or biological specimens such as the paraffin molecules studied in this paper or the protein, nucleic acid or lipid molecules in biological structures. The work of Meents et al [30] has measured hydrogen production directly and shown this to be by far the largest gaseous component released due to radiolysis of proteins. In the paraffin crystals being studied here, which contain only carbon and hydrogen, the release of hydrogen atoms is likely to be an important first step in radiation damage, pushing the adjacent chains apart locally and causing more widespread movement unless the crystal is well supported on a thick, strong carbon film. In addition, cleavage of the C-H bond also leads, almost stoichiometrically, to creation of C=C double bonds [32], which in turn leads to a large change in bond angle and resultant stress in the specimen as the deformed product molecule is accommodated as a defect in the crystal.

We note that although the best paraffin images we have now obtained can show almost perfect contrast for the three first-order spots [(1,1), (1,−1) and (2,0)], the higher resolution spots out to 1.5Å are still variable in intensity across even the best images. Thus although we have reduced the amount of specimen movement and image blurring, beam-induced movement is still present at the ~0.5Å level of movement and affects the higher-resolution spots, as opposed to the ~2.0Å level of movement that affects the first-order spots.

Images with nearly perfect contrast should be good candidates to determine the projected structure of these paraffin monolayer crystals by image processing. The projection should then have the density distribution expected from a half unit cell of the 3D crystal [29] or from model phases and experimental amplitudes [33]. However, in our low dose images, it was not easy to determine the amount of defocus, astigmatism and beam tilt that would be needed to determine the CTF and thus to correct the phases of the Fourier components that could be obtained from the average unit cell in each image. To do this, it would have been necessary to carry out more careful coma free alignment and to record some subsequent higher dose images of the carbon support after the paraffin crystals had been destroyed. Our investigation of image contrast, which was targeted only at the ~4Å resolution spots, did not require (and did not employ) this additional electron-optical characterization of the images.

Can we then transfer any lessons from these measurements on paraffin crystal images to improve the imaging of ice-embedded biological structures? Clearly a thick film of ice will itself have greater strength than a thin film. On the other hand ice itself is damaged by irradiation, releasing hydrogen and oxygen as radiation products, though at liquid helium temperature there may be more hydrogen released than oxygen. One of the major advantages of working with electron cryomicroscopic images of single particles embedded in amorphous ice is that the background between particles is very clean because images of amorphous ice itself show very little contrast. Indeed it is likely that, in amorphous ice, the water molecules themselves move around at doses as low as 1-2 el/Ų, since the electron diffraction pattern of ice at liquid helium temperature changes significantly in this dose range [34]. It is not yet known whether smaller particles embedded in amorphous ice move more than larger particles. Nor is it known whether and by how much particles of different size rotate as a result of radiation damage. Clearly there is still a lot to be done before electron cryomicroscope images of biological structures can be obtained that are as perfect as those obtained now for images of paraffin crystals on thick carbon supports.

In single particle electron cryomicroscopy, the loss of contrast at high resolution is most easily characterized by an effective B-factor that describes loss of contrast with resolution. Values from 240 [35] to over 1000Ų are observed in practice [14]. The equivalent B-factor for most paraffin images on thin carbon, where contrast is below 10% of theoretical, is over 150Ų. Thus the amount of specimen movement for paraffin crystals on thinner supports, whether measured in terms of contrast loss or an equivalent increased B-factor, is similar to that found in electron crystallography or single particle electron cryomicroscopy. By using much thicker carbon support films, the image blurring now found in our best paraffin images is described by a B-factor of less than 20Ų. The challenge is now to work out how to prevent or minimize specimen movement due to radiation damage in ice-embedded biological structures.