The X3LYP extended density functional for accurate descriptions of nonbond interactions, spin states, and thermochemical properties

Abstract

We derive the form for an exact exchange energy density for a density decaying with Gaussian-like behavior at long range. Based on this, we develop the X3LYP (extended hybrid functional combined with Lee–Yang–Parr correlation functional) extended functional for density functional theory to significantly improve the accuracy for hydrogen-bonded and van der Waals complexes while also improving the accuracy in heats of formation, ionization potentials, electron affinities, and total atomic energies [over the most popular and accurate method, B3LYP (Becke three-parameter hybrid functional combined with Lee–Yang–Parr correlation functional)]. X3LYP also leads to a good description of dipole moments, polarizabilities, and accurate excitation energies from s to d orbitals for transition metal atoms and ions. We suggest that X3LYP will be useful for predicting ligand binding in proteins and DNA.

The development of accurate functionals has made density functional theory (DFT) the method of choice for first principles predictions of fundamental processes in materials ranging from metal alloys to semiconductors, to ceramics, to new catalysts (1, 2). Despite this progress, there remain serious limitations in DFT theory. Thus, the B3LYP (Becke three-parameter hybrid functional combined with Lee–Yang–Parr correlation functional) method (3) achieves a high accuracy [mean absolute deviation (MAD) = 0.13 eV (1 eV = 1.602 × 10^-19 J)] for thermochemistry [heats of formation of the 148 molecules in the extended G2 reference set (4, 5)], but it predicts that the noble gas dimers are unstable. The PW1PW hybrid method (6, 7) leads to less accuracy (0.23 eV for G2) and far too strong bonding in noble gas dimers [≈7 times the correct answer for He₂ (7)], and indeed leads to very strong bonding even when the functional for electron correlation (which is responsible for London dispersion forces) is omitted. Similar results are obtained for other functionals of this class [mPW (7) and PBE (8–10)], suggesting that these exchange functionals include some correlation effects, making it difficult to combine them with true correlation functionals.

The particular application motivating us to reexamine the functionals in DFT is the possibility of genomewide structure-based drug design. As the genomics revolution leads first to sequences and then to 3D structures for all proteins of all forms of life, there will be an opportunity for computation and theory to help develop new generations of drugs (agonists and antagonists) that are both very active and very specific (binding maybe to just one protein of all proteins for all forms of life, so as to minimize toxic side effects). However, for theory and computation to play this role, it is essential that the noncovalent interactions of ligands to proteins be accurately predicted. Thus, it is essential to accurately describe London dispersion forces (van der Waals attraction) along with electrostatic and hydrogen bond interactions.

The current generations of DFT methods do not provide this accuracy, but we present here an extended functional, denoted as X3LYP (extended hybrid functional combined with Lee–Yang–Parr correlation functional), that significantly improves the accuracy for van der Waals and hydrogen-bonded complexes while providing an excellent description of dipole moments and polarizabilities. It also improves the accuracy in thermochemistry, ionization potentials (IPs), electron affinities (EAs), and total atomic energies over the most popular and accurate previous method, B3LYP. We expect that X3LYP will prove useful for predicting ligand binding in proteins and DNA.

Theory

Because the magnitude of the correlation energy is generally <10% of the exchange energy, it is most important that the exchange functional be accurate. In GGA (generalized gradient approximation), the exchange energy density is defined as

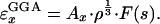[1]

Here, A_x = -3/4 (3/π)^1/3, F(s) is the GGA enhancement factor, and s is a dimensionless gradient (6), defined as

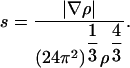[2]

The B88 (11) and PW91 (6) exchange functionals use the forms

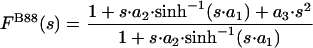[3]

and

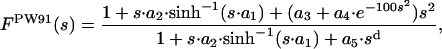[4]

where a₁ = (48π²)^1/3, a₂ = 6β·a₁, 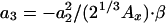, a₄ = 10/81 - a₃, 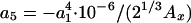, and d = 4. From fitting the HF exchange energies of the noble gas atoms, Becke obtained β = 0.0042 (11).

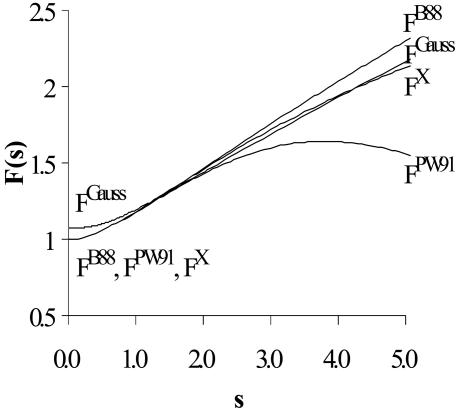
The plot of the F^B88(s) and F^PW91 (s) functions in Fig. 1 shows that these two functions differ significantly for large s, the region believed to affect significantly the performance of DFT in van der Waals systems (12, 13). For a system with spherically symmetric decaying density, i.e.,

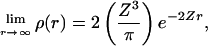F^B88(s) assures the correct asymptotic behavior of the exchange energy density (11), i.e.,

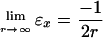(Condition 1); while Levy and Perdew showed that some scaling properties can be satisfied if the asymptotic form of the functional for large s is s^-α, where α ≥ 1/2 (Condition 2) (14). The Lieb–Oxford bound (12, 15), ε_x ≥ -1.679 · ρ(r)^1/3, suggests an upper bound on F(s) (9) (Condition 3).

Fig. 1.

The GGA enhancement factors: F^B88(s), F^PW91(s) F^Gauss(s), and F^X(s).

B88 violates Conditions 2 and 3, whereas the a₅·s^d term lets PW91 obey these conditions. However, PW91 violates Condition 1.

With modern DFT codes, most calculations on finite molecules use Gaussian basis functions, leading to a Gaussian-like long range behavior in the electron density as in Eq. 5.

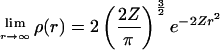[5]

The asymptotic limit for the exchange energy density of a finite system is

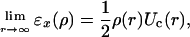[6]

where U_c is the Coulomb potential of the exchange charge, defined as

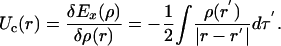[7]

Inserting Eq. 5 into Eq. 7 leads to 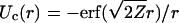. Since

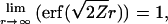Condition 1 is fulfilled for a Gaussian-like density.

Combining Eqs. 1 and 6 with Eqs. 5 and 7 gives

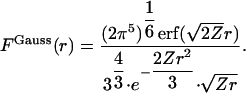[8]

Using Eq. 5, we can rewrite Eq. 2 as

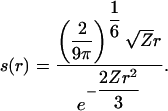[9]

Eqs. 8 and 9 determine the F^Gauss(s) for a Gaussian-like asymptotic density, which Fig. 1 shows to lies between F^B88(s) and F^PW91(s) for s ≥ 1.5, but closer to F^B88(s).

As s → 0, F^Gauss(s) → (2⁵ π/3⁴)^1/3 = 1.07466, instead of 1.0 as required to obey the limit within the local density approximation (LDA). Such a deviation may be expected for finite systems. Indeed, fitting to the unrestricted Hartree–Fock energies of the first- and the second-row atoms, Handy et al. (16) recently developed a local exchange functional, OPTX, that has an s → 0 LDA limit of 1.05151.

X3LYP Functional

Based on the F^Gauss(s) behavior for s ≥ 1.5 as shown in Fig. 1, we propose an extended exchange functional:

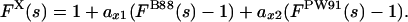[10]

Here, we choose to obey the LDA limit as s → 0, as usual in the GGA framework. We could have allowed a more general form for F^X(s) but found that combining the B88 and PW91 functionals provided sufficient flexibility. We considered that using well known functions already incorporated into computer codes could help ease the application of the X3LYP functional.

Combining F^X(s) with the LYP correlation functional (17), leads to XLYP, where the mixing parameters {a_x1, a_x2} = {0.722, 0.347} were determined through a least-square fitting to the total energies of 10 atoms {H, He, Li, Be, B, C, N, O, F, Ne}; the IPs for 16 atoms {Li, Be, B, C, N, O, F, Ne, Na, Mg, Al, Si, P, S, Cl, Ar}; the EAs for 10 atoms {H, B, C, O, F, Al, Si, P, S, Cl}; and the atomization energies for 38 molecules {H₂, He₂, Li₂, Be₂, C₂, N₂, O₂, F₂, Ne₂, Na₂, Mg₂, Si₂, P₂, S₂, Cl₂, CN, CO, CS, NO, SO, ClO, SiO, ClF, PF, AlF, SiF, CCl, SiCl, NaCl, CH, NH, OH, HF, CO₂, O₃, SO₃, OCS, CS₂}, selected to represent the important chemistry for the first- and the second-row elements (including open- and closed-shell molecules; molecules with single, double, and triple bonds; ionic systems, and systems requiring multiple determinants for proper descriptions). In particular, we include He₂ and Ne₂ as representative van der Waals systems.

All calculations used a pruned (75,434) DFT grid from jaguar (Version 4.0, Schrödinger, Portland, OR). To facilitate comparisons with literature values, we did not use the pseudospectral capabilities in jaguar. In determining the two XLYP parameters, we used the aug-cc-pVTZ basis sets (18) for all calculations. To validate the accuracy against the G2 data set, all calculations used the 6–311+G (3df, 2p) basis set with previously reported MP2 molecular geometries and scaled Hartree–Fock vibrational frequencies to calculate zero-point energies and finite-temperature corrections (4, 5, 19). This choice of geometries and basis sets allows a direct comparison of our results with previously published data obtained with other functionals (5, 7, 8, 10). For He₂, Ne₂, and (H₂O)₂, we used the aug-cc-pVTZ basis sets with no f functions. These bond energies were corrected for BSSE (basis set superposition error). For the transition metals we used the TZV(f) basis sets (20).

A big step forward for accurate DFT calculations was the introduction of hybrid methods (3), particularly the B3LYP, which uses the VWN functional III (21) based on correlation of the homogeneous electron gas in the random phase approximation, the Lee–Yang–Parr (17) correlation functional, plus a hybrid exchange functional of three terms: a portion of exact exchange, Slater local exchange, and the nonlocal gradient correction of Becke88. Thus,

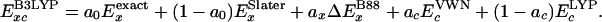[11]

Becke obtained the hybrid parameters {a₀, a_x, a_c} = {0.20, 0.72, 0.19} (3) from a least-squares fit to 56 atomization energies, 42 IPs, and 8 proton affinities (PAs) of the G2-1 set of atoms and molecules (4). B3LYP leads to excellent thermochemistry (0.13 eV MAD) and structures for covalently systems but does not account for London dispersion (all noble gas dimers are predicted unstable).

Following B3LYP, we introduce the extended hybrid functional, denoted as X3LYP:

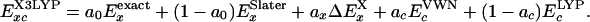[12]

We determined the hybrid parameters {a₀, a_x, a_c} = {0.218, 0.709, 0.129} in X3LYP just as for XLYP. Thus, we normalized the mixing parameters of Eq. 10 and redetermined {a_x1, a_x2} = {0.765, 0.235} for X3LYP. The F^X(s) function of X3LYP (Fig. 1) agrees with F^Gauss(s) for larger s.

Results and Discussion

We tested the accuracy of XLYP and X3LYP for a broad range of systems and properties not used in fitting the parameters. Table 1 compares the overall performance of 17 different flavors of DFT methods, showing that X3LYP is the best or nearly best for essentially all properties, leading to an acceptable accuracy for each. A few comments follow.

Table 1. MADs (all energies in eV) for various level of theory for the extended G2 set.

	G2(MAD)
Method	ΔHf	IP	EA	PA	H-Ne, Etot	TM ΔE	He2, ΔE(Re)	Ne2, ΔE(Re)	(H2O)2, De(RO...O)
HF	6.47	1.036	1.158	0.15	4.49	1.09	Unbound	Unbound	0.161 (3.048)
G2 or best ab initio	0.07a	0.053b	0.057b	0.05b	1.59c	0.19d	0.0011 (2.993)e	0.0043 (3.125)e	0.218 (2.912)f
LDA (SVWN)	3.94a	0.665	0.749	0.27	6.67	0.54g	0.0109 (2.377)	0.0231 (2.595)	0.391 (2.710)
GGA
BP86	0.88a	0.175	0.212	0.05	0.19	0.46	Unbound	Unbound	0.194 (2.889)
BLYP	0.31a	0.187	0.106	0.08	0.19	0.37g	Unbound	Unbound	0.181 (2.952)
BPW91	0.34a	0.163	0.094	0.05	0.16	0.60	Unbound	Unbound	0.156 (2.946)
PW91PW91	0.77	0.164	0.141	0.06	0.35	0.52	0.0100 (2.645)	0.0137 (3.016)	0.235 (2.886)
mPWPWh	0.65	0.161	0.122	0.05	0.16	0.38	0.0052 (2.823)	0.0076 (3.178)	0.194 (2.911)
PBEPBEi	0.74i	0.156	0.101	0.06	1.25	0.34	0.0032 (2.752)	0.0048 (3.097)	0.222 (2.899)
XLYPj	0.33	0.186	0.117	0.09	0.95	0.24	0.0010 (2.805)	0.0030 (3.126)	0.192 (2.953)
Hybrid methods
BH & HLYPk	0.94	0.207	0.247	0.07	0.08	0.72	Unbound	Unbound	0.214 (2.905)
B3P86l	0.78a	0.636	0.593	0.03	2.80	0.34	Unbound	Unbound	0.206 (2.878)
B3LYPm	0.13a	0.168	0.103	0.06	0.38	0.25g	Unbound	Unbound	0.198 (2.926)
B3PW91n	0.15a	0.161	0.100	0.03	0.24	0.38	Unbound	Unbound	0.175 (2.923)
PW1PWo	0.23	0.160	0.114	0.04	0.30	0.30	0.0066 (2.660)	0.0095 (3.003)	0.227 (2.884)
mPW1PWp	0.17	0.160	0.118	0.04	0.16	0.31	0.0020 (3.052)	0.0023 (3.254)	0.199 (2.898)
PBE1PBEq	0.21i	0.162	0.126	0.04	1.09	0.30	0.0018 (2.818)	0.0026 (3.118)	0.216 (2.896)
O3LYPr	0.18	0.139	0.107	0.05	0.06	0.49	0.0031 (2.860)	0.0047 (3.225)	0.139 (3.095)
X3LYPs	0.12	0.154	0.087	0.07	0.11	0.22	0.0010 (2.726)	0.0028 (2.904)	0.216 (2.908)
Experimental	—	—	—	—	—	—	0.0010 (2.970)t	0.0036 (3.091)t	0.236u (2.948)v

ΔH_f, heat of formation at 298 K; PA, proton affinity; E_tot, total energies (H-Ne); TM ΔE, s to d excitation energy of nine first-row transition metal atoms and nine positive ions. Bonding properties [ΔE or D_e in eV and (R_e) in Å] are given for He₂, Ne₂, and (H₂O)₂. The best DFT results are in boldface, as are the most accurate answers [experiment except for (H₂O)₂].

^aRef. 5

^bRef. 19

^cRef. 4

^dRef. 35

^eRef. 38

^fRef. 34

^gRef. 37

^hRef. 7

ⁱRef. 10

^j1.0 E_x (Slater) + 0.722 ΔE_x (B88) + 0.347 ΔE_x (PW91) + 1.0 E_c (LYP)

^k0.5 E_x (HF) + 0.5 E_x (Slater) + 0.5 ΔE_x (B88) + 1.0 E_c (LYP)

^l0.20 E_x (HF) + 0.80 E_x (Slater) + 0.72 ΔE_x (B88) + 1.0 E_c (VWN) + 0.81 ΔE_c (P86)

^m0.20 E_x (HF) + 0.80 E_x (Slater) + 0.72 ΔE_x (B88) + 0.19 E_c (VWN) + 0.81 E_c (LYP)

ⁿ0.20 E_x (HF) + 0.80 E_x (Slater) + 0.72 ΔE_x (B88) + 1.0 E_c (PW91, local) + 0.81 ΔE_c (PW91, nonlocal)

^o0.25 E_x (HF) + 0.75 E_x (Slater) + 0.75 ΔE_x (PW91) + 1.0 E_c (PW91)

^p0.25 E_x (HF) + 0.75 E_x (Slater) + 0.75 ΔE_x (mPW) + 1.0 E_c (PW91)

^q0.25 E_x (HF) + 0.75 E_x (Slater) + 0.75 ΔE_x (PBE) + 1.0 E_c (PW91, local) + 1.0 ΔE_c (PBE, nonlocal)

^r0.1161 E_x (HF) + 0.9262 E_x (Slater) + 0.8133 ΔE_x (OPTX) + 0.19 E_c (VWNS) + 0.81 E_c (LYP)

^s0.218 E_x (HF) + 0.782 E_x (Slater) + 0.542 ΔE_x (B88) + 0.167 ΔE_x (PW91) + 0.129 E_c (VWN) + 0.871 E_c (LYP)

^tRef. 27

^uRef. 33

^vRef. 32

Heats of Formation (ΔH_f). To provide a good test of the functionals for the covalent systems, we calculated the heats of formation for the 148 molecules of the extended G2 set (4, 5). X3LYP leads to MAD = 0.12 eV, which is the best DFT result. Other good results include B3LYP (MAD = 0.13 eV) (5), B3PW91 (MAD = 0.15 eV) (5), mPW1PW (MAD = 0.17) (7), and PBE1PBE (MAD = 0.21 eV) (10). All other methods lead to unacceptable errors. Table 1 makes it clear that hybrid methods dramatically improve the thermochemistry over pure GGAs. For example, PBEPBE (MAD: 0.74) compares to PBE1PBE (MAD: 0.21) (8,10); BLYP (MAD = 0.31) versus B3LYP (MAD = 0.13) (5) and XLYP (MAD = 0.33) versus X3LYP (MAD = 0.12). We should point out that the G2 energies quoted here (MAD = 0.07) include the empirical “higher-order correction” to the total energy. Without this correction, the MAD for G2-1 would have been 1.03 eV for MP2 and 0.50 eV for CCSD[T], partially limited by the use of a smaller basis set (7, 8).

Ionization Potential (IP). IPs (and EAs) are calculated as the total energy differences between the neutral and the corresponding ionic systems. GGAs generally dramatically improve the predictions of IPs of LDA (MAD = 0.67 eV) (19), suggesting that cations are more inhomogeneous than neutral systems. However, including exact exchange is not important for IP. Most GGA methods give a MAD over the 42 cases in G2 (19) lower than 0.2 eV, with O3LYP (16, 22) lowest at 0.139. X3LYP is the second best, giving MAD = 0.154.

Electron Affinity (EA). There is some debate in the literature concerning whether DFT methods are suitable for calculating EAs (10, 23, 24). Because the “self-interaction error” shifts the Kohn–Sham orbital energies upwards, the anion often has a positive (unstable) highest occupied orbital energy (this cannot ionize because of the finite size of the basis functions). In any case the numerical results lead to predicted EAs with accuracy comparable to the IPs (19). Thus, over the total 25 systems in G2 (19) we obtain MADs of 0.10 eV (B3LYP), 0.13 (PBE1PBE), and 0.09 (X3LYP). Again, inclusion of exact exchange does not improve the performance over the corresponding pure DFT methods.

Proton Affinity (PA). Adding a proton to a neutral molecule leads to a significant change in the density, making it more inhomogeneous. Thus, Table 1 shows that the proton affinities (PAs) over eight systems in G2 (19) are systematically underestimated by LDA (MAD = 0.27 eV). GGAs reduce the LDA errors significantly. B3P86 and B3PW91 (MAD = 0.03 eV) show the best performance, while B3LYP, PBE1PBE, and X3LYP lead to MAD = 0.06, 0.04 (10), and 0.07 eV, respectively.

Total Energies (E_tot). We considered the total energies for the first 10 atoms (H to Ne). Comparing to the experimental values (25, 26), LDA (SVWN) leads to significant error (MAD = 6.67 eV), which is dramatically reduced by most GGAs. X3LYP gives good result (MAD = 0.11 eV), which can be compared to B3LYP (MAD = 0.38) and PBE1PBE (MAD = 1.09). O3LYP is the best, leading to MAD = 0.06.

Bonding Properties of Rare-Gas Dimers. Rare-gas dimers provide the least ambiguous tests for the accuracy in describing van der Waals attraction (London dispersion forces). As summarized in Table 1, we calculated the equilibrium distance and bond energy of He₂ and Ne₂ as probes of the accuracy for van der Waals systems (27).

LDA leads to significant overbinding (by 12 times for He₂, with a bond too short by 0.6 Å).

Although B88 exchange is very successful in describing covalent bonds, it fails dramatically for London interactions (28, 29). Thus, every DFT method using the B88 exchange functional (pure or hybrid, with and without correlation) leads to unbound rare-gas dimers, far more unbound than HF.

On the other hand, every DFT method using the PW91 exchange functional severely overbinds rare-gas dimers, even when the correlation functional is omitted. To ameliorate this problem, Adamo and Barone modified PW91 (7) by fitting the differential exchange energies of rare-gas dimers to HF values, removing some of the overbinding tendency of PW91. The PBE functional gives an overall good description of rare-gas dimers.

The van der Waals (London) attraction between rare-gas atoms arises entirely from electron correlation (the instantaneous interaction between fluctuating dipoles). Thus, HF wave-functions give a purely repulsive interaction for all interatomic distances and we expect that exchange-only potentials should also give this behavior. However, we found that the PW91, mPW91, and PBE exchange-only potentials lead to erratic minima, as do the corresponding hybrid models.

We conclude that X3LYP provides the best description of London forces because coupled with the LYP correlation term its gives a good description of bonding for He₂ and Ne₂ while without correlation, the exchange-only (X or X3) potential is repulsive and close to the Hartree–Fock curve. Because the London forces of He and Ne are described well, we expect a good description of the London forces between electron pairs involving the first 10 atoms of the periodic table.

Note that in describing the dispersion forces, we are concerned with distances near the equilibrium configuration for van der Waals complexes, which tend to be in the range from 2.5 to 4 Å. It is at much larger distances before the neglect of overlap between the atomic distances leads to the classic 1/r⁶ London potential (30, 31).

Bonding Properties of Water Dimer. Hydrogen bonding plays a critical role in a wide range of chemical and biological phenomena. Consequently, water dimer, the prototypical hydrogen bonded system, has been studied thoroughly experimentally and theoretically (32–34). The floppiness of (H₂O)₂ has made experimental determinations of r_e and D_e difficult. Microwave measurements of the rotational moments lead to a vibrationally averaged O... O distance of R₀ = 2.976 Å, from which it was estimated that R_e = 2.946 Å (32). The most widely accepted experimental bond energy of D_e = 0.23 ± 0.03 eV (33) was based on measurements of the thermal conductivity of water vapor followed by relatively complex interpretation including an estimate of the zero-point energy calculated at the HF/4–21G level (33).

Fortunately, highly accurate values for the equilibrium geometry and dissociation energy of (H₂O)₂ have been determined computationally (34). These ab initio CCSD(T) (Full) studies used a 275 basis function interaction optimized basis set extrapolated to infinity, leading to r_e(O... O) = 2.912 ± 0.005 Å and D_e = 0.218 ± 0.004 eV (34). We conclude that the ab initio values (34) provide the most reliable data.

All DFT methods that include GGA give H bond energies within 0.04 eV of D_e = 0.218 eV and bond distances within 0.04 Å of r_e = 2.912 Å (34). This may seem adequate, but for biological applications, greater accuracy is highly desired. The best accuracy is given by PBE1PBE and X3LYP, which lead to binding energy errors of 0.002 eV and bond distance errors of 0.016 Å (PBE1PBE) and 0.004 Å (X3LYP). We should emphasize here that (H₂O)₂ was not included in the training set for these functionals, indicating that physics of hydrogen bonding is correctly described.

Electrostatics. Electrostatic interactions are quite important in the bonding of ligands to proteins and DNA in determining differential solvation also important in binding. To assess the accuracy for charge distributions from various DFT methods, we calculated the dipole moments for 70 molecules for which accurate values are available. HF generally overestimates the magnitude of dipole moments (MAD = 0.242 Debye), but all DFT methods lead to substantial improvement (e.g., MAD errors are: B3LYP, 0.083; PW1PW, 0.088; PBE1PBE, 0.084; and X3LYP, 0.088). These results were not used in optimizing the parameters.

In addition, the polarizabilities of atoms and molecules are expected to be important in electrostatic and solvation interactions. For the seven molecules for which we could find accurate experimental polarizabilities, the accuracies (MAD in au) for various DFT methods are as follows: B3LYP, 0.16; PW1PW, 0.35; PBE1PBE, 0.32; and X3LYP, 0.19. These results were not used in optimizing the parameters.

Spin States of Transition Metals. Many important biological systems involve metal atoms in various spin and oxidation states. For example, the various steps of detoxifying foreign molecules by cytochrome P450s involves high-spin Fe^III, high-spin Fe^II, and low-spin Fe^II. Consequently, it is important that the excitation energies and IPs be properly described (35, 36). We considered the nine transition metal atoms Sc–Cu and calculated the dⁿs² to dⁿ⁺¹s¹ excitation energy of the neutral atom and the dⁿs¹ to dⁿ⁺¹s⁰ (n = 1–9) excitation energy of the cation for various DFT functionals. Table 1 shows that X3LYP does quite well with a MAD of 0.22 eV, as compared to B3LYP (0.25) (37) and PBE1PBE (0.30). These results were not used in optimizing the parameters.

Summary

We deduce the form for the exact exchange energy density to describe a density decaying as a Gaussian at long range. We find that F^Gauss(s) lies between F^B88(s) and F^PW91(s), serving as the basis for the extended functional, F^X, which is described a linear combination of F^PW91 (with a sound physical basis) with F^B88 (which in B3LYP does best for thermochemistry but badly for London forces). Optimizing the four parameters [using the atomization energies of a small set (37) of diatomic and triatomic molecules along with atomic energies or IPs and EAs of the first 18 atoms] leads to the X3LYP functional with excellent accuracy for thermochemistry (heats of formation, IPs, EAs, proton affinities, and total atomic energies), a good description of London dispersion, an excellent description of hydrogen bond interactions, and excellent energetics for the spin states of transition metals. Thus, we recommend the use of X3LYP for application to a wide range of chemical, biological, and materials systems. X3LYP should also form a good starting point for continuing attempts to develop improved functionals for exchange and for correlation.