Experimental and DFT Studies: Novel Structural Modifications Greatly Enhance the Solvent Sensitivity of Live Cell Imaging Dyes

Abstract

Structural modifications of previously reported merocyanine dyes (J. Am. Chem. Soc. 2003, 125, 4132–4145) were found to greatly enhance the solvent dependence of their absorbance and fluorescence emission maxima. Density functional theory (DFT) calculations have been performed to understand the differences in optical properties between the new and previously synthesized dyes. Absorption and emission energies were calculated for several new dyes using DFT vertical self-consistent reaction field methods (VSCRF). Geometries of ground and excited states were optimized with a Conductor-like screening model (COSMO) and self-consistent-field (SCF) methods. The new dyes have enhanced zwitterionic character in the ground state, and much lower polarity in the excited state, as shown by the DFT-VSCRF calculations. Consistently, the position of the absorption bands are strongly blue-shifted in more polar solvent (methanol compared to benzene) as predicted by the DFT spectral calculations. Inclusion of explicit H-bonding solvent molecules within the quantum model further enhances the predicted shifts, and is consistent with the observed spectral broadening. Smaller, but significant spectral shifts in polar versus nonpolar solvent are predicted and observed for emission bands. The new dyes show large fluorescence quantum yields in polar hydrogen bonding solvents; qualitatively, the longest bonds along the conjugated chain at the excited S₁ state minimum are shorter in the more polar solvent, inhibiting photoisomerization. The loss of photostability of the dyes is a consequence of the reaction with and electron transfer to singlet oxygen, starting oxidative dye cleavage. The calculated vertical ionization potentials of three dyes I-SO, AI-SO(4), and AI-BA(4) in benzene and methanol are consistent with their relative photobleaching rates; the charge distributions along the conjugated chains for the three dyes are similarly predictive of higher reaction rates for AI-SO(4) and AI-BA(4) than for I-SO. Time dependent DFT (TDDFT) calculations were also performed on AI-BA(4); these were less accurate than the VSCRF method in predicting the absorption energy shift from benzene (C₆H₆) to methanol (MeOH).

1. Introduction

Fluorescent biosensors have enabled visualization of signaling activity in individual, living cells, leading to important insights into spatio-temporal control of signaling pathways.^1–4 Biosensors of protein conformational change have been produced by covalently labeling proteins with solvent-sensitive fluorescent dyes,^5–13 such that protein conformational changes affect fluorescence intensity. We have described such dyes (I-SO, I-TBA, S-SO, and S-TBA)¹⁴ optimized for use in live cell biosensors, with long-wavelength absorbance and emission, high extinction coefficient and quantum yield, water solubility, photostability, and solvent sensitive fluorescence. A novel biosensor of Cdc42 activation made with one of these dyes showed a 3-fold increase in fluorescence intensity in response to GTP-binding by Cdc42.¹⁴

Using dyes which respond to protein activity by changing fluorescence intensity presents difficulties during imaging, since the fluorescence intensity of dyes depends not only on protein conformational changes, but also on variations in cell thickness, uneven illumination, biosensor concentration etc. In the past, such problems have been overcome by normalizing the biosensor signal against other, non responsive fluorophores which distribute similarly to the biosensor in cells¹⁵. This presents significant problems that are obstacles to quantitative studies of signaling networks; i.e. the two fluorophores bleach at different rates and site-specific attachment of two fluorophores to a biosensor can be very challenging. Use of a second fluorophore for normalization is not necessary if the dye undergoes a solvent-dependent shift in its excitation or emission maxima, rather than simply an intensity change. Normalization can then be achieved by monitoring the fluorescence intensity of a single dye at two different wavelengths, rather than the relative intensities of two different dyes (see Figure 1).

Figure 1.

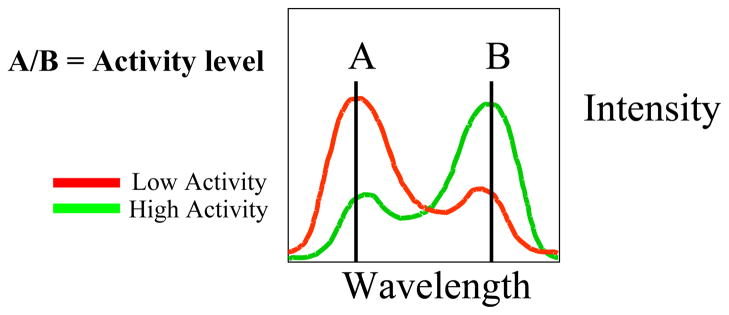
Ratio imaging. When covalently attached to a protein, the dye molecule shifts between two spectra (i.e. spectrum A and spectrum B), as the dye environment is affected by protein conformational changes. Intensity A divided by intensity B reflects the protein environment, regardless of the overall intensity of the fluorescence.

Our previously reported dyes do possess moderate solvent-dependent shifts in excitation and/or emission wavelengths, but these were insufficient for ratio imaging in cells. The absorption and emission bands present red shifts for I-SO and blue shifts for S-TBA, with increasing solvent polarity. From benzene (C₆H₆) to methanol (MeOH), the absorption and emission wavelength shifts are 15 nm and 12 nm for I-SO, and are 17 nm and 11 nm for S-TBA, respectively. The shifts of the absorption and emission bands of S-SO and I-TBA in other solvents are even smaller.¹⁴ Here we describe structural modifications that enhance the solvent-dependent shifts of excitation/emission wavelengths for these merocyanine dyes. As described by Marder and others,^16–18 merocyanine dyes are insensitive to solvent polarity when their ground states are at the “cyanine limit” (C in Figure 2), with equal contributions from the non-polar and the zwitterionic resonance structures. Dyes at the cyanine limit are characterized by equal dipole moments in the ground and excited states, so solvents affect both states similarly and there is minimal solvent-dependent change in absorption/emission maxima. We expected that by increasing the strength of the electron donor in the dye structure, the dye’s ground state structure would shift to a more polar form (D in Figure 2), and the dye would have greater solvent-dependent absorption/emission wavelengths. This increase in donor strength was accomplished by a novel introduction of a six membered ring into the dye structure. This led to additional aromaticity when the dyes adopted the zwitterionic configuration.

Figure 2.

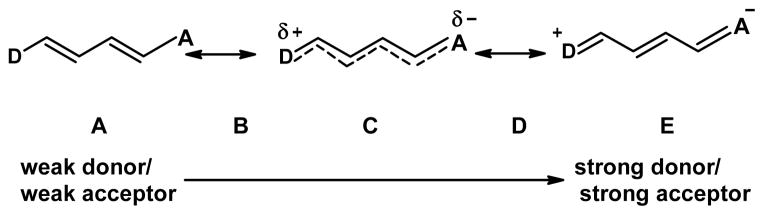
Resonance structures of merocyanine dyes. Depending on the relative electron donating and accepting strength of the “donor” (D) and “acceptor” (A) portions of the molecule, the dye can adopt different ground state structures, ranging from neutral through zwitterionic.

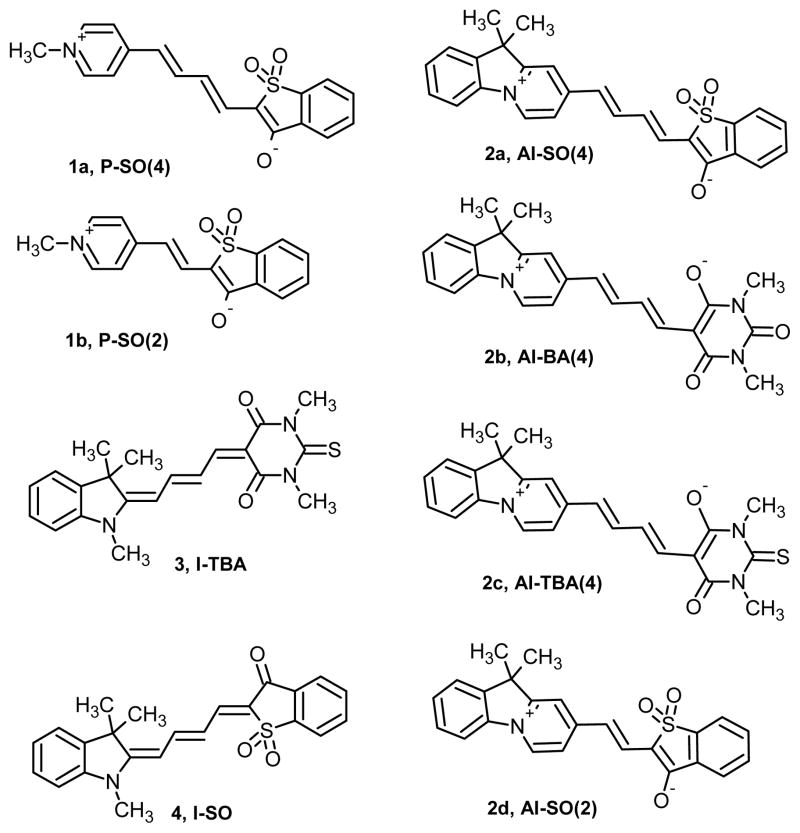
New merocyanine dyes were obtained by adding the 6-membered ring to the electron donating side of previously reported merocyanine structures (Chart 1). All the dyes are named for the combination of donor and acceptor heterocycles that make up their structure (donors: I = indolenine, S = benzothiazole, O = benzoxazole; acceptors: SO = benzothiophen-3-one-1,1-dioxide, TBA = thiobarbituric acid). In the new dyes an “A” is included in the name of the donor ring structure to denote the enhanced aromaticity imparted by the new six-membered ring (i.e. AI-SO and AI-TBA rather than the previously reported I-SO and I-TBA). The number in parentheses indicates the number of methines in the central polymethine chain.

Chart 1.

Dye structures

We will show that the absorption band positions of AI-SO(4), AI-TBA(4), and AI-BA(4) are highly solvent dependent. The shifts of the emission bands of AI-SO(4) and AI-BA(4), though not as significant as the absorption bands, are also largely increased. These two dyes are also highly fluorescent in polar solvents like methanol (MeOH).

In this paper we describe density functional theory (DFT) studies to examine how modifications of the donor structure affect dye solvent sensitivity. Several photophysical properties of these dyes were correctly predicted and analyzed using the DFT vertical self-consistent reaction field (VSCRF)^19,20 method for calculating the spectra, plus a conductor like screening (COSMO)^21–24 solvation model for optimizing geometries. This work points to structural features which can be incorporated to enhance the solvent sensitivity of a broad range of merocyanine dyes.

2. Methods

2.1. Synthesis

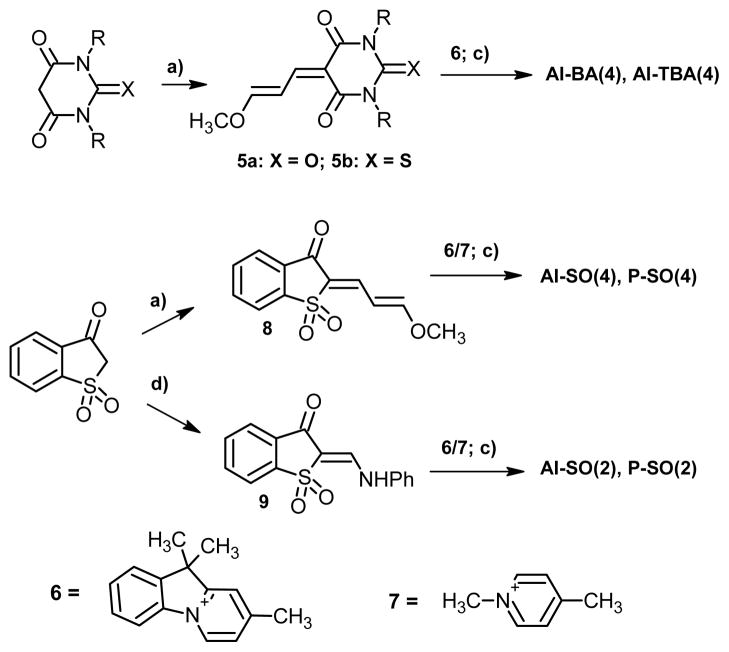
The synthesis of the new dyes 1a,b and 2a–d was accomplished according to Scheme 1. A detailed description of new synthetic procedures for this family of dyes will be published elsewhere. The synthesis of dyes 3 and 4 (I-TBA and I-SO) was described previously.¹⁴

Scheme 1.

Synthesis of dyes 1a, b, 2a-2d. Conditions: (a) malonoaldehyde bis(dimethyl acetal), CF₃COOH, 95° C, 2 hours. (b) malonoaldehyde bis(dimethyl acetal), CF₃COOH, 130° C, 2 hours. (c) N-Methylpiperidine, MeOH, reflux 30–60 min. (d) diphenylformamidine, AcOH-Ac2O, 120° C, 2 hours.

2.2. Computation

All quantum mechanical DFT calculations were performed using the Amsterdam Density Functional (ADF, Version 2000) package.²⁵ The parametrization of Vosko, Wilk and Nusair (VWN)²⁶ was used for the local density approximation term, and the corrections of Becke (1988) (B)²⁷ and Perdew (1986) (P)^28,29 were used for the non-local exchange and correlation terms. The molecular orbitals were expanded in an uncontracted triple-ζ Slater-type orbital basis set, along with a single set of polarization functions. The inner core shells of C(1s), N(1s), O(1s) and S(1s,2p) were treated by the frozen core approximation. The accuracy parameter (accint) for the numerical integration grid was set to 4.0.

We recently established a density functional vertical self-consistent reaction field (VSCRF) solvation model for predicting vertical excitation energies and the solvatochromic shift of solvent sensitive dyes in different solutions.¹⁹ We have successfully applied this method to predict the UV absorption and emission blue shifts of Brooker’s merocyanine from CHCl₃ to H₂O solutions with increasing solvent polarity, and the solvatochromic shifts of both the absorption and emission processes for S-TBA merocyanine,³⁰ Abdel-Halim’s merocyanine,³¹ the rigidified aminocoumarin C153,^32–34 and Nile red,^35,36 in different solutions.^19,20 This VSCRF model was developed in the framework of DFT with ΔSCF methodology. Its implementation is based on our original self-consistent reaction field (SCRF) development,^37–39 where the solute molecule is computed by DFT method in the presence of a solvent reaction field. The reaction field is evaluated from a finite-difference solution to the Poisson-Boltzmann equation and self-consistency between the reaction field and the electronic structure of the solute is achieved by iteration. The SCRF calculation applied to a solute geometry allows the electronic structure relaxation in both the solute and the solvent and, implicitly, the orientational (geometry) relaxation of the solvent. Once the SCRF calculation on the ground state (S₀) state (or the first excited singlet state (S₁) is achieved, the VSCRF procedure on the excited state (or the ground state) allows only the electronic structure reorganization for both the solute and solvent, and the vertical excitation (or emission) in solution is then obtained. The detailed principles and procedures for VSCRF calculations in both absorption and emission processes, including the ΔSCF spin-decontamination methodology for the first excited singlet state (S₁) energy, can be found in Refs. 19 and 20.

The solute geometries in C₆H₆ and MeOH were optimized using the COSMO (Conductor like Screening Model) model in ADF.^21–24 The COSMO model is a dielectric solvent continuum model in which the solute molecule is embedded in a molecular-shaped cavity surrounded by a dielectric medium with given dielectric constant ε. In our current COSMO and SCRF calculations, we used ε = 2.3 for C₆H₆ and ε = 32.6 for MeOH. The optical dielectric constant ε_op = 2 was used in VSCRF calculations. The dielectric boundary between the interior (with ε = 1) and the exterior of the solute region in all COSMO, SCRF and VSCRF calculations was defined by the constant surface of rolling a probe sphere (with radius r = 3.5 and 2.5 Å for C₆H₆ and MeOH, respectively) over the solute. The van der Waals radii for atoms C, O, N, S, and H were taken as 1.7, 1.4, 1.55, 1.8, and 1.2 Å, respectively. Cavitation/dispersion corrections are not included, but these should be similar for the ground and vertical excited states. For the absorption process, the S₀ state of the solute were relaxed in different solvent dielectrics (C₆H₆ and MeOH). Correspondingly, for the emission process, the geometry optimizations were performed on the S₁ state. An electron was promoted from β-HOMO to β-LUMO during the S₁ state geometry optimizations. Our SCRF/VSCRF calculations are then performed on the COSMO-optimized geometries.

As in our earlier work,^19,20 the absorption and emission energies were calculated as vertical excitations in the framework of the Franck-Condon principle^19,20,40 without explicit including of vibrational effects. We neglect zero-point-energies (ZPEs), vibrational thermal energies, and vibrational entropy contributions to the free energy in the ground state and vertical excited state for absorption (and similarly for emission). These effects will partially subtract out in the excitation energies which are energy differences. Further, in the vertical excited state (for absorption), complex issues arise about proper vibrational ensembles, time scales, and partial thermal equilibrium, involving also the solvent bath. While there can be some overall effect of these corrections on the absolute calculated excitation energies, the effects on solvent-dependent shifts are probably small. In contrast to vibrational effects, both COSMO and SCRF/VSCRF calculations include the electronic polarization of the dye by the solvent; the latter effect is important, as will be shown by the differences in dipole moment in different solvents.

3. Results and Discussions

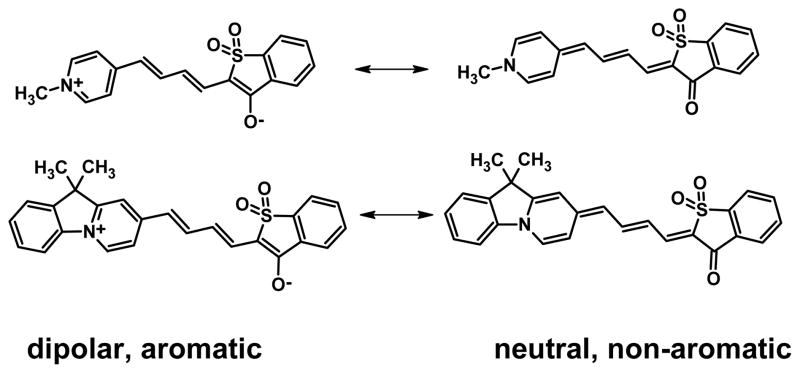
Experimentally we compared merocyanines with more zwitterionic ground states (dyes 1a, 1b and 2a–d in Chart 1) to merocyanines that should be closer to the cyanine limit (dyes 3 and 4 in Chart 1). The more zwitterionic merocyanines were made by incorporating a strong donor ring, either 4-pyridine or 10H-pyrido[1,2-a]indolenine, in the structures. These rings were predicted to stabilize the polar, zwitterionic form of the dyes in the ground state, because of the enhanced aromaticity of the zwitterionic resonance form (Figure 3).

Figure 3.

Ground state of merocyanine dyes with and without aromatic stabilization of a charged donor ring. The incorporation of an additional 6-membered ring strongly favors the charged zwitterionic resonance form.

From a theoretical perspective, we have compared DFT calculations, evaluating geometries, excitation and emission energies, H-bonding effects, molecular orbital and bonding characters, dipole moments, and the atomic charge distributions for dyes I-SO (4), I-TBA (3), AI-SO(4) (2a), AI-BA(4) (2b), and AI-TBA(4) (2c), in order to examine why the solvent dependencies in absorption and emission, the fluorescence quantum yield, and photobleaching properties change from I-SO to AI-SO(4), and from I-TBA to AI-BA(4) and AI-TBA(4). These properties are also compared in nonpolar C₆H₆ and in polar MeOH solvents.

3.1. Isomers of the Dye Molecules

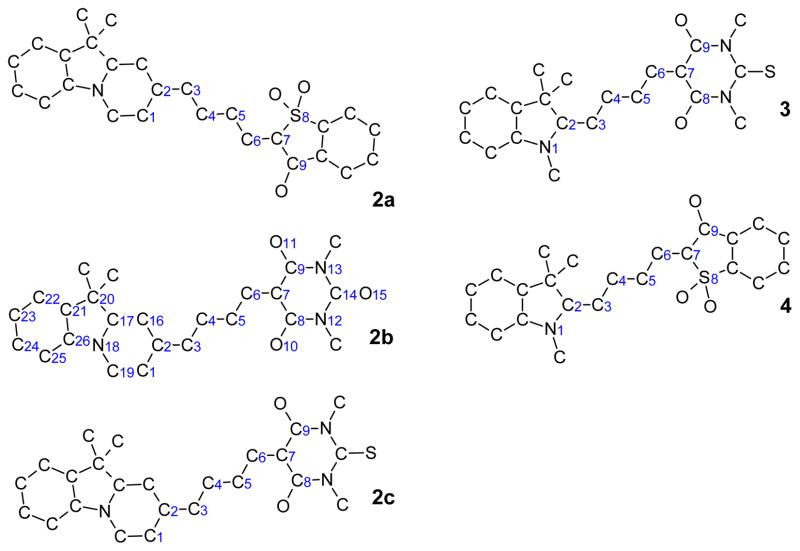
Using the COSMO model in ADF2000, we geometry optimized all the possible isomer conformations for the dyes 2a-c, 3, and 4 in C₆H₆ (ε = 2.3) and in MeOH (ε = 32.6). NMR spectra of these dyes were consistent with an all-trans configuration of the central polymethine bridge. Our calculations show that the relative energies of the different isomers for each dye are very small (overall < 2.5 kcal mol⁻¹, see Table 1). From an energetic point of view, different isomers for a certain dye may coexist in the solvents. In reality, which isomers that are measured in the experiment highly depend also on the synthetic procedure. Here we simply choose the lowest energy structures of each dye in MeOH for our further calculations in both C₆H₆ and MeOH. These structures with numbering conventions are shown in Chart 2. In fact, our tests using SCRF/VSCRF calculations show very similar electronic structures and absorption energies (with differences normally less than 0.02 eV) for different isomers of a given dye in a given solvent.

Table 1.

Calculated Relative Energies (kcal mol⁻¹) of the Different Isomers of Each Dye Molecule in C₆H₆ and MeOH.^a

Dye	Solvent	Isomers
		1 trans 4	1 cis 4	1 trans 4	1 cis 4
		9 trans 5	9 trans 5	9 cis 5	9 cis 5
I-TBA	C6H6	0.00	2.42
	MeOH	0.00	2.45
AI-TBA(4)	C6H6	0.00	0.38
	MeOH	0.00	0.56
AI-BA(4)	C6H6	0.00	1.72
	MeOH	0.00	0.63
I-SO	C6H6	0.05	0.66	0.00	1.66
	MeOH	0.00	0.80	0.43	1.95
AI-SO(4)	C6H6	0.56	0.00	1.72	1.08
	MeOH	0.75	0.00	2.04	2.03

^aSee structures in Chart 2 for the atomic labelling. Here for instance, “1 trans 4, 9 trans 5” means that “atom 1 is trans to atom 4, and atom 9 is trans to atom 5”.

Chart 2.

Geometry-optimized structures and numbering convention for the merocyanine dyes.

3.2. Absorption Spectra

The experimental absorption data for the dyes are summarized in Table 2, and Figure 4. With decreasing solvent polarity, the absorption maximum of dyes 1a–b, 2a–d shifted to longer wavelengths, and the intensity of the transition increased (Table 1, Figure 4). Such a hypsochromic (blue) shift is similar to that of Brooker’s merocyanine (Figure 5), a well known dye with a ground state predominantly in the zwitterionic form.¹⁹

Table 2.

Observed Absorption Properties of Dyes 1a–b, 2a–d, 3, 4.

Solvent	3	4	2a,	2b,	2c,	2d,	1a,	1b,
	I-TBA	I-SO	AI-SO(4)	AI-BA(4)	AI-TBA(4)	P-SO(4)	P-SO(2)	AI-SO(2)
	λmax/nm (ε)	λmax/nm (εa)	λmax/nm (ε)	λmax/nm (ε)	λmax/nm (ε)	λmax/nm (ε)	λmax/nm (ε)	λmax/nm (ε)
MeOH	583 (173000)	586 (143000)	610 (65000)	585 (83000)	576 (38000)	580 (54000)	505 (57000)	542 (92000)
EtOH	-	-	636 (83000)	604 (104000)	603 (46000)	557 (61000)	514 (65000)	549 (111000)
i-PrOH	-	-	648 (122000)	614 (132000)	618 (50000)	597 (68000)	518 (72000)	553 (132000)
BuOH	589 (190000)	587 (134000)	650 (118000)	615 (154000)	619 (53000)	593 (64000)	519 (67000)	554 (120000)
OcOH	590 (180000)	587 (125000)	660 (150000)	628 (143000)	633 (97000)	612 (80000)	524 (72000)	559 (150000)
DMF	589 (183000)	586 (143000)	651 (154000)	625 (146000)	616 (52000)	604 (99000)	522 (92000)	556 (157000)
DMSO	-	-	644 (118000)	617 (122000)	607 (56000)	599 (77000)	520 (75000)	555 (126000)
CH3CN	-	-	642 (142000)	621 (141000)	615 (54000)	596 (93000)	546 (89000)	549 (149000)
CH2Cl2	-	-	667 (278000)	647 (224000)	655 (104000)	629 (187000)	529 (128000)	561 (218000)
C6H6	584 (127000)	571 (109000)	679 (240000)	662 (201000)	683 (135000)	644 (178000)	538 (169000)	570 (235000)

Figure 4.

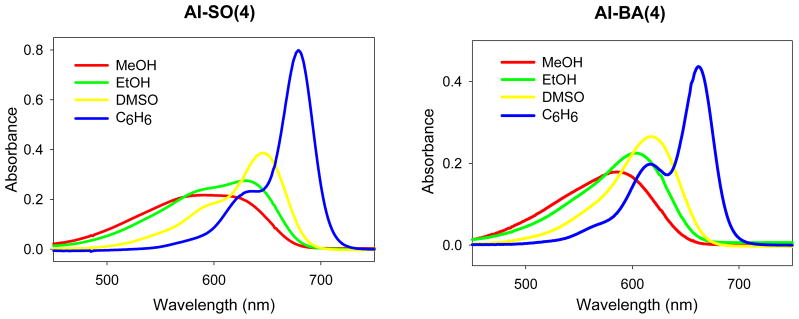
Absorbance spectra of AI-BA(4) and AI-SO(4) in methanol, ethanol, DMSO, and benzene. C(AI-BA(4)) = 2.17 μM, C(AI-SO(4)) = 3.33 μM.

Figure 5.

Brooker’s merocyanine.

For the new dyes with stronger donor rings, a decrease in solvent polarity resulted in destabilization of the zwitterionic form and moved the dye ground state towards the “cyanine limit”, increasing the contribution from the non-polar form. The calculated central C-C bond lengths of the ground state geometries are presented in Table 3. Obviously the solute structures vary with solvent polarity. Strong bond length alternations (BLA) were found for merocyanines 2a–c in MeOH, where dyes predominantly exist as zwitterions. The alternations were diminished in benzene indicating a ground state more like the ‘cyanine-limit’. For I-TBA and I-SO, the average BLA was small, suggesting that in both solvents the ground states of the dyes are close to the cyanine limit.

Table 3.

DFT Calculated Central C–C Bond Lengths (Å) of the Ground State Dye Molecules in C₆H₆ and in MeOH.

Solvent	Bond	Solute
		I-TBA	AI-TBA(4)	AI-BA(4)	I-SO	AI-SO(4)
C6H6	C2–C3	1.394	1.413	1.411	1.386	1.412
	C3–C4	1.404	1.403	1.404	1.409	1.395
	C4–C5	1.393	1.403	1.401	1.383	1.394
	C5–C6	1.397	1.396	1.399	1.404	1.401
	C6–C7	1.402	1.408	1.404	1.382	1.386
BLA(C6H6) a		0.007	0.009	0.010	0.022	0.005
MeOH	C2–C3	1.401	1.430	1.427	1.398	1.429
	C3–C4	1.395	1.389	1.393	1.399	1.382
	C4–C5	1.402	1.419	1.416	1.396	1.410
	C5–C6	1.390	1.384	1.387	1.396	1.388
	C6–C7	1.415	1.426	1.421	1.395	1.404
BLA(MeOH) a		0.009	0.038	0.032	0.0005	0.035

^aBond length alternations, BLA = {|(C₂–C₃) – (C₃–C₄)| + |(C₄–C₅) – (C₅–C₆)|}/2

The structure changes of the solutes with increasing solvent polarity from C₆H₆ are consistent with the changes of the solute dipole moment (see Table 4). The S₀ state dipole moments (μ_S0) are increased moderately by 6.15 and 4.57 D for I-TBA and I-SO, and significantly by 9.70, 8.82, and 8.45 D for AI-TBA(4), AI-BA(4), and AI-SO(4), respectively, from C₆H₆ to MeOH solutions.

Table 4.

SCRF/VSCRF Calculated and Experimentally (Exp) Observed Absorption (E_abs) Energies (eV), and the Relaxed S₀ State (μ_S0) and Vertical S₁ (μ^v_S1) State Dipole Moments (D) for the Dyes in C₆H₆ and in MeOH. TDDFT Calculated Absorption Energies (eV) for AI-BA(4) are Also Given Here.

Absorption
Solute	Solvent	μS0	μvS1	Eabs
				SCRF/VSCRF	TDDFT	Exp
I-TBA	C6H6	16.53	17.86	1.611		2.123 (585 nm)
	MeOH	22.68	22.60	1.599		2.127 (583 nm)
AI-TBA(4)	C6H6	22.84	19.77	1.349		1.816 (683 nm)
	MeOH	32.54	25.19	1.581		2.153 (576 nm)
AI-BA(4)	C6H6	19.78	18.46	1.411	2.347	1.873 (662 nm)
	MeOH	28.60	21.60	1.583	2.373	2.120 (585 nm)
I-SO	C6H6	10.07	16.91	1.637		2.172 (571 nm)
	MeOH	14.64	17.63	1.556		2.116 (586 nm)
AI-SO(4)	C6H6	17.71	18.56	1.401		1.826 (679 nm)
	MeOH	26.16	23.83	1.536		2.120 (585 nm)

The change of the solute dipole moment in different solutions, or upon S₀ → S₁ transitions, is caused by charge rearrangement or intramolecular charge transfer. We present in Figure 6 the molecular orbital plots for the electron in the HOMO of the S₀ state and the π → π promoted electron in the S₁ state of dye 2b, AI-BA(4) in C₆H₆ and in MeOH. The contributions of the atomic π orbitals to the HOMO vary with solvent type. In C₆H₆ solution, the electron in the HOMO is mainly localized at C₇(17.2%), C₃(17.0%), C₅(16.3%), N₁₈(6.6%), C₁₆(5.2%), O₁₁(4.6%), C₁(4.2%), O₁₀(3.8%), and C₂(2.5%). In MeOH solution, the localization of the electron in the HOMO is shifted rightward and localized at the atoms of C₃(17.7%), C₇(17.3%), C₅(16.6%), N₁₈(5.3%), O₁₁(5.0%), C₁₆(4.7%), O₁₀(4.2%), C₁(4.2%), C₆(3.4%), and O₁₅(2.4%). Not only the electron in the HOMO, but also the distribution of other electrons vary with solvent polarity; therefore the dipole moment of S₀ state AI-BA(4) is substantially increased with increasing solvent polarity from C₆H₆ to MeOH. During the π → π transition, the solute dipole moment decreases. The promoted electron in the π orbital moved leftward. In C₆H₆ solution, it is mainly localized at the atoms of C₄(14.1%), C₂(14.0%), C₆(13.6%), C₁₉(9.7%), N₁₈(7.2%), C₁₇(5.4%), C₅(5.1%), C₂₃(3.2%), O₁₀(3.1%), C₂₅(3.1%), C₈(3.1%), and O₁₁(2.9%) for the vertical S₁ state. In MeOH, the contributions change to C₄(14.4%), C₆(13.9%), C₂(13.0%), N₁₈(8.9%), C₁₉(8.7%), C₁₇(5.5%), C₁₆(4.9%), C₃(3.6%), C₂₃(3.1%), C₈(3.0%), C₂₅(2.9%), and C₉(2.7%).

Figure 6.

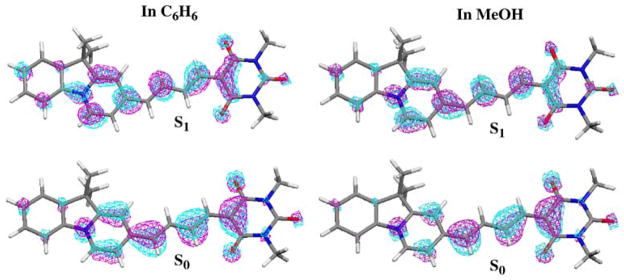
Molecular orbital plots for the electron in the HOMO of the ground state (S₀) and the π → π promoted electron in the first excited singlet state of AI-BA(4) in C₆H₆ and in MeOH.

When the solute dipole moment in the excited state is larger than that in the ground state, the excited state is better stabilized in polar solvents relative to the ground state. With increasing solvent polarity, there will be a red shift for the absorption bands. On the other hand, a blue shift with increasing solvent polarity will occur if the solute dipole moment in the ground state is larger than that in the excited state. During the π → π excitation process, the solute dipole moments of AI-TBA(4), AI-BA(4) and AI-SO(4) all decrease in MeOH solution (Table 4). Their absorption bands shift to the blue with increasing solvent polarity from C₆H₆ to MeOH. By contrast, the dipole moment of I-SO increases during the π → π transition, and we observe the red shift of its absorption band from C₆H₆ to MeOH solution.

In Table 4, we also present the SCRF/VSCRF calculated vertical excitation energies of these molecules. The ΔSCF procedure of DFT method normally under-estimates the absolute value of the S₁ state energy, and therefore also the vertical excitation energy.^19,20 However, the directions and approximate magnitudes of the solvatochromic shift are correctly predicted.

Experimentally we observed a very small red shift for I-TBA with increasing solvent polarity from C₆H₆ to OcOH (with ΔE_abs = 0.021 eV, or Δλ_max = 6nm). We did predict a slight red shift for this molecule from C₆H₆ to MeOH (with ΔE_abs = 0.012 eV). The observed blue shift from OcOH to MeOH solutions (Δλ_max = 7nm) is possibly caused by the explicit interactions (for instance H-bonding interactions) between the solute and solvent molecules.

Recently, solvent continuum models for predicting the vertical electronic transitions have also been established at the time dependent DFT (TDDFT) level.^41–46 Calculations on the n = π* transition energies of diazines performed by Mennucci⁴² and Cossi and Barone⁴⁴ have shown results which are in very good agreement with the experiments. However, calculations with TDDFT are still not straightforward in the optimization of gemetries on the excited state surfaces. In order to compare the SCRF/VSCRF and the TDDFT methods, we also applied SCRF/VSCRF calculations on the diazines (see Figure 1 of Ref. 19) to predict the blue shifts with increasing solvent polarities from n-heptane to water solutions,¹⁹ and compared our results with the TDDFT⁴⁴ and the experimental data.⁴⁷ We saw that the TDDFT method was better than the ΔSCF calculations in predicting the absolute values of the vertical excitation energies. However, the blue shifts from n-heptane to water obtained by SCRF/VSCRF calculations are much closer to those from the experimental data than those from the TDDFT results, especially for pyridazine and pyrimidine.¹⁹ Both SCRF/VSCRF and TDDFT calculations show that consideration of the explicit water H-bonding effects is very important in order to predict the correct blue shifts for diazines from n-heptane to water.¹⁹

According to ADF’s manual, it is possible to combine COSMO model with TDDFT calculations. The usually major effects (modified zeroth-order Kohn-Sham (KS) orbitals and orbital energies) are included. However, COSMO should also modify the first-order change in the KS potential. This effect has not yet been implemented in ADF and may be significant in case of a high value of the dielectric constant. To see if we can use this TDDFT version in our dye calculations in different solvents, we applied the combination of COSMO and TDDFT at the COSMO optimized geometries of S₀ state AI-BA(4). The results are also given in Table 4. As seen before, the absolute values of the excitation energies predicted by TDDFT are much larger than the ΔSCF calculations,¹⁹ and larger than the experimental spectral energies in the current case. The TDDFT calculations yield very similar excitation energies for AI-BA(4) in C₆H₆ and in MeOH. The energy difference is only 0.026 eV, which is much worse than the SCRF/VSCRF’s result (0.172 eV) comparing with the experiment (0.247 eV).

3.3. Broadening of dye absorption in alcohols; role of H-bonding

The dyes studied here have very broad absorption bands in polar, hydrogen bonding solvents such as methanol or ethanol (Figure 4). It is known that the width of a band in the absorption spectrum of a chromophore in solution is a result of two effects: homogeneous and inhomogeneous broadening.

Homogeneous broadening is due to the existence of a continuous set of vibrational sublevels in each electronic state. The homogenous broadening become important for dyes with ground state lying far from cyanine limit. This can be understood by considering that a large amount of charge transfer will result in a large displacement of the excited state potential surface along the solvent reorganization coordinate, leading to a larger degree of direct absorption into higher vibronic levels in the excited state.¹⁸ Inhomogeneous broadening results from the fluctuation of the structure of the solvation shell surrounding the solute. In MeOH solution, there will be more explicit interactions between the solute and the surrounding solvent molecules through H-bonding. Different patterns and numbers of H-bonding interactions may result in a distribution of solute-solvent configurations. The consequent variation in the local electric field leads to a statistical distribution of energies of the electronic transitions. Also, upon excitation, different solute structures and energies may result from the v = 0 vibrational level to v = n transitions in the S₁ state. Therefore, the broad absorption bands in MeOH solution result from homogeneous and inhomogeneous effects. According to our isomer geometry and energy calculations given in section 3.1, different isomers of a certain dye may coexist in a certain solvent. In polar solvents like MeOH, different isomers will have different H-bonding interactions with the solvent molecules, which is also a source for the inhomogeneous broadening.

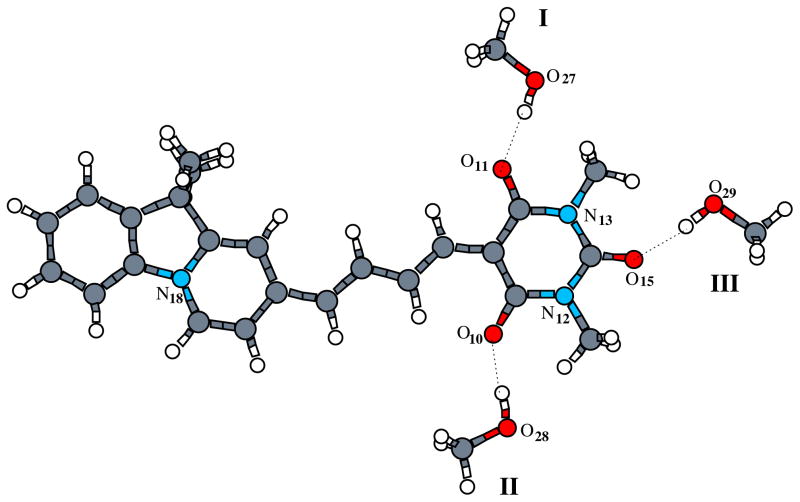
To see how explicit H-bonding and how different numbers of H-bonding interactions influence the solute structure and properties, we took AI-BA(4) as an example and put one, two and three explicit CH₃OH molecules H-bonding to the solute in different positions (Figure 7). The +1CH₃OH(I) model contains one CH₃OH molecule at position I, the +2CH₃OH(I,II) model has two CH₃OH molecules in total at positions I and II, and the +3CH₃OH(I,II,III) model contains all three H-bonding CH₃OH molecules at I, II and III, respectively. The geometries were then optimized using the COSMO model in ADF.

Figure 7.

Three possible positions of the explicit CH₃OH molecules H-bonding to AI-BA(4) in MeOH solution.

The main bond lengths of these structures are given in Table 5. For comparison, we also include the values for the structure without explicit H-bonding partners. Clearly, the geometry of AI-BA(4) changes upon interaction with the solvent molecule, and also changes with increasing numbers of the H-bonding solvent molecules. First, we look at the central C–C bonds. Without including explicit H-bonding interactions, the C₂–C₃, C₃–C₄, C₄–C₅, C₅–C₆, and C₆–C₇ bond lengths are 1.427, 1.393, 1.416, 1.387, and 1.421 Å, respectively, with obvious single, double, single, double, and single bond characters, consistent with Chart 1. By including one and two H-bonding CH₃OH molecules, these bonding characters are strengthened, with C₂–C₃, C₄–C₅, and C₆–C₇ lengthened, and C₃–C₄, and C₅-C₆ shortened. In the +3CH₃OH(I,II,III) model, the bond lengths of C₂–C₃, C₄–C₅, and C₆–C₇ reach the largest values of 1.444, 1.418, and 1.425 Å, and C₃–C₄, and C₅–C₆ are the shortest bonds 1.380 and 1.383 Å, respectively, among the calculated models. By including explicit H-bonding interactions, the bonding characters of C₁–C₁₉ and C₁₆–C₁₇ are weakend, and those of C₇–C₈ and C₇–C₉ are strengthened.

Table 5.

Main Bond Lengths (Å) of the S₀ State AI-BA(4) Structure in MeOH with 0, 1, 2 and 3 Explicit H-Bonding CH₃OH Molecules.^a

Bond	+0CH3OH	+1CH3OH(I)	+2CH3OH(I,II)	+3CH3OH(I,II,III)
C2–C3	1.427	1.435	1.443	1.444
C3–C4	1.393	1.382	1.381	1.380
C4–C5	1.416	1.414	1.418	1.418
C5–C6	1.387	1.385	1.384	1.383
C6–C7	1.421	1.420	1.424	1.425
C7–C8	1.451	1.445	1.442	1.441
C7–C9	1.450	1.445	1.447	1.444
C1–C19	1.369	1.373	1.373	1.373
C16–C17	1.371	1.385	1.390	1.390

^aSee atomic labels of AI-BA(4) in Chart 2, and the CH₃OH molecular positions of I, II, and III in Figure 7. Geometries were optimized using the COSMO model in ADF.

The SCRF/VSCRF calculated dipole moment values and vertical excitation energies for these models are given in Table 6. We see that the dipole moment of the solute increases with increasing number of H-bonding solvent molecules. Different models in MeOH produce different absorption energies (E_abs), and the E_abs value increases with increasing numbers of the H-bonding solvent molecules. In reality, the orientation and the number of the H-bonding interactions between the solute and the solvent molecules may vary and be different from our models. However, our calculations here show that the absorption energy of the solute is influenced by the number and patterns of H-bonding interactions. The excitation energy differences we predicted among the different MeOH H-bonding models are not as large as the broadening we observed experimentally. The inhomogeneous broadening includes molecular dynamics effects which we have not taken into account, and homogeneous broadening as well.

Table 6.

SCRF/VSCRF and TDDFT Calculated Absorption (or Excitation) (E_abs) Energies (eV), the Relaxed S₀ State (μ_S0) and Vertical S₁ (μ^v_S1) State Dipole Moments (D) for AI-BA(4) in different H-bonding Models in MeOH (Figure 7), and the Absorption Energy Shifts from C₆H₆ to MeOH Solvents.

Absorption
Model	μS0	μv S1	Eabs		Eabs(MeOH) – Eabs(C6 H6)a
			SCRF/VSCRF	TDDFT	SCRF/VSCRF	TDDFT	Exp
+0CH3OH	28.60	21.60	1.583	2.373	0.172	0.026	0.247
+1CH3OH	31.44	24.03	1.611	2.358	0.200	0.011
+2CH3OH	33.31	25.64	1.631	2.350	0.220	0.003
+3CH3OH	34.63	26.89	1.648	2.353	0.237	0.006

^aThe values of E_abs(MeOH) are the E_abs values given in the table for different models. E_abs(C₆H₆) = 1.411 eV for VSCRF and 2.347 eV for TDDFT, which were given in Table 4.

We note that our calculations correspond to S₀(v = 0) → S₁ vertical transitions. Specifically for absorption, these calculations are performed in the optimal ground state geometry, and the excited state is calculated in the same geometry, assuming the Frank-Condon principle. In reality, the S₀(v = 0) → S₁(v = n) (n is largely unidentified) transitions from a distribution of solute-solvent configurations will result in a large span of excitation energies, which are further broadened by the distribution of H-bonding solvent molecules.

In Table 6, we also compared the SCRF/VSCRF calculated and observed energy difference of E_abs(MeOH) – E_abs(C₆H₆), which represents the blue shift of the absorption band of AI-BA(4) with increasing solvent polarity from C₆H₆ to MeOH. The predicted energy shift gets closer to the experimental value each time we add one, two, and three explicit H-bonding CH₃OH molecules into the quantum region. Especially when considering three H-bonding CH₃OH molecules, our predicted energy shift 0.237 eV is in very good agreement with experimental value of 0.247 eV. Again, we see it is important to take into account the possible explicit H-bonding effects in the SCRF/VSCRF calculations, in order to predict the correct order and reasonable relative excitation energies of the solute molecule in different solvents.

For comparison, we also performed the TDDFT plus COSMO single-point energy calculations on these three COSMO optimized AI-BA(4) structures. Results are also given in Table 6. The current TDDFT plus COSMO calculations yield essentially no difference on the +1, +2, and +3CH₃OH models. Having the explicit H-bonding MeOH molecules with the solute, instead of increasing the blue shift from C₆H₆ to MeOH solvent, TDDFT predicted a decrease of the shift (which was already very small (0.026 eV)), making no difference of the absorption energy of AI-BA(4) in C₆H₆ and in MeOH. The current version of the combination of TDDFT and COSMO in ADF, without modifying the first-order change in the KS potential, is therefore not suitable for solvatochromic studies.

3.4. Fluorescence Spectra of the Dyes

The experimental emission data for the dyes are summarized in Table 7. The SCRF/VSCRF predicted emission energies and the solute dipole moments before and after the vertical emission process are given in Table 8. The dipole moments of AI-BA(4) and AI-SO(4) are further decreased on the S₁ surface after geometry relaxation (in MeOH solution), and then increased during the S₁ → S₀ transition. This is consistent with the blue shifts of the emission bands of AI-BA(4) and AI-SO(4) with increasing solvent polarity from C₆H₆ to MeOH. By contrast, the dipole moment of I-SO further decreases after S₁ state geometry relaxation, and then decreases significantly during the vertical emission process. This is also in agreement with the red shift of the I-SO emission band with increasing solvent polarity from C₆H₆ to MeOH. Similarly to the absorption case, we predicted a negligible red shift (ΔE_em = 0.017 eV) for the emission band of I-TBA with increasing solvent polarity. In reality, there does exist a small red shift from C₆H₆ to DMF (with ΔE_em = 0.020 eV, or Δλ_max = 6nm). The nearly equal emission energy observed in C₆H₆ and MeOH may again result in the explicit interactions between the solute and solvent molecules.

Table 7.

Observed Emission Properties of Dyes 1a, b, 2a-d, 3 and 4.

Solvent	3, I-TBA	4, I-SO	2a, AI-SO(4)	2b, AI-BA(4)	2d, P-SO(4)	1a, P-SO(2)	1b, AI-SO(2)
	λmax/nm (Φa)	λmax/nm (Φ)	λmax/nm (Φ)	λmax/nm (Φ)	λmax/nm (Φ)	λmax/nm (Φ)	λmax/nm (Φ)
MeOH	603 (0.26)	615 (0.08)	665 (0.54)	618 (0.52)	630 (0.018)	529 (0.005)	561 (0.05)
EtOH	-	-	671 (0.82)	651 (0.19)	634 (0.029)	533 (0.008)	563 (0.09)
i-PrOH	-	-	673 (0.96)	652 (0.22)	636 (0.049)	532 (0.014)	565 (0.13)
BuOH	609 (0.61)	618 (0.54)	675 (0.92)	654 (0.29)	640 (0.048)	535 (0.015)	567 (0.16)
OcOH	609 (0.99)	617 (0.98)	679 (0.88)	656 (0.64)	6443(0.082)	536 (0.024)	569 (0.21)
DMF	611 (0.94)	615 (0.97)	673 (~1.0)	658 (0.26)	635 (0.10)	534 (0.025)	567 (0.16)
DMSO	-	-	673 (~1.0)	657 (0.23)	636 (0.067)	535 (0.024)	567 (0.24)
CH3CN	-	-	667 (0.75)	652 (0.05)	632 (0.067)	531 (0.011)	561 (0.06)
CH2Cl2	-	-	681 (0.54)	664 (0.03)	650 (0.082)	541 (0.01)	571 (0.06)
C6H6	605 (0.20)	603 (0.42)	691 (0.19)	670 (0.01)	656 (0.002)	546 (0.004)	577 (0.02)

Table 8.

SCRF/VSCRF Calculated and Experimentally Observed Emission (E_em) Energies (eV), and the Relaxed S₁ State (μ_S1) and Vertical S₀ (μ^v_S0) State Dipole Moments (D) for the Dye Molecules in C₆H₆ and in MeOH.

Emission
Solute	Solvent			μS1	μvS0	Eem
						SCRF/VSCRF	Exp
I-TBA	C6H6			18.21	17.00	1.506	2.050 (605 nm)
	MeOH			23.06	21.61	1.489	2.056 (603 nm)
AI-BA(4)	C6H6			17.27	20.07	1.341	1.851 (670 nm)
	MeOH		+0	19.23	23.91	1.416	2.006 (618 nm)
			+1	21.37	26.57	1.426
			+2	23.17	28.26	1.428
			+3	24.16	29.41	1.432
I-SO	C6H6			16.85	10.55	1.629	2.056 (603 nm)
	MeOH			17.33	15.55	1.537	2.016 (615 nm)
AI-SO(4)	C6H6			18.57	18.15	1.332	1.794 (691 nm)
	MeOH			23.00	23.31	1.381	1.865 (665 nm)

For the emission energy of AI-BA(4) in MeOH, the E_em values also increase with increasing number of the H-bonding solvent molecules. The increment, however, is much less than the corresponding ones in the absorption process. This may also be explained by the smaller change of the dipole moment μ_S1 from one model to another, compared with the corresponding change of μ_S0. This may also be the reason that the width of the emission band in MeOH is not as broad as the absorption band.

3.5. Fluorescence quantum yield

The fluorescence quantum yield (Φ) is determined by the competition between fluorescence and non-radiatiative pathways. Many factors can affect the fluorescence quantum yield, such as, temperature (which influences the intramolecular vibrations, rotations or isomerizations, and the collisions of the solute and solvent, etc.), pH, polarity, viscosity, hydrogen bonding, presence of quenchers, and formation of new complex.⁴⁸

The main nonfluorescent deactivation path for the excited state of Merocyanine 540 (MC 540), which is closely related to our dyes, is photoisomerization around central double bond.^49–51 It was supposed that partial rotation around the double bond in the excited state of MC 540 will result in formation of a perpendicular transition state that collapses to a highly excited vibronic level of the ground state, with consequent thermal dissipation of energy.⁴⁹ Work with structurally similar dyes has established that in a given solvent, the height of the barrier to internal rotation decreases with decreasing bond order of isomerizing bond.⁵⁰

The quantum yield of fluorescence of MC 540 increases with increase in solvent shear viscosity, a trend which is true for dyes 1a–b, 2a–d, 3 and 4 (Table 7), suggesting the importance of photoisomerization for our dyes. It has been previously shown that the rate of photoisomerization of MC 540 can be correlated to solvent polarity. For example, in alcohols the photoisomerization rate is higher than in nitriles with similar viscosities.⁵² This is partly because the hydrogen bonding alcohols better stabilize the twisted excited state of MC 540, which has a substantial zwitterionic character leading to faster photoisomerization.

Since the explicit solute-solvent interactions vary with the solvents, and so many factors will influence the fluorescence and life times, it is not an easy task to predict or analyze the Φ values in each solvent. Here we will analyze the geometric and electronic structures of the dye molecules in C₆H₆ and in MeOH, in order to have an idea how the fluorescence quantum yield changes in general from non-polar to polar solvents, without considering the explicit solute-solvent interactions. There is a striking difference between fluorescence quantum yields in benzene and methanol for dyes AI-SO(4), AI-BA(4) and I-SO, even though these are solvents with similar viscosities (Table 7). For I-SO, we have Φ(C₆H₆) = 0.42 > Φ(MeOH) = 0.08. In contrast, for AI-SO(4), Φ(C₆H₆) = 0.19 < Φ(MeOH) = 0.54. In Table 9, we present the calculated central C-C bond lengths of the relaxed S₁ state for I-SO and AI-SO(4). The molecular orbital plots of the ground state (S₀) HOMO and the S₁ state promoted electron are shown in Figure 8 (for I-SO) and Figure 9 (for AI-SO(4)). For I-SO, after excitation in C₆H₆, the bond lengths of C₂-C₃, C₄-C₅ and C₆-C₇ are lengthened (see Tables 3 and 9), and these three bonds change from bonding to non-bonding, bonding to anti-bonding, and non-bonding to anti-bonding characters, respectively (see Figure 8). Now r(C₄-C₅) = 1.408 Å becomes the longest in the S₁ state. It is therefore very likely that the main photo-isomerization coordinate is the internal rotation of C₄-C₅ for I-SO in C₆H₆ since this is the weakest bond with the greatest single bond character. In MeOH, after excitation, the bond lengths of C₃-C₄ and C₅-C₆ are lengthened, and their bonding characters are changed from non-bonding to anti-bonding (for C₃-C₄) and bonding to non-bonding (for C₅-C₆). Now r(C₃-C₄) = 1.414 Å, and r(C₅-C₆) = 1.410 Å. Both are longer than r(C₄-C₅) in C₆H₆. Also, the central C-C bonds of the S₁ state of I-SO in MeOH have distinct single or double bond character. By contrast, these bonds show very similar distances in C₆H₆ solution. Therefore, the internal rotations around C₃-C₄ and C₅-C₆ for the S₁ state of I-SO in MeOH will be easier than any bond rotations of the S₁ state of I-SO in C₆H₆. This is probably the reason that the fluorescence quantum yield of I-SO in MeOH is smaller than in C₆H₆.

Table 9.

Calculated Central C–C Bond Lengths (Å) of the S₁ State Adiabetic Minimum Dye Molecules in C₆H₆ and in MeOH.

Solvent	Bond	Solute
		I-SO	AI-SO(4)	AI-BA(4)
C6H6	C2–C3	1.400	1.430	1.431
	C3–C4	1.402	1.403	1.400
	C4–C5	1.408	1.412	1.419
	C5–C6	1.396	1.401	1.397
	C6–C7	1.405	1.398	1.415
MeOH	C2–C3	1.393	1.420	1.422
	C3–C4	1.414	1.416	1.413
	C4–C5	1.395	1.399	1.410
	C5–C6	1.410	1.414	1.405
	C6–C7	1.397	1.392	1.414

Figure 8.

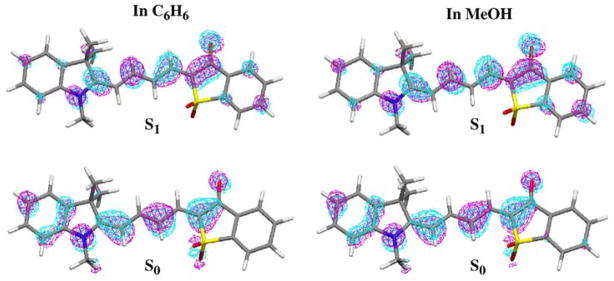
Molecular orbital plots for the electron in HOMO of the S₀ state and the π → π promoted electron in the S₁ state of I-SO in C₆H₆ and in MeOH.

Figure 9.

Molecular orbital plots for the electron in HOMO of the S₀ state and the π → π promoted electron in the S₁ state of AI-SO(4) in C₆H₆ and in MeOH.

For the S₁ state AI-SO(4) in C₆H₆, r(C₂-C₃) = 1.430 Å is obviously longer than other central C-C bonds (Table 9), and its bond character changes from bonding to non-bonding upon excitation (Figure 9). For the S₁ state AI-SO(4) in MeOH, though this bond is still the longest (1.420 Å), it has bonding character (Figure 9) and it is shortened upon excitation (Tables 3 and 9). The other possible rotating bonds are C₃-C₄ and C₅-C₆, which are lengthened after excitation, and their bonding characters change from non-bonding to anti-bonding (for C₃-C₄) and bonding to non-bonding (for C₅-C₆). These two bond lengths r(C₃-C₄) = 1.416 Å and r(C₅-C₆) = 1.414 Å in MeOH are much shorter than r(C₂-C₃) = 1.430 Å in C₆H₆. Therefore, the internal rotation or photo-isomerization for the S₁ state AI-SO(4) around C₂-C₃ in C₆H₆ will be easier than the rotation around C₂-C₃, C₃-C₄ or C₅-C₆ in MeOH, and the fluorescence quantum yield of AI-SO(4) in C₆H₆ is thus lower than that in MeOH. The same reason applies for the lower fluorescence quantum yield of AI-BA(4) in C₆H₆ relative to MeOH (Figure 6).

3.6. Photostability

The photostability of dyes is very important for applications in living cells. We have been studying the mechanism of photobleaching for merocyanines of varying structure.¹⁴ The photostability of the new dyes was characterized by exposing them to constant illumination from a halogen tungsten lamp filtered through glass. This broad spectrum light source provided essentially equal intensity throughout the spectral range where the dyes absorb, and where they would be irradiated in vivo (600–650 nm). Bleaching occurred through intermediate formation of singlet oxygen. Photobleaching rates of the new dyes are compared in Table 10.

Table 10.

Dyes Photobleaching Rates and Reactivity Towards Singlet Oxygen.

Dye	kph*106, s−1 (k ph(rel))a		kr(rel)b
	MeOH	C6H6
2a, AI-SO(4)	89 (261)	128(115)	59.2
2b, AI-BA(4)	68 (200)		25.6
1a, P-SO(4)	28 (82)		60.3
2d, AI-SO(2)	0.7(2.1)		20.3
3, I-SO	0.53 (1.56)	1.11(1.00)	5.24
4, I-TBA	0.34 (1.00)		1.00
Cy5	1.89 (5.56)

^ak_ph = absolute rate of photobleaching, k_ph(rel) = relative rate of photobleaching with respect to standards I-TBA in MeOH and I-SO in C₆H_6.

^bk_r(rel) = relative rates constants for product formation during reaction of the dyes with singlet oxygen produced chemically in DMSO. All measurements were done at 25 °C.

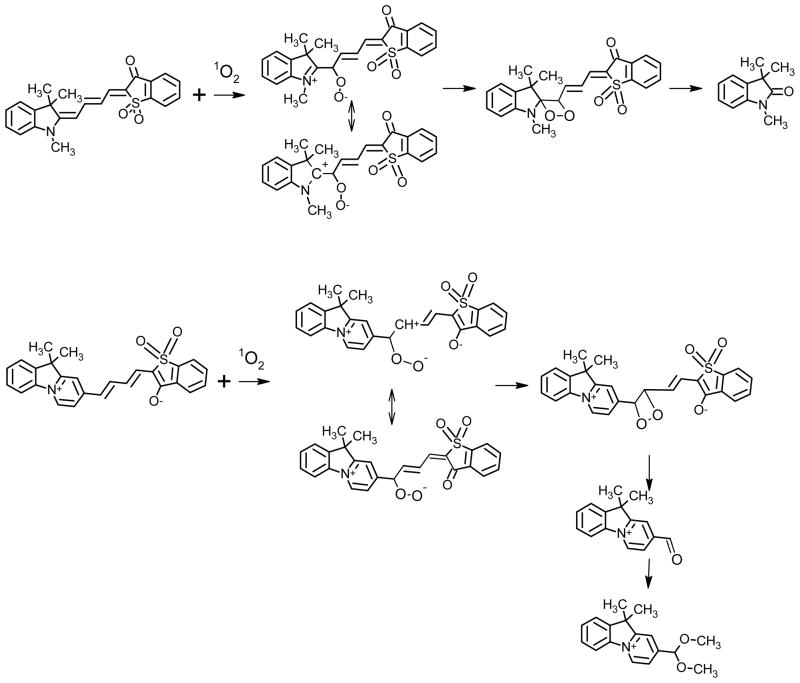
The bleaching rates for the dyes differed by two orders of magnitude. The relative rate constants k_r (rel) for product formation during reaction with singlet oxygen were measured by comparing the percent conversions for dyes dissolved in DMSO containing a fixed amount of ¹O₂ (2.5 mM solutions; ¹O₂ generated by decomposition of 1,4-dimethylnaphtalene-1,4-endoperoxide). The rates were generally higher for dyes with a polar ground state (1a, 2a, 2b, 2d) than for the dyes with their ground state at the “cyanine limit” (3, 4). Careful analysis of reaction mixtures revealed that the major product of dye 3 photooxidation was indol-2-one 10, while the major product of photooxidation of dye 2a is acetal 11 (Figure 10). The detailed analysis of these reactions and reactions products will be published elsewhere. Olefins without allylic hydrogens react with singlet oxygen to form dioxetanes. Dioxetanes are unstable and decompose, to form two carbonyl compounds.

Figure 10.

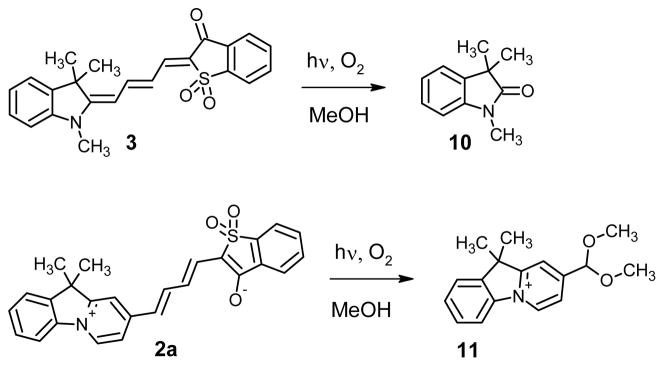
Products of photobleaching reactions of merocyanine dyes.

The mechanism of the reaction can be a concerted [2+2] addition of singlet oxygen or it can be a polar reaction, depending on the olefin structure. Olefins with donor substituents react with singlet oxygen to form dioxetanes via zwitterionic 1,4-dipolar species. Because our dyes have donor substituents (nitrogens) it is likely that the reaction proceeds through a zwitterionic mechanism. (Scheme 2). The incipient reactivity of the dyes will be determined by the extent of negative charge at carbon atom C₃, which is the most negatively charged atom in the dye molecules (Table 11, also see Figure S1 in Supporting Information). One can think of this as a charge-induced dipole interaction between C₃ and ¹O₂. Our calculation showed that this charge is higher for AI-SO(4) and AI-BA(4), which react faster with singlet oxygen.

Scheme 2.

Photooxidation of I-SO and AI-SO(4) dyes.

Table 11.

Calculated Atomic Eletrostatic Potential (ESP) Charges of the Central C atoms of Ground State I-SO, AI-SO(4) and AI-BA(4) in MeOH.

Dyes	C3	C4	C5	C6
I-SO	−0.36	−0.10	−0.36	0.02
AI-SO(4)	−0.40	−0.11	−0.35	−0.02
AI-BA(4)	−0.47	−0.09	−0.32	−0.04

It has been suggested that the initial interaction of ¹O₂ with C=C bonds is a single-atom, end-on interaction.⁴⁰ Previous studies show that the initial stage of the reaction generally proceeds through charge transfer (substrate electron donor ¹O₂ electron acceptor).⁴⁰ Therefore the rates of reaction with ¹O₂ normally increase as the ionization potential of the substrate decreases. We calculated the vertical ionization potentials (ΔE_I) of I-SO, AI-SO(4) and AI-BA(4), and compared them in Table 12. ΔE_I is defined as:

$$\mathrm{\Delta }{E}_{\text{I}}=E^{+}-E_0$$ (1)

where E₀ is the full SCRF energy calculated at the COSMO-optimized geometry of the neutral ground state dye molecule in a certain solvent, and E⁺ is the VSCRF energy for the dye with a positive charge at the same geometry in the same solvent. Clearly, the calculated ionization potentials of AI-SO(4) and AI-BA(4) are lower than the corresponding value of I-SO in both C₆H₆ and MeOH solutions. It is therefore easier for AI-SO(4) and AI-BA(4) to transfer an electron to ¹O₂; AI-SO(4) and AI-BA(4) show much higher photobleaching rates (Table 10) than I-SO, as expected based on the calculated ionization potentials. We also see that ΔE_I(MeOH) > ΔE_I(C₆H₆) for each of the dye molecules. This is consistent with the fact that the experimentally observed photobleaching rates of AI-SO(4) and I-SO are higher in C₆H₆ than in MeOH.

Table 12.

Vertical Ionization Potential ΔE_I (eV) of I-SO, AI-SO(4) and AI-BA(4).

Solvent	Solute
	I-SO	AI-SO(4)	AI-BA(4)
C6H6	6.083	5.953	5.908
MeOH	6.296	6.130	6.234

4. Conclusion

New merocyanine dyes with an enhanced contribution of the zwitterionic ground state resonance form have been prepared through incorporation of a six membered ring in the electron donor portion of the molecule. Positions of the absorption and emission bands for the new dyes strongly depend on solvent polarity. Their photophysical properties were correctly predicted using the SCRF/VSCRF method plus COSMO solvation model. We found that explicit H-bonding solvent interactions were important to include in calculations to predict the correct order of the excitation and emission energies. In contrast to MC540, the new dyes show large fluorescence quantum yields in polar hydrogen-bonding solvents. This can be explained by the DFT results that charge transfer upon excitation produces an excited state with a low contribution from the zwitterionic form. The non-polar excited state is less susceptible to hydrogen bond formation with solvent and consequent non-radiative activation through photoisomerization.

Since the positions of singlet oxygen attack in the dye molecules are predicted (atom C₃), efforts are being made to improve the photostability of these dyes by attaching an electron-accepting group to atom C₃ to inhibit the charge transfer from C₃ to ¹O₂. The cyano-group (C≡N) has been chosen for this purpose and attached to I-SO and S-SO.⁵³ This greatly improved the photostability of the dyes.⁵³ Efforts to improve the photostability of other solvent-sensitive dyes are ongoing. On the other hand, photobleaching of the new dyes can be useful in making powerful phototoxins. It is well known that certain cyanine dyes, such as MC540, are selectively assimilated into leukemia cells, even in the presence of a large excess of healthy cells.^{49,51,54–56} They can be used to detect labelled cells, and then function as potent phototoxins toward the host cells after photobleaching. MC540, however, suffers from its very modest quantum yields of both triplet formation and singlet molecular oxygen generation. There is scope for an increase in cytotoxicity by improving the photophysical properties without significantly changing molecular properties such as selectivity and cellular/tissue localization.⁵⁷