Detection of Correlated Sources in EEG using Combination of Beamforming and Surface Laplacian Methods

Abstract

Beamforming offers a way to estimate the solution to the inverse problem in EEG and MEG but is also known to perform poorly in the presence of highly correlated sources, e.g during binaural auditory stimulation, when both left and right primary auditory cortices are activated simultaneously. Surface Laplacian, or the second spatial derivative calculated from the electric potential, allows for deblurring of EEG potential recordings reducing the effects of low skull conductivity and is independent of the reference electrode location. We show that anatomically constrained beamforming in conjunction with the surface Laplacian allows for detection of both locations and dynamics of temporally correlated sources in EEG. Whole–head 122 channel binaural stimulus EEG data were simulated using a boundary element method (BEM) and realistic geometry forward model. We demonstrate that in contrast to conventional potential–based EEG beamforming, Laplacian beamforming allows to determine locations of correlated source dipoles without any a priori assumption about the number of sources. We also show (by providing simulations of auditory evoked potentials) that the dynamics at the detected source locations can be derived from subsets of electrodes. Deblurring auditory evoked potential maps subdivides EEG signals from each hemisphere and allows for the beamformer to be applied separately for left and right hemispheres.

1. Introduction

Electric potential, measured on the skull surface during electroencephalography (EEG), is generated by extracellular currents that originate from simultaneous activation of large populations of neuronal sources in the cortical gray matter. The task of determining the spatio-temporal dynamics of the neural activity in the cerebral cortex from EEG (or MEG) recordings (the inverse problem) is intrinsically ill-posed due to non-uniqueness of the solution (von Helmholtz, 1853). However, using a spatial filtering method that is relatively new in EEG known as beamforming in combination with additional constraints from electrophysiology and neuroanatomy allows for estimation of the solution to the inverse problem.

A number of MEG and EEG source localization methods have been developed in the past few decades (for review see e.g. (Pizzagalli, 2007)). Beamforming (Frost III, 1972; van Veen et al., 1997; Robinson and Vrba, 1999) is a spatial filtering technique widely used to estimate both locations and dynamics of neural sources without prior knowledge of the number of active sources. There are two major drawbacks of beamforming. First, it requires an accurate forward solution, which is especially important when applied to EEG recordings due to conductivity and anisotropy of the head tissues (Murzin et al., 2011). Second, the performance of beamforming severely degrades if the sources have the same dynamics, e.g. their time-courses of activity are highly correlated within a certain period of time. A classic example of such a situation is auditory evoked potentials under binaural stimulation, where the sources are located in the primary and secondary auditory cortices and are spatio-temporally overlapping (Scherg and Von Cramon, 1985).

Different approaches have been developed in recent years that aim to improve source reconstruction of correlated sources in MEG beamforming, such as nulling beamformer (Hui et al., 2010), coherent source region suppression (Dalal et al., 2006), dual-source beamforming (Brookes et al., 2007) and most recently dual-core beamforming (Diwakar et al., 2011). The software packages BESA (www.besa.de) and FieldTrip (http://fieldtrip.fcdonders.nl) deal with correlated sources in MEG using dynamic imaging of coherent sources (DICS) (Gross et al., 2001), which requires an assumption about the number of sources and/or the location of one of the two sources. While most authors suggest that such methods may also be applied to EEG analysis, to our knowledge correlated sources in EEG beamforming have not previously been addressed perhaps due to inaccuracy of the forward models and the effects of low skull conductivity resulting in spatial smearing (blurring) of the electric potential as it transitions from the brain to the scalp surface.

One of the methods of deblurring EEG is to calculate the second spatial derivative also called the surface Laplacian (SL) (Gevins, 1989; Nunez and Srinivasan, 2006). Shown to be essentially an estimate of the cortical potential and independent of the reference electrode location (Nunez and Srinivasan, 2006), SL allows to increase the spatial resolution of the EEG, but there is no previous work, to our knowledge, that incorporates the Laplacian forward solution in EEG beamforming. Here we provide a novel framework in which SL is used in the LCMV beamforming approach to the inverse problem. The surface Laplacian acts as a deblurring filter and allows for spatial separation of sources which overlap in raw scalp EEG recordings. Moreover, we demonstrate that our method allows to detect the spatio-temporal neural activity of highly correlated sources, such as auditory evoked potentials (AEP).

2. Laplacian Beamforming

Most source localization methods start with the calculation of the forward field (the set of forward solutions) G_Θ - the collection of electric potential distributions at the sensor locations from all individual neural sources Θ in the volume of the brain. Anatomically constrained beamforming is based on calculation of the neural activity index N_a for predefined locations in the brain (explicit derivations are available elsewhere), where the neural activity is typically modeled as dipolar sources constrained to the neocortex and perpendicular to the gray-white matter boundary. Calculation of N_a involves the inverse of the covariance matrix of the measured EEG signal $C_{ij}=\frac{1}{T}{\int }_0^T{X}_i(t)X_j(t)dt$ (where X is the electric potential time series at the electrodes) and the forward field vector G_Θ

$$N_a=\frac{{\mathbf{G}}_{\mathrm{\Theta }}·{\mathbf{C}}^{-1}\mathbf{\Sigma }{\mathbf{C}}^{-1}{\mathbf{G}}_{\mathrm{\Theta }}}{{\mathbf{G}}_{\mathrm{\Theta }}·{\mathbf{C}}^{-1}{\mathbf{G}}_{\mathrm{\Theta }}},$$ (1)

where Σ is the noise covariance matrix.

The forward solution vector G_Θ is calculated using a whole-head 122 electrode EEG array (for explicit details see Murzin et al. (2011)). We use a CT-guided realistic geometry boundary element method, while the brain surface derived from the same subject’s high-resolution MRI scan (Fischl et al., 1999; Dale et al., 1999) serves as an anatomical constraint for source locations and directions.

In the next step, from the electric potential forward solution G_Θ and the time series X we compute the surface Laplacian L_Θ and the Laplacian converted time series X_L. Now beamformer neural activity indices are calculated using

$$N_a=\frac{{\mathbf{L}}_{\mathrm{\Theta }}·{\mathbf{C}}_L^{-1}\mathbf{\Sigma }{\mathbf{C}}_L^{\_1}{\mathbf{L}}_{\mathrm{\Theta }}}{{\mathbf{L}}_{\mathrm{\Theta }}·{\mathbf{C}}_{\mathbf{L}}^{\_1}{\mathbf{L}}_{\mathrm{\Theta }}},$$ (2)

where C_L is the covariance matrix of the Laplacian-treated signal X_L. Covariance matrices C and C_L are close to singular and therefore are non-invertible. To deal with this problem we add a small constant (regularization parameter) to the diagonal of the covariance matrix (Fuchs, 2007).

The source dynamics (reconstructed time series) at source location Θ is computed as the dot product of the signal at the sensors X(t) and the beamformer weights for this location H_Θ

$$X_{\mathrm{\Theta }}^{\mathit{\text{rec}}}(t)={\mathbf{X}}_L(t)·{\mathbf{H}}_{\mathrm{\Theta }}$$ (3)

where the beamformer weights for each Θ are given by

$${\mathbf{H}}_{\mathrm{\Theta }}=\frac{{\mathbf{C}}_L^{-1}{\mathbf{L}}_{\mathrm{\Theta }}}{{\mathbf{L}}_{\mathrm{\Theta }}·{\mathbf{C}}_L^{-1}{\mathbf{L}}_{\mathrm{\Theta }}}.$$ (4)

One important aspect of using the surface Laplacian in place of potential is that taking the second derivative of the potential on the surface results in an activity pattern that is independent of the reference electrode location. The choice of reference has long been debated in the EEG community (Hagemann et al., 2001; Nunez, 2010) and plays an important role in the waveform analysis of EEG/EP/ERP. However, most EEG source estimation techniques, including beamforming, depend only on the topography of the potential maps (Michel et al., 2004). Using the Laplacian instead of potentials as beamformer input bypasses the reference issue and allows greater flexibility in terms of choice of reference for the experimenter.

While surface Laplacian allows to estimate dura potentials and might be the appropriate final step in some EEG studies, the use of MRI-guided brain models of the source space is justified by the ability to distinguish between gyral and sulcal sources and to make use of brain atlases (such as Destreaux atlas in Freesurfer and others) in order to estimate the dynamics of the activity in different cortical structures.

3. Surface Laplacian: computational aspects

Many different approaches on how to compute the surface Laplacian have been developed in the past such as the so-called Hjort Laplacian (Hjorth, 1975), spherical spline (Perrin et al., 1989), finite difference method (Oostendorp and van Oosterom, 1996) and their variations including different spline techniques and inhomogeneous conductors of arbitrary shape. While the choice of method is important when it comes to specific aims of cortical potential estimation, in our settings it is only important to use the same method for Laplacian calculation from both the forward solution and the time series representing the EEG signal. The finite difference method, chosen for our purposes for simplicity, assumes potential values ϕ on a rectangular grid

$$L_{i,j}=\frac{1}{d^2}({\varphi }_{i-k,j}+{\varphi }_{i+k,j}+{\varphi }_{i,j-k}+{\varphi }_{i,j+k}-4{\varphi }_{i,j})$$ (5)

where d represents the distance between the nodes and k is the Laplacian finite element size (discussed below).

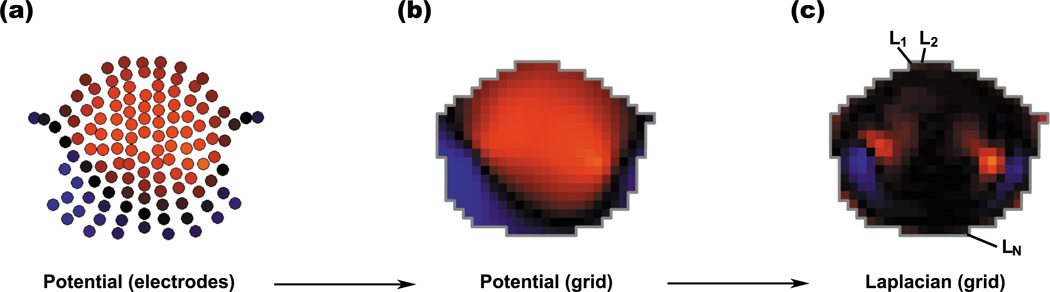
Usually, the EEG electrodes are located on a non-rectangular (placement on a head) grid, prompting for interpolation (Nunez and Srinivasan, 2006). In our work we use a biharmonic spline interpolation (Sandwell, 1987) conveniently implemented in the ’V4’ data gridding method in Matlab. The first step, however consists of a one-time linear interpolation in order to define an area for the spline interpolation as shown in Fig. 1, corresponding to the length of the Laplacian vector L = (L₁, L₂, ..., L_N) for both the forward model and the analyzed EEG time series.

Figure 1.

Computation of surface Laplacian. (a) Electric potential on the scalp electrodes from two single source dipoles, located in the primary auditory cortices, (b) spline interpolation of electric potential on a rectangular grid (c) surface Laplacian calculated from (b) using a finite difference method. The mask is derived from a linear interpolation of the potential on the electrodes (see text for details).

Another important aspect is to choose the interpolation resolution Nand the size of the Laplacian finite element k. Coarse spatial resolution N results in loss of information and large values of N disproportionately increase the computation time of the beamforming algorithm. The size of the finite difference step k in (5) affects how fine or coarse the spatial derivative is. If the step is too small, it will result in overestimation of fine details at the electrode locations. On the other hand if k is too large, it will result in blurring of the current density estimate and increased boundary effects. This notion of small Laplacian (nearest neighbor electrodes) and large Laplacian (next nearest neighbor) was previously addressed by McFarland and colleagues (McFarland et al., 1997) where they concluded that large Laplacian performs better in some situations. In our simulations we have used a grid of 40 × 40, N = 377 and k = 4.

The procedural steps were performed as follows. Brain surfaces (from high resolution T₁ MRI scan using Freesurfer), scalp and skull surfaces (from high resolution CT scan and standard graphical software package) and electrode locations (Polhemus 3D motion tracker) were acquired from a human subject in one of the studies performed in our lab in the past. Coregistration was performed in SPM 5.0 and Matlab. In the next step electric potential forward solutions G_Θ for the cortical sources were computed using a boundary element method (for explicit details see Murzin et al. (2011)), followed by computation of the Laplacian forward solutions L_Θ. EEG time series were simulated using the principle of superposition of electromagnetic fields and by superposing the forward solutions from the intended sources in the primary auditory cortices and randomly positioned dipoles, representing noise. The signal to noise ratio in our simulations is defined as 20 log $\frac{A_S}{A_N}$ , where A_S and A_N are the amplitudes of the signal and the noise respectively and was kept in the range of 12–16 dB. The Laplacian distributions at each time point were then obtained by spline interpolation and equation (5) as described above.

4. Simulations

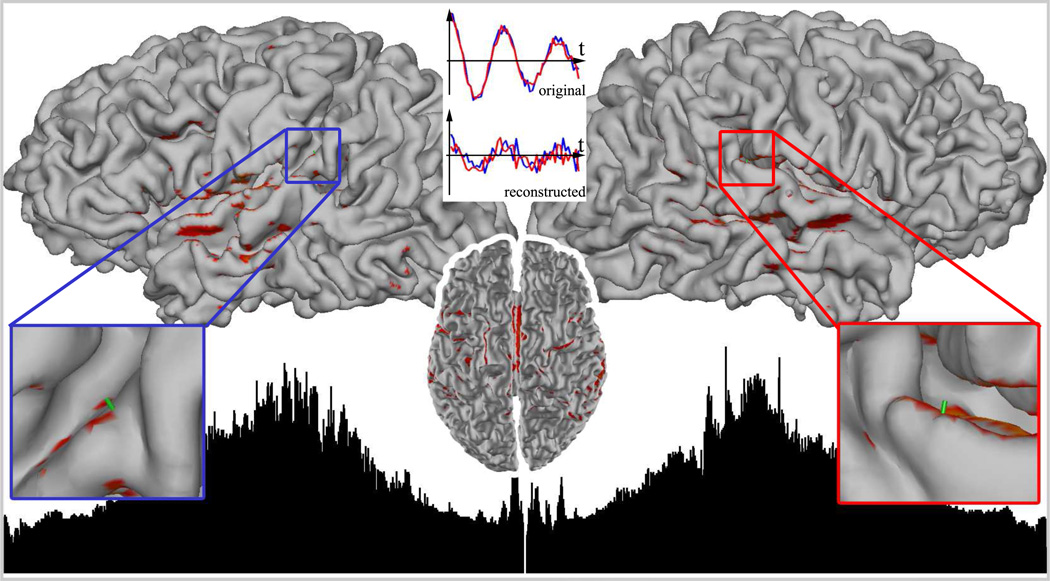
EEG beamforming works well with uncorrelated sources (Murzin et al., 2011), i.e., as long as the time series of any one of the sources cannot be represented as a linear superposition of the rest of them. In real situations, however, there are regions in the brain that are activated simultaneously, for instance, when a subject is exposed to binaural auditory stimuli or makes a movement of two hands (e.g. Banerjee et al. (2012)). In the former case, both left and right primary auditory cortices are active at the same time, and the two areas as sources are spatially distant but temporally correlated. Simulated EEG patterns (whole head, 122 channels), which correspond to the described setup are shown in Figure 2(a). The electric potential distributions, due to the source dipoles being mostly parallel to each other, overlap and reinforce each other. If we apply the potential-based beamforming algorithm (1) to such an EEG data set, the calculated activity index shows a broad area of neural activity in and around temporal lobes as shown in Figure 3.

Figure 2.

Simulated EEG data set and corresponding surface Laplacian: binaural stimulus. The sources are located in the left and right auditory cortices.

Figure 3.

Beamforming activity index calculated from the EEG forward solution is shown in black (arbitrary units) below the subjects’ brain surfaces (arranged left to right: left hemisphere anterior to posterior, right hemisphere posterior to anterior) and is also plotted color-coded on the cortical surface with the threshold of 3 standard deviations. Two highly correlated sources are located in the primary auditory cortices. The results indicate that the neural activity is detected as originating from an area around and between the auditory cortices. The top middle insert shows the simulated and reconstructed time series of the 2 correlated sources.

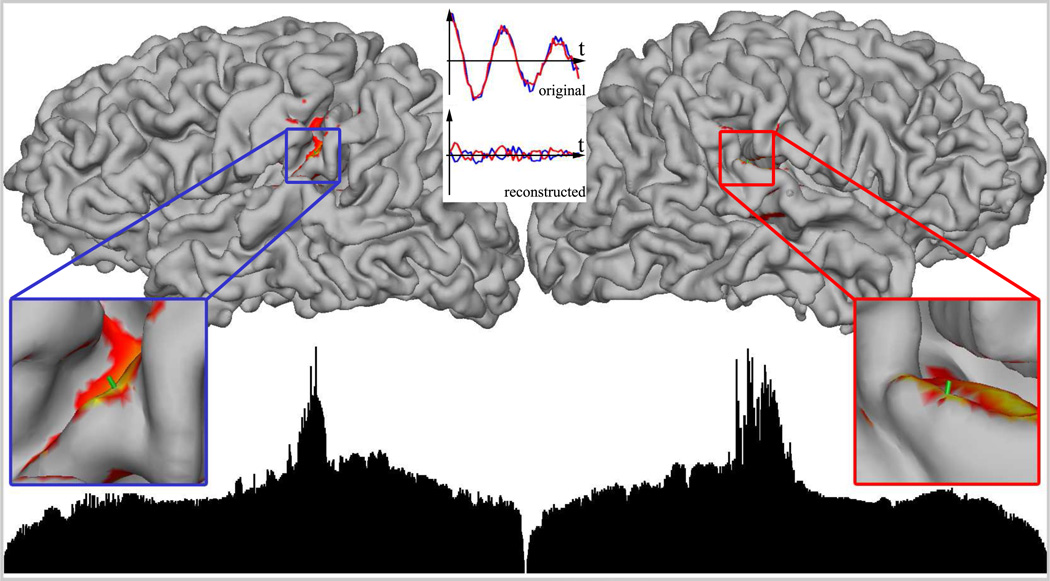
Figure 2(b) shows the surface Laplacian calculated from the simulated EEG data set. As shown in detail in Appendix A, the surface Laplacian allows one to estimate the cortical potential (eqn. A.10). The two areas of activity are now visually distinguishable. The surface Laplacian of each of the forward solutions corresponding to a unique location and direction on the cortical surface is calculated in order to apply the beamforming algorithm. The beamformer weights are obtained the same way as before, but using the values of the surface Laplacian instead of the electric potential as time series X(t). The results are shown in Figure 4. Two areas of strong activity, one in each hemisphere, are now detected, and when plotted on the cortical surface, reveal locations in the primary auditory cortices. Localization errors can be estimated by calculating the distance between the simulated source location and the ”center of mass” of the cortical locations crossing a certain threshold of the values of the neural activity index. The average error from 100 simulations for the potential beamforming was found to be 28 ± 6mm and for the Laplacian beamforming 9 ± 8mm. The higher variability in the latter case is due to increased sensitivity of the Laplacian to the noise in the model.

Figure 4.

Beamforming activity index calculated using the surface Laplacian derived from the EEG forward solution. Now the detected neural activity is localized near the auditory cortices. Notably the reconstructed time series (top middle insert) does not reproduce the simulated dynamics.

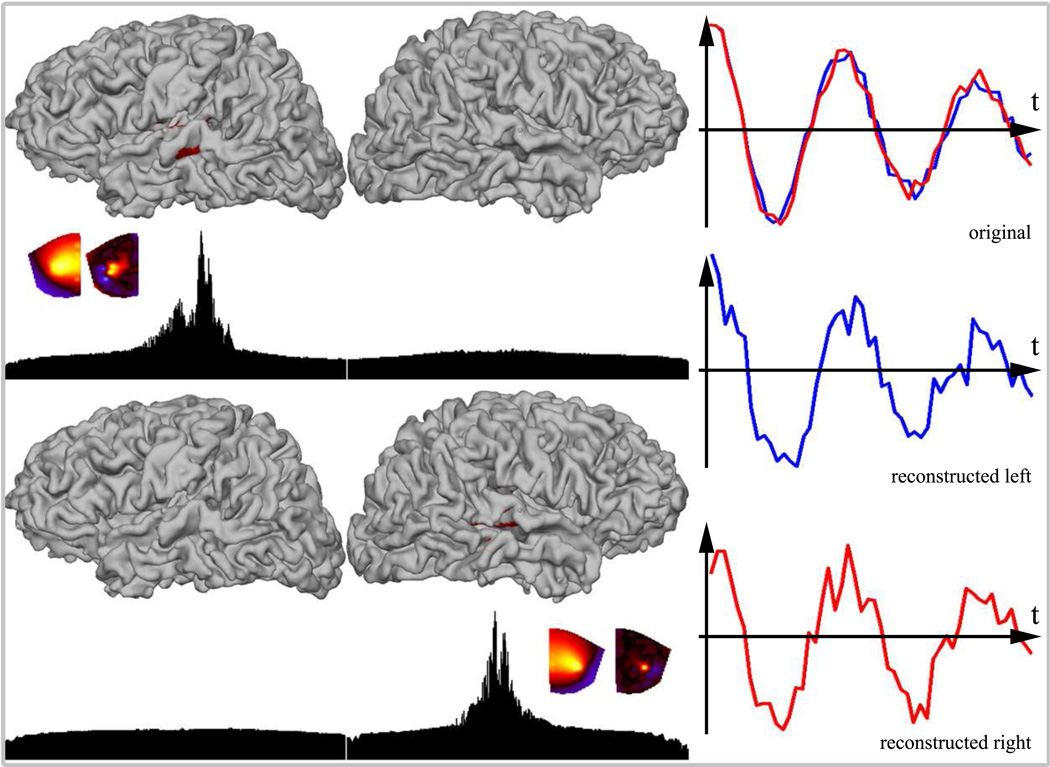
The reconstructed time series, however, are extremely noisy and do not match the original activation as shown in Figure 4 (top center). Since neural activity in the auditory cortices is highly correlated, the beamforming analysis (based on covariance) fails to return the oscillatory behavior of the sources (Figure 4). To determine the dynamics at the source locations in AEP simulations, we subdivide the electrode space into two arrays corresponding to the left and right hemisphere, which leads to two sets of forward solution matrices L_Θ. While the sensor space is divided, the source space for each simulation is still the whole brain, i.e. the neural activity index is calculated for locations in both hemispheres based on the electrodes over the left hemisphere in the first step and the right hemisphere in the second step. This procedure is applied to both hemispheres and the results are shown in Figure 5. The time series corresponding to the sources in the left and right hemisphere are shown in blue and red, respectively. The middle and bottom graphs on the right in Figure 5 show how the time courses are reconstructed when only half of the sensors are used in the beamforming analysis: left source activity (blue) is accurately reproduced as shown in the middle and the red curve in the bottom graph corresponds to the dipole in the right hemisphere.

Figure 5.

Beamforming activity index and reconstructed time courses calculated using surface Laplacian from two subsets of EEG sensors over the left or right hemisphere. This allows to estimate the dynamics at the source locations which was not possible when beamforming was applied to the whole-head EEG.

5. Conclusions

Here, we proposed and theoretically investigated a novel method to detect temporally correlated sources in EEG by using the surface Laplacian in LCMV beamforming. The second spatial derivative of the potential, or surface Laplacian, one of the popular deblurring tools for EEG, is suggested to be used in place of the electric potential in the beamforming algorithm. Our simulations show that it is possible to not only correctly detect the source locations but also to reconstruct the corresponding time series by using partial sensor arrays.

LCMV beamforming is based on suppressing interference from everywhere else but the point of interest Θ If there are locations in the source space that share the time course of activity with Θ, then the beamformer outputs contain leakages from Θ to other correlated locations and may lead to errors in the amplitude and time course estimates (Sekihara et al., 2002). Belardinelli and colleagues have recently performed an MEG phantom study (Belardinelli et al., 2012) where it was shown that LCMV is able to detect two distant (more than 3cm apart) highly correlated (95%) sources in a realistic noise environment even though such high levels of correlation negatively affect power and spatial blurriness of the reconstructed sources. In our simulations of auditory evoked potentials we demonstrate that it is possible to localize the sources also in EEG, but only with a key additional step, namely spatial de-blurring. The surface Laplacian allows one to spatially separate the potential distributions originating from the auditory cortices and apply beamforming to estimate source locations. In order to estimate the time-courses of the sources in question, we use partial sensor arrays, corresponding to left and right hemispheres.

Although our suggested method may best be implemented with averaged EEG, such as evoked and event-related potentials, application to raw EEG is also possible in the case of clean EEG signals. For example, since an auditory response from a brief stimulus is relatively strong, it can be captured in single-trial EEG. What may be a good strategy in EP/ERP studies is to perform source estimation from windowed raw EEG, followed by calculation of the average of the neural activity index. This is a subject for future research.

Highlights.

We present a novel method to detect temporally correlated sources in EEG by using the surface Laplacian in LCMV beamforming.

EEG data were simulated using a boundary element method (BEM) and realistic geometry forward model.

We validate the method by applying it to the well known problem of source reconstruction under binaural auditory stimulation.

Appendix A. Surface Laplacian: physical meaning

EEG measurements are known to produce blurry images due to low skull conductivity, greatly affecting the overall accuracy of source reconstruction. One way to deal with this problem is to calculate the surface Laplacian or second spatial derivative of the scalp potential with respect to the two surface coordinates (Gevins, 1989; Nunez and Srinivasan, 2006). The physical meaning of the surface Laplacian (Nunez et al., 1994) can be derived starting from the general form of Maxwell’s equations for the electric field E and magnetic field B

$$\begin{array}{cc}\text{curl}\mathit{E}=-\frac{1}{c}\frac{\partial \mathit{B}}{\partial t}\hfill & \text{curl}\mathit{B}=\frac{1}{c}\frac{\partial \mathit{E}}{\partial t}+\frac{4\pi }{c}\mathit{j}\hfill \\ \text{div}\mathit{E}=4\pi \rho \hfill & \text{div}\mathit{B}=0\hfill \end{array}$$ (A.1)

where j is the current density and ρ is the electric charge density. Assuming that the electromagnetic fields are changing slowly (f < 10² Hz), so that the time-derivatives in (A.1) are negligible¹, we obtain the quasi-static approximation

$$\begin{array}{cc}\text{curl}\mathit{E}=\mathbf{0}\hfill & \text{curl}\mathit{B}=\frac{4\pi }{c}\mathit{j}\hfill \\ \text{div}\mathit{E}=4\pi \rho \hfill & \text{div}\mathit{B}=0\hfill \end{array}$$ (A.2)

As the curl of the electric field vanishes, E can be written as the negative gradient of a potential function ϕ

$$\mathit{E}=-\text{grad}\varphi =-\nabla \varphi$$ (A.3)

which leads to

$$\nabla \times \nabla \varphi =\mathbf{0}\text{and}\nabla ·\nabla \varphi =-4\pi \rho$$ (A.4)

where ▽ ▽ ϕ = ∆ϕ is the Laplacian of the potential. The second equation in (A.4) is the well-known Poisson equation

$$\mathrm{\Delta }\varphi (\mathit{x},\mathit{y},\mathit{z})=-4\pi \rho (\mathit{x},\mathit{y},\mathit{z})$$ (A.5)

which states that the Laplacian of the electric potential at every point in space is proportional to the electric charge density at this point. This means that the Laplacian is a physical quantity in contrast to the electric potential, which depends on the reference used. Now we consider the three-dimensional Laplacian in spherical coordinates

$$\mathrm{\Delta }\varphi (r,\theta ,\phi )=\frac{1}{r^2}\left[\frac{\partial }{\partial r}\right(r^2\frac{\partial \varphi }{\partial r})+\frac{1}{\text{sin}\theta }\frac{\partial }{\partial \theta }(\text{sin}\theta \frac{\partial \varphi }{\partial r})+\frac{1}{{\text{sin}}^2\theta }\frac{{\partial }^2\varphi }{\partial {\phi }^2}]$$

where we can distinguish between the first term inside the square brackets as the radial part ∆_r and the other two terms as the tangential part ∆_θφ

$$\mathrm{\Delta }\varphi (\mathit{r},\theta ,\phi )={\mathrm{\Delta }}_{\mathit{r}}\varphi +{\mathrm{\Delta }}_{\theta \phi }\varphi =-4\pi \rho (\mathit{r},\theta ,\phi )$$ (A.6)

Since there is no free charge on the surface of the conducting volume (scalp), the charge density ρ(r,θ, φ) vanishes and it follows that

$$\rho (\mathit{r},\theta ,\phi )=\Rightarrow {\mathrm{\Delta }}_r\varphi =-{\mathrm{\Delta }}_{\theta \phi }\varphi$$ (A.7)

The tangential part of the Laplacian ∆_θφϕ can be calculated from surface measurements of the electric potential. Its radial part is given by

$${\mathrm{\Delta }}_r\varphi =\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial \varphi }{\partial r}\right)=\frac{1}{r^2}[2r\frac{\partial \varphi }{\partial r}+r^2\frac{{\partial }^2\varphi }{\partial r^2}]=\frac{2}{r}\frac{\partial \varphi }{\partial r}+\frac{{\partial }^2\varphi }{\partial r^2}$$ (A.8)

The gradient of the potential in the radial direction $\frac{\partial \varphi }{\partial r}$ is the radial part of the electric field E_r, and since the electric field, according to Ohm’s law, is proportional to the current density (j =σ E), it follows that

$$\frac{\partial \varphi }{\partial r}~j_r$$ (A.9)

The second derivative $\frac{{\partial }^2\varphi }{\partial r^2}$ in (A.8) can be neglected due to the fact that the electric potential in a homogeneous conductor falls off linearly, leading to

$${\mathrm{\Delta }}_r\varphi ~j_r$$ (A.10)

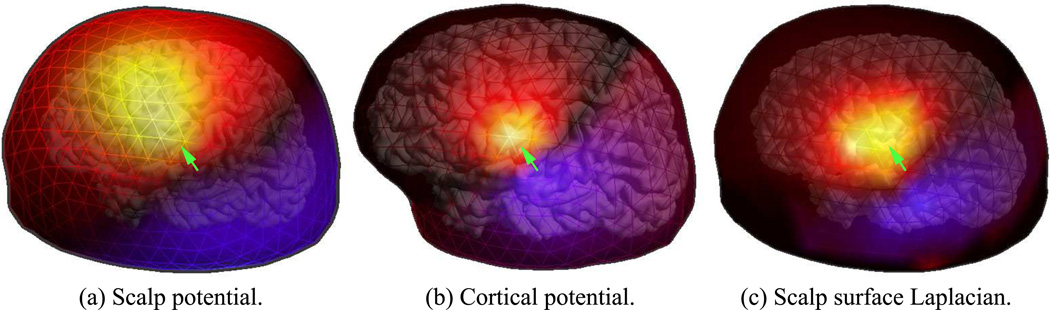
i.e. the radial part of the Laplacian is proportional to the radial component of the current density, which represents currents entering or leaving the surface of the scalp (current sources and sinks). Figure A.6 shows a comparison between the negative of the surface Laplacian, and the electric potential (forward solution) calculated on the scalp (a) and on the cerebrospinal fluid (b), the latter representing the cortical potential. The surface Laplacian (c) is localized similarly to the cortical potential and can serve as its estimate.

Figure A.6.

Surface Laplacian derived from the electric potential on the scalp is an estimate of the electric current density or cortical potential. (a) Electric potential on the scalp surface from a single source dipole, located in the left primary auditory cortex, (b) electric potential on the cerebrospinal fluid surface from the same source, (c) negative of the surface Laplacian calculated from (a).