Abstract
The Brownian motion of a nanoparticle in an incompressible Newtonian fluid (quiescent or fully developed Poiseuille flow) has been investigated with an arbitrary Lagrangian-Eulerian based finite element method. Results for the motion in a compressible fluid medium are estimated. Thermal fluctuations from the fluid are implemented using a fluctuating hydrodynamics approach. The instantaneous flow around the particle and the particle motion are fully resolved. Carriers of two different sizes with three different densities have been investigated (nearly neutrally buoyant). The numerical results show that (a) the calculated temperature of the nearly neutrally buoyant Brownian particle in a quiescent fluid satisfies the equipartition theorem; (b) the translational and rotational decay of the velocity autocorrelation functions result in algebraic tails, over long time; (c) the translational and rotational mean square displacements of the particle obeys Stokes-Einstein and Stokes-Einstein-Debye relations, respectively. Larger the particle, longer the time taken to attain this limit; and (d) the parallel and perpendicular diffusivities of the particle closer to the wall are consistent with the analytical results, where available.
1 INTRODUCTION
The major motivation for the present study is the simulation of a nanoparticle thermal motion in a fluid flow that occurs in targeted drug delivery where the drug carrying nanocarriers are intravascularly introduced into the vasculature. Nanoparticles allow more precise and successful infiltration of drugs to target cells. In general, nanoparticle drug-delivery systems have been shown to enhance the solubility of compounds, and to reduce the impact of drugs on non-target tissue, thereby eliminating unwanted and dangerous side effects. In order to more broadly integrate this technology into medicine, a precise understanding of how to guide the nanoparticle to the target site is necessary. To achieve this goal, as a first step, it is necessary to determine the motion of a nanocarrier (due to thermal and hydrodynamic effects) in a fluid medium.
A nanoparticle suspended in a fluid undergoes random motion due to the thermal fluctuations in the fluid. As a consequence, translational and rotational degrees of freedom become important. In determining the translational and rotational motions of the nanoparticle in an incompressible Newtonian medium, there exist two methods that couple the thermal fluctuations with the hydrodynamic interactions. These are the generalized Langevin method [1] and the fluctuating hydrodynamics method [5]. Either procedure would require numerical simulations for covering extensive parameter space. Over the years, many numerical simulation schemes, such as the finite volume method, Lattice-Boltzmann method, and stochastic immersed boundary method have been employed for this purpose. In the present study, the fluctuating hydrodynamics approach is considered. This essentially consists of adding stochastic stresses to the stress tensor (random stress) in the momentum equation and stochastic fluxes to the heat flux where an energy equation is present in the formulation. The fluctuating hydrodynamic equations for the fluid coupled with the equations of motion for the nanoparticle result in the description of the Brownian motion of a nanoparticle in a fluid [5].
In this paper, a direct numerical simulation adopting an arbitrary Lagrangian-Eulerian based finite element method is employed to simulate the Brownian motion of a nanoparticle in an incompressible Newtonian fluid contained in a horizontal micron sized circular tube. Both translational and rotational motions of a nanoparticle in a (i) stationary fluid medium, and (ii) Poiseuille flow are investigated. The results for the attainment of thermal equilibrium between the particle and the surrounding medium, diffusivity for the particle in the medium, effect of the presence of the confining vessel wall on particle displacement and diffusivity are evaluated and discussed in detail. The result as appropriate to a compressible fluid medium are also reported.
2 THEORETICAL FORMULATION
The Brownian motion of a nanoparticle in an incompressible Newtonian fluid contained in a horizontal circular vessel is considered. The fluid and particle equations are formulated in an inertial frame of reference with the origin coinciding with the center of the vessel. The diameter, D, and the length, L, of the vessel (tube) are very large compared to the particle size, d, the diameter of the particle. Two different cases for the fluid medium are considered: a fluid at rest in a cylindrical vessel, and a fully developed Poiseuille flow in a circular tube. Initially, a nanoparticle is introduced either at the vessel (tube) centerline or at suitably chosen locations away from the center line towards the bounding wall. In the numerical simulation for Poiseuille flow, the particle is initially fixed at the starting location and the flow is allowed to evolve until the flow is fully developed in the entire domain. Then the particle is released and allowed to move (see, [5]). This way, the velocity profiles in the flow cases are fully developed in the domain of interest and calculations are effected in the fully developed regime. No body force is considered either for the particle or for the fluid domain. At time t = 0, the nanoparticle is subjected to Brownian motion in each case. The motion of the nanoparticle is determined by the hydrodynamic forces and torques acting on the particle and the wall interactions.
The motion of an incompressible Newtonian fluid satisfies the conservation of mass and momentum given by
| (1) |
| (2) |
where U and ρ(f) are the velocity and density of the fluid, respectively, σ is the stress tensor, p is the pressure, J is the identity tensor, and μ is the dynamic viscosity. The random stress tensor S is assumed to be a Gaussian with
| (3) |
where 〈 〉 is the ensemble average, kB is the Boltzmann constant, T is the absolute temperature, δij is the Kronecker delta, and the Dirac delta function δ(x − x′) denotes that the components of the random stress tensor are spatially uncorrelated (Markovian). The right hand side of equation (3) shows that the mean and variance of the thermal fluctuations are chosen to be consistent with the fluctuation-dissipation theorem [2, 3] for an incompressible fluid.
For a rigid particle suspended in an incompressible Newtonian fluid, the translational and rotational motions of the particle satisfies Newton’s second law and the Euler equation, respectively,
| (4) |
where m is the mass of the particle, I is its moment of inertia, and, U and ω are the translational and angular velocities of the particle, respectively. The hydrodynamic force F and torque T acting on the particle are given by
| (5) |
where X is the position of the centroid of the particle, (x − X) is a vector from the center of the particle to a point on its surface, ∂Σp denotes the particle surface, and n̂ is the unit normal vector on the surface of the particle pointing into the particle.
The initial and boundary conditions for the problem are
| (6) |
| (7) |
| (8) |
where up is the prescribed velocity (zero or fully developed Poiseuille flow inlet profile), Σ0 is the domain occupied by the fluid and ∂Σi and ∂Σo are the inlet and outlet boundaries, respectively. The stochastic governing equations (1) – (5) along with the initial and boundary conditions (6) – (8) are solved numerically. It is assumed that there is no body torque acting at any point in the fluid and the viscous stress tensor, σ, is symmetric. A numerical simulation at a mesoscopic scale involving a particle in a fluid could be based on a discretization of the equations (1) – (8). However, the discrete forms have to satisfy the fluctuation-dissipation theorem [4]. The details of the finite-element spatial and temporal discretization, and, mesh movement algorithm are discussed in [5].
3 RESULTS AND DISCUSSION
A solid spherical particle of radius a = 200nm or 300nm is initially placed at the center of a cylindrical tube (R = 5μm) containing a Newtonian fluid. Both, quiescent and fully developed Poiseuille flows are considered. The computational domain moves with the particle, and from the particle location, the ends of the computational domain are at a distance of 20a at any instant of time [5]. The physical parameters chosen are: kB = 1.3806503 × 10−23 kgm2/s2K; μ = 10−3 kg/ms; ρ(f) = 103 kg/m3; and three particle densities in the range, 990kg/m3 ≤ ρ(p) ≤ 1010 kg/m3. The temperature of the fluid is initially set to Tp = 310K and the particle at zero degrees. The maximum fluid velocity for Poiseuille flow presented in this study is Umax = 10mm/s, relevant to some biological applications. For this Umax, the flow Reynolds number, Ref = ρ(f)RUmax/μ = 5 × 10−2 and the particle Reynolds number, Rep = ρ(f)aUmax/μ = 2.5 × 10−3.
The different time scales involved in this study are: (i) hydrodynamic time scale, τv = a2/v; Brownian time scales, (ii) τb = m/ζ(t) and (iii) τd = a2ζ(t)/kBT. Here, v is the kinematic viscosity and ζ(t) = 6πμa is the Stokes dissipative friction force coefficient for a sphere. It is required that the time step for the numerical simulation Δt be smaller than the smallest of all the physical time scales. The simulations presented in this study have been carried out for long enough durations to allow for the temperature of the particle to equilibrate - i.e., if N is the number of simulated time steps then N · Δt = t ? τv. The number of time steps depends upon equilibration of particle temperature, or determination of velocity autocorrelation functions (VACFs) and mean square displacements (MSDs). In order to ensure the uniqueness of the realizations, different initial seeds are chosen for a Gaussian random number generator. To account for compressibility effects, the particle mass m is augmented by an added mass m0/2, M = m + m0/2, where m0 is the mass of the displaced fluid [6].
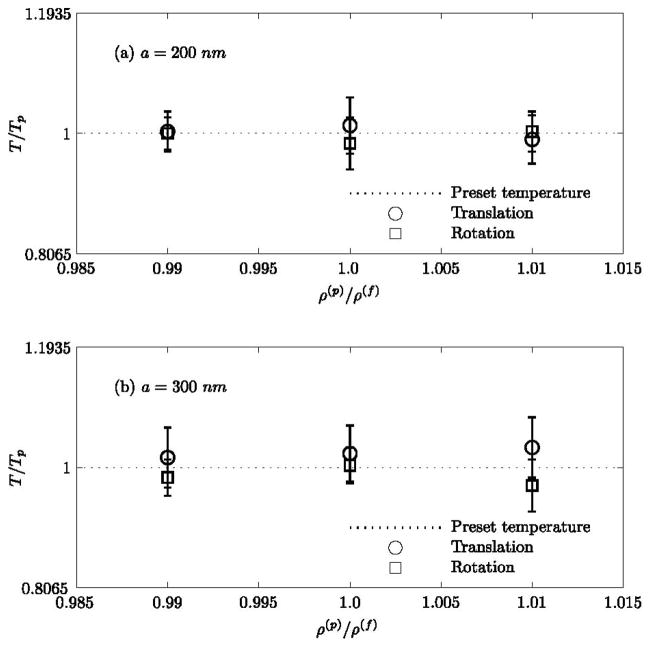
Figure 1 shows that translational and rotational temperatures of nearly neutrally buoyant Brownian particles, thermally equilibrated, in a quiescent fluid medium are independent of the density of the particle in relation to that of fluid. The error bars have been plotted from standard deviations of the temperatures obtained with 15 different realizations.
Figure 1.
Translational and rotational temperatures of a nearly neutrally buoyant nanoparticle in a stationary fluid medium as a function of the particle density normalized with fluid density.
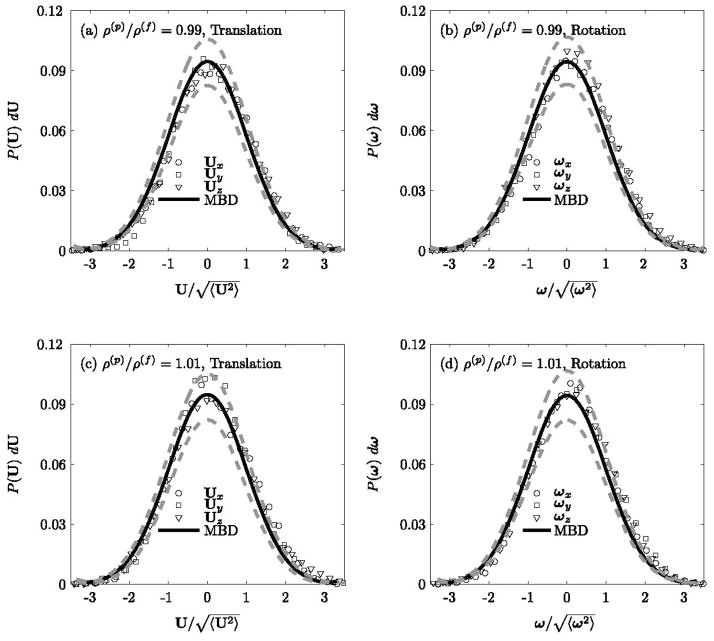
Figure 2 shows the numerically simulated components of (U − Ū) (Figure 2(a),(c)) and (ω − ω̄) (Figure 2(b),(d)) (represented by three different symbols) of the nanoparticle (a = 200nm) are compared with the analytical Maxwell-Boltzmann distribution (MBD) with a zero mean and variance of kBT/M and kBT/I, respectively. It is observed that each degree of freedom individually follows MBD within 5% error (see dotted line in Figure 2). This validates the numerical procedure employed in this study.
Figure 2.
Equilibrium probability of the (a) translational and (b) rotational velocities of the nanoparticle (a = 200nm) in a stationary fluid medium for ρ(p)/ρ(f) = 0.99 and 1.01.
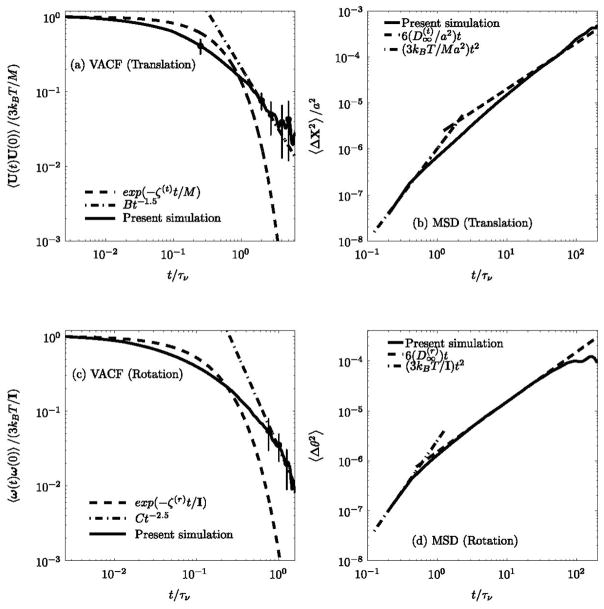
Figures 3 (a) and (c) show the numerically obtained translational and rotational VACFs of a nearly neutrally buoyant nanoparticle (a = 300nm) in a quiescent fluid medium. It is observed that the translational and rotational VACFs of the Brownian particle have power-law decays, Bt−3/2 and Ct−5/2, respectively, over long times, where B = M ρ(f)1/2/12π3/2μ3/2 and C = Iρ(f)3/2/32π3/2μ5/2. The error bars have been plotted from standard deviations of the decay at particular time instants obtained with 15 different realizations.
Figure 3.
Translational and rotational VACFs and MSDs of a nanoparticle particle of radius a = 300nm and ρ(p)/ρ(f) = 0.99 in a stationary fluid medium.
Figures 3 (b) and (d) show the numerically obtained translational and rotational MSDs of nearly neutrally buoyant nanoparticle (a = 300nm) in a quiescent fluid medium, initially placed at the center of the vessel (R = 5μm), for both short and long times. It is observed that in the regime where the particle’s motion is dominated by its own inertia (ballistic), the translational and rotational motions of the particle follow (3kBT/M)t2 and (3kBT/I)t2, respectively. In the diffusive regime, t ? τb, the translational and rotational MSDs increase linearly in time to follow (Stokes-Einstein relation) and (Stokes-Einstein-Debye relation), respectively, where , and are the translational and rotational self-diffusion coefficients.
Tables 1 and 2 respectively show the numerically obtained translational and rotational, ballistic and diffusive regimes for various size of nanoparticle. It is observed that higher the radius of the particle, longer the time taken by the translational and rotational motion of the particle to attain the Stokes-Einstein and Stokes-Einstein-Debye limits, respectively, in the diffusive regime.
Table 1.
Translational ballistic and diffusive regimes for different size of particles.
| a | Ballistic regime | Diffusive regime |
|---|---|---|
| 200nm | 0.107 ≤ t/τv ≤ 0.178 | t/τv ≥ 5.98 |
| 300nm | 0.251 ≤ t/τv ≤ 0.501 | t/τv ≥ 19.95 |
Table 2.
Rotational ballistic and diffusive regimes for different size of particles.
| a | Ballistic regime | Diffusive regime |
|---|---|---|
| 200nm | 0.045 ≤ t/τv ≤ 0.1 | t/τv ≥ 0.8 |
| 300nm | 0.214 ≤ t/τv ≤ 0.428 | t/τv ≥ 2.8 |
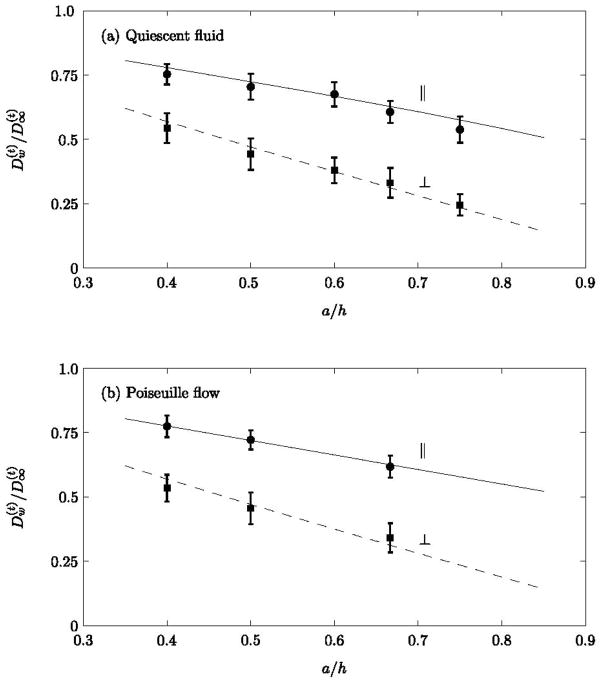
Figure 4 shows the numerically obtained parallel (x direction) and perpendicular (y direction) MSDs of nearly neutrally buoyant particles of different radii initially placed at various distances, h, from the tube wall, both in a quiescent medium and in a Poiseuille flow.
Figure 4.
The translational diffusion coefficient of nearly neutrally buoyant Brownian particles of different radii a initially placed at different locations h from the wall of the circular vessel in a quiescent medium. Solid and dashed lines correspond to the perturbation solutions given in [7].
It is observed that for a given particle of radius a, the diffusivity of the particle decreases closer to the wall (i.e., as h → 0, Dw/D∞ decreases). Similarly, for a given location of the particle from the wall, h, the diffusivity of the particle decreases for the larger particle (i.e., as a increases).
Acknowledgments
This work was sponsored by National Institute of Health (NIH) Grant R01 EB006818 (D.M.E.); National Science Foundation (NSF) Grant CBET-0853389. Computational resources were provided in part by the National Partnership for Advanced Computational Infrastructure under Grant No. MCB060006.
References
- 1.Uma B, Swaminathan TN, Ayyaswamy PS, Eckmann DM, Radhakrishnan R. Generalized Langevin dynamics of a nanoparticle using a finite element approach: Thermostating with correlated noise. The Journal of Chemical Physics. 2011;135:114104. doi: 10.1063/1.3635776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Landau LD, Lifshitz EM. Fluid Mechanics. Pergamon Press; London: 1959. [Google Scholar]
- 3.Hauge EH, Martin-Löf A. Fluctuating hydrodynamics and Brownian motion. Journal of Statistical Physics. 1973;7(3):259–281. [Google Scholar]
- 4.Serrano M, Gianni DF, Español P, Flekkøy EG, Coveney PV. Mesoscopic dynamics of Voronoi fluid particles. Journal of Physics A: Mathematical and General. 2002;35(7):1605–1625. [Google Scholar]
- 5.Uma B, Swaminathan TN, Radhakrishnan R, Eckmann DM, Ayyaswamy PS. Nanoparticle Brownian motion and hydrodynamic interactions in the presence of flow fields. Phys Fluids. 2011;23:073602. doi: 10.1063/1.3611026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Huang R, Chavez I, Taute KM, Lukic B, Jeney S, Raizen MG, Florin E. Direct observation of the full transition from ballistic to diffusive Brownian motion in a liquid. Nature Physics. 2011;7:576–580. [Google Scholar]
- 7.Happel J, Brenner H. Low Reynolds number hydrodynamics. Martinus Nijhoff Publishers; The Hague, Netherlands: 1983. [Google Scholar]