A Tutorial on Rank-based Coefficient Estimation for Censored Data in Small- and Large-Scale Problems

Abstract

The analysis of survival endpoints subject to right-censoring is an important research area in statistics, particularly among econometricians and biostatisticians. The two most popular semiparametric models are the proportional hazards model and the accelerated failure time (AFT) model. Rank-based estimation in the AFT model is computationally challenging due to optimization of a non-smooth loss function. Previous work has shown that rank-based estimators may be written as solutions to linear programming (LP) problems. However, the size of the LP problem is O(n² + p) subject to n² linear constraints, where n denotes sample size and p denotes the dimension of parameters. As n and/or p increases, the feasibility of such solution in practice becomes questionable. Among data mining and statistical learning enthusiasts, there is interest in extending ordinary regression coefficient estimators for low-dimensions into high-dimensional data mining tools through regularization. Applying this recipe to rank-based coefficient estimators leads to formidable optimization problems which may be avoided through smooth approximations to non-smooth functions. We review smooth approximations and quasi-Newton methods for rank-based estimation in AFT models. The computational cost of our method is substantially smaller than the corresponding LP problem and can be applied to small- or large-scale problems similarly. The algorithm described here allows one to couple rank-based estimation for censored data with virtually any regularization and is exemplified through four case studies.

1 Introduction

Survival analysis is a ubiquitous concept in statistics and widely used in biomedical, clinical, and reliability studies. Various semiparametric models and estimators have been proposed for survival analysis. Cox’s proportional hazards model (Cox, 1972), for example, has been studied extensively for four decades and is widely used partly due to its ease of computation. While the accelerated failure time (AFT) model (Cox and Oakes, 1984; Kalbeisch and Prentice, 1980) is, as suggested by Sir David Cox, “in many ways more appealing because of its quite direct physical interpretation” as compared to the more popular proportional hazards model (Reid, 1994), it has not been adopted in practice because of theoretical and computational challenges. Over the past several years, there have been technical and computational advances in this area and we build on this work to present a strategy for simultaneous coefficient estimation and variable selection. The current paper provides a detailed account of a fitting algorithm applied to regularized rank-based coefficient estimation in the semiparametric AFT model for both small- and large-scale problems; that is, where the dimension of the predictors can be smaller or larger than the sample size.

The AFT model asserts that the natural logarithm of the survival endpoint T_i is linearly related to explanatory variables, i.e.,

$$\text{log }{T}_i={\mathbf{x}}_i^{\top }\mathit{\beta }+{\zeta }_i,(i=1,\dots ,n),$$ (1)

where x_i is a p-vector of fixed predictors for the ith subject, β is a p-vector of regression coefficients, and (ζ₁, …, ζ_n) are independent and identically distributed errors with an unspecified distribution function. If C_i is a stochastic, subject-specific censoring variable, then the observed data are ${\{(U_i,{\delta }_i,{\mathbf{x}}_i)\}}_{i=1}^n$, where U_i = min(T_i, C_i), δ_i = I(T_i ≤ C_i) and I(·) is the indicator function. The goal is to estimate the regression coefficients β using the observed data. Rank-based coefficient estimation was first proposed by Prentice (1978) but the first general asymptotic theory was not developed for more than decade later (Tsiatis, 1990; Wei et al, 1990) and the most general theory under the weakest conditions appeared a few years later (Ying, 1993). A detailed history of early rank-based methods for censored data is provided elsewhere (Kalbeisch and Prentice, 1980).

From the beginning, rank-based coefficient estimation in the AFT model has been difficult and statistical inference even more challenging. The difficulty in estimation arises from the non-smooth nature of the estimating function. The difficulty in inference arises because the asymptotic slope matrix of the estimating function depends on the hazard function of the errors and cannot be directly estimated from the observed data; thus, the sandwich covariance matrix cannot be directly estimated for statistical inference. The earliest coefficient estimation techniques were based on direct search (Tsiatis, 1990; Wei et al, 1990; Lin and Geyer, 1992) and only truly suitable for low-dimensional problems, i.e., small p. Jin et al (2003) provided the the first reliable and accurate estimation procedure through explicit use of linear programming (LP) techniques to compute the Gehan (1965) estimator, a special version of the weighted logrank estimator. Compared to earlier approaches, this was a substantial improvement due to the accuracy of the method and its availability in standard software packages.

Unfortunately, the LP problem in Jin et al (2003) has O(n² + p) unknown parameters subject to n² linear constraints and the size of optimization problem can quickly overwhelm many standard LP solvers running on desktop computers. Furthermore, the inference procedure by Jin et al (2003) was based on resampling which meant that a perturbed LP problem of the same dimension as the original LP problem had to be solved multiple times (See Section 6). The computational complexity of the inference procedure by Jin et al (2003) prompted investigators to propose other methods. In particular, Heller (2007) proposed to directly approximate the Heaviside function in the Gehan (1965) estimating function with a distribution function while Brown and Wang (2005, 2007) proposed a pseudo-Bayesian approach which effectively estimates the coefficients and sandwich covariance simultaneously, again based on a smooth estimating function. In both cases, statistical inference can be performed immediately after coefficient estimation because the sandwich matrix is directly estimable.

Building on earlier work for smoothed rank-based methods and the need for practical solutions, here we provide a general tutorial for regularized rank-based coefficient estimation based on smooth approximation. In particular, we are interested in the optimization problem,

$$\underset{\mathit{\beta }}{\text{arg min}}\left\{f(\mathit{\beta })+𝒮(\lambda ,\mathit{\beta })\right\},$$ (2)

where f(β) is a smooth rank-based loss function, λ is a regularization parameter, and 𝒮(λ, β) is a generic penalty function or regularization term. Optimizing (2) for general loss functions is currently a hot topic in the areas of data mining, machine learning, engineering, and computational statistics. One reason for this is that the minimizer of (2) leads to a sparse solution for some convex but non-differentiable penalty functions with singularities at the origin. As a result, the minimizer of (2) also serves the role of a variable selection and model construction procedure at the same time. No author has tackled the specific problem here for f(β) pertaining to smoothed rank-based loss functions and only three authors have considered (2) for non-smooth f(β) (Johnson, 2008, 2009a; Xu et al, 2010; Cai et al, 2009).

The objective of the current paper is to provide a tutorial on a general numerical algorithm for smoothed rank-based loss functions f(β) and various penalty functions 𝒮(λ, β). Where earlier proposals for ℓ₁-regularized rank-based coefficient estimation provided exact solutions (Johnson, 2009a; Xu et al, 2010; Cai et al, 2009), the motivation behind our current approach is to provide a practical numerical solution of low computational complexity. In order to maximize the efficiency of our procedure, we adopt gradient-based Newton methods for minimizing smooth objective functions. In order to minimize computational complexity for ill-posed problems, we adopt limited-memory quasi-Newton algorithms. The algorithm outlined here applies to general smooth rank-based loss functions f(β) (Heller, 2007; Brown and Wang, 2005, 2007; Johnson and Strawderman, 2009) and current regularizations (Hoerl and Kennard, 1970; Tibshirani, 1996; Zou and Hastie, 2005; Yuan and Lin, 2006; Tibshirani et al, 2005; Zou, 2006; Johnson et al, 2008; Candes and Tao, 2007; Wu et al, 2009).

The contribution of the current paper is two-fold. First, after a brief history of the problem in Section 2, we provide in Section 3 a detailed tutorial on how to compute rank-based coefficient estimates in the AFT model using a smoothed loss function. In addition to reviewing recent trends in this area, we also propose a new estimator derived from polynomial-based smoothing and complements other estimators based on a smoothed loss function (Heller, 2007; Brown and Wang, 2005, 2007; Johnson and Strawderman, 2009). Second, in Section 4, we review regularized rank-based coefficient estimation and provide a tutorial on how to implement these procedures for rank-based estimators in a computationally efficient manner. We demonstrate unregularized and regularized coefficient estimation through three examples in Section 6. This tutorial is comprehensive for the topic and the framework described here may be applied to other loss functions and regularizations.

2 Background

Tsiatis (1990) proposed coefficient estimation through the weighted logrank estimating function,

$${\mathit{\Psi }}_{\vartheta }(\mathit{\beta })=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\delta }_i\vartheta (e_i,\mathit{\beta })\left\{{\mathbf{x}}_i-\frac{{\displaystyle {\sum }_{j=1}^n}I(e_j\ge e_i){\mathbf{x}}_j}{{\displaystyle {\sum }_{j=1}^n}I(e_j\ge e_i)}\right\},$$

where $e_i=\text{log }{U}_i-{\mathbf{x}}_i^{\top }\mathit{\beta }$ and ϑ(·, β) is a user-specified, data-dependent, non-negative weight function. Due to the discrete nature of the estimating function, the weighted logrank estimator β̂_ϑ is defined as a zero-crossing of Ψ_ϑ(β); that is, β̂_ϑ satisfies,

$${\Psi }_{\vartheta ,j}(\mathit{\beta ̂}-){\Psi }_{\vartheta ,j}(\mathit{\beta ̂}+)\le 0,$$

for all j = 1, …, p. The class of weighted logrank coefficient estimators has been studied extensively in the statistics literature. It is well-known that the weighted logrank coefficient estimator β̂_ϑ is consistent and asymptotically normal, under certain regularity conditions (Tsiatis, 1990; Wei et al, 1990; Ying, 1993). Unfortunately, the estimating function Ψ_ϑ(β) is not monotone, in general, and may contain multiple roots, thus, making parameter estimation troublesome. Fygenson and Ritov (1994) showed that the weighted logrank estimating function with Gehan (1965) weight, i.e.,

$$\vartheta (t,\mathit{\beta })=n^{-1}{\displaystyle \sum _{j=1}^n}I(e_j\ge t),$$ (3)

is monotone. In this case, it can be shown that the weighted logrank estimating function simplifies to

$${\mathit{\Psi }}_G(\mathit{\beta })=\frac{1}{n^2}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{\delta }_i({\mathbf{x}}_i-{\mathbf{x}}_j)I(e_i\le e_j),$$ (4)

which is often referred to as the Gehan estimating function. The Gehan estimating function Ψ_G(β) in (4) is the p-dimensional quasi-gradient of the following convex loss function,

$$f_G(\mathit{\beta })=\frac{1}{n^2}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{\delta }_i(e_j-e_i)I(e_i\le e_j),$$ (5)

and the Gehan estimator is defined as the minimizer of the objective function f_G(β),

$${\mathit{\beta ̂}}_G=\underset{\mathit{\beta }}{\text{arg min}}{f}_G(\mathit{\beta }).$$ (6)

The function f_G(β) in (5) is a piecewise-linear convex function and the global minimizer β̂_G lies in a p-dimensional polytope. Hence, although the objective function is convex, its minimizer may not be unique. Since f_G(β) is a non-differentiable function, gradient-based optimization methods cannot be applied directly to solve for β̂_G. In order for the rank-based estimator to be adopted in practice, efficient numerical methods are needed to solve the optimization problem. There are basically three ways to solve (6): direct search, linear programming, or smoothing.

Direct search methods are widely used in fields such as computational biology. Methods such as evolutionary algorithms and the Nelder-Mead algorithm are easy to implement and, therefore, very popular. In addition, bisection can be applied rather straightforwardly and effectively for low-dimensional problems. However, these methods lack of a comprehensive convergence theory and are well known to perform poorly on medium- to high-dimensional problems (Nocedal and Wright, 2006).

A second way to address optimization problem (6) is to reformulate it as a linear programming (LP) problem. Jin et al (2003) were the first authors to make successful use of the LP formulation,

$$\underset{u,\mathit{\beta }}{\text{min}}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{\delta }_i{u}_{\mathit{\text{ij}}}$$ (7)

subject to:	uij = (ej − ei),
	uij ≤ 0,
	for i, j = 1, …, n.

Either simplex or interior point methods may be engaged to solve the LP problem in (7). The advantage of the simplex method is that this method provides an exact solution after a finite number of iterations. However, a major drawback is the rate at which the dimension of the optimization problem increases. While the optimization problem (6) deals with p unknown parameters, the LP problem (7) has O(n² + p) parameters: one for every u_ij pair and one for each coefficient parameter, β_j, j = 1, …, p. Furthermore, the LP problem has n² linear constraints. When n and/or p are large, the complexity of the method increases and the convergence rate drops dramatically (Nocedal and Wright, 2006). Interior point methods belong to a class of inexact methods and, unlike simplex, they utilize gradient information. While interior point methods are better than simplex for moderately-sized problems (in terms of the sample size n and dimension of predictors p), they are computationally costly for large n and moderate to large p.

3 Smooth Gehan Loss Functions

3.1 Induced Loss Functions

Several authors have noted practical challenges in inferential procedures for estimators derived from non-smooth loss functions. Two recent germane contributions include the monotone estimating function by Heller (2007) and the pseudo-Bayesian method by Brown and Wang (2005, 2007). Both Heller (2007) and Brown and Wang (2005, 2007) cite simplified standard error estimation as a principal motivation for their smoothing procedures.

3.1.1 Brown and Wang (2005, 2007)

Brown and Wang (2005) proposed an intriguing pseudo-Bayesian method of simultaneous coefficient and standard error estimation in non-smooth parameter estimation problems. Brown and Wang (2007) considered the same parameter estimation discussed here and is directly relevant. Recently, Johnson and Strawderman (2009) reviewed the work by Brown and Wang (2005, 2007), provided theoretical justification for the censored data problem (Brown and Wang, 2007), and extended the method to clustered failure time data. Let Z ~ N(0, I_p) and Γ be a p-dimensional matrix, such that ‖Γ‖ = O(1), Γ² = Ω, and Ω is a symmetric, positive definite matrix. Then, the Brown and Wang (2007) estimating function is the perturbed Gehan estimating function, Ψ_B(β) = E_Z{Ψ_G(β) + ΓZ}; that is,

$${\mathit{\Psi }}_B(\mathit{\beta })=\frac{1}{n^2}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{\delta }_i({\mathbf{x}}_i-{\mathbf{x}}_j)\mathrm{\Phi ̅}\left(\frac{e_i-e_j}{r_{\mathit{\text{ij}}}}\right),$$ (8)

Φ(t) is the standard normal cumulative distribution function, Φ̅(t) = 1 − Φ(t), and $r_{\mathit{\text{ij}}}^2={({\mathbf{x}}_i-{\mathbf{x}}_j)}^{\mathrm{T}}\mathit{\Omega }({\mathbf{x}}_i-{\mathbf{x}}_j)$. Furthermore, the Brown and Wang (2007) coefficient estimator, say β̂_B, is consistent and $\sqrt{n}({\mathit{\beta ̂}}_B-{\mathit{\beta }}_0)$ converges in distribution to a mean-zero random vector with asymptotic covariance that is automatically computed as part of the estimation procedure (Brown and Wang, 2005, 2007; Johnson and Strawderman, 2009).

The estimator by Brown and Wang (2007) can be shown to minimize a convex loss function as well. Using integration by parts and facts about normal distribution functions, Johnson and Strawderman (2009) showed that the estimating function Ψ_B(β) has an associated convex loss function for which ∇f_B(β) = Ψ_B(β); in particular,

$$f_B(\mathit{\beta })=\frac{1}{n^2}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{\delta }_i\left[(e_j-e_i)\Phi \left(\frac{e_j-e_i}{r_{\mathit{\text{ij}}}}\right)+r_{\mathit{\text{ij}}}\varphi \left(\frac{e_j-e_i}{r_{\mathit{\text{ij}}}}\right)\right].$$ (9)

3.1.2 Heller (2007)

Heller (2007) proposed a estimating function by smoothing the indicator function in Ψ_G(β), i.e.,

$${\mathit{\Psi }}_H(\mathit{\beta })=\frac{1}{n^2}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{\delta }_i({\mathbf{x}}_i-{\mathbf{x}}_j)\mathrm{G̅}\left(\frac{e_i-e_j}{a}\right),$$ (10)

where G(t) is a cumulative distribution function, G̅(t) = 1 − G(t), and ‘a’ is a tuning parameter. Heller proved that, under suitable regularity conditions, the solution to 0 = Ψ_H(β), say β̂_H, was a consistent estimator of β₀. Moreover, he showed that $\sqrt{n}({\mathit{\beta ̂}}_H-{\mathit{\beta }}_0)$ converges in distribution to a normal random vector with mean zero and whose covariance could be directly estimated.

A common and convenient choice of the distribution function is the standard normal distribution, i.e., G(t) ≡ Φ(t). With this distribution function, one can again use integration by parts to show that Ψ_H(β) is the p-dimensional gradient of the following convex loss function,

$$f_H(\mathit{\beta })=\frac{1}{n^2}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{\delta }_i\left[(e_j-e_i)\Phi \left(\frac{e_j-e_i}{a}\right)+a\varphi \left(\frac{e_j-e_i}{a}\right)\right].$$ (11)

A straightforward calculation confirms that ∇f_H(β) = Ψ_H(β).

3.2 The Polynomial-smoothed Gehan Loss Function

A third approach for the optimization problem (6), is to approximate the objective function f_G(β) directly by a smooth approximating function. This is a common technique in applied mathematics and has been used for at least six decades (Huber, 1964). The gain of this approach is that we can adopt computationally efficient gradient-based methods to minimize a surrogate loss function.

Define the following smooth approximation to the Gehan loss function,

$$f_{G,\epsilon }(\mathit{\beta })=\frac{1}{n^2}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{\delta }_i{c}_{\epsilon }(e_i-e_j),$$ (12)

where c_ε is a sufficiently smooth real-valued function. Here, we choose a polynomial smoothing function

$$c_{\epsilon }(z)=\{\begin{array}{cc}-z,\hfill & \text{if }z\le -\epsilon ,\hfill \\ -\frac{1}{16{\epsilon }^3}{(\epsilon -z)}^4+\frac{1}{4{\epsilon }^2}{(\epsilon -z)}^3\hfill & \text{if }z\in (-\epsilon ,\epsilon ],\hfill \\ 0,\hfill & \text{if }z>\epsilon ,\hfill \end{array}$$

with sufficiently small but strictly positive ε (e.g., ε = 10⁻⁴). As shown in Figure 1, the function c_ε(z) = −z for all z ≤ −ε and c_ε(z) = 0 for all z > ε and, hence, matches the Gehan loss function exactly for |z| > ε. The smoothing takes place within the interval (−ε, ε]. Straightforward calculations reveal that the function c_ε and its first two derivatives $c_{\epsilon }^{\prime },c_{\epsilon }^{″}$ are continuous in the points −ε and ε for any ε > 0. Hence the loss function f_G,ε(β) is twice-differentiable in β for ε > 0. Note, f_G,ε(β) also inherits convexity from c_ε for every ε ≥ 0. Given our definition of c_ε, it is evident that lim_ε→0 f_G,ε(β) = f_G(β).

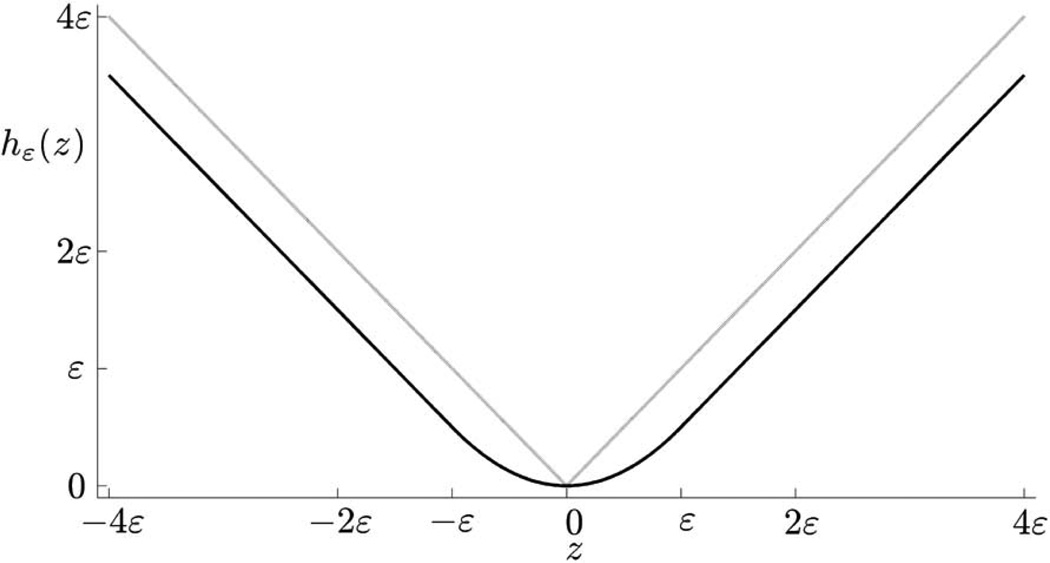
Fig. 1.

Graph of the smoothing function c_ε. Compared with the function [·]⁻ the error c_ε(z) − [z]⁻ is largest at z = 0 with an absolute error of 3/16ε.

The estimator is defined as the minimizer of the polynomial-smoothed objective function, i.e.,

$${\mathit{\beta ̂}}_{G,\epsilon }=\underset{\mathit{\beta }}{\text{arg min}}{f}_{G,\epsilon }(\mathit{\beta }).$$ (13)

The following theorem establishes the main consistency result.

Theorem 1 Under Conditions A1–A4 in Johnson and Strawderman (2009, p.586), β̂_G,ε is a strongly consistent estimator of β₀.

The proof of Theorem 1 as well as other large sample results are outlined in the Appendix. The result is a direct consequence of a strong law of large numbers for U-statistics.

Remark 1. Although asymptotic analysis suggests ε decreases as n increases, here, we simply view ε as a tuning constant that weighs two objectives: numerical accuracy versus the speed of algorithmic convergence. We used ε = 10⁻⁴ in numerous real and simulated examples and found this value to a suitable rule-of-thumb. In statistical computing, it is not uncommon that algorithms include fixed tuning constants; see, for example, MM algorithms (Hunter and Lange, 2004).

3.3 Connections, Contrasts

To facilitate comparisons to other estimators, the first-order partial derivatives of f_G,ε(β) with respect to β leads to the monotone estimating function,

$${\mathit{\Psi }}_{G,\epsilon }(\mathit{\beta })=\frac{1}{n^2}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{\delta }_i({\mathbf{x}}_i-{\mathbf{x}}_j)K_{\epsilon }(e_i-e_j),$$ (14)

where $K_{\epsilon }(z)=-c_{\epsilon }^{\prime }(z)$,

$$K_{\epsilon }(z)=\{\begin{array}{cc}1,\hfill & \text{if }z\le -\epsilon ,\hfill \\ -\frac{1}{4{\epsilon }^3}{(\epsilon -z)}^3+\frac{3}{4{\epsilon }^2}{(\epsilon -z)}^2\hfill & \text{if }z\in (-\epsilon ,\epsilon ],\hfill \\ 0,\hfill & \text{if }z>\epsilon .\hfill \end{array}$$

Evidently, K_ε(z) is a weight function operating on the differences in residuals (e_i − e_j) : the weight is 1 if (e_i − e_j) < −ε, 0 if (e_i − e_j) > ε, and values between 0 and 1 if −ε < (e_i − e_j) ≤ ε. When ε = 0, the polynomial-smoothed Gehan estimating function is exactly the Gehan estimating function, Ψ_G,ε(β) = Ψ_G(β).Written in this way, the difference between Ψ_H(β) and the polynomial-smoothed estimating function Ψ_G,ε(β) is how the weight is assigned to the difference (e_i − e_j). This fact leads to a useful heuristic for standard error estimation for the polynomial-smoothed estimator β̂_G,ε and is outlined in the Appendix.

Compared with f_H(β) or f_G,ε(β), f_B(β) is self-contained in the sense that there is no independent tuning parameter a or ε, respectively. The price one pays for the automatic data-dependent bandwidth r_ij is mostly computational: a sandwich matrix must be computed at every iteration to update Ω. However, simultaneous coefficient and covariance estimation is a principal motivation behind the method of Brown and Wang (2005, 2007) and one expects a proportional increase in the computational burden.

3.4 Inference Procedures

Tsiatis (1990) showed that, under suitable regularity conditions, the Gehan estimator is asymptotically normal, i.e. n^1/2(β̂_G − β₀) converges in distribution to a mean-zero normal random vector with covariance

$${\mathit{\Omega }}_G={\mathbf{A}}_G^{-1}{\mathbf{B}}_G{\mathbf{A}}_G^{-1},$$

where

$${\mathbf{A}}_G=\underset{n\to \mathrm{\infty }}{\text{lim}}{n}^{-1}{\displaystyle \sum _{i=1}^n}[{\delta }_i\vartheta (e_i,\mathit{\beta })\frac{h_{\varsigma }^{\prime }(e_i)}{h_{\varsigma }(e_i)}{\{{\mathbf{x}}_i-\frac{{\displaystyle {\sum }_{j=1}^n}I(e_j\ge e_i){\mathbf{x}}_j}{{\displaystyle {\sum }_{j=1}^n}I(e_j\ge e_i)}\}}^{\otimes 2}],$$

$${\mathbf{B}}_G=\underset{n\to \mathrm{\infty }}{\text{lim}}{n}^{-1}{\displaystyle \sum _{i=1}^n}\left[{\delta }_i{\{\vartheta (e_i,\mathit{\beta })\}}^2{\{{\mathbf{x}}_i-\frac{{\displaystyle {\sum }_{j=1}^n}I(e_j\ge e_i){\mathbf{x}}_j}{{\displaystyle {\sum }_{j=1}^n}I(e_j\ge e_i)}\}}^{\otimes 2}\right],$$

ϑ(t, β) is the Gehan weight in (3), h_ζ(t) is the hazard function of the errors ζ_i in (1), $h_{\zeta }^{\prime }(t)=(d/\mathit{\text{dt}})h_{\zeta }(t)$, and v^⊗2 = vv^⊤. For the inference procedures here, it is assumed that A_G is full-rank. Because the matrix A_G involves the hazard function of the errors, it cannot be directly evaluated without non-parametric smoothing or numerical differentiation, but these techniques can incur substantial instability in finite samples. This was the impetus for the resampling technique by Jin et al (2003). The idea is to generate n independent, exponentially-distributed random variables Z_i ~ Exp(1), i = 1, …, n, and define

$${\mathit{\beta ̂}}_G^{*}=\underset{\mathit{\beta }}{\text{arg min}}{f}_G^{*}(\mathit{\beta })$$

where f_G(β)* is the perturbed loss function,

$$f_G^{*}(\mathit{\beta })=\frac{1}{n^2}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{\delta }_i(e_j-e_i)I(e_i\le e_j)Z_i.$$

The perturbation is repeated a large number of times, say M, and an estimate of var(β̂_G) is the sample covariance of the M resampled vectors ${\mathit{\beta ̂}}_G^{*}$. The key to the success of perturbing the minimand is that E(Z_i) = var(Z_i) = 1 and the mechanism that generates Z_i is completely independent of the data-generating mechanism for {(x_i, U_i, δ_i), i = 1, …, n}. Note, that perturbing the minimand is a general technique and it applies to any of the smooth loss functions, f_G,ε(β), f_B(β) or f_H(β).

Of course, resampling is computationally demanding and a direct solution is preferable. Similar to the Gehan estimator, the asymptotic covariance of the smooth estimators β̂_• takes the usual sandwich form,

$${\mathit{\Omega }}_{•}={\mathbf{A}}_{•}^{-1}{\mathbf{B}}_{•}{\mathbf{A}}_{•}^{-1},$$

where B_• is the asymptotic covariance of n^1/2Ψ_•(β₀) and A_• is the asymptotic slope matrix of lim_n→∞ Ψ_•(β₀). However, unlike the original Gehan estimator whose asymptotic slope matrix could not be directly evaluated, the derivative of the smoothened estimating function may be evaluated analytically and A_• = lim_n→∞ −(∂/∂β)Ψ_•(β₀). The sample estimator for A_• is

$${\mathbf{Â}}_{•}=\frac{1}{n^2}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{\delta }_i{({\mathbf{x}}_i-{\mathbf{x}}_j)}^{\otimes 2}{w}_{\mathit{\text{ij}}},$$

where w_ij is a weight on the difference (e_i − e_j). If ϕ(z) is the normal probability density function evaluated at z, then for Brown and Wang, w_ij = ϕ{(e_i − e_j)/r_ij)}/r_ij; Heller, w_ij = ϕ{(e_i − e_j)/a)}/a; polynomial-smoothed, w_ij is obtained by straightforward differentiation of K_ε(z). We also need an estimator for B_•. Due to the asymptotic equivalence of n^1/2Ψ_•(β₀) and n^1/2Ψ_G(β₀), we may use the sample estimator of the asymptotic covariance of n^1/2Ψ_G(β₀) for the smoothened estimators β̂_• (cf. Brown and Wang, 2005, 2007; Johnson and Strawderman, 2009); namely,

$${\mathbf{B̂}}_{•}=\frac{1}{n}{\displaystyle \sum _{i=1}^n}\left[{\delta }_i{\{\vartheta (e_i,\mathit{\beta })\}}^2{\{{\mathbf{x}}_i-\frac{{\displaystyle {\sum }_{j=1}^n}I(e_j\ge e_i){\mathbf{x}}_j}{{\displaystyle {\sum }_{j=1}^n}I(e_j\ge e_i)}\}}^{\otimes 2}\right].$$

Both Heller (2007) and Brown and Wang (2005, 2007) provide other estimators for B_• based a theory of U-statistics. The estimator by Johnson and Strawderman (2009) reduces to B̂_• when the survival times are independent as we have here. Consequently, our estimator of the asymptotic covariance Ω_• is

$${\mathit{\Omega ̂}}_{•}={\mathbf{Â}}_{•}^{-1}{\mathbf{B̂}}_{•}{\mathbf{Â}}_{•}^{-1}.$$

4 Regularized Rank-based Estimation in AFT Models

Regularized regression has drawn substantial interest among researchers in statistics and biostatistics in recent years because it achieves simultaneous model selection and parameter estimation (Tibshirani, 1996; Zou and Hastie, 2005; Tibshirani et al, 2005; Yuan and Lin, 2006). A second reason regularized regression has gained popularity is due to high-dimensionality of today’s data sets. In particular, when the dimension of the predictors p exceeds the sample size n, the estimation problem is said to be ill-posed. In 1902, Hadamard defined a mathematical problem to be well-posed if a solution exists, the solution is unique, and depends continuously on the data in some reasonable topology (Hadamard, 1902). In general, every least-squares-based or likelihood-based estimation problem will be ill-posed with no unique solution when n < p. In order to construct a well-posed parameter estimation problem for high-dimensional data, one needs to incorporate prior knowledge to overcome the ambiguity of the global minimizers. In the Bayesian framework, the prior knowledge is reflected by a-priori information on the estimators, leading naturally to additive regularization terms (Vogel, 2002; Kaipio and Somersalo, 2005).

4.1 Exact Solutions

Few authors have offered algorithms for regularized rank-based coefficient estimation for censored outcomes. To clarify the challenges, the familiar Lagrangian form of the ℓ₁-regularized Gehan estimator is:

$$\underset{\mathit{\beta }}{\text{arg min}}\{f_G(\mathit{\beta })+\lambda {\displaystyle \sum _{j=1}^p}|{\beta }_j|\}.$$ (15)

Building on the earlier LP problem for the unregularized optimization in (7) and noting that $|{\beta }_j|={\beta }_j^{+}+{\beta }_j^{-}$, the optimization problem in (15) can be rewritten as the following LP problem:

$$\underset{u,\mathit{\beta }}{\text{min}}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{\delta }_i{u}_{\mathit{\text{ij}}}$$

subject to:	uij = (ej − ei),
	uij ≤ 0,
	${\displaystyle \sum _k}({\beta }_k^{+}+{\beta }_k^{-})\le \tau ,$
	${\beta }_k^{+}\ge 0,{\beta }_k^{-}\ge 0,$
	for i, j = 1, …, n,
	for k = 1, …, p,

where τ is a regularization parameter. Johnson (2008) was the first to attempt to solve a class of general problems related to (15) through direct search methods. In that paper, he noted that the optimization in (15) was of the form, ℓ₁ loss plus ℓ₁ penalty, and could be written as another LP problem but provided no algorithm to produce an exact solution. Then, Johnson (2009a) developed a practical solution for the ℓ₁-regularized Gehan estimator that made explicit use of linear programming. In independent work, Xu et al (2010) offered the same algorithm as in Johnson (2009a) and extended it to correlated survival times.

Both Johnson (2009a) and Xu et al (2010) extended an earlier algorithm by Jin et al (2003) to accommodate the ℓ₁ penalty. Their procedures use the ubiquitous quantreg package in R, developed by Roger Koenker and coauthors (Koenker and Bassett Jr, 1978; Koenker and D’Orey, 1987; Koenker and Ng, 2005), and were primarily developed for problems where n > p. As mentioned earlier in Section 1, it is possible to use interior point methods to solve large-scale LP problems with p > n. But our experience is that procedures built on quantreg in R will not suffice and another solution is needed. Two alternatives are (a) to use another LP solver, or (b) to write new code to solve the specific LP problem. A caveat to (a) is that many off-the-shelf LP solvers used to solve large-scale problems are unfamiliar to most statisticians and would be rarely adopted in practice. Cai et al (2009) chose the second route (b) and developed a path-finding algorithm that computes the entire ℓ₁-regularized coefficient path. Unfortunately, this path-finding algorithm cannot be easily extended to general penalty functions.

4.2 Newton-type Solutions

For large-scale problems, it becomes almost imperative to utilize efficient algorithmic methods to solve optimization problem (15) and gradient-based optimization algorithms are efficient. However, for the same reason that gradient-based algorithms cannot be applied to minimize f_G(β) alone, gradient-based optimization cannot be applied directly to minimize (15) because of the non-differentiability of ℓ₁-norm at zero. A natural way to proceed here is to approximate the absolute value function with a piecewise quadratic function. For example, the Huber function (Huber, 1964) is often used to smoothen the ℓ₁-norm and is given by

$$h_{\epsilon }(z)=\{\begin{array}{c}\hfill \frac{1}{2\epsilon }{z}^2,\text{ if }|z|<\epsilon ,\\ \hfill |z|-\frac{\epsilon }{2},\text{ if }|z|\ge \epsilon ,\end{array}$$ (16)

as illustrated in Figure 2. Let f_•(β) be short-hand for any smoothed rank-based loss function: f_B(β), f_H(β), or f_G,ε(β). So, by substituting f_•(β) for f_G(β) and the Huber ε-approximation h_ε(β_j) for |β_j| in (15), we arrive at a new optimization problem,

$$\underset{\mathit{\beta }}{\text{arg min}}\{f_{•}(\mathit{\beta })+\lambda {\displaystyle \sum _{j=1}^p}{h}_{\epsilon }({\beta }_j)\}.$$ (17)

Fig. 2.

Graph of the smoothing function h_ε. Compared with the function | · | the absolute error stays below ε/2 for any z.

Because the convex objective function in (17) is twice-differentiable in β, we may use gradient-based algorithms to minimize it. Newton-type algorithms possess quadratic convergence rates and are, thus, very efficient.

The current literature provides various types of regularization methods and penalty functions, say 𝒮(λ, β), where 𝒮 is a convex function and λ ≥ 0 is a regularization parameter. Many methods depend on the ℓ₁-norm and Huber’s ε-approximation provides a recipe for smoothing. Along the lines discussed above, we will replace a non-differentiable function 𝒮(λ, β) with a smooth approximation 𝒮_ε(λ, β). Then, we characterize the family of regularized smooth Gehan estimators as

$$\underset{\mathit{\beta }}{\text{arg min}}\{f_{•}(\mathit{\beta })+{𝒮}_{\epsilon }(\lambda ,\mathit{\beta })\}.$$ (18)

While it is impossible to provide a comprehensive list of all available penalty functions, we enumerate below a list of seven common regularization methods, i.e., 𝒮(λ, β), which have been proposed for penalized least squares and penalized likelihood problems. In Table 1, we exemplify the smoothed penalty function 𝒮_ε(λ, β) alongside the original function 𝒮(λ, β) for all seven penalty functions.

1. The ${\ell }_2^2$ regularization (Hoerl and Kennard, 1970) with $𝒮(\lambda ,\mathit{\beta })=\lambda {\Vert \mathit{\beta }\Vert }_2^2$ penalizes β quadratically, leading to greater penalties for large values of β, and straightforward numerical algorithms can be used to handle the optimization problem (18).

2. The ℓ₁ regularization, a. k. a. lasso (Tibshirani, 1996), with 𝒮(λ, β) = λ ‖β‖₁ penalizes all parameters β linearly and leads to sparse representations (Boyd and Vandenberghe, 2004). ℓ₁ regularization methods are broadly used such as in signal processing, statistics and geophysical applications. Since ℓ₁ regularization is not differentiable at 0 (i.e., for any β_j = 0), computationally this approach needs special attention. Applicable methods to solve the optimization problem (18) include linear programming, interior point, and iterative re-weighted least squares methods.

3. The elastic net (Zou and Hastie, 2005) $𝒮(\lambda ,\mathit{\beta })={\lambda }_1{\Vert \mathit{\beta }\Vert }_1+{\lambda }_2{\Vert \mathit{\beta }\Vert }_2^2$, with λ = (λ₁, λ₂)^⊤ combines the ℓ₁ and ${\ell }_2^2$ regularization. Dependent on the sizes of λ₁ and λ₂ this regularizer penalizes large values quadratically and small values linearly.

4. A regularizer of “opposite” behavior to the elastic net is the Berhu regularizer (Owen, 2006), 𝒮(λ, β) = ∑_j 𝒮_j(λ, β_j), and

   $${𝒮}_j(\lambda ,{\beta }_j)=\lambda \{\begin{array}{cc}|{\beta }_j|,\hfill & \text{if }|{\beta }_j|\ge \epsilon ,\hfill \\ \frac{{\beta }_j^2+{\epsilon }^2}{2\epsilon },\hfill & \text{if }|{\beta }_j|<\epsilon ,\hfill \end{array}$$

   penalizing small values of β quadratically and large values linearly.

5. The discrete total variation type regularizer $𝒮(\lambda ,\mathit{\beta })=\lambda {\displaystyle {\sum }_{j=1}^{p-1}}|{\beta }_{j+1}-{\beta }_j|$ induces smoothness in the parameters β. Note, this regularizer presumes a neighboring/ordering structure of the β_j’s, j = 1, …, p.

6. To induce sparsity and smoothness at the same time the two dimensional fused lasso regularization $𝒮(\lambda ,\mathit{\beta })={\lambda }_1{\Vert \mathit{\beta }\Vert }_1+{\lambda }_2{\displaystyle {\sum }_{j=1}^{p-1}}|{\beta }_{j+1}-{\beta }_j|$ has been introduced by Tibshirani et al (2005).

7. Let the G_k’s be the mutually exclusive subsets of {1, …, p}. The group lasso can now be seen as the grouped ℓ₂ regularization,

   $$𝒮(\lambda ,\mathit{\beta })=\lambda {\displaystyle \sum _{k=1}^K}\sqrt{\mathrm{\aleph }(G_k)}{\Vert {\mathit{\beta }}_{G_k}\Vert }_2,$$

   where ℵ(G_k) is the cardinality of G_k (Yuan and Lin, 2006; Meier et al, 2008) and reduces to ℓ₁ regularization when ℵ(G_k) = 1. Note, β_Gk is the vector of elements β_k for which k ∈ G_k. Group lasso requires prior knowledge on the grouping of the parameters β_k. Note, ‖ · ‖₂ is not differentiable in a singular point, i.e., 0. Typically, this is neglected in numerical investigations using gradient-based methods.

Table 1.

Table of some common penalty functions and their Huber-type approximation.

Penalty	𝒮(λ,β)	𝒮ε(λ,β)
ridge	$\lambda {\displaystyle {\sum }_{j=1}^p}{\beta }_j^2$	$\lambda {\displaystyle {\sum }_{j=1}^p}{\beta }_j^2$
lasso	$\lambda {\displaystyle {\sum }_{j=1}^p}|{\beta }_j|$	$\lambda {\displaystyle {\sum }_{j=1}^p}\{\begin{array}{cc}\frac{1}{2\epsilon }{\beta }_j^2,\hfill & \text{if }|{\beta }_j|<\epsilon ,\hfill \\ |{\beta }_j|-\frac{\epsilon }{2},\hfill & \text{if }|{\beta }_j|\ge \epsilon ,\hfill \end{array}$
elastic net	${\lambda }_1{\displaystyle {\sum }_{j=1}^p}|{\beta }_j|+{\lambda }_2{\displaystyle {\sum }_{j=1}^p}{\beta }_j^2$	${\displaystyle {\sum }_{j=1}^p}\{\begin{array}{cc}(\frac{{\lambda }_1}{2\epsilon }+{\lambda }_2){\beta }_j^2,\hfill & \text{if }|{\beta }_j|<\epsilon ,\hfill \\ {\lambda }_1(|{\beta }_j|-\frac{\epsilon }{2})+{\lambda }_2{\beta }_j^2,\hfill & \text{if }|{\beta }_j|\ge \epsilon ,\hfill \end{array}$
Berhu	$\lambda {\displaystyle {\sum }_{j=1}^p}\{\begin{array}{cc}|{\beta }_j|,\hfill & \text{if }|{\beta }_j|\le \gamma ,\hfill \\ \frac{{\beta }_j^2+{\gamma }^2}{2\gamma },\hfill & \text{if }|{\beta }_j|>\gamma ,\hfill \end{array}$	$\lambda {\displaystyle {\sum }_{j=1}^p}\{\begin{array}{cc}\frac{1}{2\epsilon }{\beta }_j^2,\hfill & \text{if }|{\beta }_j|<\epsilon ,|{\beta }_j|\le \gamma \hfill \\ |{\beta }_j|-\frac{\epsilon }{2},\hfill & \text{if }|{\beta }_j|\ge \epsilon ,|{\beta }_j|\le \gamma \hfill \\ \frac{{\beta }_j^2+{\gamma }^2}{2\gamma },\hfill & \text{if }|{\beta }_j|>\gamma ,\hfill \end{array}$
total variation	$\lambda {\displaystyle {\sum }_{j=1}^{p-1}}|{\beta }_{j+1}-{\beta }_j|$	$\lambda {\displaystyle {\sum }_{j=1}^{p-1}}\left(\begin{array}{cc}\frac{1}{2\epsilon }{({\beta }_{j+1}-{\beta }_j)}^2\hfill & \text{if }|{\beta }_{j+1}-{\beta }_j|<\epsilon \hfill \\ |{\beta }_{j+1}-{\beta }_j|-\frac{\epsilon }{2},\hfill & \text{if }|{\beta }_{j+1}-{\beta }_j|\ge \epsilon \hfill \end{array}\right)$
fused lasso	${\lambda }_1{\displaystyle {\sum }_{j=1}^p}|{\beta }_j|+{\lambda }_2{\displaystyle {\sum }_{j=1}^{p-1}}|{\beta }_{j+1}-{\beta }_j|$	combined lasso and total variation smoothing
group lasso	$\lambda {\displaystyle {\sum }_{k=1}^K}\sqrt{\mathrm{\aleph }(G_k)}{\Vert {\mathit{\beta }}_k\Vert }_2$	$\lambda {\displaystyle {\sum }_{k=1}^J}\sqrt{\mathrm{\aleph }(G_k)}{\Vert {\mathit{\beta }}_k\Vert }_2$

5 Algorithm

Every regularization procedure consists of two parts: (a) estimating the regression parameters β for fixed regularization parameter λ, and (b) tuning λ for optimal performance. For coefficient estimation in part (a), the computational advantage of our approximation lies in the smoothness and convexity of f_G,ε(β) and 𝒮_ε(λ, β). Due to these properties, we may use gradient-based optimization algorithms for which the optimization theory provides numerous iterative methods. One of the foremost gradient-based optimization algorithm is Newton’s method, which converges locally at a quadratic rate and uses the gradient and Hessian to form the search direction and step length at each iteration. In our experiments, we observe that the numerical calculations of the Hessian of the smoothed Gehan estimator and solving the inner system are at unreasonable costs (in particular for large scale problems) and we try to avoid utilizing Hessian information, i.e., curvature information; as a result, we prefer quasi-Newton methods in our investigations. The fundamental concept behind quasi-Newton methods is to provide curvature information of a loss function f_G,ε(β) and the regularizer 𝒮_ε(λ, β) in order to calculate an efficient search direction at each iteration without calculating the Hessian matrix explicitly and solving the inner system.

Algorithm 1.

L-BFGS method

Require:
fε	{smooth model function}
𝒮ε	{smooth regularizer function}
β0	{initial guess}
d	{data}
λj	{regularization parameter}
1: while ∇ J(β) ≠ 0 do
2:    calculate J(β) = fε(β) + 𝒮ε(λj, β) and ∇ J(β)
3:    estimate Hessian inverse approximation ℋ by last K update steps
4:    s = −ℋ⊤ ∇ J(β)	{quasi Newton search direction}
5:    calculate α via Armijo line search
6:    β = β + αs	{update step}
7: end while
8: β̂ = β
Ensure:
β̂	{optimal parameter}

The limited memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) method is one such quasi-Newton method, which is designed to target large scale optimization problems. The L-BFGS method avoids forming the Hessian and solving the inner linear system and only incorporates curvature information of the last few iterates, as outlined in pseudo-code in Algorithm 1. Throughout this work, we use the L-BFGS with an Armijo line search algorithm. For all our experiments we use a relative tolerance of 10⁻⁶ for the stopping criteria of the optimization algorithm (Gill et al, 1981).

The choice of the regularization parameter λ in part (b) is also crucial. To get a good estimate of the regularization parameter λ one may utilize information-based rules, cross validation, generalized cross validation, discrepancy principle and statistical learning techniques (Chung et al, 2011). In the interest of space, we refer readers to Hastie et al (2009) for a detailed description of cross-validation but provide a summary in our pseudo-code in Algorithm 2. The whole procedure, including coefficient estimation in part (a) and parameter tuning in part (b), is described in Algorithm 3. Our general framework is implemented in Matlab and is available upon request.

6 Worked Examples

As discussed previously, we divide the rank-based estimation problems for AFT models into two categories. First, the problems deal with low-dimensional predictors x relative to the number of the observation n, where n could be small or large. These problems are typically well-posed. The other case is when we have p > n or even p ≫ n. These problems are typically ill-posed and a regularization 𝒮_ε, often driven by prior knowledge on x, is used.

In this section we present four data examples where the AFT model relates lifetime or survival to risk factors. The first three examples have low-dimensional predictors and intended to compare accuracy, computational complexity, and inference between the original Gehan estimator β̂_G and the smoothened estimators, β̂_•: β̂_B, β̂_H, and β̂_G,ε. For smoothing in Ψ_H(β), we use Heller’s suggested estimate and rate, â = σ̂n^−0.26, where σ̂² is the sample variance of the uncensored residuals based on an initial Gehan fit. We estimate standard errors for β̂_H and β̂_B directly through a sandwich estimator Ω̂_• for the asymptotic covariance Ω_•. For the polynomial-smoothed estimator, β̂_G,ε, our experience is that perturbing the loss function works better in this case and, hence, results from resampling are presented below. Finally, in the fourth example, we present a data analysis of high-dimensional microarray data using the group lasso regularization. In this last example, no standard error estimates are presented because, at the time of this writing, there is no theoretically-justified inference procedure for the class of regularized estimators considered here.

Algorithm 2.

Cross Validation

Require:
fε	{smooth model function}
𝒮ε	{smooth regularizer function}
β0	{initial guess}
d	{data}
λj	{regularization parameter}
1: choose n cross validation sample sets {di}i=1, …,n
2: for i = 1 to n do
3:    extract sub-sample set
4:    ${\mathit{\beta ̂}}_j^n={\text{arg min}}_{\mathit{\beta }}{f}_{\epsilon }(\mathit{\beta })+{𝒮}_{\epsilon }(\lambda j,\mathit{\beta })$ using di
{optimization method see Algorithm 1}
5:    calculate $f_i=f_{\epsilon }({\mathit{\beta }}_i^n)$
6: end for
7: calculate Vj = mean (fi’s)
Ensure:
Vj

Algorithm 3.

Driver for Smooth Statistical Models

Require:
fε	{smooth model function}
𝒮ε	{smooth regularizer function}
β0	{initial guess}
d	{data}
{λ1, …, λm}	{set of regularization parameters}
1: for j = 1 to m do
2:    β̂j = arg minβ fε (β) + 𝒮ε(λj, β)
{optimization method, see Algorithm 1}
3:    calculate fj
{Cross-Validation method, see Algorithm 2}
4: end for
5: ĵ = arg minj=1, …, m Vj
{choose minimal cross validation set}
6: set β̂= β̂ĵ
Ensure:
β̂	{optimal parameter}

6.1 Multiple Myeloma Data

First, we exemplify the methods using multiple myeloma data set, given in the online SAS/STAT User’s Guide. This is the primary example in the PHREG procedure and was also used for illustration in Jin et al (2003). The data consist of survival outcomes and two independent variables, hemoglobin (HGB) and the natural logarithm of blood urea nitrogen (BUN), for a total of n = 65 patients. The covariates are standardized to have mean zero and unit variance. For HGB and log(BUN), Jin et al (2003) report estimated coefficients β̂_G as −0.532 and 0.292 with estimated standard errors 0.146 and 0.169, respectively. Using our polynomial-smoothed estimator β̂_G,ε, the coefficient estimates are −0.532 and 0.292 with estimated standard errors 0.149 and 0.164. The Brown and Wang coefficient estimates are −0.510 and 0.304 with standard error estimates 0.212 and 0.208. Using a smoothing parameter â = 0.987, Heller’s estimates are −0.510 and 0.302 and standard error estimates 0.190 and 0.196, respectively. In short, the polynomial-smooth estimate β̂_G,ε is similar to the original Gehan estimate β̂_G in both point estimate and standard error estimate. The point and standard error estimates of β̂_B and β̂_H are similar to one another, but the point estimates are 3–4% different in absolute magnitude than the Gehan coefficient estimates and the standard error estimates 20–30% larger than resampling. When a different covariance estimator is used, Brown and Wang (2007) find standard error estimates of the same magnitude as in Jin et al (2003).

6.2 Mayo PBC Data

The Mayo primary biliary cirrhosis (PBC) data set (Fleming and Harrington, 1991) contains information about the survival time and prognostic variables for 418 patients who were eligible to participate in a randomized study of the drug D penicillamin. Of 418 patients who met standard eligibility criteria, a total of 312 patients participated in the randomized portion of the study. Using the smaller randomized cohort, the study investigators used stepwise deletion to build a Cox proportional hazards model for the natural history of PBC (Dickson et al, 1989). Of the original ten predictors, stepwise deletion selected five significant variables: age, albumin, bilirubin, edema, and prothrombin time (protime). We take the natural logarithmic transformation of albumin, bilirubin, and prothrombin time to conform to the analysis in Fleming and Harrington (1991). These five variables constitute the natural history model for PBC (Dickson et al, 1989).

We present in Table 2 the coefficient estimates β̂_B, β̂_H, β̂_G,ε (here we set ε = 10⁻⁴) based on (13), and β̂_G based on (6) using linear programming. We note that the coefficient and standard error estimates between β̂_G and β̂_G,ε are nearly identical. The proposed BFGS algorithm runs in less than one-half of one second and the linear programming method of Jin et al (2003) is still reasonable at 5.3 seconds (on our MacBook Pro running R 2.9.1) given the moderate sample size. Heller’s smoothing parameter is â = 1.607 and the resulting coefficient estimates tend to be stronger, i.e. farther from the null; the corresponding standard error estimates are larger. The coefficient estimates from Brown and Wang generally differ from the other estimators and the standard error estimates lie between those computed for β̂_H and β̂_G,ε.

Table 2.

Coefficients estimates for Mayo PBC data.

Parameter	β̂B	β̂H	β̂G,ε	β̂G
age	−0.344 (0.073)	−0.470 (0.102)	−0.270 (0.057)	−0.271 (0.062)
albumin	0.226 (0.089)	0.200 (0.113)	0.205 (0.070)	0.204 (0.069)
bilirubin	−0.721 (0.082)	−0.925 (0.110)	−0.593 (0.068)	−0.594 (0.071)
edema	−0.248 (0.083)	−0.231 (0.099)	−0.223 (0.069)	−0.224 (0.070)
protime	−0.295 (0.086)	−0.347 (0.106)	−0.238 (0.071)	−0.237 (0.080)

6.3 Nursing Home Data

From 1980–1982, the National Center for Health Services Research conducted a study to determine the effect of financial incentives on variation of patient care in nursing homes. In particular, 18 out of 36 nursing homes from San Diego, California, received higher per diem payments for accepting and admitting Medicaid patients and additional bonuses when the patient’s prognosis improved. The study collected data from an additional 18 control nursing homes where no financial incentives were used. A complete description is given in Morris et al (1994). The total sample size from all 36 nursing homes is n = 1601. Our data set consists of seven co-variables: treatment (trt), age, sex, marital status, and three health status indicators (h1–h3), ranging from the best health to the worst health. For the polynomial-smoothed estimator, we used ε = 10⁻⁴. Our results are presented in Table 3.

Table 3.

Coefficient estimates for nursing home data.

Parameter	β̂B	β̂H	β̂G,ε	β̂G
trt	0.141 (0.107)	0.140 (0.108)	0.145 (0.107)	0.144 (0.103)
age	0.096 (0.055)	0.096 (0.055)	0.096 (0.052)	0.096 (0.054)
sex	−0.633 (0.125)	−0.633 (0.125)	−0.628 (0.127)	−0.629 (0.118)
mar stat	−0.249 (0.144)	−0.249 (0.145)	−0.247 (0.142)	−0.252 (0.135)
h1	−0.093 (0.146)	−0.095 (0.148)	−0.092 (0.145)	−0.091 (0.141)
h2	−0.589 (0.130)	−0.591 (0.131)	−0.588 (0.126)	−0.587 (0.131)
h3	−1.073 (0.174)	−1.076 (0.176)	−1.071 (0.169)	−1.071 (0.160)

In Table 3, coefficient estimates for all four estimators are displayed. For the nursing home data set, we computed Heller’s smoothing parameter as â = 0.7056. In this data set, we found very minor differences among the coefficient and standard error estimates. Among the three smoothened estimators, the polynomial-smoothed estimator took the longest took converge at 35 iterations. Both β̂_H and β̂_B converged in less than 10 iterations.

The sample size of the nursing home data is sufficiently “large” where the smoothing algorithm makes a significant impact. Using the algorithm of Jin et al (2003) along with Barrodale-Roberts simplex optimization (Koenker and D’Orey, 1987) via quantreg in R, the computation fails. However, the improved Frisch-Newton (Koenker and Ng, 2005) algorithm performs better and finishes in just under two minutes (i.e., 1.75 minutes on our MacBook Pro running R 2.9.1). For the nursing home data set, our quasi-Newton algorithm runs in five seconds. To highlight the differences in CPU times, consider computing standard error estimates using the resampling scheme by Jin et al (2003) with M = 1000 resamples. In this case, their resampling procedure would take more than one day on our desktop computer. In order to compute the standard error estimates for β̂_G in Table 3, we submitted our job to the Emory University Rollins School of Public Health high performance computing cluster. On our cluster, the resampling procedure of Jin et al (2003) applied to the nursing home data took 4 hours for M = 500 resamples. All of the other standard error estimates can be computed on an ordinary desktop computer in a matter of seconds.

6.4 CAMDA Data

We investigate a large scale data analysis using data from the Critical Assessment of Microarray Data Analysis (CAMDA) 2003 program, the details of which can be found on their website (CAMDA, 2003). For this analysis, we use gene expression data that were obtained through microarray experiments and the outcome of interest is a survival endpoint measured as time-to-death (in months) due to lung andenocarcinoma. The sample includes n = 200 subjects and gene expression data for 1036 gene probe sets; we refer to the probe sets as “gene biomarkers.” Our goal is to identify the gene biomarkers that are associated with survival of patients with lung andenocarcinoma using the AFT model with the group lasso penalty (see Table 1).

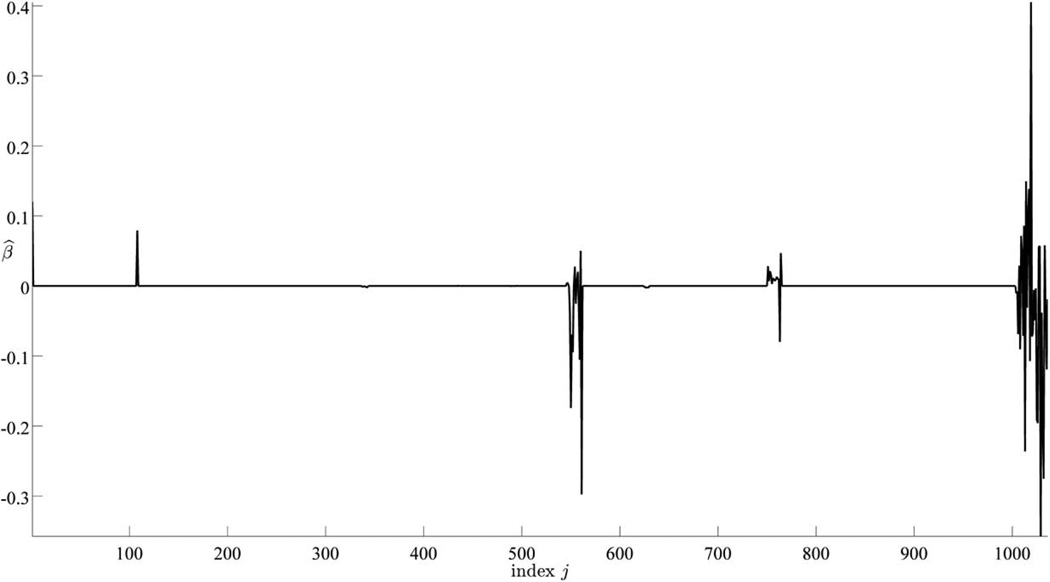
To identify the group structure, we first perform k-mean clustering to divide the gene biomarkers into 50 groups and rearrange the biomarkers so that the biomarkers in the same group have consecutive indices; of note, the group size ranges from 1 to 66. When fitting the AFT model with f_•(β) ≡ f_G,ε(β) and the group lasso penalty, we use a five-fold cross validation technique as presented in Algorithm 2 to select the optimal regularization parameter λ_ĵ = 0.01773. The resulting sparse model includes 78 biomarkers with nonzero regression coefficient estimates from 13 different groups and the regression coefficient estimates are presented in Figure 3.

Fig. 3.

Estimated parameters β for the CAMDA data using group lasso regularization.

7 Conclusions

In this paper, we present a general framework to efficiently compute rank-based coefficient estimates for semiparametric AFT models in small- or large-scale problems. Exact rank-based estimates are computed by optimization a linear programming (LP) problem. Although computing exact solutions is a laudable goal and may be required in some unusual settings, it is rarely needed in practical work. For those instances when an accurate Gehan estimate is required, our polynomial-based smoothing yields coefficient estimates nearly identical to Gehan estimates but only take a fraction of the computational resources compared to solving the LP problem. Moreover, the same ideas to smoothen the non-smooth loss function can be applied to the smoothing non-differentiable regularizations as well.

In addition to the polynomial-smooth Gehan estimator, Brown and Wang (2005, 2007) and Heller (2007) have each offered alternative rank-based coefficient estimators that are consistent, asymptotically normal, and whose asymptotic covariance matrix is directly estimable. Hence, one can estimate standard errors easily for large data set without resorting to computationally-intensive resampling. We reviewed standard error estimation for non-regularized Gehan estimators but not for regularized Gehan estimators. At the time of this writing, this is still an open question. If future researchers find that perturbing the minimand is a theoretically-sound resampling technique for regularized estimators, then our description in Section 3.4 will be germane for all estimators reviewed in this paper.

The fact that many constrained optimization problems can be closely approximated by an unconstrained optimization problem with a smooth objective function is an old idea. However, the application to regularized rank-based estimation for censored data is new and relevant to emerging data sets. We can apply our algorithm to penalty functions that have been proposed in the least squares framework but not yet extended to rank-based estimators, e.g. large-scale rank-based coefficient estimation with group lasso penalty. The general form of the computational framework makes it applicable for a wide range of optimization problems beyond the survival analysis applications discussed here.

Finally, as with most scientific problems, there is more than one approach, more than one technique to achieve the scientific objective. Rank-based estimation in the AFT model is but one technique and competing methods include those based on least squares, imputation, or inverse weighting. Over the past decade, several authors have advanced these competing methods to the regularized estimation setting yet were not discussed here (cf. Huang et al, 2006; Johnson, 2008; Johnson et al, 2008; Johnson, 2009b; Johnson et al, 2011). This omission is unabashedly self-serving and partly reflects our bias for rank-based estimators in the AFT model. Compared with least-squares estimators, rank-based estimators lose only a small amount of efficiency for (log)-normal errors but are more efficient for skewed and heavy-tailed error distributions. Inverse weighting is a powerful and convenient technique but whose finite sample behavior can be tied closely to the magnitude of the weights and hence the tail of the censoring distribution. This tutorial aims to be more or less comprehensive for unregularized and regularized rank-based estimation in the AFT model but falls well short as a comprehensive review of small- or large-scale coefficient estimation in the AFT model, in general. Nevertheless, we hope researchers interested in robust coefficient estimation in the AFT model find this tutorial helpful.

Appendix

Operating Characteristics of Polynomial-smoothed Gehan Estimator

In this section, we outline the large sample properties of the estimator β̂_G,ε. Let the parameter β belong to a parameter space 𝔹, a compact subset of ℜ^p and let f₀(β) be a convex function for β ∈ 𝔹. The proof of Theorem 1 relies on the following two facts regarding the loss functions f_G(β) and f_G,ε(β).

Lemma 1 Under Conditions A1–A3 in Johnson and Strawderman (2009, p.586),

$$\underset{\mathit{\beta }\in 𝔹}{\text{sup}}|f_G(\mathit{\beta })-f_0(\mathit{\beta })|\to 0\mathit{\text{ almost surely}}.$$

Lemma 2 Under Conditions A1–A3 in Johnson and Strawderman (2009, p.586),

$$\underset{\mathit{\beta }\in 𝔹}{\text{sup}}|f_{G,\epsilon }(\mathit{\beta })-f_0(\mathit{\beta })|\to 0\mathit{\text{ almost surely}}.$$

Lemma 1 is also Lemma 1 in Johnson and Strawderman (2009) under exactly the same conditions and stated without proof.

Outline proof of Lemma 2. By the triangle inequality, we have

$$|f_{G,\epsilon }(\mathit{\beta })-f_0(\mathit{\beta })|\le |f_{G,\epsilon }(\mathit{\beta })-f_G(\mathit{\beta })|+|f_G(\mathit{\beta })-f_0(\mathit{\beta })|.$$ (19)

By Lemma 1, the second term in (19) can be made arbitrarily small, uniformly for all β ∈ 𝔹, except on a set of probability measure zero. The first term in (19) is

$$|f_{G,\epsilon }(\mathit{\beta })-f_G(\mathit{\beta })|\le \frac{1}{n^2}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}|(c_{\epsilon }(-u_{\mathit{\text{ij}}})-c_0(-u_{\mathit{\text{ij}}}))|\le \text{max }|(c_{\epsilon }(-u_{\mathit{\text{ij}}})-c_{\epsilon }(-u_{\mathit{\text{ij}}}))|=\frac{3}{16}\epsilon .$$

Hence, the absolute difference between the Gehan loss and its smooth approximation can be made arbitrarily small, for every β ∈ 𝔹. The conclusion then follows.

Proof of Theorem 1. Under Conditions A1–A3 of Johnson and Strawderman, f_G(β) and f_G,ε(β) converge uniformly to the convex function f₀(β) by Lemmas 1 and 2, respectively. By Condition A4, f₀(β) is strictly convex at its unique minimizer, β₀. Thus, the minimizers of the random convex functions f_G,ε(β) and f_G(β) converge almost surely to β₀.

Asymptotic Distribution The polynomial-smoothed Gehan estimator bears a close similarity to Heller’s (2007) estimator and one expects the asymptotic distribution theory follows similarly. A straightforward calculation confirms that K_ε(z) in Ψ_G,ε(β) in (14) is a survivor function and k_ε(z) = (d/dz)K_ε(z) is symmetric about zero with finite second moment (that is, Heller’s, 2007, Condition C3, p. 553). Define the asymptotic slope matrix A_ε(β) and asymptotic covariance B_ε(β),

$${\mathbf{A}}_{\epsilon }(\mathit{\beta })=\underset{n\to \mathrm{\infty }}{\text{lim}}E[(\partial /\partial \mathit{\beta }){\mathit{\Psi }}_{G,\epsilon }(\mathit{\beta })]{|}_{\mathit{\beta }={\mathit{\beta }}_0},$$

$${\mathbf{B}}_{\epsilon }(\mathit{\beta })=\underset{n\to \mathrm{\infty }}{\text{lim}}\text{ var }\{n^{1/2}{\mathit{\Psi }}_{G,\epsilon }({\mathit{\beta }}_0)\}.$$

Then, assuming the covariate matrix has finite second moment and the non-singularity of A_ε(β) in a neighborhood of the true value β₀, one can show $\sqrt{n}({\mathit{\beta ̂}}_{G,\epsilon }-{\mathit{\beta }}_0)$ converges in distribution to a mean-zero normal random vector with asymptotic covariance

$${\{{\mathbf{A}}_{\epsilon }({\mathit{\beta }}_0)\}}^{-1}{\mathbf{B}}_{\epsilon }({\mathit{\beta }}_0){\{{\mathbf{A}}_{\epsilon }({\mathit{\beta }}_0)\}}^{-1},$$

(see Heller, 2007, Appendix). As with Heller’s estimator, both A_ε(β) and B_ε(β) are directly estimable from the data, the latter derived from a theory of U-statistics.