Time domain Removal of Irrelevant Magnetization (TRIM) in CEST Z-spectra

Abstract

Purpose

To evaluate the possibility of processing Z-spectra using time domain analysis.

Methods

An inverse Fourier transform (IFT) is applied on Z-spectra thus transforming the CEST data into the time domain. Here large interfering signals from solvent and semisolid magnetization transfer can be fit and filtered out. The method is demonstrated on a range of phantoms (creatine, a paraCEST agent, and hen egg white) and also in vivo on a mouse brain.

Results

Using time domain analysis, signal components in Z-spectra could be fit very well thus enabling irreverent or nuisance components to be removed. The method worked equally well for samples in a solution or a gel where the large contribution from conventional magnetization transfer contrast (MTC) was easily separated out. Results from egg white and mouse brain in vivo data showed the large water resonance could easily be removed thus allowing the remaining signal to be analyzed without interference from direct water saturation.

Conclusions

This method successfully filtered out the large nuisance signals from bulk water and MTC in Z-spectra in a large variety of phantom types and also in vivo. It is expected to be a potentially powerful tool for CEST studies without needing asymmetry analysis.

Introduction

Chemical exchange saturation transfer (CEST) is a relatively new type of MRI contrast that indirectly detects labile protons from low concentration solutes through the bulk water signal with enhanced sensitivity [1-7]. It is particularly promising for in vivo applications because it is sensitive to many physiological parameters (e.g., pH [8-12] or protein concentration [5,9,13]) and the sensitivity enhancement of low concentration solutes can be up to several orders of magnitude [14]. In addition, many exogenous contrast agents can be designed to exploit the CEST effect for molecular and functional imaging applications [4,15-19]. Currently, the most common method of conducting CEST experiments is to selectively saturate low concentration solute protons, which have some chemical shift difference (ω) from the water resonance, using RF irradiation. When these solute protons exchange with water protons, the saturation is also transferred to the water pool thus causing the water signal to attenuate. This frequency dependent saturation transfer experiment can be visualized similar to conventional magnetization transfer contrast (MTC) spectra by measuring the saturated water signal (S_sat), normalized by the signal without saturation (S₀), as a function of saturation frequency. The resulting plot has been dubbed a Z-spectrum [20] or CEST spectrum. Z-spectra are characterized by a symmetric direct saturation (DS) around the water resonance frequency that interferes with the detection of CEST effects (“spillover”). To remove this interference, it is common to perform a so-called MT ratio (MTR) asymmetry analysis [21] with respect to the water frequency. This process is characterized by subtracting the downfield (ω) from the upfield (−ω) signal ratios through

$${\mathrm{MTR}}_{\mathrm{asym}}\left(\nu \right)=S_{\mathrm{sat}}(-\nu )∕S_0-S_{\mathrm{sat}}\left(\nu \right)∕S_0$$ (1)

where ν = ω/2π. Asymmetry analysis is based on an inherent assumption of symmetry of non-CEST contributions (such as DS) around the water signal, so that the residual signal would show only contributions of the saturated exchangeable protons. However for in vivo studies and some in vitro studies, other residual signals are commonly observed in MTR_asym plots [22]. The reason is that chemical exchange is only one of several possible types of MT pathways that may contribute to saturation experiments. Another pathway is the transfer of nuclear Overhauser enhancements (NOEs) by dipolar cross-relaxation. This happens efficiently by spin diffusion in semi-solid tissue components [23,24] as well as, slower, in mobile macromolecules [2,22,25-28]. The signals due to these mechanisms are not centered about the water resonance frequency [29,30] and can, together with any B₀ field inhomogeneity, complicate the extraction of pure CEST contrast when using asymmetry analysis. Depending on the saturation field strength, the relative contributions of the CEST and NOE effects change [25,31] as does the MTR_asym. Alternative methods have been proposed for Z-spectra to address these issues using postprocessing approaches (Bloch equation fitting [32,33] or Lorentzian line fitting [25,34,35]) as well as new image collection schemes [36]. However, their interpretation often remains problematic because it is difficult to discriminate between different overlapping contributions in the Z-spectrum (frequency domain) and thus the fits can have several minima for a set of given variables. Here we propose to extract CEST effects from Z-spectra using time domain analysis, which provides the possibility to remove the large effects of direct saturation as well as effects from broad components, such as MTC. We therefore dubbed this approach “Time-domain Removal of Irrelevant Magnetization” (TRIM).

Methods

To demonstrate the possibility of TRIM processing for Z-spectra, we analyzed CEST data from the following phantoms: 5 mM creatine at pH = 7.3 in PBS and in a gel (2% agarose), and 100% hen egg white. In addition, we reanalyzed 10 mM EuDOTA-(gly)⁻₄ paraCEST data from a previous paper [37] and performed a CEST experiment on a mouse brain in vivo. CEST-MRI experiments on phantoms were performed using a 6 s continuous wave (CW) saturation pulse followed by a single-shot fast spin-echo (FSE) MRI readout (32 × 32 acquisition matrix, field of view = 20 mm × 20 mm, slice thickness 2 mm, TR/TE = 20 s /5 ms). B₁ strengths for the saturation pulse were 2 μT for creatine phantoms and 1 μT for egg white. Z-spectra were acquired over a range from −10 ppm to 10 ppm from water in steps of 0.2 ppm for creatine and in steps of 0.1 ppm for egg white. The CEST data for mouse brain were acquired using a 1.6 μT, 4 s CW saturation pulse followed by a FSE readout with an echo train length of 12 (48 × 32 acquisition matrix, field of view = 15 mm × 15 mm, slice thickness 1 mm, TR/TE = 6 s /5 ms). All experiments, excluding the re-analyzed data, were performed using an 11.7 T Bruker Biospec preclinical MRI system.

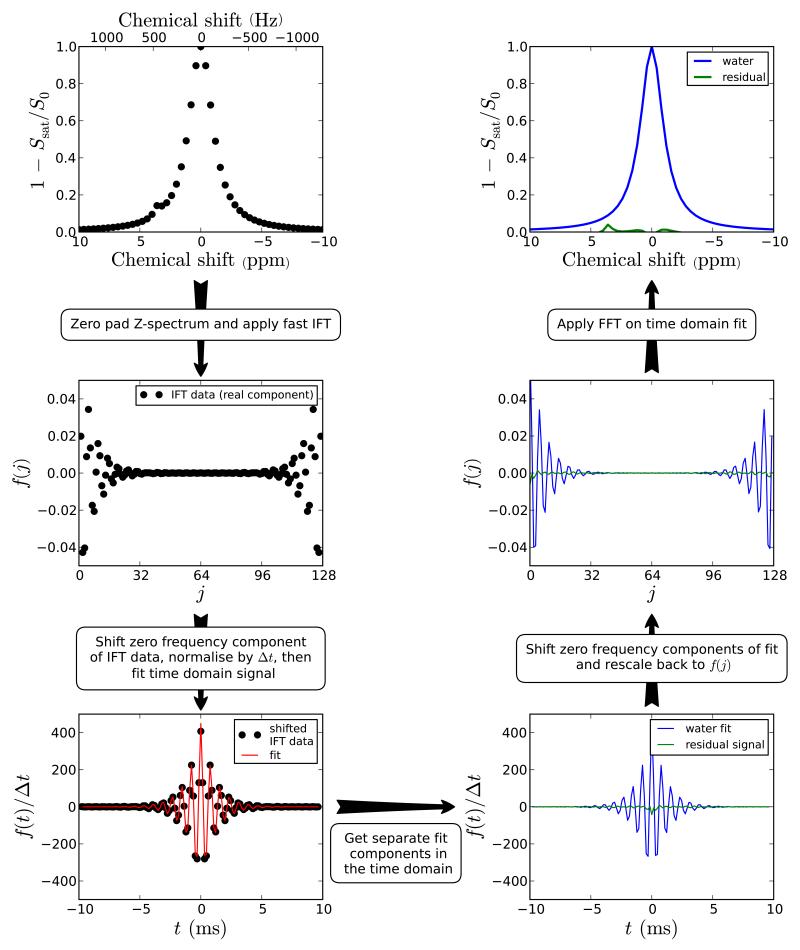
The TRIM procedure for analyzing CEST spectra (see Figure 1) requires transforming the data collected in the frequency domain (by varying the saturation offset frequency, ν) to the time domain. To do this, we first invert the Z-spectrum. Such an inverted Z-spectrum (1 – S_sat/S₀) can be seen as being a sum of arbitrary functions F_s(ν):

$$1-S_{\mathrm{sat}}\left(\nu \right)∕S_0=\Sigma F_{\mathrm{s}}\left(\nu \right).$$ (2)

Figure 1.

Schematic diagram showing the procedure for processing Z-spectra using time domain analysis. In the first section, a Z-spectrum was simulated for two pools (water at 0 ppm and amide at 3.6 ppm) and 51 offset frequencies between 10 to −10 ppm at 3 T (128 MHz). The processing steps before the fitting are outlined on the figure with the Z-spectrum zero padded to a total of 128 points (N). After the multicomponent fit, the reverse procedure is applied to the fitted data and residual signal in order to obtain the Z-spectra. The peak amplitude of the 3.6 ppm in the resiudal spectrum is 0.040 compared to 0.044 for MTR_asym. This amplitude may be used to assess the proton transfer ratio_.

For a conventional Z-spectrum, acquired with 2N saturation frequency offsets every Δν, the discrete Fourier transform of F_s(ν) is given by:

$$f_{\mathrm{s}}\left(t\right)=\Delta \nu \sum _{k=-N}^{N-1}{F}_{\mathrm{s}}\left(k\Delta \nu \right)e^{i2\pi tk\Delta \nu },$$ (3)

with t given at points t_j = jΔt where j = −N, −N+1, …, 0, … N-1 and the dwell time Δt = 1/(2NΔν). Consequently, from Eq. 3, we can simply fit the components in a Fourier transformed inverted Z-spectrum using a series of damped sinusoids:

$$f\left(t\right)=\sum _{\mathrm{s}}{f}_{\mathrm{s}}\left(t\right)=\Delta \nu \sum _{\mathrm{s}}{A}_{\mathrm{s}}\left[\cos \right({\nu }_{s}t)+i\sin ({\nu }_{s}t\left)\right]e^{-g_s\left(t\right)},$$ (4)

where A_s is the integral of each signal component (s), ν_s is the frequency of the peak from the reference point in Hz (since Z-spectra contain no imaginary component, we reference ν_s to the lowest saturation frequency in the Z-spectrum), and g_s is a factor for the shape of the peak. A_s is related to the proton transfer ratio (PTR) [2] and can potentially be used to quantify the CEST effect. In the case of a saturation line shape, g_s is related to T₁, T₂, the exchange rate (k_sw), and saturation power (B₁). Notice that this is different from normal NMR spectroscopy, where the line broadening is a function of T₂* and k_sw. Equation 3 provides a general description of the time domain signal for which any line shape or sum of line shapes can be used to fit out components. To simplify things, one could make assumptions such as using either Lorentzian (g_s(t) = d_s|t|) or Gaussian line shapes (g_s(t) = (d_st)²) where d_s is the damping factor. In principle, this would then be the same as fitting these shapes in the inverted Z-spectrum. In the case that MTC effects are present and the spectral width too limited, the use of the IFT approach can cause truncation artifacts due to non-zero spectral intensities at the edges, but we can remove those by moving the baseline. Notice that fitting multiple components in the frequency domain would also be complicated in the presence of non-zero spectral intensities in the inverted Z-spectrum and that a similar approach (shift of baseline or addition of constant) would have to be used to be able to fit the data but that this is technically changing the line shape and may affect the correctness of the fit.

In our data processing, we used the fast Fourier transform (FFT) algorithm [38] to transform the Z-spectra to the time domain. When using this algorithm, the limits in Eq. 3 are shifted to range from 0 to 2N-1. Consequently, the Fourier transformed data requires a shift (see Figure 1) before its analysis by Eq. 3 because the points from −t_j,max to 0 in Eq. 3 are aliased to between t_j,max to 2t_j,max. Additionally, the FFT algorithm requires N to be a power of two, so before the analysis, the data needs to be padded with zeros up to the next highest power of 2. Since Δν stays constant, the spectral width becomes larger and the dwell time smaller. Notice that if the inverted Z-spectra are non-zero at upper or lower saturation frequencies (truncation in frequency domain) the damped sinusoids shown in Eq. 4 will be convolved with an additional function. To avoid this, the baseline in the frequency domain can simply be shifted down before the inverse Fourier transform (IFT) to avoid truncation. An advantage of zero padding in the frequency domain is that the time-domain signal is interpolated (see definition of Δt above), which is of assistance in the fitting procedure because more points should give a more reliable fit. Here, we fit for A_s, ν_s, and d_s for each component s using all points in the real and imaginary parts of Eq. 4 concurrently. Subsequently, the interfering components are removed from the data. Notice that the time domain data are normalized by Δt to give the actual integral of the Z-spectrum in the time domain amplitude. An additional benefit of this is to make the time domain data independent of the number of points (N) used including any zero filling. Finally, the fitted data are again frequency shifted before the FFT back to the frequency domain where the residual Z-spectrum can be analyzed with only the CEST and CEST-NOE effects of mobile components.

The procedure for choosing the type of line shape and number of components in the fits was based on the width of the lines (e.g., free water was initially set to Lorentzian and bound water was initially set to Gaussian) and the number of significant peaks in the Z-spectrum (e.g., creatine in a gel initially had three pools to account for free water, bound water, and creatine). After the initial fit, the residual signal was analyzed to test the goodness of fit. For poor fits, the number of pools/line shapes was varied manually in order to find a better fit). All simulations and experimental data were processed using Python, Scipy, and Numpy (www.python.org, scipy.org, and numpy.scipy.org, respectively) using code written in-house.

Results

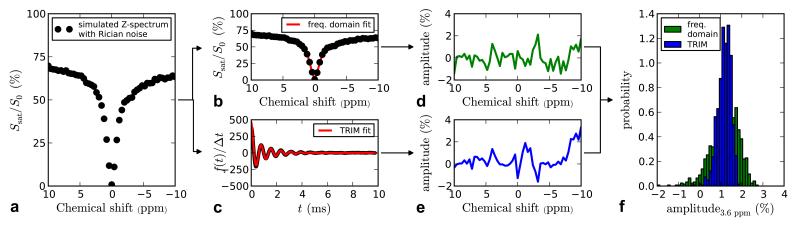
Due to linearity between the time and frequency domain, it could be argued that Z-spectra can also by analyzed by fitting multiple Lorentzian and/or Gaussian line shapes [34]. Therefore to compare the TRIM method with fitting multiple Lorentzians in the frequency domain, we first performed a Monte-Carlo simulation on a simulated Z-spectrum with Rician noise [34,41]. The Z-spectrum was simulated by numerically solving the Bloch-McConnell equations for a three-pool (free water, bound water, and amide) system. Next, noise was generated (based on a Rician distribution) and added to the Z-spectrum. The resulting “noisy” spectrum was processed using both the TRIM method and the frequency domain method using two Lorentzian line shapes (to account for the free and bound water pools). Finally, the fitted lines were subtracted from the simulated data and the amplitude at the amide resonance frequency in the residual spectrum measured. This process was repeated 1000 times. The results, shown in Figure 2, indicate that the TRIM method produced more consistent values for the APT signal at 3.6 ppm (due to the narrower distribution in the histogram).

Figure 2.

Result of a Monte-Carlo simulation comparing the TRIM and frequency domain fitting methods. A Z-spectrum is simulated (a) by numerically solving the Bloch equations for 3 pools (free water, bound water, amide). Noise is added to this Z-spectrum and it is subsequently fit in both the frequency (b) and time domains (c). The amplitude of the signal in the residual spectra (i.e., after the two fitted components are removed) at the amide proton frequency is then measured. This process is repeated 1000 times and the distribution in the APT signal plotted in (f).

Figure 3 shows the results of TRIM processing for CEST experimental data acquired from an egg white phantom. The original inverted Z-spectrum is displayed in Figure 3a with the data in the time domain displayed in Figure 3b (For clarity, only the real component of the IFT data beginning at the top of the echo (t = 0) is shown in Figure 3b and subsequent figures). The data in Figure 3b was fit using a three-pool model of Eq. 4 with each component displayed in the frequency domain in Figure 3c. The component corresponding to the free water pool was subtracted from the data in the time domain and the residual signal (shown in Figure 3d) transformed back into the frequency domain according to the scheme shown in Figure 1. The residual spectrum (Figure 3e) shows the free water component is almost completely removed thus the residual signal can be analyzed with minimal interference from direct water saturation.

Figure 3.

CEST experimental data from a hen egg white phantom (a). In (b), the inverted Z-spectrum is transformed into the time-domain and fit using three Lorentizian line shapes (the fitted line shapes are also displayed in the frequency domain in (c)). The component corresponding to the water peak (red line in (c)) is subtracted from the experimental data in the time domain and then the residual signal (d) is transformed back in the frequency domain. The filtered Z-spectrum (e) shows that the water component is largely removed thus leaving the residual signal to be analyzed with minimal interference.

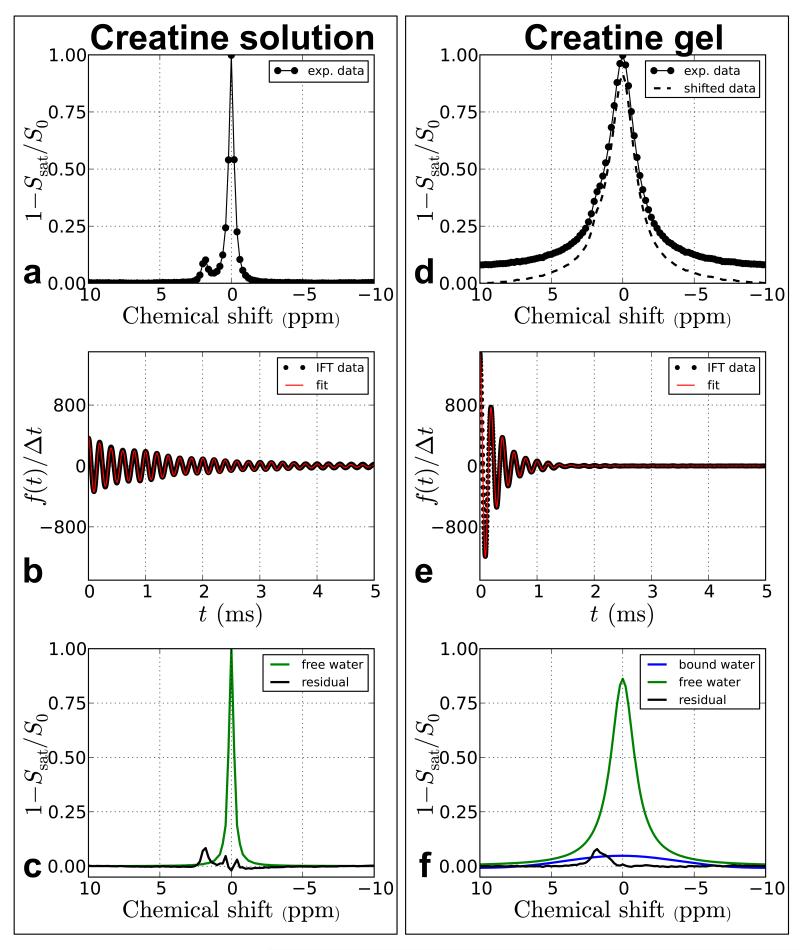
To demonstrate the possibility to deal with semi-solid MTC data, the time domain method was also compared between CEST agents in solution and in a gel. Figure 4 shows the TRIM results from 5 mM creatine (Cr) in solution and in a gel phantom. IFT data from Cr in solution (Figure 4b) were fit to a two-pool model while Cr in a gel (Figure 4e) was fit to a three-pool model (free water using a Lorentzian line shape, bound water using a Gaussian line shape, and creatine using a Lorentzian lineshape) in the time domain. For the creatine solution, Eq. 4 fit the data in Figure 4b very well and a component at ~2 ppm was the largest peak in the residual spectrum. For the creatine gel, the baseline of the inverted Z-spectra in Figure 4d did not reach zero for the frequency range over which we collected our Z-spectra (±10 ppm). To remove this truncation in the frequency domain, we shifted the baseline to zero (“Shifted data” in Figure 4d). Using the TRIM method on the shifted Z-spectrum, we were still able to remove the broad nuisance components, which subsequently provided a remaining distinct peak corresponding to the creatine resonance in the residual spectrum. Figure 4e clearly shows how absorption lineshapes that are difficult to resolve in the frequency domain can be resolved in the time-domain based on the decay rate.

Figure 4.

CEST experimental data from 5 mM creatine at pH 7.3 in solution (a-c) and in a gel (d-f). The narrow water resonance in a decays more slowly in the time domain (b) compared to the broad resonance in d. Differences in decay rates can assist in separating out overlapping resonances with different linewidths.

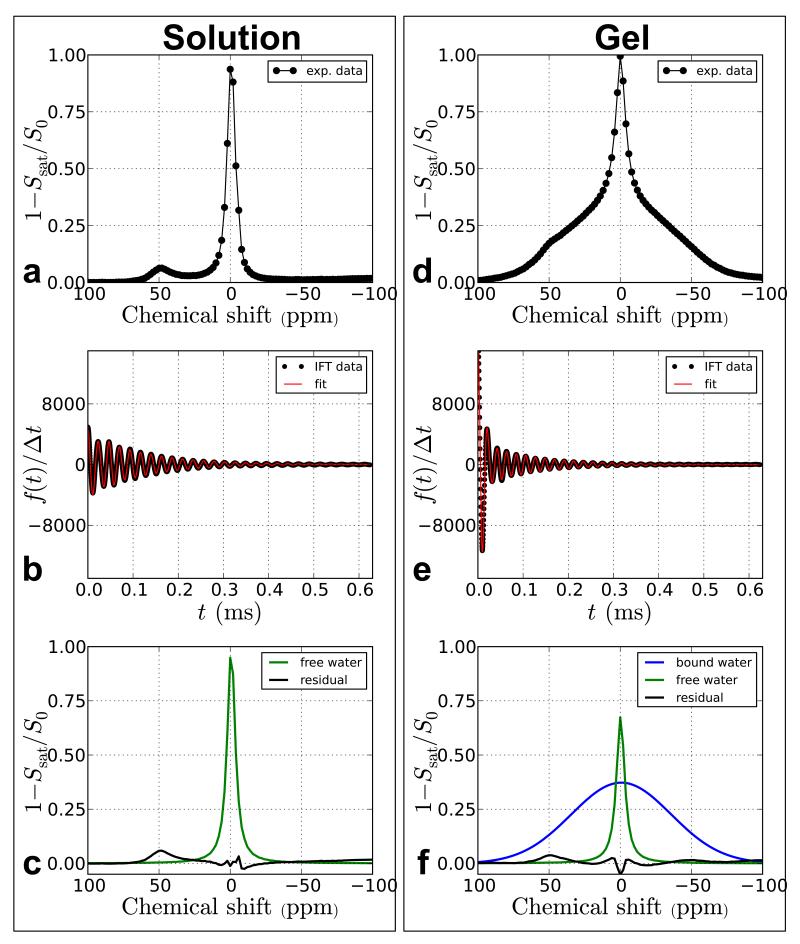
Similarly, Figure 5 shows the results of TRIM analysis using data from a previous paraCEST study [37]. The Z-spectra are from two phantoms containing 10 mM EuDOTA-(gly)⁻₄ in tris buffer (pH = 7), one in solution and the other in a gel matrix created by adding 4% agarose. The broad bound water component in Figure 5d was fit using a Gaussian line shape while the other two components (free water and paraCEST agent) were fit using Lorentzian line shapes.

Figure 5.

Time-domain processing of paraCEST data (10 mM EuDOTA-(gly)⁻₄) in solution and in a 4% agarose gel. The gel data has an additional component which appears as a large rapidly decaying component in the time domain that is simply separated out from the free water and paraCEST agent components.

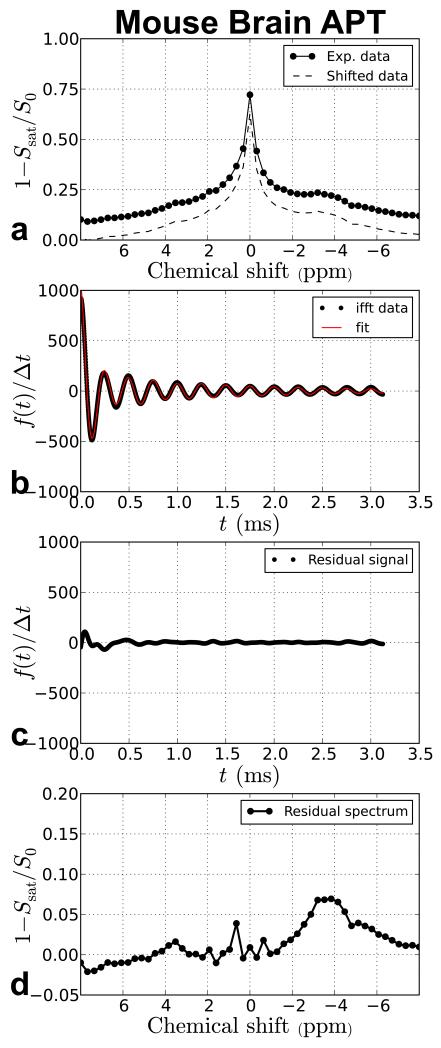
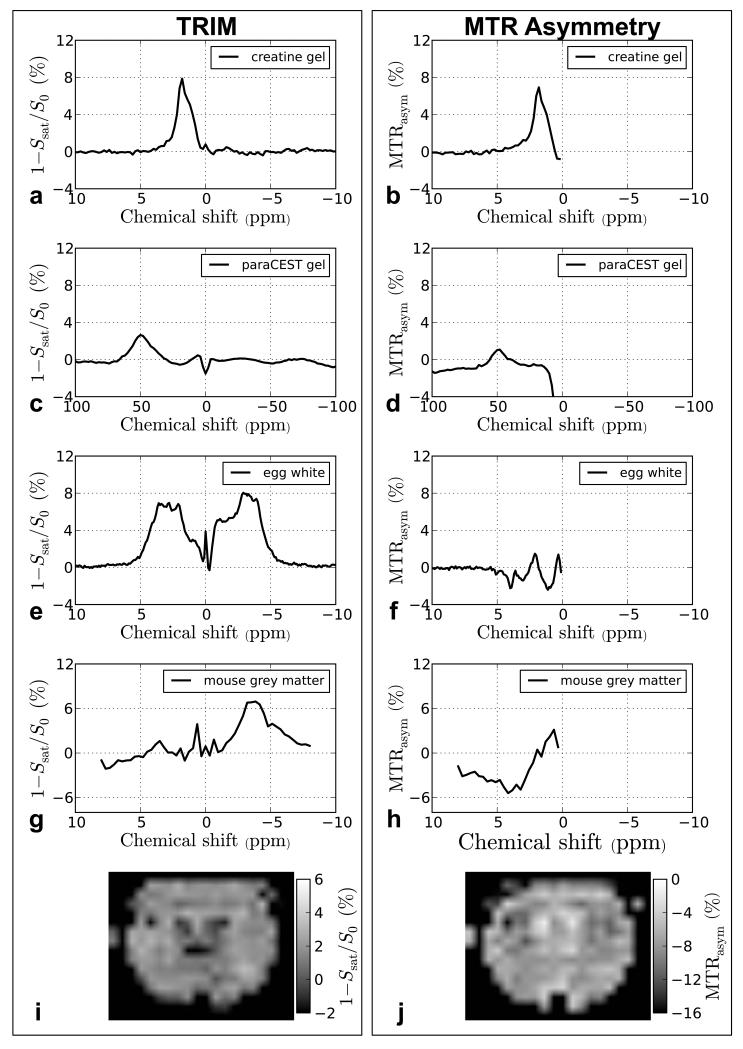
In Figure 6, we demonstrate the TRIM approach on in vivo data from mouse grey matter, which also has significant signal components up- and down field from water. However, here we fitted out two interfering components, namely a broad Lorentzian one representing MTC (d_s = 8800 s⁻¹) and another Lorentzian free water component (d_s = 650 s⁻¹). The residual spectrum shows a resonance with maximum at about 3.5 ppm and a large CEST-NOE contribution upfield from water. In Figure 7, we compare the TRIM procedure with MTR asymmetry analysis. For the creatine gel (Figures 7a-b), the time domain filtering approach yields comparable results to MTR asymmetry analysis. However, for the other cases (Figures 7c-h), the results differ appreciably. The TRIM approach yields higher signal intensity with less baseline distortion compared to asymmetry analysis. For the egg white phantom and mouse brain, the signal intensity using asymmetry are difficult to interpret due to interference of the upfield NOE-CEST signals, while the time domain analysis shows discernable resonances. Finally, two maps created using the signal intensity at 3.6 ppm from the mouse in vivo data are compared in Figures 7i-j. The maps show opposite levels of contrast between the TRIM-analyzed and MTR_asym-analyzed data. This is not surprising, because the scale in Figure 7j is negative due to most of the contrast in the MTR_asym map originating from the −3.6 ppm signal (also note that the scale range in Figure 7j is twice as large as the scale in Figure 7i). Thus, while the map in Figure 7i can be used to estimate the proton transfer ratio for the 3.6 ppm resonance, this would not be possible using the asymmetry analysis.

Figure 6.

TRIM processing of in vivo mouse brain data. The data is taken from a region of interest (ROI) drawn in the caudate/putamen region of normal appearing grey matter.

Figure 7.

Comparison of the time domain filtering approach (left) and MTR asymmetry analysis method (right) for isolating CEST effects. In a, the residual creatine signal after TRIM processing is very similar to the creatine peak obtained using MTR_asym analysis (b). This is not the case for the paraCEST agent in a gel. After TRIM analysis, the residual signal from the paraCEST agent (c) is larger than the signal obtained using MTR analysis (d). It is difficult to compare the results of TRIM processing and MTR_asym for the egg white and mouse grey mater data (e-h) because MTR_asym convolves the upfield and downfield effects from water. In (g), a peak corresponding to the expected APT frequency is clearly visible. We compare two maps that were obtained from TRIM analysis (i) and MTRasym (j). In j, the upfield and downfield peaks are also convolved and it seems that most of the contrast is from upfield effects from water because the signal for each voxel is negative. In the map obtained from TRIM processing, the signal is mostly positive and the map has inversed contrast compared to the MTR_asym map.

Discussion

We have demonstrated a potentially power technique for processing Z-spectra in the time domain for removing large nuisance or irrelevant signal components which can interfere with the analysis of CEST experiments. In phantoms, the TRIM method almost completely removed the free water component in hen egg white thus leaving up- and down-field peaks to be analyzed with minimal interference. The possibility to remove broad components, such as due to MTC effects was also demonstrated on creatine and paraCEST phantoms. In both cases, the broad MTC component was fit out very well, together with the free water component and thus leaving easy to interpret residual spectra. Finally, we also demonstrated the TRIM approach on in vivo data acquired from mouse grey matter. Similar to the other situations, the residual spectrum had minimal interference from direct water saturation and conventional MTC effects.

Compared to asymmetry analysis (Figure 7), the TRIM approach performed as well or better for the sample types tested here. In cases where MTR_asym convolves upfield and downfield phenomena, one could argue that Z-spectra can alternatively be analyzed by fitting Lorentzian line shapes or the Bloch equations to the experimental data. In the case of Bloch equation fitting, knowledge of B₁ and relaxation parameters would be required for each component, making this more involved. However, due to the linear properties of the Fourier transform, the Z-spectrum should in principle be fittable directly in the frequency domain when using multiple Lorentzian and/or Gaussian line shapes [34]. This expectation was substantiated when simulating this for theoretically generated noise-free spectra (results not shown), but when processing “noisy” spectra using both the TRIM method and the frequency domain method with two Lorentzian line shapes (to account for the free and bound water pools) the TRIM method produced more consistent values for the APT signal (based on the narrower distribution in the histogram, Figure 2f). One reason for the more consistent value could be that since the signal amplitude in the time domain is equal to the integral of each component in the frequency domain, the fitting is weighted much more towards large solvent signals in the time domain compared to the frequency domain. Therefore it is less important for account for each solute peak in the time domain because the fitting parameters are more sensitive to the larger components in the spectrum compared to small solute signals and noise. As a consequence, the time domain analysis may be advantageous in vivo where Z-spectra are often composed of two large nuisance components (DS and MTC) and many smaller peaks which are of interest.

Figure 7 demonstrates a number of potential issues with the TRIM approach. One problem, observed in the filtered Z-spectra is that the large solvent components are sometimes not completely filtered out. This could be because the line shape in the original Z-spectrum is not a perfect Lorentzian or Gaussian, which is what we assumed here when using Eq. 4 to fit the data. The baseline distortion seen Figure 5e could also be due to fitting a Gaussian to a line that is not explicitly Gaussian. This issue can be easily accounted for by adding additional terms in Eq. 4 to account for other line shapes (e.g., super Lorentzian). Other possibilities for reducing interference from large rapidly decaying components is time-shifting, windowing the time-domain signals, or band pass filtering. Also seen in Figure 3 is that when Z-spectra are acquired with more offset frequencies at a sufficiently narrow saturation bandwidth, more information will be present in the signal and a better fit can be obtained. Acquiring more points in the Z-spectrum of course increases total scan duration. However, this is less of a problem for steady-state methods [25,39] that often require high-resolution Z-spectra to be acquired if the water lineshape has to be fitted out.

Another potential problem is deciding how many signal components (s) to fit to the experimental data. The proteins in hen egg white and mouse brain have a large number of exchangeable peaks, but here we were able to get a reasonable fit using just 3 components for both sets of data thus, allowing us to remove the unwanted magnetization components. Each component for these two datasets had a Lorentzian line shape. Fitting a large number of components to account for small signal contributions would have improved the fit for some of the solute components, but we feel this would have had minimal effect on the water signal filtering since the water and MTC components are much larger than these additional solute components. We felt that a three-component model adequately fit the major components in the IFT data but determining the number of components to fit could be further refined using methods such as independent component analysis (ICA) or Bayesian modeling [40].

Another adjustment that was required in our analysis of the creatine gel and mouse brain data was that the baseline of the inverted Z-spectrum needed to be shifted to zero. If we didn’t perform the baseline correction, inverse Fourier transformation of the zero-padded Z-spectrum would result in the damped sinusoids from the Lorentzian peaks convolved with a truncation function. This would have to be addressed by adding additional terms to Eq. 4. However, since this function is not straightforward, we decided to just shift the baseline to zero. This shift may complicate the model function in Eq. 4 for extreme cases but for the phantom data and in vivo data analyzed here, it was not an issue. This shift also only has a minor impact on the quantification of the non-bound water components since the magnitude of their effect is not expected to change much when shifting the baseline of the inverted Z-spectra (see Figures 7a-b).

It is important to note the differences between this analysis approach and the FLEX [42] acquisition and analysis method. In FLEX experiments, the time domain signal is collected directly and analyzed using time-domain analysis. This FLEX signal has an additional phase term in the time domain signal which is not present in the CEST data since all Z-spectra are absorption line shapes. Another difference between FLEX and this method is that the PTR values of the signal components will be different. The CEST signal components are a result of saturation transfer whereas the FLEX signal consists of signal components that have been frequency encoded before transferring to the water and have a frequency dependent intensity weighting depending on the pulsed excitation profile. These different labeling schemes report on protons in different exchange regimes and different magnetization transfer effects.

Conclusion

We demonstrated a new approach for processing Z-spectra, namely using time domain analysis. The method successfully separated different components in a wide range of phantoms and we demonstrated the potential for filtering out large nuisance signal components such as due to direct water saturation and MTC effects in phantoms and in vivo. This relatively simple TRIM method is easy to implement, allowing the analysis of Z-spectra without the need for MTR asymmetry processing.