Diastolic chamber properties of the left ventricle assessed by global fitting of pressure-volume data: improving the gold standard of diastolic function

Abstract

In cardiovascular research, relaxation and stiffness are calculated from pressure-volume (PV) curves by separately fitting the data during the isovolumic and end-diastolic phases (end-diastolic PV relationship), respectively. This method is limited because it assumes uncoupled active and passive properties during these phases, it penalizes statistical power, and it cannot account for elastic restoring forces. We aimed to improve this analysis by implementing a method based on global optimization of all PV diastolic data. In 1,000 Monte Carlo experiments, the optimization algorithm recovered entered parameters of diastolic properties below and above the equilibrium volume (intraclass correlation coefficients = 0.99). Inotropic modulation experiments in 26 pigs modified passive pressure generated by restoring forces due to changes in the operative and/or equilibrium volumes. Volume overload and coronary microembolization caused incomplete relaxation at end diastole (active pressure > 0.5 mmHg), rendering the end-diastolic PV relationship method ill-posed. In 28 patients undergoing PV cardiac catheterization, the new algorithm reduced the confidence intervals of stiffness parameters by one-fifth. The Jacobian matrix allowed visualizing the contribution of each property to instantaneous diastolic pressure on a per-patient basis. The algorithm allowed estimating stiffness from single-beat PV data (derivative of left ventricular pressure with respect to volume at end-diastolic volume intraclass correlation coefficient = 0.65, error = 0.07 ± 0.24 mmHg/ml). Thus, in clinical and preclinical research, global optimization algorithms provide the most complete, accurate, and reproducible assessment of global left ventricular diastolic chamber properties from PV data. Using global optimization, we were able to fully uncouple relaxation and passive PV curves for the first time in the intact heart.

diastolic dysfunction is present to some degree in virtually all structural myocardial diseases, and, independent of its primary cause, this condition per se has become a major source of cardiovascular morbidity and mortality (23). Although the physiology of diastole has been a key field of preclinical research for decades, all treatments aimed to improve clinical outcome on the basis of modifying diastolic properties have been unsuccessful (8). Diastolic dysfunction is a generic term designating diverse abnormalities of left ventricular (LV) mechanical chamber properties, which all share a final stage of elevated left atrial pressure, pulmonary congestion, and heart failure. To improve therapeutic strategies, it is recognized that developing independent, unbiased, and robust indexes of each intrinsic diastolic property is mandatory (16).

At the full-organ integration level, the analysis of LV pressure-volume (PV) data obtained during acute load manipulation is the current gold standard method for assessing diastolic chamber properties in vivo as well as ex vivo in isolated beating-heart preparations (1, 10). This method is used in cardiovascular research to characterize new animal models of disease, to analyze the effect of therapies, and to validate noninvasive surrogate indexes of diastolic function.

Active and volume mediated passive mechanical properties are the major determinants of diastolic function, and a number of constitutive equations have been established (3, 15, 39). Relaxation designates the active phenomenon related to myofilament unbridging. Passive mechanical properties regulate chamber deformation below (elastic restoring) or above ventricular equilibrium volume (V₀). Because active and passive properties act simultaneously during diastole, uncoupling their physical effects is particularly challenging. Current methods attempt to isolate diastolic properties by focusing on specific temporal windows of diastole (18). The rate of relaxation has been characterized using several mathematical models, most frequently using exponential (35), or logistic (15), functions, or even a kinematic-inspired differential equation (3). These approaches share in common that they fit the pressure-time data during the nonfilling period of diastole, under the assumption that passive volume dependent forces are negligible or constant during this period. Stiffness is estimated by fitting the curvilinear end-diastolic PV relationship (EDPVR) from a number of beats during preload manipulation, with each beat contributing with a single point, and assuming that relaxation has been completed by end diastole (ED) (1).

These assumptions do not always hold in vivo (34). Also, confining parameter fitting to the isovolumic phase and to the instants of ED heavily penalizes statistical power, because all data recorded during filling are dismissed. Additionally, determining the fitting window landmarks introduces an important source of error and variability. But most importantly, current methods cannot account for passive mechanical properties of the LV below its V₀. Today, the role of negative suction pressure generated by elastic restoring forces requires complex volume clamp experiments (21, 27, 33) and has never been addressed in the intact beating heart. Finally, previous efforts to obtain a robust single-beat measurement of chamber stiffness without acute preload interventions are conceptually oversimplified, because they have always denied elastic restoring forces during diastole (9, 25, 43).

Current computation methods used to assess chamber properties from PV signals use linear or nonlinear numerical algorithms developed more than 20 years ago (3, 15, 35). Since then, curve-fitting methods have evolved substantially, and algorithms for multidimensional optimization have been widely implemented (7). Stochastic optimization methods are particularly useful in biology, as they are able to fit nonlinear equations in a multivariate environment under prespecified constraints representative of physically sound parameter values (2).

We hypothesized that global optimization is a suitable numerical method for uncoupling active and passive diastolic mechanical chamber properties of the LV from conventional PV data, which improves current methods used to characterize diastolic function in the experimental and clinical environments.

The general objective of the present study was to improve the analysis of diastolic PV data by developing and validating a novel numerical algorithm based on global optimization. We aimed to fully implement well-established constitutive equations, obtaining indexes of diastolic function by multivariate fitting of all points in multiple-beat data sets. Specific objectives were as follows: 1) to test the accuracy, reliability, and uncertainty of the global optimization method when analyzing data from in silico, animal, and clinical sources; 2) to test its performance when assessing single beats; and 3) to analyze the correlation of indexes obtained with the optimization method with those obtained noninvasively using Doppler echocardiography.

METHODS

The algorithm was first tested using Monte Carlo simulation to assess its capacity to recover a prespecified parameter space as in reverse engineering (14). Next, we performed animal experiments to test the algorithm's performance under acute hemodynamic interventions. We finally studied a human population to demonstrate its accuracy in the clinical setting. We introduced individual sensitivity analyses, plotting the relative contribution of each mechanical property to instantaneous diastolic pressure on an individual per-patient basis. We also analyzed the performance of the new method for the purpose of single-beat analysis. Finally, we tested the optimization algorithm when fitting alternative, more complex mathematical models of relaxation (3, 15).

Mathematical modeling and optimization algorithm.

We attempted to implement a numerical algorithm capable of fitting constitutive equations that, until now, were only obtainable using volume clamp interventions (see appendix) (39). Thus we did not intend to establish a new conceptual scheme of formulation of diastolic properties. Instead, we aimed to combine previously validated models to obtain a global fitting of the diastolic data. For this purpose, we adapted numerical methods frequently used for the analysis of other multidimensional processes in biology, such as allosteric protein regulation (7).

Diastolic pressure is defined as the resultant of adding active (P_a) and passive (P_p) forces acting throughout the full diastolic period (Fig. 1). Although passive forces are modulated by energy-consuming phosphorylation processes (and therefore are not fully passive sensu stricto), for the purpose of this study, we use the term “passive forces” to summarize the changes in LV chamber pressure caused by changes in volume.

Fig. 1.

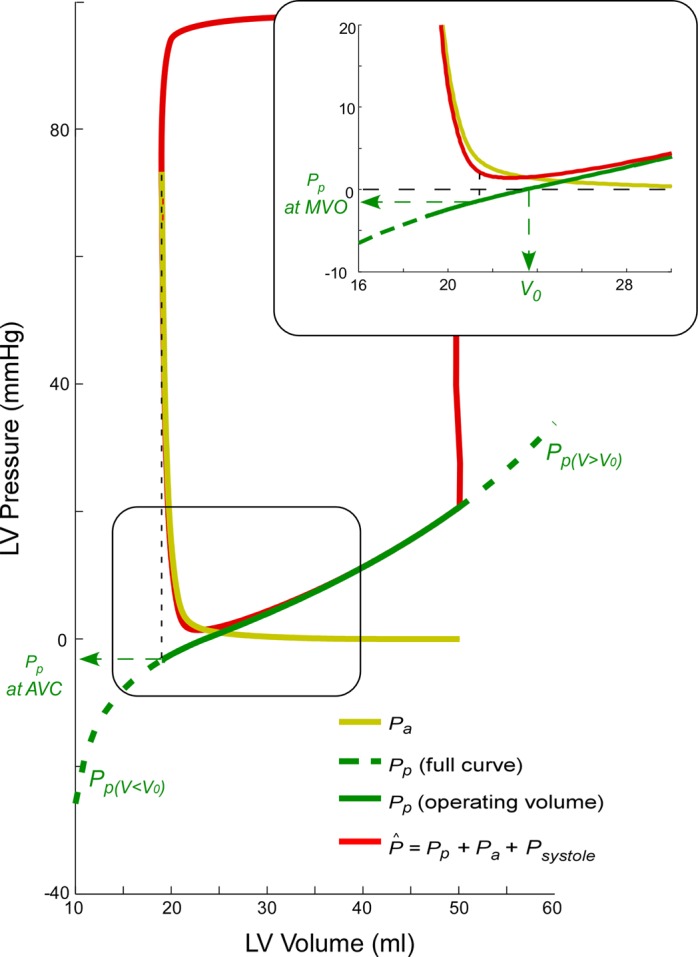
Theoretical model decoupling of active (yellow) and passive (green) left ventricular (LV) diastolic pressures. Total pressure is shown in red. Early filling is shown in detail in the inset. P_a, active diastolic pressure; P_p, passive diastolic pressure; AVC, aortic valve closing; MVO, mitral valve opening; V, LV volume; V₀, equilibrium volume; P̂, estimated pressure; P_systole, systole pressure.

As the LV relaxes during the isovolumic phase, pressure falls toward the volume-dependent value of passive pressure. The time constant of relaxation (τ) characterizes the rate of relaxation and is generally calculated from a monoexponential equation. In our global model, the passive time-varying volume-dependent pressure is taken as the asymptote of relaxation used in the conventional method for measuring τ (coefficient A in appendix Eq. A7). Additionally, because signals are analyzed for the full diastolic period at a time, fitting τ is not only confined to the isovolumic phase. Instead, the P_a waveform is obtained from aortic valve closing to mitral valve opening. Alternative to the experimental formulation of relaxation, a logistic model has been proposed that has shown P_a to be less load dependent (15). And recently, a more complete physical model has been implemented that best fits the pressure phase plane and integrates both the exponential and logistic relationships (3). Designated “kinematic” model of diastole, the latter includes an additional parameter to define diastolic properties. We tested the performance of the optimization algorithm to fit these alternative formulations, which include additional degrees of freedom (see appendix for details).

Passive pressure is defined using a piecewise continuous and differentiable function that has different constitutive parameters for volume values below and beyond V₀. Consequently, LV instantaneous pressure is expressed as a function of volume and time, as well as of six parameters that define diastolic properties: τ, V₀, the passive stiffness constants below (S₋) and above V₀ (S₊), and well as LV minimum dead (V_d) and maximal achievable volumes (V_m).

Until today, these mathematical foundations could only be fully solved using volume clamp experiments to uncouple P_a from P_p. We hypothesized that a proper optimization algorithm is capable of separating both effects if solutions are confined to physiologically sound values of the parameters. First, one degree of freedom was reduced by the smoothness assumption for the piecewise expression of P_p below and beyond V₀ (22). Second, we defined a cost function as the squared distance from observed to predicted pressure, based on the remaining five parameters. Third, we implemented a global optimization algorithm to search for the best set of solutions that minimizes this cost function (7). Notice that, because of the high input dimensionality, conventional nonlinear fitting algorithms are highly sensitive to initialization, frequently reaching convergence on spurious solutions. Instead, global optimization methods are designed to provide solutions to problems that may contain multiple local minima. Thus we selected a multiple-initialization trust-reflective algorithm, allowing constrained boundaries of parameters, within user-defined values (4, 5). We seeded the algorithm with 50 random initializations in parallel. When more than one local minimum was reached, the solution with lowest cost function was automatically selected. Importantly, if time is referenced to end systole and constitutive indexes remain unchanged by definition, the algorithm can process multiple or single beats, interchangeably. Normalized Jacobian and resolution matrices were calculated and plotted to assess dependencies and index sensitivity.

We defined “conventional methods” as the exponential fitting of τ confined to the isovolumic period for characterizing relaxation (as defined in the appendix Eq. A7) and the curvilinear fitting of the EDPVR for assessing stiffness. We described the active relaxation curve using τ, as well as the estimated residual active pressure at ED. To describe the fitted passive PV curve we used the following: 1) the coefficients from Eqs. A2 and A3; 2) the estimated P_p at aortic valve closure and filling onset (optimization method only); and 3) its slope dP/dV_{V ≥ V0} = S₊/(V_m − V) at V = V₀ and V = end-diastolic volume (EDV) (EDPVR and global optimization methods).

Monte Carlo simulation.

Because there is no true gold standard of diastolic function in vivo, we used synthetic data to compare the performance of the global fitting algorithm against the conventional isovolumic and EDPVR methods (see appendix for details). From measured volume signals, we generated 1,000 synthetic pressure tracings by entering random values of τ, S₊, V₀, V_m, and V_d and forcing physiological bounds. We added random noise and compared the capability of conventional and global optimization algorithms to recover the input space of randomly entered values.

Animal study.

Twenty-six adult minipigs (60 ± 10 kg) underwent high-fidelity instrumentation experiments. Animals were preanesthetized with ketamine and xylazine and mechanically ventilated. Complete anesthesia and relaxation were maintained by propofol infusion (0.2 mg·kg⁻¹·min⁻¹), as well as repetitive intravenous boluses of pentobarbital (15 mg/kg + 5 mg·kg⁻¹·15 min⁻¹) and pancuronium (0.2 mg·kg⁻¹·15 min⁻¹). Through the right carotid artery, we placed a 7F pigtail conductance PV catheter (CD-Leycom) into the LV and connected it to a dual-field conductance processor (Sigma 5DF, CD-Leycom). An occlusion balloon was placed in the inferior vena cava (IVC) for preload manipulation. Twenty-two animals were studied in a closed-chest design, at baseline, and during dobutamine (1–10 μg·kg⁻¹·min⁻¹) and esmolol (25–200 μg·kg⁻¹·min⁻¹) infusions. Fourteen animals underwent median sternotomy without opening the pericardium. These animals were studied at baseline, during dobutamine (1–10 μg·kg⁻¹·min⁻¹) and esmolol (25–200 μg·kg⁻¹·min⁻¹) infusions, after acute volume overload (1,000- to 1,500-ml saline isotonic solution in 5–10 min), and after left main coronary artery microembolization (CME) of polystyrene microspheres (mean diameter 45 μm, Polysciences, Warrington, PA). PV data were acquired during transient IVC occlusion, three times for each state. Simultaneous B-mode echocardiographic images and V signals were recorded for calibration (40). All data were collected during ventilator disconnection and digitized at 1,000 Hz. Animals were euthanized at the end of the experiments. Experimental protocols were approved by the local Institutional Animal Care Committee.

Clinical study.

Twenty-eight patients (58 ± 11 yr old, 13 women) in sinus rhythm undergoing left heart catheterization were included. Indications for catheterization were ruling out coronary artery disease in 7 patients with dilated cardiomyopathy (DCM), 12 patients with chest pain and normal ejection fraction, and 9 cirrhotic patients under evaluation for liver transplantation. A conductance PV 7F pig-tail catheter was placed in the LV, connected to a dual-field conductance processor (CD Leycom CFL-512), and calibrated by the hypertonic saline method (36). For acute preload reduction, an occlusion balloon (Nu-Vasive 40 mm) was introduced by the right femoral vein and placed in the junction of IVC and right atrium. PV loops were acquired during transient IVC occlusion at end-expiration apnea (36). Simultaneous Doppler-echocardiographic examinations were performed during the catheterization study. We used a broadband 1.75–4 MHz transducer on a Vivid 7 ultrasound system (General Electric Healthcare). We measured pulsed-wave Doppler flow parameters (transmitral E-wave deceleration time, E/A ratio, and isovolumic relaxation time), and averaged septal and lateral tissue-Doppler mitral annulus velocities (20, 41). The study protocol was approved by the local Institutional Review Committee, and all subjects provided written informed consent.

Statistical analysis.

Animal experiments were analyzed using paired t-tests and linear mixed-effects models (S-Plus version 8.0, Tibco), where appropriate. The effects of interventions on hemodynamic indexes were calculated as the fixed-effect estimates and their 95% confidence intervals. Fixed effects were adjusted for an open/closed chest design. Differences among phases were tested using simulation contrasts against baseline measurements. For the clinical study, three to five beats were averaged for each patient, and variables are described as means ± SD. Determinants of error of the conventional methods was assessed by multivariate linear regression and backwards stepwise variable selection based on Akaike's information criterion. Asymptotic confidence intervals are inaccurate in nonlinear fitting problems. Instead, we used the Monte Carlo method (1,500 random replicates of a clinical example) (7) to calculate the confidence intervals and cross-correlation of stiffness coefficients. Bland-Altman analysis and intraclass correlation coefficient (R_ic) were used to assess agreement and reproducibility. Values of P < 0.05 were considered significant.

RESULTS

Monte Carlo simulation study.

The algorithm recovered accurate and unbiased values of the original values of τ and V₀ in the 1,000 PV data sets. Agreement with entered values of S₊, V_m, and V_d was also good (Table 1). The slopes of the passive PV curve were also accurately estimated, and the performance of the global fitting algorithm outweighed that of the conventional methods.

Table 1.

Monte Carlo simulation study: agreement between the conventional and the optimization methods to fit the prespecified indexes of diastolic function

	Conventional Method			Optimization Method
	Ric	Bias	Random error	Ric	Bias	Random error
τ, ms	0.92	2	5	0.99	0	2
V0, ml	0.98	0	4	1.00	0.04	0.5
S−, mmHg				0.99	0.06	1.6
Vd, ml				0.84	0.09	3.6
S+, mmHg	0.92	0.21	5	0.99	0.15	1.41
Vm, ml	0.93	0.56	11	0.99	0.26	3.4
dP/dV at V0, mmHg/ml	0.94	10−4	0.1	0.99	10−4	0.02
dP/dV at EDV, mmHg/ml	0.97	0.04	0.1	0.99	10−4	0.05

R_ic, intraclass correlation coefficient; τ, time constant of left ventricular (LV) relaxation; V₀, equilibrium volume; S₋, constant of diastolic elastic recoil; V_d, dead volume asymptote; S₊, constant of diastolic passive stiffness; V_m, maximum volume asymptote; dP/dV, derivative of LV pressure with respect to volume; EDV: end-diastole volume.

Animal study.

The algorithm converged in all except 8 of 274 data sets (97%), with a root mean square error (RMSE) between measured and fitted pressure of 1.62 ± 1.13 mmHg (Table 2). The full decoupled active and passive pressure curves were obtained in all experimental conditions. Pooled data from all experiments showed good agreement between the optimization algorithm and the conventional EDPVR method for assessing V₀ (R_ic = 0.74, error = 8 ± 8 ml), but limited agreement to assess LV stiffness both in terms of dP/dV at V₀ (R_ic = 0.41, error = 0.40 ± 0.19 mmHg/ml), and dP/dV at EDV (R_ic = 0.43, error = 0.43 ± 0.36 mmHg/ml).

Table 2.

Animal study: effects of acute hemodynamic interventions on diastolic properties

	Baseline	Esmolol	Dobutamine	Volume	CME
Animals, n	25	15	18	6	4
Runs, n	102	75	69	18	10
Hemodynamic data
Heart rate, beats/min	91 (83–99)	79 (71–87)*	111 (103–118)*	90 (81–100)	74 (63–85)*
Duration of diastole, ms	357 (304–410)	435 (381–488)*	308 (255–362)*	296 (235–357)*	470 (400–539)*
ESV, ml	23 (20–26)	24 (21–27)	18 (15–21)*	26 (22–30)	41 (37–45)*
EDV, ml	48 (43–53)	49 (44–53)	44 (39–49)*	57 (51–63)*	60 (53–66)*
EDP, mmHg	9 (7–10)	9 (8–11)	9 (7–10)	14 (12–16)*	14 (12–17)*
Peak systolic pressure, mmHg	94 (85–103)	85 (76–94)*	105 (96–113)*	95 (84–105)	47 (35–59)*
ESP, mmHg	63 (56–70)	55 (47–62)*	63 (56–71)	63 (54–71)	25 (15–36)*
dP/dtmin, mmHg/s	1,497 (1,228–1,766)	1,237 (965–1,509)*	1,629 (1,360–1,899)	1,278 (967–1,590)	618 (470–1,163)*
dP/dtmax, mmHg/s	1,805 (1,468–2,142)	1,215 (869–1,562)*	3,822 (3,482–4,161)*	1,796 (1,338–2,255)*	1,113 (509–1,185)*
Diastolic properties (conventional methods)
Isovolumic τ, ms	54 (47–61)	53 (46–60)	43 (36–50)*	66 (58–75)*	94 (83–104)*
EDPVR V0, ml	16 (12–20)	15 (11–19)	15 (11–19)	18 (13–24)	25 (18–32)*
EDPVR S+, mmHg	12 (9–14)	15 (12–18)	13 (10–16)	15 (11–19)	25 (20–30)*
EDPVR Vm, ml	72 (65–80)	77 (69–85)	69 (61–77)	85 (74–96)*	91 (77–105)*
EDPVR dP/dV at V0, mmHg/ml	0.19 (0.14–0.25)	0.19 (0.13–0.25)	0.22 (0.17–0.28)	0.18 (0.08–0.28)	0.50 (0.37–0.63)*
EDPVR dP/dV at EDV, mmHg/ml	0.84 (0.36–1.32)	0.69 (0.2–1.18)	1.15 (0.68–1.63)	1.25 (0.57–1.93)	1.90 (1.03–2.76)*
Diastolic properties (optimization method)
τ, ms	53 (46–59)	48 (41–55)	47 (41–54)*	68 (59–76)*	89 (79–99)*
Pa at ED, mmHg	0.3 (0.1–0.5)	0.1 (−0.2–0.3)	0.3 (0–0.5)	0.8 (0.4–1.1)*	1.5 (1.1–1.9)*
V0, ml	21 (16–26)	15 (10–20)*	20 (15–25)	21 (15–28)	30 (22–38)*
S−, mmHg	4 (2–6)	3 (1–5)	5 (3–7)	5 (2–8)	21 (17–24)*
Vd, ml	3 (2–4)	4 (3–5)	4 (3–6)	6 (4–8)	2 (0–5)
Pp at aortic valve closure, mmHg	−0.1 (−1.1–0.9)	1.1 (0–2.2)*	−1.4 (−2.4–−0.3)*	0.2 (−1.2–1.7)	0.0 (−1.8–1.7)
Pp at filling onset, mmHg	0.4 (−0.5–1.3)	1.7 (0.7–2.6)*	−0.7 (−1.6–0.2)*	1.3 (0.1–2.6)	1.5 (0–3.1)
S+, mmHg	8 (6–10)	10 (8–12)*	11 (9–13)*	15 (12–17)*	13 (9–16)*
Vm, ml	67 (60–74)	71 (63–78)	66 (59–73)	83 (72–93)*	81 (68–94)
dP/dV at V0, mmHg/ml	0.21 (0.17–0.26)	0.20 (0.16–0.25)	0.28 (0.23–0.32)*	0.26 (0.20–0.32)	0.44 (0.36–0.52)*
dP/dV at EDV, mmHg/ml	0.67 (0.51–0.82)	0.58 (0.42–0.75)	0.66 (0.5–0.82)	0.73 (0.47–0.98)	1.47 (1.13–1.8)*

Values show the estimated fixed effects (with 95% confidence interval in parentheses) from mixed models controlling for repeated measures within animal and open/closed chest design. CME, coronary microembolization; ESV, end-systolic volume; EDP, end-diastolic pressure; ESP, end-systolic pressure; dP/dt_min and dP/dt_max, minimal and maximal derivative of LV pressure with respect to time, respectively; EDPVR, end-diastolic pressure-volume relationship; P_a, active diastolic pressure; P_p, passive diastolic pressure.

^*P < 0.05 vs. baseline.

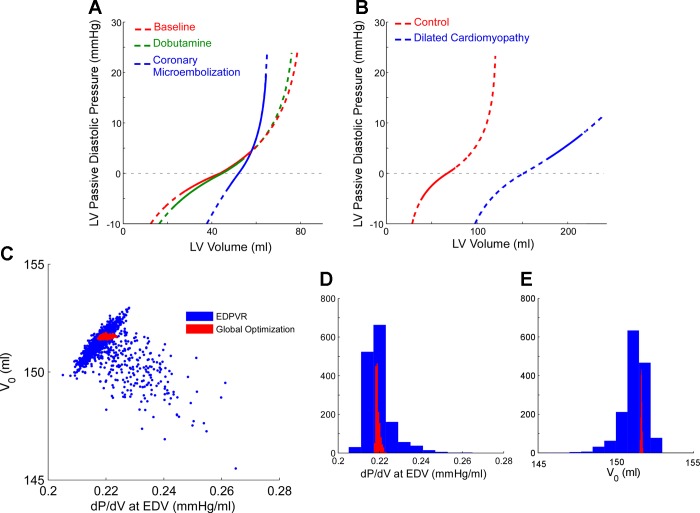
As expected, the most extreme changes in LV passive properties (dP/dV and V₀) were obtained by CME (Table 2 and Fig. 2A). Inotropic interventions did not modify passive properties below V₀ (no changes in S₋ or V_d). However, inotropic modulation changed the operative V range and/or the V₀, resulting in significant changes in P_p at aortic valve closure and at mitral valve opening. Importantly, small changes in LV volume during the isovolumic phase increased passive pressure from −0.8 ± 3.6 mmHg at aortic valve closure to −0.1 ± 3.3 mmHg (P < 0.0001) at mitral valve opening (pooled data sets). In 32 of the data sets (12% of total number), P_a at ED was > 0.5 mmHg, reflecting incomplete relaxation during volume infusion and CME.

Fig. 2.

Full characterization of passive diastolic pressure-volume (PV) relationship. A: three phases obtained during hemodynamic interventions in a representative animal experiment. B: curves obtained from a control subject (red) and a dilated cardiomyopathy (DCM) patient (blue). Dotted lines represent the full PV relationship, whereas solid lines represent the curve operated by the ventricle during the cardiac cycle. C–E: uncertainty of stiffness parameters measured from the DCM patient in B. Charts show the scatter plot (C) and distribution functions (D and E) results of Monte Carlo estimation of stiffness parameters obtained by the end-diastolic PV relationship (EDPVR) (blue) and global methods (red) for that particular data set. Notice the narrowing in confidence intervals and reduction in cross-correlation between parameters obtained using the global optimization method. dP/dV, derivative of LV pressure with respect to volume; EDV, end-diastolic volume.

Clinical study.

The algorithm converged in all data sets with a RMSE of 2.6 ± 2.9 mmHg. A wide range of relaxation rates, elastic restoring forces, and stiffness was observed (Table 3; Figs. 2B and 3). The agreement with the isovolumic method to assess τ was good. The EDPVR method returned higher autocorrelation and much wider confidence intervals of stiffness parameters than the global optimization method (Fig. 2, C–E). The agreement of the optimization algorithm with the EDPVR method for dP/dV was only moderate, particularly at EDV (Table 3). The V₀ was below end-systolic volume (ESV) in 16 patients and between ESV and EDV in 12. In consequence, the role of passive forces during early diastole was found to be highly variable (P_p at mitral valve opening ranging from −5.3 to +13.7 mmHg). P_p at mitral valve opening was the only determinant of the error of the conventional method to estimate τ (P < 0.001). Absolute error of the EDPVR to estimate dP/dV at V₀ and at EDV was higher in patients with ejection fraction < 0.45 (P < 0.001 and P = 0.02, respectively).

Table 3.

Clinical study

	Optimization Method		Conventional Method		Agreement
	Mean ± SD	Range	Mean ± SD	Range	Ric	Absolute error	Relative error, %
τ, ms	50 ± 10	36–77	50 ± 9	37–75	0.85	0 ± 5	0 ± 10
V0, ml	55 ± 47	8–166	53 ± 33	18–130	0.88	8 ± 20	13 ± 38
S−, mmHg	9 ± 11	0–39
Vd, ml	15 ± 17	1–60
S+, mmHg	23 ± 17	5–80	18 ± 14	2–46	0.23	8 ± 16	41 ± 71
Vm, ml	160 ± 77	61–354	149 ± 74	56–353	0.86	18 ± 36	12 ± 22
dP/dV at V0, mmHg/ml	0.22 ± 0.12	0.07–0.51	0.20 ± 0.11	0.05–0.43	0.23	0.05 ± 0.13	27 ± 58
dP/dV at EDV, mmHg/ml	0.46 ± 0.30	0.13–0.46	0.73 ± 0.65	0.05–2.78	0.26	−0.27 ± 0.60	−16 ± 64

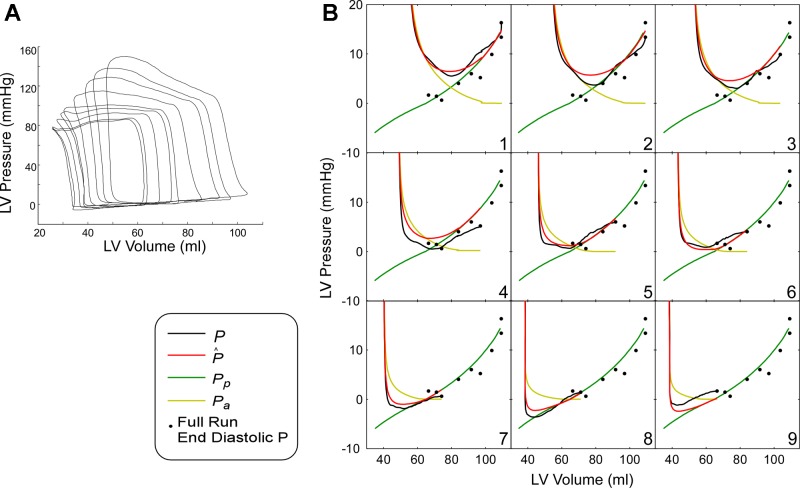
Fig. 3.

Full characterization of LV main diastolic properties by PV analysis in a control subject. A: PV data sets of 9 beats obtained during inferior vena cava (IVC) occlusion. B: beat-by-beat representation of each measured diastolic PV curve (black), fitted pressure (red), as well as active (yellow) and passive (green) contributions to total pressure. End-diastolic PV points for all beats are also shown (black dots).

Doppler-derived transmitral E-wave deceleration time, E/A ratio, isovolumic relaxation time, or tissue-Doppler mitral annulus velocity did not correlate with reference indexes of diastolic properties obtained using the optimization algorithm (τ, V₀, S₊, S₋, dP/dV at V₀ and at EDV, all P > 0.05).

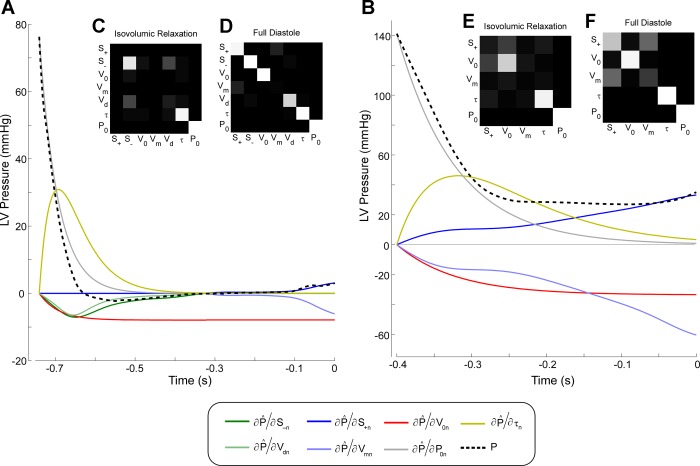
The sensitivity analysis demonstrated the relative contribution of each property to the instantaneous LV pressure (Fig. 4). Resolution matrices showed relatively low autocorrelation among diastolic parameters (Fig. 4). Incomplete relaxation was observed in two patients with DCM (P_a values of 0.6 and 1.4 mmHg at ED, respectively; Fig. 4B).

Fig. 4.

Sensitivity analysis of LV main diastolic properties. A: normalized Jacobian matrix of a control subject. Measured pressure is shown in the black dotted line. The impact of each diastolic index on instantaneous pressure is shown as the partial derivative of fitted pressure with respect to each index, normalized by its value. Elastic restoring forces are shown in green [constant of diastolic elastic recoil (S₋) and LV minimum dead volume (V_d)], diastolic stiffness in blue [constant of diastolic passive stiffness (S₊) and LV maximal achievable volume (V_m)], V₀ in red, time constant of relaxation (τ) in yellow, and LV pressure at the onset of diastole (P₀) in gray. Notice that early filling is governed by P₀, τ, V₀, and elastic restoring forces, whereas late filling is only influenced by V₀ and diastolic stiffness. B: identical analysis as in A, in a patient with DCM. This ventricle does not contract below V₀, so there is no contribution to filling of restoring forces. Additionally, notice that relaxation is not completed by end diastole, so end-diastolic pressure (EDP) is partially influenced by τ. C–F: resolution matrices of isovolumic relaxation (C and E) and full diastolic period (D and F). In this representation, the degree of autocorrelation among parameters is shown as the hue of gray, from no relationship (black) to full correlation (white).

Reliability analysis.

High R_ic values for intra- and interobserver reproducibility (15 randomly selected data sets, blinded analysis 3 mo apart) were obtained for τ (0.96 and 0.99, respectively), V₀ (0.99 and 0.92), dP/dV at V₀ (0.96 and 0.83), and dP/dV at EDV (0.81 and 0.87) using the global optimization method. Inter- and intraobserver reproducibility R_ic values of the EDPVR method for assessing LV stiffness were remarkably lower for V₀ (0.89 and 0.75), dP/dV at V₀ (0.70 and 0.67), and dP/dV at EDV (0.73 and 0.25, respectively).

Single-beat analysis.

Excellent agreement between entered values and single-beat coefficients were obtained for τ and dP/dV in the Monte Carlo simulation study. Also, the accuracy of the single-beat method was acceptable in the animal and clinical studies for dP/dV and V₀ (Table 4).

Table 4.

Agreement between single-beat and multiple-beat analysis using the global optimization method

	Ric	Bias	Random Error
Monte Carlo study*
τ, ms	0.97	0.20	3.8
V0, ml	0.98	0.17	2.6
dP/dV at V0, mmHg/ml	0.99	2 × 10−4	0.02
dP/dV at EDV, mmHg/ml	0.99	4 × 10−3	0.04
Animal study
τ, ms	0.77	14	20
V0, ml	0.59	10	11
dP/dV at V0, mmHg/ml	0.14	0.36	0.52
dP/dV at EDV, mmHg/ml	0.41	0.02	0.44
Clinical study
τ, ms	0.69	3	8
V0, ml	0.94	8	15
dP/dV at V0, mmHg/ml	0.39	0.08	0.16
dP/dV at EDV, mmHg/ml	0.65	0.07	0.24

^*Compared with entered reference values.

Alternative models of relaxation.

The RMSE of the logistic and kinematic models for the full animal hemodynamic runs was similar to that of the exponential fitting: 1.50 ± 1.58 and 1.96 ± 1.06 mmHg, respectively. Correlation between exponential and logistic values of τ was R = 0.95. Correlation of exponential τ with the kinematic parameters of relaxation (μ·E_K) was R = 0.71. An example of different model fitting in the pressure-phase plane during relaxation is shown in Fig. 5.

Fig. 5.

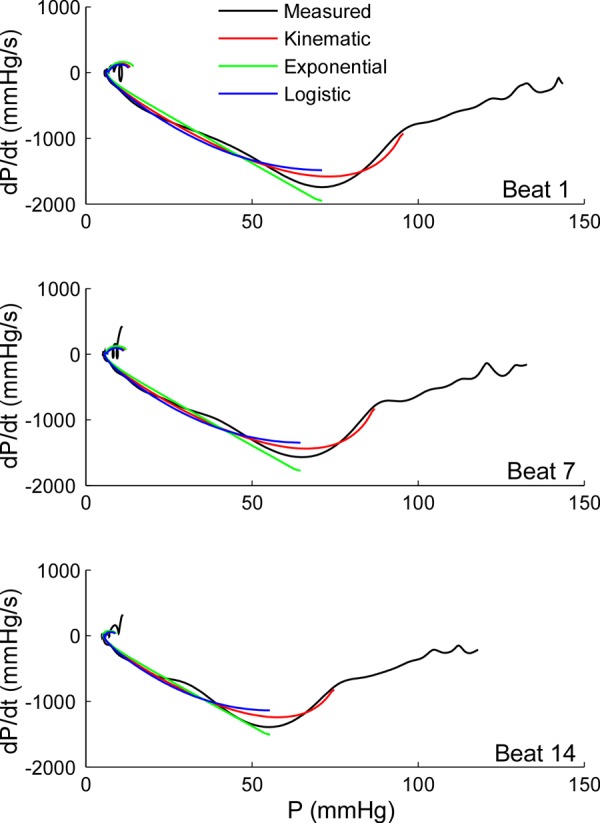
Alternative mathematical model fittings for pressure data during isovolumic relaxation shown in the pressure phase plane. The results of adjusting pressure-time data using the optimization algorithm implementing different relaxation functions are shown in a representative animal data set of 14 beats obtained during IVC occlusion. Active relaxation is described using the exponential (Eq. A1, green), the logistic (Eq. A9, blue), and the kinematic models (Eq. A10, red), overlaid on measured pressure (black, from peak LV pressure to end diastole). In the pressure-phase plane, these models are depicted as linear, one parameter curvilinear, and two parameter curvilinear, respectively. Beats 1, 7, and 14 are shown. Notice that, by design, the optimization algorithm estimates a single set of relaxation parameters [τ, τ-logistic, and μ (resistive parameter equivalent to τ) and E_k (lumped elastic parameter accounting for the elastic restoring force)] for the exponential, logistic, and kinematic models, respectively, from the 14 beats in the data set. Thus individual beat fitting results are necessarily worse than if each beat were fitted independently. dP/dt, minimal derivative of LV pressure with respect to time.

DISCUSSION

The present study validates a new method that yields the most complete, accurate, and reproducible assessment of main diastolic chamber properties available to date for the intact heart. Global fitting methods have demonstrated increased robustness in a number of biological processes (7, 17), but had never been used to analyze LV chamber properties. With this method, we have been able to assess for the first time the full active and passive mechanical properties in the intact heart (1, 18, 24) using conventional PV data. A number of factors account for this improved characterization: 1) increased statistical power resulting from combining within-beat and between-beat analysis, thereby including all measured data points during diastole; 2) simultaneous fitting multiple beats; 3) reduced sensitivity to exact identification of ED; and 4) accurate identification of the full passive PV relationship below and beyond the V₀. The performance of the method to fit a number of mathematical models demonstrates that the well-established foundations of diastolic function can now be incorporated to the data analysis, improving the reliability of translational and clinical research without any modification in the experimental setups.

The present study shows important limitations of the EDPVR method to characterize LV stiffness. A number of sources of error were identified. Among them were single-point fitting, variable degrees of residual relaxation at ED, the development of negative ED pressure (EDP) during severe occlusions, and the wide confidence intervals of fitted parameters in vivo (Fig. 2, C–E). We believe these findings question the single-point EDPVR fitting method as the true gold standard of passive stiffness in cardiovascular research.

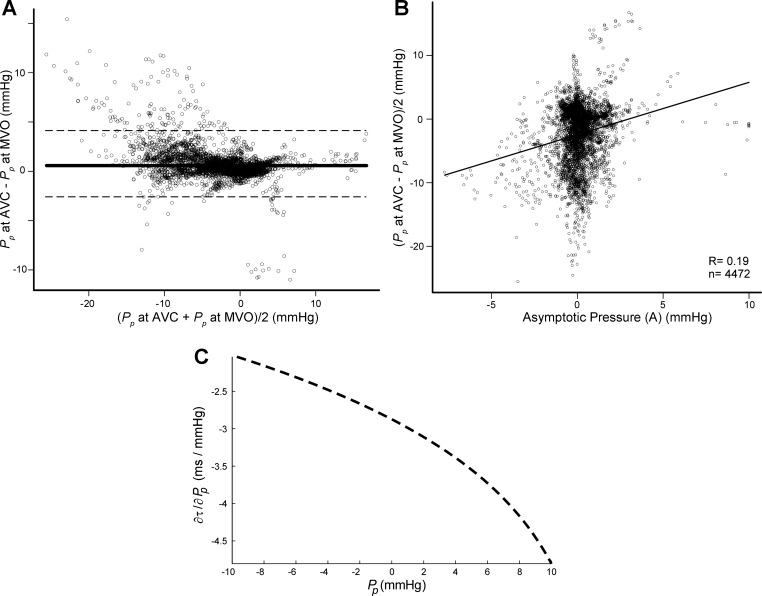
According to our findings, current methods for measuring relaxation can also be improved. Because of the impossibility of decoupling passive pressure, it is recognized that the isovolumic τ amalgamates, in variable degrees, the effects of relaxation and restoring forces in ways that are not fully understood (11, 38). Conventional algorithms for measuring τ in the intact heart are based on fitting the LV pressure-time data during the time interval between aortic valve closure [or at minimal derivative of left ventricular pressure with respect to time (dP/dt)] and 5 mmHg above EDP. The kinematic model represents a comprehensive approach to the physical properties of relaxation, is capable of fitting pressure data even before minimal dP/dt, and has established a causal connection between the parametric limits of isovolumic relaxation as a physical process (3). However, whatever formulation is preferred (3, 6, 15, 38), all of these methods share in common the assumption of a constant volume (and therefore asymptotic pressure) throughout the isovolumic period (10). A number of factors acting immediately after aortic valve closure, including aortic valve regurgitation or valve bulging, frequently cause small changes in chamber volume. Because the slope of the negative passive PV curve is steep at that point, even small changes in volume during the early relaxation phase translate into a significant time-varying pressure (average 80% in our animal data set). Whenever instantaneous volume data are available, our global fitting can measure pure active relaxation in the intact heart, dissecting it from the effect of elastic recoil during early diastole (39). Importantly, we showed that the asymptote of conventional single-beat nonfilling methods (A in appendix Eq. A7) does not capture the variable passive pressure during relaxation. This inaccuracy induces a significant error in the estimation of τ and may be partially responsible for the previously reported load dependence of relaxation constants (Fig. 6) (28). The finding of a significant effect of inotropic state on restoring forces (e.g., P_p at aortic valve closure and mitral valve opening in Table 2) suggests that the lusotropic effects in vivo of drugs that concomitantly affect inotropy may need to be revisited. In fact, we found that esmolol had no effect on true relaxation. Instead, by shifting the passive PV relationship to the left (i.e., lowering V₀), this drug blunted negative suction pressure.

Fig. 6.

Impact of passive pressure during the isovolumic phase on the estimation of relaxation. A: Bland-Altman plot of pooled data of all beats from all animal experiments showing the bias (solid line) ± SD (dashed line) showing the individual variation of passive pressure from AVC to MVO. The lack of full agreement demonstrates volume-mediated changes in passive pressure in this phase. B: scatterplot between asymptotic pressure obtained by single-beat analysis using Eq. A7 (horizontal axis) and average isovolumic passive pressure obtained by the global optimization method (vertical axis). The lack of correlation demonstrates the limitations of the conventional method for measuring relaxation to accurately uncouple passive pressure during the isovolumic phase. C: impact of the uncertainty of estimating passive pressure during the isovolumic phase for the characterization of relaxation using the conventional exponential method (Eq. A7 analytic derivative solved for a τ value of 50 ms and P₀ of 80 mmHg). Notice that 1-mmHg error in the estimation of P_p induces an error up to 4.5 ms in measured τ. As shown in B, these errors are frequently much higher. We believe that this mechanism may partially account for the preload dependence of relaxation previously reported using the conventional single-beat isovolumic method.

For the first time in humans, we have been able to quantify the effects of restoring forces facilitating depressurization and early filling in the intact heart. Our observations confirm the findings of volume clamp experiments demonstrating the abolition of restoring forces in the failing ventricle (33). By means of the Jacobian matrix, the new solving method additionally provided a sensitivity analysis of the contribution of each parameter to diastolic pressure in every particular data set, as illustrated in Fig. 4. It is now possible to identify to what extent impaired relaxation, stiffness, or operating stiffness (changes in the operating EDV and ESV volume values, which shift position in the PV curve) is responsible for abnormal filling pressures in a particular patient (12, 16, 33). The automatic identification of those cases in which incomplete relaxation may mimic increased stiffness (34) constitutes an illustrative example of the advantages of uncoupling active diastolic forces from passive ones.

Based on fitting all of the PV diastolic data, the global optimization method does not require identifying the end of the isovolumic period and is much less sensitive to an exact identification of ED. These features render the method particularly promising in the right ventricle, a location where precisely defining these temporal events is challenging (26).

To avoid the need for IVC occlusion, three studies have proposed using within-beat filling data to measure stiffness (9, 25, 43). These methods rely on first subtracting isovolumic relaxation pressure to measured pressure and then nonlinearly fitting the resultant PV curve. However, all single-beat methods estimate relaxation pressure assuming a zero asymptote (9, 25, 43). As shown in our study, conditions of extreme loading, inotropic interventions, CME, and DCM can remarkably shift the ESV away from V₀, introducing a significant contribution of the passive component to total early diastolic pressure. Figure 6 clearly confirms volume clamp observations that passive forces during early filling cannot be denied, yielding previous single-beat methods (9, 25, 43) ill posed. Moreover, our method has an additional advantage over these previous single-beat approximations. Because the algorithm processes data from multiple beats in an integral fashion, the spontaneous variations in load caused by breathing (19) can be incorporated in future developments. For these reasons, we believe that global optimization is the most accurate method available to date to characterize diastolic properties in vivo without the need of occluding the vena cava. In the future, when combined with image based methods for measuring LV volume values, this type of algorithms will improve the assessing of LV diastolic properties in clinical practice.

Doppler echocardiography is the noninvasive method most frequently used to assess diastolic function in bedside clinical examinations, but the present study showed a poor correlation of currently recommended methods (20) with intrinsic global chamber properties. E-wave deceleration time is known to physically depend on average diastolic operating stiffness, measured as the average intrabeat PV linear relationship, from minimum pressure to ED (13). The lack of correlation of the deceleration time with passive PV curve parameters observed in our study is probably related to its sensitivity to relaxation (32). Operating stiffness during diastasis can also be accurately determined by fitting the transmitral flow spectrogram to a kinematic mathematical model (19). Despite the fact that LV relaxation is still frequently not completed during this phase (Fig. 4B), the relationship of Doppler-derived diastatic operating stiffness with passive PV curve parameters deserves further investigation. Advances in imaging techniques are rapidly improving the clinical assessment of myocardial deformation. Further studies on how deformation-based measurements, such as myocardial strain, untwisting, and detorsion, reciprocally interact with intrinsic global chamber properties are warranted; the possibility of now measuring global chamber elastic recoil is particularly promising in this context.

Limitations and future directions.

Analyzing the effects of inotropic interventions in patients would have added interesting translational evidence from the clinical setting. However, we did not perform repeated-measures experiments in patients due to the highly invasive nature of the simultaneous left and right catheterization procedure of measuring PV loops during balloon caval occlusion.

Although our method fitted the PV-time relationship acceptably well during rapid filling, there are additional factors influencing this relationship that were not taken into account (30). Flow inertia, vorticity, ventricular interdependence, pericardial properties, myocardial viscoelasticity, and non volume dependent untwisting deformation may have a complementary effect on the PV relationship (39). Also, extreme concentric remodeling moves the pressure-decay curve away from the exponential model (10). Additionally, it has been suggested that atrial inotropic attributes may confound the EDPVR (42), and the interpretation of the V₀ is a matter of debate (31, 37). By design, our method assumes fixed indexes of relaxation for all beats during preload manipulation. Because it accounts for volume-dependent passive pressure during relaxation, we introduce, for the first time, a method that is not sensitive to the assumption of a free asymptote (Fig. 6). However, relaxation per se may be dependent both on volume and on cycle length (28, 29). It is also well recognized that passive properties (as characterized by our method) are influenced by chamber stiffness, and also by myocardial stiffness and chamber size remodeling (1). Due to these factors, there is still room for improvement in the mathematical modeling of diastole (Fig. 3). However, the choice of extra parameters should be guided by physiological insight and verified by experimental and clinical data. The sensitivity and resolution analyses proposed in this study provide an efficient systematic methodology to benchmark these prospective models. For example, incorporating an additional coefficient that accounts for load-influencing τ can be readily tested. Also, further mathematical modeling can be incorporated to characterize the passive stress-strain relationship and account for true myocardial diastolic stiffness (1). Finally, the implementation of data weights to particularly meaningful events of diastole (e.g., minimum dP/dt) may further improve the robustness of fitted parameters, particularly when using the largest parameter space such as required for Eq. A10.

Conclusions.

The results of accuracy, precision, applicability, sensitivity, and reliability demonstrate that optimization algorithms are the best methods for assessing LV global diastolic chamber properties in clinical and preclinical research. A more accurate, robust, reliable, and complete characterization of diastolic function may have important applications in clinical cardiovascular research. With the type of methods proposed, the independent role of a prolonged relaxation, increased passive stiffness, and operating volume can be isolated as the cause of diastolic chamber function in a given patient. This can be relevant in conditions of extreme load, such as valvular regurgitation or congenital heart disease, in which true chamber abnormalities are particularly complex to address. In patients with hypertrophic or hypertensive cardiomyopathy, prolonged relaxation frequently coexists with increased stiffness, and the mechanism responsible for high filling pressures can now be isolated. Interestingly, the role of elastic recoil forces in these conditions has never been addressed. Finally, due to the issues discussed above, the global optimization tool seems a promising tool for understanding the particular forces governing the diastolic function of the right ventricle. The combination of imaging modalities and data processing algorithms that do not require a catheter-driven manipulation of preload will facilitate a better understanding of diastolic dysfunction in these clinical disorders. Therefore, we believe that global optimization of PV data is the best available method to characterize diastolic function. Researchers aiming to understand the effects of drugs on diastolic function, to characterize new animal models of disease, or to test noninvasive surrogate techniques for assessing diastolic function in the clinical setting should benefit from this new method.

GRANTS

This study was supported by Grants PIS09/02603, RD12/0042 (Red de Investigación Cardiovascular), BA11/00067 (to J. Bermejo), and CM12/00273 (to C. Pérez del Villar) from the Instituto de Salud Carlos III, Spain. A. Gonzalez-Mansilla and C. Pérez del Villar were partially supported by grants from the Fundación para Investigación Biomédica Gregorio Marañón, Spain. J. Bermejo, P. Martizez-Legazpi, and J. C. del Álamo were partially supported by National Heart, Lung, and Blood Institute Grant 1R21 HL-108268-01 (to J. C. del Álamo).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: J.B., R.Y., J.C.d.A., D.R.-P., and J.C.A. conception and design of research; J.B., R.Y., C.P.d.V., D.R.-P., P.M.-L., Y.B., J.C.A., M.M.D., A.G.-M., A.B., and J.E. performed experiments; J.B., R.Y., C.P.d.V., J.C.d.A., P.M.-L., Y.B., J.C.A., M.M.D., A.G.-M., and A.B. analyzed data; J.B., R.Y., C.P.d.V., J.C.d.A., D.R.-P., P.M.-L., Y.B., J.C.A., and M.M.D. interpreted results of experiments; J.B., P.M.-L., and A.G.-M. prepared figures; J.B., C.P.d.V., and J.E. drafted manuscript; J.B., R.Y., C.P.d.V., J.C.d.A., D.R.-P., P.M.-L., J.C.A., and F.F.-A. edited and revised manuscript; J.B., R.Y., C.P.d.V., J.C.d.A., D.R.-P., P.M.-L., J.C.A., M.M.D., A.G.-M., A.B., J.E., and F.F.-A. approved final version of manuscript.

APPENDIX

Theoretical model.

To date, active and passive mechanical properties can only be completely decoupled by driving nonfilling beats using volume clamp experiments (22, 27, 38, 39). In these experiments, relaxation is typically described using an exponential equation as

$${\text{P}}_{\text{a}(t\text{,V})}=[{\text{P}}_0-{\text{P}}_{\text{p}(\text{V})}]\cdot e^{-t/\tau }$$ (A1)

where P_a designates active relaxation pressure, P₀ measures LV pressure at the onset of diastole, P_p designates passive pressure, t is diastolic time measured from end systole to mitral valve closing, and τ is the time constant of LV relaxation. Passive mechanical diastolic properties are governed by a piecewise PV logarithmic relationship. The elastic restoring pressure generated when volume V < V₀ is modeled by

$${\text{P}}_{\text{p}(\text{V}<{\text{V}}_{\text{0}})}=S_{-}\cdot \log \frac{{\text{V}}_{(\text{V}<{\text{V}}_0)}-{\text{V}}_{\text{d}}}{{\text{V}}_0-{\text{V}}_{\text{d}}}$$ (A2)

where V₀ is defined as LV V when P_p = 0, S₋ designates the stiffness constant for V < V₀, and V_d is the LV dead V asymptote. Above V₀, the PV relationship is

$${\text{P}}_{\text{p}(\text{V}>{\text{V}}_{\text{0}})}=-S_{+}\cdot \log \frac{{\text{V}}_{\text{m}}-{\text{V}}_{(\text{V}>{\text{V}}_0)}}{{\text{V}}_{\text{m}}-{\text{V}}_{\text{0}}}$$ (A3)

where S₊ designates the stiffness constant for V > V₀, and V_m is the maximal achievable volume asymptote.

For a relatively homogenous solid body undergoing elastic deformation, the slope of P_p is continuous. Therefore, at V₀, it must hold that dP_{V < V0}/dV = dP_{V > V0}/dV (22), and S₋ can be expressed as a volume normalization of S₊:

$$S_{-}=\frac{S_{+}({\text{V}}_0-{\text{V}}_{\text{d}})}{{\text{V}}_{\text{m}}-{\text{V}}_0}$$ (A4)

thereby reducing the number of parameters by one.

Active and passive mechanical properties act simultaneously during the full diastolic period, from aortic valve closure to mitral valve opening, such that full estimated pressure P̂ is a function of time and volume (Fig. 1):

$${\widehat{\text{P}}}_{(t,\text{V})}={\text{P}}_{\text{a}(t,\text{V})}+{\text{P}}_{\text{p}(\text{V})}$$ (A5)

If Eqs. A1–A4 are substituted into Eq. A5, the characterization of diastolic properties (τ, V₀, S₊, V_m, and V_d) can be formulated as the minimization of a cost function defined by the following expression of the difference between the theoretical pressure and the measured pressure, i.e.

$$\underset{\tau ,{\text{V}}_0,S_{+},{\text{V}}_{\text{m}},{\text{V}}_{\text{d}}}{\min }{\Vert {\widehat{\text{P}}}_{(t,\text{V})}-\text{P}\Vert }_2^2$$ (A6)

where P stands for measured pressure, and ${\Vert \overrightarrow{d}\Vert }_2$ is the Euclidean norm of the vector d, in this case, the vector of differences between the pressures estimated, P̂_(t,V), and measured, P, at all of the recorded time points. If all diastolic parameters are assumed to be load independent and time is normalized at end systole, Eq. A5 is valid for all beats in a data set. Thus Eq. A6 can be fitted interchangeably for a single beat and for a full hemodynamic run of IVC occlusion. S₋ and V_d are undetermined, if V does not fall below V₀ in any of the beats. Notice that identifying V < V₀ in a data set is not equivalent to measuring negative diastolic pressures, because P_a contributes with positive pressure (Eq. A5).

Algorithm solving.

For solving Eq. A6, we adapted Matlab built-in global optimization algorithms (release 7.13, Optimization and Global Optimization toolboxes, Natick, MA). All pressure and volume signals underwent low-pass filtering at 50 Hz. End systole (aortic valve closure) was defined as the instant of peak negative pressure derivative. End diastole (ED) was defined as the peak of the R-wave slope, confirmed visually beat by beat at the bottom-right corner of the PV diagram. Tolerance values for P̂ and input space (V,t) were set to 10⁻¹⁰ mmHg, 10⁻¹⁰ ml, and 10⁻¹⁰ s, respectively, with a maximum of 300 iterations and 10⁴ function evaluations. Due to the nonlinear nature of the fit, it is probable that the cost function has more than one minimum. This probability is enhanced by the relatively large (five) number of degrees of freedom in Eq. A6. To ensure that the optimization method finds the global minimum and neglects spurious local minima, we selected a trust-reflective algorithm because prespecified lower and upper constraints can be entered for each parameter (4, 5). Additionally, 50 random initialization sets of constrained parameters were seeded to the global optimization algorithm and processed in parallel. Upper and lower constraints for S₊, V₀, V_m, V_d, and τ were 6–80 mmHg, 20% of mean volume to 100% of EDV of first beat, 100% of EDV to 180% of EDV of first beat, 1% of EDV to 30% of EDV of first beat, and 15–150 ms, respectively.

The Jacobian matrix for all indexes was obtained from Eqs. A1–A4 from the analytic partial derivative of fitted P with respect to each parameter (∂P̂/∂τ, ∂P̂/∂V₀, …) and entered in the fitting algorithm for solving. For the sensitivity analysis, the Jacobian matrix was normalized to account for different parameter scaling [∂P̂/(∂τ/τ), ∂P̂/(∂V₀/V₀), …] and plotted for each data set for the first beat in each run, adding the term for P₀, ∂P̂/(∂P₀/P₀). Resolution matrices were also computed to rule out interdependencies among different parameters (17). Average processing time for a 10-beat data set was 1 min using a 2-GHz, quad-core i5 Intel workstation. The value of P_p was estimated at onset of diastole and time of mitral valve opening, as well as P_a at ED.

For the conventional method used for comparison, relaxation pressure was fitted to

$${\text{P}}_{\text{a}(t)}={\text{P}}_0\cdot e^{-t/\tau }+A$$ (A7)

during the isovolumic period only (up to 5 mmHg above EDP). The constant A represents a positive or negative asymptotic pressure value that is equivalent to the term P_p(V) in Eq. A5, if the volume is constant. The same applies to τ (Fig. 1). Conventional values of this parameter were fitted to Eq. A7 beat by beat (41) and then averaged for the full data set. Conventional assessment of the EDPVR was done by fitting Eq. A3 to ED multiple-beat PV data (12, 39). Single-beat analysis was performed on all Monte Carlo, animal, and clinical data, with reprocessing of the data only for the first beat in the data set.

Monte Carlo simulation.

We used Monte Carlo simulation (14) to test the performance of the novel fitting algorithm in finding a prespecified set of diastolic parameters (6). First, 20 experimental volume signals recorded during IVC occlusion (10 animals and 10 patients; 7–15 beats each) were randomly selected. Next, 50 synthetic “pressure” series were generated applying model equations (Eqs. A1–A5) to each of these experimentally measured volume signals, using physiologically sound random parameters for equation parameters. Thus a total of 1,000 PV data sets were obtained. The simulated P₀ was calculated from measured ESVs by assuming a linear end-systolic PV relationship, and entering random values for peak elastance (range: 0.7 to 5 mmHg/ml) and volume intercept (80–300% of ESV). We generated random values for τ, S₊, V₀, V_m, and V_d uniformly distributed in the same parameter intervals used for the constrains described for solving. Parameters and volume values were then entered in Eqs. A1–A4 to obtain a simulated pressure measurement. Because not all parameter combinations are physiologically plausible, we regenerated random values of the parameters until the following constrains were met: 1) P₀ < 200 mmHg for the first beat and >50 mmHg for the last one; 2) EDP < 30 mmHg; 3) minimal pressure achieved during the first half of the diastolic period; and 4) pressure span during diastole from P₀ to minimum pressure > 30 mmHg. The final entered values of diastolic parameters were stored as reference. Before entering the fitting algorithm, Gaussian white noise was added to the simulated pressure signals, matching the signal-to-noise ratio found in animal and clinical experiments (45 and 42 dB, respectively). Each PV simulated waveform was visually verified before processing. An example is shown in Fig. 7.

Fig. 7.

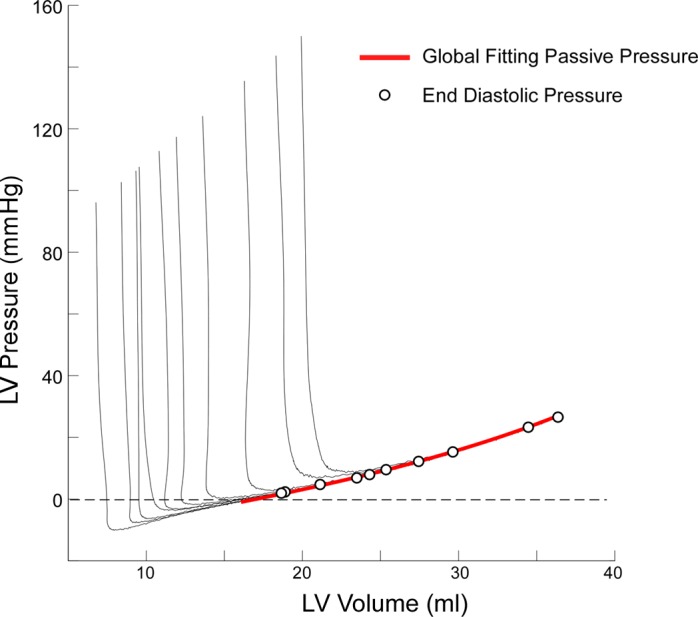
Example of Monte Carlo synthetic PV curves generated from an animal volume data set. Pressure is generated from instantaneous volumes using random values for indexes of active and passive diastolic properties, and random noise is added, as detailed in the text. End-diastolic PV values are shown in the black dots. The global fitting passive pressure curve is shown in red.

Alternative models of relaxation.

Additionally, to the exponential function showed in Eq. A1, other models have been proposed to describe the pressure-time relationship during isovolumic relaxation. We also attempted to test the performance of the global fitting algorithm to incorporate these alternative mathematical relationships. The physical assumptions underlying the different models of isovolumic relaxation are best illustrated plotting the time derivative of pressure against instantaneous pressure (as a pressure-phase plot) (3).

The logistic function defines:

$${\text{P}}_{\text{a}(t)}=\frac{A}{1+e^{t/{\tau }_{\text{L}}}}$$ (A8)

Where A is an amplitude constant, and τ_L is the time constant of relaxation measured using this method (15). A can be expressed in terms of P₀, and Eq. A8 becomes:

$${\text{P}}_{\text{a}(\text{V},t)}=\frac{2[{\text{P}}_0+{\text{P}}_{\text{p}(\text{V})}]}{1+e^{t/{\tau }_{\text{L}}}}$$ (A9)

Alternatively, a more generic relationship of the pressure-time relationship has been proposed that does incorporate passive pressure in its definition (3). This approach has been coined “kinematic” model and is based on a differential equation:

$$\frac{{\text{d}}^2\text{P}}{\text{d}{t}^2}+\frac{1}{\mu }\frac{\text{dP}}{\text{d}t}+E_k(\text{P}-{\text{P}}_{\infty })=0$$ (A10)

Where μ is the resistive parameter equivalent to τ, and E_k is a lumped elastic parameter accounting for the elastic restoring force. Equation A10 includes a static pressure asymptote, P_∞, representing the passive pressure of the fully relaxed ventricle. In the original work, the parameters of this equation were estimated using a nonlinear fitting algorithm on the dP/dt (3). However, the P-time data can be fitted to the exact analytic solution of Eq. A10:

$$\begin{array}{c}{\text{P}}_{\text{a}(\text{V},t)}=\frac{e^{\frac{t\left(\sqrt{1-4E_k{\mu }^2}-1\right)}{2\mu }}\left[{\text{P}}_0-{\text{P}}_{\text{p}(\text{V})}-{\text{P}}_{\text{p}(\text{V})}\sqrt{1-4E_k{\mu }^2}+2{\dot{\text{P}}}_0\mu +{\text{P}}_0\sqrt{1-4E_k{\mu }^2}\right]}{2\sqrt{1-4E_k{\mu }^2}}-\frac{{\text{P}}_0-{\text{P}}_{\text{p}(\text{V})}-{\text{P}}_{\text{p}(\text{V})}\sqrt{1-4E_k{\mu }^2}+2{\dot{\text{P}}}_0\mu -{\text{P}}_0\sqrt{1-4E_k{\mu }^2}}{2e^{\frac{t\left(\sqrt{1-4E_k{\mu }^2}+1\right)}{2\mu }}\sqrt{1-4E_k{\mu }^2}}\end{array}$$ (A11)

Where P₀ and Ṗ₀, respectively, account for the values of pressure and dP/dt at the beginning of fitting. Notice that Eq. A11 is equivalent to merging the proposed combination of solutions in the original work (3). This approach avoids the noise amplification caused by numerically differentiating the measured pressure signal. As in Eqs. A1 and A9, in Eq. A11 the asymptote of P_a is replaced by P_p(V), allowing the merge of active and passive constitutive equations throughout the full diastolic period. A more complex integration of passive restoring forces in Eq. A11 is beyond the scope of this study. Local minima algorithms were forced to iterate until noncomplex values of the coefficients were returned.

In Eqs. A10 and A11, LV relaxation properties are characterized by two parameters, μ and E_k, representing a more generic formulation of the relaxation pressure decay than the exponential and logistic models. Furthermore, it has been shown that the kinematic model is capable of fitting the pressure data before minimal dP/dt. Replicating previously published methodology (3), we begun analyzing from the instant where the second time derivative of pressure fell below 50% of the peak value (a few ms earlier than dP/dt_min).

Notice that using the global optimization method, instead of single-beat fitting of pressure data measured before mitral valve opening, we fit Eq. A11 for the full hemodynamic run obtained during IVC occlusion. The returned single values of μ and E_k, therefore, account for the best fit to all of the diastolic period of a number of beats. Individual beat fitting must be necessarily worse than if beats were fitted individually. Differences between the exponential, logistic, and kinematic methods for fitting early diastolic filling data are best illustrated in the pressure phase plane (Fig. 5), as previously proposed (3).

Glossary

CME

Left main coronary artery microembolization

DCM

Dilated cardiomyopathy

dP/dV

Derivative of left ventricular pressure with respect to volume

ED

End diastole

EDV

End-diastolic volume

ESV

End-systolic volume

EDPVR

End-diastolic pressure-volume relationship

IVC

Inferior vena cava

PV

Pressure-volume

P_a

Active diastolic pressure

P_p

Passive diastolic pressure

S₊

Constant of diastolic passive stiffness

S₋

Constant of diastolic elastic recoil

τ

Time constant of relaxation

V₀

Equilibrium volume

V_d

Left ventricular minimum dead volume

V_m

Left ventricular maximal achievable volume