Mechanisms of adaptation in human auditory cortex

Abstract

This study investigates the temporal properties of adaptation in the late auditory-evoked potentials in humans. The results are used to make inferences about the mechanisms of adaptation in human auditory cortex. The first experiment measured adaptation by single adapters as a combined function of the adapter duration and the stimulus onset asynchrony (SOA) and interstimulus interval (ISI) between the adapter and the adapted sound (“probe”). The results showed recovery from adaptation with increasing ISI, as would be expected, but buildup of adaptation with increasing adapter duration and thus SOA. This suggests that adaptation in auditory cortex is caused by the ongoing, rather than the onset, response to the adapter. Quantitative modeling indicated that the rate of buildup of adaptation is almost an order of magnitude faster than the recovery rate of adaptation. The recovery rate suggests that cortical adaptation is caused by synaptic depression and slow afterhyperpolarization. The P2 was more strongly affected by adaptation than the N1, suggesting that the two deflections originate from different cortical generators. In the second experiment, the single adapters were replaced by trains of two or four identical adapters. The results indicated that adaptation decays faster after repeated presentation of the adapter. This increase in the recovery rate of adaptation might contribute to the elicitation of the auditory mismatch negativity response. It may be caused by top-down feedback or by local processes such as the buildup of residual Ca²⁺ within presynaptic neurons.

the amplitude of the response of the brain to a sensory stimulus decreases when the stimulus is repeated over time. This decrease, which is often referred to as “repetition suppression” or “adaptation” (Grill-Spector et al. 2006), is one of the most ubiquitous features of sensory processing and has been proposed to play a role in the generation of the auditory mismatch negativity (MMN) response (Garrido et al. 2009; Jääskeläinen et al. 2004; May and Tiitinen 2010). Adaptation has also been widely used in both psychophysical and functional MRI (fMRI) studies as a tool for probing functional properties of sensory neural populations in humans. Typically, these studies have measured the response to a probe stimulus after presentation of an adapting stimulus. The adapter and probe are either identical or differ in a given feature (e.g., orientation in vision, Blakemore and Campbell 1969, or frequency modulation rate in hearing, Kay and Matthews 1972). If neurons are selective for the feature along which the adapter and probe differ, the different probe will recruit unadapted neurons and thus show a release from adaptation compared with the identical probe.

There is indication that the size of this release from adaptation depends on the temporal properties of the adapter and probe. Fang et al. (2005), for instance, used both short and long adapters to measure adaptation to visual orientation in humans with fMRI. They found that, in primary visual cortex, the long, but not the short, adapter yielded a release from adaptation for different vs. same adapter and probe orientations. This was likely because the long adapter produced more adaptation overall than the short adapter. More adaptation for the longer adapter suggests that adaptation was predominantly caused by the ongoing response to the adapter. Eggermont (2000) measured adaptation in single- and multiunit responses in cat primary auditory cortex using noise-burst adapters and probes with varying durations and interstimulus intervals (ISIs). In contrast to Fang et al. (2005), Eggermont (2000) found that adaptation decreased with increasing adapter duration and thus stimulus onset asynchrony (SOA) between the adapter and probe. This suggests that, in Eggermont (2000), adaptation was predominantly caused by the onset, rather than the ongoing, response to the adapter. The discrepancy between the findings of Fang et al. (2005) and Eggermont (2000) may be due to the fact that the two studies used different species (human and cat) or because they investigated different sensory modalities (visual and auditory). Alternatively, it might be attributable to the fact that the measurement modalities used by the two studies are sensitive to different aspects of the neural activity: Fang et al. (2005) used fMRI, which is sensitive to synaptic activity (Logothetis and Wandell 2004), whereas Eggermont (2000) measured spiking activity. Finally, the subjects of Eggermont (2000) were anesthetized, whereas the subjects of Fang et al. (2005) were alert.

The aim of the current study was to reinvestigate the finding of Eggermont (2000) that adaptation in auditory cortex is predominantly determined by the adapter onset response using alert human subjects and a measurement modality that, like fMRI, is sensitive to synaptic, rather than spiking, activity. Adaptation was measured for a pure-tone probe, which was preceded by a pure-tone adapter of the same frequency. The amount of adaptation was measured as a combined function of the adapter duration and the SOA and ISI between the adapter and probe. In addition to single adapters, we also used trains of multiple adapters, presented at different rates. Previous neurophysiological data from the rat barrel cortex suggest that the rate of recovery from adaptation might depend on the number and presentation rate of the adapters (Chung et al. 2002). To be better able to dissociate the probe from the preceding adapter response, the measurements were conducted with EEG. Like fMRI, EEG is sensitive to synaptic activity but has a much superior temporal resolution.

METHODS

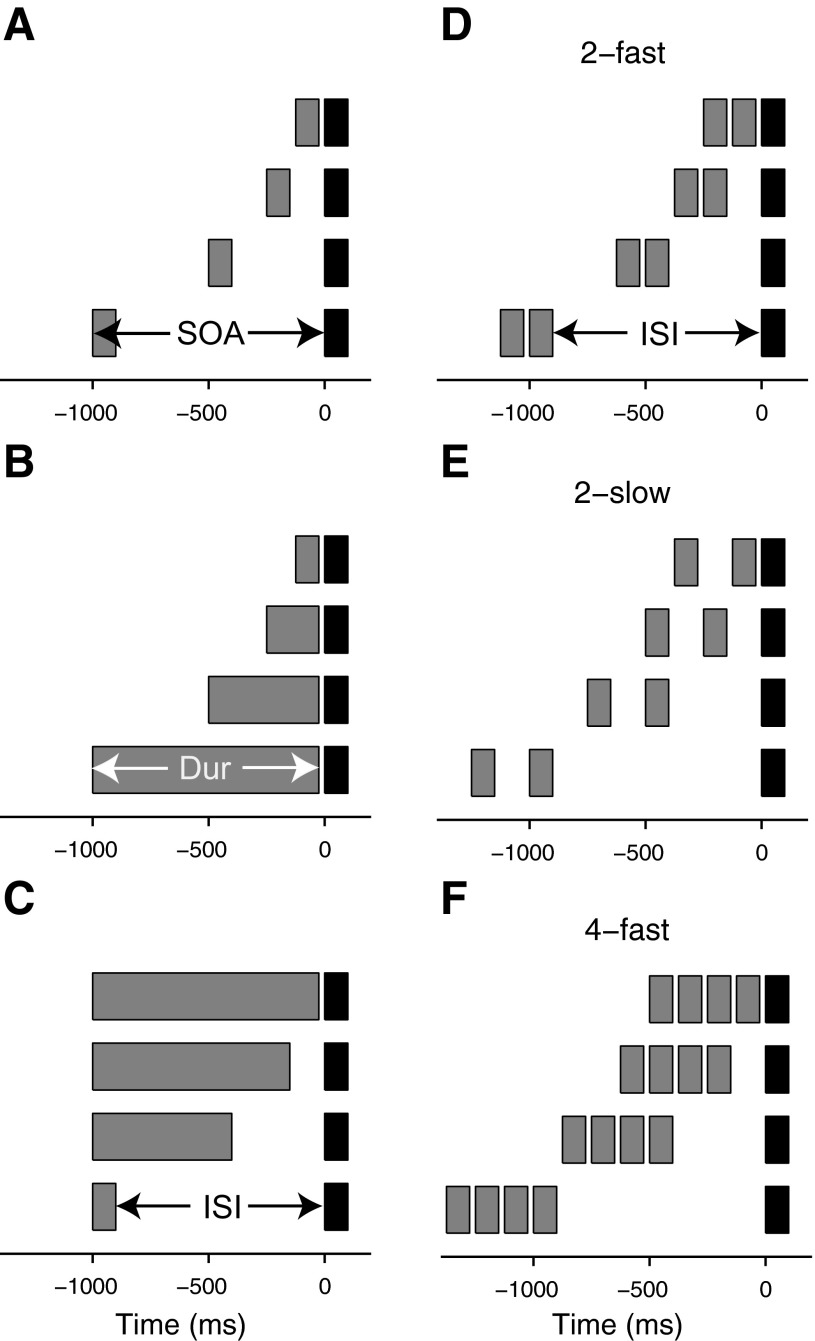
This study measured the adaptational effect of single or multiple adapter stimuli on the late auditory cortical potentials evoked by a probe stimulus. Both the adapters and the probe were pure tones with the same nominal frequency of 1 kHz. The probe duration was fixed at 100 ms. In the first experiment, the probe was preceded by a single adapter, and the probe response size was measured as a combined function of: 1) the SOA and ISI between the adapter and probe, with the adapter duration fixed at 100 ms (Fig. 1A); 2) the SOA and the adapter duration, with the ISI fixed at 25 ms (Fig. 1B); and 3) the adapter duration and the ISI, with the SOA fixed at 1,000 ms (Fig. 1C). In the second experiment, the probe was preceded by multiple adapters, which had a duration of 100 ms each and were presented at either a fast (8/s) or slow (4/s) rate. For the fast presentation rate, either two (Fig. 1D) or four (Fig. 1E) adapters were used; for the slow rate, only two adapters were used (Fig. 1F). For each of these adapter configurations, the probe response size was measured as a function of the interval between the offset of the last adapter and the probe onset (referred to as ISI as before; Fig. 1D).

Fig. 1.

Stimulus conditions used in experiments 1 (A–C) and 2 (D–F). In experiment 1, the probe (black) was preceded by a single adapter (gray), and the stimulus onset asynchrony (SOA; A), adapter duration (Dur; B), or interstimulus interval (ISI; C) was varied parametrically. In experiment 2, either 2 (D and E) or 4 (F) adapters were used, and the adapters were presented either at a fast (8 Hz; D and F) or slow (4 Hz; E) rate. As in experiment 1, the ISI was varied parametrically in all 3 cases.

Stimuli

All stimuli were generated digitally at a sampling rate of 24.414 kHz using MATLAB (The MathWorks, Natick, MA), digital-to-analog-converted with a 24-bit amplitude resolution using TDT System 3 (RP2.1 Real-Time Processor, HB7 headphone amplifier; Tucker-Davis Technologies, Alachua, FL), and presented diotically through K240 DF headphones (AKG, Vienna, Austria). The adapter and probe stimuli were gated on and off with 10-ms quarter-cosine ramps and presented at a root-mean-square level of 70-dB sound pressure level (SPL). They were presented in discrete trials of 3,990 ms each. Within each trial, the adapter(s) and probe had the same frequency, selected randomly from a -octave range around the nominal frequency (1 kHz) to minimize across-trial adaptation. A continuous noise, filtered to yield equal excitation across all cochlear filters, was presented throughout the data acquisition. The noise was presented at a level of 30-dB SPL per cochlear-filter bandwidth (defined as equivalent rectangular bandwidth, or ERB; Glasberg and Moore 1990). It was intended to equalize the stimulus sensation level across frequencies and participants.

In the first experiment, the adapter was a single stimulus. In the first part of this experiment (experiment 1A; Fig. 1A), the SOA between the adapter and probe was varied from 125 to 1,000 ms in doublings (125, 250, 500, and 1,000 ms), and the adapter duration was kept constant at 100 ms. This meant that the ISI varied from 25 to 900 ms (25, 150, 400, and 900 ms). To disambiguate the effects of SOA and ISI in experiment 1A, experiment 1B used the same SOAs but with a constant ISI of 25 ms (Fig. 1B). This meant that the adapter duration varied from 100 to 975 ms (100, 225, 475, and 975 ms). Finally, we also measured adaptation as a combined function of adapter duration and ISI, with a constant SOA of 1,000 ms (experiment 1C; Fig. 1C). The ISIs in experiment 1C matched those used in experiment 1A, and the adapter duration varied from 975 to 100 ms (975, 850, 600, and 100 ms). Some of the conditions in the different parts of experiment 1 were identical and were therefore measured only once. In total, there were nine unique conditions in experiment 1.

In the second experiment, the adapters were trains of either two or four stimuli, which had a duration of 100 ms each and were presented at a rate of either 8 or 4/s (Fig. 1, D–F). The ISIs between the last stimulus in the adapter trains and the probe matched those in experiment 1A (25, 150, 400, and 900 ms). In total, experiment 2 contained 12 stimulus conditions.

In the conditions with the two shortest ISIs (25 and 150 ms), the response to the adapter (experiment 1) or adapter trains (experiment 2) overlapped the response to the subsequent probe. To isolate the probe response in these conditions, we also measured the responses to the respective adapters in isolation and subtracted them from the overlapping adapter and probe responses (see Data Analysis). There were five adapter-alone conditions in experiment 1 and three in experiment 2.

EEG Data Acquisition

The EEG recordings were conducted in four separate sessions, two for experiment 1 and two for experiment 2. The sessions lasted ∼80 min each and were conducted on different days. The experiment 1 sessions were conducted before the experiment 2 sessions. Each session was divided into 4 blocks. There was a total of 14 conditions in experiment 1 (9 stimulus conditions + 5 adapter-alone conditions) and 15 conditions in experiment 2 (12 stimulus conditions + 3 adapter-alone conditions). Each block contained 20 repetitions of all 14 or 15 conditions, presented in a randomly permuted order, and lasted ∼20 min.

The participant was seated on a comfortable chair in a double-walled, sound-attenuating booth [Industrial Acoustics Company (IAC), Winchester, United Kingdom]. Auditory-evoked cortical potentials were recorded with a 32-channel EEG amplifier system (BrainAmp DC, Brain Products, Gilching, Germany) and an EEG cap fitted with 33 Ag/AgCl ring electrodes arranged according to the standard 10-20 system (EASYCAP, Herrsching, Germany). Skin-to-electrode impedances were kept below 5 kΩ. The recording reference was the vertex channel (Cz), and the ground was placed on the central forehead (AFz). The data were recorded continuously at a sampling rate of 500 Hz and band-pass-filtered online between 0.1 and 250 Hz.

This was a passive listening experiment; participants watched a self-chosen silent movie with subtitles throughout the recordings to remain alert.

Data Analysis

The raw EEG data were preprocessed with EEGLAB (Delorme and Makeig 2004), which runs under MATLAB. They were: 1) low-pass-filtered at 35 Hz using a zero-phase infinite impulse response filter with a −48 dB/octave roll-off; 2) downsampled to a 250-Hz sampling rate; 3) rereferenced to average reference; and 4) divided into 2,100-ms epochs covering the period from −100 to 2,000 ms relative to the onset of the adapter stimulus. Epochs with nonstereotypical artifacts were rejected automatically using the EEGLAB “joint-probability” function. This function identifies artifacts by detecting occurrences of uncharacteristically large (≥3.5 SDs) potentials across many electrodes. This led to the rejection of an average of 9.2% of epochs in experiment 1 and 11.2% in experiment 2. Electro-ocular and electrocardiac artifacts were then removed by applying an independent component analysis based on the extended infomax algorithm (Bell and Sejnowski 1995; Lee et al. 1999). Artifactual components were removed by manual inspection of the response time courses and scalp topographies of the components. Epochs were then averaged for each participant and condition and baseline-corrected to the 100-ms silent period preceding the adapter onset.

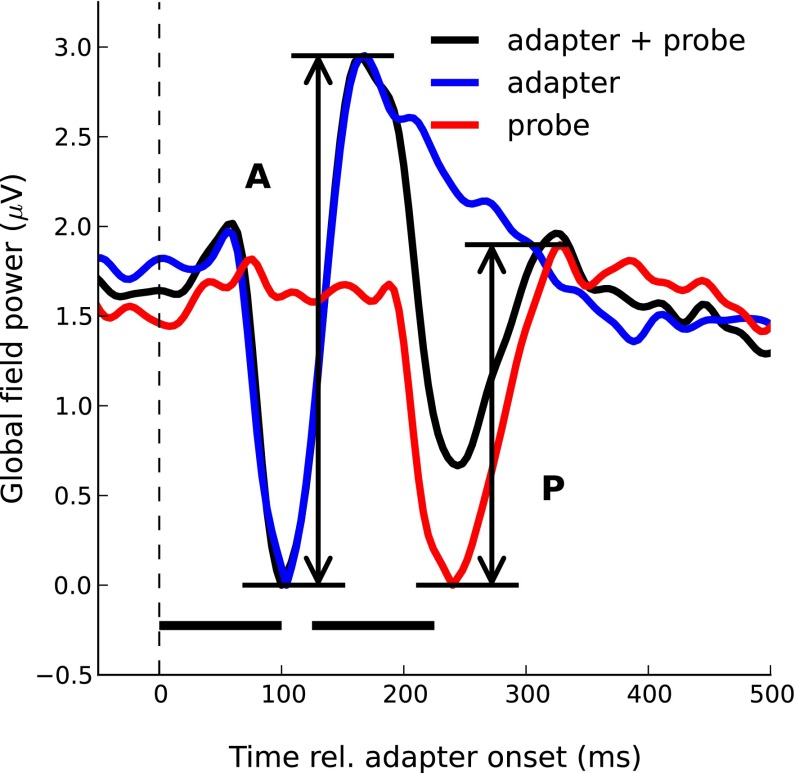
In all but one condition in experiment 1 and in all conditions in experiment 2, the probe response was isolated by subtracting the response to the respective adapter in isolation from the composite response to the adapter and probe (Fig. 2). In experiment 1A, the adapter was identical across conditions, so the response to the adapter in isolation was measured only once. The amount of adaptation was measured by expressing the size of the probe response (Ρ) as a fraction of the size of the adapter response (Α), subtracting the result from unity, and expressing it in percentage [(1 − Ρ/Α) × 100]. The adapter and probe response sizes were measured as the peak-to-peak difference between the P2 and N1 deflections in the global field power (GFP) of the adapter and probe responses. The GFP represents a model-free and reference-independent measure of response strength as a function of time, which takes into account all, rather than just a few, data channels (Murray et al. 2008). The disadvantage is that it is positive, irrespective of the vertex-polarity of the underlying data. This is why the P2-N1 difference cannot be derived from the GFP of responses baseline-corrected to the silent period preceding the stimulus onset. Instead, we baseline-corrected the responses to the N1 peak and derived the P2-N1 difference by measuring the height of the P2 peak in the GFP of these N1 baseline-corrected responses (Fig. 2). We also measured the sizes of the N1 and P2 deflections separately by comparing the respective peaks in the GFP of the N1 baseline-corrected responses with the average GFP within the 100-ms silent period preceding the stimulus onset. Normally, the N1 and P2 peaks are measured in the GFP of the silent, baseline-corrected responses. However, in the current experiment, the P2 was small and rode on a large vertex-negative N1 and thus did not reach vertex positivity in some of the conditions. In such cases, the P2 does not produce a peak in the GFP of the silent baseline-corrected responses.

Fig. 2.

Grand-average responses (across 12 participants) to the single-adapter and probe pair with the 100-ms adapter Dur and 25-ms ISI (black line). Here and in the following, the traces show the global field power (GFP) of the N1 baseline-corrected responses (see text). The stimulus timing is indicated by the black bars above the abscissa. The blue line shows the response to the adapter in isolation. The probe response (red line) was derived by subtracting the adapter response from the response to the adapter and probe pair. The size of the adapter (Α) and probe (Ρ) responses was measured as the peak-to-peak difference between the N1 and P2 deflections. rel., Relative to.

Participants

The same 12 participants (9 female; age range = 21–26 yr) took part in both experiments 1 and 2 after giving written, informed consent. All participants had normal hearing (hearing thresholds of 20-dB hearing level or better at octave frequencies between 0.25 and 8 kHz) in both ears and had no history of audiological or neurological disease. Ten of the participants were right-handed according to the Edinburgh inventory (Oldfield 1971). The experimental procedures used conformed with the International Code of Medical Ethics of the World Medical Association (Declaration of Helsinki) and were approved by the Ethics Committee of the University of Nottingham Medical School.

RESULTS

Experiment 1

Figure 2 shows that the responses to the adapters contained a transient onset response, consisting of an initial vertex-positive deflection at, on average, 56 ms (P1), a vertex-negative deflection at 100 ms (N1), and another vertex-positive deflection at 168 ms (P2). The responses to the probes had a similar morphology but were smaller in size than the adapter responses as would be expected.

Is adaptation caused by the onset or ongoing response to the adapter?

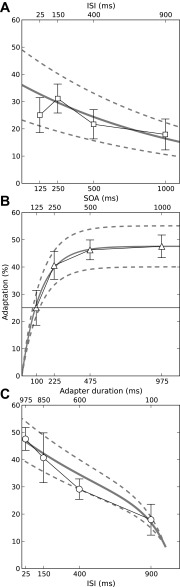
In experiment 1, the probe was preceded by a single adapter. In the first part (experiment 1A), adaptation was measured as a combined function of the SOA and ISI between the adapter and probe with the adapter duration fixed at 100 ms (Fig. 1A). Given that the adapter duration was fixed, adaptation was expected to decrease with increasing SOA or ISI irrespective of whether adaptation is caused by the onset or ongoing response to the adapter. This was indeed the case; the size of the probe response (measured as the P2-N1 peak-to-peak difference) increased (Fig. 3, A–D), and thus the amount of adaption decreased (Fig. 4A), with increasing SOA/ISI. A one-way ANOVA with repeated measures (RM-ANOVA) confirmed that this effect was significant [F(3,33) = 3.293, P = 0.02]. Since SOA and ISI were varied in proportion with one another (SOA = ISI + 100 ms), the change in adaptation could have been caused by either one or both variables.

Fig. 3.

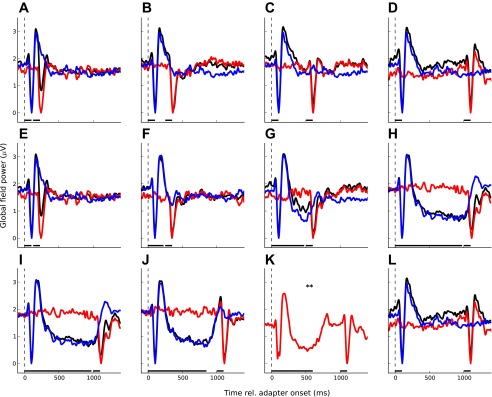
Grand-average responses for experiment 1. Each panel shows 1 experimental condition; the top (A–D) shows the conditions with varying SOA (experiment 1A; see Fig. 1A), the middle (E–H) shows the conditions with varying adapter Dur (experiment 1B; Fig. 1B), and the bottom (I–L) shows the conditions with varying ISI (experiment 1C; Fig. 1C). The stimulus timing is indicated by the black bars above the abscissa. As in Fig. 2, the black lines show the responses to the adapter-probe pairs, the blue lines show the responses to the adapter in isolation, and the red lines show the probe responses. In the 400-ms ISI condition (K; indicated by **), the response to the adapter was not measured separately because the adapter response did not overlap the probe response and measuring it would have added another condition. A and E, D and L, and H and I represent identical conditions and thus show the same data. The adapter responses in isolation in A–D are also the same.

Fig. 4.

Amount of adaptation produced by single adapters (experiment 1) as a function of ISI or SOA (A), SOA or adapter Dur (B), and adapter Dur or ISI (C), indicated by the upper and lower abscissae in each panel. The symbols show the average across 12 participants, and the error bars show the standard error (SE). The gray lines in A and B show least-squares exponential function fits to the data (see text). The gray line in C shows a prediction of the experiment 1C data based on the function fits to the data from experiments 1A and 1B. The prediction was derived by adding to the function fit for experiment 1A the difference between the function fit for experiment 1B and the measured adaptation for the shortest (100-ms) adapter Dur (marked thin horizontal line in B). The dashed gray lines show the confidence intervals of the fitted functions (A and B) and the derived prediction (C).

To disambiguate the effects of SOA and ISI, experiment 1B measured adaptation for the same set of SOAs as used in experiment 1A but with the ISI fixed at 25 ms (Fig. 1B). For that, the adapter duration was increased in proportion with the SOA (duration = SOA − 25 ms). If, as suggested by Eggermont (2000), adaptation is caused by the onset rather than ongoing adapter response, adaptation would be expected to decrease with increasing SOA as in experiment 1A. This, however, was not the case; Fig. 4B shows that, instead of decreasing, adaptation increased with increasing SOA/adapter duration [F(3,33) = 7.30, P < 0.001; see also Fig. 3, E–H]. This finding is consistent with the results of Fang et al. (2005) and suggests that adaptation was mainly caused by the ongoing adapter response.

To test whether adaptation was exclusively caused by the ongoing adapter response or whether there was at least some contribution from the onset response, we conducted another experiment (experiment 1C) where we varied only the ISI and adapter duration and kept the SOA fixed (at 1,000 ms; Fig. 1C). With the SOA fixed, any effect of the adapter onset response would have been constant across the conditions in experiment 1C, creating a mismatch between the experiment 1C results and the combined results from experiments 1A and 1B, both of which used a variable SOA. Such a mismatch, however, was not observed. The gray line in Fig. 4C shows a prediction of the adaptation in experiment 1C based on the combined results from experiments 1A and 1B. The prediction was calculated by combining a decrease in adaptation with increasing ISI with a further decrease in adaptation as a result of the concomitant decrease in adapter duration (duration = 1,000 ms − ISI). The adaptation decrease with increasing ISI was taken from experiment 1A. The adaptation decrease with decreasing adapter duration was derived from the experiment 1B results by subtracting the adaptation for the shortest adapter duration (100 ms, indicated by the thin horizontal line in Fig. 4B) from the adaptation for the longer durations. The prediction was based on exponential function fits to the experiments 1A and 1B data described below (gray lines in Fig. 4, A and B) rather than the measured data points. An F-test showed that the observed and predicted adaptation for experiment 1C did not differ significantly [F(1,3) = 0.67, P = 0.47]. This suggests that the adapter onset response had little or no contribution to adaptation in experiment 1.

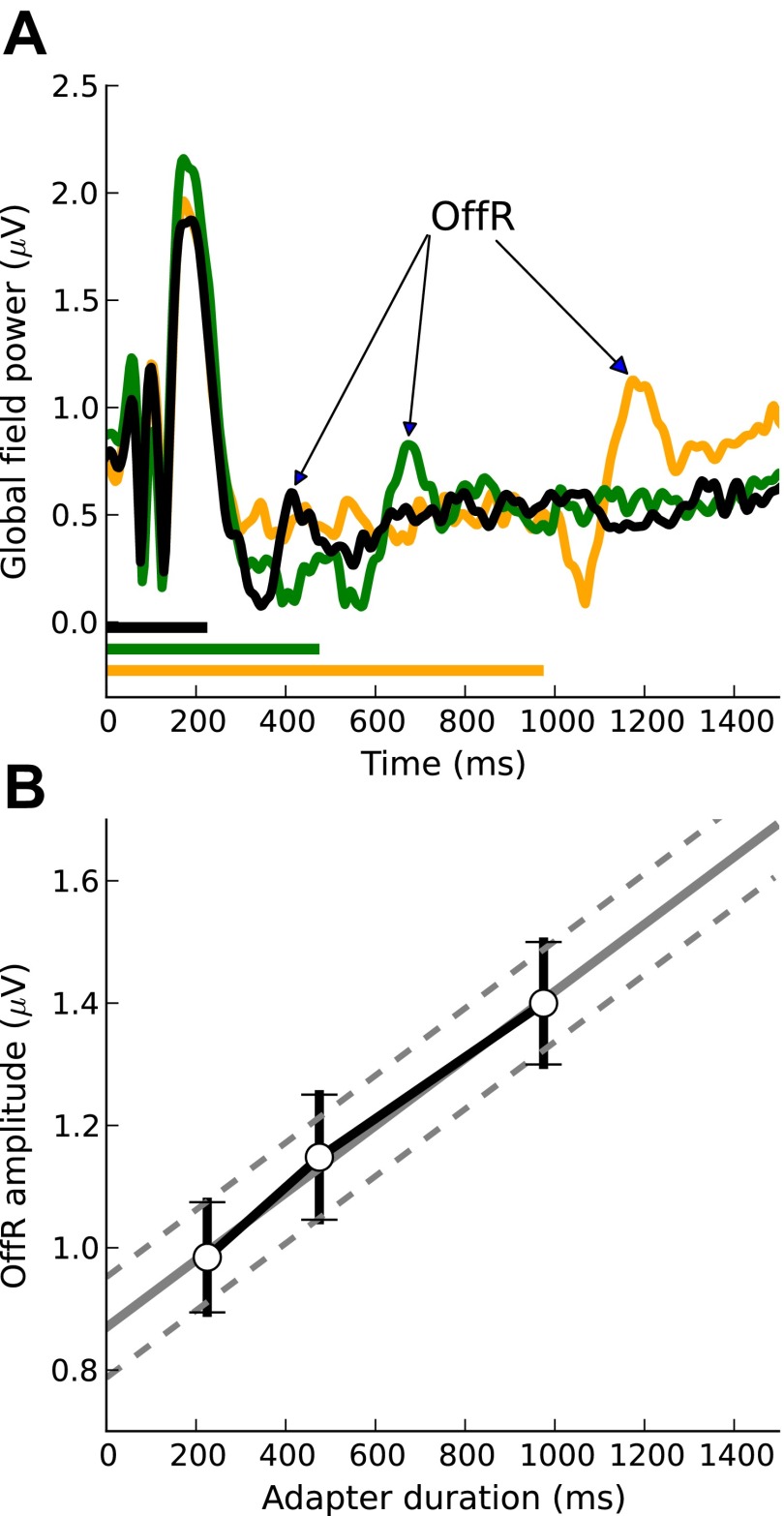
It is possible, however, that adaptation was caused, not by the ongoing adapter response but by the off-response (OffR) to the adapter. To test this possibility, we examined the relationship between the OffR size and adapter duration (Fig. 5A) and compared this relationship with the adaptation observed in experiment 1B. We found that there was no discernible OffR for the shortest adapter duration used (100 ms) when that duration already produced a substantial proportion (52%) of the asymptotic adaptation. For the longer durations (225–975 ms), the OffR size increased linearly with increasing duration (Fig. 5B), whereas adaptation increased exponentially; the gray line in Fig. 4B shows a least-squares fit of the experiment 1B data with an exponential function of the form Α = Α_∞·(1 − e^{−β·duration}) (Eq. 1), where Α is adaptation, β is the rate with which adaptation changes as a function of the adapter duration, and Α_∞ is the asymptotic adaptation for very long durations. In fitting this function, we assumed that adaptation would tend to zero toward zero adapter duration. An F-test showed that the exponential function fitted the data significantly better than a linear function [F(1,4) = 2.329, P < 0.001]. This and the fact that the shortest adapter duration caused substantial adaptation but no OffR indicates that adaptation was not caused by the adapter OffR.

Fig. 5.

The size of the off-response (OffR) to the adapter increased with increasing adapter Dur (A). There was no discernible OffR for the shortest (100-ms) adapter. For the longer adapters, the relationship between the OffR size and adapter Dur was approximately linear (B).

The N1 and P2 have different adaptational properties.

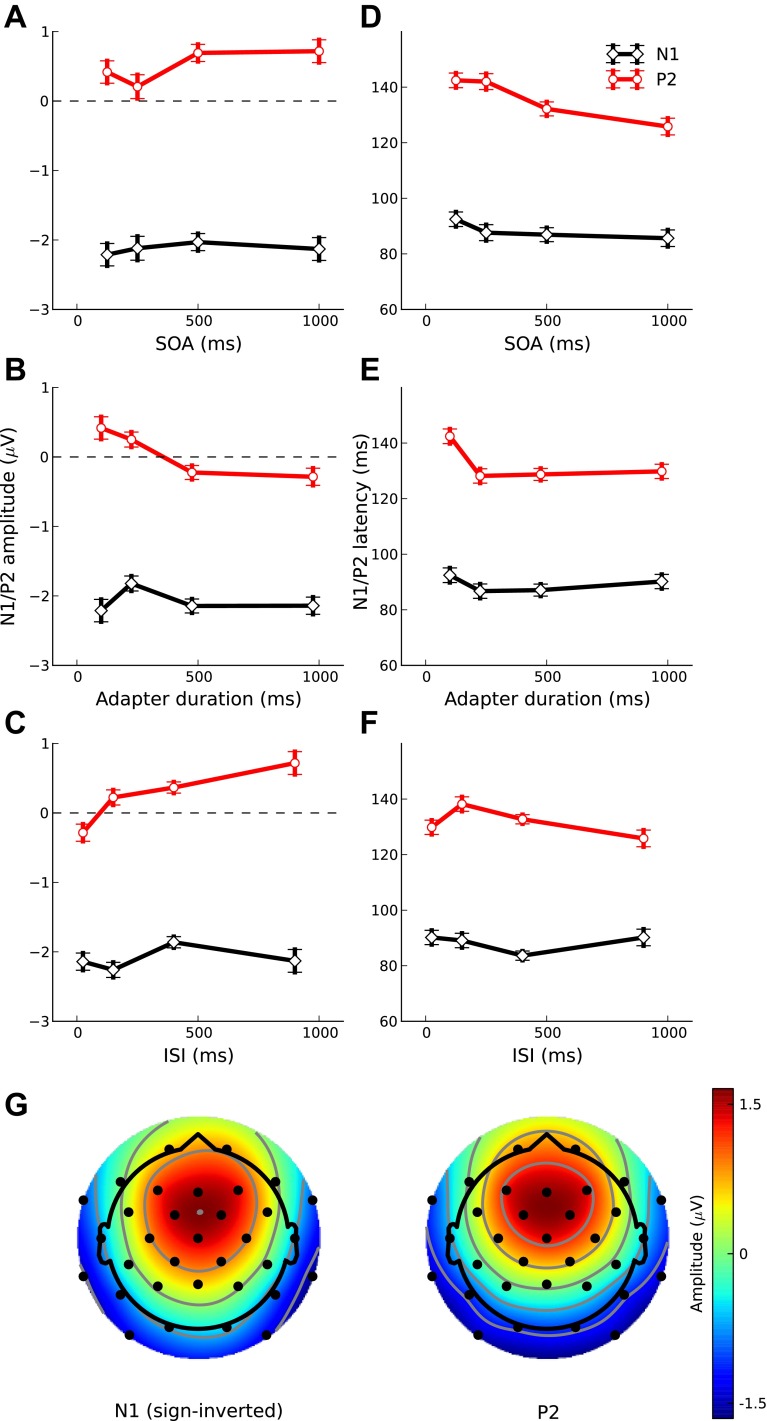
Closer examination of the probe responses in Fig. 3 suggests that the variation in adaptation as a function of the temporal stimulus parameters observed in experiment 1 was mainly due to changes in the size of the P2 rather than the N1. To test this, we measured the sizes of the N1 and P2 separately. This showed that, in all three parts of experiment 1 (A, B, and C), the variation in the size of the P2 as a function of the independent variables (SOA, ISI, and duration) was greater than the variation in the N1 size (Fig. 6, A–C). Separate one-way RM-ANOVAs on the N1 and P2 showed that the P2 effect was significant and the N1 effect nonsignificant in all three experiments. The interaction between the N1 and P2 effects as a function of the independent variable, tested with two-way RM-ANOVAs, was significant for experiments 1B [F(3,33) = 5.03, P = 0.003] and 1C [F(3,33) = 6.58, P < 0.001] but not for experiment 1A [F(3,33) = 1.36, P = 0.25].

Fig. 6.

Dependence on SOA (top), adapter Dur (middle), and ISI (bottom) of the N1 (red symbols and lines) and P2 (black) deflections in the probe response. The left (A–C) shows the average peak amplitudes and the right (D–F) the latencies of the deflections. The error bars show the SE. G shows the scalp topographies of the N1 (left) and P2 (right), derived by averaging over the 20-ms time windows around the N1 and P2 peaks in the grand-average response to the adapters in isolation. The N1 topography was sign-inverted to account for the polarity difference between the N1 and P2.

These results indicate that the N1 and P2 have different adaptational properties, suggesting that they arise from different neural generators. In particular, they might arise from different locations or from different layers at the same cortical location. To test these alternatives, we compared the scalp topographies of the N1 and P2 using a modified version of the global dissimilarity (DISS) analysis (Lehmann and Skrandies 1980). Two deflections arising from different cortical layers at the same location can differ in polarity but not in topography. To eliminate the polarity difference between the N1 and P2, we sign-inverted the scalp topography of the N1 (Fig. 6G, left) before calculating its DISS with the P2 (Fig. 6G, right) as described by Murray et al. (2008). Although the N1 and P2 showed some differences in topography, a permutation test (with 1,000 within-participant permutations) showed that these differences did not reach significance (P = 0.08).

Adaptation effects on response latency.

To test whether adaptation has an effect on the speed of the processing of the probe stimulus, we also measured the N1 and P2 latencies. However, rather than using the conventional peak latency measure, we measured the latencies of the onset flanks of the deflections by finding the point of the steepest rising slope (see Lütkenhöner et al. 2003 for a similar procedure). The flank latency represents a less confounded measure of processing speed than the peak latency; the peak latency is influenced not only by the latency of the current deflection (e.g., the N1), but also by the latency and relative amplitude of the subsequent deflection (the P2 in the case of the N1). The N1 and P2 flank latencies were submitted to one- and two-way RM-ANOVAs. These analyses showed no significant effect of the independent variable (SOA, ISI, or duration) except for a slight effect of SOA/ISI on the P2 latency in experiment 1A [F(3,33) = 3.44, P = 0.022; Fig. 6D]. This indicates that adaptation mainly affects the size of the probe response and has relatively little effect on its latency.

Experiment 2

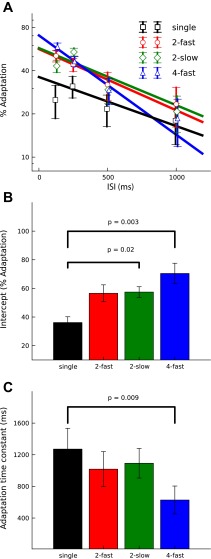
In experiment 2, the probe was preceded by either two or four adapters presented either at a faster (8/s) or a slower (4/s) rate (labeled “2-fast,” “2-slow,” and “4-fast”; Fig. 1, D–F). Figure 7 shows that, as for the single adapters used in experiment 1A, adaptation for the multiple adapters decreased with increasing ISI between the offset of the last adapter and the onset of the probe. A two-way RM-ANOVA of the single-adapter condition from experiment 1A and the three multiple-adapter conditions from experiment 2 (2-fast, 2-slow, and 4-fast) confirmed the significance of this effect [main effect of ISI: F(3,33) = 18.3, P < 0.001]. Figure 8A shows that the functions relating adaptation to ISI, henceforth referred to as “adaptation decay functions,” were approximately linear when adaptation was expressed in logarithmic units. This was true for both the single- and multiple-adapter conditions and suggests that adaptation decays exponentially with time. The rate of decay of adaptation appears to differ between the different adapter conditions. The significance of these differences was confirmed by the interaction between adapter condition and ISI [F(9,33) = 3.23, P = 0.007].

Fig. 7.

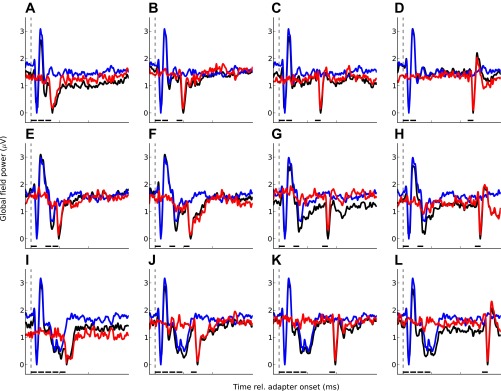
Grand-average responses for experiment 2. As in Fig. 3, each panel shows 1 experimental condition; the top (A–D) shows the 2-fast conditions (see Fig. 1D), the middle (E–H) shows the 2-slow conditions (Fig. 1E), and the bottom (I–L) shows the 4-fast conditions (Fig. 1F). The stimulus timing is indicated by the black bars above the abscissa. The black lines show the responses to the adapter and probe sequences, the blue lines show the responses to the adapter trains in isolation, and the red lines show the probe responses.

Fig. 8.

Decay of adaptation as a function of ISI for the single-adapter conditions from experiment 1A and the multiple-adapter conditions from experiment 2 (see key in A). The symbols in A show the average amount of adaptation as a function of ISI; the error bars show the SE. The data were least-squares-fitted with exponential decay functions, which appear linear when adaptation is plotted on a logarithmic scale (straight lines in A). B shows the function intercepts, which represent the maximum adaptation strength at 0 ISI. C shows the function slopes, which represent the decay rate of adaptation, expressed as time constants. The colors in B and C are the same as in A.

To assess the differences between the adapter conditions further, the data for each condition were fitted with an exponential function of the form Α = Α₀·e^−μ·ISI (Eq. 2), where Α is adaptation, Α₀ is the maximum adaptation at zero ISI, and μ is the rate with which adaptation decays. Α₀ can be read from the intercepts of the fitted functions in Fig. 8A, and μ from their slopes. The adaptation decay rate, μ, is often expressed as a time constant, which is the reciprocal of the decay rate (1/μ; e.g., Eggermont 1985). The fits yielded stronger maximal adaptation, Α₀, for the multiple adapters than for the single adapters as would be expected. For the single adapters, Α₀ was 36% compared with an average of 57% for the two-adapter conditions (2-fast and 2-slow) and 67% for the four-adapter condition (4-fast). Planned comparisons showed that the differences between the single-adapter condition and both the two- and four-adapter conditions were significant [2: t(11) = 2.51, P = 0.016; 4: t(11) = 3.27, P = 0.003]. The fits also yielded faster adaptation decay rates, μ, for the single than multiple adapters; μ corresponded to a time constant of 1,271 ms for the single adapters compared with 1,055 ms, on average, for the two-adapter conditions and 738 ms for the four-adapter condition. Planned comparisons showed that the difference between the single- and four-adapter conditions was significant [t(11) = 2.83, P = 0.009].

DISCUSSION

Here, we measured adaptation in the late auditory-evoked cortical potentials as a function of the adapter temporal parameters. We found that adaptation increases with increasing adapter duration and decreases with increasing time interval between the adapter offset and the probe onset (ISI) with little or no added effect of the onset asynchrony between the adapter and probe (SOA). These results indicated that adaptation was not caused by the transient onset response (OnR) to the adapter. Adaptation was also not caused by the transient response to the adapter offset (OffR). This was shown by comparing the size of the OffR with the amount of adaptation as a function of adapter duration. Instead, adaptation has to have been caused by the ongoing response to the adapter. In the auditory-evoked cortical potentials, ongoing activity is reflected by the sustained response, which is itself relatively little affected by adaptation (Picton et al. 1978). Our results suggest that, as for the visual modality (Fang et al. 2005), studies that want to use adaptation as a tool for investigating auditory stimulus representations should employ long adapters and short ISIs between the adapter and probe to maximize the amount of adaptation and thus the likelihood of detecting stimulus-specific release from adaptation.

In contrast to our results, Eggermont (2000) found that adaptation in single- and multiunit spiking activity in cat primary auditory cortex decreased with increasing SOA (for short adapter durations) and ISI (for long durations) but depended little on adapter duration. This suggested a strong contribution to adaptation by the transient adapter OnR. Eggermont (2000) assumed that the adaptation elicited by the adapter OnR was caused by medium-duration afterhyperpolarization (mAHP; Schwindt 1988a) and, potentially, lateral inhibition (Brosch and Schreiner 1997; Calford and Semple 1995); like mAHP and lateral inhibition, adaptation by the OnR persisted for only ∼50 ms. In contrast, the adaptation observed in the current study persisted for several hundred milliseconds, suggesting that it was caused by slow afterhyperpolarization (sAHP; Schwindt 1988b) and by depression of synaptic neurotransmitter release (synaptic depression; Zucker and Regehr 2002; see Kohn 2007 for review). Both synaptic depression (see Asari and Zador 2009 and Wehr and Zador 2005 for measurements from auditory cortex) and sAHP (reviewed in Faber and Sah 2003) persist for hundreds of milliseconds or even seconds. The difference in the persistence of adaptation in the results of Eggermont (2000) and our results may be due to the fact that Eggermont (2000) used anesthesia. Anesthesia would be expected to diminish or even abolish the ongoing response to the adapter (e.g., Cheung et al. 2001; Rennaker et al. 2007), allowing synapses to recover from depression and abolishing sAHP (Schwindt 1988a). Anesthesia may also be expected to affect the processes involved in the reuptake of neurotransmitter after its release into the synaptic cleft and thus shorten the recovery from synaptic depression (Richards 2002).

Both the increase in adaptation with increasing adapter duration and the recovery from adaptation with increasing ISI followed exponential functions. Under the simplest assumption that adaptation is caused by depletion of releasable neurotransmitter, the rate of recovery from adaptation, μ (Eq. 2), would be determined by the rate at which neurotransmitter is replenished, and the rate of increase of adaptation with adapter duration, β (Eq. 1), would reflect a combination of the neurotransmitter replenishment rate (μ) and the rate of neurotransmitter depletion, λ (β = λ + μ; Eggermont 1985). The exponential fits of the adaptation functions with ISI and adapter duration indicated that, in human auditory cortex, adaptation increases with a time constant of 1/β = 125.9 ms and recovers with a time constant of 1/μ = 1,271 ms. This means that the time constant for neurotransmitter depletion, calculated as 1/λ = 1/(β − μ), is 139.7 ms, which is ∼9 times faster than time constant for neurotransmitter replenishment (1,271 ms). The rate of neurotransmitter depletion, λ, would be expected to depend on the rate at which the presynaptic neuron is activated as well as the efficiency with which neurotransmitter is released as a result of each activation; the faster the presynaptic activation rate and the greater the efficiency of neurotransmitter release, the faster the rate of neurotransmitter depletion (Tsodyks and Markram 1997). The presynaptic activation rate would be expected to depend on the strength of the stimulus. The efficiency of neurotransmitter release, on the other hand, can be influenced, transiently, by neuromodulators such as acetylcholine and, longer-term, by spike time-dependent plasticity (Markram and Tsodyks 1996; Markram et al. 1998). Neurophysiological results suggest that the rate of neurotransmitter replenishment, μ, decreases toward higher processing levels (Eggermont 1985, 2000). This explains why neural responses to prolonged sounds become more transient and less sustained (Harms and Melcher 2002; Seifritz et al. 2002 and references therein).

Our results showed that the P2 was more strongly affected by adaptation than the N1; both the increase in adaptation with increasing adapter duration and the recovery from adaptation with increasing ISI were much more apparent in the P2 than N1. This finding is consistent with previous results (reviewed in Crowley and Colrain 2004). It suggests that the N1 and P2 have at least partially distinct neural generators. It has been proposed that the N1 might reflect stimulus-specific thalamocortical input, whereas the P2 might represent a combination of nonspecific thalamocortical and more widespread corticocortical responses (Barth et al. 1993; Ohl et al. 2000; Shaw 1988; von der Behrens et al. 2009). A comparison of the topographies of the N1 and P2 suggests that they arise from different layers within the same or similar cortical patch.

The recovery from adaptation for the multiple adapters occurred with a considerably faster time constant (e.g., 738 ms for the 4-adapter trains) than for the single adapters (1,271 ms). This accords with the results of Chung et al. (2002) inasmuch as it shows that repeated exposure to the adapter can change the parameters of adaptation. Our finding of faster recovery from adaptation for repeated adapters may also be related to the recent finding by Taaseh et al. (2011) that, in the auditory oddball paradigm (see Näätänen et al. 2012 for a review), the standard (i.e., frequently presented) stimuli are less effective at adapting the deviant (i.e., rarely presented) stimuli than would be expected on the basis of adaptation by single adapters. Taaseh et al. (2011) hypothesized that this reduction in the adaptational effectiveness of the standards may be due to a sharpening of the specificity of adaptation. The current results suggest that it might also be due to an increase in the adaptation recovery rate. Changes in adaptation parameters with repeated exposure to the adapting stimulus, and indeed adaptation itself, may be mediated by top-down feedback from higher-order brain areas involved in setting up expectations based on past stimulus input (Friston 2005). This is consistent with the finding that adaptation, at least in human macroscopic brain responses, is stronger for expected than for unexpected stimuli (Costa-Faidella et al. 2011; Lange 2009; Summerfield et al. 2008; Todorovic et al. 2011; Wacongne et al. 2011; however, see Farley et al. 2010 for contrary evidence in animal multiunit recordings). However, given that stimulus expectancy was fixed in the current study, we cannot exclude the possibility that our finding of a faster adaptation recovery rate for multiple than for single adapters reflects a local, rather than a top-down, effect. For instance, our finding could be related to the previous finding in slice recordings that the recovery from synaptic depression is accelerated by the buildup of residual presynaptic Ca²⁺ as a result of repeated stimulation (reviewed in Zucker and Regehr 2002). Alternatively, our finding could also be due to the involvement of more than one layer of depressing synapses with different recovery rates as suggested by Mill et al. (2011).

Throughout this paper, we have assumed that the adapter and probe responses represent stimulus-evoked phasic activity, which is superimposed on a background of unrelated ongoing EEG activity. At various times, this classic view has been challenged by the proposal that event-related scalp potentials are instead caused by phase resetting of the ongoing EEG activity. In the phase-resetting mode, adaptation would have to be assumed to reflect a reduction, not in neural excitability, but in the degree of phase resetting. Although appealing theoretically, the phase-resetting model has been difficult to validate empirically. This is because phase resetting and phasic activity have similar physical characteristics. As a result, many of the key methods that have previously been used to test for phase resetting have subsequently been shown to be unspecific (Yeung et al. 2004). Moreover, it has been shown that sensory-evoked intracortical potentials, which underlie the scalp potentials, are predominantly caused by phasic activity rather than phase resetting (Shah et al. 2004).

GRANTS

This research was funded by the United Kingdom Medical Research Council (MRC) Intramural Programme.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

C.P.L., P.M.B., and K.K. conception and design of research; C.P.L. performed experiments; C.P.L. analyzed data; C.P.L., C.J.S., and K.K. interpreted results of experiments; C.P.L. prepared figures; C.P.L. and K.K. drafted manuscript; C.P.L., P.M.B., C.J.S., and K.K. edited and revised manuscript; C.P.L. approved final version of manuscript.