Abstract
Repetitive one-per-day seizures induced in otherwise normal rats by the volatile convulsant flurothyl decrease the accuracy of locating a hidden goal without changing the mean location of goal selection. We now show that an 8-d series of such seizures degrades the spatial signal carried by the firing of hippocampal pyramidal cells and specifically reduces the information conveyed by the place cell subset of pyramidal cells. This degradation and a concomitant slowing of the hippocampal theta rhythm occur over time courses parallel to the development of the behavioral deficit and plausibly account for the impairment. The details of how pyramidal cell discharge weakens are, however, unexpected. Rather than a reduction in the precision of location-specific firing distributed evenly over all place cells, the number of place cells decreases with seizure number, although the remaining place cells remain quite intact. Thus, with serial seizures there is a cell-specific conversion of robust place cells to sporadically firing (<0.1 spike/s) “low-rate” cells as opposed to gradual loss of place cell resolution. This transformation occurs in the absence of significant changes in the discharge rate of hippocampal interneurons, suggesting that the decline in the number of place cells is not a simple matter of increased inhibitory tone. The cumulative transformation of place cells to low-rate cells by repetitive seizures may reflect a homeostatic, negative-feedback process.
Introduction
In accord with expectations from the extreme seizure susceptibility of the hippocampus (Wieser, 2004) and the role of the rodent hippocampus in spatial learning and memory (O'Keefe and Nadel, 1978), repetitive convulsions induced in otherwise healthy adult rats impair their ability to learn and recall spatial navigational tasks. Specifically, ∼10 brief (<1 min) flurothyl-induced generalized seizures given once or twice per day slow the rate at which rats learn to swim to a hidden platform (Zhou et al., 2007) and reduce the accuracy with which rats locate an unmarked goal to release food pellets (Lin et al., 2009).
Based on a great deal of evidence linking normal function of hippocampal place cells to proper performance in spatial navigational tasks (McHugh et al., 1996; Rotenberg et al., 1996; Cho et al., 1998; Liu et al., 2003), repetitive seizures should alter location-specific firing in a manner that plausibly accounts for the behavioral impairment. This prediction was apparently borne out by the finding that 5 d of two-per-day flurothyl seizures reduced the stability and intensity of place cell activity 24 (or more) hours after the last seizure (Zhou et al., 2007).
The protocol used by Zhou et al. (2007) reveals persistent seizure effects but leaves unexplored the kinetics of place cell modifications. Thus, the magnitude and time course of place cell impairment after each convulsion are unknown. Similarly, the nature of place cell recovery after each convulsion is unclear. Moreover, there is little information concerning possible cumulative effects during the sequence of daily seizures, although behavioral data imply that cumulative changes should occur (Lin et al., 2009).
For these reasons, we designed a protocol to look for place cell degradation in healthy rats caused by repeated seizures given once per day for 8 d. In this procedure, which mimics measurements of navigational accuracy before and after each day's seizure (Lin et al., 2009), we recorded the same place cells four times in each day, twice before and twice after the convulsion; no attempt was made to identify cells across days.
The overall pattern of results is in line with expectations from the spatial theory of hippocampal function. Thus, we see short-term (within-day) and long-term (across-day) effects that potentially explain the navigational deficits caused by a very similar protocol. In detail, however, the outcome is very surprising: the predominant effect is not increasing instability of location-specific discharge but rather a process whereby place cells are converted to sporadically spiking “low-rate” cells (<0.1 Hz). While this happens there is hardly any degradation in the quality of the remaining place cells; it is as if the size of the active subset of place cells that represents the environment is reduced by seizures with little accompanying loss of spatial firing precision by the survivors. We suggest, in other words, that the primary change induced by repetitive seizures is a reduction of the amount of neural machinery used to compute position rather than a decrease of average resolution of place cells.
Materials and Methods
Subjects.
Adult male Long–Evans rats (Taconic) were used. They were treated in accordance with NIH guidelines for the humane treatment of animals. Rats had ad libitum access to water but food was restricted to bring their weight to ∼85% of the ad libitum level; 5 g of weight gain was allowed per week. They weighed ∼350 g at the time of the experiment. The rats were individually housed in plastic cages under diurnal lighting conditions (12 h on/12 h off). Twelve rats were used, six in the seizure group and six in the control group.
Apparatus.
The experimental chamber was a 76-cm-diameter, 50-cm-high gray-colored cylinder that was enclosed by a 190-cm-high black curtain. The cylinder floor was a sheet of gray photographic backdrop paper renewed after each recording session. There were two cue cards on the cylinder wall that occupied the upper half of the wall and 45° of the cylinder arc; one card was white, and the other was black. The card centers were separated by 135° such that the white card center was clockwise relative to the black card center. In the view of the overhead TV camera used for rat tracking, the midpoint between the cards was at 3 o'clock; this was also 0° in the angular coordinate system whose value increased in the counterclockwise direction.
Recording implant and surgery.
The recording implant contains eight independently drivable tetrodes (VersaDrive; Neuralynx). Each tetrode is made from four 25-μm-diameter nichrome wires twisted together (California Fine Wire).
For surgery, the rat was anesthetized with Nembutal (50 mg/kg) and injected with atropine (0.25 mg/kg) to minimize respiratory difficulty. The scalp was shaved and wiped with iodine. The head was immobilized in a stereotaxic instrument with two blunt ear bars and a nose clamp. A midline incision was made, and the skull was exposed and cleaned with cotton swabs. Two bone screws were put above the left and right olfactory bulbs; two more screws were inserted over the left and right cerebellar hemispheres. A circular hole 2 mm in diameter was drilled above the left dorsal hippocampus (centered 3.9 mm posterior to bregma and 2.5 mm lateral to the midline). The dura was removed and the implant was slowly lowered so that the tetrode tips were placed ∼1.6 mm below the dura. Petroleum jelly was used to cover the trephine hole. Four ground wires from the implant were soldered to the two cerebellar screws. Grip cement was used to bond the implant to the anchoring screws and the skull. Hydrogen peroxide was used to clean the wound, and a layer of antibiotic ointment was applied. The wound was closed with surgical clips. Rats were given a week to recover from the surgery.
Acute seizure induction.
Flurothyl(bis-2,2,2-triflurothyl ether), a potent, rapidly acting CNS convulsant, induces seizure due to its antagonism to GABAA receptors (Krasowski, 2000). Rats that inhale flurothyl go through a series of five convulsive stages (Racine, 1972): I, mouth and facial movements; II, head nodding; III, forelimb clonus; IV, rearing; and V, rearing and falling. Seizure induction was done in a room different from the recording room. Seizure group rats were placed in a 22 L glass fish tank (40 × 20 × 27 cm) covered with a glass sheet and placed inside a fume hood. Using a syringe pump, liquid flurothyl was dripped onto a strip of filter paper just beneath the chamber cover at a rate of 3 ml/h. The rat was exposed to the convulsant until tonic extension of forelimbs and hind limbs was observed and the animal fell down (stage V seizure). The time to the seizure start was ∼7 min. Immediately after the rat fell, the tank was flushed with room air. There were individual and daily variations in the stage V seizure duration, but the typical time was 30–60 s. Control group rats were placed in the same glass tank but tap water was delivered instead of flurothyl.
Behavioral training.
Hungry rats were handled for several days. They were then trained in the “pellet chasing” task (Muller et al., 1987) in which they learned to forage for randomly scattered 25 mg sugar pellets dropped at ∼3 per minute on a pseudorandom schedule from an overhead feeder. Rats were trained for ∼10 d before implant surgery. After a week of recovery, they were trained for a minimum of another week during screening for CA1 pyramidal cells. Thus, rats were familiar with the environment and task when the experiment began.
The experimental protocol.
Single-unit screening sessions were run twice daily >2 h apart. Tetrodes that showed no single-unit signals were lowered ∼30–60 μm (1/8–1/4 of a screw turn) after each screening session until single units were detected on most tetrodes. The typical screening time ranged from 1 to 2 weeks. During this period, the tetrodes were lowered ∼500 μm (approximately two turns) from their initial depth to place them near the pyramidal cell layer of dorsal CA1.
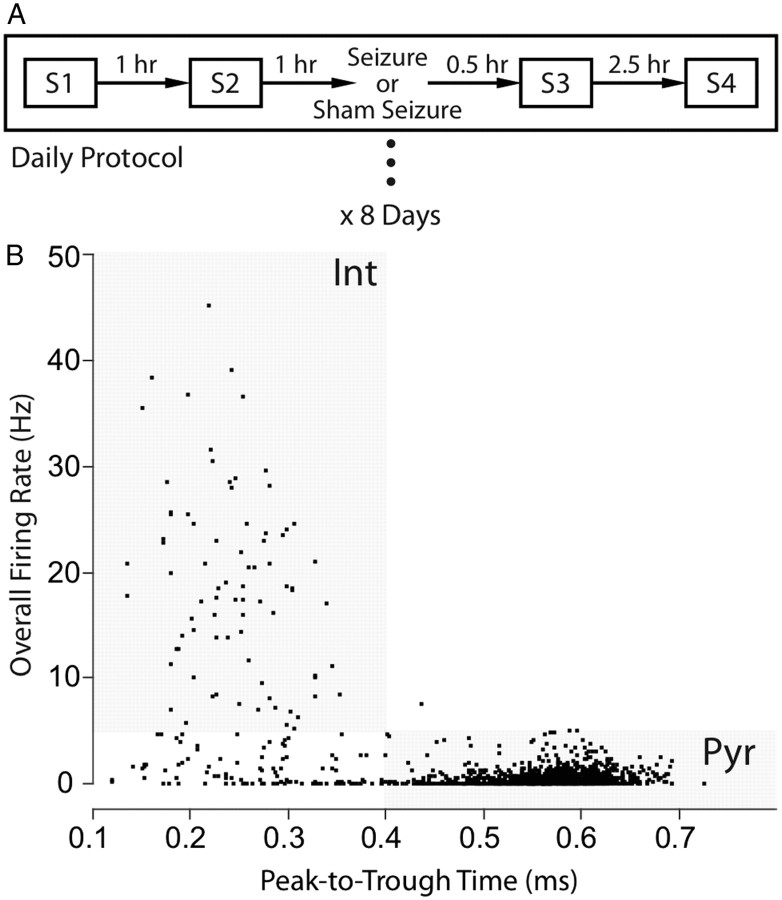
The experiment, summarized in Figure 1A, consisted of 8 consecutive recording days. Four 16 min sessions were done each day at −2, −1, +0.5, and +3 h relative to the seizure induction. Either a flurothyl seizure or a sham seizure was given after session 2.
Figure 1.
Experimental protocol and single-unit classification. A, Daily procedure. Each day consists of four 16 min sessions at −2, −1, +0.5, and +3 h relative to the seizure induction procedure; a generalized flurothyl seizure or a sham seizure is given once daily after session 2. The same sequence is repeated for 8 consecutive days. B, Pyramidal cells and interneurons are separated by overall firing rate and peak-to-trough time of the extracellular waveform. For pyramidal cells, the peak-to-trough time is ≥0.4 ms and the mean firing rate is ≤5 Hz. For interneurons, the waveform peak-to-trough time is <0.4 ms and the mean firing rate is >5 Hz. Inclusion of cells into the sample was also determined by the peak-to-trough amplitude of the spike (see Materials and Methods).
During each of the 8 recording days, tetrodes were never moved between any of the four sessions. However, after the last daily session, tetrodes with no units were lowered ∼30 μm to enhance single-unit yield the next day. Seizures or sham seizures were stopped after day 8.
Rats became harder to handle with increasing numbers of seizures. This made it impossible to record session 3 of day 8 for one rat and session 4 of day 8 for another rat. For a third seizure rat, no units were obtained beyond day 6. Data for this rat from days 3 and 6 were therefore analyzed and treated as equivalent to days 4 and 8 for other seizure group rats.
For three seizure rats, good EEG signals were detectable for 11 consecutive postseizure days during each of which we ran two 16 min sessions separated by an hour. Attempts to record more place cells during the postseizure period were unsuccessful.
Data acquisition.
The eight-tetrode implant on a rat's head was plugged into a head stage that contained unity gain amplifiers. The head stage was attached to a 32-channel cable connected to an electrophysiology recording system (Neuralynx). Single-unit signals were amplified 10,000 times by default (or 5000 times to prevent saturation if there were cells with large-amplitude waveforms). Signals were bandpass filtered between 0.3 and 6 kHz, and digitized at 30 kHz with a 12 bit A/D converter. The threshold for spike detection was set at 100 μV.
EEG signals were amplified 2000–5000 times, sampled at 1894 Hz, and filtered from 1 to 275 Hz. Each tetrode could be assigned by software to record either single units or EEG signals. The experimental priority was to record single units. The tetrode with the lowest background noise was used as the reference.
The rat's position was tracked by detecting two red LEDs on the head stage. Video frames from a digital camera were processed at 30 Hz. A brightness threshold was set in the red video channel to accept only light from the LEDs. The rat's position was taken as the center of gravity of all above-threshold pixels.
Single-unit isolation, matching, and classification.
Single-cell data were analyzed only for days 1, 4, and 8. Off-line Sorter software (Plexon) was used to identify single units. They were isolated and clustered using a 3D scatter view of peak waveform amplitudes on three of the four tetrode wires. After a single unit was isolated from other waveforms, the cluster was refined using a rotating 3D scatter view of the first three principal components of the four tetrode waveforms.
Single-unit matching was done across the four daily sessions. Session 1 waveforms were first clustered and then used as references for recognizing waveforms in sessions 2, 3, and 4. Waveforms for each individual unit were visually matched using the 3D scatter views of peak waveform amplitudes of the four tetrode wires, as well as the relative ratio of their peak amplitudes. For the most part, waveforms were stable and matched across the four daily sessions. When the waveforms for a tetrode failed to match across the sessions, the putative clusters were excluded from the data set. No waveform matching was done across days since it was much harder to identify the same cells with high consistency and because lowering the silent tetrodes after a day's final session could potentially disturb signals on other tetrodes. Thus, we treated data from different days as if they were from independent neuronal populations.
Pyramidal cells and interneurons were identified using waveform properties and temporal firing characteristics (Ranck, 1973; Fox and Ranck, 1975, 1981; Kubie et al., 1990; Csicsvari et al., 1999). The separation criteria were as follows: (1) the extracellular waveform peak-to-trough time was ≥0.4 ms for pyramidal cells and <0.4 ms for interneurons (Fig. 1B); (2) the time-averaged firing rate for pyramidal cells was ≤5 spikes/s and >5 spikes/s for interneurons (Fig. 1B); (3) the minimum peak-to-trough spike amplitude for pyramidal cells was 200 μV; the minimum for interneurons was 150 μV (Fox and Ranck, 1975); (4) pyramidal cells were able to fire complex spikes (bursts of spikes with decrementing amplitude and interspike intervals <5 ms), whereas interneurons did not generate complex spikes.
Pyramidal cell classification.
A pyramidal cell was considered to be a place cell if it met the following criteria: (1) 0.1 spikes/s ≤ overall rate ≤ 5 spikes/s, (2) coherence ≥ 0.4, and (3) nine contiguous pixels ≤ field size ≤ 50% of cylinder area. The minimum field size was defined as a set of nine contiguous pixels in which the firing rate was nonzero. If a pyramidal cell did not meet the criteria for a place cell and its overall rate was <0.1 spikes/s, it was called a “low-rate cell.” The few (∼10%) remaining pyramidal cells that were neither place cells nor low-rate cells were called “other” cells.
Since there were two baseline (preseizure) sessions 1 and 2, it was decided that a pyramidal cell had to satisfy place cell criteria in both baseline sessions of a day to be treated as a place cell. If the firing rate of a cell was below threshold (<0.1 Hz) in both baseline sessions, it was classified as a low-rate cell. The remaining pyramidal cells were categorized as “other” cells. The number of cells recorded per rat is given in Table 1 along with the number in each pyramidal cell class in the two baseline sessions.
Table 1.
Cell class distribution in baseline sessions
| Cell type | Control group |
Seizure group |
||||
|---|---|---|---|---|---|---|
| Day 1 | Day 4 | Day 8 | Day 1 | Day 4 | Day 8 | |
| Pyramidal cells | 80 | 79 | 77 | 115 | 122 | 103 |
| Pyramidal cells per rat | 24, 2, 7, 10, 8, 29 | 3, 2, 11, 8, 1, 54 | 10, 4, 15, 2, 0, 46 | 9, 10, 10, 17, 56, 13 | 3, 28, 6, 9, 60, 16 | 3, 38, 10, 15, 19, 18 |
| Place cells | 44 (55%) | 48 (61%) | 41 (53%) | 66 (57%) | 46 (38%) | 20 (19%) |
| Low-rate cells | 22 (28%) | 23 (29%) | 25 (32%) | 28 (24%) | 55 (45%) | 68 (66%) |
| Other cells | 14 (17%) | 8 (10%) | 13 (17%) | 21 (18%) | 21 (17%) | 15 (15%) |
| Interneurons | 5 | 6 | 5 | 9 | 2 | 6 |
Cell class distributions in baseline (preseizure) sessions 1 and 2 for days 1, 4, and 8. Pyramidal cells have to satisfy the place cell criteria in both baseline sessions of a day in order to be treated as a place cell in the analysis of spatial firing properties. If a pyramidal cell has below-threshold (<0.1 Hz) firing rate in both sessions, it is classified as a low-rate cell. Any leftover pyramidal neurons are considered as “other” cells. For interneurons, the firing rate threshold is 5 Hz.
By matching waveforms across daily sessions, we could track changes in individual cells within a day. For control (sham seizure rats), pyramidal cell classification was stable across multiple daily sessions. In contrast, for seizure rats, our main finding was that the classification of a cell often changed after the daily seizure. No attempt was made to match cells across days so it is possible that the same cell was recorded for 2 or more successive days.
Pyramidal cell firing field properties.
We measured five field properties: (1) field smoothness estimated by coherence score, (2) primary field spatial information, (3) primary field mean firing rate, (4) primary field size, and (5) overall firing rate. The primary field is the largest field if there were multiple fields in a rate map. The five measures were defined as follows: (1) coherence, the z-transform of the correlation between the firing rate in a pixel and the average rate in the eight nearest-neighbor pixels (Muller and Kubie, 1989); (2) primary field spatial information, the average of the “positional information” of each pixel in the largest field (Olypher et al., 2003); positional information is a measure of relative entropy; it calculates the distance between the probability distribution of firing rates for a given location and the distribution of firing rates across all locations; (3) primary field mean rate, the total number of spikes fired in the largest field divided by the total time spent in the field; (4) primary field size, the number of pixels in the largest field (pixel side, 3.2 cm); (5) overall firing rate, the total number of spikes fired by the cell divided by the session duration. If the spatial firing pattern of a pyramidal cell did not have the nine contiguous pixel minimum required for a firing field, its primary field properties (spatial information, mean rate, and size) were assigned values of zero.
Place cell cross-session analysis.
Analysis of place cell rate maps across sessions was done in two ways: (1) field similarity score, the pixel-by-pixel correlation between two rate arrays from different sessions of the same place cell (Bostock et al., 1991); (2) rate change score, the signed difference-over-sum score as opposed to the unsigned “rate remapping” score used by Leutgeb et al. (2005). Session 1 (S1) of each day was the baseline to which subsequent daily sessions were compared. Thus, the rate change score for session 3 (S3) was the difference in primary field mean rates divided by the sum of the two rates as follows: (S3 − S1)/(S3 + S1). The range of possible scores is from −1 (S3 ≪ S1), to 0 (no rate change), to 1 (S3 ≫ S1).
EEG analysis.
A speed range of 10–30 cm/s was used to select EEG segments with “movement-related theta” (Vanderwolf, 1969; Huxter et al., 2007) for frequency domain analysis. Rat locomotor speed was calculated in 333 ms intervals. If the average moving speed of a 1 s window was within the speed range, the corresponding 1.08 s EEG data segment was extracted and zero-padded out to 8.64 s for fast Fourier transform analysis. The magnitude spectrum was characterized in the range of 0–100 Hz using 866 frequency bins. Theta peak frequency was taken as the largest peak in the 5–12 Hz range and theta magnitude as the height of the peak.
For the control group, qualified EEG data were analyzed in six rats up to day 4 and four rats up to day 8. For the seizure group, qualified data from five rats were analyzed up to day 5 and three rats up to day 8. In the postseizure period, three seizure rats with good EEG signals were recorded for 11 additional days.
Histology.
At the end of the experiment, rats were administered a lethal dose of urethane and perfused transcardially with 200 ml of normal saline followed by 200 ml of 4% paraformaldehyde (PFA). The brains were removed and postfixed in PFA and stored in a refrigerator. Before slicing, brains were placed in 30% sucrose for at least 24 h until they sank. Coronal sections along the entire extend of the hippocampus were cut at 15 μm on a freezing microtome. Every third slide was stained with cresyl violet. The slices were imaged with a video microscope, and cell counts were made for CA1 and CA3. We estimated ∼30 cells in 100 μm2 patches in the pyramidal cell layers in both control and seizure rat brains. Thus, we detected no obvious cell loss after eight serial flurothyl-induced seizures given once per day.
Statistics.
To determine within-day effects of a seizure, repeated-measure ANOVAs of four daily sessions were done for single-cell firing properties for days 1, 4, and 8. For post hoc comparisons, Wilcoxon's rank sum tests with Bonferroni's correction were used to detect specific session differences within the seizure and control groups (sessions 1 and 3 for seizure effect; sessions 3 and 4 for recovery). The use of session 1 rather than session 2 is arbitrary; to emphasize this, we used session 2 rather than session 1 in the kinetic model (see Results), although the outcome is indistinguishable regardless of which preseizure session was considered. To determine across-day effects of multiple seizures, repeated-measure two-way ANOVAs of group by session were performed for days 1, 4, and 8; planned post hoc comparisons using Wilcoxon's tests with Bonferroni's correction were done for preseizure session 1 of each day between the two groups. Similar ANOVAs and post hoc t tests were applied to the theta peak frequency data set that includes days 1 through 8 during the seizure period and days 9–19 for postseizure recordings. Chi-square (χ2) goodness-of-fit tests were done for the cell class distributions; similar session comparisons for the within- and across-day effects were conducted. JMP statistical discovery software (SAS) and KaleidaGraph (Synergy Software) were used. Values of p < 0.05 were considered statistically significant. Error bars indicate SEMs.
Results
After 8 d of one-per-day flurothyl-induced generalized seizures in otherwise normal rats, single hippocampal cell activity and the hippocampal EEG became abnormal in several ways. First, pyramidal cell firing was reduced in the first postseizure session (session 3) on a given day, followed by partial recovery during the second postseizure session (session 4). In addition to these short-term (within-day) effects, there was a cumulative across-day decrease in the overall activity of pyramidal cells even during the preseizure sessions (sessions 1 and 2) of the day. This long-term decrease mainly reflected a progressive reduction in the size of the place cell subset and a concomitant increase in the size of the low-rate cell subset. Third, place cells recorded on later seizure days were more vulnerable to the effects of the day's seizure. Fourth, at the network level, the peak frequency of hippocampal theta oscillations declined in a fashion parallel to the decreased number of active single pyramidal cells. Finally, although the number of recorded interneurons was not very large, we saw no obvious short- or long-term increase in their activity that might account for the conversion of place cells to low-rate cells.
Short- and long-term effects of repeated seizures on pyramidal cells: examples from individual rats
To illustrate the short- and long-term effects of serial seizures, we show firing rate maps for representative pyramidal cells from a single control rat (Fig. 2) and a single seizure rat (Fig. 3) on the first and last experiment days (days 1 and 8).
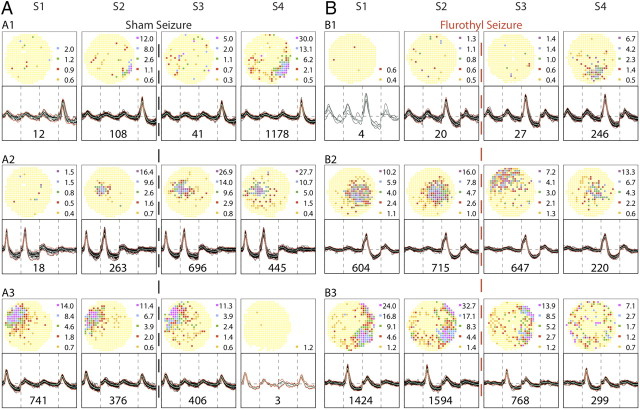
Figure 2.
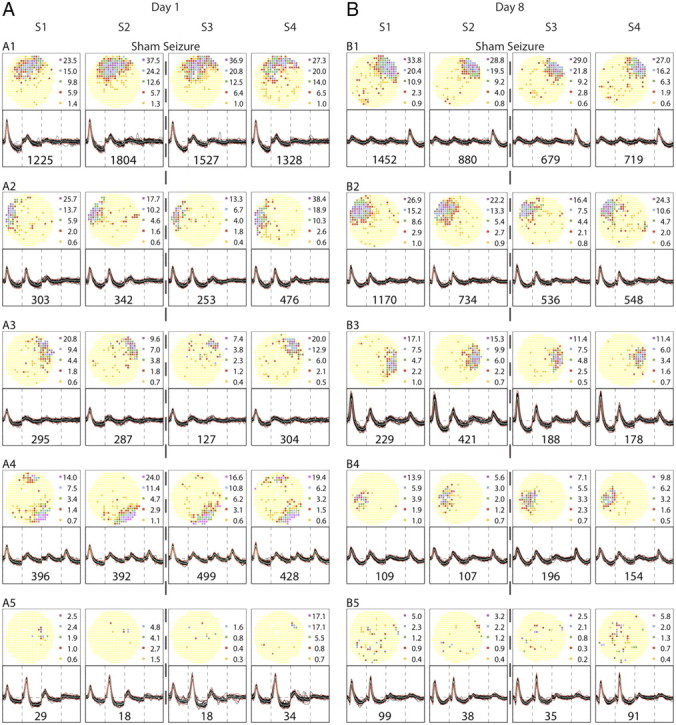
Firing rate maps and spike waveforms for cells recorded from an example control rat. The five half-rows on the left are for recording day 1; the five half-rows on the right are for recording day 8. Note that the two cell samples are independent; there was no attempt to hold the same cells across days. Each half-row summarizes the results of four daily sessions, S1 and S2 before the sham seizure and S3 and S4 after the sham seizure. The outcome of each session is shown with a firing rate map at the top and waveforms at the bottom. Thirty (or fewer) tetrode waveforms are overlaid and the number of spikes fired by the cell during the session is given below the traces. Recording stability is demonstrated by the constancy of waveforms within each half-row despite disconnection and reconnection of the cable between each session. In firing rate maps, yellow codes pixels in which exactly zero spikes were fired during the session. Pixels with higher rates are colored in the ascending order orange, red, green, blue, purple; the rate (spikes/second) in the median pixel in each color category is shown to the right of the map. A, Day 1. The four pyramidal cells in the top half-rows show during each session the stable firing fields typical of place cells. Field location is fixed, although the discharge rate varies. Fields are stable even though the rat was exposed to a different environment between sessions 2 and 3. The cell in the bottom half-row is a sporadically firing “low-rate” cell more commonly seen in seizure rats after each seizure and especially after multiple seizures. B, Day 8. The four pyramidal cells in the top half-rows are again clear place cells; the cell in the bottom half-row is a low-rate cell. The constant nature of recordable cells over the 8-d protocol is emphasized by the fact that only details would change if A and B were interchanged.
Figure 3.
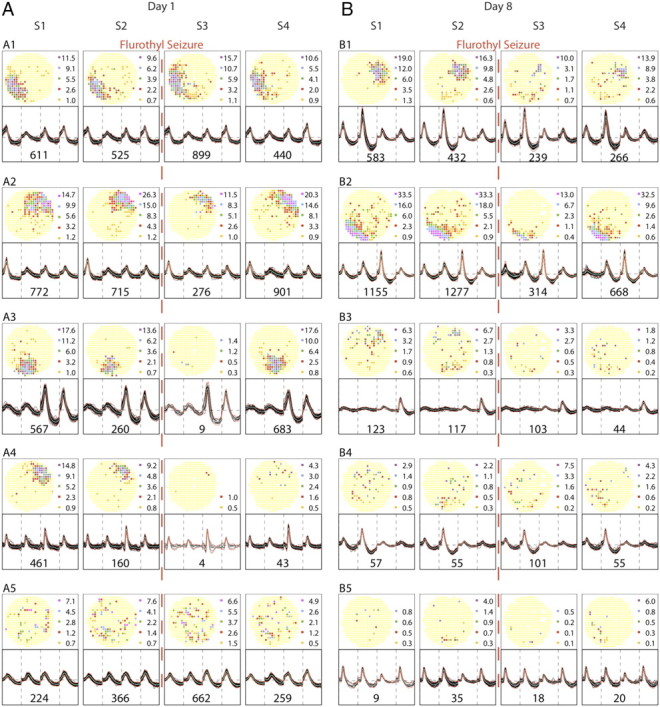
Rate maps and spike waveforms for cells recorded from an example seizure rat. Alterations in cell-specific spike activity were seen within a day and between days 1 and 8. The layout of the figure is the same as in Figure 2. Note that tetrode waveforms are stable despite the mechanical and biochemical effects of the seizure between sessions 2 and 3. A, Day 1. During sessions 1 and 2, the spatial firing patterns of the five example pyramidal cells parallel the patterns of the example cells from the control rat; the top four half-rows show place cells, whereas the bottom half-row shows a nonplace cell. The dashed vertical red line between sessions 2 and 3 indicates induction of a brief, generalized seizure. The spatial firing patterns of the cells in the top two half-rows are not strongly altered after the seizure, although during session 3 there is a transient rate increase for cell A1 and a transient rate decrease for cell A2. In contrast, cell A3 is nearly silent during session 3, although it recovers during session 4. The seizure effects on cell A4 are even stronger; it is virtually inactive during session 3 and recovers little if at all during session 4. The nonplace cell A5 in the bottom half-row appears hardly affected by the seizure. By comparing sessions 3 and 4 of day 1 for the seizure rat and the control rat (Fig. 2), the changes seen here are plausibly attributed to the seizure rather than exposure to a different environment between sessions 2 and 3. B, Day 8. The rate maps for sessions 1 and 2 capture the state of the neural system after seven seizures. The top two half-rows show there are still apparently normal place cells, but including only two such cells indicates that a long-term, cumulative change has occurred; the nature of the change is depicted by including three sporadically firing cells.
The recordings from the control rat emphasize several properties of normal hippocampal pyramidal cells (Fig. 2). First, on both days, tetrode waveforms are constant across the four recording sessions, indicating that individual cells can be reliably recognized and matched when the cable is disconnected after each session and reconnected before the next session. Second, there are no consistent changes in the spatial firing distribution across the four recording sessions within a day, although the rat experienced a very different environment during the sham seizure. Finally, the selected ensembles of spatial firing patterns (four place cells and one low-rate cell) are interchangeable between day 1 and day 8; this implies that there has been no systematic alteration in the underlying neuronal population as a function of time.
Recordings from the seizure rat (Fig. 3) reveal that tetrode waveforms are as well preserved as for the control rat; waveforms are unchanged by disconnection and reconnection of the recording cable, by transport to a different environment, and by the convulsion itself. After exposure to flurothyl, however, waveform constancy is often accompanied during both days by major changes in spatial firing patterns.
Before the seizure on day 1, the selected ensemble of spatial firing patterns (four place cells and one nonplace cell) is equivalent to the day 1 and day 8 ensembles for the control rat. After the seizure, the spatial firing patterns of these pyramidal cells are altered in two main ways. In the short term (within day 1 or day 8), firing is often suppressed for at least 0.5 h after seizure (Fig. 3A2–A4,B1–B2). Not uncommonly (on both days), there is partial recovery 3 h after the seizure (Fig. 3A2,A3,B2). Strikingly, there are also cells that persist in near-silence with no signs of a recovery (Fig. 3A4). In the long term, on day 8, the character of the preseizure ensemble is altered so that there are fewer place cells; by our criteria, only cells B1 and B2 qualify as place cells in both sessions 1 and 2.
The statistical analyses in the next sections show that the selected examples in Figures 2 and 3 capture the overall behavior of pyramidal cells in control and seizure rats. Nevertheless, anomalous place cells in both groups (see Fig. 9) suggest there are additional sources of variation in the hippocampal representation of space.
Figure 9.
Examples of anomalous place cells. The layout is the same as Figures 2 and 3. A, Control group examples. The cells in A1 and A2 show spatially selective firing patterns emerging from initial near silence in S1. For the cell in A1, the firing field is present in sessions 2 and 4. The cell in A3 has a stable firing field in sessions 1–3 that disappears in session 4. B, Seizure group examples. A new field develops for the cell in B1 in session 4 that could be due either to seizure-induced synaptic plasticity or the intrinsically dynamic nature of the place representation, as seen also in control rats. The frequency of such occurrences is not noticeably different from the control group. The cell in B2 shows a transient remapping in S3 before returning to its preseizure state in S4. This instability may be a seizure effect but again is rare. The cell in B3 exhibits both reduced firing rate and disintegration of its firing field in S4.
How pyramidal cells are affected by repeated seizures
Changes in spatial firing properties are described by coherence and three measures of the primary firing field, namely, spatial information, mean rate, and size; coherence and information estimate spatial firing organization, whereas field rate and size estimate firing intensity. If a cell had no field, its field measures were assigned values of zero (see Materials and Methods). When these quantities are plotted for the entire pyramidal cell sample (Fig. 4A) for the four sessions of days 1, 4, and 8, visual inspection reveals for each day a short-term postseizure drop in session 3 and partial recovery in session 4. In addition, a long-term, across-day decline is seen for preseizure sessions 1 and 2.
Figure 4.
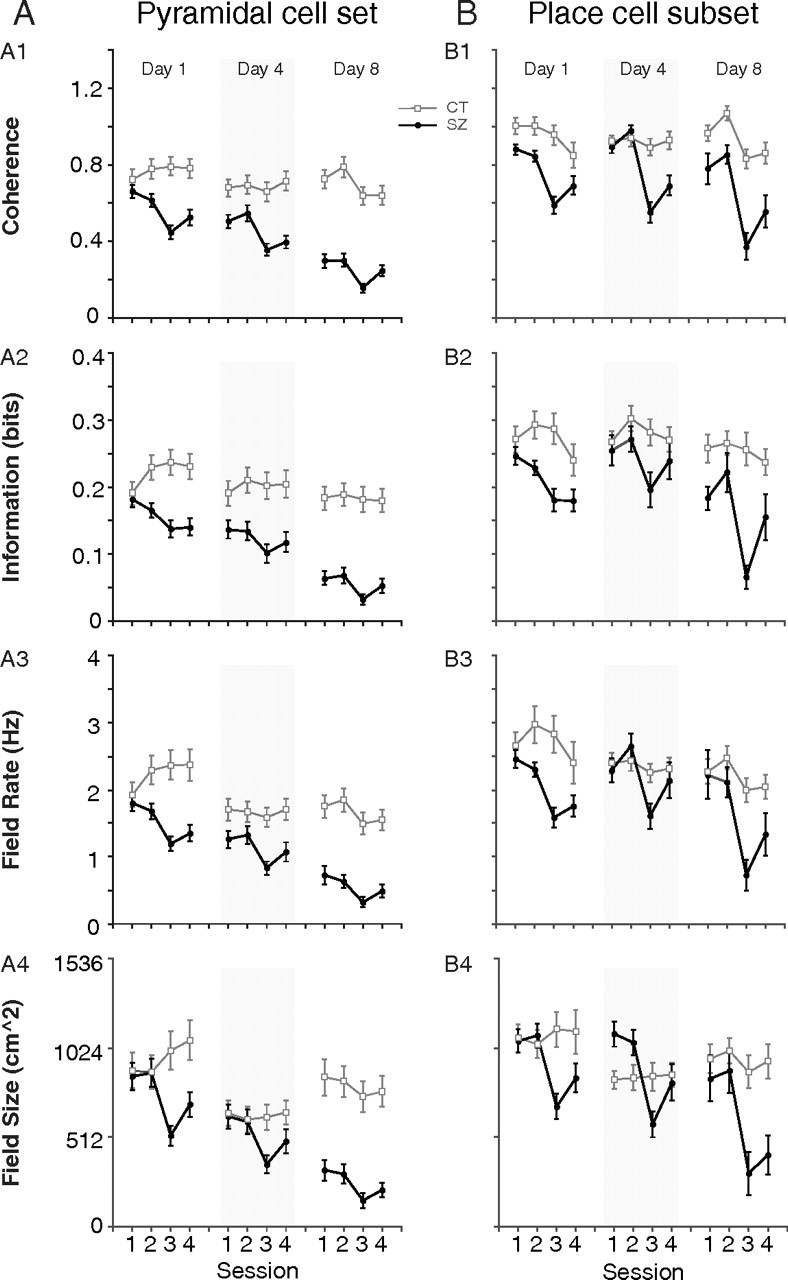
Spatial firing properties for the pyramidal cell sample and the place cell subset across days. The spatial organization of pyramidal cell discharge is measured by coherence and primary field spatial information; discharge intensity is quantified by primary field mean firing rate and primary field size. If a pyramidal cell does not have a qualifying field, then its primary field measures of information and rate and size are set to zero (see Materials and Methods). A, Spatial firing properties for the entire pyramidal cell sample (place plus low-rate plus other cells). For the seizure group (filled circle), all four properties exhibit a sharp short-term drop in postseizure session 3 of each day followed by a partial recovery in session 4. Spatial firing properties also display a cumulative long-term decline seen by comparing preseizure sessions 1 and 2 across days. For the control group (open square), there are no strong short- or long-term trends within a day or from day 1 to day 8. B, The same four spatial firing properties are plotted for the place cell subset. A pyramidal cell has to satisfy place cell criteria in both preseizure sessions 1 and 2 to be included in the analysis. The seizure group shows a sharp short-term drop in postseizure session 3 of each day followed by partial recovery in session 4. Unlike plots for the pyramidal cell set in A, the spatial firing properties for the place cell subset in preseizure sessions 1 and 2 are mostly preserved across days 1, 4, and 8. The place cell subset for the control group shows essentially constant spatial firing property values across all sessions in each day. Error bars indicate SEM.
To formally characterize the short-term effects on pyramidal cells, we did repeated-measure ANOVAs of session for each day for the control and seizure groups. For control rats, there was a significant session effect for coherence and field rate on day 8 only. Planned comparisons did not reveal, however, a reliable difference between sessions 1 and 3 or between sessions 3 and 4 for either measure (data not shown). In contrast, for the seizure group, there was a significant session effect for all four measures on each day (Table 2). For each property, we then made within-day planned Wilcoxon's comparisons between sessions 1 and 3 to test the reliability of the seizure-induced decreases; we also compared sessions 3 and 4 to test the reliability of the partial recoveries.
Table 2.
Repeated-measure ANOVAs of session for pyramidal cells
| Day | Coherence | Field info | Field rate | Field size |
|---|---|---|---|---|
| D1 | F (3,342) = 14.5 | F (3,342) = 6.0 | F (3,342) = 13.0 | F (3,342) = 17.1 |
| p = 1.1e-7 | p = 0.002 | p = 6.9e-7 | p = 5.4e-9 | |
| D4 | F (3,360) = 19.9 | F (3,360) = 3.7 | F (3,360) = 9.3 | F (3,360) = 18.2 |
| p = 9.3e-11 | p = 0.02 | p = 3.1e-5 | p = 7.8e-10 | |
| D8 | F (3,306) = 12.3 | F (3,306) = 5.4 | F (3,306) = 5.5 | F (3,306) = 8.5 |
| p = 3.1e-7 | p = 0.002 | p = 0.005 | p = 0.0001 |
The post hoc results for the seizure group indicate that each measure (except field information on day 4) decreased significantly from session 1 to session 3 (Table 3). Thus, the organization and intensity of pyramidal cell firing are reduced during the first postseizure session.
Table 3.
Short-term effects of seizures on pyramidal cells
| Compared sessions | Day | Coh | Info | Rate | Size |
|---|---|---|---|---|---|
| S1–S3 | D1 | S | S | S | S |
| D4 | S | NS | S | S | |
| D8 | S | S | S | S | |
| S3–S4 | D1 | NS | NS | NS | S |
| D4 | NS | NS | NS | S | |
| D8 | S | S | S | S | |
S, significant; NS, not significant; D, day; S, session.
Comparisons of session 3 to session 4 (Table 3) show that on days 1 and 4, recovery is reliable only for field size. On day 8, however, each measure indicates significant recovery. We conclude there is indeed some recovery of pyramidal cell spatial signaling between sessions 3 and 4. This conclusion is bolstered by the fact that each property shows an uptick from session 3 to session 4 on each day. From the binomial distribution, the chance probability of this outcome is 2−12 ≈ 2.4e-4.
We next looked for long-term changes in pyramidal cell activity by doing group by session repeated-measure ANOVAs. The group effect was significant for all properties on all 3 d with the exception of field size on day 4 (data not shown). We then compared the control and seizure groups during session 1 for the 3 d and found an increasing effect of seizures from the pattern of significant differences for the four measures. On day 1, there were no group differences; on day 4, coherence and field information were different; on day 8, all of the properties differed (Table 4).
Table 4.
Long-term effects of seizures on pyramidal cells
| Compared sessions | Coh | Info | Rate | Size |
|---|---|---|---|---|
| D1S1–D1S1 | NS | NS | NS | NS |
| D4S1–D4S1 | S | S | NS | NS |
| D8S1–D8S1 | S | S | S | S |
S, significant; NS, not significant; D, day; S, session.
We also did ANOVAs of session 1 across days for the seizure group (data not shown). The main effect of day is significant for each property; goodness-of-fit tests indicate that partitioning into days accounts for significant amounts of variance. Post hoc Wilcoxon's tests show that, for each property, there are significant declines from day 1 to day 4 and from day 4 to day 8. Thus, from comparisons with control animals and from comparisons within the seizure group, we conclude that the seizure-induced degradation of spatial signaling by pyramidal cells is cumulative over days.
How place cells are affected by repeated seizures
The plots in Figure 4B for place cells parallel those in Figure 4A for pyramidal cells. In Figure 4B, however, the values for each property tend to be higher, as expected if they are valid measures of place cell activity. Short-term seizure effects are still visible from the drop in each property between sessions 2 and 3 for each day. In contrast to the entire pyramidal cell sample (Fig. 4A), however, the long-term effect of seizures on place cells is much harder to discern by comparing preseizure values across days; it is as if the properties of those pyramidal cells considered to be place cells hardly changed with repeated seizures.
To look for short-term effects on place cells, we did repeated-measure ANOVAs of session for each day for both groups. For the control group (data not shown), there were significant coherence variations across sessions on days 1 and 8 and a significant field rate variation across sessions on day 8, but overall the ANOVAs suggest that place cell activity in the control rats was quite constant. In contrast, for the seizure group, there was a significant session effect for each measure on each day (Table 5).
Table 5.
Repeated-measures ANOVAs of session for place cells
| Day | Coherence | Field info | Field rate | Field size |
|---|---|---|---|---|
| D1 | F (3,195) = 16.15 | F (3,195) = 9.04 | F (3,195) = 15.71 | F (3,195) = 12.20 |
| p = 7.05e-8 | p = 5.11e-5 | p = 3.36e-8 | p = 1.84e-6 | |
| D4 | F (3,135) = 27.22 | F (3,135) = 2.79 | F (3,135) = 7.14 | F (3,135) = 17.10 |
| p = 1.58e-10 | p = 0.07 | p = 0.0009 | p = 1.71e-7 | |
| D8 | F (3,57) = 13.39 | F (3,57) = 8.85 | F (3,57) = 7.95 | F (3,57) = 8.19 |
| p = 1.01e-6 | p = 0.0005 | p = 0.001 | p = 0.001 |
For the control group, planned post hoc Wilcoxon's comparisons of sessions 1 and 3 were not significant for any day, suggesting that no systematic trend was revealed by the three significant ANOVAs of session. However, for the seizure group, the session 1 to session 3 comparison for each property was significant for each day except for field information on day 4 (Table 6).
Table 6.
Short-term effects of seizures on place cells
| Compared sessions | Day | Coh | Info | Rate | Size |
|---|---|---|---|---|---|
| S1–S3 | D1 | S | S | S | S |
| D4 | S | NS | S | S | |
| D8 | S | S | S | S | |
| S3–S4 | D1 | NS | NS | NS | NS |
| D4 | NS | NS | NS | NS | |
| D8 | NS | S | NS | NS | |
S, significant; NS, not significant; D, day; S, session.
For recovery in session 4, there were no significant differences between sessions 3 and 4 for the control group according to Wilcoxon's tests. Similar statistical tests revealed little evidence for recovery between sessions 3 and 4 for the seizure group; only field information on day 8 reliably increased between the postseizure sessions (Table 6), although several of the other measures on different days show a strong recovery trend from session 3 to session 4. Following this indication, we note that the overall appearance in Figure 4B of the property versus session functions for the seizure group suggests a pattern of partial recovery. This is borne out by a binomial test that shows that the probability of improvement in at least 11 of 12 cases is 0.0029.
To detect long-term seizure effects on place cells, we performed group by session repeated-measure ANOVAs (data not shown). The group main effects for place cells were not as pronounced as for the pyramidal cell sample; there were significant differences for all properties except field size on day 1, only for coherence on day 4 and for all properties on day 8. Crucially, when the groups were compared for session 1 over the 3 d, the only significant difference was for field size on day 4 (Table 7). In other words, for place cells, there was virtually no discernable long-term effect of multiple seizures. This unintuitive result is confirmed by across-day ANOVAs of session 1 for the seizure group (data not shown), which revealed no significant effect for any property. Even post hoc pairwise comparisons between days showed no change. Therefore, it appears that place cell discharge properties are preserved in the face of multiple seizures even though the pyramidal cell sample is affected. In additional analyses (data not shown), we found that decreasing the coherence threshold for place cell selection from 0.4 to 0.3 had no effect on the conclusion that the quality of place cells is quite constant in session 1 across days. Similarly, increasing the threshold for separating low-rate and place cells from 0.1 to 0.2 spikes/s did not alter any of our conclusions.
Table 7.
Long-term effects of seizures on place cells
| Compared sessions | Coh | Info | Rate | Size |
|---|---|---|---|---|
| D1S1–D1S1 | NS | NS | NS | NS |
| D4S1–D4S1 | NS | NS | NS | S |
| D8S1–D8S1 | NS | NS | NS | NS |
S, significant; NS, not significant; D, day; S, session.
Repeated seizures reduce the number of place cells and increase the number of low-rate cells
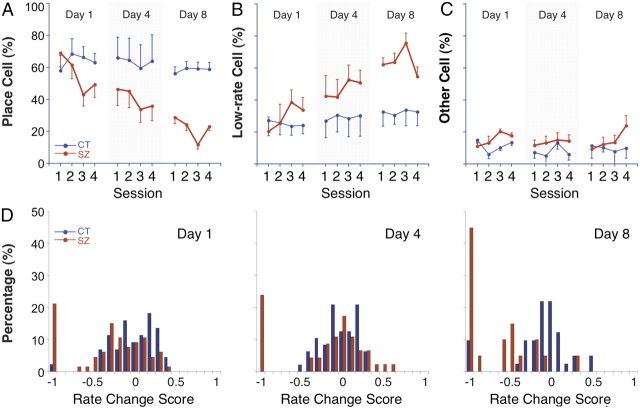
To reconcile the cumulative effects of repeated seizures on pyramidal cells and the lack of such effects on the place cell subset, we analyzed changes in the fraction of pyramidal cells classified as place, low-rate, and “other” cells. Figure 5 shows how the fractions of these cell types vary in the four daily sessions for days 1, 4, and 8. Generally, the fraction of other cells is relatively constant and approximately equal for control and seizure rats, although for seizure rats this class doubles in session 4 of day 8. There are also no major changes in the fractions of place cells or low-rate cells for control rats within or across days. In contrast, the fractions of place cells and low-rate cells vary in opposite directions for the seizure group, both within each day and across days. Thus, long-term differences in spatial firing properties between the entire pyramidal cell sample and the place cell subset appear to stem from systematic, across-day shifts in the distribution of place cells and low-rate cells. The implication is that the degradation of spatial firing of pyramidal cells depends on a decrease in the fraction of pyramidal cells that are place cells rather than an evenly distributed, across-cell decline of the spatial firing properties of place cells.
Figure 5.
Percentage of place cells, low-rate cells (<0.1 Hz), and other cells; histograms of rate change score. A, Place cell percentage. The seizure group (red) shows a short-term drop in postseizure session 3 of each day followed by a partial rebound in session 4; a long-term decline is seen in preseizure sessions 1 and 2 across days 1, 4, and 8. The control group (blue) shows no short- or long-term effect; its percentage stays around 60% across sessions and days. B, Low-rate cell percentage. The fraction of low-rate cells for the seizure group is complementary to the fraction of place cells within and across days. In each day, there is a short-term increase in session 3 and a partial reversal during session 4. There is also a long-term increase seen by comparing preseizure sessions across days. The control group shows no short- or long-term effect; its percentage stays around 25–30% range across sessions and days. C, Other cell percentage. Pyramidal cells that do not qualify as place cells or low-rate cells are classified as “other” cells (see Materials and Methods). The fraction of the other cells fluctuates within the range of 5–20%, but there is no obvious short- or long-term trend for either group. D, Histograms of rate change score comparing discharge rate in session 3 to discharge rate in session 1. The most striking feature for all 3 d is the large percentage of cells from seizure rats whose rate change score falls into the −1 category, indicating that the spike activity of the cell underwent a great decline. In addition to this within-day effect, the cell percentage in the −1 category increases from day 1 to day 8. Error bars indicate SEM.
Numeric analyses of cell class percentages were done with chi-square (χ2) goodness-of-fit tests. In regard to short-term effects for seizure rats, the percentage of place cells decreased from session 1 to session 3 on all 3 d (Table 8); the percentage of low-rate cells increased significantly from session 1 to session 3 on days 1 and 8 but not on day 4 (Table 8). No changes were detected for the fraction of other cells. Comparisons of sessions 3 and 4 revealed that the apparent recovery on days 1 and 4 was unreliable but that on day 8 the fraction of place cells increased and the fraction of low-rate cells decreased between the postseizure sessions (Table 8).
Table 8.
Short-term effects of seizures on cell class
| Compared sessions | Day | Place | Low rate | Other |
|---|---|---|---|---|
| S1–S3 | 1 | S | S | NS |
| 4 | S | NS | NS | |
| 8 | S | S | NS | |
| S3–S4 | 1 | NS | NS | NS |
| 4 | NS | NS | NS | |
| 8 | S | S | S | |
S, significant; NS, not significant; S, session.
For long-term effects, we first showed that the distributions of three cell classes for the control and seizure groups diverged in session 1 across days. For each day, we used the fraction of each class for control rats as expected values and the corresponding fraction for seizure rats as observed values. In agreement with inspection of Figure 5, the distributions (df = 2) were the same for day 1 (p = 0.06) but increasingly different for day 4 (p = 1.3e-05) and day 8 (p = 2.9e-10).
To confirm session 1 trends seen in Figure 5 for each individual cell category, we collapsed cell fractions into three dichotomous partitions, namely, place/not-place, low-rate/not-low-rate, and other/not-other. We then used these partitions in χ2 tests to look for changes in the fraction of each cell class across days. For the control group, no significant differences were detected between days. In contrast, for the seizure group, the place cell fraction declined significantly, the low-rate cell fraction increased significantly, and the other cell fraction was unchanged; this pattern was seen comparing day 1 to day 4 or to day 8, and comparing day 4 to day 8 (Table 9).
Table 9.
Long-term effects of seizures on cell class
| Compared sessions | Place | Low rate | Other |
|---|---|---|---|
| D1S1–D4S1 | S | S | NS |
| D1S1–D8S1 | S | S | NS |
| D4S1–D8S1 | S | S | NS |
S, significant; NS, not significant; D, day; S, session.
The tendency of seizures to convert place cells to low-rate cells is illustrated in a different way in the histograms of Figure 5D, which show distributions of rate change scores between sessions 1 and 3 for cells that were place cells in session 1; cells that are silenced or nearly silenced by the seizure fall into the −1 value bin. In Figure 5D, it is seen that nearly all cells with such an extreme negative rate change score are from seizure rats, that the percentage of such cells increases with seizure number, and, crucially, that there is an excluded range of negative scores, which is indicative of a bimodal distribution. Thus, in nearly all cases, place cells either remain place cells or are shifted to the extreme bin by the seizure; see example cells A3 and A4 in Figure 3.
Two additional aspects of Figure 5D are worth noting. First, on day 8 there is some indication that place cells whose rate change score are not in the −1.0 bin are nevertheless shifted in the negative direction more than cells from control rats and more than on days 1 and 4. This suggests either an additional process beyond a conversion of place cells to low-rate cells or a slowing in the rate of recovery from the seizure. Figure 4B nevertheless indicates that place cells at the start of day 8 are no worse than on days 1 and 4.
We also made a rate change figure for “other cells” (data not shown) whose general appearance resembles that of Figure 5D. This implies that the conversion of pyramidal cells with initially rapid rates but without additional place cell properties follow the same pattern as place cells.
Suppression of place cell activity is greater after multiple seizures
A careful inspection of Figure 4B suggests greater seizure-induced declines in each of the spatial firing quantities for place cells on day 8 than day 1. To test this impression, each spatial firing property during session 3 was normalized to its value in session 1 on the same day and the normalized values were compared. According to Wilcoxon's tests, there were no differences for the control group between days 1 and 8. In contrast, for the seizure group, the decline in session 3 was greater on day 8 than day 1 for all four measures (Coh, z = −2.42, p = 0.015; Info, z = −3.05, p = 0.002; rate, z = −3.01, p = 0.003; size, z = 2.16, p = 0.03). We therefore think there is an additional, cumulative effect of repeated seizures beyond the reduction in place cell numbers. Thus, although the spatial signaling of the remaining place cells before the seizure on day 8 appears normal, these cells are more vulnerable to the seizure.
Kinetic model of seizure effects on place cell and low-rate cell numbers
We modeled seizure-induced changes of the state of hippocampal pyramidal cells (PY) using first-order kinetics in which place cells (PC) can turn to low-rate cells (LC) and vice versa as follows:
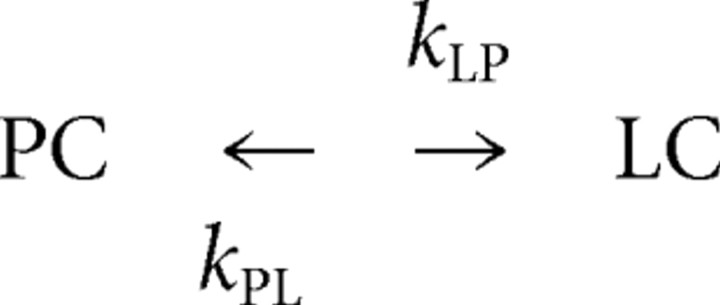 |
In this analysis, we ignore “other” cells so that PC/PY + LC/PY = 1. The frequency of converting place cells to low-rate cells is equal to the relative number of place cells [PC] = (PC/PY) multiplied by the rate constant KPL. Equation 1 expresses this process as a probability as follows:
Similarly, the frequency of converting low-rate to place cells is given by the following:
In the steady state, the two probabilities are equal as follows:
We simulated these reversible changes of spatial firing characteristics as continuous time discrete state Markov processes, selecting the next event and the time it happens according to the above probabilities.
The effects of repeated seizures were calculated by starting the kinetic system from the steady state. The relative numbers of place cells and low-rate cells in the model were set according to the number of the cell types seen before the first seizure so that [PC] = 70.75%. The initial value of one of the rate constants was set during the optimization for finding the best fit; the other rate constant was calculated according to Equation 3. We investigated the following models.
Model 1
Each seizure caused an immediate decrease in the number of place cells with a concurrent increase in the number of low-rate cells. Place cells were decreased by a fraction of either their current number (model 1A) or their total number (model 1B). This model had two parameters, one to set the initial rate constants (kPLo) and one to determine the extent of seizure effects.
Model 2
Seizures caused an abrupt increase in kPL. In model 2A, the rate constant relaxed to its initial value with an exponential decay (kPLt = eA−Bt, where t stands for time). In model 2B, the return of the rate constant to its initial value was implemented with a power law (kPLt = AT−B). The three parameters of these models are kPLo, B, and A.
Model 3
A combination of model 1A and model 2A, in which seizures are followed by changes in place cell proportion and rate constant kPL (four parameters).
Model 4
Seizures induced two types of changes. An abrupt decrease of relative place cell numbers was modified by an abrupt increase in kLP, enhancing the recovery of low-rate cells to place cells. kLP relaxed to its original value with an exponential decay. Place cell decrease was implemented by either a multiplicative constant (model 4A) or a (negative) additive constant (model 4B). The four parameters were kLPo, B, and A controlling kLP dynamics and a constant determining the seizure-induced drop in place cell number.
Each model was fit to the place cell and low-rate cell proportions in the seizure group (Fig. 5A,B). The best fit was determined by a least-square error measure, using the program fminsearch.m in MATLAB. This program implements the Nelder–Mead simplex method for nonlinear optimization. Optimization was started from multiple initial states to ensure that solutions were general and not local. Model selection was performed by calculating Akaike information criterion (AIC) (Akaike, 1974) and Bayesian information criterion (BIC) (Schwarz, 1978); these measures are capable of comparing models with different number of parameters.
Our choice of a first-order process to model seizure effects is parallel to the empirical division of pyramidal cells into place cells and low-rate cells in which each pyramidal cell can switch between these two types. The models considered only the second, third, and fourth sessions of each day. By disregarding the first session, we avoided the need for the optimization algorithm to take preseizure variance into account, thereby emphasizing immediate seizure effects and within-day recovery.
To find an acceptable parsimonious model, we imagined that seizures do not change the structure of the kinetic model by introducing, for example, unobserved states. In addition, since we had no evidence for irreversible effects, we only tested models that did not change the steady state although the kinetics may be arbitrarily slow.
The simplest way seizures can perturb the dynamics of the model is that they directly cause changes in cell numbers. Thus, in the first approach, we simulated the aftermath of a seizure as an immediate reduction in relative place cell number, either by a fraction of their current number (model 1A) or by a fraction of their original number (model 1B). In this simple model, place cell and low-rate cell proportions relaxed after each seizure toward the steady state determined by the invariant rate constants. The optimization algorithm failed to find a good fit to the data with either model 1 variant; it was impossible to simultaneously capture the within-day and across-day effects. The optimized predictions for models 1A and 1B are shown, respectively, in Figure 6, A and B, where it is clear that the fit is reasonable for across-day effects but poor for within-day effects. The quantitative estimates for the quality of the fit are shown in Table 10, which summarizes least-square error, AIC, and BIC for all models.
Figure 6.
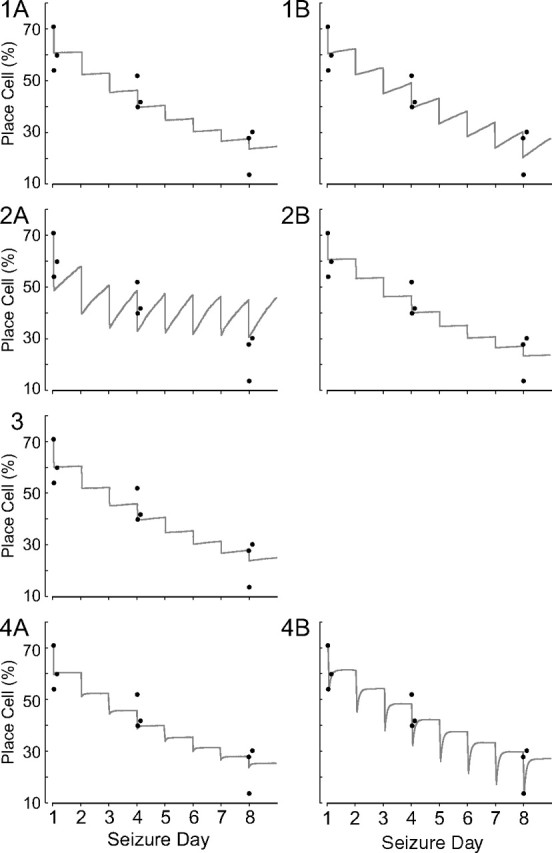
Changes in place cell percentages predicted by variants of the first order kinetic model; each plot also displays as filled black circles the observed number of place cells for sessions 2, 3, and 4 for experimental days 1, 4, and 8. Models 1A, 1B, 2A, 2B, and 3 all fail because they do not reproduce the rapid recovery between session 3 and session 4. Model 4A begins to capture this crucial feature of how place cell numbers are altered by repetitive seizures. Model 4B, however, mimics the initial large loss of place cells in session 3 and the rapid recovery in session 4; it also has a reasonable fit for the long-term, across-day cumulative effect of seizures.
Table 10.
Error measures for kinetic models
| Model | Least-squares error | AIC | BIC |
|---|---|---|---|
| 1A | 224.99 | 32.97 | 33.36 |
| 1B | 191.16 | 31.50 | 31.90 |
| 2A | 844.18 | 46.87 | 47.46 |
| 2B | 220.33 | 34.78 | 35.37 |
| 3 | 222.94 | 36.89 | 37.68 |
| 4A | 218.98 | 36.73 | 37.51 |
| 4B | 91.70 | 28.89 | 29.68 |
We next asked whether the failure of the first model to predict the fast within-day, slow across-day recovery sequence would be corrected if the rate constants were time dependent, changing suddenly after a seizure and then quickly falling back to their initial values. In one variant (model 2A), we assumed that a seizure abruptly increased kPL after which it reverted, on an exponential time course, to its preseizure level. The consequence is that a large number of place cells are immediately converted to low-rate cells followed by rapid recovery. Nevertheless, we could not find an acceptable combination of initial change in rate constant and exponential decay; when the fit for within-day recovery was acceptable, the relaxation of the rate constant was so fast that across-day recovery was complete and the cumulative result of seizures disappeared. The requirement to simultaneously fit changes within and across days could not be rectified by substituting a power law for the exponential decay (model 2B). Combining the approaches of model 1 and model 2 by abruptly changing cell type concentrations and making the kPL rate constant time dependent also failed to provide a good fit (model 3).
In the last model type, we retained the assumption that seizures cause immediate decreases of place cell numbers that are compensated by an increase in kLP, which promotes the reverse process of switching low-rate cells to place cells. The time-dependent decay of kLP to its preseizure value was assumed to follow an exponential course. When the effect of a seizure was to switch a fraction of current place cells to low-rate cells, the within-day loss was not reproduced (model 4A). In contrast, when the number of place cells was reduced by a constant, namely, a fixed fraction of the initial (day 1 preseizure) place cell population (model 4B), the fit was greatly improved.
Interneuron firing rates
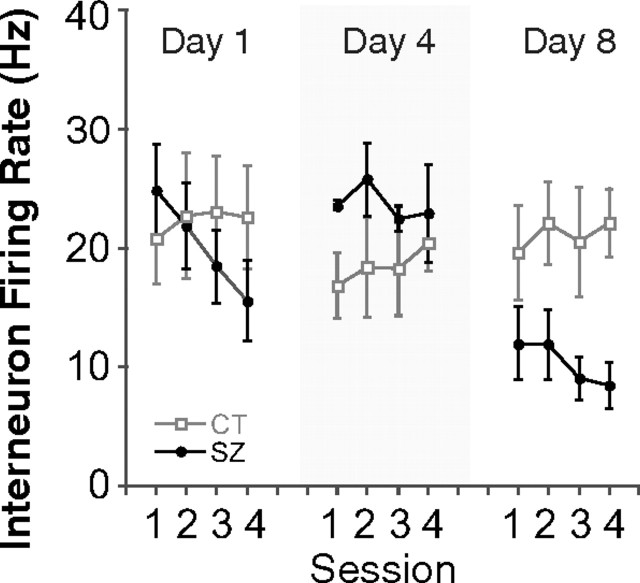
Repeated seizures might suppress pyramidal cell firing via enhanced activity of inhibitory interneurons. This notion is, however, contrary to the finding that the mean interneuron firing rate undergoes a small decrease after each seizure (Fig. 7). Repeated-measure ANOVAs of session for the control group found no significant variation on any day. Similar ANOVAs for the seizure group found a significant effect on day 1 but not on days 4 or 8. The rate change between sessions 1 and 3 on day 1 was significant (df = 8; p = 0.02), but in fact the change was a decrease. Two-way repeated-measure ANOVAs of group by session for overall interneuron firing rate revealed no significant interactions on any day and the main group effect was significant only on day 8 (F(1,8) = 6.55; p = 0.03). Once again, however, the discharge rate for inhibitory interneurons in the seizure group was lower. It is clear that more interneurons must be recorded to fully reject the idea that increased inhibitory activity suppresses pyramidal cells, but our tentative conclusion is that interneuron and pyramidal cell excitability are reduced in parallel.
Figure 7.
The average interneuron firing rate shows no systematic change within or across days. The average discharge rates for interneurons recorded from control and seizure rats are plotted as a function of session and day. No clear short- or long-term trend is seen for the seizure group (filled circle). In fact, the rate for seizure group interneurons on day 8 appears to be lower than day 4 or day 1. Error bars indicate SEM.
Repeated seizures cause decreases of peak theta frequency
Along with single-cell recordings, the hippocampal EEG was monitored and analyzed for power spectrum changes. We focused on possible shifts in peak frequency in the 5–12 Hz theta oscillation band. Theta amplitude changes were ignored, since they are unavoidably induced by the tetrode movements used to maximize single-unit yield (Bragin et al., 1995; Buzsáki, 2002). In control rats, the peak theta frequency was ∼8.3 Hz for the initial 8-d experimental period (Fig. 8A). For seizure rats, however, there was a large drop in peak theta frequency for session 3 after each day's seizure followed by an increase indicative of recovery during session 4 (Fig. 8A). Thus, the theta frequency effects mimicked the changes in single-unit firing properties described above. In a simple statistical analysis, if there is an equal chance that the peak frequency will increase or decline between sessions 1 and 3, the probability of eight of eight decreases is 0.004. The probability of partial recovery (i.e., an increase of peak frequency) between sessions 3 and 4 in eight of eight cases is also 0.004. It is interesting that theta frequency increases from session 1 to session 2 on all days for control and seizure rats, suggesting a “warm-up” effect, which is reminiscent of the increase in theta frequency as a novel environment becomes more familiar (Jeewajee et al., 2008).
Figure 8.
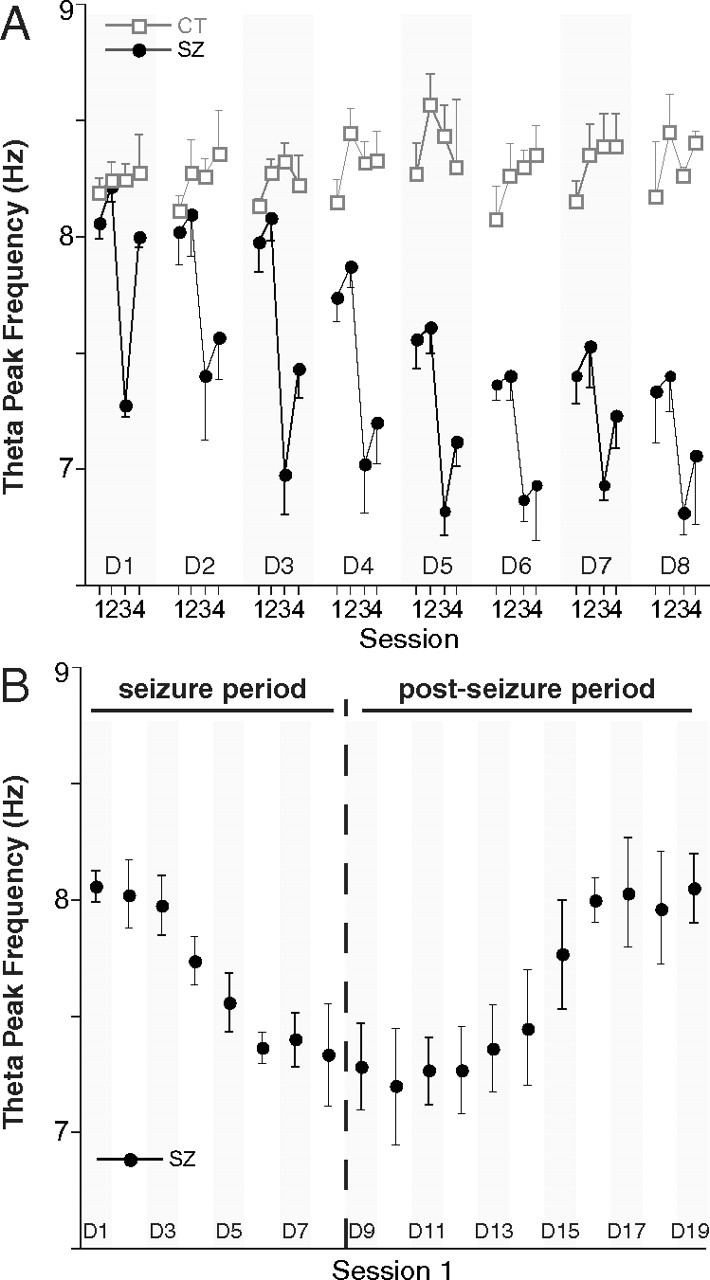
Seizures cause within-day and across-day slowdowns of theta oscillations (5–12 Hz). Only theta data recorded while the rat ran between 10 and 30 cm/s were analyzed. A, Frequency of the peak power in the theta band for four daily sessions during the 8-d seizure period. For control rats (open square), there is little change in the frequency for peak power across days. For seizure rats (filled circle), each convulsion causes a drop in peak power frequency in session 3 of each day as well as a cumulative, long-term decline in peak frequency across days. B, Peak theta frequency for session 1 only during the seizure and postseizure periods; seizure induction is stopped after day 8. The peak theta frequency starts at ∼8.3 Hz on day 1, declines to ∼7.4 Hz on day 8, and returns to the day 1 level around days 15 and 16. Error bars indicate SEM.
Repeated-measure ANOVAs of theta frequency for session were done for each day for the control and seizure groups. After Bonferroni's correction to α = 0.0063 for eight tests, no significant session variations were found for the control group. For the seizure group, there were significant session variations on days 1, 3, 4, and 5 (data not shown). The lack of significant session effects on days 6, 7, and 8 is attributed to the cumulative reduction of preseizure session 1 frequency from previous seizures and the apparent asymptote near 7.0 Hz (Fig. 8A).
We next asked on which day the cumulative seizure effect on peak theta frequency caused a reliable group separation. According to a two-way ANOVA of group by day for session 1, the interaction was significant (F(7.28) = 3.83; p = 0.005). Bonferroni's corrected t tests for individual days revealed that the group difference was first reliable on day 5 (t(6) = 4.23; p = 0.0055).
Peak theta frequency recovers when seizure inductions are terminated
At the end of the 8-d seizure period, we continued to record EEG from three seizure rats that still had large-amplitude raw signals for 11 additional “postseizure” days. The peak theta frequency in session 1 for days 1–19 is plotted in Figure 8B, where the initial decline and a subsequent recovery are evident. By eye, the return of peak theta frequency to its preseizure value is essentially complete by day 16. The existence of an upward trend during the postseizure period is confirmed by a repeated-measure ANOVA for day (F(10,20) = 28.2; p = 1.3e-9). T tests of peak theta frequency for each day in the postseizure interval against peak frequency in session 1 of day 1 are significant up until day 14 but not thereafter (data not shown). Thus, according to this measure, it takes only a week for recovery to occur; this is comparable with the time it takes navigational behavior to recover from seizure-induced deficits due to a near-identical protocol (Lin et al., 2009). We also saw that the warm-up effect between sessions 1 and 2 was largest on days 11–15, near the steepest part of the recovery process (data not shown).
Locomotor velocity and other behavioral observations
To ask how seizures affect locomotion, average running speed was examined in session 1 for days 1, 4, and 8 with a two-way repeated-measure ANOVA for group by day. Neither main effect nor the interaction was significant (data not shown). To ask whether there was a postseizure effect on running speed, we did a similar ANOVA for session 3 with the same lack of significant results. Thus, inducing a limited number of seizures does not affect locomotor velocity either cumulatively or as a result of the day's seizure.
Direct observation of rats suggests that emotional changes occurred with increasing numbers of seizures. Minutes or even hours after a seizure, some rats were more reactive to touch, were more likely to assume a defensive stance, and were harder to handle. For these reasons, it was impossible on day 8 to do session 3 for one rat and session 4 for a second rat. Even though average running speed did not change, some seizure rats exhibited a tendency to remain idle and neglected for 1–2 min intervals to chase sugar pellets in postseizure sessions on days 7 and 8. In the home cage, seizure rats were more likely to stay in a sleeping posture; they were less alert or less responsive to external noises. However, paroxysmal movements were not observed nor was there any EEG evidence of spontaneous seizures during 16 min of daily recordings.
Anomalous place cells
The hippocampal place representation of a familiar environment includes intriguing temporal variation sources (Fenton and Muller, 1998; Fenton et al., 2010). We show in Figure 9 similar effects that operate on the timescale of entire sessions rather than the much briefer intervals reported earlier.
Although both seizure and control rats were familiar with the cylinder from at least 3 weeks of training and cell screening, we sometimes saw place cells appear or disappear for entire formal recording sessions. For example, two pyramidal cells from control rats (Fig. 9A1,A2) were barely active in session 1 but subsequently developed firing fields; one of these (Fig. 9A1) stopped firing in the session 3 and then resumed in session 4. Another cell (Fig. 9A3) had a stable firing field in sessions 1–3 that disappeared in session 4; other cells recorded on the same tetrode were stable in session 4, implying that the disappearance is not due to probe movement. These observations further indicate that the hippocampal representation of space is intrinsically dynamic; some place cells can turn on and off without any changes to the external environment. In the same vein, the observation that place cells can become low-rate cells and low-rate cells can become place cells suggests that the postulated rate constants in our kinetic models represent the existence of real processes.
The cell recorded from a seizure group rat in Figure 9B1 was weakly active in sessions 1–3 but developed a clear firing field in session 4. The formation of this new place field could be due to seizure-induced plasticity, or it may reflect the dynamic nature of the place representation suggested by the cells from a control rat in Figure 9A. A different dynamic pattern is seen in Figure 9B2, where the cell undergoes transient remapping in session 3 before reverting to the initial field location in session 4. Finally, the cell in Figure 9B3 fires less in session 4 and shows a disintegration of its firing field. This is in contrast to the more usual process in which residual firing after seizures is confined to the region of the original field (Fig. 3A2–A4,B1,B2).
Discussion
The predominant effect of repetitive convulsant-induced seizures on hippocampal pyramidal neurons is the transformation of individual, initially robust place cells into sporadically firing low-rate cells. Both the within-day and across-day time courses of such conversions parallel the slowing of theta oscillations at the network level and the reduced precision of self-localization at the behavioral level (Lin et al., 2009). Since sporadically discharging cells are effectively removed from the spatial map, we contend that the primary consequence of repetitive seizures is a reduction in hippocampal information processing capacity.
Transient and persistent conversion of place cells to low-rate cells
One-half of an hour after a single flurothyl seizure, the number of place cells clearly decreases. The process underlying this decrease is transient since place cell numbers return toward their original level only 2.5 h later. This same sequence of initial decrease followed by partial recovery is recapitulated on other days, but there is a key difference across days: the starting number of place cells markedly decreases with the additional seizures. Intuitively, the progressive loss of place cells with additional seizures seems to demand an additional, slower process, a conclusion supported by our simple kinetic model (Fig. 6). The notion of a long-term change is supported by the greater susceptibility to seizures of the remaining place cells on day 8 than on day 1 (Fig. 4B). Since the decreased pyramidal cell activity occurs with no significant change in CA1 interneuron activity (Fig. 7), place cell conversion is not due to increased inhibitory tone unless other interneurons are involved.
Evidence suggests that place cell transformation is on a cell-by-cell basis so that signal degradation is not homogenous in the population. Inspection of rate maps for a seizure rat (Fig. 3) reveals cell-specific transformation during session 3 and cell-specific recovery in session 4. Added evidence comes from plots of place cell properties (Fig. 4B), where little long-term decline is seen in the session 1 firing properties of remaining place cells on days 4 and 8 compared with day 1. Of direct relevance are the rate change plots (Fig. 5D), which have a bimodal character; place cell discharge in seizure rats is strongly suppressed (score, −1) or mainly intact.
The within- and across-day place cell transformations to low-rate cells may reflect seizure-triggered homeostasis. Reducing place cell numbers may be a form of negative feedback that reduces overall network activity, possibly via synaptic plasticity processes (Turrigiano et al., 1994, 1998; Turrigiano, 1999). The involvement of plastic processes is suggested by experiments in which seizure-like stimulation depotentiates or disrupts established hippocampal LTP in vitro (Hu et al., 2005) and in vivo (Hesse and Teyler, 1976).
Are place cells randomly converted to low-rate cells? In one model of the hippocampal spatial representation (Touretzky and Muller, 2006; Jackson and Redish, 2007), place cells are grouped in multiple, relatively independent “maplets,” each of which is a complete but low-resolution representation of the environment. Thus, reduced place cell numbers might reflect loss of one or more maplets, consequently reducing the precision of the whole representation.
Our account of how flurothyl seizures impact place cells is considerably different from that provided by Zhou et al. (2007). They reported decreases in average coherence, information content, and field center rate 24 h after 5 d of 2 seizures per day (with some recovery by 72 h). Zhou et al. (2007) also noted that firing field locations were less stable, but we only rarely saw field displacements of this kind (Fig. 9B2). The proffered explanations of behavioral deficits is also different; for Zhou et al. (2007), the problems stem from reduced place cell stability and resolution, whereas we suggest the problems arise because decreased computational resources are devoted to navigation. Nevertheless, the day 8 rate change score distribution (Fig. 5D) and the increased vulnerability of place cells to later seizures leave room for the possibility that the processes reported by Zhou et al. (2007) may help explain how repeated seizures affect spatial information processing.
Modeling the dynamics of converting place cells to low-rate cells
To explain within- and across-day changes of place cell and low-rate cell numbers, we proposed first-order kinetic models with only two cell types. Thus, the numbers and identities of “other cells” were constant allowing only interconversions of place cells and low-rate cells.
Unquestionably, other models might be developed including those with a population of truly silent cells (Thompson and Best, 1989). Silent cells are pyramidal cells that are fully suppressed in awake rats but fire during slow-wave sleep or light barbiturate anesthesia. For parsimony, we considered only models with two classes of pyramidal cells. Note that this implies that silent cells are not recruited into the representation after seizures. Instead, the combined place cell plus low-rate cell set is fixed for a given environment (Epsztein et al., 2011). This assumption is consistent with the within-day waveform constancy of the place cells that were transformed to low-rate cells by the seizure. We assume that across-day effects follow the same pattern.
Several models were tested for their fit to place cell percentages during sessions 2, 3, and 4 on days 1, 4, and 8. The best model had two key features: (1) each seizure caused a certain number of place cells to switch to low-rate cells; (2) the rate constant kLP for converting low-rate cells back to place cells increased suddenly at seizure time and then returned over an exponential time course to its preseizure value.
The first feature postulates a zeroth-order process, independent of place cell “concentration” that converts place cells to low-rate cells. The high postseizure value of kLP allows for an initially rapid recovery of place cell numbers; the exponential decay of kLP back to its original level allows seizure effects to persist for long times, resulting in the cumulative across-day effect.
The requirement of a zeroth-order PC → LC process suggests that place cell loss is a rather direct consequence of the seizure. Perhaps plastic LTP-like synaptic strength increases that cause each place cell to have a firing field are rapidly reversed in a cell-specific manner.
Importantly, the proposed place cell → low-rate cell and reverse processes seem to exist, as shown by the spontaneous interconversions for anomalous place cells in control rats (Fig. 9A). That place cells can shut off for entire recording sessions suggests there is indeed a mechanism for converting them to low-rate cells; reappearance of the same firing field for the cell suggests the existence of the reverse mechanism. Of further interest is the possibility that the interconversion of place cells and low-rate cells is triggered each time the rat enters the environment.
Theta network oscillations
In addition to within-day and across-day conversions of place cells to low-rate cells, repetitive seizures have parallel effects on theta frequency; there is a sharp drop after each seizure and a cumulative reduction with multiple seizures.
There are several candidate mechanisms for theta slowing including changes in the medial septal pacemaker (Petsche et al., 1962), modified interactions between medial septal ⇆ hippocampal projection cells (Manseau et al., 2008), weakened coupling of local CA1 oscillators (Goutagny et al., 2009), and reduced hippocampal neuronal activity (Leung and Yim, 1991; Chapman and Lacaille, 1999). Theta slowing is likely not confined to CA1 but probably occurs in medial septum, CA3, and entorhinal cortex.
Another mechanism involves GLUK5-containing kainate receptors (Dolman et al., 2006). Injecting a kainate receptor antagonist transiently reduces theta frequency in a way reminiscent of short-term seizure effects (Huxter et al., 2007). Thus, the slowing of theta oscillations due to repeated seizures may reflect downregulation of kainate receptors, which would likely affect several of the suggested mechanisms above.
Exposure to novel environments transiently decreases theta frequency (Jeewajee et al., 2008). Although the mechanism behind novelty-induced frequency drops may not overlap seizure-induced drops, seizures may return the brain to a less experienced spatial state, similar to initial exposure to a novel environment.
Reversal of seizure effects
After stopping seizure induction, theta frequency gradually returned to its initial value (Fig. 8B). This reversal had a time course parallel to the return of normal performance in a hidden goal task (Lin et al., 2009). The similar time courses of theta frequency and performance recovery suggest that place cell numbers would return to their preseizure levels when no more convulsions were induced. The dynamics of recovery, however, are uncertain. For example, increasing seizure numbers or rate might irreversibly change single-cell activity, theta frequency modifications, and navigational precision.
Summary
Brief, daily flurothyl seizures for 8 d in otherwise healthy adult rats induce short-term and long-term reductions in place cell numbers and theta frequency, reductions that plausibly explain deficits in spatial hidden goal tasks caused by similar seizure protocols (Zhou et al., 2007; Lin et al., 2009). Reversal of EEG changes after the cessation of seizures suggests that place cell numbers would recover, in line with the recovery of performance in spatial tasks. We conclude that preventing seizures in humans may result in improved memory and learning.
Footnotes
This work was supported by NIH Grant NS20464. We thank Dr. Jeremy Barry for teaching surgical techniques to H.L., Matthew Holtzer and Bruno Rivard for the design and production of recording implants, and anonymous reviewers for their comments and suggestions.
References
- Akaike H. A new look at the statistical model identification. IEEE Trans Automat Contr. 1974;19:716–723. [Google Scholar]
- Bostock E, Muller RU, Kubie JL. Experience-dependent modifications of hippocampal place cell firing. Hippocampus. 1991;1:193–205. doi: 10.1002/hipo.450010207. [DOI] [PubMed] [Google Scholar]
- Bragin A, Jandó G, Nádasdy Z, Hetke J, Wise K, Buzsáki G. Gamma (40–100 Hz) oscillation in the hippocampus of the behaving rat. J Neurosci. 1995;15:47–60. doi: 10.1523/JNEUROSCI.15-01-00047.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki G. Theta oscillations in the hippocampus. Neuron. 2002;33:325–340. doi: 10.1016/s0896-6273(02)00586-x. [DOI] [PubMed] [Google Scholar]
- Chapman CA, Lacaille JC. Intrinsic theta-frequency membrane potential oscillations in hippocampal CA1 interneurons of stratum lacunosum-moleculare. J Neurophysiol. 1999;81:1296–1307. doi: 10.1152/jn.1999.81.3.1296. [DOI] [PubMed] [Google Scholar]
- Cho YH, Giese KP, Tanila H, Silva AJ, Eichenbaum H. Abnormal hippocampal spatial representations in alphaCaMKIIT286A and CREBalphaDelta− mice. Science. 1998;279:867–869. doi: 10.1126/science.279.5352.867. [DOI] [PubMed] [Google Scholar]
- Csicsvari J, Hirase H, Czurkó A, Mamiya A, Buzsáki G. Oscillatory coupling of hippocampal pyramidal cells and interneurons in the behaving rat. J Neurosci. 1999;19:274–287. doi: 10.1523/JNEUROSCI.19-01-00274.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dolman NP, More JC, Alt A, Knauss JL, Troop HM, Bleakman D, Collingridge GL, Jane DE. Structure-activity relationship studies on N3-substituted willardiine derivatives acting as AMPA or kainate receptor antagonists. J Med Chem. 2006;49:2579–2592. doi: 10.1021/jm051086f. [DOI] [PubMed] [Google Scholar]
- Epsztein J, Brecht M, Lee AK. Intracellular determinants of hippocampal CA1 place and silent cell activity in a novel environment. Neuron. 2011;70:109–120. doi: 10.1016/j.neuron.2011.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fenton AA, Muller RU. Place cell discharge is extremely variable during individual passes of the rat through the firing field. Proc Natl Acad Sci U S A. 1998;95:3182–3187. doi: 10.1073/pnas.95.6.3182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fenton AA, Lytton WW, Barry JM, Lenck-Santini PP, Zinyuk LE, Kubík S, Bures J, Poucet B, Muller RU, Olypher AV. Attention-like modulation of hippocampus place cell discharge. J Neurosci. 2010;30:4613–4625. doi: 10.1523/JNEUROSCI.5576-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox SE, Ranck JB., Jr Localization and anatomical identification of theta and complex spike cells in dorsal hippocampal formation of rats. Exp Neurol. 1975;49:299–313. doi: 10.1016/0014-4886(75)90213-7. [DOI] [PubMed] [Google Scholar]
- Fox SE, Ranck JB., Jr Electrophysiological characteristics of hippocampal complex-spike cells and theta cells. Exp Brain Res. 1981;41:399–410. doi: 10.1007/BF00238898. [DOI] [PubMed] [Google Scholar]
- Goutagny R, Jackson J, Williams S. Self-generated theta oscillations in the hippocampus. Nat Neurosci. 2009;12:1491–1493. doi: 10.1038/nn.2440. [DOI] [PubMed] [Google Scholar]
- Hesse GW, Teyler TJ. Reversible loss of hippocampal long term potentiation following electronconvulsive seizures. Nature. 1976;264:562–564. doi: 10.1038/264562a0. [DOI] [PubMed] [Google Scholar]
- Hu B, Karnup S, Zhou L, Stelzer A. Reversal of hippocampal LTP by spontaneous seizure-like activity: role of group I mGluR and cell depolarization. J Neurophysiol. 2005;93:316–336. doi: 10.1152/jn.00172.2004. [DOI] [PubMed] [Google Scholar]
- Huxter JR, Zinyuk LE, Roloff EL, Clarke VR, Dolman NP, More JC, Jane DE, Collingridge GL, Muller RU. Inhibition of kainate receptors reduces the frequency of hippocampal theta oscillations. J Neurosci. 2007;27:2212–2223. doi: 10.1523/JNEUROSCI.3954-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson J, Redish AD. Network dynamics of hippocampal cell-assemblies resemble multiple spatial maps within single tasks. Hippocampus. 2007;17:1209–1229. doi: 10.1002/hipo.20359. [DOI] [PubMed] [Google Scholar]
- Jeewajee A, Lever C, Burton S, O'Keefe J, Burgess N. Environmental novelty is signaled by reduction of the hippocampal theta frequency. Hippocampus. 2008;18:340–348. doi: 10.1002/hipo.20394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krasowski MD. Differential modulatory actions of the volatile convulsant flurothyl and its anesthetic isomer at inhibitory ligand-gated ion channels. Neuropharmacology. 2000;39:1168–1183. doi: 10.1016/s0028-3908(99)00221-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kubie JL, Muller RU, Bostock E. Spatial firing properties of hippocampal theta cells. J Neurosci. 1990;10:1110–1123. doi: 10.1523/JNEUROSCI.10-04-01110.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leung LW, Yim CY. Intrinsic membrane potential oscillations in hippocampal neurons in vitro. Brain Res. 1991;553:261–274. doi: 10.1016/0006-8993(91)90834-i. [DOI] [PubMed] [Google Scholar]
- Leutgeb S, Leutgeb JK, Barnes CA, Moser EI, McNaughton BL, Moser MB. Independent codes for spatial and episodic memory in hippocampal neuronal ensembles. Science. 2005;309:619–623. doi: 10.1126/science.1114037. [DOI] [PubMed] [Google Scholar]
- Lin H, Holmes GL, Kubie JL, Muller RU. Recurrent seizures induce a reversible impairment in a spatial hidden goal task. Hippocampus. 2009;19:817–827. doi: 10.1002/hipo.20565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Muller RU, Huang LT, Kubie JL, Rotenberg A, Rivard B, Cilio MR, Holmes GL. Seizure-induced changes in place cell physiology: relationship to spatial memory. J Neurosci. 2003;23:11505–11515. doi: 10.1523/JNEUROSCI.23-37-11505.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manseau F, Goutagny R, Danik M, Williams S. The hippocamposeptal pathway generates rhythmic firing of GABAergic neurons in the medial septum and diagonal bands: an investigation using a complete septohippocampal preparation in vitro. J Neurosci. 2008;28:4096–4107. doi: 10.1523/JNEUROSCI.0247-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McHugh TJ, Blum KI, Tsien JZ, Tonegawa S, Wilson MA. Impaired hippocampal representation of space in CA1-specific NMDAR1 knockout mice. Cell. 1996;87:1339–1349. doi: 10.1016/s0092-8674(00)81828-0. [DOI] [PubMed] [Google Scholar]
- Muller RU, Kubie JL. The firing of hippocampal place cells predicts the future position of freely moving rats. J Neurosci. 1989;9:4101–4110. doi: 10.1523/JNEUROSCI.09-12-04101.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller RU, Kubie JL, Ranck JB., Jr Spatial firing patterns of hippocampal complex-spike cells in a fixed environment. J Neurosci. 1987;7:1935–1950. doi: 10.1523/JNEUROSCI.07-07-01935.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Keefe J, Nadel L. The hippocampus as a cognitive map. Oxford: Clarendon; 1978. [Google Scholar]
- Olypher AV, Lánský P, Muller RU, Fenton AA. Quantifying location-specific information in the discharge of rat hippocampal place cells. J Neurosci Methods. 2003;127:123–135. doi: 10.1016/s0165-0270(03)00123-7. [DOI] [PubMed] [Google Scholar]
- Petsche H, Stumpf C, Gogolak G. The significance of the rabbit's septum as a relay station between the midbrain and the hippocampus. I. The control of hippocampus arousal activity by the septum cells. Electroencephalogr Clin Neurophysiol. 1962;14:202–211. doi: 10.1016/0013-4694(62)90030-5. [DOI] [PubMed] [Google Scholar]
- Racine RJ. Modification of seizure activity by electrical stimulation. II. Motor seizure. Electroencephalogr Clin Neurophysiol. 1972;32:281–294. doi: 10.1016/0013-4694(72)90177-0. [DOI] [PubMed] [Google Scholar]
- Ranck JB., Jr Studies on single neurons in dorsal hippocampal formation and septum in unrestrained rats. I. Behavioral correlates and firing repertoires. Exp Neurol. 1973;41:461–531. doi: 10.1016/0014-4886(73)90290-2. [DOI] [PubMed] [Google Scholar]
- Rotenberg A, Mayford M, Hawkins RD, Kandel ER, Muller RU. Mice expressing activated CaMKII lack low frequency LTP and do not form stable place cells in the CA1 region of the hippocampus. Cell. 1996;87:1351–1361. doi: 10.1016/s0092-8674(00)81829-2. [DOI] [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimension of a model. Ann Stat. 1978;6:461–464. [Google Scholar]
- Thompson LT, Best PJ. Place cells and silent cells in the hippocampus of freely behaving rats. J Neurosci. 1989;9:2382–2390. doi: 10.1523/JNEUROSCI.09-07-02382.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Touretzky DS, Muller RU. Place field dissociation and multiple maps in hippocampus. Neurocomputing. 2006;69:1260–1263. [Google Scholar]
- Turrigiano G, Abbott LF, Marder E. Activity-dependent changes in the intrinsic properties of cultured neurons. Science. 1994;264:974–977. doi: 10.1126/science.8178157. [DOI] [PubMed] [Google Scholar]
- Turrigiano GG. Homeostatic plasticity in neuronal networks: the more things change, the more they stay the same. Trends Neurosci. 1999;22:221–227. doi: 10.1016/s0166-2236(98)01341-1. [DOI] [PubMed] [Google Scholar]
- Turrigiano GG, Leslie KR, Desai NS, Rutherford LC, Nelson SB. Activity-dependent scaling of quantal amplitude in neocortical neurons. Nature. 1998;391:892–896. doi: 10.1038/36103. [DOI] [PubMed] [Google Scholar]
- Vanderwolf CH. Hippocampal electrical activity and voluntary movement in the rat. Electroencephalogr Clin Neurophysiol. 1969;26:407–418. doi: 10.1016/0013-4694(69)90092-3. [DOI] [PubMed] [Google Scholar]
- Wieser HG ILAE Commission on Neurosurgery of Epilepsy. ILAE Commission Report. Mesial temporal lobe epilepsy with hippocampal sclerosis. Epilepsia. 2004;45:695–714. doi: 10.1111/j.0013-9580.2004.09004.x. [DOI] [PubMed] [Google Scholar]
- Zhou JL, Shatskikh TN, Liu X, Holmes GL. Impaired single cell firing and long-term potentiation parallels memory impairment following recurrent seizures. Eur J Neurosci. 2007;25:3667–3677. doi: 10.1111/j.1460-9568.2007.05598.x. [DOI] [PubMed] [Google Scholar]