The General Factor of Personality: A General Critique

Abstract

Recently, it has been proposed that all non-cognitive measures of personality share a general factor of personality. A problem with many of these studies is a lack of clarity in defining a general factor. In this paper we address the multiple ways in which a general factor has been identified and argue that many of these approaches find factors that are not in fact general. Through the use of artificial examples, we show that a general factor is not:

1. The first factor or component of a correlation or covariance matrix.

2. The first factor resulting from a bifactor rotation or biquartimin transformation

3. Necessarily the result of a confirmatory factor analysis forcing a bifactor solution

We consider how the definition of what constitutes a general factor can lead to confusion, and we will demonstrate alternative ways of estimating the general factor saturation that are more appropriate.

1. Is there a general factor of personality?

Fundamental questions in the assessment of cognitive and non-cognitive aspects of personality are what is the appropriate number of factors/dimensions to extract from a data set and what is the structure of these factors. Hierarchical models have been used frequently in the cognitive domain (Carroll, 1993; Horn and Cattell, 1966, 1982) to reveal higher-order factors (e.g., gc, gf, and one highest order factor, g). In the personality domain, hierarchical models were used by Cattell (1957, 1966), Eysenck and Himmelweit (1947), Eysenck (1967), and more recently by DeYoung et al. (2002) and Digman (1997) but stopped with two to six highest level variables. At a more narrow level of analysis, hierarchical modeling of anxiety (Zinbarg and Barlow, 1996; Zinbarg et al., 1997) has revealed lower order factors as well as a higher order one. Few have applied this procedure to the entire domain of non-cognitive personality, but there has been a surge of interest in this topic over the last five years.

The first empirical support for the “General Factor of Personality” (GFP) was reported by Musek (2007), who analyzed various inventories assessing Big-Five traits in three large-scale samples. Results of exploratory and confirmatory factor analyses showed that extraversion, agreeableness, conscientiousness, emotional stability, and openness all loaded positively on one factor, which Musek labeled as the “Big One.” Musek suggested that the Big One likely reflected a mixture of positively valued personality characteristics and postulated that it should be related to positive psychological outcomes such as well-being, satisfaction with life, and self-esteem.

Philippe Rushton and his colleagues followed Musek’s initial paper with a series of studies (Rushton et al., 2008, 2009; Rushton and Irwing, 2008, 2009a,b,c) claiming to find the GFP in a multitude of commonly used personality inventories. Two of these studies (Rushton et al., 2008, 2009)as well as a group of follow-up studies (Figueredo and Rushton, 2009; Veselka et al., 2009a,b)used twin samples to establish the genetic basis of the GFP. These papers also presented the view that the GFP reflects individual differences in reproductive strategies initially outlined by Wilson (1975). It was theorized that individuals scoring high on the general factor favored the so-called ‘K-strategy’, whereby a large parental investment is made in a relatively low number of high-quality, slow-maturing offspring. Conversely, individuals scoring low on the general factor were thought to favor the ‘r-strategy’, investing a low level of care in a large number of offspring.

The next wave of studies set about showing that the GFP could predict theoretically relevant outcome variables. Erdle et al. (2010) found that the GFP was highly related to self-esteem in an internet sample of over 600,000 people, and then published a follow-up study (Erdle and Rushton, 2011a) showing that this association could not be explained by social desirability. Using undergraduate samples, Erdle and Rushton (2011b) also found an association between the GFP and self-esteem that was not accounted for by social desirability. This paper also reported positive associations between the GFP and positive affect and expectations of reward, along with negative associations between the GFP and negative affect and expectations for punishment. The GFP was also shown to be related to peer-ratings of likeability and popularity in classmates in a sample of adolescents (van der Linden et al., 2010) and to supervisor-rated job-performance in a sample of individuals working in the chemical industry, consultancy and personnel agencies, telemarketing, education, or catering service.

As evidence in support of the GFP accumulated, studies that called the validity of the GFP into question began to emerge. de Vries (2011) reanalyzed the data from van der Linden et al. (2010) and concluded that the GFP found in that study was essentially identical to extraversion. Donnellan et al. (2012) failed to replicate in an independent sample the GFP in the Multidimensional Personality Questionnaire that was reported by Rushton and Irwing (2009a); rather, a three-factor solution fit the original data as well as the independent sample data better than did a one-factor solution. Hopwood et al. (2011) noted that most studies confirming the GFP had extracted the GFP from one personality inventory at a time. They instead examined whether a GFP could be extracted across eight personality inventories included in a large (N = 680 community sample. Hierarchical analyses suggested that the Big-Five were evident across inventories but that they were relatively independent of each other. Additionally, confirmatory factor analyses were unable to generate an acceptable fit for a one-factor model.

A large portion of the studies summarized above are presented in more detail in comprehensive reviews that present favorable (Just, 2011; Rushton and Irwing, 2011) and unfavorable (Ferguson et al., 2011) perspectives on the GFP. Novel results that support (Loehlin and Martin, 2011; Loehlin and Horn, 2012; Loehlin, 2013) and fail to support (Muncer, 2011; Pettersson et al., 2012) the GFP continue to emerge at a rapid rate. Although there is much value in assessing the merits of individual studies on the GFP, we believe that the plethora of conflicting viewpoints presented across individual studies is due in part to a lack of clarity about the conceptual and statistical issues regarding what constitutes a general factor. Therefore, in this paper we take a step back in order to examine the premise upon which any general factor may be deemed as a valid construct. In doing so, we show that a) there are fundamental flaws in the analytical procedures used to extract the GFP, b) when correcting for these errors, the magnitude of a GFP is not large enough to be psychologically meaningful, and c) the utility of a GFP is less than that of using lower level factors as predictors.

2. Multiple ways of evaluating the importance of a factor

Although there is some confusion in the literature as to what constitutes a general factor, it is perhaps easiest to think of it as analogous to the general 3° background radiation in radio astronomy used as evidence for the “Big Bang”. That is, the general factor pervades all items. This is, of course, the basic logic behind reliability theory, where the general factor of a test is the variance common to all of the items on the test and item variances can be decomposed into that part due to a general factor and other parts due to group and specific factor variance as well as unique variance (Revelle and Zinbarg, 2009).

There are at least five different methods that have been commonly used to measure the importance of a factor or component in factor or components analysis. Each method has also been applied to examining the importance of a general factor. We first describe these methods and then apply them to simulated correlation matrices with known structures to demonstrate how these methods differ in recovering the latent structure of each correlation matrix. We then apply these same techniques to five of the data sets reported by Rushton and his colleagues as well as three reported by Musek and then finally compare these results to several well known data sets of cognitive ability.

2.1. Method 1:Eigen Values of first principal component or first factor

Some early claims for a general factor emphasized the size of the eigen value of the first factor or principal component¹. But this measure is insensitive to the structure of the correlation matrix, but rather is a function of the average correlation of the matrix. Consider a correlation matrix, R, with a factor F with loadings f_i and eigen value $\lambda =\mathbf{F}\prime \mathbf{F}=\sum f_i^2$. The first measure of importance is a direct comparison of the magnitude of the factor’s eigen value to the rank of the matrix. For non-singular correlation matrices, the rank will be the number of variables and so this is just $\frac{\lambda }{N}$ where N is the number of variables. This ratio will indicate the amount of variance in the correlation matrix associated with that factor (or component). If all correlations are positive, it is also an index of the average correlation between any two items (or tests) accounted for by that factor or component. (More precisely, the average correlation associated with this component is $\overline{r}=\frac{\lambda -1}{N-1}$ (Kaiser, 1968)). Because the numerator and denominator will both increase with N, it is insensitive to the number of tests being analyzed. This is the approach of Musek (2007) and in at least one case, by Rushton and Irwing (2009c). Although referred to as a general factor, which normally implies a hierarchical or multilevel solution, this is just the first (usually unrotated) factor or component (see footnote 1).

2.2. Scores on the first unrotated component or factor

Although some interpret the size of the eigen value of the first unrotated component or factor as an index of a general factor, others (e.g., Loehlin (2012); van der Linden et al. (2011); Veselka et al. (2012)) find scores on this first unrotated factor (or component) scores. This is done to find the correlation with solutions from other inventories (Loehlin, 2012; van der Linden et al., 2011) or across twin pairs (Veselka et al., 2012). Although we applaud this concern for validation, because the factors/components so found do not represent a general factor, the correlation between two such estimates is potentially flawed. As we will show with an example later, the problem is that since the first factor is not the general factor, correlating it with another incorrect estimate from another inventory does not add any useful information.

2.3. Method 3: Correlations between Lower Order Factors

A third approach is to extract a higher order factor (or even sometimes, a higher order component) from the correlations between the lower order factors (or sometimes, the lower order components). In the case of just two lower order factors, loadings on this higher order factor are underdetermined and a typical solution is just to use the square root of the interfactor correlation. The importance of such a “general factor” is then interpreted in terms of its loadings on the lower order factors. This seems to be the approach favored by Rushton and his colleagues in some of their earlier analyses.

2.4. Method 4: Explained Common Variance

An anonymous reviewer suggested yet another estimate of the amount of the general factor saturation, the Explained Common Variance or ECV (Reise et al., 2010, 2013; Ten Berge and Socan, 2004). When used in conjunction with a bi-factor rotation, the ECV is an index of the amount of variance accounted for by the general factor compared to the total amount of common variance explained by the factor model. The ECV is just the ratio of the eigen value for the general factor divided by the sum of the eigen values of all of the factors. Although the ECV is an excellent indication of unidimensionality, it is not an estimate of the amount of the total test variance that is explained by the general factor. In particular, the ECV will remain the same even if all of the correlations in a matrix are divided by a constant. As an index of unidimensionality, this is good, as an index of the general factor saturation, this is not helpful.

2.5. Method 5: ^ωhierarchical (^ωh)

The fifth method to estimate the importantance of general factor is to use the approach of McDonald (1999), Revelle and Zinbarg (2009) or Zinbarg et al. (2005) and is the ratio of the sum of the correlations accounted for by the general factor divided by the sum of the original correlations. If F is a general factor of the set of variables, then

$${\omega }_{\mathit{hierarchical}}={\omega }_h=\frac{\mathbf{1}\mathbf{\prime }\mathbf{F}\mathbf{F}\prime \mathbf{1}}{\mathbf{1}\mathbf{\prime }\mathbf{R}\mathbf{1}}=\frac{{(\sum f_i)}^2}{\sum \sum r_{ij}}$$

may be thought of as the reliability due to the general factor of that set of variables. ω_h is the ratio of the sum of correlations reproduced by a factor to the sum of all correlations². ω_h can be conceptualized briefly as examining the direct effect of the second or third order factor not on the lower order factors, but on the variables themselves (Holzinger and Swineford, 1937; Jensen and Weng, 1994; Reise et al., 2007; Schmid and Leiman, 1957). A general factor can be found either by Exploratory Factor Analysis (EFA) or Confirmatory Factor Analysis (CFA). When using EFA, lower order factors are allowed to correlate and a higher order (general) factor is found from these correlations. The loadings of this general factor on the variables may then found by using a Schmid Leiman transformation (Schmid and Leiman, 1957). An alternative technique for finding the general factor is to use EFA with a bifactor rotations (Jennrich and Bentler, 2011) or CFA to directly find a bifactor solution (Holzinger and Swineford, 1937; Reise et al., 2010, 2013). Hierarchical models are found merely by allowing the first order factors to,correlate and then finding a second order factor to account for their correlations.

Given the normal meaning of the word hierarchy to represent a tree like structure, there is an unfortunate naming confusion in these models. While Gustafsson and Balke (1993), McDonald (1999) and Yung et al. (1999) refer to the structure in the left panel of Figure 1 as a higher order model and to solutions similar to those of Schmid and Leiman (1957) as a hierarchical models or nested models, Mulaik and Quartetti (1997) refers to the left panel as hierarchical and the right panel as nested. Continuing the confusion, Chen et al. (2006) refer to the left panel as a second order factoring, and the right panel as a bifactor solution. We prefer to follow normal English usage and use hierarchy to represent tree like structures.

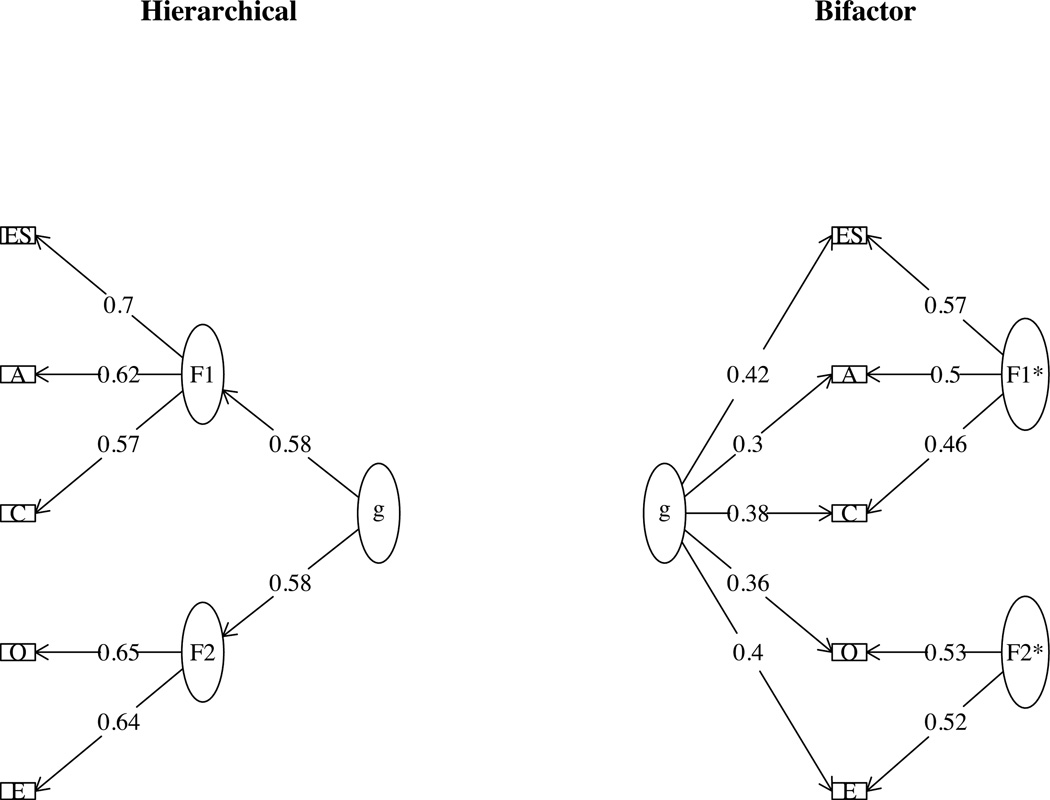
Figure 1.

An example of an exploratory hierarchical solution versus a exploratory bifactor solution of the Digman median correlations. The exploratory procedure allows some small cross loadings between the two lower level factors and the tests. When using a confirmatory factor model for the hierarchical model, the loadings are .61, .56, and .72 for the first factor and .55 and .76 for the second factor with general factor loadings of .60. The confirmatory bifactor model produces general factor loadings of .44, .20, .48, .32 and .45 for C, A, ES, O, and E respectively. This leads to an ω_hvalue of .36. All analyses done using the psych and sem packages in R.

As is true with other estimates of reliability, ω_h is sensitive to the number of items or subtests being examined. Unlike a which tends towards 1 as test length increases, ω_h tends towards the asymptotic value of

$${\omega }_{h_{\infty }}=\frac{\mathbf{1}\mathbf{\prime }\mathbf{F}\mathbf{F}\mathbf{\prime }\mathbf{1}}{\mathbf{1}\mathbf{\prime }(\mathbf{R}-{\mathbf{U}}^{\mathbf{2}})\mathbf{1}}$$

where U² represents the unique residual variation in the basic factor model of R = FF′ + U².

2.6. Exploratory versus Confirmatory Factor Analysis

When estimating the parameters for methods 3 – 5, it is possible to use EFA or CFA. The seeming advantage of CFA is that goodness of fit statistics are available for the overall model. However, more recent factor analytic procedures (e.g., those available in the psych package (Revelle, 2013) in 𝖱 ‘ (R Development Core Team, 2012)) can find these statistics as well. Most of the various CFA and EFA fit statistics consider the size of the elements of the residual matrix (R* = R − FF′) for a hypothesized F matrix. Conceptually, all of these approaches consider the size of the squared residuals, R*², and either find the root mean square of these residuals or sum the squared residuals divided by their standard error to find a χ². Other goodness fit • indices derived from this χ ² compare the magnitude of the residual χ² with the x² of the original correlation matrix. When using maximum likelihood (ML) techniques to find the solution, a χ² statistic may be derived from the ML fit statistic. Root Mean Square Errors of Approximation (RMSEA) are then derived from this χ². All of these later set of approaches indicate whether the overall model fits the data, not whether a general factor is or is not necessary. Some of the analyses reported by Rushton and his colleagues use CFA and compare fits with and without a general factor (Rushton and Irwing, 2008; Rushton et al., 2008; Rushton and Irwing, 2009c). But such comparisons are asking no more than are the lower order factors themselves correlated.

We have used EFA and a Schmid-Leiman transformation (Schmid and Leiman, 1957) to find ω_h. As an anonymous reviewer points out, there are problems with this approach that can lead to an overestimation of ω_h as well as ECV. Alternatives which we have used include the bifactor rotations discussed by Holzinger and Swineford (1937); Reise et al. (2010, 2013) and implemented by Jennrich and Bentler (2011). Further discussion of this problem may be found in Chen et al. (2006). However, in our experience, in comparison to the Schmid-Leiman procedure, the direct bifactor approach using SEM, or the indirect by using a bifactor rotation tend to overestimate the general factor. But in all cases, these approaches are to be preferred to methods 1–3.

2.7. Application of Eigen Values, ω_h, and Correlations between Lower-Order Factors to simulated Correlation Matrices

What is important to realize is that the simple question of what is the percentage of variance due to a general factor will have different answers depending upon which approach is used. Thus, it is possible that the different methods may yield estimates of general factor saturation that are not equally valid. To show this, we evaluate the validity of each of the estimates using example correlation matrices differing in their amount of general factor saturation.

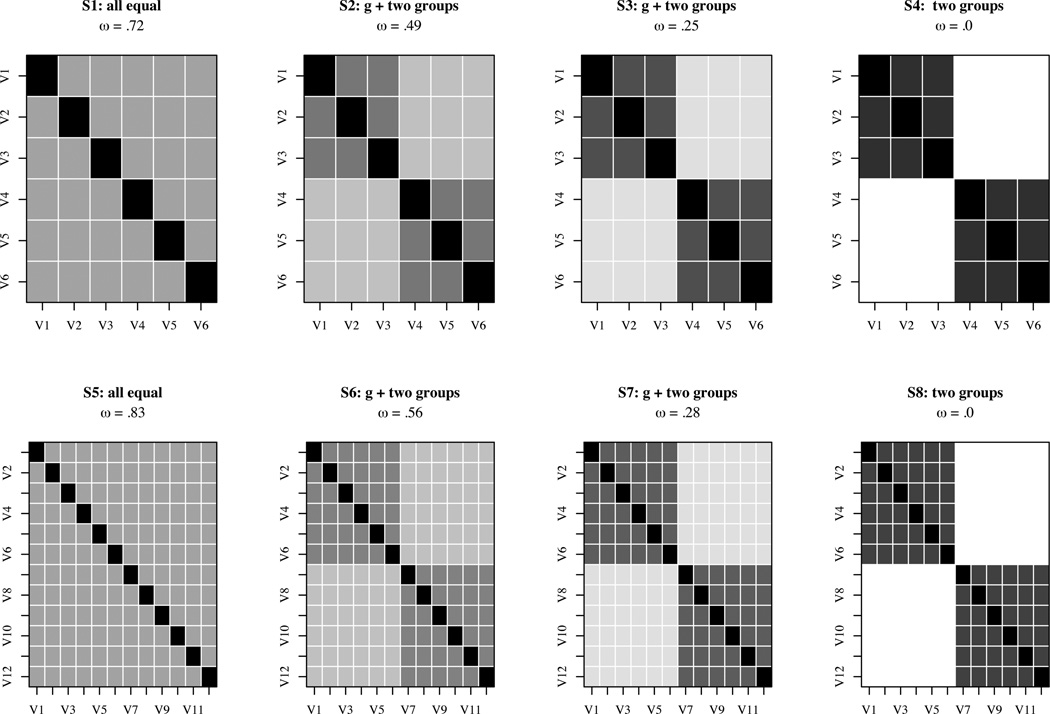
We first apply Methods 1–5 to eight example correlation matrices (S1–S8) with equal average item intercorrelations that differ in their general factor saturation (Table 1). Each set is made up of two groups of items, with equal correlations within both groups but progressively smaller correlations of items between the groups. While the between group inter-item correlations reflect the general factor, the within group correlation reflect a mixture of general + group factor. All eight example matrices have the same overall average inter-item correlation, .30. Sets S1 . S4 are formed from two groups of size three with average correlations of .30, .45, .60 and .75 within groups, but with between group inter-item correlations of .3, .2, .1, and 0 respectively. Sets S5 S8 have similar structures, also with an overall average correlation of .3, but for two groups of size 6 with within group correlations of .30, .42, .54, and .66 and between group inter-item correlations of .3, .2, .1, or 0 between the first and last six tests. This pattern of correlations leads to between group correlations of .56, .32, .14, and .00 for S1 … S4 and .72, .39, .16 and .00 for sets S5 … S8. When corrected for attenuation these correlations become 1, .44, .17, and .00 for S1 … S4, and 1, .48, .19 and .00 for S5 … S8. This structure may be seen graphically in Figure 2. The shading within each box represents the magnitude of the correlations for that set. Thus, the diagonal (correlations of 1.0) are darkest, and equal levels of shading imply equal magnitude of the correlations.

Table 1.

Eight example matrices all with an average inter item correlation of .3 but that differ drastically in their structures. α reliabilities of the first four sets are all .72 and for the last four are all .84. ω_hierarchical for these sets range from .72 to 0 for sets 1–4 and from .84 to 0 for sets 5–8. The last set (S8) is then rearranged to show two subsets, 8A and 8B which are discussed in section 2.8. See Figure 1 for a graphical display of these correlation matrices and Table 2 for an analysis of their general factor saturation.

Set S1							Set S2
Variable	V1	V2	V3	V4	V5	V6	V1	V2	V3	V4	V5	V6
V1	1.00	0.30	0.30	0.30	0.30	0.30	1.00	0.45	0.45	0.20	0.20	0.20
V2	0.30	1.00	0.30	0.30	0.30	0.30	0.45	1.00	0.45	0.20	0.20	0.20
V3	0.30	0.30	1.00	0.30	0.30	0.30	0.45	0.45	1.00	0.20	0.20	0.20
V4	0.30	0.30	0.30	1.00	0.30	0.30	0.20	0.20	0.20	1.00	0.45	0.45
V5	0.30	0.30	0.30	0.30	1.00	0.30	0.20	0.20	0.20	0.45	1.00	0.45
V6	0.30	0.30	0.30	0.30	0.30	1.00	0.20	0.20	0.20	0.45	0.45	1.00
Set S3							Set S4
V1	1.00	0.60	0.60	0.10	0.10	0.10	1.00	0.75	0.75	0.00	0.00	0.00
V2	0.60	1.00	0.60	0.10	0.10	0.10	0.75	1.00	0.75	0.00	0.00	0.00
V3	0.60	0.60	1.00	0.10	0.10	0.10	0.75	0.75	1.00	0.00	0.00	0.00
V4	0.10	0.10	0.10	1.00	0.60	0.60	0.00	0.00	0.00	1.00	0.75	0.75
V5	0.10	0.10	0.10	0.60	1.00	0.60	0.00	0.00	0.00	0.75	1.00	0.75
V6	0.10	0.10	0.10	0.60	0.60	1.00	0.00	0.00	0.00	0.75	0.75	1.00
Set S5
Variable	V1	V2	V3	V4	V5	V6	V7	V8	V9	V10	V11	V12
V1	1.00	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30
V2	0.30	1.00	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30
V3	0.30	0.30	1.00	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30
V4	0.30	0.30	0.30	1.00	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30
V5	0.30	0.30	0.30	0.30	1.00	0.30	0.30	0.30	0.30	0.30	0.30	0.30
V6	0.30	0.30	0.30	0.30	0.30	1.00	0.30	0.30	0.30	0.30	0.30	0.30
V7	0.30	0.30	0.30	0.30	0.30	0.30	1.00	0.30	0.30	0.30	0.30	0.30
V8	0.30	0.30	0.30	0.30	0.30	0.30	0.30	1.00	0.30	0.30	0.30	0.30
V9	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30	1.00	0.30	0.30	0.30
v10	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30	1.00	0.30	0.30
V11	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30	1.00	0.30
V12	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30	0.30	1.00
Set S6
Variable	V1	V2	V3	V4	V5	V6	V7	V8	V9	V10	V11	V12
V1	1.00	0.42	0.42	0.42	0.42	0.42	0.20	0.20	0.20	0.20	0.20	0.20
V2	0.42	1.00	0.42	0.42	0.42	0.42	0.20	0.20	0.20	0.20	0.20	0.20
V3	0.42	0.42	1.00	0.42	0.42	0.42	0.20	0.20	0.20	0.20	0.20	0.20
V4	0.42	0.42	0.42	1.00	0.42	0.42	0.20	0.20	0.20	0.20	0.20	0.20
V5	0.42	0.42	0.42	0.42	1.00	0.42	0.20	0.20	0.20	0.20	0.20	0.20
V6	0.42	0.42	0.42	0.42	0.42	1.00	0.20	0.20	0.20	0.20	0.20	0.20
V7	0.20	0.20	0.20	0.20	0.20	0.20	1.00	0.42	0.42	0.42	0.42	0.42
V8	0.20	0.20	0.20	0.20	0.20	0.20	0.42	1.00	0.42	0.42	0.42	0.42
V9	0.20	0.20	0.20	0.20	0.20	0.20	0.42	0.42	1.00	0.42	0.42	0.42
V10	0.20	0.20	0.20	0.20	0.20	0.20	0.42	0.42	0.42	1.00	0.42	0.42
V11	0.20	0.20	0.20	0.20	0.20	0.20	0.42	0.42	0.42	0.42	1.00	0.42
V12	0.20	0.20	0.20	0.20	0.20	0.20	0.42	0.42	0.42	0.42	0.42	1.00
Set S7
V1	1.00	0.54	0.54	0.54	0.54	0.54	0.10	0.10	0.10	0.10	0.10	0.10
V2	0.54	1.00	0.54	0.54	0.54	0.54	0.10	0.10	0.10	0.10	0.10	0.10
V3	0.54	1.00	0.54	0.54	0.54	0.10	0.10	0.10	0.10	0.10	0.10	0.10
V4	0.54	0.54	0.54	1.00	0.54	0.54	0.10	0.10	0.10	0.10	0.10	0.10
V5	0.54	0.54	0.54	0.54	1.00	0.54	0.10	0.10	0.10	0.10	0.10	0.10
V6	0.54	0.54	0.54	0.54	0.54	1.00	0.10	0.10	0.10	0.10	0.10	0.10
V7	0.10	0.10	0.10	0.10	0.10	0.10	1.00	0.54	0.54	0.54	0.54	0.54
V8	0.10	0.10	0.10	0.10	0.10	0.10	0.54	1.00	0.54	0.54	0.54	0.54
V9	0.10	0.10	0.10	0.10	0.10	0.10	0.54	0.54	1.00	0.54	0.54	0.54
V10	0.10	0.10	0.10	0.10	0.10	0.10	0.54	0.54	0.54	1.00	0.54	0.54
V11	0.10	0.10	0.10	0.10	0.10	0.10	0.54	0.54	0.54	0.54	1.00	0.54
V12	0.10	0.10	0.10	0.10	0.10	0.10	0.54	0.54	0.54	0.54	0.54	1.00
Set S8
Variable	V1	V2	V3	V4	V5	V6	V7	V8	V9	V10	V11	V12
V1	1.00	0.66	0.66	0.66	0.66	0.66	0.00	0.00	0.00	0.00	0.00	0.00
V2	0.66	1.00	0.66	0.66	0.66	0.66	0.00	0.00	0.00	0.00	0.00	0.00
V3	0.66	0.66	1.00	0.66	0.66	0.66	0.00	0.00	0.00	0.00	0.00	0.00
V4	0.66	0.66	0.66	1.00	0.66	0.66	0.00	0.00	0.00	0.00	0.00	0.00
V5	0.66	0.66	0.66	0.66	1.00	0.66	0.00	0.00	0.00	0.00	0.00	0.00
V6	0.66	0.66	0.66	0.66	0.66	1.00	0.00	0.00	0.00	0.00	0.00	0.00
V7	0.00	0.00	0.00	0.00	0.00	0.00	1.00	0.66	0.66	0.66	0.66	0.66
V8	0.00	0.00	0.00	0.00	0.00	0.00	0.66	1.00	0.66	0.66	0.66	0.66
V9	0.00	0.00	0.00	0.00	0.00	0.00	0.66	0.66	1.00	0.66	0.66	0.66
V10	0.00	0.00	0.00	0.00	0.00	0.00	0.66	0.66	0.66	1.00	0.66	0.66
V11	0.00	0.00	0.00	0.00	0.00	0.00	0.66	0.66	0.66	0.66	1.00	0.66
V12	0.00	0.00	0.00	0.00	0.00	0.00	0.66	0.66	0.66	0.66	0.66	1.00
Rearranged Set 8 to show why correlating the first general factor across measures doesn’t work.
Set 8A							Set 8B
Variable	V1	V2	V3	V7	V8	V9	V4	V5	V6	V10	V11	V12
V1	1.00	0.66	0.66	0.00	0.00	0.00	0.66	0.66	0.66	0.00	0.00	0.00
V2	0.66	1.00	0.66	0.00	0.00	0.00	0.66	0.66	0.66	0.00	0.00	0.00
V3	0.66	0.66	1.00	0.00	0.00	0.00	0.66	0.66	0.66	0.00	0.00	0.00
V7	0.00	0.00	0.00	1.00	0.66	0.66	0.00	0.00	0.00	0.66	0.66	0.66
V8	0.00	0.00	0.00	0.66	1.00	0.66	0.00	0.00	0.00	0.66	0.66	0.66
V9	0.00	0.00	0.00	0.66	0.66	1.00	0.00	0.00	0.00	0.66	0.66	0.66
V4	0.66	0.66	0.66	0.00	0.00	0.00	1.00	0.66	0.66	0.00	0.00	0.00
V5	0.66	0.66	0.66	0.00	0.00	0.00	0.66	1.00	0.66	0.00	0.00	0.00
V6	0.66	0.66	0.66	0.00	0.00	0.00	0.66	0.66	1.00	0.00	0.00	0.00
V10	0.00	0.00	0.00	0.66	0.66	0.66	0.00	0.00	0.00	1.00	0.66	0.66
V11	0.00	0.00	0.00	0.66	0.66	0.66	0.00	0.00	0.00	0.66	1.00	0.66
V12	0.00	0.00	0.00	0.66	0.66	0.66	0.00	0.00	0.00	0.66	0.66	1.00

Figure 2.

Examples of a general factor for data sets 1–8. Each figure graphically portrays a correlation matrix with shading representing the magnitude of the correlation. The diagonal is a correlation of 1. The first row shows 6 and the second 12 variables with just a general factor, a large general with two group factors, a small general and two groups, and just two group factors. The average intercorrelation of the items .3 for all eight sets and thus α = .72 for all sets in the first row and α = .84 for all sets in the second row. See Table 2 for a comparison of alternative methods of estimating a general factor for these eight data sets.

It is clear by construction (and inspection) that there is just one factor (a general factor) in sets S1 and S5, and two uncorrelated factors (no general factor) in sets S4 and S8. What is somewhat less clear is how much is the general factor saturation in sets S2, S3, S6 and S7. By construction, Sets S1 … S4 have total variance of 15 and have general factor variance of rbg * 6² =10.8, 7.2, 3.6, and 0 where r_bg is the inter-item correlation for items in different groups. Similarly, sets S5 … S8 have total variance of 51.6 and general factor variance of r_bg* 12² = 43.2, 28.8, 14.4, and 0. Thus, the general factor saturations (the ratio of the amount of general factor variance to the total variance) are .72, .48, .24, .00, .84, .56, .28, and 0.00 for sets S1 … S8.

A number of different estimates of the general factor are listed in Table 2. The ratio of the first eigen value to the rank of the matrix for either a components solution (C₁/N) or a factor solution (Λ₁/N) (Method 1) is clearly not an indication of a general factor, for this is sensitive just to the average correlation and in the case of principal components, to the size of the data set. These estimates are not at all sensitive to the hierarchical structure of the data. The correlation between the lower order factors (Method 3) either significantly over estimates (sets S1 and S5) or under estimates (sets S3 and S7) the item variance associated with a general factor. The square root of the correlation over estimates the general factor saturation for all the cases, except when the correlation between lower order factors is zero. For these examples, with just two factors, the Explained Common Variance (Method 4) • provides estimates which are practically identical to the correlations between the factors. ω_h and the ratio of the eigen value of the general factor to the rank of the matrix (Λ_g/N, Method 5), found by EFA using the omega function in the psych package Revelle (2013) in 𝖱 (R Development Core Team, 2012) are sensitive, as they should be, to the average between group correlation. For cases with a clear two group factor structure, ω_h is underdetermined and was found by the setting the two group factors to have equal loadings on the general factor (Zinbarg et al., 2007). Note how the ω_h estimate correctly identifies the amount of general factor variance and the ratio Λ_g/N correctly identifies the average between group inter-item r associated with the general factor.

Table 2.

Alternative estimates of general factor saturation for the eight simulated data sets (S1:S8) in Figure 1, data sets in which the general factor of personality has been extracted, and classic cognitive ability data sets. Method 1: The first Eigen Value from a principal components analysis or factor analysis divided by number of items (N) equals the proportion of variance accounted for by that component or factor. C₁ is the eigen value of the first principal component, Λ₁ is the eigen value for the first factor found by minimal residual factor analysis. Method 3: Correlation between group factors. Browne’s target rotation function was used with a cluster structure target. r_Λ is the correlation between the first and second group factors, or, in the case of the MMPI and ability items, the average of the between factor correlations. Method 4: The Explained Common Variance found from exploratory factor analysis. Method 5: ω analyses. Λ_g is the eigen value of the general factor found by a Schmid-Leiman transformation; ω_h is MacDonald’s ω_hierarchical ω_h∞ is the asymptotic value of ω_h. R² is the amount of factor variance accounted for by the original variables. It is a direct function of the inverse of the correlation matrix and the factor structure loadings. R/M is the estimate of GFP saturation appearing in empirical articles authored by Rushton and Musek. For Rushton’s first four analyses, this is r_Λ emerging from structural equation modeling. For the MPQ, this is Λ₁/N. Each of Musek’s estimates is C₁/N

	Method 1		Method 3	Method 4	Method 5
	C1/N	Λ1/N	rΛ	ECV	Λg/N	ωh	ωh∞	R2	R/M
S1	.42	.30	.99	.98	.30	.72	.99	.72
S2	.42	.30	.44	.44	.20	.48	.62	.48
S3	.42	.30	.17	.17	.10	.24	.29	.24
S4	.42	.30	.00	.00	.00	.00	.00	.00
S5	.36	.30	.97	.99	.30	.83	1.00	.83
S6	.36	.30	.48	.48	.20	.56	.65	.56
S7	.36	.30	.19	.19	.10	.28	.31	.28
S8	.36	.30	.00	.00	.00	.00	.00	.00
Rushton’s Analyses
Digman’s Medians	.40	.27	.33	.34	.14	.35	.50	.36	.45
Mount’s meta anal.	.44	.30	.37	.38	.17	.40	.54	.41	.44
Comrey Scales	.29	.19	.26	.26	.08	.27	.38	.31	.41
MMPI	.39	.35	.15	.25	.16	.37	.41	.41	.49
MPQ	.46	.33	.25	.33	.17	.35	.45	.37	.33
Musek’s Analyses
Big Five Inventory	.50	.39	.38	.40	.22	.43	.52	.51	.50
IPIP	.42	.29	.30	.32	.17	.37	.48	.46	.40
Big Five Observer	.45	.32	.42	.46	.20	.43	.58	.46	.45
Cognitive Ability Data	Sets
Thurstone’s 9	.54	.50	.55	.60	.40	.74	.79	.74
Bechtoldt’s 17	.37	.31	.29	.47	.28	.71	.76	.77
Holzinger’s 14	.37	.33	.40	.59	.28	.72	.80	.85
Brigham 9	.56/	.39	.56	.76	.49	.85	.91	.89
Holzinger 24	.34	.31	.31	.45	.22	.66	.70	.67
Means
Rushton & Musek	.42	.30	.31	.34	.16	.37	.48	.41	.43
Cognitive Ability	.44	.37	.42	.57	.33	.74	.79	.78

2.8. Why correlating “general factor scores” across inventories might not be informative

If a GFP from one inventory is important, then it should correspond to that found in other inventories, or with other methods. In an attempt to show that the GFP is general across inventories and correlates between twin pairs, several investigators have found component scores on the first principal component (Loehlin and Horn, 2012; Veselka et al., 2009b) or estimated factor scores on the first factor (Loehlin, 2012; Veselka et al., 2012) and then reported the correlation of these scores across inventories. Although seemingly a reasonable approach, it is not informative unless the factor scores actually measure the general factor. If they do not, then this approach is not useful. This is best shown with a simple example.

Consider the 12 variables shown in example data set S8. As is clear from the correlations, this set is composed of two independent clusters of 6 items < each, with a within cluster correlation of .66. Consider the variables in Set S8 as made up of two related sets such that variables 1–3 and 7–9 form one set (8A) and variables 4–6 and 10–12 forming another set (8B). (This rearranged set is shown as the last set in Table 1). Then all six items in set 8A have loadings of .57 on a “general factor” of set A as do all six items in set 8B on that “general factor”. These two “general factors” in turn correlate .85 with each other even though in fact there is no general factor in either set 8A or 8B!

Most people would think of the structure in either set 8A or 8B as representing 2 different factors. In fact, by construction the amount each item should load on a general factor is 0 and as was shown for sets S4 and S8, the ω_h = 0.0. However, when extracting two factors from either 8A or 8B and examining the first unrotated factor³, we discover that each item loads on the “general factor” with a loading of .574 and that the amount of variance associated with this general factor (what Revelle and Zinbarg (2009) would call ω_total) is (.574 * 6)²/(.66 * 6 * 2 + 6) = .85. Why should this be? Because each first unrotated factor is fitting the diagonal and off diagonal elements with the assumed average correlation of .33. The two “general factors” correlate so highly because each “general factor” is a sum of two unrelated parts, the first and second clusters of both sets 8A and 8B.

3. Extending the analysis on the “General Factor of Personality”

The preceding analyses show that ω_h properly estimates the general factor saturation McDonald (1999); Zinbarg et al. (2005, 2006); Revelle and Zinbarg (2009) and suggest that Rushton’s and others’ failure to use ω_h to estimate the general factor saturation in different personality inventories may have resulted in less than optimal solutions. Musek (2007) also did not use ωh to evaluate the importance of a general factor. Our strategy in the remainder of the paper is to apply ω_h analyses to data sets originally used to establish the importance of a general factor in personality (Musek, 2007; Rushton and Irwing, 2008; Rushton et al., 2008; Rushton and Irwing, 2009c).⁴ We then compare estimates of a general factor in personality to the general factor saturation found in classic cognitive ability data sets.

In addition to the example data sets, Table 2 shows estimates of the importance of a general factor emerging from an ω_h analysis for the personality and cognitive ability data sets discussed below, and Figure 3 graphically represents the general factor in a selected sample of these data sets. Even a cursory analysis of the table and figure shows that a general factor is not as well-represented in personality (mean ω_h = .37) as it is in cognitive ability (mean ω_h = .74). Note that the means for analyses using Method 1 (comparing the magnitude of the first principal component or first factor to the rank of the matrix) do not differ between the Rushton and Musek analyses (means < = .42 and .30) and the Cognitive measures (means = .44 and .37). Nor do they differ substantially when using Method 3 (the correlation between the subfactors), means = .31 and .42 for the Personality and Cognitive measures, respectively. However, when using the appropriate methodology for estimating the Explained Common Variance (Method 4) or a general factor (Method 5) there are substantial differences between the two content domains. The average magnitude of the size of the general factor divided by the rank of the matrix is more than twice as large in the cognitive domain (.33) than it is in the personality domain (.16). Converting these to estimates of ω_h lead to values of .73 and .38 for cognitive and personality measures, respectively.

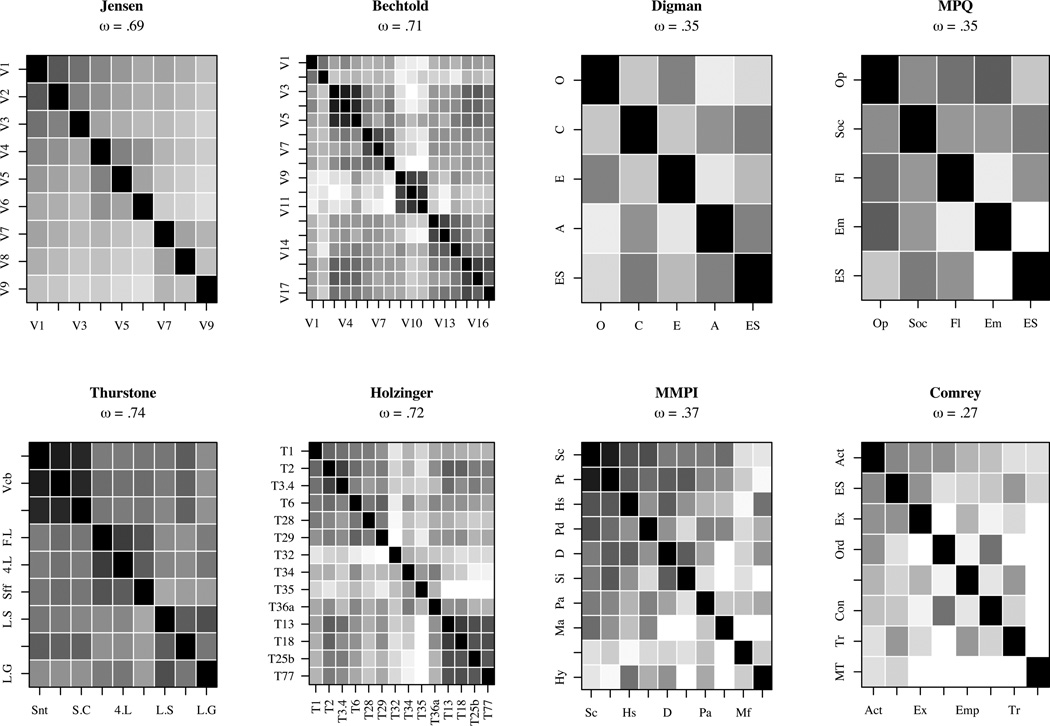
Figure 3.

The general factor of seven real data sets and one simulated data set. Thurston, Bechtoldt and Holzinger are examples from the cognitive domain, Digman, MPQ, MMPI and Comrey are from Rushton and colleagues. Jensen is a prototypical general factor example. ω_h is found using EFA. Shading represent values from 0 to 1. Those less than 0 are shown as white (e.g., the Comrey data set).

3.1. Digman’s 1997 Analysis of Big 5 Traits

Although the “Big 5” model of non-cognitive aspects of personality is partly credited to John Digman’s influential chapter in the Annual Review (Digman, 1990), Digman also proposed a higher order structure of two super factors (Digman, 1997). As is clear from inspection of the correlation matrices of the Big 5 reviewed by Digman, the five factors are not orthogonal. In a meta-analysis of the Digman study, Rushton and Irwing (2008) have presented both median and weighted average correlation matrices. Rushton and Irwing (2008) used confirmatory procedures to extract a higher order general factor from these correlations.

An alternative solution, using the procedure of Schmid and Leiman (1957) is to calculate the g loadings from the hierarchical solution, extract the general factor, and the find the residual loadings on the remaining orthogonal factors (Figure 1). The amount of general factor saturation, McDonald’s coefficient ω_h (McDonald, 1999; Revelle and Zinbarg, 2009; Zinbarg et al., 2005), is found by squaring the sum of the general factor loadings and dividing by the sum of the total correlation matrix. The resulting value, .35, is the percentage of variance accounted for by the general factor. Note that this is a smaller value than Rushton and Irwing (2008) obtained (.45) using the correlation between lower-order factors found through structural equation modeling to estimate the general factor saturation. This same analyses can be repeated on other data sets reported by Rushton and Irwing (2008) and Rushton and Irwing (2009c).

3.2. Mount et al.’s (2005) meta-analysis

Rushton and Irwing (2008) extracted a general factor from Mount et al. (2005)’s meta-analytic results for Big 5 scale intercorrelations that were derived from four inventories assessing Big 5 content: the NEO-PI-R (Costa and McCrae, 1992); the Hogan Personality Inventory, HPI (Hogan and Hogan, 1995), the Personal Characteristics Inventory (Mount et al., 1999), and the International Personality Item Pool (Goldberg, 1999). Rushton and Irwing (2008)’s estimate of the general factor saturation, computed again by the correlation between lower-order factors emerging from structural equation modeling, was .44. This is slightly higher than MacDonald’s ω_h, .40.

3.3. The Comrey Personality Scales

The bi-factor solution for the Comrey Personality Scales (correlations taken from the 1995 manual) (Comrey, 1995, 2008), originally analyzed for a general factor in Rushton and Irwing (2009c), is also given in Table 2. Once again, the low saturation of the general factor (ω_h = .27, compare with Rushton and Irwing (2009c)’s estimate of 41% general factor saturation) combined < with several low loadings of primary scales on the general factor suggest that the higher order factor alone may not provide an adequate description of the data. When examining the CFA solution to the Comrey (Rushton and Irwing, 2008, Figure 1) it is clear that their “general factor” is actually just a measure of what they label as “Extraversion” but could better be described as a blend of Activity, Emotional Stability, and Extraversion.

3.4. The MMPI

Yet another data set reported by Rushton and Irwing (2009c) that shows the general factor is the MMPI-2 (Helmes, 2008). However, when we applied a bifactor analysis, this general factor accounts for 37% of the variance in a total score obtained by averaging all of the MMPI-2 scales (Table 2) rather than the 49% Rushton and Irwing (2009c) found from the correlations between lower order factors.⁵ Additionally, various scales showed extremely low loadings on the general factor.

3.5. The Multicultural Personality Questionnaire

The last dataset that Rushton and Irwing (2009c) reported a general factor for is the Multicultural Personality Questionnaire, MPQ (Van der Zee and Van Oudenhoven, 2001).⁶ Rushton and Irwing (2009c) used principal axis factoring to show that the general factor accounted for 33% of the common item variance, however, structural equation modeling suggested that a bifactor model provided a better fit than a general factor alone. Additionally, structural equation modeling showed that not all scales included in the MPQ loaded on the general factor. The general factor emerging from our exploratory bifactor analysis (Table 2) accounted for a similar 31% of the variance in the MPQ.

3.6. Re-analyzing Musek (2007)

Musek (2007) relied on the variance accounted for by the first principal component to estimate a general factor in three independent samples. Each sample was assessed with a different Big 5 assessment, translated into Slovenian: Sample 1 was assessed with the Big Five Inventory, BFI (John et al., 1991), sample 2 the IPIP, and sample 3 the Big Five Observer, BFO (Caprara et al., 1994). The proportion of scale variance in the Big 5 attributable to the general factor was .50 for the BFI, .40 for the IPIP, and .45 for the BFI. Although not recommended for reasons discussed earlier, Musek’s first principal component analyses agree very well with the more appropriate ω_h calculation

4. Comparison to mental ability tests

We can compare these solutions of personality tests to what is found when analyzing some classic data sets. Five sets are considered: a) 9 mental tests from Thurstone (McDonald, 1999; Thurstone and Thurstone, 1941); b) 17 mental tests from Thurstone and Bechtoldt (Bechtoldt, 1961); c) 14 tests from Holzinger and Swineford (1937); d) 9 tests from Brigham (Thurstone, 1933) and e) 24 mental tests from Harman (1967). The first four data sets are included as data sets in the psych package. The last is in core R. The interested reader is encouraged to repeat our analyses on these open source data sets.

4.1. 9 mental tests from Thurstone

A classic data set is the 9 variable Thurstone problem which is discussed in detail by R. P. McDonald (1985, 1999). These nine tests were grouped by Thurstone and Thurstone (1941) (based on other data) into three factors: Verbal Comprehension, Word Fluency, and Reasoning. The original data came from Thurstone and Thurstone (1941) but were reanalyzed by Bechtoldt (1961) who broke the data set into two. McDonald (1999), in turn, selected these nine variables from a larger set of 17. The general factor saturation of the 9 tests, estimated by ω_h, was .74.

4.2. 17 mental tests from Thurstone/Bechtoldt

This set is the 17 variables from which the clear 3 factor solution used by McDonald (1999) is abstracted. ω_h, of these variables was .72.

4.3. 14 mental tests from Holzinger

These 14 variables are from Holzinger and Swineford (1937) who introduced the bifactor model (one general factor and several group factors) for mental abilities. This is a nice demonstration data set of a hierarchical factor structure that can be analyzed using the omega function, ω_h = 71.

4.4. 9 mental tests from Brigham/Thurstone

These 9 mental tests reported by Thurstone (1933) are the data set of 4,175 students reported by Professor Brigham of Princeton to the College Entrance Examination Board. This set also has a high general factor saturation, ω_h = .85.

4.5. 24 mental tests from Holzinger/Harman

The 24 mental tests from Holzinger and Swineford have been analzyed by Harman (1967) and many others as an example of factor analysis. ω_h, for these tests was .65.

It is clear from all five of these classic data sets that the general factor saturation of cognitive tests is much higher than the general factor saturation of non-cognitive measures.

5. Creating a general factor when it is not there

Before extolling the benefits of finding ω_h either by EFA or CFA techniques, it is important to report that for simulations suggest that even when the true value of ω_h = 0, sample based estimates can be positively biased. This occurs because automatic calculations of ω_h will sometimes identify one or another group factor as a “general factor”, even though inspection of the general factor loadings suggest it is just a group factor. For example, in 50 _r simulations of population values of 0.0, sample estimates for EFA for 12 variables averaged .28 (s.e. = .02), while sample estimates using CFA techniques were even more biased (mean =.34, s.e.= .03). This bias disappears as the population value increases beyond about .4 (Revelle and Wilt, 2012). The bias may be controlled for by noting when the general factor loadings have a large variance (some very small, some very large) which is an indication of a group rather than a general factor.

Another problem that can lead to the appearance of a general factor is when the data are not simple structured. Most analyses of personality scales or items have attempted to rotate to a simple structure where each marker variable has substantial loadings on one and only one factor. That is, items or sub scales are thought to be of complexity 1. Personality variables probably do not have such a structure for rather many constructs are at least of complexity 2. Indeed, the the work on the Abridged Big 5 Circumplex Structure (AB5C) of Hofstee et al. (1992) shows that many items are in the “interstitial space” between the Big 5 dimensions. This issue of cross loadings has been discussed by Ashton et al. (2009) who suggest that the observed higher level correlations are due to scales measuring blends of lower order, orthogonal constructs.

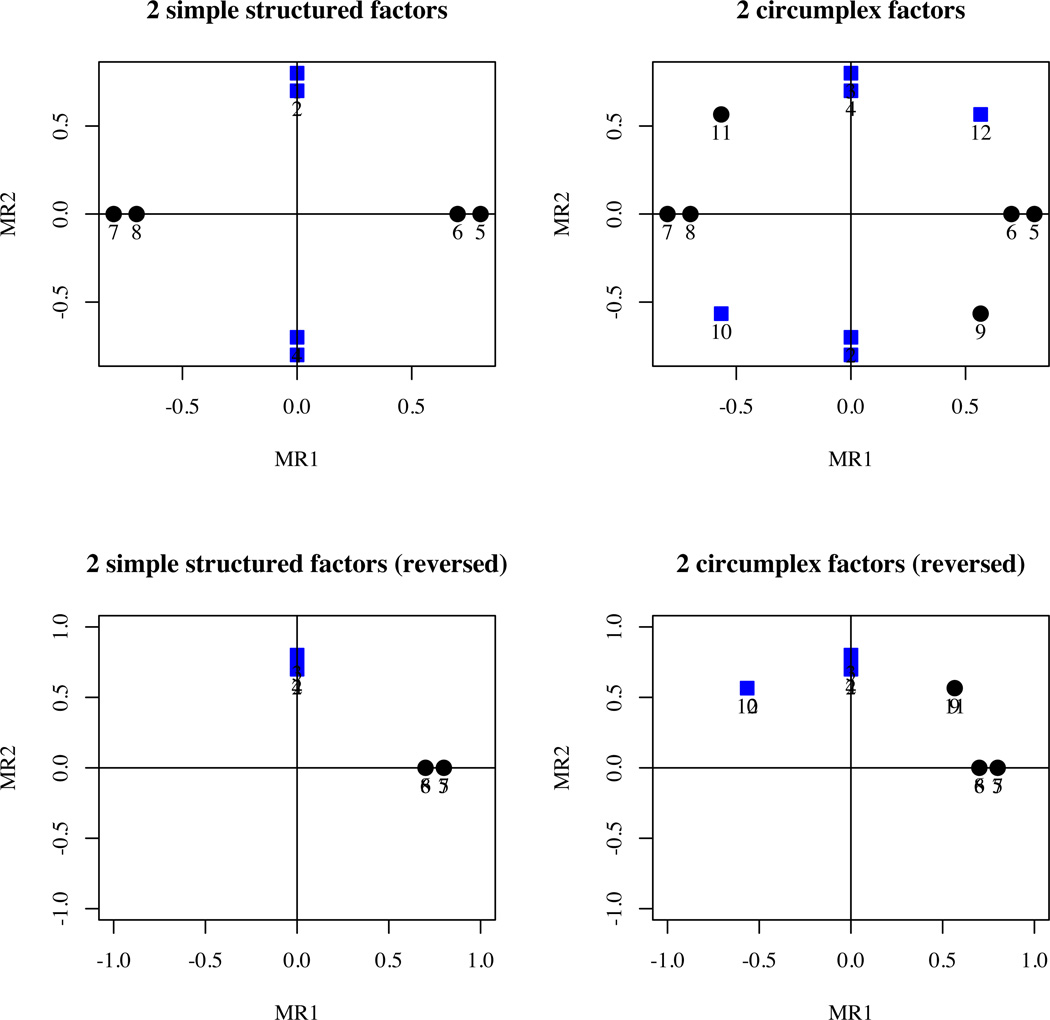
Consider 8 items representing two bipolar factors (Figure 4 upper left) or two unipolar factors (Figure 4 lower left) formed by reverse scoring the negative items. It is clear by inspection (and calculation either by EFA or CFA) that ω_h = 0. But, when adding in four variables on the major and minor diagonals of the variables, several alternative solutions are possible. Applying a CFA bifactor model or just not rotating the two factor solution leads to a “general factor” defined by variables 1–4 and 9–11, with an ω_h = .63. But, of course, the other factor is equally important and should be considered just as general. A two factor EFA also identifies two factors (MR1 and MR2) that are orthogonal and thus there is no evidence for a general factor. We suspect that similar problems account for some of the proposed GFP solutions.

Figure 4.

Two orthogonal factors may be bipolar or reversed scored as to be unipolar (Column 1). When items are added to the diagonals of these structures (Column 2), there is a tendency to find a general factor, even though one is not present.

6. Discussion and conclusions

Yes, it is possible to find a general factor of personality. One can do this be defining the first unrotated factor to be “general”. But is this the most useful level of analysis? We do not believe so. Based upon the psychometric principal that a measure should be interpreted in terms of its common variance, it is hard to justify the conclusion that Rushton and others advocate, namely thinking about measures when less than half of the variance is associated with that construct. The examples we have used are extreme cases, but we have done so in order to help people think about what it means to have a general factor. .

We have previously considered the hierarchical structure of personality inventories and suggested that items or tests should be combined as long as an internal consistency estimate based upon the worst split half reliability, β (Revelle, 1979), increases for the combined scale. Applying this logic to the examples from the cognitive domain results in one, high level scale. But applying the same algorithm to the personality inventories discussed above does not. Rather, the β estimates for the lower level constructs are greater than when they are combined. That is, normally, internal consistency estimates increase when combining measures of one domain. But a sign of multiple domains is when the lower level measures are more internally consistent than the higher level measure. This is the case of the personality measures, but not of the ability measures.

Just as some have claimed that affect reflects one common dimension from happy to sad (Russell and Carroll, 1999), others have shown that it is better to consider happy and sad as separate dimensions (Rafaeli and Revelle, 2006). This debate between forming higher order constructs versus focusing on lower order, but correlated constructs is long running. In the field of intelligence, the introduction of the bifactor model (Holzinger and Swineford, 1937) clarified the use of hierarchical models and allowed for the estimation of the relative importance of each. When g has large saturations on each test, it is clearly useful to think in terms of g. But when the saturation is low, and when there is good biological evidence for separate, although correlated systems associated with the lower order constructs (e.g., the three brain systems model of reinforcement sensitivity theory (Corr, 2008; Gray and McNaughton, 2000; Revelle, 2008), it will prove more useful to develop theories at the lower order level.

When we compare the general factor solutions of the personality tests to those of the ability tests, it is apparent that what is a clear g in ability is much muddier in personality.

Highlights.

Many have claimed there exists a general factor of personality.

We show this is a mistaken understanding of basic psychometrics.

We give a brief tutorial how to find a general factor.

We compare supposed GFPs to those found in the cognitive domain.