Dissociation of first- and second-order motion systems by perceptual learning

Abstract

Previous studies investigating transfer of perceptual learning between luminance-defined (LD) motion and texture-contrast-defined (CD) motion tasks have found little or no transfer from LD to CD motion tasks but nearly perfect transfer from CD to LD motion tasks. Here, we introduce a paradigm that yields a clean double dissociation: LD training yields no transfer to the CD task, but more interestingly, CD training yields no transfer to the LD task. Participants were trained in two variants of a global motion task. In one (LD) variant, motion was defined by tokens that differed from the background in mean luminance. In the other (CD) variant, motion was defined by tokens that had mean luminance equal to the background but differed from the background in texture contrast. The task was to judge whether the signal tokens were moving to the right or to the left. Task difficulty was varied by manipulating the proportion of tokens that moved coherently across the four frames of the stimulus display. Performance in each of the LD and CD variants of the task was measured as training proceeded. In each task, training produced substantial improvement in performance in the trained task; however, in neither case did this improvement show any significant transfer to the nontrained task.

Introduction

Substantial evidence has now accrued to suggest that there exist separate first- and second-order mechanisms (Cavanagh & Mather, 1989) for extracting luminance-defined (LD) motion versus texture-contrast-defined (CD) motion.

Mather and West (1993) showed that the motion of two-frame random dot kinematograms (RDKs) was detectable either if the two types of checks composing the RDK differed in luminance or if they had equal luminance but differed in texture contrast. They reasoned that if the input to motion extraction consists of the output from a single, up-front transformation that is differentially activated by luminance and also by texture contrast, the motion of a RDK should be detectable if one frame has checks differing in luminance and the other frame has checks differing in texture contrast. They proceeded to show that observers are at chance in trying to judge the motion of such hybrid RDKs, leading them to conclude that separate preprocessing transformations are used to extract LD versus CD motion.

Lu and Sperling (1995) also presented evidence supporting the existence of separate first- and second-order systems. They investigated this issue using two drifting sinusoidal gratings, one defined by luminance, the other by texture contrast (a drifting sinusoidal envelope was used to modulate the contrast of a field of static binary noise). The contrast of each stimulus was set at threshold for detection of motion direction. Lu and Sperling proceeded to additively combine two stimuli, varying the relative phases of the two components. They reasoned that if a single system is responsible for sensing the motion of both of these stimuli, the up-front nonlinearity used by that system must be converting each of the two threshold physical modulations into an equivalent neural modulation. In this case, we would expect that when these two stimuli are combined, motion direction judgments should be much easier in some phases (when the corresponding neural images reinforce each other), but much more difficult in others (when the neural images cancel). Contrary to this prediction, Lu and Sperling found that performance was independent of the relative phase with which the LD and CD gratings were combined. Moreover, performance was enhanced at all phases. This finding suggests that the two motion signals (LD and CD) were processed by separate systems, each analyzing its own, separate neural image for motion.

Scott-Samuel and Georgeson (1999) used a similar strategy and came to a similar conclusion. They first used a motion nulling method to estimate the effective difference in intensity injected into textures of different contrasts by early nonlinearities. They then proceeded to test whether this estimated distortion was sufficient to account for the motion produced by spatiotemporal variation in texture contrast. Specifically, they attempted to add luminance modulations to CD motion stimuli so as to cancel the motion they produced. This proved to be impossible, leading them to conclude that although there do indeed exist early visual distortions through which CD motion stimuli can drive first-order mechanisms, there also exist distinct second-order mechanisms selective for CD motion.

Further evidence supporting the claim that there exist separate first- and second-order motion mechanisms has come from Allard and Faubert (2008), who measured the effectiveness with which each of LD and CD noise (i.e., noise defined by luminance modulations and noise defined by texture contrast modulations) mask each of LD and CD motion. For low temporal frequencies, they observed a double dissociation: LD noise was much more effective at masking LD than CD motion, and CD noise was much more effective at masking CD than LD motion. Interestingly, however, for stimuli presented at 8 Hz, no such dissociation was observed; that is, LD noise proved just as effective at masking CD motion as it was at masking LD motion, and similarly, CD noise was just as effective at masking LD motion as it was at masking CD motion. This suggests that at high temporal frequencies, both LD and CD motion are detected by the same mechanism.¹

Additional support for the existence of separate first- and second-order motion mechanisms has come from Ashida, Lingnau, Wall, and Smith (2007), who used a fast fMRI adaptation procedure to probe this question. Specifically, they used radial (rotating) LD and CD motion stimuli. On a given test trial, the participant first viewed (for 2 s) an adapting stimulus S1 that consisted of either the LD or the CD stimulus rotating either clockwise or counterclockwise; then there was a 2-s blank interval, followed by a 1-s stimulus S2 consisting of either the LD or the CD stimulus rotating in either the same or the opposite direction as S1. They observed direction-selective adaptation independently for each of CD and LD motion in each of areas MT, MST, and V3A; that is, when S1 was an LD (CD) stimulus and S2 was the LD (CD) stimulus rotating in the same direction as S1, the bold signal in the time window between 1 and 7 s after the presentation of S2 showed significant suppression, as compared with the case in which S2 was the LD (CD) stimulus rotating in the opposite direction. However, no cross-adaptation between LD and CD motion stimuli was observed in any of these areas; that is, when S1 was an LD (CD) stimulus and S2 was the CD (LD) stimulus rotating in the same direction as S1, there was no suppression. In addition, the authors conducted a psychophysical experiment in which participants viewed the same sorts of stimulus sequences as were used in the fMRI study and strove to judge the rotation direction of S2. Threshold modulation amplitudes were elevated for precisely the conditions that had shown bold signal suppression in the fMRI study, but not for the other (cross-adaptation) conditions, confirming that behavior was consistent with the imaging results.

Further support for separate first- and second-order mechanisms has come from studies focused on patients with localized brain lesions. Using the same stimuli as those used in the present study, Vaina and Cowey (1996) demonstrated that patient F.D. was selectively impaired in the contralesional visual field on discriminating the direction of the CD stimulus (as well as on other non-Fourier motion tests). This contrasted with his normal performance on tasks using LD motion stimuli, including the LD motion task discussed here. His lesion involved the left lateral occipital lobe extending into the angular gyrus and the middle temporo-occipital cortex, sparing, however, the human homologue of the middle temporal region (MT). On the other hand, patients R.A. (Vaina, Makris, Kennedy, & Cowey, 1998) and T.F. (Vaina, Soloviev, Bienfang, & Cowey, 2000), with lesions centered on the dorsal V2, were selectively impaired on the discrimination of direction in LD motion, including the present LD motion judgment, but their performance was normal on all the non-Fourier motion stimuli tested (including the CD motion task used in the present study). These data strongly suggest that detecting the motion of LD versus non-Fourier (including CD) motion stimuli is accomplished by different mechanisms in the human brain. To explain these dissociations, Clifford and Vaina (1999) suggested a model consisting of two parallel channels separately mediating the perception of Fourier and non-Fourier motion. They proposed that the non-Fourier channel first applies a texture-grabbing transformation to the visual input and then submits the output to motion analysis. The motion analysis mechanism is hypothesized to be the same in both channels; however, the non-Fourier channel is assumed to operate only at a coarse spatial scale.

One result that seems to contradict the existence of separate first- and second-order motion mechanisms has come from a study by Ukkonen and Derrington (2000). They investigated this issue using the “pedestal test” introduced by Lu and Sperling (1995), which we now describe. When a drifting sinusoid is added to a static sinusoid (the pedestal) with the same orientation and spatial frequency but with twice the amplitude as the drifting sinusoid, all the potentially trackable features (e.g., peaks, zero-crossings, troughs) in the resulting stimulus oscillate back and forth. Because the net motion of any given feature is ambiguous, any motion extraction process based on feature tracking should be unable to detect the motion of the drifting grating. On the other hand, Reichardt detectors (Reichardt, 1989; van Santen & Sperling, 1984, 1985), motion energy analyzers (Adelson & Bergen, 1985), and related computations yield an unambiguous, time-averaged response to the moving grating that is invariant with respect to the presence versus absence of the pedestal. Thus, if performance at detecting the motion, right versus left, of a drifting sinusoid is uninfluenced by the presence versus absence of a stationary pedestal, one can conclude that the most sensitive system available for making the judgment uses motion energy analysis or some similar computation.

Lu and Sperling (1995) showed that high temporal frequency LD and CD motion stimuli pass the pedestal test. Specifically, in the case of LD motion, Lu and Sperling showed that if a vertical grating whose amplitude A is adjusted to yield threshold performance in a left-versus-right task is added to a stationary vertical grating of the same spatial frequency with amplitude 2A, performance changes hardly at all. In the case of CD motion, Lu and Sperling first measured the amplitude A required to support threshold performance in judging the direction, left versus right, of a drifting sinusoid used to modulate the contrast of a field of static, binary noise, where the mean noise contrast was 0.5 [so the maximum amplitude of the sinusoid-modulated noise field was (1 + A) * 0.5, and the minimum amplitude was (1 − A) * 0.5]. This moving sinusoid was then added to a stationary sinusoid of the same orientation and spatial frequency with amplitude 2A, and the resulting dynamic pattern was used to modulate the amplitude of a field of static binary noise. As in the case of LD motion, Lu and Sperling observed that for CD motion, performance was influenced very little by the presence of the pedestal, leading them to conclude that, like LD motion, CD motion is detected by applying motion energy analysis to the moving contrast envelope.

Instead of binary noise carriers, Ukkonen and Derrington (2000) used stationary sinusoidal carriers (with spatial frequency 5 times that of the moving sinusoid used to modulate carrier contrast). Consistent with the results of Lu and Sperling (1995), they confirmed that when the mean contrast of the carrier was high (45%), the resulting CD motion passed the pedestal test. However, they noted that when carrier contrast is high, one might well expect intensive nonlinearities to operate prior to motion extraction to transform the CD motion stimulus into a stimulus with significant LD content. (For example, a compressive nonlinearity would operate to lower the effective mean intensity of regions of high carrier contrast, relative to regions of low carrier contrast, thus injecting an LD signal into the stimulus.) These up-front nonlinearities would enable CD motion to be extracted by the first-order system.

They reasoned further that the influence of such up-front nonlinearities would be minimized in CD stimuli that use low-contrast carriers (because any standard, monotonic nonlinearity is likely to be locally linear across the small range of contrasts used in the carrier). Thus, by using a low-contrast carrier in the pedestal test for CD motion, it is possible to rule out the possibility that the motion is being detected by the first-order system operating on a distortion product. On the other hand, if there does indeed exist a second-order motion system that applies motion energy analysis to a rectified transformation of the visual input, CD motion should pass the pedestal test even if mean carrier contrast is low. As Ukkonen and Derrington (2000) documented, however, when the mean contrast of the carrier was low (4.5%), CD motion failed the pedestal test, leading the authors to question the existence of a second-order motion system in human vision.

Perceptual learning and motion sensing

Notwithstanding the contrary results of Ukkonen and Derrington (2000), the mass of evidence accrued from psychophysical, fMRI, and brain lesion studies tips the balance strongly in support of separate first- and second-order motion mechanisms. Strikingly, however, to our knowledge, no previous studies investigating transfer of perceptual learning between LD and CD motion have shown a clean dissociation between first- and second-order motion mechanisms.

Zanker (1993) was the first to study transfer of learning across judgments of different varieties of motion. As in the present study, he used RDKs whose tokens could be defined by various properties. In particular, Zanker used tokens defined by (1) luminance (LD), (2) temporal frequency (FD), and (3) local LD motion (MD). LD tokens had higher mean luminance than the background; FD tokens were filled with static texture, whereas the background was composed of flickering texture; MD tokens were filled with random patterns that translated smoothly in a direction perpendicular to the motion of the tokens. The dependent variable was the threshold percent of noise tokens (tokens that are randomly replaced from frame to frame, instead of moving coherently). Zanker had participants first practice one of the LD, FD, or MD motion tasks by running 20 staircases (3-up, 1-down); each staircase started at %-noise equal to 0 (maximum strength motion signal) and terminated after eight reversals. The mean of the reversals was taken as an estimate of %-noise threshold. Then each participant ran 20 more staircases in one of the two tasks other than the task they had practiced.

In summary, Zanker (1993) found (1) complete transfer of skill acquired in the MD motion task to the LD motion task but very little transfer from the LD motion task to the MD motion task, (2) substantial but incomplete transfer of skill acquired in the FD motion task to the LD motion task but no transfer from the LD to the FD motion task, and (3) complete transfer from the MD to the FD motion task and complete (or nearly complete) transfer from the FD to the MD task. Thus, skill acquired in detecting each of the two varieties of non-Fourier motion included by Zanker in his study transferred effectively to performance in his LD motion task. However, skill acquired through training in the LD task failed to transfer to either of his non-Fourier motion tasks.

Chen et al. (2009) used stimuli that seem well-chosen to address the question of transfer between first- and second-order motion systems.² Their task required participants to judge the movement direction of a parafoveal, 2-cpd drifting grating. Prior to training, all participants were tested in their ability to make directional judgments with LD and with CD gratings across six temporal frequencies between 2 and 30 Hz; specifically, the threshold amplitude of grating modulation was measured for each of the six temporal frequencies. Then each participant was trained with either CD gratings or LD gratings at a fixed temporal frequency of 8 Hz. After training, all participants went through a posttest like the pretest to assess changes in contrast thresholds resulting from the training. The design also included a control group that performed the pretest and the posttest but did not undergo training to estimate improvement due merely to the pre- and posttests. Chen et al. found strong transfer of learning from the CD motion task to the LD motion task but very little transfer from the LD to the CD motion task. Furthermore, training in the 8-Hz CD motion task improved performance in both the CD and LD motion tasks across all six temporal frequencies. As was observed by Petrov and Hayes (2010), this suggests that the third-order motion system (Lu & Sperling, 1995), which cuts off around 4 Hz, probably plays a negligible role with these stimuli.

A similar result was obtained by Petrov and Hayes (2010). Their LD stimuli consisted of dynamic white noise combined additively with isotropically, band-pass filtered noise fields translating rigidly so as to produce 10-Hz temporal modulation at the center spatial frequency of the filtered noise. Their CD stimuli consisted of dynamic white noise whose contrast was multiplicatively modulated by the same sort of translating band-pass filtered noise fields as were used in the LD stimuli. The task was to make a fine directional judgment. Specifically, observers had to judge whether the direction of translation was displaced clockwise or counterclockwise relative to a fixed, standard direction that was indicated explicitly by a line drawn on the screen in two demo trials at the start of a given block and, thereafter, had to be remembered. A given participant was pretested in either the LD or the CD motion task, then trained in the other motion task, and ended with a posttest for whichever task he/she had been pretested.

The results are clear: Training in the CD motion task translates very effectively to the LD motion task; however, training in the LD motion task translates very little, if at all, to the CD motion task.

In summary, the three studies reviewed here all documented asymmetric transfer between LD and CD (or other non-Fourier) motion tasks. The common finding was that skill acquired through training in CD (or other non-Fourier) motion tasks transferred effectively to analogous LD motion tasks, but the reverse was not true: Skill acquired through training in LD motion tasks does not seem to transfer to analogous CD (or other non-Fourier) motion tasks.

The results we present here depart from this pattern. As we detail below, we obtained substantial learning in both of our LD and CD tasks. However, in neither case did this learning transfer at all to the other task. This result offers strong support for the claim that separate mechanisms subserve detection of LD versus CD motion, at least for the specific global motion judgment studied here. We will address the implications of this result for theories of motion sensing in the Discussion section.

Method

Presentation conditions

All the experiments took place in a quiet dark room, in which the only source of illumination was the monitor. Observers adapted 5 min before starting training session. Viewing was binocular, from a distance of 60 cm from the display device.

Apparatus

All stimuli were generated and presented, and responses were collected and analyzed using a Macintosh computer. Stimuli were presented in the center of a color monitor (Apple Trinitron, 0.25-mm pitch, 13 in.; 640 × 480 pixels; active viewing area, 235 × 176 mm; vertical scanning frequency, 66.7 Hz, and P22 phosphor). The system had 8 bits/gun pixel quality. The stimuli were generated using a color table of 256 gray levels. The monitors were calibrated using VideoToolbox software (Pelli, 1997), and prior to each experimental session, the internal z-axis linearization of the monitors was confirmed with a Minolta LC-1500 for the range of contrasts used.

Stimuli

The stimulus field subtended 10 × 10 deg² at a viewing distance of 60 cm and was presented against a uniform gray background (9.5 cd/m²). The stimulus area was divided into a notional grid of 38 × 38 blocks, each subtending 16 × 16 arcmin². Each block consisted of 10 × 10 pixels of binary noise texture. Specifically, any given block B was characterized by high and low luminance values, L_high(B) and L_low(B). Half of B’s pixels had luminance L_high(B), and half had luminance L_low(B). The locations of high and low values were randomly assigned within B. Thus, B’s mean luminance was (L_high + L_low)/2, and B’s Michelson contrast was (L_high − L_low)/(L_high + L_low).

A given stimulus comprised two sorts of blocks, background blocks and (motion) tokens. In each frame of every stimulus used here, 14% (200 out of 1,444) of the blocks were tokens, with the others being background blocks.

Each background block B had a mean luminance of 9.5 cd/m² and a mean contrast of 0.2 [L_low(B) was slightly above 7 cd/m², and L_high(B) was slightly less than 12 cd/m²].

The LD motion tokens had a contrast of 0.2 (equal to the contrast of the background) but a mean luminance of 12.3 cd/m² (30% greater than background mean luminance). The CD motion tokens had a mean luminance of 9.5 cd/m² (equal to the mean luminance of the background) but a contrast of 0.6 (3 times the background contrast).

In each of the LD and CD motion stimuli, the luminances in any given block (whether a background block or a motion token) were randomly rescrambled from frame to frame, inducing flicker across the display.

A given stimulus comprised four frames, each presented for 45 ms. Observers were instructed to maintain fixation on a central cue spot that remained present throughout the display. The task was to judge whether motion was to the right or to the left. On a given trial, the strength of the motion signal in the stimulus was varied by changing the number n of the 200 tokens that carried the same unidirectional motion signal. Specifically, on a given trial, n signal tokens appearing in frame 1 were selected to generate systematic motion between frames 1 and 2. Then, in frame 2, a new set of n signal tokens was chosen to generate motion between frames 2 and 3, and in frame 3, yet another set of n signal tokens was chosen to generate motion between frames 3 and 4. Each of the n signal tokens selected in frame k (for k = 1, 2, 3) was displaced half its width (5 pixels) in the correct direction (either left or right) in frame k + 1, yielding a translation speed of 2.92 deg/sec. All the other (200 − n) noise tokens were painted in random locations in frame k + 1. If the motion of a signal token carried it out of the stimulus field, it reappeared at the same vertical location on the opposite side (wrap-around procedure). When all tokens were selected to move systematically, the display appeared as a cluster of tokens all moving to the left or to the right across the flickering background. In the case in which the number of tokens moving coherently on a given trial was n, we say the proportion coherence was n/200; threshold proportion coherence will be our standard dependent variable.

On a given trial, the observer first fixated a cue spot centered in a uniform field of luminance 9.5 cd/m² (equal to the mean luminance of the background blocks used in all stimuli). The observer then initiated the trial with a button-press. Following a delay of 100 ms, the stimulus was presented. After the four frames of the stimulus, the cue spot remained on alone. The observer then registered his/her response with a buttonpress.

Participants

There were 14 participants in the study. Eight were trained in the LD motion task, and 6 were trained in the CD motion task.

All the participants were recruited from the Boston University undergraduate student population (8 females). The study conformed to the Ethics of the World Medical Association (Declaration of Helsinki), and informed consent was obtained from each participant prior to the start of the experiment. Participants were required to be free of current or past neurological or psychiatric disorders, to have normal or corrected-to-normal visual acuity and contrast sensitivity (measured with a Pelli–Robson contrast sensitivity chart; Brian GriffithsClement Clarke Intl/Haag-Streit U.K.). Participants were included in the data analysis if they completed all the sessions in the perceptual learning protocol detailed below.

Training procedures

Each of the participants came to the lab between 6 and 8 p.m. on a sequence of 5 successive days. On each day, the procedure was the same:

1. Training calibration. The session began with an adaptive assessment procedure in the participant’s training task (LD motion for 8 participants and CD motion for 6 participants). This assessment procedure was controlled by a staircase as follows. The maximum number of targets in a display was 200. The full range of steps the staircase could visit spanned 64 possible signal levels, where the number of signal tokens presented on a trial at staircase level k was the integer nearest to 200^k/643 To minimize the number of trials in a single run, the staircase had two parts (Vaina et al., 2003). The first consisted of three steps down until the first error, followed by nine steps up until the next correct response, then two steps down until the next error, followed by six steps up until the next correct response. The second part was a standard 3-up, 1-down staircase. That is, on each trial, if the last three responses were correct, the staircase got one step harder; otherwise, the staircase got one step easier. The 3-up, 1-down staircase was continued until it comprised 10 reversals. Threshold (mean and standard deviation) was computed from the last 6 reversals.

2. Training. After the initial staircase, each participant was trained in eight blocks of constant stimuli, each comprising 100 trials. The coherence proportions used in these training blocks were derived as follows. For μ and σ, the mean and standard deviation of coherence proportion across the last six reversals of the assessment staircase, let N₁, N₂, N₃, N₄, and N₅ be the nearest integers to 200 × (μ − 3σ), 200 × (μ − σ), 200 × μ, 200 × (μ + σ), and 200 × (μ + 3σ). Then each block contained 20 trials in which the number of coherently moving tokens was N_k, for k = 1, 2, …, 5.

3. Testing. At the end of each session, two more assessment staircases were run, the first one for the training task, and the second one for the other (nontrained) task.

Finally, there was also a follow-up visit. Ten to 12 days after the last day of training and testing, the participant returned for a testing session in which two assessment staircases were run, one for the trained task and one for the other (nontrained) task. The purpose of this test was to check the stability of the learning observed at the end of training.

Results

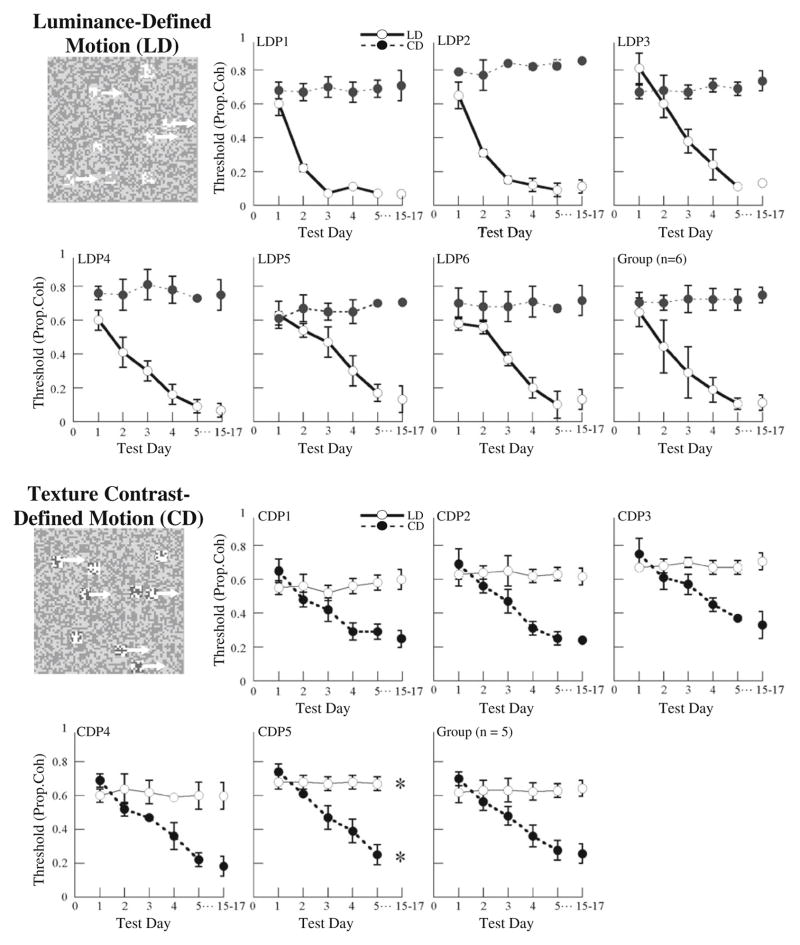
Of the 8 participants who trained in the LD motion task, 2 showed no learning; their final proportion-coherence thresholds did not differ from their initial thresholds. In addition, 1 of the 6 participants trained in the CD motion task showed no learning. We restrict our consideration only to those participants who showed significant learning in their training task. The results for the 6 participants who showed learning in the LD motion task are shown in the upper panel of Fig. 1. Solid lines give the proportion-coherence thresholds for the LD motion task (shown in boldface to indicate that this was the training task), and dashed lines give the thresholds in the (nontrained) CD motion task. The unconnected markers on the right side of this figure show the thresholds measured in the follow-up visit. The thresholds for a given participant are all marked with the same plotting marker. Thus, for example, the solid and dashed lines marked with squares give the thresholds for the LD and CD tasks for a single participant. Error bars show the standard deviations of the coherence proportions visited by the staircases.

Fig. 1.

Effects of training on sensitivity to luminance-defined (LD) motion (solid lines) and texture-contrast-defined (CD) motion (dashed lines). The top panel shows the results for 6 participants trained in the LD motion task and the mean performance of the group. In this panel, the solid lines are bold to indicate that this was the training task. The bottom panel shows the results for 5 participants trained in the CD motion task and mean results for the group. The dashed lines are bold to indicate that CD motion was the training task. The disconnected markers on the far right of each panel show the results of the posttraining test, which occurred 10–12 days after the completion of training (1 observer who was trained in the CD motion task did not take the posttraining test). In each of the top and bottom panels, each different marker type shows the thresholds measured for a single observer in both the LD and CD motion tasks. Note that for each observer, although performance improved substantially in the training task, performance in the nontrained task remained flat

Results for the 5 participants who showed learning in the CD motion task are plotted in the lower panel of Fig. 1. As above, solid lines give the proportion-coherence thresholds for the (nontrained) LD motion task, and dashed lines give the thresholds for the thresholds in the CD motion task. The dashed curves are shown in boldface in this figure to indicate that these are the curves for the training task.

The main point to note for all participants in both panels is that although performance in the training task improved dramatically over the course of the 5 days of training, performance in the nontrained task showed no improvement. Paired comparison t-tests comparing the proportion coherence on day 5 versus 1 of training confirm that the participants trained in the LD motion task improved significantly in the LD motion task, t(5) = 15.75, p < .0001, but not in the CD motion task, t(5) = 0.8991, p = .4098. Similarly, across the 5 days of training, participants trained in the CD motion task improved significantly in the CD motion task, t(4) = 17.00, p < .0001, but not in the LD motion task, t(4) = 0.5898, p = .5870.

Note also that thresholds measured in each task for each observer in the follow-up visits 10–12 days after training were not markedly different from the thresholds measured immediately after the last training session, showing that the learning observed at the end of training was stable at least across the 10–12 days between the last day of training and the posttraining test. Stability of learning was assessed using paired comparison t-tests comparing proportion coherence in the retention test versus day 5 of training. For participants trained in the LD motion task, performance in the LD motion task did not change significantly over the retention period, t(5) = 0.4732, p = .6560, while performance in the CD motion task showed slight but significant deterioration, t (5) = 3.3127, p = .0212. For the participants trained in the CD motion task, performance in the CD motion task showed a slight but significant improvement between the last day of training and the retention test, t(3) = 5.9604, p = .0094, while performance in the LD motion task showed no significant change, t(3) = 0.6765, p = .5472.

Discussion

Implications for theories of motion sensing

The only difference between the two motion tasks being compared is in the way in which tokens are defined relative to the background (which is identical in the two tasks). Yet, despite the close similarity between the two tasks compared in this study, we find a clean dissociation between training-driven changes in skill:

1. A participant trained in the LD motion task shows sharp improvement in this task, while performance in the CD motion task remains at baseline.

2. Exactly the opposite pattern is obtained for a participant trained in the CD motion task.

What implications does this finding have for theories of human motion sensing? Ultimately, we shall argue that these results support the existence of entirely distinct first- and second-order motion systems tuned to motion carried by luminance versus texture contrast, respectively. However, there are several competing theories of the different mechanisms used to sense motion and several a priori possible alternative explanations of the observed dissociation.

In considering any motion mechanism, it is important to distinguish two stages of the computation used by that system:

1. (preprocessing transformation) The system first applies some rapid, spatially local image transformation to the visual input, and

2. (motion extraction) then submits the resulting transformation to some variety of motion analysis—that is, a computation that is sensitive to correspondences in its input across space and time.

For example, standard models of first- and second-order motion processing propose that the first-order system skips the preprocessing transformation and extracts motion directly from the luminance variations impinging on the retina; by contrast, the second-order system is hypothesized to use a preprocessing transformation that converts regions of high texture contrast into regions of high mean value prior to extracting motion (e.g., Chubb & Sperling, 1988; Clifford, Freedman, & Vaina, 1998; Ledgeway & Smith, 1994; Lu & Sperling, 1995; Yo & Wilson, 1992).

For the motion tasks used in this study, there are two reasons to think that the primary site of learning is likely to be the motion extraction stage of processing. First, for each of the LD and CD motion stimuli, the physical difference between motion tokens and the background is (1) chosen so that tokens are clearly distinct from the background at the outset of training and (2) fixed throughout the experiment. This limits the amount of improvement that is likely to be available through increasing the sensitivity of the up-front transformation in either task. Second, in our tasks, difficulty is controlled by varying the proportion of tokens that move coherently. Thus, at any stage in training, the factor limiting performance is not the distinctness with which tokens are defined against the background but, rather, the clarity of the motion signal produced by matches between tokens across frames. This manipulation promotes improvement primarily through heightening sensitivity to the specific sorts of spatiotemporal correlations in the input stream that the participant is required to detect—a form of sensitivity presumably resident in the motion extraction stage of processing.

We submit that these considerations make it unlikely that the learning occurs in the third-order system of Lu and Sperling (1995). This system is hypothesized to extract motion from a time-varying “salience map” whose value at any given spatiotemporal point in the visual field reflects the degree to which that point has been promoted to figure (rather than relegated to ground) in the perceptual organization achieved though the interaction of top-down attention and bottom-up stimulation. Suppose that the observed improvement in performance due to training is due to heightened sensitivity of the third-order system. Then if, as we have argued above, the primary locus of learning is in the motion extraction stage, the learning should show strong transfer between the LD and CD motion tasks. In each task, the motion tokens are highly salient, relative to the background. Thus, any improvement in processing in the motion extraction stage should benefit performance in both tasks quite strongly. This prediction is contradicted by the present results.

A similar argument shows that the locus of learning is unlikely to be in a position-tracking mechanism of the sort posited by Seiffert and Cavanagh (1998). The specific computation used by this hypothetical system to extract motion is not clearly articulated. However, if we assume that whatever computation this system uses, the improvement produced by training in either the LD or the CD motion task is due primarily to heightened sensitivity in this motion extraction stage, then once again transfer should be strong between the LD and CD motion tasks.

It should be noted, however, that Seiffert and Cavanagh (1998) hold that in addition to the position-tracking system, human vision also comprises a first-order mechanism of the sort posited by Lu and Sperling (1995). Are the present results consistent with this view? Suppose that the first-order system is the site of improvement due to training in the LD motion task and that the position-tracking system is the site of improvement due to training in the CD motion task. In this case, although it is plausible to suppose that improved performance in the LD motion task might not transfer to the CD motion task, it is hard to see why improvement in the CD motion task should fail to transfer to the LD motion task. The features to be tracked (i.e., the tokens as distinct from the background) are roughly equivalent in salience in the two tasks. (This is implied by the fact that at the outset of training, performance in the LD and CD tasks is roughly equivalent for all participants.) Therefore, if the site of improvement in the CD motion task is the motion extraction computation used by the position-tracking system, it is hard to see how the observed improvement in performance in the group trained in the CD motion task should fail to transfer to the LD motion task.

The results also argue forcefully against theories proposing that LD and CD motion are extracted by a single mechanism whose preprocessing transformation is sensitive both to luminance and to texture-contrast variations (e.g., Johnston & Clifford, 1995a, 1995b; Johnston, McOwan, & Buxton, 1992; Taub, Victor, & Conte, 1997). Once again, if the site of the learning were at the motion extraction stage of any such hypothetical mechanism, we should observe strong transfer between the LD and CD motion tasks.

Our findings thus support the conclusion that there exist distinct first- and second-order motion-sensing mechanisms and that the sensitivity of the first-order system (but not of the second-order system) gets heightened by training in the LD motion task, whereas the sensitivity of the second-order system (but not of the first-order system) gets heightened by training in the CD motion task.

It should be noted that substantial evidence supports the claim that although the first- and second-order systems extract motion separately from the visual input, the outputs from the two systems are combined at an early stage of processing (e.g., Goutcher & Loffler, 2009; Lu & Sperling, 1995; Nishida & Ashida, 2000; Nishida & Sato, 1995; Wilson & Kim, 1994). The present results clearly imply that the site of learning in each of the LD and CD motion tasks is localized to a stage of processing prior to any combination of the signals from the first- and second-order systems.

Finally, we note that the present results are consonant with previous findings showing that LD and CD motion signals do not interact in enabling extraction of global motion (Cassanello, Edwards, Badcock, & Nishida, 2011; Edwards & Badcock, 1996).

Why did previous learning experiments fail to find a double dissociation?

None of the three previous experiments investigating transfer of learning between Fourier and non-Fourier motion tasks (Chen et al., 2009; Petrov & Hayes, 2010; Zanker, 1999) yielded the clean double dissociation observed in the present study. On the contrary, the finding common to all three of these studies was that skill acquired through training in non-Fourier motion tasks transfers effectively to LD motion tasks; however, skill acquired through training in LD motion tasks fails to transfer to non-Fourier tasks. In this section, we outline the differences between the previous studies and the present study, with an eye toward understanding the possible sources of the differences in results.

The study of Zanker (1999) is similar to the present study in one respect. As in the present study, Zanker’s basic motion task was a global motion task, and his dependent variable was the threshold proportion of noise tokens (i.e., tokens randomly resituated across stimulus frames) that the participant could tolerate in making his/her left–right judgments.⁴ We have argued above that this task is well suited to produce learning focused predominantly in the motion extraction phase of processing.

Importantly, however, Zanker’s (1999) study did not include a CD motion task. The physical contrast of motion tokens versus background was equated in each of the FD and MD stimulus types he studied. That this difference may be critical is suggested by the fact that participants who trained in Zanker’s FD and MD motion tasks showed very limited improvement in performance. As is shown by Zanker’s Fig. 2c, e, in each of these tasks, learning is roughly at asymptote after the first out of 20 training staircase runs, and the total improvement in each task is around 10% motion noise tolerance (from around 17% noise tokens to 27% noise tokens in the FD motion task; from around 32% noise tokens to 42% noise tokens in the MD motion task). By contrast, in our CD motion task, learning is both more gradual and also shows much larger magnitude. Our CD motion task trainees begin at noise tolerance levels between 20% and 30% and show linear improvement across five sessions, achieving final noise tolerance levels near 80%.

The limited extent of the learning observed by Zanker (1999) in his two non-Fourier tasks leads us to question whether these stimuli are actually being processed by the second-order system. First, we note that all empirical support for a distinct second-order system has come from studies that used CD motion, suggesting that physical variations that do not introduce a difference in texture contrast may well not engage the second-order system. We speculate that Zanker’s FD and MD motion trainees are actually using the third-order system (Lu & Sperling, 1995) to make their judgments. Since the third-order system extracts motion from the “salience map,” it is expected that learning in either the FD or the MD task should transfer effectively to any other global motion task in which tokens are at least as clearly defined, relative to the background, as are the tokens in the training task. Thus, one expects skill acquired through training in the FD or MD task to transfer to the LD task.

The Chen et al. (2009) experiment differed from the present experiment in a number of ways. First, Chen et al. used drifting sinusoids rather than the global motion displays used here. In addition, their stimuli were presented parafoveally, whereas observers in the present study fixated the center of the stimulus display. Most intriguingly, in contrast to the present study, in which task difficulty was controlled by varying the proportion of tokens in the stimulus that moved coherently across frames, in the study of Chen et al., task difficulty was controlled by varying the physical amplitude (defined either by texture contrast or by luminance) of the signal whose motion was to be detected. Thus, in the task used by Chen et al., the factor limiting performance at any stage in training is the distinctness with which the physical variations defining the motion are registered by the up-front transformation. This implies that the training used by Chen et al. tends to promote improvement by increasing the gain (relative to noise) of the up-front transformation (rather than by increasing the sensitivity of the motion extraction processing stage, as in the present study).

Although the focus of Chen et al. (2009) on the up-front transformation might seem to be an important difference from the present study, it is difficult to see how it helps to explain the divergence in the results. Suppose that training in the CD motion task increases the sensitivity of the up-front transformation used by the second-order system. Why should this learning transfer to the LD motion task? Perhaps the up-front transformation used by the second-order system is sensitive not only to variations in texture contrast, but also to variations in luminance. If so, the second-order system should be useful for performing the LD motion task, and one might therefore expect learning in the CD task to transfer to the LD task. However, the results from the present study give no indication that this is the case. In our CD task, training yields dramatic improvements in performance without improving performance in the LD task at all. Thus, our data suggest that the second-order system is useless for detecting LD motion, implying that the up-front transformation used by the second-order system has negligible sensitivity to luminance variations.

These considerations leave us in doubt as to the source of the difference between the results of Chen et al. (2009) and those of the present study.

All of the tasks used by Zanker (1999), Chen et al. (2009), and the present study require a coarse directional motion judgment (left vs. right). By contrast, the task used by Petrov and Hayes (2010) required a fine direction discrimination. We speculate that this is the crucial difference between their experiment and ours. Neurons with relatively precise direction selectivity first emerge in the visual-processing stream in area MT (e.g., Rust, Mante, Simoncelli, & Movshon, 2006; Zeki, 1974), and it seems likely that the decision statistics participants used to perform the tasks in Petrov and Hayes combine information from the ensemble of responses produced by neurons in this area. Several groups have tested the responses of neurons in monkey areas MT and MST to various sorts of non-Fourier motion stimuli (Albright, 1992; Churan & Ilg, 2001; O’Keefe & Movshon, 1998). Although these studies document a broad spectrum of sensitivity to CD versus LD motion, with many neurons showing sensitivity to both sorts of variations, a common finding is that there exist many neurons sensitive to LD motion but not to CD motion. It thus seems likely, on the one hand, that a participant might well derive a decision statistic effective for performing the LD variant of the Petrov and Hayes task that failed to work for the CD variant. On the other hand, nearly all neurons in MT with sensitivity to CD motion also are sensitive to LD motion; thus, it is probable that a decision statistic effective for performing the CD variant of the Petrov and Hayes task would also be effective for the LD variant of their task.

Although this account explains why one might expect asymmetric transfer of learning in the Petrov and Hayes (2010) study, it raises questions about the present results. Despite the fact that the LD and CD motion tasks used in the present study required coarse, rather than fine, discriminations of motion direction, it nonetheless seems likely that participants referred to the responses of MT neurons in making their judgments. Thus, it is unclear why the argument we have just presented fails to apply to the present results. The answer to this question awaits further investigation.

Final remarks

We have used a perceptual learning paradigm to document a complete dissociation between first-order and second-order processing. Training in a global motion task that uses LD motion tokens yields substantial improvement across 5 days of training. However, this improvement shows no transfer to the corresponding CD motion task. Similarly, training in the CD motion task yields substantial improvement with training but no transfer to the corresponding LD motion task. It should be noted that training in each task variant results in a level of performance that far outstrips the level of performance the participant is able to achieve in the untrained task variant. This implies that the computation the participant learns in mastering each task provides no purchase for the other task. Two corollaries of this observation are (1) the up-front transformation used in performing the LD version of the task is completely insensitive to texture contrast variations and (perhaps more surprisingly) (2) the up-front transformation used in performing the CD version of the task is completely insensitive to luminance variations.